下载文档原格式
4《大学物理》（下）复习提纲第6章恒定电流的磁场（1） 掌握磁场，磁感应强度，磁力线，磁通量等概念，磁场中的高斯定理，毕奥一沙伐 一拉普拉斯定律。
（2） 掌握安培环路定律，应用安培环路定律计算磁场（3）掌握安培定律，会用安培定律计算磁场力。
会判断磁力矩的方向。
会判断霍尔效应 电势的方向。
1.边长为2a 的等边三角形线圈，通有电流 I ，则线圈中心处的磁感强度的大小为 —9戶°门（4丸可 _______________ .I （其中ab 、cd 与正方形共面）,C2.边长为I 的正方形线圈，分别用图示两种方式通以电流 在这两种情况下，线圈在其中心产生的磁感强度的大小分别为3.—无限长载流直导线，通有电流 I ，弯成如图形状.设各线段皆在纸面内，一无限长载4流直导线，通有电流I ，弯成如图形状.设各线段皆在纸面内，则P 点磁感强度B 的大小为•则P 点磁感强度B的大小为5=51-B 2=A O ZW,(B 方向指向纸内)6.如图所示，用均匀细金属丝构成一半径为 R 的圆环C ,电流I 由导线1流入圆环A 点，并由圆环B 点流入导线2•设导线1和导线2与圆环共面，则环心 O 处的磁感强度大小为 ________________ (4n/?i ,。
_________________ ,方向 ___________ 垂直纸面向内 ___________7.真空中电流分布如图，两个半圆共面，且具有公共圆心，试求 O 点处的磁感强度.设半径分别为R 和2R 的两个载流半圆环在 O 点产生的磁感强度的大小分别 为B i 和B 2 .§ 二 “0(47?) B 厂坯！ ©R)O 点总磁感强度为4. 一无限长载有电流I 的直导线在一处折成直角， P 点位于导线所在 平面内，距一条折线的延长线和另一条导线的距离都为 a ,如图•求P点的磁感强度B . B 1i(^ ―)方向为4na 2B 2 二 J Q I (1 -、2)”.FAG4na 2B = Bj - B 2 = 2.L 0l /(4~.a) 方向为：5•无限长直导线在P 处弯成半径为R 的圆，当通以电流I 时，则在圆心O 点的磁感强度大 小等于 D(A)(B)%1、2 4R(C) 0, (D)伍)&均匀磁场的磁感强度B与半径为r的圆形平面的法线n的夹角为a ,今以圆周为边界，作一个半球面S，S与圆形平面组成封闭面如图.则通过S面的磁通量①9 •如图，两根直导线ab和cd沿半径方向被接到一个截面处处相等的铁环上，稳恒电流10. 端流入而从d端流出，则磁感强度B沿图中闭合路径如图，流出纸面的电流为阳曲=2人(B)11.如图，在一圆形电流定理可知(A)(B)(C)(D)21，流进纸面的电流为I，则下述各式中哪一个是正确的?jH-dl = 1(D) i H*dl = -I.I所在的平面内,-B dl =0，且环路上任意一点L:B dl =0，且环路上任意一点L\ B dl -0，且环路上任意一点LB dl - 0，且环路上任意一点L 选取一个同心圆形闭合回路B =常量.12. 有一同轴电缆，其尺寸如图所示，它的内外两导体中的电流均为分布，但二者电流的流向正相反，则且在横截面上均匀(1) 在r < 0处磁感强度大小为Ri< r< R2处磁感强5D.――Z4L,则由安培环路&川(2宾Rj) , o(2) _______________________________________ 在 r > R 处磁感强度大小为313.两根长直导线通有电流I ，图示有三种环路；在每种情况下， {B dl 等于:在图(a)和(b)中各有一半径相同的圆形回路 L i 、L 2，圆周内有电流l i 、丨2，其分布相同,且均在真空中，但在(b)图中L 2回路外有电流13, P i 、P 2为两圆形回路上的对应点，则：(A)B dl =:B dl , B P I=B P 2L i P(lQl#P i ( l i °l ?严O(B)B dl--B dl ,B P I二 B P 2 .L i J"L 2 l3L iL 2(a)(b)(C)B dl =:B dl ,B PI=B P 2 .L iL 2(D)；B dl --B dl , ‘ B P i =B P 2 .[C:L iL215.把轻的导线圈用线挂在磁铁N 极附近，磁铁的轴线穿过线圈中心，且与线圈在同一平面内，如图所示•当线圈内通以如图 所示方向的电流时，线圈将(A) 不动.(B) 发生转动，同时靠近磁铁. (C) 发生转动，同时离开磁铁. (D) 不发生转动，只靠近磁铁.______________________ (对环路a).(E) 不发生转动，只离开磁铁. 16.如图，一根载流导线被弯成半径为 R 的1/4圆弧，放在磁感强度为 B 的均匀磁场中，则载流导线ab (电流I 顺时针方向流动)所受磁场的作用力的大小为 方向 __________ 沿y 轴正向 ________17. 如图，均匀磁场中放一均匀带正电荷的圆环，其线电荷密度为 与环面垂直的转轴旋转. 当圆环以角速度 3转动时，圆环受到的磁力矩为其方向 ________ 在图面中向上18.有两个半径相同的环形载流导线 A 、B ,它们可以自由转动和移动，把它们放在相互垂直的位置上，如图所示，将发生以下哪一种运动？(A) A 、B 均发生转动和平动，最后两线圈电流同方向并紧靠在一起. (B) A 不动，B 在磁力作用下发生转动和平动. (C) A 、B 都在运动，但运动的趋势不能确定.(D) A 和B 都在转动，但不平动，最后两线圈磁矩同方向平行.19. 如图，在一固定的无限长载流直导线的旁边放置一个可以自由移动和转动的圆形的刚性 线圈，线圈中通有电流，若线圈与直导线在同一平面，见图 (a),则圆线圈的运动将是平移，靠向直导线；若线圈平面与直导线垂直，见图(b)，则圆线圈将受力矩，绕通过直导线的线圈直径转动，同时受力向直导线平移 __________________________________。
《大学物理》（下）复习提纲第八章静止电荷的电场（1）掌握电场强度的迭加法计算。
掌握库仑定律。
（2）掌握电场强度通量计算方法、高斯定理。
（3）掌握静电场的环路定律，电势能和电势的定义和计算公式。
（4）掌握导体静电平衡时电荷如何分布。
导体静电平衡后的电势计算方法以及平行板电容器的电容公式。
（5）掌握电介质在外电场中极化性质和电介质中的高斯定理。
要会用介质中高斯定理定性分析介质中电场和电势，掌握电场能量计算公式。
1．如图所示，真空中一长为L的均匀带电细直杆，总电荷为q，试求在直杆延长线上距杆的一端距离为d 的P点的电场强度．2．电荷为＋q 和－2q 的两个点电荷分别置于x＝1 m和x＝－1 m处．一试验电荷置于x 轴上何处，它受到的合力等于零？3．若匀强电场的场强为E ，其方向平行于半径为R 的半球面的轴，如图所示．则通过此为半球面的电场强度通量Φe___________________，如果图是B，通量Φ为___________________。
e4．如图所示，一个电荷为q 的点电荷位于立方体的A 角上，则通过侧面abcd 的电场强度通量等于___________________，如果电荷为q 的点电荷位于立方体的中心上，通过侧面abcd 的电场强度通量等于通量e Φ为___________________。
5．根据高斯定理的数学表达式∑⎰=⋅0/εq S d E S可知下述各种说法中，正确的是：(A) 闭合面内的电荷代数和为零时，闭合面上各点场强一定为零．(B) 闭合面内的电荷代数和不为零时，闭合面上各点场强一定处处不为零． (C) 闭合面内的电荷代数和为零时，闭合面上各点场强不一定处处为零． (D) 闭合面上各点场强均为零时，闭合面内一定处处无电荷．6．三个平行的“无限大”均匀带电平面，其电荷面密度都是＋σ，如图所示，则A 、B 、C 、D 三个区域的电场强度分别为：E A ＝_________________，E B ＝_____________，E C ＝_______________，E D =_________________ (设方向向右为正)．7. 真空中一“无限大”均匀带电平面，其电荷面密度为σ (>0)．在平面附近有一质量为m 、电荷为q (>0)的粒子．试求当带电粒子在电场力作用下从静止开始垂直于平面方向运动一段距离l 时的速率．设重力的影响可忽略不计．8. 如图所示，两个“无限长”的、半径分别为R 1和R 2的共轴圆柱面均匀带电，沿轴线方向单位长度上所带电荷分别为λ1和λ2，则在各个区域距离轴线为 r 处的 P 点的电场强度大小E 为 _______________________.9．如图，A 点与B 点间距离为2l ，OCD 是以B 为中心，以l 为半径的半圆路径. A 、B 两处各放有一点电荷，电荷分别为＋q 和－q ．把另一电荷为Q (Q ＜0 )的点电荷从D 点沿路径DCO 移到O 点，则电场力所做的功为___________________10. 将电荷均为q 的三个点电荷一个一个地依次从无限远处缓慢搬到x 轴的原点、x = a 和x = 2a 处．求证外界对电荷所作之功为设无限远处电势能为零．11. 如图所示,两同心带电球面，内球面半径为r 1＝5 cm ，带电荷q 1＝3×10-8C ；外球面半径为r 2＝20 cm ， 带电荷q 2＝－6×10-8C ，设无穷远处电势为零，则空间另一电势为 零的球面半径r ＝ __________________．12. 如图所示，两个同心的均匀带电球面，内球面半径为R1、带电荷Q1，外球面半径为R2、带有电荷Q2．设无穷远处为电势零点，试求下图(A),(B),(C)三图中、距离球心为r 处的P点的电势U为分别为__________________，__________________，__________________。
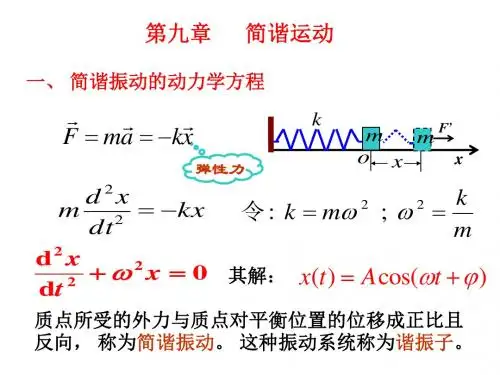
大学物理内容复习（下）大学物理（下）复习一、 稳恒磁场 基本槪念，基本定律：磁感应强度：m P M B max=，磁矩： n S I P m⋅∆⋅=0 磁通量：⎰⎰⋅=ΦS m S d B高斯定理：0=⋅⎰⎰S S d B环流定理：∑⎰=⋅I l d B 0μ―――稳恒磁场无源有旋磁感应强度的计算：1．电流产生的磁场（毕—萨定律）：⎰⨯⋅=−−−→−⨯⋅=L r r l Id B r r l Id B d 303044πμπμ磁场叠加原理2。
运动电荷产生的磁场：304rr v q dN B d B nSdldN q ⨯⋅=−−→−==πμ 几种典型载流导线的磁场：有限长直导线：()120sin sin 4ββπμ-=aIB 无限长直导线：r I B πμ20=圆形电流轴线上：()2322202Rx IRB +=μ圆形电流圆心处：R IB o 20μ=无限长直螺线管内部：nI I LNB 00μμ==螺绕环内部： nI I LNB 00μμ== 无限长载流直圆柱体： 柱内：202R IrB πμ= 柱外：r I B πμ20=轴线上：0=B磁场对载流导线及运动电荷的作用：安培力：⎰⨯=⨯=LB l Id f B l Id f d磁力矩：B P M m⨯=洛仑兹力：B v q f ⨯=磁力的功：∆Φ=Φ==⎰⎰I Id dA A例题：一、一载流导线弯成如图所示形状，电流由无限远处流来，又流向无限远处。
则圆的圆心o 点的磁感应强度大小为多少？方向如何？图1图2(1) RIRIπμμ44320+⋅; (2)RIRIπμμ44320-⋅(3)RIRIRIπμμπμ443240-⋅+- (4)RIRIRIπμμπμ443240+⋅+-(5) RIRIRIπμμπμ443240-⋅+(6) 2120⋅RIμ(7) RIRIRIπμμπμ421240+⋅+- (8)RIRIRIπμμπμ421240-⋅+-(9) RIRIπμμ440- (10)RIRIπμμ440+图9图8二、氢原子中的电子（电量为e ），在一半径为R 的圆轨道上以速率v 做匀速率圆周运动，则圆心处的磁感应强度大小为 多少？圆心处磁场能量密度为多少？等效圆电流的磁矩?=mR ev I π2=, 20022Rev R I B πμμ==, 422200282R v e B w m πμμ== n R Rev n Is m 22ππ== 三、两个电子e 1和e 2同时射入某均匀磁场后，分别作螺旋运动。
《大学物理》（下）复习资料第二部分：电学基本要求一. 基本概念电场强度, 电势；电势差, 电势能，电场能量。
二.基本定律、定理、公式 1.真空中的静电场： 库仑定律：r r q q F 321041πε=。
=041πε9×109 N·m 2·C -2电场强度定义：0q F=， 单位：N·C -1 ，或V·m -1 点电荷的场强：r q 3041πε=点电荷系的场强：N E E E E +++= 21,（电场强度叠加原理）。
任意带电体电场中的场强：电荷元dq 场中某点产生的场强为： r dqd 3041πε=，整个带电体在该产生的场强为：⎰=E d E电荷线分布dq=,dl λ 电荷面分布dq=dS σ, 电荷体分布dq=dV ρ电通量：S d E Se ⋅=⎰⎰φ=⎰⎰SdS E θcos高斯定理：在真空中的静电场中，穿过任一闭合曲面的电场强度的通量等于该闭合曲面所包围的电荷电量的代数和除以0ε 。
ε∑⎰⎰=⋅iSq S d E 。
物理意义：表明了静电场是有源场注意理解： 是由高斯面内外所有电荷共同产生的。
∑i q 是高斯面内所包围的电荷电量的代数和。
若高斯面内无电荷或电量的代数和为零，则0=•⎰⎰d ,但高斯面上各点的E 不一定为零。
在静电场情况下，高斯定理是普遍成立的。
对于某些具有对称性场强分布问题，可用高斯定理计算场强。
典型静电场：均匀带电球面：=（球面内）；r q3041πε=（球面外）。
均匀带电无限长直线：E=r02πελ, 方向垂直带电直线。
均匀带电无限大平面：E=2εσ, 方向垂直带电直线。
均匀带电圆环轴线上： E=2/3220)(4x R qx+πε , 方向沿轴线（R 为圆环半径）。
电场力：q 0= , 电场力的功：A ab =⎰⎰=•ba ba dl E q l d E q θcos 00,特点：积分与路经无关, 说明静电场力是保守力。
第7章 静电场（是保守力场）教学要求：1．会求解描述静电场的两个重要物理量：电场强度E 和电势V 。
2．掌握描述静电场的重要定理：高斯定理和安培环路定理（公式内容及物理意义）。
3．掌握电容、电势差的计算。
主要公式： 一、 电场强度12．点电荷系场强：n E E E E+⋅⋅⋅++=21（矢量和）3（五步走积分法）(建立坐标系、取电荷元、写E d、分解、积分) (线元，面元，体元)4．对称性带电体场强：二、电势12．点电荷系电势：n V V V V +⋅⋅⋅++=21（代数和）3（四步走积分法）(建立坐标系、取电荷元、写dV 、积分)4．已知场强分布求电势：⎰⎰⋅=⋅=lv pdr E l d E V 0三、电势差：⎰⋅=∆B AAB l d E U四、电场力做功：⎰⋅=∆=2100l l l d E q U q A五、基本定理(1) 静电场高斯定理：（有源场）物理意义：表明静电场中，通过任意闭合曲面的电通量（电场强度沿任意闭合曲面的面积分），等于该曲面内包围的电荷代数和除以0ε。
(3)静电场安培环路定理：（无旋场）物理意义：表明静电场中，电场强度沿任意闭合路径的线积分为0。
第8章 恒定电流和恒定磁场（非保守力场）教学要求：1．电流连续性方程，熟悉毕奥-萨伐尔定律的应用，会解任意形状载流导线周围磁感应强度大小，并由右手螺旋法则求磁感应强度方向； 2．会求解载流导线在磁场中所受安培力；3．掌握描述磁场的两个重要定理：高斯定理和安培环路定理（公式内容及物理意义）。
主要公式：0. 电流的连续性方程：1．毕奥-萨伐尔定律表达式1）有限长载流直导线，垂直距离r（其中。
向之间的夹角流方向与到场点连线方分别是起点及终点的电和21θθ）2）无限长载流直导线，垂直距离r 处磁感应强度3）半无限长载流直导线，过端点垂线上且垂直距离r 处磁感应强度4）圆形载流线圈，半径为R ，在圆心O 处5）半圆形载流线圈，半径为R ，在圆心O 处6）圆弧形载流导线，圆心角为)(弧度制θ，半径为R ，在圆心O（θ用弧度代入）2．安培力：⎰⨯=lB l Id F （方向沿B l Id⨯方向，或用左手定则判定）dq d d sj S t⋅=-⎰积分法五步走:1.建坐标系;2.取电流元l Id;3.写θsin IdlB dF =;4.分解;5.积分. 安培的分子电流假说3．洛伦兹力： B v q F⨯=（磁场对运动电荷的作用力）当带电粒子同时受到电场力和磁场力时：()F q E B υ→→→→=+⨯4．磁场高斯定理：无源场）(因为磁场线是闭合曲线,从闭合曲面一侧穿入,必从另一侧穿出.)物理意义：表明稳恒磁场中，通过任意闭合曲面的磁通量（磁场强度沿任意闭合曲面的面积分）等于0。
大学物理（下）复习十、真空中的稳恒磁场： （一）基本概念：1、电流密度：n dS dI=δ， 导体内 υδnq = （此式对正负电荷q 都成立，对电子q=-e ；v 为载流子漂移速度）.电流：⎰⋅=S S d I δ，dt dqI = 对负电荷，规定电流沿-v 方向.2、稳恒电流：0=⋅⎰SS dδ（稳恒电流的条件）稳恒电场：稳定电荷分布产生的电场。
满足0=⋅⎰Ll d3、电动势：定量描述电源非静电力做功本领的物理量。
⎰+-⋅=电源内）(ld ε 或⎰⋅=Ll dε4、磁矩：n S I m∆0=（I 0为线圈电流，△S 为线圈面积，n 为线圈法向，与I 0成右旋关系）.5、磁感应强度： 量值 mM B m a x =； 或 ⊥=dS d B max Φ （n S I m∆0=）方向：试验线圈稳定平衡后，其磁矩的方向。
6、磁通量：⎰⋅=Sm S d BΦ7、霍耳效应：在磁场中，载流导体上出现横向电势差的现象。
（二）基本定律、定理：1、毕奥—萨伐尔定律： 204rr l Id d ⨯⋅=πμ 遵从磁场叠加原理，对一段载流导线L 的磁场：⎰⨯⋅=−−−−→−⨯⋅=L r r l Id B r r l Id B d 20020044πμπμ磁场叠加原理2、运动电荷的磁场： 2004r r q ⨯⋅=υπμ 3、磁场中的高斯定理： 0=⋅⎰⎰SS d B；4、安培环路定理：∑⎰=⋅I l d B L0μ磁介质中，安培环路定理：∑⎰=∙0I l d H L.磁场强度 M B H-=0μ，M 为介质磁化强度.对各向同性磁介质，H Bμ=，磁导率 r μμμ0=磁场中的高斯定理和安培环路定理，分别说明了磁场是无源场、有旋场。
5、电流元所受磁场的作用力——安培定律： B l Id d⨯=，⎰⨯=LB l Id6、载流线圈在匀强磁场中所受磁力矩： m ⨯=磁力矩总是要使线圈转到它的磁矩方向与磁场方向相一致的位置，此时，0=⨯=B m M7、运动电荷在磁场中所受力——洛仑兹力： q ⨯=υ8、磁力的功： ⎰=Φd I A ； 当I 恒定 ()12ΦΦ∆Φ-==I I A（三）几种典型载流导体的磁感应强度公式：1、载流直导线： ()⎪⎪⎩⎪⎪⎨⎧=-=aI B aIB πμθθπμ2c o s c o s 40210无限长有限长2、圆形电流：()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=⋅==+=RI R I B RIB x RR IB πθμπθμμμ42222002/32220圆弧圆心处圆心处轴线上任一点3、载流直螺线管：()⎪⎩⎪⎨⎧=-=I n B nI B 0120cos cos 2P μββμ无限长轴线上任一点 间的夹角）与螺线管轴线的位矢点到螺线管端口为（r P β 4、无限长载流直圆柱体：⎪⎪⎪⎩⎪⎪⎪⎨⎧=>=<=)(2)(2020B R r rI B R r R rI B 轴线上柱外柱内πμπμ5、螺绕环： I n I lNB 00μμ== 6、面密度为i 的无限大均匀带电平面两侧的磁场： 20iB μ=（匀强磁场）7、电荷在空间中激发的磁场： 2004rr v q B dN B d B q nSdl dN q ⨯⋅=−−−→−==πμ十二、电磁感应：（一）法拉第电磁感应定律： dt d m i Φ-=ε， N 匝线圈：dtN d m i )(Φ-=ε ).(间的夹角位矢与电流为r Iθ).(圆弧的张角为θ).(成右螺旋关系方向与I B ).(成右螺旋关系与方向垂直于电流环，I B说明：（1）这是计算感应电动势的普遍适用公式，但必须在闭合回路情况下计算。
大学物理复习提纲(下册)大学物理复习纲要（下册）第九章 静电场一、 基本要求 1、 理解库仑定律2、 掌握电场强度和电势概念3、 理解静电场的高斯定理和环路定理4、 熟练掌握用点电荷场强公式和叠加原理以及高斯定理求带电系统电场强度的方法5、 熟练掌握用点电荷的电势公式和叠加原理以及电势的定义式来求带电系统电势的方法 二、 内容提要 1、 静电场的描述描述静点场有两个物理量。
电场强度和电势。
电场强度是矢量点函数，电势是标量点函数。
如果能求出带电系统的电场强度和电势分布的具体情况。
这个静电场即知。
（1） 电场强度 0q E =点电荷的场强公式 r e rq 2041πε=（2） 电势 a 点电势 0.a a V E dl =⎰ （00V =） （3） a 、b 两点的电势差 .bab a b aV V V E dl =-=⎰（4） 电场力做功 00.()ba b aW q E dl q V V ==-⎰（5） 如果无穷远处电势为零，点电荷的电势公式： 04a q V rπε=2、表征静电场特性的定理(1)真空中静电场的高斯定理： 1.nii sqE d s ε==∑⎰高斯定理表明静电场是个有源场，注意电场强度通量只与闭合曲面内的电荷有关，而闭合面上的场强和空间所有电荷有关 （2）静电场的环路定理： .0lE dl =⎰表明静电场是一种保守场，静电力是保守力，在静电场中可以引入电势的概念。
3、电场强度计算（1） 利用点电荷的场强公式和叠加原理求 点电荷 21014ni i i q E r πε==∑ 带电体 2014r dqE e r πε=⎰ （2） 高斯定理求E高斯定理只能求某些对称分布电场的电场强度，用高斯定理求电场强度关键在于做出一个合适的高斯面。
4、电势计算（1）用电势的定义求电势（E 的分布应该比较容易求出）.a aV E dl =⎰电势零点（2）利用点电荷的电势公示和电势叠加原理求电势： 014P dqV rπε=⎰第十章 静电场中的导体和电介质 一、基本要求1、 理解静电场中的导体的静电平衡条件，能从平衡条件出发分析导体上电荷分布和电场分布。
2、 了解电介质极化的微观机理，理解电位移矢量D 的概念，及在各向同性介质中D 和E 关系，理解电介质中的高斯定理并会利用它求介质中对称电场的场强。
3、理解电容的定义，能计算常用电容器的电容4、了解电场能量密度的概念，能计算电场能量。
二、内容提要 1、静电场中的导体当导体处于静电平衡时，导体内部场强处处为零；导体内任意两点电势差为零。
整个导体是一个等势体，导体表面是一个等势面，导体内部没有静电荷。
电荷按表面的曲率分布在表面上。
导体表面附近的场强和该处导体表面的电荷面密度有0E σε=的关系。
2、静电场中的电介质电介质的极化位于静电场中的电解质表面产生极化电荷，介质中的场强： '0E E E =+ 3、介质中的高斯定理0.sD d s Q =⎰ 00DE E εε==4、电容：电容的定义: 12QC V V =- 计算电容器电容步骤：（1） 设电容器两极板带有电荷Q +和Q -。
（2） 求两极板之间的场强分布（3） 利用电势定义式求出两极板之间的电势差： 2121.V V E dl -=⎰（4） 利用电容公式求电容: Q C V= 5、电容器储存的能量22111222e Q W CU QU C === 电场能量体密度 12e DE ω=利用能量体密度求电场能量:12e e VW dV DE ω==⎰⎰ V 为场不为零的空间三、解题的思路和方法静电场中放置导体，应先根据静电平衡条件求出电荷分布，而后根据电荷分布求场强分布.静电场中放置电介质，应先根据电荷分布，求电位移矢量D ，而后根据D 和E 的关系求E ，由E 分布求电势或电势差。
第十一章 恒定磁场一、 基本要求1、掌握描述磁场的物理量－磁感应强度。
2、理解毕奥-萨伐尔定律，能用它和叠加原理计算简单电流的磁场。
3、理解恒定电流的磁场的高斯定理和安培环路定理，学会用安培环路定理计算磁感应强度的方法4、理解洛伦兹力和安培力公式，能分析电荷在均匀电场和磁场中的受力和运动情况，了解磁矩概念，能计算简单几何形状载流导体和载流平面线圈载在磁场中受的力和力矩。
二、 内容提要1、描述磁场的物理量－磁感应强度B 矢量B 矢量大小：maxF B q υ=B 矢量方向：规定为正的运动电荷在磁场中受力为零时的运动方向为该点的磁场方向。
2、恒定电流在磁场中的基本定律-毕奥-萨伐尔定律024r Idl e d B rμπ⨯=式中70410./T m A μπ-=⨯ d B 方向： 与r Idl e ⨯的方向相同 d B 的大小为：02sin()4r Idl e dB r μπ⨯=由毕奥-萨伐尔定律求出几种典型电流的磁场 （1）无限长载流直导线的磁场 02IB rμπ= （2）圆电流中心的磁场 02IB Rμ=（3）长直螺线管的磁场 0B nI μ= 三、 表征磁场特性的定理1、磁场的高斯定理:.0sB d s =⎰ 说明磁场是无源场2、安培环路定理.lB dl I μ=⎰ 说明磁场是非保守场四、 磁感应强度计算1、用毕奥-萨伐尔定律求B2、用安培环路定理求B五、 用安培环路定理解题的方法和思路用安培环路定理可以非常方便的求某些电流的磁感应强度，具体步骤是： a ）先要分析磁场分布是否具有空间的对称性，包括轴对称、点对称等 b ）根据磁场的对称性特征选取适当的回路，：该回路一定要通过求磁场的点，积分回路的回转方向不是和磁场方向垂直便是和磁场方向平行，且B 作为一个常量可以从积分号中提出，积分时只对回路的长度积分。
六、 磁场对运动电荷和电流的作用1、磁场对运动电荷的作用力-洛伦兹力：F q B υ=⨯2、磁场对载流导线的作用力-安培力 d F Idl B =⨯ F Idl B =⨯⎰3、用安培力公式计算电流在磁场中受力步骤: a) 根据磁场的分布情况选取合适的电流元 b) 由安培力公式求出电流元受力d F c) 用分量式积分求出F可以证明：在均匀磁场中，任意形状的平面载流导线所受的磁力与该导线始终点连线相同的直导线所受磁力相同，平面闭合线圈所受的合力为零。
七、 载流线圈在磁场中所受的磁力矩M m B =⨯ n m NISe =磁力矩的大小 sin M NBIS θ= 方向：遵循右手螺旋法则第十二章 电磁感应一、基本要求1、掌握并熟练应用法拉第电磁感应定律和楞次定律计算感应电动势，并判断其方向及电势高低。
2、理解动生电动势和感生电动势，会计算动生电动势和感生电动势。
3、了解自感和互现象，会计算几何形状简单的导体的自感和互感。
4、了解磁场能量和能量密度概念。
二、内容提要1、法拉第电磁感应定律： i d dtξΦ=-一个回路，不管什么原因，只要穿过回路的磁通量随时间变化，回路中就有感应电动势。
应用该式只要求出.sB d s Φ=⎰，若它是时间的函数，则磁通量对时间求导即得i ξ感应电流，若电路闭合，回路电阻为 R : 1i d I R dtΦ=-式中负号是楞次定律的数学表达式。
2、楞次定律 判定感应电流方向回路中感应电流所激发的磁场，总是使它反抗任何引起感应电流的原因。
3、动生电动势和感应电动势（1）动生电动势：().bi a B dl ξυ=⨯⎰ dl 式中为线元，B 为外磁场，υ为线元的速度（2）感应电动势..i k s ld d BE dl d s dt dtξΦ==-=-⎰⎰感应电动势的计算公式实质上就是法拉第电磁感应定律，不过这种通量的变化只是由于B 的变化引起的。
4、求动生电动势和感生电动势的思路和方法（1） 导体或导体回路在恒定磁场中运动时（即导体切割磁力线运动时），产生的 电动势为动生电动势。
应用().bi a B dl ξυ=⨯⎰时，应先选一个合适的线元dl ，并注意线元所在处的B 和它的运动速度υ，并注意各矢量之间的夹角。
正确写出().i d B dl ξυ=⨯，而后积分，注意积分的上下限。
（2）变化的磁场在其周围空间产生涡旋电场，这种涡旋电场力是一种非静电力。
正是它驱使载流子运动产生电动势，在不要求计算k E 时，仍可按法拉第电磁感定律求感应电动势。
第十四章 光学一、 基本内容：11.1、11.2、11.3、11.4、11.6、11.7、11.9、11.10、11.11 二、 基本要求： （一） 光的干涉：1、 理解光的相干性及获得相干光的两种方法；2、掌握杨氏双缝的相干条件和条纹分布规律；3、 掌握光程概念及光程差与相位差的关系；4、 理解半波损失概念并掌握产生条件；5、掌握薄膜等厚干涉（劈尖、牛顿环）的干涉条件及条纹分布规律。
（二） 光的衍射：1、 理解研究夫琅禾费单缝衍射的半波带法，掌握其条纹分布规律；2、能用光栅衍射公式确定谱线位置，了解光栅的缺级问题。
（三） 光的偏振1、 理解自然光、偏振光、部分偏振光、起偏、检偏等概念；2、 掌握马吕斯定律；3、理解反射和折射时光的偏振现象，掌握布儒斯特定律。
三、 内容摘要（一） 光的干涉1、怎样获得相干光：将普通光源上同一点发出的光，利用双缝（分波振面法）和反射和折射（分振幅法）使一束光“一分为二”，沿两条不同的路径传播并相遇，这样，单束的每一个波列都分成了频率相同，振动方向相同，相位差恒定的两部分，当它们相遇时，符合相干条件，产生干涉现象。
2、杨氏双缝干涉：波程差⎪⎪⎩⎪⎪⎨⎧=-±=±=暗纹明纹)3,2,1(2)12()3,2,1,0(22' k k k k d x d λλ'12sin d x d d r r r ==-=∆θ条纹坐标：相邻明纹或相邻暗纹之间的距离3、光程：光在介质中通过L 距离引起的相位差：nL 为光程，即光通过介质中的几何路程折合成的光在真空中的路程。
4、等厚干涉（劈尖、牛顿环）（1）等厚干涉的成纹公式：垂直入射时，上下表面反射的光的光程差（假设有半波损失）（2）劈尖条纹分布规律: (a) 如果反射光有半波损失，棱处d=0, 零级暗纹 (b) 条纹等间距(c)相邻明纹（或暗纹）对应的劈尖的厚度差⎪⎪⎩⎪⎪⎨⎧-±±=2)12(22''λλk d d k d d x λddx '=∆nLL nλπλπϕ22==∆⎪⎩⎪⎨⎧=+==+减弱，加强 3,2,102)12(3,2,122k k k k nd λλλnd λλ==∆（3）牛顿环：光垂直入射，反射光有半波损失时，明纹半径暗纹半径 条纹不是等间距的。
（4）关于半波损失（产生的条件）：入射光从光疏介质到光密介质的反射光，相位有π的跃变。
