【全国校级联考】福建省龙岩市一级达标校2020-2021学年高一下期期末考试数学试题

龙岩市一级达标校2020-2021～2020学年第二学期期末高一教学质量检查
化学试题参考答案
一、选择题（共4４分，其中1-10题每题2分，11-18题每题3分）
题号 1 2 3 4 5 6 7 8 9 10 答案 C D B C B B D D C D 题号11 12 13 14 15 16 17 18
答案 A D A B C C A A
二、非选择题（除标注外，其余每空均为2分）
19．（14分）
（1）第2周期第VIA族
（2）H2O 氧原子的半径比较小，与氢形成的键更稳定（其他合理答案也可）
（3）Na（1分） a、c
（4）SO2 +2OH－==SO3 2－+ H2O 或SO2 +OH－==HSO3 －
（5）
（方程式2分，单线桥1分）
20．（14分）
（1）分液漏斗
（2）还原
（3）F、E、B(或F、E、B)
（4）
（5）除去氯化氢气体氢氧化钠溶液（其他合理答案也可）
（6）<
21．（14分）
（1）催化剂红黑交替（其他合理答案也可）
（2）收集生成的乙醛，防止其挥发到空气中产生污染
（3） 2CH3CH2OH+O22CH3CHO+2H2O（或CuO与乙醇反应）④⑤
（4）该反应是放热反应
（5）还原
22．（14分）
（1）作涂料（其他合理答案也可）
（2）Fe3+ 、H+
（3）CO 、CO2
（4）将Fe2+ 氧化成Fe3+ a 50/a （5）。

福建省龙岩市一级达标校2021-2021学年高一化学下学期期末质检试题〔考试时间：90分钟 总分值：100分〕注意：1.请将试题的全部答案填写在答题卡上。

2.可能用到的相对原子质量：H-1 C-12 O-16 Ca-40 Fe-56第I 卷〔选择题，共44分〕一、选择题〔共18题，其中1-10题每题2分，11-18题每题3分。

每题只有1个选项符合题意〕1.科学家通过粒子加速器进行实验，获得了一种罕见的4526Fe 原子。

对于4526Fe 和5626Fe ，以下有关数目不相同．．．的是〔 〕 A.质子数 B.最外层电子数 C.中子数D.核外电子数2.人体所需元素中，有一种对人类智力起重要作用的主族元素R 。

R 元素处于第五周期，其最高价氧化物的化学式为27R O ，那么R 元素的名称为〔 〕 A.氟B.氯C.溴D.碘3.化学家维勒在制备氰酸铵〔4NH CNO 〕时得到结晶物尿素[()22CO NH ]，这一发现打破了当时化学界流行的“不能通过人工方法将无机物转化为有机物〞的“生命力论〞。

氰酸铵和尿素两种物质互为〔 〕 A.同种物质 B.同分异构体 C.同位素D.同素异形体4.1991年，我国著名化学家张清莲准确测得In 的相对原子质量为114.818，被国际原子量委员会采用为新的标准值。

铟〔In 〕的原子结构如下图，以下说法错误的选项是．．．．．．〔 〕A.In 为长周期元素B.In 易导电导热C.In 在反响中易得电子D.结构示意图中X=495.木薯粉〔主要成分是淀粉〕、食盐〔主要成分是氯化钠〕、料酒〔有效成分为乙醇〕、食醋〔有效成分为乙酸〕等都是厨房常备的物品，它们主要成分或有效成分对应物质属于离子化合物的是〔 〕 A.木薯粉B.食盐C.料酒D.食醋6.以下化学用语中，错误的选项是．．．．．．〔 〕 A.22H O 的电子式： B.乙烯的结构简式：22CH CH C.羟基的电子式：D.2+Mg 的结构示意图：7.锂不仅在军事工业中占有举足轻重的地位，而且在民用工业也是一种重要的材料。

福建省龙岩市2020-2021学年高一地理下学期期末考试试题（考试时间：75分钟满分：100分）注意：请将试题的全部答案填写在答题卡上。

第I卷（选择题共50分）本大题共25小题，每小题2分，共50分。

每小题只有一个答案最符合题意，多选、错选、漏选均不得分。

2020年11月1日，中国第七次人口普查正式开启，与以往相比，普遍存在的“人户分离”给人口普查带来难。

“人户分离”现象指中华人民和国境内公民的经常居住地和常住户口登记地不一致，可分为“有户（籍）无人”和“有人无户（籍）”两种情况。

据此完成1～2题。

1．下列地区中，“人户分离”现象中“有户（籍）无人”现象相对普遍的是A．广东省B．黑龙江省C．浙江省D．江苏省2．下列现象与“人户分离”无关的是A．沿海城市常住人口快速增长B．暑假期间新疆游客众多C．春节期向交通运输压力增大D．南方山区农田撂荒严重2021年中央经济工作会议确定，力争我国二氧化碳排放2030年前达到峰值，2060年前实现碳中和。

据此完成3～4题。

3．下列产业部门的转型升级，对“碳达峰”影响最大的是A．金融业B．零售业C．采掘业D．制造业4．实现“碳中和”的可行措施是①缩小工业规模②参与植树造林③大力发展火电④提高环保标准A．①②B．①③C．③④D．②④2019年4月，国家发改委发布《2019年新型城镇化建设重点任务》，首次提出了“收缩型城市”的概念，并针对性地提出要“促进城市精明增长”。

图1示意我国主要“收缩型城市”分布。

据此完成5～6题。

图15．造成该类型城市收缩的原因最有可能是A．产业结构升级B．矿产资源枯竭C．自然灾害频发D．长期低生育率6．“精明增长”理论对现阶段我国城市规划的借鉴意义是A．推动郊区城市化B．推进棚户区改造C．优先发展制造业D．大量兴建卫星城7．下列城市中，宜将“精明增长”理念用于实践的是A．广州B．青岛C．福州D．鹤岗某大数据平台对2017年上半年城市人流量进行统计，图2示意我国某特大城市甲、乙两功能区之间工作日6时至22时人流量状况。

2020-2021学年福建省龙岩市高一（下）期末化学试卷一、单选题（本大题共14小题，共42.0分）1.化学与生活密切相关，下列有关说法错误的是()A. 无水乙醇可直接用于医用消毒B. 燃煤中加入CaO可以减少SO2的排放C. 用灼烧的方法可区分蚕丝和人造纤维D. 加热能灭活新型冠状病毒是因为蛋白质受热变性2.以下六种核素： 36Li、 37Li、 614C、 714N、 1123Na、 1224Mg.下列相关说法错误的是()A. 36Li和 37Li在元素周期表中的位置相同B. 614C可用于鉴定文物年代C. 614C和 714N质量数相等，二者互为同位素D. 1123Na和 1224Mg的中子数相同3.短周期主族元素X、Y、Z、W的原子序数依次增大，X原子最外层电子数是其电子层数的2倍，X、Y的核电荷数之比为3：4，单质Z在空气中燃烧有黄色火焰，W−的最外层为8电子结构。

下列说法正确的是()A. 简单氢化物的稳定性：X>YB. 原子半径大小：X<Y<Z<WC. Z与Y形成的化合物都只含离子键D. 化合物ZWY可作漂白剂和消毒剂4.下列有关化学用语的表示方法中正确的是()A. 硫化钠的电子式：B. Mg2+的结构示意图：C. CO2分子比例模型：D. HCl的形成过程：5.下列有关铝、硅及其化合物的叙述错误的是()A. 二氧化硅可用于生产电脑芯片和光导纤维B. 常温下可用铝槽车运输浓硫酸或浓硝酸C. 二氧化硅制备单晶硅涉及氧化还原反应D. 氢氧化铝可用于治疗胃酸过多6.下列叙述正确的是()A. 糖类、油脂、蛋白质都能水解B. 纤维素、蛋白质、油脂都是高分子化合物C. 鸡蛋清中加入硫酸铵浓溶液会出现盐析现象D. 淀粉和纤维素的通式均为(C4H10O5)n，二者互为同分异构体7.某兴趣小组设计的原电池装置如图，下列叙述错误的是()A. 负极的电极反应式为：Fe−2e−=Fe2+B. 石墨棒为正极，一段时间后质量增加C. 离子导体中的Fe3+向石墨棒方向移动D. 电子的流动方向是：铁片→导线→石墨棒8.含硒(Se)的保健品已进入市场，硒与氧同主族、与溴同周期。

龙岩市一级达标校2020-2021～2020学年第二学期期末高一教学质量检查物理试题参考答案一、选择题（13小题，每小题4分，共52分。

在每小题给出的4个选项中，第1-8题只有一项符合题目要求，第9-13题有多项符合题目要求。

全部选对得4分，选对但不全的得2分，有选错得0分）14. （1）需要 （2）不需要 （3）B t d )11(2222AB t t Md FL -=15. （1）1.5（1.4~1.6） 0.22（0.21~0.24） 0.24（0.23~0.25） （3）甲三、计算题（3小题，共32分。

请把正确答案填写在答题卡上。

解答时请写出必要的文字说明、方程式、重要的演算步骤和答案，只写最后答案的不能得分。

） 16．（10分） 解：（1）平直的公路上，速度最大时，加速度a=00.1f mg =牵引力 1F f = （1分） 由11P F v = （2分） 得130m v = （2分） （2）上坡行驶时速度最大时，加速度a=02sin 0F mg f α--= （1分）牵引力32310N F =⨯ （1分）由22P F v = （2分）得220m s v = （1分）17．（10分） 解：（1）“套环”在竖直方向上做自由落体运动，根据2g 21h t H =- （2分） 解得：t=0.4s （2分） （2）当“套环”刚好贴着木桩左侧落下时，速度有最大值，即：s m td d ax /9.2v m =+=环（2分） 当“套环”刚好贴着木桩右侧落下时，速度有最小值，即：s m tdin /5.2v m ==（2分）所以小红抛出“套环”的初速度范围是：s m v s m /9.2/5.20<< （2分） 18．（12分） 解：（1）设滑块质量为m ，滑块恰好能通过第1个圆轨道，有：Rv m mg 2= （2分）解得：v = （1分）滑块从A 点到圆轨道最高点过程机械能守恒，有：221)2(mv R h mg =- （2分）联立解得：h =5m （1分） （2）如果滑块停止在D 点，从A 点到D 点，根据动能定理，有：0CD mgh mgL μ-= （1分）解得h =2.4m<5m （1分） 若h <5m ，滑块会脱离圆轨道，故必须h ≥5m （1分） 如果小球停止在E 点，从A 点到E 点根据动能定理，有： （1分） 0cos )sin (=---αμμαDE CD DE mgL mgL L h mg解得h =6.12m （1分） 综上可得5m≤h≤6.12m （1分）。

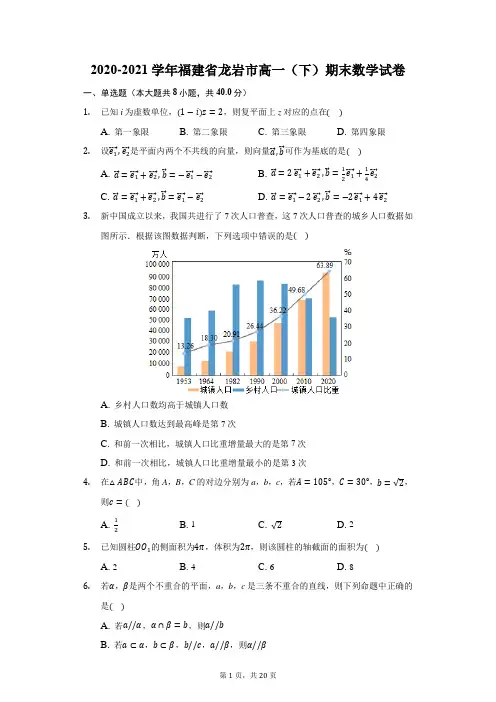
2020-2021学年福建省龙岩市高一（下）期末数学试卷一、单选题（本大题共8小题，共40.0分）1.已知i为虚数单位，(1−i)z=2，则复平面上z对应的点在()A. 第一象限B. 第二象限C. 第三象限D. 第四象限2.设e1⃗⃗⃗ ,e2⃗⃗⃗ 是平面内两个不共线的向量，则向量a⃗,b⃗ 可作为基底的是()A. a⃗=e1⃗⃗⃗ +e2⃗⃗⃗ ,b⃗ =−e1⃗⃗⃗ −e2⃗⃗⃗B. a⃗=2e1⃗⃗⃗ +e2⃗⃗⃗ ,b⃗ =12e1⃗⃗⃗ +14e2⃗⃗⃗C. a⃗=e1⃗⃗⃗ +e2⃗⃗⃗ ,b⃗ =e1⃗⃗⃗ −e2⃗⃗⃗D. a⃗=e1⃗⃗⃗ −2e2⃗⃗⃗ ,b⃗ =−2e1⃗⃗⃗ +4e2⃗⃗⃗3.新中国成立以来，我国共进行了7次人口普查，这7次人口普查的城乡人口数据如图所示．根据该图数据判断，下列选项中错误的是()A. 乡村人口数均高于城镇人口数B. 城镇人口数达到最高峰是第7次C. 和前一次相比，城镇人口比重增量最大的是第7次D. 和前一次相比，城镇人口比重增量最小的是第3次4.在△ABC中，角A，B，C的对边分别为a，b，c，若A=105°，C=30°，b=√2，则c=()A. 12B. 1C. √2D. 25.已知圆柱OO1的侧面积为4π，体积为2π，则该圆柱的轴截面的面积为()A. 2B. 4C. 6D. 86.若α，β是两个不重合的平面，a，b，c是三条不重合的直线，则下列命题中正确的是()A. 若a//α，α∩β=b，则a//bB. 若a⊂α，b⊂β，b//c，a//β，则α//βC. 若a ⊂α，b ⊂α，且c ⊥a ，c ⊥b ，则c ⊥αD. 若a ⊥α，α∩β=c ，b//c ，则a ⊥b7. 已知菱形ABCD ，AC =2，BD =4，且AE ⃗⃗⃗⃗⃗ =2BE ⃗⃗⃗⃗⃗ ，则∠DEC 的余弦值为( )A. 6√3131B. 6√3731C. 6√3137D. 6√37378. 现有5个相同的小球，分别标有数字1，2，3，4，5，从中有放回的随机抽取两次，每次抽取一个球，记：事件A 表示“第一次取出的球数字是2”，事件B 表示“第二次取出的球数字是3”，事件C 表示“两次取出的球的数字之和为8”，事件D 表示“两次取出的球的数字之和为6”，则下列选项正确的是( )A. 事件A 和事件C 相互独立B. 事件B 和事件C 相互独立C. 事件B 和事件D 相互独立D. 事件C 和事件D 相互独立二、多选题（本大题共4小题，共20.0分） 9. 设z 1，z 2，z 3为复数，则( )A. 若z 1>z 2，则z 1−z 2>0B. 若z 1z 2=z 2z 3，则z 1=z 3C. 若z 2−=z 1，则|z 1z 3|=|z 2z 3|D. 若z 1满足|z 1|=1，则|z 1−2|的最小值为110. 已知正四面体PABC 的棱长为2，M 、N 分别为PA 、PB 的中点．下列说法正确的有( )A. MN ⊥PCB. 异面直线BM 与PC 所成角的余弦值为√36C. 该正四面体的体积为√23D. 该正四面体的内切球体积为√627π11. 在平行四边形ABCD 中，AB =2，AD =2√3,AB⃗⃗⃗⃗⃗ ⋅AD ⃗⃗⃗⃗⃗⃗ =−6,AM ⃗⃗⃗⃗⃗⃗ =λAD ⃗⃗⃗⃗⃗⃗ ,λ∈[0,1]，则下列选项正确的是( )A. MB ⃗⃗⃗⃗⃗⃗ ⋅MC ⃗⃗⃗⃗⃗⃗ 的最小值是−3B. MB ⃗⃗⃗⃗⃗⃗ ⋅MC ⃗⃗⃗⃗⃗⃗ 的最小值是−2C. MB ⃗⃗⃗⃗⃗⃗ ⋅MC ⃗⃗⃗⃗⃗⃗ 的最大值是10D. MB ⃗⃗⃗⃗⃗⃗ ⋅MC ⃗⃗⃗⃗⃗⃗ 的最大值是2512. 在△ABC 中，角A ，B ，C 对边分别为a ，b ，c ，设向量m⃗⃗⃗ =(c,a +b),n ⃗ =(a,c)，且m⃗⃗⃗ //n ⃗ ，则下列选项正确的是( ) A. A =2B B. C =2AC. 1<ca <2D. 若△ABC 的面积为c 24，则C =π2三、单空题（本大题共4小题，共20.0分）13. 已知向量a ⃗ =(1,3),b ⃗ =(3,4)，若(λa ⃗ −b ⃗ )⊥b ⃗ ，则λ=______．14. 记一组数据x i (i =1,2，…，n)的平均数为x −，且x −=1.6,1n ∑(n i=1x i −x −)2=1.44，则1n∑x i 2n i=1=______．15. 已知圆C 的弦AB 的长度为2√3，则AB ⃗⃗⃗⃗⃗ ⋅AC⃗⃗⃗⃗⃗ =______． 16. 已知三棱锥P −ABC ，PB =PC =AB =BC =AC =2√3，侧面PBC ⊥底面ABC ，则PA =______，三棱锥P −ABC 外接球的表面积为______． 四、解答题（本大题共6小题，共70.0分） 17. 已知复数z =a +(a −1)i(a ∈R)．(1)若z ⋅z −=5，求a ； (2)求|z|的最小值．18. 如图，S 是圆锥的顶点，AB 是底面圆O 的直径，C 为底面圆周上异于A ，B 的点，D 为BC 的中点．(1)求证：平面SOD ⊥平面SBC ；(2)若圆锥的侧面积为3√5π，且BC =4，AC =2，求该圆锥的体积．19.为了解某班级学生期末考试数学成绩情况，抽取该班40名学生的数学成绩，将所得数据整理后，画出其频率分布直方图(如图)，已知从左到右各长方形高的比为2：3：5：6：3：1．(1)根据频率分布直方图，计算抽取的数学成绩的平均数和第65百分位数(同一组中的数据用该组区间的中点值为代表)；(2)若从分数在[80,90)和[130,140]的同学中随机抽取两位同学，求抽取的两位同学中至少有一位同学的数学成绩在[130,140]的概率．=bsinA这两个条件中任选一个，补20.在①√3(a−bcosC)=csinB；②√3acos A+C2充在下面问题中的横线上，并解答相应的问题．在△ABC中，角A，B，C的对边分别为a，b，c，且满足______，BD平分∠ABC交AC于点D，且BD=2，AC=3，求△ABC的面积．21.甲、乙两人组成“星队”参加猜成语活动，每轮活动由甲、乙各猜一个成语，已知甲每轮猜对的概率为p，乙每轮猜对的概率为q.在每轮活动中，甲和乙猜对与否互，恰有一人猜不影响，各轮结果也互不影响．已知每轮甲、乙同时猜错的概率为112．错的概率为512(1)求p和q；(2)若p>q，求“星队”在两轮活动中猜对2个成语的概率．22.已知等边三角形ABC，D，E分别是边AB，AC上的三等分点，且AD=CE(如图甲)，将△ADE沿DE折起到△A1DE的位置(如图乙)，M是A1D的中点．(1)求证：EM//平面A1BC；(2)若二面角A1−DE−B的大小为2π，求直线DE与平面A1CE所成角的正弦值．3答案和解析1.【答案】A【解析】解：首先由(1−i)z=2求得z=21−i =2(1+i)(1−i)(1+i)=1+i，对应点为(1,1)，在第一象限．故选：A．首先由(1−i)z=2求得z，然后可确定复平面上z对应的点所在象限．本题考查复数除法运算，考查复数几何意义，属于基础题．2.【答案】C【解析】解：对于A，a⃗=−b⃗ ，∴a⃗,b⃗ 共线，不能作基底，∴不选A；对于B，a⃗=4b⃗ ，∴a⃗,b⃗ 共线，不能作基底，∴不选B；对于C，不存在λ，使得a⃗=λb⃗ ，能作基底，∴选C；对于D，a⃗=−12b⃗ ，∴a⃗,b⃗ 共线，不能作基底，∴不选D．故选：C．依据向量共线定理可解决此题．本题考查平面向量基本定理，考查数学运算能力及直观想象能力，属于中档题．3.【答案】A【解析】解：因为2020年城镇人口高于乡村人口，故选项A错误；因为城镇人口数达到最高峰是2020年，即第7次，故选项B正确；第2次和第1次相比，城镇人口比重增量为18.3%−13.26%=5.04%，第3次和第2次相比，城镇人口比重增量为20.91%−18.3%=2.61%，第4次和第3次相比，城镇人口比重增量为26.44%−20.91%=5.53%，第5次和第4次相比，城镇人口比重增量为36.22%−26.44%=9.78%，第6次和第5次相比，城镇人口比重增量为49.68%−36.22%=13.46%，第7次和第6次相比，城镇人口比重增量为63.89%−49.68%=14.21%，所以和前一次相比，城镇人口比重增量最大的是第7次，故选项C正确；前一次相比，城镇人口比重增量最小的是第3次，故选项D正确．故选：A．利用题中柱形图和折线图中的数据信息以及变化趋势，对四个选项逐一分析判断即可．本题考查了条形图和折线图的应用，读懂统计图并能从统计图得到必要的信息是解决问题的关键，属于基础题．4.【答案】B【解析】解：在△ABC中，角A，B，C的对边分别为a，b，c，A=105°，C=30°，所以B=45°，b=√2，则c=bsinCsinB =√2×12√22=1．故选：B．利用三角形的内角和求解B，然后利用正弦定理求解c即可．本题考查正弦定理的应用，是基础题．5.【答案】B【解析】解：设底面圆的半径为r，圆柱的高为h，则有{V=πr2ℎ=2πS侧=2πrℎ=4π，解得r=1，ℎ=2，所以该圆柱的轴截面的面积为S=2rℎ=2×2=4．故选：B．设底面圆的半径为r，圆柱的高为h，由体积和侧面积公式求出r和h，由轴截面的面积公式求解即可．本题考查了圆柱几何性质的应用，圆柱体积公式的应用，轴截面的理解与应用，考查了空间想象能力与逻辑推理能力，属于基础题．6.【答案】D【解析】解：若a//α，α∩β=b，则a//b或a与b异面，故A错误；若a⊂α，b⊂β，b//c，a//β，则α//β或α与β相交，故B错误；若a⊂α，b⊂α，且c⊥a，c⊥b，则c⊂α或c//α或c与α相交，相交也不一定垂直，只有添加条件a与b相交，才有c⊥α，故C错误；若a ⊥α，α∩β=c ，则a ⊥c ，又b//c ，所以有a ⊥b ，故D 正确． 故选：D ．由空间中直线与直线、直线与平面的位置关系判断A 与B ；由直线与平面垂直的判定判断C ；由异面直线所成角的求法判定D ．本题考查空间中直线与直线、直线与平面、平面与平面位置关系的判定，考查空间想象能力与思维能力，是基础题．7.【答案】D【解析】解：根据题意，菱形ABCD ，AE⃗⃗⃗⃗⃗ =2BE ⃗⃗⃗⃗⃗ ，则A 、B 、E 三点共线，且B 是AE 的中点， 如图：AC =2，BD =4，则AB =√(AC2)2+(BD 2)2=√5，则AE =2AB =2√5， 在△ABD 中，cos∠BAD =AB 2+AD 2−2AB⋅AD2AB⋅AD =−35，在△ADE 中，DE 2=AE 2+AD 2−2AE ⋅AD ⋅cos∠BAD =37，则DE =√37， 又由EC =BD =4，DC =AB =√5， 则cos∠DEC =DE 2+EC 2−DC 22DE⋅EC=6√3737，故选：D ．根据题意，分析A 、B 、E 三点的关系可得B 是AE 的中点，求出AB 的值，在△ABD 中，由余弦定理求出cos∠BAD ，进而求出DE ，分析求出EC 和DC 的值，进而利用余弦定理计算可得答案．本题考查三角形中的几何计算，涉及余弦定理的应用，注意分析A 、B 、E 三点的关系，属于中档题．8.【答案】C【解析】解：由题意，P(A)=15,P(B)=15,P(C)=325,P(D)=15， 对于A ，P(AB)=0≠P(A)P(B)，故选项A 错误；≠P(B)P(C)，故选项B错误；对于B，P(BC)=125=P(B)P(D)，故选项C正确；对于C，P(BD)=125≠P(C)P(D)，故选项D错误．对于D，P(CD)=125故选：C．利用相互独立事件的概率乘法公式，对四个选项逐一分析判断即可．本题考查了相互独立事件的判断，解题的关键是掌握相互独立事件的概率公式，考查了逻辑推理能力，属于基础题．9.【答案】ACD【解析】解：∵z1>z2，∴z1−z2>z2−z2=0，故A选项正确，若z1z2=z2z3，则z2(z1−z3)=0，当z2=0，z1≠z3时，等式也成立，故B选项错误，∵z2−=z1，∴z2=z1−，设z1=a+bi，则z2=a−bi，∴|z1|=|z2|=√a2+b2，∴|z1||z3|=|z2||z3|，即|z1z3|=|z2z3|，故C选项正确，设z1=a+bi，(a,b∈R)，∵|z1|=1，∴a2+b2=1，−1≤a≤1，∴z1−2=a−2+bi，∴|z1−2|=√(a−2)2+b2=√(a−2)2+1−a2=√5−4a，∵−1≤a≤1，∴|z1−2|min=√5−4=1，故D选项正确．故选：ACD．根据已知条件，结合共轭复数的概念和复数模的求法，以及复数模的几何意义，即可求解．本题主要考查了共轭复数的概念和复数模的求法，考查了复数模的几何意义，需要学生有较强的综合能力，属于中档题．10.【答案】ABD【解析】解：正四面体PABC 的棱长为2，M 、N 分别为PA 、PB 的中点． 如图所示：对于A ：取AB 的中点D ，连接PD ，DC ， 由于AP =BP ，AC =CB ，所以PD ⊥AB ，CD ⊥AB ，故AB ⊥平面PCD ，所以AB ⊥PC ，由于NM//AB ，所以MN ⊥PC ，故A 正确；对于B ：取AC 的中点E ，连接ME ，BE ，所以异面直线BM 与PC 所成角为∠BME ， 由于ME =12PC =1，BM =√4−1=√3，BE =√3， 故cos∠BME =√3)22√3)22×√3×1=√36，故B 正确；对于C ：BE 和DC 交点O 为底面△ABC 的中心， 故OC =(2√33)=2√63，所以V P−ABC =13×12×2×2×√32×2√63=2√23，故C 错误；对于D ：利用等体积转换法：设内切球的半径为r ， 所以V P−ABC =4×13×12×2×2×√32⋅r =2√23，解得r =√66，故V 球=43⋅π⋅(√66)3=√6π27，故D 正确． 故选：ABD ．直接利用线面垂直的判定和性质的应用，异面直线的夹角的求法，余弦定理的应用，勾股定理的应用，等体积转换法，球的体积公式的应用判断A 、B 、C 、D 的结论． 本题考查的知识要点：线面垂直的判定和性质的应用，异面直线的夹角的求法，余弦定理的应用，勾股定理的应用，等体积转换法，球的体积公式的应用，主要考查学生的运算能力和数学思维能力，属于中档题．11.【答案】BC【解析】解：由图可得MB⃗⃗⃗⃗⃗⃗ ⋅MC ⃗⃗⃗⃗⃗⃗ =(AB ⃗⃗⃗⃗⃗ −AM ⃗⃗⃗⃗⃗⃗ )(MA ⃗⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ ) =AB ⃗⃗⃗⃗⃗ ⋅MA ⃗⃗⃗⃗⃗⃗ +AB ⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ −AM ⃗⃗⃗⃗⃗⃗ ⋅MA ⃗⃗⃗⃗⃗⃗ −AM ⃗⃗⃗⃗⃗⃗ ⋅AC⃗⃗⃗⃗⃗ =−λAB ⃗⃗⃗⃗⃗ ⋅AD ⃗⃗⃗⃗⃗⃗ +AB ⃗⃗⃗⃗⃗ ⋅(AB ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ )+AM ⃗⃗⃗⃗⃗⃗ ²−λAD ⃗⃗⃗⃗⃗⃗ ⋅(AB ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ )=−λAB ⃗⃗⃗⃗⃗ ⋅AD ⃗⃗⃗⃗⃗⃗ +|AB ⃗⃗⃗⃗⃗ |²+AB ⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ +λAD ⃗⃗⃗⃗⃗⃗ ²−λAD ⃗⃗⃗⃗⃗⃗ ⋅AB ⃗⃗⃗⃗⃗ −λAD ⃗⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ =6λ+4−6+12λ+6λ−12λ =12λ−2， 因为λ∈[0,1]，所以MB ⃗⃗⃗⃗⃗⃗ ⋅MC ⃗⃗⃗⃗⃗⃗ =12λ−2∈[−2,10]， 故选：BC ．作图，利用向量三角形法则、平面向量数量积性质等用含λ的式子表示出MB ⃗⃗⃗⃗⃗⃗ ⋅MC ⃗⃗⃗⃗⃗⃗ =12λ−2，然后根据λ取值范围即可得到答案．本题考查平面向量数量积法则的应用，考查数形结合思想、转化思想，属于基础题．12.【答案】BC【解析】解：△ABC 中，角A ，B ，C 对边分别为a ，b ，c ，设向量m ⃗⃗⃗ =(c,a +b),n ⃗ =(a,c)，且m⃗⃗⃗ //n ⃗ ， 所以可得：c 2=a(a +b)=a 2+ab ， 而c 2=a 2+b 2−2abcosC ， 所以可得：ab =b 2−2abcosC ， 可得a =b −2a ⋅cosC ，由正弦定理可得：sinA =sinB −2sinAcosC =sin(A +C)−2sinAcosC =sinAcosC +cosAsinC −2sinAcosC =sin(C −A)， 所以可得A =C −A 或A +C −A =π，可得C =2A 或C =π(舍)所以B 正确，A 不正确． C =2A <π，所以A <π2所以B=π−A−C=π−3A，可得π−3A>0，所以A<π3，可得0<A<π3由正弦定理可得ca =sinCsinA=sin2AsinA=2sinAcosAsinA=2cosA∈(1,2)，所以C正确；S△ABC=12absinC=c24，由正弦定理可得12sinAsinBsinC=14sin2C，所以sinAsinB=12sinC，即sinAsin3A=12sin2A，整理可得：sin3A=cosA，所以3A=π2±A，可得A=π4或π8，进而可得C=π2或π4，所以D不正确；故选：BC．由向量的关系可得a，c的关系，再由余弦定理可得A，C的关系，进而求出B与A的关系，再由三角形的内角和可得A的范围，由正弦定理可得ca=2cosA，由A的范围求出ca的范围，由面积公式及面积的值可得A角，进而求出C的值，可判断命题的真假．本题考查三角形的正余弦定理的应用，向量的运算，属于中档题．13.【答案】53【解析】解：∵向量a⃗=(1,3),b⃗ =(3,4)，(λa⃗−b⃗ )⊥b⃗ ，∴(λa⃗−b⃗ )⋅b⃗ =λa⃗⋅b⃗ −b⃗ 2=λ(3+12)−25=15λ−25=0，则λ=53，故答案为：53．由题意利用两个向量垂直的性质，两个向量的数量积公式，计算求得λ的值．本题主要考查两个向量垂直的性质，两个向量的数量积公式，属于基础题．14.【答案】4【解析】解：因为数据x i(i=1,2，…，n)的平均数为x−=1.6，方差为1n ∑(ni=1x i−x−)2=1n∑(ni=1x i2−nx−2)=1n∑x i2ni=1−x−2=1.44，所以1n ∑x i 2n i=1=1.44+1.62=4．故答案为：4．根据平均数和方差的计算公式，计算即可．本题考查了平均数和方差的计算公式应用问题，是基础题．15.【答案】6【解析】解：取AB 的中点O ；连接CO ； 则CO ⊥AB ；∵在圆C 中弦AB 的长度为2√3，∴AB ⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ ==(AO ⃗⃗⃗⃗⃗ +OC ⃗⃗⃗⃗⃗ )⋅AB ⃗⃗⃗⃗⃗ =AO ⃗⃗⃗⃗⃗ ⋅AB ⃗⃗⃗⃗⃗ +OC ⃗⃗⃗⃗⃗ ⋅AB ⃗⃗⃗⃗⃗ =12AB ⃗⃗⃗⃗⃗ 2=12×2√3×2√3=6； 故答案为：6．取AB 的中点O ；连接CO ；则CO ⊥AB ；利用向量的三角形法则即可求出结论． 本题考查向量的数量积的应用，考查向量的表示以及计算，考查计算能力，是基础题．16.【答案】3√2 20π【解析】解：三棱锥P −ABC ，PB =PC =AB =BC =AC =2√3， 如图所示：侧面PBC ⊥底面ABC ，则PF =√(2√3)2−(√3)2=3，同理AF =√(2√3)2−(√3)2=3， 所以PA =√32+32=3√2， 根据勾股定理的应用： DF =EF =13×3=1，所以DC =2，所以OC =√22+12=√5， 所以S 球=4⋅π⋅(√5)2=20π． 故答案为：3√2；20π．首先利用勾股定理的应用求出PA 的长，进一步利用勾股定理的应用求出外接球的半径和球的表面积．本题考查的知识要点：三棱锥体和球体的关系，球的表面积公式的应用，主要考查学生的运算能力和数学思维能力，属于基础题．17.【答案】解：(1)∵z =a +(a −1)i(a ∈R)，∴z −=a −(a −1)i(a ∈R)， ∴z ⋅z −=(a −1)2+a 2=5，∴a 2−a −2=0，解得a =2或a =−1．(2)∵|z|=√(a −1)2+a 2=√2a 2−2a +1=√2(a −12)2+12 ∴a =12时，|z|的最小值为√22．【解析】(1)根据共轭复数的概念，可得z −=a −(a −1)i(a ∈R)，再结合复数代数形式的乘法运算，即可求解．(2)根据已知条件，结合复数模的公式，即可求解．本题考查了复数代数形式的乘法运算，以及复数模的公式，需要学生熟练掌握公式，属于基础题．18.【答案】解：(1)证明：由圆锥的性质可知，SO ⊥底面圆O∵BC 在底面圆O 上，∴BC ⊥SO ， ∵C 在圆O 上，AB 为直径，∴AC ⊥BC ， 又点O ，D 分别为AB ，BC 的中点，∴OD//AC ，∴OD ⊥BC ，又OD ∩SO =O ，且OD ，SO ⊂平面SOD ，∴BC ⊥平面SOD ，又BC ⊂平面SBC ，∴平面SOD ⊥平面SBC ．(2)∵BC=4，AC=2，∴AB=√AC2+BC2=√42+22=2√5，∴底面周长为2√5π，∴S侧=12×SA×2√5π=3√5π，∴SA=3，∴SO=√SA2−AO2=2，∴V圆锥=13×5π×SO=10π3．【解析】(1)推导出SO⊥底面圆O，BC⊥SO，AC⊥BC，OD//AC，OD⊥BC，从而BC⊥平面SOD，由此能证明平面SOD⊥平面SBC．(2)求出底面周长为2√5π，S侧=3√5π，从而SA=3，SO=√SA2−AO2=2，由此能求出该圆锥的体积．本题考查面面垂直的证明，考查该圆锥体积的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力、推理论证能力，是中档题．19.【答案】解：(1)因为频率分布直方图中，高的比就是频率的比，所以各区间上的频率可依次设为2x，3x，5x，6x，3x，x，则2x+3x+5x+6x+3x+x=1，解得x=120，所以各区间上的频率从左往右依次为：0.1，0.15，0.25，0.3，0.15，0.05，所以平均数为：85×0.1+95×0.15+105×0.25+115×0.3+125×0.15+135×0.05=109，假设第65百分位数为y，则0.1+0.15+0.25+(y−110)×0.03=0.65，解得y=115；所以所求平均数为109，第65百分位数为115．(2)由(1)可知数学成绩在[80,90)共有40×0.1=4人，分别记为a，b，c，d，数学成绩在[130,140]共有40×0.05=2人，分别记为A，B，从这6人中随机抽出两位同学的样本空间Ω={AB,Aa，Ab，Ac，Ad，Ba，Bb，Bc，Bd，ab，ac，ad，bc，bd，cd}，n(Ω)=15，记事件M表示“至少有一位同学的数学成绩在[130,140]”，n(M)=9，所以至少有一位同学的数学成绩[130,140]的概率为P(M)=915=35．【解析】(1)因为频率分布直方图中高的比就是频率的比，从而求各区间的频率，再求平均数与第65百分位数，(2)可知数学成绩在[80,90)共有4人，在[130,140]共有2人，利用列举法及古典概率模型公式求概率．本题考查了频率分布直方图的应用及古典概率模型的应用，属于基础题．20.【答案】解：若选①，由正弦定理，得√3(sinA−sinBcosC)=sinCsinB．由sinA=sin(B+C)=sinBcosC+cosBsinC，得√3cosBsinC=sinCsinB，由0<C<π，得sinC≠0，所以√3cosB=sinB，所以tanB=√3．又0<B<π，得B=π3．若选②，因为√3acos A+C2=bsinA，由正弦定理得√3sinAcos A+C2=sinBsinA，因为0<A<π，sinA≠0，所以√3cos A+C2=sinB，又因为A+B+C=π，所以A+C2=π2−B2，所以cos A+C2=cos(π2−B2)=sin B2，所以√3sin B2=2sin B2cos B2，又因为B2∈(0,π2)，sin B2≠0，所以cos B2=√32，所以B=π3，因为S△ABD+S△CBD=S△ABC，所以12×2×c×sinπ6+12×2×a×sinπ6=12×a×c×sinπ3，化简得a+c=√32ac①，由余弦定理得b2=a2+c2−2accosB，所以9=a2+c2−ac，所以(a+c)2=3ac+9②，联立①②化简得a2c2−4ac−12=0，所以(ac−6)(ac+2)=0，解得ac=6或ac=−2(舍去)，又因为S△ABC=12acsinB，所以S△ABC=12×6×√32=32√3．【解析】若选①，由正弦定理，两角和的正弦公式，同角三角函数基本关系式可求tan B 的值，结合0<B <π，可得B 的值；若选②，利用三角函数恒等变换的应用化简已知等式可得cos B2=√32，即可求解B 的值，由于S △ABD +S △CBD =S △ABC ，利用三角形的面积公式可得a +c =√32ac ，由余弦定理得(a +c)2=3ac +9②，联立得a 2c 2−4ac −12=0，解得ac 的值，根据三角形的面积公式即可求解．本题主要考查了正弦定理，三角函数恒等变换，三角形的面积公式，余弦定理在解三角形综合应用，考查了计算能力和转化思想，属于中档题．21.【答案】解：(1)根据题意，设M 表示事件“每轮甲、乙同时猜错”；N 表示事件“恰有一人猜错”，则P(N)=(1−p)q +p(1−q)=512， P(M)=(1−p)(1−q)=112，解可得：p =23，q =34或p =34，q =23； (2)根据题意，若p >q ，则p =34，q =23，设A i 表示事件“甲在两轮中猜对i 个成语”，B i 表示事件“乙在两轮中猜对i 个成语”，(i =0、1、2)，E 表示“星队”在两轮活动中猜对2个成语， 由于两轮猜的结果相互独立，所以P(E)=P(A 0B 2)+P(A 1B 1)+P(A 2B 0)=14×14×23×23+2×14×34×2×13×23+34×34×13×13=4144+24144+9144=37144； 故“星队”在两轮活动中猜对2个成语的概率为37144．【解析】(1)设M 表示事件“每轮甲、乙同时猜错”；N 表示事件“恰有一人猜错”，分析可得关于p 、q 的方程组，解可得p 、q 的值，即可得答案；(2)根据题意，设A i 表示事件“甲在两轮中猜对i 个成语”，B i 表示事件“乙在两轮中猜对i 个成语”，(i =0、1、2)，E 表示“星队”在两轮活动中猜对2个成语，分析可得P(E)=P(A 0B 2)+P(A 1B 1)+P(A 2B 0)，由相互独立事件的概率公式计算的可得答案． 本题考查相互独立事件的概率计算，涉及互斥事件概率的加法公式，属于基础题．22.【答案】解：(1)证法一：过点E作EF//BD交BC于点F，取A1B的中点G，∵△ABC是等边三角形，AD=CE，∴EF//BD，EF=12BD，又∵M、G分别为A1D和A1B的中点，∴MG为△A1BD的中位线，∴MG//BD，MG=12BD，∴EF//MG，EF=12MG，∴四边形EFGM为平行四边形，∴EM//FG，又∵FG⊂面A1BC，EM⊄面A1BC，∴EM//平面A1BC，证法二：取点F为BD中点，连EF，则EC=BF，因此EF//BC，又∵BC⊂平面A1BC，EF⊄平面A1BC，∴EF//平面A1BC，连MF，∵点M为A1D中点，∴MF//A1B，又∵A1B⊂平面A1BC，MF⊄平面A1BC，∴MF//平面A1BC，又MF∩EF=F，∴平面MFE//平面A1BC，∵EM⊂平面MPE，∴EM//平面A1BC(2)设AB=3，则AD=1，AE=2，∵∠A=60°，∴在△ADE中，由余弦定理，得DE=√AD2+AE2−2AD⋅AE⋅cosA=√3，∵22=12+(√3)2，∴AE2=AD2+DE2，∴∠ADE=90°，∴DE⊥AD，DE⊥BD，∴DE⊥BD，DE⊥A1D，又∵A1D⊂面A1DE，BD⊂面BDE，∴∠A1DB为二面角A1−DE−B的平面角，∴∠A1DB=2π3设A1在面BDEC内的投影为P，则P在BD的延长线上，∴A1P⊥BD，∵∠A1DB=2π3，∴∠A1DP=π3，在△A1DP中，A1D=AD=1，由正弦定理，得DP=12，A1P=√32，连接CP，且BP=52，在△BCP中，由余弦定理，得CP=√BP2+BC2−BP⋅BC⋅ cosB=√312，在Rt △A 1PC 中，A 1C =√A 1P 2+CP 2=√342，∴在△A 1CE 中，cos∠A 1EC =4+1−3444=−78，∴sin∠A 1EC =√158，∴S △A 1CE =12×2×1×√158=√158， 设DE 与平面A 1CE 所成角为θ，点D 到平面A 1CE 的距离为d ， 由V D−A 1CE =V A 1−DCE ，∴13×S △A 1CE ×d =13×S △DCE ×A 1P ， 又∵S △DCE =12×√3×1×sin5π6=√34，∴d =√15，∴sinθ=d DE=√55， ∴直线DE 与平面A 1CE 所成角的正弦值为√55．【解析】(1)证法一：过点E 作EF//BD 交BC 于点F ，取A 1B 的中点G ，利用线面平行判定定理证明，证法二：取点F 为BD 中点，连EF ，先证明面面平行，再证明线面平行；(2)设AB =3，在△ADE 中求出DE ，可判断∠A 1DB 为二面角A 1−DE −B 的平面角，再结合条件，利用等体积法求解即可．本题考查了线面平行的判定定理和性质，直线与平面所成的角，同时考查了空间想象力，属于中档题．。

福建省龙岩市一级达标校2020-2021学年高一语文下学期期末质检试题(考试时间：150分钟满分：150分)注意：请将试题的全部答案填写在答题卡上。

一、现代文阅读(24分)(一)论述类文本阅读(本题共3小题，9分)阅读下面的文字，完成1～3题。

①“网红”一词的兴起似乎是近些年的事情。

《咬文嚼字》2015年年度十大流行语排名中，“网红”入榜。

次年，网红社会关注度、产业化程度集中爆发。

而实际上，网红发展沿革几乎与中国互联网发展同步。

②上世纪90年代末，一批网络作家及各大贴吧、论坛的知名吧主、版主可以称作中国第一代网红。

在网速较慢，智能手机、轻便摄录设备还未普及的年代，网红们主要依靠文字聚拢大批粉丝。

2004年前后，第二代网红崭露头角，他们在互联网上通过图像、照片等更加直观的形式展示自我、分享生活、表达态度，积极与网友互动。

这一代网红恰逢中国互联网由“搜索”阶段向社交化阶段发展的关键时期。

与初代网红相比，他们更接近普通人，也更多依靠独特个性赢得大众关注。

2015年以来，随着互联网尤其是移动互联网发展，人们能够随时随地享受高速网络，轻松便捷分享高清影像，视频网站、直播平台也日益蓬勃。

第三代网红赶上短视频内容创作风口，各具风格的视频作品走入人们视野，内容更加专业和精致。

③成为网红，看起来容易，其实需要辛苦耕耘。

在互联网早期，一些人以噱头博取眼球成为网红，虽短时间内为众人瞩目，但因未能持续提供内容而迅速淡出公众视野。

事实证明，网红要“长红”，必须有鲜明突出的自身定位、个人特色以及强大的内容输出能力，才能获得稳定、持续的粉丝吸引力，形成自身品牌。

④网红本质上是互联网社交的产物，是个人与互联网用户共同参与、相互选择的结果。

网红知名度和影响力归根结底是广大互联网用户赋予的。

带有鲜明互联网属性的网红，容纳更广泛的大众趣味，也更直观地反映时代风尚。

出于互联网用户的主动选择，网红与其追随者之间具有很强的黏性，这种黏性往往形成特定的网络社群，转化为粉丝经济的消费主体。

福建省龙岩市一级达标校2020-2021学年高一生物下学期期末质检试题(考试时间：90分钟满分：100分)注意：请将试题的全部答案填写在答题卡上一、选择题(本大题共35小题。

1－20题每小题1分；21－35题每小题2分，共50分。

每小题列出的四个选项中，只有一项是最符合题目要求的。

)1.下列性状中，属于相对性状的是A.番茄的圆果与黄果B.狗的卷毛与白毛C.豌豆的高茎与矮茎D.兔的长毛与狗的短毛2.光反应和暗反应是光合作用过程的不同阶段，下列叙述正确的是A.光反应必须在光照条件下进行B.暗反应必须在黑暗条件下进行C.二氧化碳的固定在光反应中进行D.影响光反应的环境因素不会影响暗反应3.科学家用含有14C的二氧化碳来追踪光合作用中的碳原子，这种碳原子的转移途径是A.二氧化碳→ADP→NADPHB.二氧化碳→NADPH-→ATPC.二氧化碳→糖类→五碳化合物D.二氧化碳→三碳化合物→糖类4.一个胃癌患者发现肺部也出现了癌细胞，原因可能是A.癌细胞能够无限增殖B.癌细胞形态结构发生变化C.癌细胞表面糖蛋白减少容易分散和转移D.癌细胞选择性表达了原癌基因和抑癌基因5.离体的叶绿体在光照下进行稳定光合作用时，如果突然撤去光照，短暂时间内叶绿体中物质相对含量的变化是A.ATP增多，NADPH减少B.ATP减少，NADPH增多C.C3化合物减少，C5化合物增多D.C3化合物增多，C5化合物减少6.右图是光合作用探索历程中恩格尔曼的实验示意图，有关叙述正确的是A.用水绵做实验材料是因为其叶绿体呈球形便于观察B.实验前需“黑暗”处理，以消耗细胞中原有淀粉C.实验通过观察好氧细菌的分布来确定氧气产生的位置D.实验证明叶绿体主要吸收红光和蓝紫光7.下列关于抗维生素D佝偻病的叙述，错误的是A.女性患者中部分患者病症较轻B.男性患者的女儿都是患者C.表现正常的夫妇也可能携带致病基因D.人群中女性患者的数量多于男性患者8.右图中4、6、7号为色盲患者，7号个体的色盲基因来源于A.1号B.2号C.4号D.3号9.下列一定属于同源染色体的是A.分别来自父方和母方的两条染色体B.形状和大小都相同的两条染色体C.着丝点分裂后形成的两条染色体D.减数分裂中配对的两条染色体10.正常情况下果蝇体内等位基因不可能存在于A.精细胞B.四分体C.同源染色体D.次级卵母细胞11.假如有15个初级卵母细胞和5个初级精母细胞，都能正常发育产生配子并受精，则最多能形成的受精卵数目是A.60B.20C.15D.512.一对夫妇表现型正常，却生了一个白化病女儿。

2020-2021学年福建省龙岩市高一（下）期末语文试卷一、单选题（本大题共6小题，共12.0分）1.下列选项中字音字形全都正确的一项是（）A. 切中肯綮．（qìng）瞋．（chēn）目商贾．（gǔ）汗涔涔．（cén）B. 抢．（qiǎng）呼欲绝庖．（páo）厨孝悌．（dì）庇．（bì）佑C. 豁．（huò）然开朗悚．（sǒng）然踌著．（chú）迂讷．（nà）D. 纷繁无．（wú）杂搠．（shuò）倒青蒿．（gāo）素撮．（cuò）合2.下列句子中加点的字不全是通假字的一项是（）A. 鼓瑟希．，铿尔盖．亦反其本矣B. 向使四君却客而不内．手裁．举C. 旦日不可不蚤．自来谢项王微．夫人之力不及此D. 不宜卤．莽暴．霜露，斩荆棘3.下列各句中加点的词解释不正确的一项是（）A. 道芷阳间．行间：从小路B. 善．刀而藏之善：措拭C. 骊山北．构而西折北：向北D. 当以乐．牺牲吾身乐：快乐4.下列各句中加点词的意义和用法相同的一项是（）A. 后人哀之而．不鉴之源不深而．岂望流之远B. 如其．礼乐，以俟君子吾其．还也C. 臣之．壮也，犹不如人未之．有也D. 斯亦伐根以．求木茂五亩之宅，树之以．桑5.下列各选项句式分类正确的一项是（）A. ①③⑨/②⑧/④⑤⑩/⑥⑫/⑦⑪B. ①③⑪②④⑧/⑤⑨/⑥⑫/⑦⑩C. ①⑫/②④/③⑪/⑤⑨/⑥⑦/⑧⑩D. ①③⑪/②④/⑤⑨/⑥⑦⑫/⑧⑩6.下列各项中对《红楼梦》作品故事情节的表述，正确的一项是（）A. 甄士隐的女儿英莲在元宵看社火灯花时走失。

三月十五葫芦庙着火把隔壁的甄家烧成一片瓦砾。

甄家从此渐渐走向破败。

疯跛道人吟唱了《好了歌》，甄士隐听后便彻悟，并为《好了歌》作解注。

B. “听了宝玉这番话，心中虽然有万句言语，只是不能说得，半日，方抽抽噎噎的说道：‘你从此可都改了罢!’”这是宝玉挨打后，被抬回怡红院后，恍惚听到悲泣之声，看是宝钗，又心疼她暑天跑来看他。

龙岩市一级达标校2021-2021～2021学年第二学期期末高一教学质量检查语文试题参考答案一、现代文阅读〔一〕论述类文本阅读1．〔3分〕C 〔A项以偏概全，“与中国互联网开展同步〞错，原文为“几乎与中国互联网开展同步〞。

B项张冠李戴，“互联网〞错，原文为“恰逢中国互联网……〞；“第二代网红的社会关注度暴增〞错，原文为“?咬文嚼字?2021年年度十大流行语排名中……次年，网红社会关注度、产业化程度集中爆发〞，而非“第二代网红〞时期。

D项指代有误，“网红群体……助推了互联网文化开展，营造了健康社会风气〞错，原文为“多一些这样的网红群体〞，即“具备丰富的知识、出众的才华……〞的网红群体。

〕2．〔3分〕A 〔A项无中生有。

“阐释了‘网红’的概念〞错，文章首段并没有对“网红〞的概念进行阐释。

〕3．〔3分〕B 〔B项不合逻辑。

“只要……就……〞错，原文为“网红要‘长红’，必须有鲜明突出的自身定位……才能获得稳定、持续的粉丝吸引力……〞〕〔二〕文学类文本阅读4．〔3分〕D 〔D项主要原因是老秤匠在发现儿子制作“吃客秤〞一事后，决定让儿子出去闯一闯，让他领悟“人有良心、秤有准星〞的道理。

〕5．〔6分〕①老秤匠与小秤匠的比照。

在制作“吃客秤〞一事上，老秤匠与小秤匠的态度截然不同，突出老秤匠的诚信。

②老秤匠与王老板的比照。

王老板企图利用孙记良好的声誉来谋取不义之财，老秤匠发现儿子捣鼓的“猫腻〞后，将一百五十杆杆秤劈断，突出老秤匠恪守传统道德，坚持为人处世的底线。

③老秤匠制秤与砸秤的态度比照。

制秤时非常细心重视，但砸秤时毫不吝惜，突出了老秤匠坚持原那么、珍视信誉的形象。

6．〔6分〕小说最后两段不能删去。

①这两段是补叙，补充交代了夜里秤匠父子对砸秤事件的反思和所做出的行动，使故事情节更完整。

②尾秤杆上的金字“炫得儿子的双眼泪盈盈的〞与开头“炫得老孙头的眼也发出熠熠的亮光〞，首尾照应。

③写出老秤匠用心良苦、理解孩子，也展示了小秤匠知错能改，使人物形象更加真实、饱满。