北航解析几何课件总复习

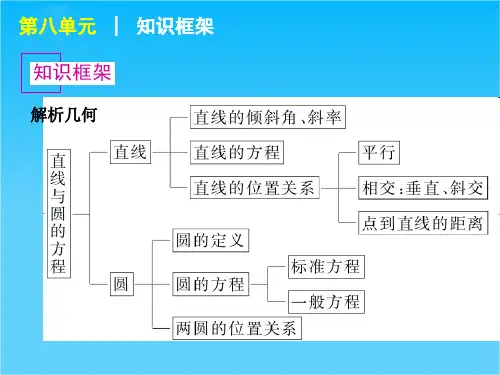
《解析几何》知识点复习1解析几何是数学中一个非常重要的分支，它将代数与几何巧妙地结合在一起，通过建立坐标系，用代数方法来研究几何图形的性质和相互关系。

接下来，让我们一起对解析几何的一些关键知识点进行复习。

一、坐标系坐标系是解析几何的基础，最常见的是直角坐标系（也称为笛卡尔坐标系）。

在直角坐标系中，我们通过两条互相垂直的数轴，即 x 轴和 y 轴，来确定平面上点的位置。

一个点的坐标就是它在 x 轴和 y 轴上的投影所对应的数值，通常表示为（x, y)。

此外，还有极坐标系。

在极坐标系中，一个点的位置由极径和极角来确定。

极径是该点到极点的距离，极角是极轴（通常为 x 轴的正半轴）到该点的连线与极轴所成的角。

二、直线1、直线的方程点斜式：若已知直线上一点（x₁, y₁) 以及直线的斜率 k，则直线方程为 y y₁＝ k(x x₁)。

斜截式：若直线的斜率为 k，且在 y 轴上的截距为 b，则直线方程为 y ＝ kx ＋ b。

两点式：若已知直线上两点（x₁, y₁) 和（x₂, y₂)，则直线方程为（y y₁)／（y₂ y₁) ＝（x x₁)／（x₂ x₁)。

一般式：Ax ＋ By ＋ C ＝ 0 （A、B 不同时为 0）。

2、直线的位置关系平行：两条直线斜率相等。

垂直：两条直线斜率之积为－1。

3、距离公式点到直线的距离：d ＝｜Ax₁＋ By₁＋ C| ／√（A²＋ B²) ，其中（x₁, y₁) 是点的坐标，Ax ＋ By ＋ C ＝ 0 是直线方程。

三、圆1、圆的方程标准方程：（x a)²＋（y b)²＝ r²，其中（a, b) 是圆心坐标，r 是半径。

一般方程：x²＋ y²＋ Dx ＋ Ey ＋ F ＝ 0 （D²＋ E² 4F ＞ 0），圆心坐标为（D/2, E/2) ，半径为√（D²＋ E² 4F) ／ 2 。

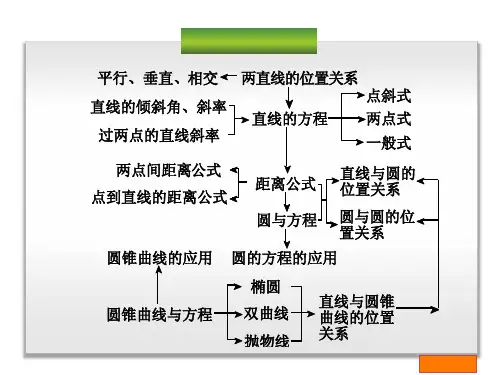
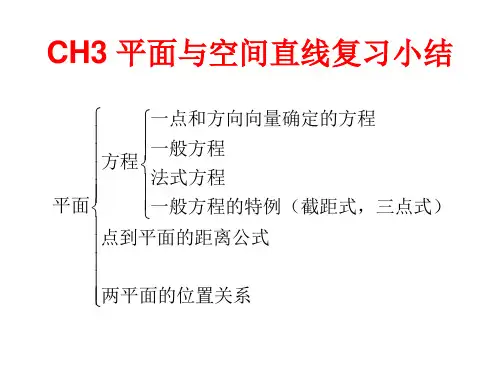
第1页 共4页第八章 解析几何复习讲义第一部分 圆锥曲线圆锥曲线的统一定义：平面内到定点F 和定直线l 的距离之比为常数e 的点的轨迹.①当10<<e 时，轨迹为椭圆； ②当1=e 时，轨迹为抛物线；③当1>e 时，轨迹为双曲线； 一、椭圆1. 椭圆方程的第一定义：212121212121212,2,2F F F F a PF PF F F a PF PF F F a PF PF 线段无轨迹椭圆==+<=+>=+ 2.椭圆方程.①椭圆的标准方程：i. 焦点在x 轴上：)0(12222>>=+b a b y a x . ii. 焦点在y 轴上：)0(12222>>=+b a bx a y .②一般方程：)0,0(122>>=+B A By Ax .3.性质：①顶点：②对称轴:③焦点：④焦距：⑤准线：⑥离心率:⑦焦半径：i. 设),(00y x P 为椭圆)0(12222>>=+b a by a x 上的一点，21,F F 为左、右焦点，则由椭圆方程的第二定义可以推出. ii.设),(00y x P 为椭圆)0(12222>>=+b a ay b x 上的一点，21,F F 为上、下焦点，则由椭圆方程的第二定义可以推出. ⑧通径：垂直于x 轴且过焦点的弦叫做通径. a b d 22=；坐标：，),(2ab c -和),(2a b c4.直线与椭圆位置关系----------抓住代数与几何图形的紧密联系将直线方程与椭圆方程联立的方程组解的个数即为交点个数。

故用判别式法判别①相交等价于0>∆（2个交点）②相切等价于0=∆（1个交点）③相离等价于0<∆（无交点）例、已知直线1+-=x y 与椭圆22221(0)x ya b a b+=>>相交于A 、B 两点，且线段AB 的中点在直线02:=-y x l 上，则此椭圆的离心率为22例、椭圆284722=+y x 上的点到直线01623=--y x 的最短距离为13138 5.共离心率的椭圆系的方程：椭圆)0(12222>>=+b a by a x 的离心率是a c e =)(22b a c -=，方程t t b y a x (2222=+是大于0的参数，)0>>b a 的离心率也是ace = 我们称此方程为共离心率的椭圆系方程.6.共焦点的椭圆系的方程：)0(12222>>=+++b a k b y k a x 或)0(12222>>=+++b a kb x k a y 二、双曲线1. 双曲线的第一定义：201,ex a PF ex a PF -=+=0201,ey a PF ey a PF -=+=第2页 共4页▲yxF 1F 21234533的一个端点的一条射线以无轨迹方程为双曲线21212121212121,222F F F F a PF PF F F a PF PF F F a PF PF ==->=-<=-2. 双曲线方程⑴双曲线标准方程：①焦点在x 轴上：)0,(12222>=-b a by a x .②焦点在y 轴上)0,(12222>=-b a b x a y⑵一般方程： )0(122<=+AC Cy Ax .3.性质① )0,(12222>=-b a by a x 顶点： 焦点： 准线方程 渐近线方程：②对称轴 ③离心率 ④准线距c a 22；通径a b 22. ⑤参数关系a ce b a c =+=,222.⑥焦半径公式：对于双曲线方程12222=-by a x （21,F F 分别为双曲线的左、右焦点或分别为双曲线的上下焦点） “长加短减”原则： a ex MF a ex MF -=+=0201 构成满足a MF MF 221=- a ex F M aex F M +-='--='0201（与椭圆焦半径不同，椭圆焦半径要带符号计算，而双曲线不带符号）aey MF a ey MF +=-=0201 ,aey F M a ey F M -'-='+'-='02014.等轴双曲线：双曲线222a y x ±=-称为等轴双曲线，其渐近线方程为x y ±=，离心率2=e .5.共轭双曲线：以已知双曲线的虚轴为实轴，实轴为虚轴的双曲线，叫做已知双曲线的共轭双曲线.λ=-2222b y a x 与λ-=-2222b y a x 互为共轭双曲线，它们具有共同的渐近线：02222=-b y a x .6.共渐近线的双曲线系方程：)0(2222≠=-λλby ax 的渐近线方程为02222=-by ax ;如果双曲线的渐近线为0=±b ya x 时，它的双曲线方程可设为)0(2222≠=-λλb y a x .7. 共焦点的双曲线系方程12222=--+k b y k a x 或 12222=--+kb x k a y 8.过定点的直线与双曲线的位置关系：抓住代数与几何图形的紧密联系；抓直线与渐近线的位置关系 区域①：无切线，2条与渐近线平行的直线，合计2条；区域②：即定点在双曲线上，1条切线，2条与渐近线平行的直线，合计3条； 区域③：2条切线，2条与渐近线平行的直线，合计4条；区域④：即定点在渐近线上且非原点，1条切线，1条与渐近线平行的直线，合计2条； 区域⑤：即过原点，无切线，无与渐近线平行的直线.相交等价于0>∆或直线与渐近线平行（1个或2个交点）▲y xM'MF 1F 2▲yxM'MF 1F 2第3页 共4页相切等价于0=∆（一个交点） 相离等价于0<∆（无交点）⑴过定点作直线与双曲线有且仅有一个交点，可以作出的直线数目可能有0、2、3、4条. 2）若直线与双曲线交点为2个时，可用韦达定理来判断两交点的分布情况例 直线1+=kx y 与双曲线1322=-y x 相交于A 、B 两点，当a 为何值时，A 、B 在双曲线的同一支上？当a 为何值时，A 、B 分别在双曲线的两支上？当36-<<-a 或63<<a 时，A 、B 两点在同一支上； 当33<<-a 时，A 、B 两点在双曲线的两支上三、抛物线px y 22=px y 22-=py x 22=py x 22-=图形▲yxO▲yxO▲y xO▲yxO焦点 )0,2(pF )0,2(pF -)2,0(p F )2,0(p F -准线 2p x -=2p x =2p y -=2p y =范围 R y x ∈≥,0 R y x ∈≤,0 0,≥∈y R x 0,≤∈y R x 对称轴 x 轴y 轴顶点 （0，0） 离心率 1=e焦半径 12x pPF +=12x p PF += 12y p PF +=12y pPF +=焦点弦)(21x x p AB ++=)(21x x p AB +-=)(21y y p AB ++=)(21y y p AB +-=通径：过焦点且垂直于对称轴的相交弦 通径：p d 2=2.抛物线)0(22>=p px y 的参数方程：⎩⎨⎧==222pt y pt x （t 为参数）3.直线与抛物线的位置关系相交等价于0>∆或直线与对称轴平行（1个或2个交点）相切等价于0=∆（一个交点） 相离等价于0<∆（无交点）4.过抛物线px y 22=（0>p ）焦点的直线AB ，设),(11y x A ，),(22y x B ，弦AB 所在直线的倾斜角为α，则有下列性质：①)(21x x p AB ++=；α2sin 2pAB =②4221p x x =，221p y y -= ③以AB 为直径的圆与准线相切第4页 共4页④F 对A 、B 在准线上的射影点所形成的张角为2π ⑤pBF FA 211=+ 几种常见的题型及解法①定义及标准方程问题（先定型再定式后定量） ②中点弦问题（点差法）③最值问题（距离或角的最值）⎩⎨⎧数形结合思想配方法：（利用定义）.2.1从代数、三角、几何三种途径寻求解决④离心率问题 ⑤弦长问题、焦半径问题 ⑥渐近线的到角与夹角问题 ⑦最值、范围问题 数学思想方法及能力①数形结合思想②转化化归思想③分类讨论思想④分析与综合能力⑤良好的运算能力四、直线与圆锥曲线的位置关系一、几种常见的题型:①直线与圆锥曲线的位置关系判断：从几何角度可分为三类：无公共点，仅有一个公共点及有两个相异公共点。

高考数学总复习第六讲解析几何高考解析几何试题一样共有4题(2个选择题, 1个填空题, 1个解答题), 共计30分左右, 考查的知识点约为20个左右. 其命题一样紧扣课本, 突出重点, 全面考查. 选择题和填空题考查直线, 圆, 圆锥曲线, 参数方程和极坐标系中的基础知识. 解答题重点考查圆锥曲线中的重要知识点, 通过知识的重组与链接, 使知识形成网络, 着重考查直线与圆锥曲线的位置关系, 求解有时还要用到平几的差不多知识, 这点值得考生在复课时强化. 一、圆锥曲线的几类差不多习题 一. 弦的中点问题具有斜率的弦中点问题，一样设曲线上两点为(,)x y 11，(,)x y 22，代入方程，然后两方程相减，再应用中点关系及斜率公式，消去四个参数。

例1 给定双曲线x y 2221-=。

过A （2，1）的直线与双曲线交于两点P 1及P 2，求线段P 1P 2的中点P 的轨迹方程。

分析：设P x y 111(,)，P x y 222(,)代入方程得x y 121221-=，x y 222221-=。

两式相减得 ()()()()x x x x y y y y 12121212120+--+-=。

又设中点P （x,y ），将x x x 122+=，y y y 122+=代入，当x x 12≠时得 22201212x yy y x x ---=·。

又k y y x x y x =--=--121212，代入得24022x y x y --+=。

当弦P P 12斜率不存在时，其中点P （2，0）的坐标也满足上述方程。

因此所求轨迹方程是8174127122()()x y ---=。

例2 已知椭圆x y 22651+=，通过点（1，1）引一弦，使它在这点被平分，求此弦所在的直线方程。

略解：有()()()()x x x x y y y y 12121212650+-++-=，代入得13251212+--=()()y y x x 0，得k y y x x =--=-121256。