高数勘误汇总
- 格式:pdf
- 大小:94.44 KB
- 文档页数:5

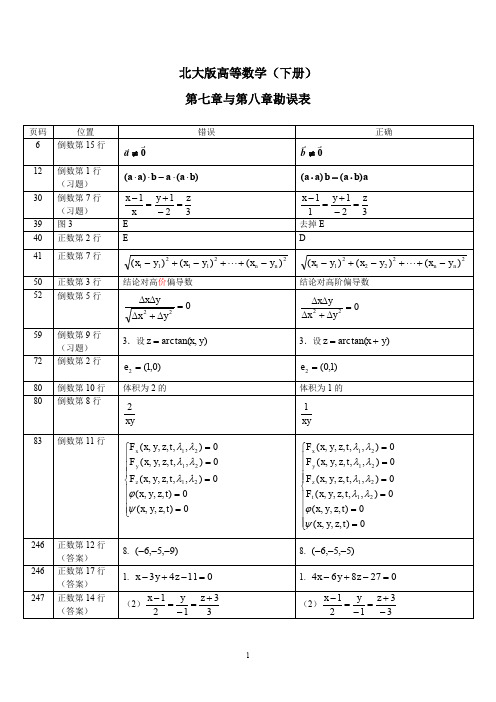


《线性代数与解析几何》勘误表第1章:行列式p.13,例题4.1:解的第二个等号后,应加一个负号。
p.15,第三行(等号后):去掉;p.17,第7-8 行: (t=1,2,…,j-1,j+1,…,n)p.19倒数第4-5行:假设对于n-1阶范德蒙行列式V_{n-1}结论成立,p. 20,第 2 行:D_{n-1}改为V_{n-1}p.20,第6行,定理5.2中:去掉“若”字p.21,倒数第3行:…展开代入而得,p.2 4倒数第1行:(-1)的指数应为“ 1+2 - k+1+2 ----- k ” 习题1:第1题(2)答案有误:应为sin2x-cosx A2.第6题(3)答案有误:(3)n(3n-1)/2,当n=4k或者n=4k+3时为偶数,当n=4k+1 或4k+2时为奇数.第10 题(4)(5)答案有误:(4)(-1)A{(n-2)(n-1)/2}; (5)(-1)A{ n-1}a_n第11题(6)答案有误:….,当a\neq 0时,D=(-1)A{n( n-1)/2}aA{n-2}国八2-(n-1)xA2]y1 +z1z1 +x1禺+ y1p.26,第12题(2):改为:y2 +z2z2 +x2X2 + y丫3 +Z3 Z3 +X3 X3 + y―-.(n -1)(n+2)…八n A.(3): •••= [a + —1) J2“-n(4):…二送a i b n_Li =ep.27,第14题(4):(此题较难,可以去掉!)答案有误,应为:D n = [(x 、x2-4yz)n 1_(x _ I x2_4yz)n勺]/2n 1x2-4yz,当 x2= 4yz ;D n =(n1)(|)n,当 x2=4yz。
第15题答案有误:为60(11- .2)p. 27,第16题:去掉条件“若x_1+x_2+x_3+x_4=1,则”第二章:矩阵p.32,第7 行: 称其为n阶对角矩阵,…..p.35,第5-6 b_21和b_12互换位置(两处)p.36,第7行:去掉“设A , B, C分别为….矩阵,”在第10行后增加:当然, 这里假定了矩阵运算是有意义的.p.39,第 4 行: 就得到一个2*2的分块矩阵。

高等数学下册勘误1.P7 B 组第2题,将“不共面”改为“不共线”。
2.P21 第2行,将“设方程”改为“设平面π的方程”。
3.P46 最后1行,将“点(,)P x x y y '+∆+∆”改为“点(,)P x y '∆∆”。
4.P63 第11行,将“函数(,)z x y =”改为“函数(,)z f x y =”。
5.P69 倒数第3行,将“324u xyz x∂==-∂”改为“324MMu xyzx∂==-∂”;将“234u x z y∂==-∂”改为“234MMu x zy∂==-∂”;将“22312u x yz z∂==∂”改为“22312MMu x yzz∂==∂”。
6.P69 倒数第2行,将“gradu ”改为“(2,1,1)gradu -”。
7.P71 第11行,将“22(,)8324046U x y xy x y x y =++--”改为 “(,)40(,)(104)P x y U x y x y =-+”。
8.P72 第7行,删去“,而0x x ≠”。
9.P73 第19行,将“达到最佳花费效果,”改为“的花费”。
10.P78 倒数第1,2, 4行,将“1ni =∑”改为“101i =∑”。
11.P90 第7行,将“定理1.3”改为“定理1.2”。
12.P122 第14行,将“DS =⎰⎰”改为DS =⎰⎰。
13.P137 第14,15行,将“13”改为“112”。
14.P142 第10行将“131cos (cos )3θθ--”改为“3cos (cos )3πθθ-”15.P145 习题8.2 B 组第1题,将“正向边界曲线”改为“边 界曲线(取逆时针方向)”。
16.P150 最后1行,将“()0LDDQ P Pdx Q dy dxdy dxdy xy∂∂+=-=∂∂⎰⎰⎰⎰⎰ ”改为“()0LDDQ P Pdx Q dy dxdy dxdyxy∂∂+=±-=±∂∂⎰⎰⎰⎰⎰ ”。
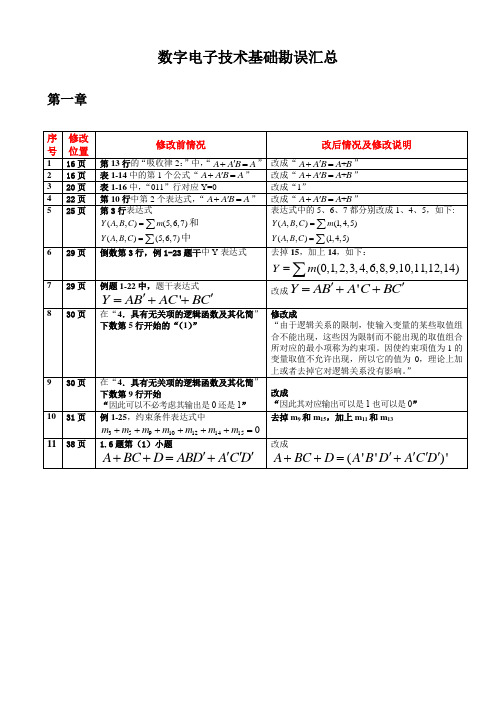
数字电子技术基础勘误汇总第一章I第1行中“T导通”将“T导通”改成“T截止”。
上下交换“I A<B”和“I A>B”文字的位置同上,上下交换“I A<B”和“I A>B”文字的位置(两个逻辑符号的都交换)交换“E1”和“E3”文字的位置表4-9中T=0的第2行,Q=1,Q*=0;如下:将前2行的R D’和S D’信号互换。
如下所示:D D图4-23中将K图表头上的“SR”改成“RS”,即交换一下顺序,其它不变。
图4-44中的最后一个小图,如下所示第五章)修改说明:在对应计数值4的的两个位置,在RD ’信号上画“窄的负脉冲”上的负脉冲向后延迟,即应先出现“状态5”,才能出现RD ’的负脉冲信号。
驱动方程22102111022000210FF : =, = FF : , () FF : (), 1J Q Q K Q J Q K Q Q J Q Q K ⎧⎪'''==⎨⎪'==⎩图5-51 CLK线上加上一个黑点,如下所示2、设计实例,第2段中“327687”修改为“32768”,即去掉最后一位的图5-56(a)修改说明:图5-56(a)中,在最下两图数字“1”,如同最上面两图的RD’端一样。
如图所示:的勘误如下(见红色部分,共12处):解:该电路为具有输入变量(A)的莫尔型同步时序逻辑电路,其中使用了两个下降沿触发的边沿JK触发器(编号为FF2、FF1),触发器的状态组合Q2Q1代表了时序电路的工作状态。
另外,整个电路有一个输出信号Y。
(1)首先根据电路连接情况列出各种方程(同步电路不必列时钟方程)。
①触发器驱动方程。
1112221FF : 1FF : J K J K A Q ==⎧⎨==⊕⎩ ② 触发器次态方程。
将上述驱动方程分别代入到JK 触发器的通用特性方程(*Q JQ K Q ''=+)中,整理后得到次态方程,即电路的状态方程。
高中高考数学易错易混易忘题分类汇总及解析“会而不对,对而不全”一直以来成为制约学生数学成绩提高的重要因素,成为学生挥之不去的痛,如何解决这个问题对决定学生的高考成败起着至关重要的作用。
本文结合笔者的多年高三教学经验精心挑选学生在考试中常见的66个易错、易混、易忘典型题目,这些问题也是高考中的热点和重点,做到力避偏、怪、难,进行精彩剖析并配以近几年的高考试题作为相应练习,一方面让你明确这样的问题在高考中确实存在,另一方面通过作针对性练习帮你识破命题者精心设计的陷阱,以达到授人以渔的目的,助你在高考中乘风破浪,实现自已的理想报负。
【易错点1】忽视空集是任何非空集合的子集导致思维不全面。
例1、 设{}2|8150A x x x =-+=,{}|10B x ax =-=,若A B B =,求实数a 组成的集合的子集有多少个?【易错点分析】此题由条件A B B =易知B A ⊆,由于空集是任何非空集合的子集,但在解题中极易忽略这种特殊情况而造成求解满足条件的a 值产生漏解现象。
解析:集合A 化简得{}3,5A =,由A B B =知B A ⊆故(Ⅰ)当B φ=时,即方程10ax -=无解,此时a=0符合已知条件(Ⅱ)当Bφ≠时,即方程10ax -=的解为3或5,代入得13a =或15。
综上满足条件的a 组成的集合为110,,35⎧⎫⎨⎬⎩⎭,故其子集共有328=个。
【知识点归类点拔】(1)在应用条件A ∪B =B⇔A ∩B =A⇔AB时,要树立起分类讨论的数学思想,将集合A是空集Φ的情况优先进行讨论.(2)在解答集合问题时,要注意集合的性质“确定性、无序性、互异性”特别是互异性对集合元素的限制。
有时需要进行检验求解的结果是满足集合中元素的这个性质,此外,解题过程中要注意集合语言(数学语言)和自然语言之间的转化如:(){}22,|4A x y x y =+=,()()(){}222,|34B x y x y r =-+-=,其中0r >,若A B φ=求r 的取值范围。
《高等数学(经管类)》(上)勘误表页码、行号错误内容正确内容 (说明)P2第13行 a ∈b ,但a ∉A , a ∈B ,但a ∉A , P2第16行 若A ⊆B ,且B ⊇A , 若A ⊆B ,且A ⊇B ,P3倒第1行 oU (x 0,δ), 即oU ( a , δ), 即P4第1行 oU ( x 0,δ)={x |0<|x - a |<δ}. oU ( a , δ)={x |0<|x - a |<δ}. P4第2行 o U ( a ,δ)=U (a ,δ)-{ a }.o U ( a ,δ)=U (a ,δ)\{ a }.P7第17行 库存量 库存费P10倒第12行 12x x -,12x x -<0,P13第8行 y = f (x ) 的图形上的点,y = f -1(x ) 的图形上的点,P20图1-22 图1-23原图中误将虚线为实线,正确如右图P21图1-24 图1-25原图中虚线与实线不准确,正确如右图P22倒第10行注: 由基本初等函数经过有限次四则运算后所成的函数称为简单函数,注:一般由常数和基本初等函数经过四则运算后所成的函数称为简单函数,P26第3行需求函数的反函数1()d f Q p -=需求函数的反函数1()d f Q P -=P29倒第2行 0<x <38.0<x <138.P29倒第5行 221146)((6100)39x x x x -=+-++ 221146)((6100)39x x x x =+++--P30倒第11行 6.已知某厂单位产品时 6.已知某厂生产一个单位产品时P31倒第9行 9.下列函数是由哪些基本初等函数复合而成的?9.下列函数是由哪些简单函数复合而成的? P32倒第6行 7.若)(x f 对其定义域上的一切, 7.若)(x f 对其定义域上的一切x , P36倒第11行 则∃N 1>0, 则∃正整数N 1, P36倒第8行 ∃N 2>0,∃正整数N 2,P37第3行 ∃N >0,当n >N 时, ∃正整数N ,当n >N 时, P37第9行 ∃N >0,当n >N ∃正整数N ,当n >N P37第11行 ∃N >0,当n >N 时, ∃正整数N ,当n >N 时, P37第13行 ∃N >0,当n >N 时,∃正整数N ,当n >N 时,2)(10)2)1)(0x x +-2)(10)2)1)(0x x -+,3(4ks ka k ⎧⎪⎨+⎪⎩,03(),4ks ka k s a ⎧⎪⎨+-⎪⎩。