(新课标)2020年高考数学一轮总复习 6_4推理与证明课时规范练(理)(含解析)新人教A版

第四节　推理与证明
教 材 回 顾 考 点 突 破
栏目导航
最新考纲考情考向分析
1.了解合情推理的含义，能进行简单的归纳推理和类比推理，体会并认识合情推理在数学发现中的作用．
2．了解演绎推理的含义，掌握演绎推理的“三段论”，并能运用“三段论”进行一些简单推理．
3．了解直接证明的两种基本方法——分析法和综合法；了解分析法和综合法的思考过程和特点．
4．了解反证法的思考过程和特点.1.以理解类比推理、归纳推理和演绎推理的推理方法为主，常以演绎推理的方法根据几个人的不同说法作出推理判断进行命题．注重培养学生的推理能力．2．直接证明的方法——综合法和分析法，间接证明的方法——反证法，常以立体几何中的证明和不等式的证明为载体加以考查，注重考查学生分析问题、解决问题的能力．在高考中主要以解答题的形式考查，难度中档.
部分
全部部分整体个别一般。

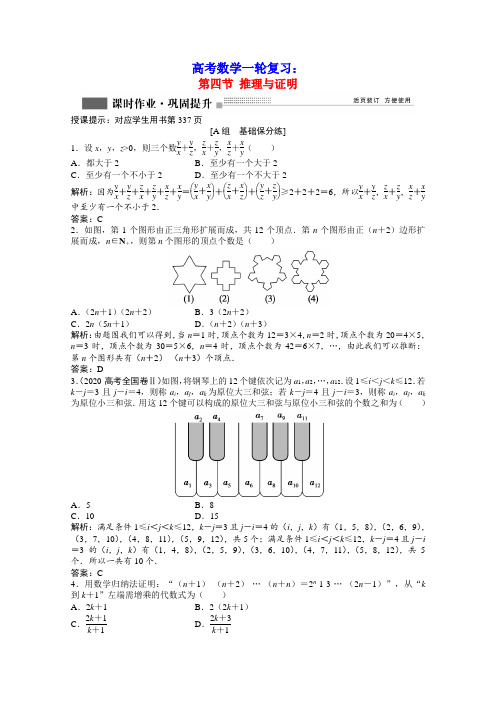
高考数学一轮复习：第四节 推理与证明授课提示：对应学生用书第337页[A 组 基础保分练]1．设x ，y ，z >0，则三个数y x ＋y z ，z x ＋z y ，x z ＋xy（ ）A ．都大于2B ．至少有一个大于2C ．至少有一个不小于2D ．至少有一个不大于2解析：因为y x ＋y z ＋z x ＋z y ＋x z ＋x y ＝⎝⎛⎭⎫y x ＋x y ＋⎝⎛⎭⎫z x ＋x z ＋⎝⎛⎭⎫y z ＋z y ≥2＋2＋2＝6，所以y x ＋y z ，z x ＋z y ，x z ＋xy中至少有一个不小于2． 答案：C2．如图，第1个图形由正三角形扩展而成，共12个顶点．第n 个图形由正（n ＋2）边形扩展而成，n ∈N ＋，则第n 个图形的顶点个数是（ ）A ．（2n ＋1）（2n ＋2）B ．3（2n ＋2）C ．2n （5n ＋1）D ．（n ＋2）（n ＋3） 解析：由题图我们可以得到，当n ＝1时，顶点个数为12＝3×4，n ＝2时，顶点个数为20＝4×5，n ＝3时，顶点个数为30＝5×6，n ＝4时，顶点个数为42＝6×7，…，由此我们可以推断：第n 个图形共有（n ＋2）·（n ＋3）个顶点． 答案：D 3．（2020·高考全国卷Ⅱ）如图，将钢琴上的12个键依次记为a 1，a 2，…，a 12．设1≤i ＜j ＜k ≤12．若k －j ＝3且j －i ＝4，则称a i ，a j ，a k 为原位大三和弦；若k －j ＝4且j －i ＝3，则称a i ，a j ，a k 为原位小三和弦．用这12个键可以构成的原位大三和弦与原位小三和弦的个数之和为（ ）A ．5B ．8C ．10D ．15解析：满足条件1≤i ＜j ＜k ≤12，k －j ＝3且j －i ＝4的（i ，j ，k ）有（1，5，8），（2，6，9），（3，7，10），（4，8，11），（5，9，12），共5个；满足条件1≤i ＜j ＜k ≤12，k －j ＝4且j －i ＝3的（i ，j ，k ）有（1，4，8），（2，5，9），（3，6，10），（4，7，11），（5，8，12），共5个．所以一共有10个． 答案：C4．用数学归纳法证明：“（n ＋1）·（n ＋2）·…·（n ＋n ）＝2n ·1·3·…·（2n －1）”，从“k 到k ＋1”左端需增乘的代数式为（ ） A ．2k ＋1 B ．2（2k ＋1）C ．2k ＋1k ＋1D ．2k ＋3k ＋1解析：依题意当n ＝k 时，左边＝（k ＋1）（k ＋2）（k ＋3）…（k ＋k ），当n ＝k ＋1时，左边＝（k ＋1＋1）（k ＋1＋2）（k ＋1＋3）…（k ＋1＋k ）（k ＋1＋k ＋1），从“k 到k ＋1”左端需增乘的代数式为（2k ＋1）（2k ＋2）k ＋1＝2（2k ＋1）．答案：B 5．（2021·孝义期末测试）我们知道：在平面内，点（x 0，y 0）到直线Ax ＋By ＋C ＝0的距离公式d ＝|Ax 0＋By 0＋C |A 2＋B 2，通过类比的方法，可求得：在空间中，点（2，4，1）到直线x ＋2y ＋2z＋3＝0的距离为（ ） A ．3 B ．5C ．5217D ．3 5解析：类比平面内点到直线的距离公式，可得空间中点（x 0，y 0，z 0）到直线Ax ＋By ＋Cz ＋D＝0的距离公式为d ＝|Ax 0＋By 0＋Cz 0＋D |A 2＋B 2＋C 2，则所求距离d ＝|2＋2×4＋2×1＋3|12＋22＋22＝5．答案：B6．已知a ，b ，c ∈R ，若b a ·c a >1且b a ＋ca≥－2，则下列结论成立的是（ ）A ．a ，b ，c 同号B ．b ，c 同号，a 与它们异号C ．a ，c 同号，b 与它们异号D ．b ，c 同号，a 与b ，c 的符号关系不确定解析：由b a ·c a >1知b a 与ca 同号，若b a >0且c a >0，不等式b a ＋ca ≥－2显然成立， 若b a <0且c a <0，则－b a >0，－ca >0， ⎝⎛⎭⎫－b a ＋⎝⎛⎭⎫－c a ≥2⎝⎛⎭⎫－b a ·⎝⎛⎭⎫－c a >2，即b a ＋c 2<－2， 这与b a ＋c a ≥－2矛盾，故b a >0且ca >0，即a ，b ，c 同号．答案：A7．用反证法证明“若x 2－1＝0，则x ＝－1或x ＝1”时，应假设________． 解析：“x ＝－1或x ＝1”的否定是“x ≠－1且x ≠1”． 答案：x ≠－1且x ≠18．将1，2，3，4…这样的正整数按如图所示的方式排成三角形数组，则第10行左数第10个数为________．解析：由三角形数组可推断出，第n 行共有2n －1个数，且最后一个数为n 2，所以第10行共19个数，最后一个数为100，左数第10个数是91． 答案：919．已知x ，y ，z 是互不相等的正数，且x ＋y ＋z ＝1，求证：⎝⎛⎭⎫1x －1⎝⎛⎭⎫1y －1⎝⎛⎭⎫1z －1>8． 证明：因为x ，y ，z 是互不相等的正数，且x ＋y ＋z ＝1，所以1x －1＝1－x x ＝y ＋z x >2yz x ，①1y －1＝1－y y ＝x ＋z y >2xz y，② 1z －1＝1－z z ＝x ＋y z >2xy z，③ 又x ，y ，z 为正数，由①×②×③， 得⎝⎛⎭⎫1x －1⎝⎛⎭⎫1y －1⎝⎛⎭⎫1z －1>8．10．（2021·常德模拟）设a >0，f （x ）＝axa ＋x，令a 1＝1，a n ＋1＝f （a n ），n ∈N ＋．（1）写出a 2，a 3，a 4的值，并猜想数列{a n }的通项公式； （2）用数学归纳法证明你的结论．解析：（1）∵a 1＝1，∴a 2＝f （a 1）＝f （1）＝a1＋a，a 3＝f （a 2）＝a ·a 1＋a a ＋a 1＋a ＝a2＋a ；a 4＝f （a 3）＝a ·a 2＋a a ＋a 2＋a ＝a3＋a ．猜想a n ＝a（n －1）＋a（n ∈N ＋）．（2）证明：①易知，n ＝1时，猜想正确． ②假设n ＝k （k ∈N ＋）时猜想正确，即a k ＝a（k －1）＋a，则当n ＝k ＋1时，a k ＋1＝f （a k ）＝a ·a k a ＋a k ＝a ·a（k －1）＋a a ＋a （k －1）＋a＝a （k －1）＋a ＋1＝a[（k ＋1）－1]＋a．这说明，n ＝k ＋1时猜想正确．由①②知，对于任何n ∈N ＋，都有a n ＝a（n －1）＋a．[B 组 能力提升练]1．正弦函数是奇函数，f （x ）＝sin （x 2＋1）是正弦函数，因此f （x ）＝sin （x 2＋1）是奇函数，以上推理（ ）A ．结论正确B ．大前提不正确C ．小前提不正确D ．全不正确解析：因为f （x ）＝sin （x 2＋1）不是正弦函数，所以小前提不正确． 答案：C2．分析法又称执果索因法，若用分析法证明“设a >b >c ，且a ＋b ＋c ＝0，求证：b 2－ac <3a ”索的因应是（ ） A ．a －b >0 B ．a －c >0 C ．（a －b ）（a －c ）>0 D ．（a －b ）（a －c ）<0 解析：b 2－ac <3a ⇔b 2－ac <3a 2⇔（a ＋c ）2－ac <3a 2⇔a 2＋2ac ＋c 2－ac －3a 2<0⇔－2a 2＋ac ＋c 2<0⇔2a 2－ac －c 2>0 ⇔（a －c ）（2a ＋c ）>0⇔（a －c ）（a －b ）>0． 答案：C3．下面图形由小正方形组成，请观察图①至图④的规律，并依此规律，写出第n 个图形中小正方形的个数是（ ）A ．n （n ＋1）B ．n （n －1）2C ．n （n ＋1）2D ．n （n －1）解析：由题图知第1个图形的小正方形个数为1，第2个图形的小正方形个数为1＋2，第3个图形的小正方形个数为1＋2＋3，第4个图形的小正方形个数为1＋2＋3＋4，…，则第n个图形的小正方形个数为1＋2＋3＋…＋n ＝n （n ＋1）2．答案：C4．如图所示，面积为S 的平面凸四边形的第i 条边的边长记为a i （i ＝1，2，3，4），此四边形内任一点P 到第i 条边的距离记为h i （i ＝1，2，3，4），若a 11＝a 22＝a 33＝a 44＝k ，则1×h 1＋2×h 2＋3×h 3＋4×h 4＝2Sk．类比以上性质，体积为V 的三棱锥的第i 个面的面积记为S i （i ＝1，2，3，4），此三棱锥内任一点Q 到第i 个面的距离记为H i （i ＝1，2，3，4），若S 11＝S 22＝S 33＝S 44＝k ，则H 1＋2H 2＋3H 3＋4H 4值为（ ）A ．4V kB ．3V kC ．2V kD ．V k解析：∵V ＝13S 1H 1＋13S 2H 2＋13S 3H 3＋13S 4H 4＝13（kH 1＋2kH 2＋3kH 3＋4kH 4）∴H 1＋2H 2＋3H 3＋4H 4＝3Vk．答案：B 5．（2021·兰州市高考实战模拟）观察下列式子：1，1＋2＋1，1＋2＋3＋2＋1，1＋2＋3＋4＋3＋2＋1，…，由以上可推测出一个一般性结论：对于n ∈N ＋，1＋2＋…＋n ＋…＋2＋1＝________．解析：因为1＝12，1＋2＋1＝22，1＋2＋3＋2＋1＝32，1＋2＋3＋4＋3＋2＋1＝42，…，所以归纳可得1＋2＋…＋n ＋…＋2＋1＝n 2． 答案：n 26．在平面内，三角形的面积为S ，周长为C ，则它的内切圆的半径r ＝2SC．在空间中，三棱锥的体积为V ，表面积为S ，利用类比推理的方法，可得三棱锥的内切球（球面与三棱锥的各个面均相切）的半径R ＝________．解析：若三棱锥表面积为S ，体积为V ，则其内切球半径R ＝3VS．理由如下：设三棱锥的四个面的面积分别为S 1，S 2，S 3，S 4， 由于内切球的球心到各面的距离等于内切球的半径，所以V ＝13S 1R ＋13S 2R ＋13S 3R ＋13S 4R ＝13SR ，所以内切球的半径R ＝3VS．答案：3V S7．我们将具有下列性质的所有函数组成集合M ：函数y ＝f （x ）（x ∈D ），对任意x ，y ，x ＋y2∈D均满足f ⎝⎛⎭⎫x ＋y 2≥12[f （x ）＋f （y ）]，当且仅当x ＝y 时等号成立．（1）若定义在（0，＋∞）上的函数f （x ）∈M ，试比较f （3）＋f （5）与2f （4）的大小； （2）设函数g （x ）＝－x 2，求证：g （x ）∈M ．解析：（1）对于f ⎝⎛⎭⎫x ＋y 2≥12[f （x ）＋f （y ）]， 令x ＝3，y ＝5得f （3）＋f （5）≤2f （4）．（2）证明：g ⎝⎛⎭⎫x 1＋x 22－12[g （x 1）＋g （x 2）]＝－（x 1＋x 2）24＋x 21＋x 222＝（x 1－x 2）24≥0，当且仅当x 1＝x 2时取等号，所以g ⎝⎛⎭⎫x 1＋x 22≥12［g （x 1）＋g （x 2）］，所以g （x ）∈M ．［C 组〓创新应用练］1．（2021·惠州市高三二调）《周易》历来被人们视作儒家群经之首，它表现了古代中华民族对万事万物深刻而又朴素的认识，是中华人文文化的基础，它反映出中国古代的二进制计数的思想方法．我们用近代术语解释为：把阳爻“”当作数字“1”，把阴爻“”当作数字“0”，则八卦所代表的数表示如下：卦名 符号 表示的二进制数 表示的十进制数坤 000 0艮0011坎010 2巽011 3 依次类推，则六十四卦中的“屯”卦，符号为“[XCS 346．TIF ；BP ]”，其表示的十进制数是[JY ]（ ） A ．33 B ．34 C ．36 D ．35 解析：由题意可知，六十四卦中的“屯”卦的符号“”表示的二进制数为100010，转化为十进制数为0×20＋1×21＋0×22＋0×23＋0×24＋1×25＝34． 答案： B2．一布袋中装有n个小球，甲、乙两个同学轮流抓球，且不放回，每次最少抓一个球，最多抓三个球．规定：由乙先抓，且谁抓到最后一个球谁赢，那么以下推断中正确的是（）A．若n＝9，则乙有必赢的策略B．若n＝7，则甲有必赢的策略C．若n＝6，则甲有必赢的策略D．若n＝4，则乙有必赢的策略解析：若n＝9，则乙有必赢的策略．（1）若乙抓1个球，甲抓1个球时，乙再抓3个球，此时剩余4个球，无论甲抓1～3的哪种情况，乙都能保证抓最后一个球；（2）若乙抓1个球，甲抓2个球时，乙再抓2个球，此时剩余4个球，无论甲抓1～3的哪种情况，乙都能保证抓最后一个球；（3）若乙抓1个球，甲抓3个球时，乙再抓1个球，此时剩余4个球，无论甲抓1～3的哪种情况，乙都能保证抓最后一个球．所以若n＝9，则乙有必赢的策略．答案：A。

课时作业(三十四)-+_>0, ••• M>N 故选 A2 2 2 2 2 22. B ［解析］当a>b>0时,a >b 成立.当a=- 3,b=-1时，满足a >b 但a>b>0不成立，所以“a >b "是"a>b>0” 的必要不充分条件，故选B.2 23. D ［解析］选项AB 中，当c=0时，显然不成立；选项C 中，当a=-2,b=-3时,a>b 成立，但a >b 不成立；选项2D 中，Tc +1>0 一定成立，且a>b,.・——>一一定成立，故选D4. (- n ,2 n )［解析］结合题意可知 3 a - 3 =2( a - 3 )+( a + 3 )，且 2( a - 3 ) € (- n , n ), a + 3 € (0, n )，利 用不等式的性质可知3a - 3的取值范围是(-n ,2n ).5. d>b>a>c ［解析］■/ a+b=c+d,a+d>c+b,「. 2a>2c,即 a>c,「. b<d. ■/ a+c<b,^ a<b.综上可得 d>b>a>c.6. D ［解析］因为当x=2,y=1时，一v_, 一 < 一 ,cos x<cos y 所以排除选项A,B,C 故选D7. C ［解析］由于原料A 每天的限额为21吨所以3x+5y < 21;由于原料B 每天的限额为13吨，所以2x+3y < 13.故选C8. B ［解析］ Tb -a= ------- = ---------- = ------ >0, • b>a;又 a-c= --------- = -----------= ---------->0二 a>c. • b>a>c, 即c<a<b.故选B.9. C ［解析］设 3a-2b=x(a+b)+y(a-b),易得 x=-,y=-,「. 3a-2b=-(a+b)+(a-b) € ［-2,10］,故选 C.10. B ［解析］设厶ABC 的三边长分别为b-m,b,b+mb>m ：0). •••△ ABC 满足两边之和大于第三边,^b -m+b>b+r? b>2m 即一>2;b-m+b+m>? b>0;b+(b+n)>b-m? b>- 2m. •最小边与最大边长度的比值为 ——=—=1-「,T ->2, •——>,显然 —<1,据此可得,△ ABC 的最小边与最大边长度的比值的取值范围 是-.故选B.11. 乙［解析］由题意得甲购买鸡蛋的平均单价为 ——=——，乙购买鸡蛋的平均单价为二一.由21. A ［解析］TM -N=x+x+1 =>0,.・. ，•乙的购买方式更优惠条件得a^ b.12. P >Q ［解析］由a,b是非负实数，作差可得3 3 2 2 2 255P-Q=a+b- (a+b)=a ( - )+b (-)=(-)［()-()］.当a> b 时，> > 0,.・.()> ()，得( - )［( )-( ) ］> 0;__ _ _ 5 — 5 ——__ 5 — 5当a<b时,o w < ,•••() <()，得(-)［()-()］>0.•••a3+b3》—(a2+b2),即p> Q.13. ［2,27］［解析］因为一=——,8€ — < 27,1 < (xy ) < 4,所以一€ ——，即一€ ［2,27］.14. A ［解析］当x=1,y=-1时,-6< a-b+c < 4,所以a-b+c的最小值为-6,最大值为4,故B,D错误当x=-1 ,y=-1 时,-12W -a-b+c w - 2,则2W a+b-c w 12,所以a+b-c 的最小值为2,最大值为12.故选A15. -一［解析］•••实数a,b,c满足a>c-2且3 +3 <3 ,• 3 >3 =,3 +3 <3，由3 >0,可得3a-c-3b-c<3①.由3b-c<3-3a-c<3--—，可得川、-—,• 3=3^>-—②.由①②可得-—<3a-c-3b-c<3,即一的取值范围为-一.课时作业（三十五）21. A ［解析］由12X+X-1W 0,得(3x+1)(4x-1) w 0,解得--w x w-，即不等式的解集为l x -—w x w-.2 22. B ［解析］由题意知,2为方程--x+2x=mx的一个根所以--X 2 +2X 2=2n,解得m=,故选B3. A ［解析］由-<1得1<x<3,由x2-3x<0得0<x<3,所以“ -<1"是“x2-3x<0"的充分不必要条件，故选A2 2 2 2 24. (a +2,3a)［解析］Tx - (a +3a+2)x+3a但+2)<0,二［x-(a+2)］(x-3a)<0. Va €2 2 2(1,2),「.a+2<3a,「.a +2<x<3a, •不等式的解集为(a+2,3a).5. ［0,1］［解析］因为f (x)的定义域为R,所以x -6kx+k(k+8)>0在R上恒成立，则△ =36k -4k(k+8)w 0, 解得0w k w 1.6. B ［解析］因为xf (x-1) >a的解集为［3,+r 所以3为方程xf (x-1)=a的根所以a=3f (3-1 )=3 X (2-1)=3, 故选B2 27. A ［解析］设f(x)=2x-x =-(x-i)+i < 1,因为存在x o € ［-2,3］,使不等式2X o- > a 成立所以a< f(x)max 所以a< 1,故选A28. B ［解析］当a=0时,符合题意.当0时,丁关于x的不等式4ax +4ax+1>0的解集为R二-解得0va<1.综上可知实数a的取值范围是［0,1),故选B.9. D ［解析］由一> 1 得一-1 > 0,即 _—》0,二［(a-1)x- 1］(x+1) > 0 且X K -1,解得XV-1或x》一，则不等式的解集为(-,-1)U 一g ,故选D10. B ［解析］由题意知征收耕地占用税后每年损失耕地-- 万亩,则税收收入为-- X 24000Xt%由题意得-- X 24 000 Xt%> 9000，整理得t2-8t+15W 0,解得3< t < 5, At的取值范围是［3,5］,故选B11. D ［解析］关于x的不等式x - (a +1)x+a<0可化为(x- 1)(x-a)<0.当a>1时，不等式的解集为(1,a);当a<1 时，不等式的解集为(a,1).要使得解集中至多包含2个整数则a<4且a>-2.又当a=1时,不等式的解集为？，符合题意.所以a的取值范围是［-2,4］,故选D.2 2 2集为{x|x> 2};当x<0时,不等式-x + +2<0化为-x -x+ 2<0,即x +x- 2>0,此时不等式的解集为-.综上所述，原不等式的解集为{x|x<- 2或x>2}.13. a < 4 ［解析］当a=0时，不等式化为4x+1< 0,解得x<--,符合题意；当a>0时，若满足题意，则△ =16- 4a >0,得0<a< 4;当a<0时，满足题意.综上可得a的取值范围是a< 4.2 2 212. {x|x<- 2或x>2}［解析］当x>0时,不等式-x + +2<0化为-x +x+2<0,即x -x- 2>0,此时不等式的解2 2.设f (x)=x+_ ,x 14. D [解析]当x€ [1,5]时,不等式x-ax+2>0 可化为x+2>ax,即a<x+_,.・.a<€ [1,5],则易知f(x)的最大值为f(5)=5+-=—,•••a的取值范围是亠一.故选D15. a >——［解析］当a=0 时,f (x) =2x+1 ,f ［f (x)］=4x+3,不满足题意;当a<0 时,f (x)=a - +1_- < 1--,令t=f (x)< 1--,所以f ［f (x)］=f (t)一定有负值，不满足题意；当a>0 时,f (x)=a - +1--> 1--,令t=f (x)> 1--,所以f［f(x)］=f(t)的图像的对称轴为t=--，因为--<1--,所以f(t)在-- 上单调递增，即f(t)mm=f --=a+i--,依题意得a+1--> 0,得a> ——.综上可得,a的取值范围为a>——.课时作业(三十六)1. C ［解析］作岀直线x+2y+4=0,取其左下方，作岀直线x-y+ 1=0,取其左上方，故选C2. C ［解析］因为点P(- 2,t)在直线2x- 3y+6=0的上方所以-4- 3t+ 6<0,即t>-,故选CJ\Lx+y=l3. B ［解析］画岀满足约束条件的平面区域，如图中阴影部分所示，易知区域M为图中的△ ABC及其内4. B ［解析］画岀表示的可行域，如图中阴影部分所示部,A(2,0),B(1,1),C(3,3),可得区域M的周长为3 一+ 一,故选B.由得A(0,1),平移直线y=-2x+z.由图知，当直线y=-2x+z经过理0,1)时z取得最小值，最小值为2 X 0+1 =1，故选B.5. -［解析］由题可得(1+2a-1)(- 1+3a-1)<0,即a(3a-2)<0,解得0<a<,故实数a的取值范围是-6. B ［解析］作岀不等式组表示的可行域，如图中阴影部分所示，则-=y-x,所以当直线z=y-x过点A(0,1)时,z取得最大值1,故选B.卜7. A ［解析］画岀约束条件表示的可行域，如图中阴影部分所示.——的几何意义为可行域内的点与点(-1,0)连线的斜率的倒数.由图可知目标函数分别在点—和点—处取得最大值11与最小值-，故8. C ［解析］作岀不等式组表示的可行域，如图中阴影部分所示.易知当直线y=-ax+c- 3平行于直线AB 或平行于直线BC时，满足题意，o oJ/ID6%I■山,■■—-10-8 -6 —4 f 210 J；•・kAB=--=-a,或k B(=3=-a，…a=-或-3,故选C9. B ［解析］作岀不等式组- 表示的平面区域，如图中阴影部分所示.•••平面区域内存在点(x0,y o),使得x0+ay o+2W 0成立,•直线x+ay+2=0与平面区域有交点.解方程组得B(0,2),「.点B在直线x+ay+2=0 上方,• 0+2a+2< 0,解得a<-1.故选B.10. -- ［解析］由题意，画岀约束条件所表示的平面区域，如图中阴影部分所示.把目标函数z=ax+y化为y=-ax+z，当直线y=-ax+z在y轴上的截距最大时，目标函数取得最大值.当a< 0时,由目标函数z=ax+y在点(3,2)处取得最大值，得-a <-,即0》a>--;当a>0时,显然满足题意.•实数a的取值范围是--11. (0,1] U - [解析]画岀不等式组表示的平面区域，如图中△ OAB及其内部所示.平移直线x+y=m)当x+y=m过点(1,0)与——时,m的值分别是1和由图知，当1<m<时，原不等式组表示的平面区域为四边形当m<0时，区域不存在；当m€ (0,1] U - %时，原不等式组表示的平面区域是三角形，二实数m的取值范围是(0,1] U - g .12.解:设甲、乙两种产品分别生产加工厂获得的利润为z元,由已知可得不等式组§€目标函数z=700x+1200y.画岀不等式组表示的平面区域，如图中阴影部分内的整点.目标函数可变形为y=-—x ------------- ，由图可知，当直线y=-—x+——过点M时,z最大.由可得M(20,24).所以z max=700 X 20+1200 X 24=42 800(元),故该厂分别生产甲、乙两种产品20,24件才能使该厂月利润最大，最大利润为42 800元13. C ［解析］作岀不等式组-€€对应的平面区域，如图中阴影部分内的点所示设z=3x+4y,由z=3x+4y 得y=--x+_z.平移直线y=--x+-z,由图可知当直线y=--x+-z经过点A时，直线y二_x+_z在y轴上的截距最小，此时z最小.由图可得A(4,1), 则Z min=12+4=16,故选C14. - ［解析］作岀约束条件表示的可行域，如图中阴影部分所示.联立x+3y=3与x-y=- 1,可得2 2A(0,1). (x-a) +(y+a)表示点(x,y)与点(a,-a)的距离的平方，即可行域内的点到直线x+y=0的距离的平方其最小值为点A到直线x+y=0的距离的平方，易得所求最小值为-.课时作业(三十七)1. D ［解析］a+——=a+1+-> 1+2 -=5，当且仅当a=2时取等号，故选D.2. B ［解析］因为a>o,b>o，所以4=2a+b》2 —,当且仅当a=i,b=2时取等号，二0<ab< 2,则一》-,故一的最小值为-，故选B.3. D ［解析］T a>0,b>0,.・——> _,一w^= —.又Ta+b》2ab,「. 2(a+b2)>(a+b),二------------- >——.二——> ——> _ >——,故选D.4. 2 ［解析］Tx € - g,.•. y=x+ > 2 =2 ，当且仅当x=_,即x= 时，等号成立，「.y的最小值为2 一5. 4 ［解析］y=x+一=x- 2+一+2,令t=x- 2，则t> 0,又m»,「y=t+—+2》2 —+2=2 _+2,当且仅当t=—时取等号,Ty的最小值为6,. 2 —+2=6,解得mW.6. A ［解析］T 3x+2y=2,. 8 +4 =2 +2 >2 =2 =4,当且仅当3x=2y,即x二,y亠时等号成x y立,.8 +4的最小值为4.故选A7. A ［解析］因为-------- =—，所以—+-+5=—，因为—+->2 —-^,当且仅当—=时取等号，所以—+5,解得—> 6,即mr o 36,所以mn的最小值为36,无最大值，故选A.8. C ［解析］T x>2,.x-2>0,.f(x)=x+—=x-2+—+2 >2 - —+2=4,当且仅当X-2=—且x>2,即x=3 时等号成立,.a=3,故选C9. C ［解析］T一+一=2a,.——+——=2sin A又——+一o2 ————=2,当且仅当——=一时，等号成立，二sin A o 1,又sin A< 1,. A=,b=c,.A ABC是等腰直角三角形，故选C.10. 8 ［解析］T a>0, b>0,且a+2b=8,••• ab=-a 2bw- -------- =- x 16=8,当且仅当a=2b=4时取等号,• ab的最大值为8.11. 4 ［解析］由a>0,b>0,lg a+lg b=lg (a+b),得lg ab=lg (a+b),即ab=a+b即-+-=1,则a+b=(a+b) - - =2+_+_>2+2 - _=4,当且仅当a=b=2时,取等号，则a+b的最小值为4.12. 20 ［解析］由题意得一年的总运费为——万元.•••一年的总存储费用为4x万元，.••一年的总运费与总存储费用之和为——万元.T——+4x >2X 一=160,当且仅当——=4x,即x=20时取等号.••一年的总运费与总存储费用之和最小时,x=20.13.3+ 一［解析「••正实数a,b 满足一+—=1,二3a+2b=._(a+b)+-(a-b)_ ——一=3 --------------- +―-— >3+ 一，当且仅当5(a+b)2=(a-b)2时取等号,.•. 3a+2b的最小值为3+ 一.14.解:(1)由题得yd(2x-3)+——+-=-• xv_, 3-2x>0,.•.一+一 > 2 ————=4,当且仅当——=—,即x二-时取等号..•.yW-4+-=--,故函数y=x+ ------ 的最大值为--.(2) • 0<x<2, . 2-x>0,.y= - = - W ——=,当且仅当x=2-x ,即x=1时取等号，.函数y= - 的最大值为15. 解:(1)由题设得S=(x- 8) 一- =-2x-——+916,x € (8,450).⑵因为8<x<450,当且仅当2x=——，即x=60时等号成立， 从而 S < -240+916=676.2故当矩形温室的室内长为 60 m 时,三块种植植物的矩形区域的总面积最大，最大为676 m .16. D ［解析］因为0<m<所以_+ ------ =----------= -------------> -------------- =8,当且仅当2m=-2m 即卩m=时取等2 2号,所以由—+—— >k-2k 恒成立，得k-2k < 8,解得-2< k < 4,故选D.17. B ［解析］由题意可得 p=f( —)=ln—=_ln ab=_(in a+lnb),q=f — =ln —>ln —=P,v=—［f (a)+f (b)］=-(ln a+ln b),二 p=v<q 故选 B.课时作业(三十八)2 2 2 21. B ［解析］由不等式的基本性质知 若a>b>0,则a >b ，当a,b 的符号不确定时，a 与b 无法比较大小，二 这个推理的大前提是错误的，故选B.2. C ［解析］平面上关于正三角形的内切圆的性质可类比为空间中关于正四面体的内切球的性质 ，我们可以推断，在空间中有“正四面体的内切球与各面相切，切点是各面的中心”，故选C3333. B ［解析］第一组内各数之和为1 ,第2组内各数之和为2,第3组内各数之和为3……观察规律，归纳3可得第n 组内各数之和为n ,故选B.4. D ［解析］从公元1984年开始算起，公元2032年为第49年天干表10个数为一个周期，地支表12个 数为一个周期，则公元2032年对应的天干为壬，地支为子，故应为壬子年，故选D.5. ln ［n+(n+1)+(n+2)+…+(3n-2)］=2ln (2n-1) 懈析］可以发现已知的四个等式左边自然对数的真数都 是从n 开始，连续2n-1个正整数的和，右边都是2ln (2n-1),可猜想第n 个等式为ln ［n+(n+1)+(n+2)+… +(3n-2)］=2ln (2n-1).6. A ［解析］该推理的大前提是“对于可导函数 f(x),如果f' (x c )=0那么x=X 0是函数f(x)的极值点”. 对于可导函数f(x),如果f' (x o )=0,且满足当X>X 0时的导函数值与当XVX 0时的导函数值异号，那么X=X 0是 函数f (x)的极值点,所以大前提错误.故选A7. A ［解析］类比平面几何的射影定理，可以推理岀：在三棱锥A-BCD 中,ADL 平面ABC^AOL 平面BCDO2为垂足，则(S M B C ) =&BOC S ^BDC 故选 A.28. C ［解析］Tm =1+3+5+…33333+11=——X 6=36, ••• m= •/ 2=3+5,3=7+9+11,4 =13+15+17+19,二 5 =21+23+25+27+29. Tp 的分解式中最所以2x+——> 2=240,3 3小的数是21, •p =5，即p=5. • m+p6+5=11.故选C.9. ［解析］因为△ ABC勺顶点B在双曲线一-—=1(a>0,b>0)上，顶点AC分别是双曲线的左、右焦点,所以有||BA|-|BC||= 2a,所以-J= ，由正弦定理可得——=一=一所以二,故答案为一-一=-.10. 7 ［解析］J A得25票,E只得4票,••• B,CD共得46-25-4=17(票). C,D得票同样多，且要大于4票,二若CD得5票，则B得7票若C,D得6票则B得5票不满足条件;若C,D得7票，则B得3票，不满足条件; 若C,D得8票,则B得1票，不满足条件.故满足条件时,B得7票.11. A=B=0 ［解析］利用类比推理可得A=B=0.12. -- 懈析］由题意,g(x)- 6=---- 1+ ----- 1 + ----- 1 + ---- 1 + ---- 1 + ------ 1 =—+—+ ------ + --- +——+——,g -一 -6 ------ + ------ + ---- + ------- + ----- + ----- =—+一+一+——+——+—— h(x),因为h(-x)=——+——+——+ ----- + ---- +=-h (x),所以h(x)是奇函数，所以函数g(x)=——+—+•••+——的图像关于点-- 对称.课时作业(三十九)1. A ［解析］用分析法证明的实质是证明结论成立的充分条件成立•②是①的充分条件，故选A.2. A ［解析］根据反证法的定义，可知“若a € R则函数y=x3+ax+b至少有一个零点”的反设应为“若a € R则函数y=x3+ax+b没有零点”，故选A3. C ［解析］因为A,B,C€ (0° ,90° ),所以A+B：90° ,则sin A>sin (90° -B)，即sin A>cos B.同理,sinB>cos A,sin C>cos B,由以上三个不等式可得M>N故选C4. ③［解析］因为a>b>c，且a+b+c=0所以b=-a-c ,c<0,要证-< _a,只需证b2-ac< 3a2,只需证2 2 2 2 2(-a-c ) -ac< 3a，即证a -ac+a -c >0,即证a(a-c)+(a+c)(a-c)>0,即证(a-b )(a-c)>0.5. C ［解析］根据用反证法证明时反设的格式知①的假设正确，②的假设错误.②的假设应该是与都小于-,故选C.6. C ［解析］由a2,a3,a6成等比数列，可得=a2aq可得(a1+2d)2=(a1+d)(a 1+5d),即2a1d+d2=0, J公差d不等于零，.・.a1d<0,2a1+d=0,.・. dS=d(3a1+3d)hd2>0.故选C.7. C ［解析］由题意，乙、丙均不跑第一棒和第四棒，则跑第三棒的人只能是乙、丙中的一个.当丙跑第三棒时,乙只能跑第二棒，这时丁跑第一棒，甲跑第四棒，符合题意.故跑第三棒的人是丙，故选C1.C ［解析］因为多边形的边数最少是3,所以在应用数学归纳法证明凸n边形的对角线为—n(n-3)条时,8. B ［解析］T x>0,y>0 且y-x>l.x<y-1, /• -x> 1-y , ••• 一J=-1.T x<y-1 ,• 3x<3y- 3,• 1+3x<3y- 2,• ------ < --- 3-_,当y>1 时,1<3--<3,可小于1,可等于1,可大于1,故一, ---- 中至少有一个小于1.故选B9. sin 0 ad=bc ［解析］连接BQ根据勾股定理可得AB=CD= ,AD=BC= ，所以可得△ ABD^A ABE=&CD〜sin 0，所以图②中阴影部分的面积是2ABD+0CDB=sin 0 .由(ac+bd) =(a+b)(c+d)可得a2c2+2acbd+b2d2=a2c2+a2d2+b2c2+b2d2,即a2d2-2acbd+b2c2=(ad-bc)2=0，即ad=bc，所以当且仅当a,b,c,d 满足条件ad=bc时，等号成立.10. D ［解析］假设m+,n—,t+—这三个数都小于4,则-+ - + - <12.利用基本不等式可得-+ - + - = - + - + - > 2 -+2 -+2 -=12（当且仅当m=n=t=2时等号成立），得到矛盾的结论，可见假设不成立，即m+,n+,t+-三个数中至少有一个不小于4. 故选D11. A ［解析］根据题意知(X1+X2+X3+X4)(y1+y2+y3+y4)>0,又(x 1+x2+x a+x4)(y1 +y2+y a+y4)=T1+T2+T a+T4所以可知T1,T2,T3,T4中至少有一个为正数，故选A.课时作业（四十）第一步应验证n等于3,故选C2. D ［解析］由题意“ n=k” 时,左边为(k+1)(k+2)…(k+k), “n=k+1” 时，左边为(k+2)(k+3)…(k+1+k+1)，从而可得因式中增加的项为(2k+1)(2k+2),减少的项为(k+1)，故选D.3. C ［解析］当n=k+1 时,x2n-1+y2n-1=x2k+1+y2k+1,故选c4. -+-+-+- ［解析］n=4时，等式右边的式子是-+_+_+_.5. (k3+5k)+3k(k+1)+6 ［解析］因为当n=k时,k3+5k能被6整除所以当n=k+1时，式子(k+1)3+5(k+1)应变3形为(k +5k)+3k(k+1)+6.6. A ［解析］根据逆否命题和原命题的真假一致得，当n=k+1(k € N*)时命题不成立，则当n=k(k€ N*)时命题也不成立，所以当n=8时命题不成立，则当n=7时命题也不成立，故选A.2 n-1 n 27. D ［解析］将式子1+2+2+-+2 =2-1中的n用k+1替换得，当n=k+1时应证明的等式为1+2+2 +… k- 1 k k+1 +2 +2 =2 - 1,故选D.8. D ［解析］由题意，知p(k)对k=2,4,6，…,2002成立，当k取其他值时不能确定p(k)是否成立.故选D.9. D ［解析］当n=k+1时，不等式应为——+——+…+——>-，则左边增加——+——+一并减少----- +----- ，故选D.10. D ［解析］根据题意若f (4)> 5 成立，则f( n0+1) > n °+2(n。

第四课时推理课前预习案1.了解合情推理的含义，能进行简单的归纳和类比推理，体会合情推理在数学发现中的作用。

2.了解演绎推理的含义，了解合情推理和演绎推理之间的联系和差异；3.掌握演绎推理的“三段论”进行一些简单演绎推理。

1．合情推理(1)归纳推理：由某类事物的部分对象具有某些特征，推出该类事物的全部对象都具有这些特征的推理，或者由个别事实概括出的推理，称为归纳推理．简言之，归纳推理是由的推理．(2)类比推理：由两类对象具有某些类似特征和其中一类对象的某些已知特征，推出另一类对象也具有这些特征的推理称为类比推理．简言之，类比推理是由特殊到的推理．(3)合情推理：归纳推理和类比推理都是根据已有的事实，经过观察、分析、比较、联想，再进行归纳、，然后提出猜想的推理，我们把它们统称为合情推理．2．演绎推理演绎推理：从一般性的原理出发，推出某个特殊情况下的结论，我们把这种推理称为演绎推理．简言之，演绎推理是由的推理．它的特点是：前提为真时，结论必然_________.(1)“三段论”是演绎推理的一般模式，包括：①大前提——已知的一般原理；②小前提——所研究的特殊情况；③结论——根据一般原理，对特殊情况作出的判断(2)传递性关系推理推理规则是：“如果，则”（其中表示具有传递性的关系），这种推理叫传递性关系推理，如：推出。

（3）完全归纳推理把所有情况都考虑在内的演绎推理规则叫做完全归纳推理.1.（2011江西理7）观察下列各式： =3125， =15625， =78125，…，则的末四位数字为（）A．3125 B．5625 C．0625 D．81252.(2010山东文10)观察，，，由归纳推理可得：若定义在上的函数满足，记为的导函数，则=( )（A） (B) (C) (D)课堂探究案考点一归纳推理【典例1】观察下列等式：可以推测：13＋23＋33＋…＋n 3＝________ (n ∈N *，用含有n 的代数式表示)【变式1】 已知经过计算和验证有下列正确的不等式：3＋17＜210，7.5＋12.5＜210，8＋2＋12－2＜210，根据以上不等式的规律，请写出一个对正实数m ，n 都成立的条件不等式________ ． 【变式2】（2011山东理15）设函数()(0)2x f x x x =>+,观察:1()(),2x f x f x x ==+21()(()),34x f x f f x x ==+32()(()),78x f x f f x x ==+43()(()),1516x f x f f x x ==+根据以上事实，由归纳推理可得： 当且2n ≥时，1()(())n n f x f f x -== .【变式3】（2012江西理 6）观察下列各式： 3344554,7,11,a b a b a b +=+=+=则（ ）A ．28B ．76C ．123D ．199考点二 类比推理【典例2】在平面几何里，有“若△ABC 的三边长分别为a ，b ，c ，内切圆半径为r ，则三角形面积为S △ABC ＝12(a ＋b ＋c )r ”，拓展到空间，类比上述结论，“若四面体ABCD 的四个面的面积分别为S 1，S 2，S 3，S 4，内切球的半径为r ，则四面体的体积为__________________________【变式4】在正三角形中，设它的内切圆的半径为r ，容易求得正三角形的周长面积，发现，这是平面几何中的一个重要发现。

本社目为敕和专用"第六单元不等式、推理与证明I便用建议■ SHIYONGJIANY1. 编写意图(1) 重视不等式本身的知识、方法的讲解和练习力度，以基本的选题和细致全面的讲解进行组织，使学生掌握好不等式本身的重要知识和方法，为不等式的应用打下良好的基础.(2) 二元一次不等式(组)所表示的平面区域和简单的线性规划问题，是高考重点考查的两个知识点，我们不把探究点设置为简单的线性规划问题，而是设置为目标函数的最值(这样可以涵盖线性规划和非线性规划)，含有参数的平面区域以及生活中的优化问题，这样在该讲就覆盖了高考考查的基本问题.(3) 对于合情推理，主要在于训练学生的归纳能力，重点在一些常见知识点上展开.2. 教学建议(1) 在各讲的复习中首先要注意基础性，这是第一位的复习目标.由于各讲的选题偏重基础，大多数例题、变式题学生都可以独立完成，在基础性复习的探究点上要发挥教师的引导作用，教师引导学生独立思考完成这些探究点，并给予适度的指导和点评.(2) 要重视实际应用问题的分析过程、建模过程.应用问题的难点是数学建模，本单元涉及了较多的应用题，在这些探究点上教师的主要任务就是指导学生如何通过设置变量把实际问题翻译成数学问题，重视解题的过程.(3) 不等式在高考数学各个部分的应用，要循序渐进地解决，在本单元中涉及不等式的综合运用时，我们的选题都很基础，在这样的探究点上不要试图一步到位，不等式的综合运用是整个一轮复习的系统任务在本单元只涉及基本的应用，不要拔高.(4) 推理与证明是培养学生良好思维习惯，学习和运用数学思想方法，形成数学能力的重要一环.要站在数学思想方法的高度，对多年来所学习的数学知识和数学方法进行较为系统的梳理和提升.务必使学生对数学发现与数学证明方法有一个较为全面的认识.3. 课时安排本单元共7讲,1个小题必刷卷,1个单元测评卷，建议每讲1个课时完成，小题必刷卷、单元测评卷各1个课时完成，本单元建议用9个课时完成复习任务.第34讲不等关系与不等式考试说明了解现实世界和日常生活中存在大量的不等关系；了解不等式(组)的实际背景.【课前双基巩固】知识聚焦1. (1)> = < (2)> = <2. (1)b<a (3)> a+c>b+d (4)> < > (5)>对点演练2 2 21. (3,8)［解析］T 1<a<2,二1<a<4.又2<b<4,^3<a+b<8,即卩a+b 的取值范围为(3,8).2 22. f (x)>g(x)［解析］••fx)-g(x)=x-2x+2=(x- 1) +1>0,「.f (x)>g(x).2 2 o3.2 ［解析］①ac >bc,两边同时除以c可得到a>b,符合题意；②->-，当c<0时，不能得到a>b,不符合题2 2意③ >b，当a=-2,b=-1时，不能得到a>b,不符合题意;@由2018-a<2018-b，得-a<-b，则a>b,符合题意.综上可知①④符合题意，则能得到a>b的条件的个数为2.4. (-7,7)［解析］由题可知-1<a<2,-3<b<5,A - 2<2a<4,-5<-b<3,结合不等式的性质可得2a-b € (-7,7). 5(24,8)［解析］当-3<a< 0时-€ (-24,0］;当0<a<1时，一€ (0,8).综上可知-的取值范围是(-24,8).6.A > B ［解析］2 2 2 2 2 2 2 2 2 2A-B=a +b - (ab+a+b-1)d(2a +2b - 2ab- 2a-2b+2)=_［(a +b -2ab)+(a -2a+1)+(b- 2b+1)］ = ［(a-b) + (a-1) +(b-21)］>0,故A>B.【课堂考点探究】2 2例1 ［思路点拨］(1)由于Q含有根号，所以可考虑先得到P-Q，然后利用因式分解与配方法进行变形，a b c确定P-Q的符号，进而判断P,Q的大小关系;(2)令3 =4 =6 =k将a,b,c转化为对数形式，然后作商比较大小.例2 ［思路点拨］(1)利用不等式的性质与特殊值法求解；(2)利用不等式的性质，特殊值法及函数的单调性求解.(1)B ⑵D ［解析］(1)v a<b<1,.・. a+<b+1<0, •••-------------- >0且> ，则2 2-------------• (a+1)<--------------- •(b+1),(a+1) >(b+1)，则一>一,• A,CD中不等式成立;由a<b<-1,知当a=-3, b=-2时,一=-1,——二一,—<——，因此B中不等式不成立，故选B⑵由a>b,c<0,得ac<bc,选项A错误设幕函数f (x)=X，因为c<0,所以f (x)在(0,+切上是减函数，又a>b>0, 所以a<b ，选项 B 错误取 a=4,b=2,c=-4,则 log a (a-c )=log 48<2,log b (b-c )=log 26>2,此时 log a (a-c)<log b (b-c), 选项C 错误;一一=-「_ =_ >0,所以=>「选项D 正确.故选D.变式题 (1)B (2)D ［解析］(1)由 2“>2：得 m>n.当 m>n» 时，可得 m>n,|卩 m|m|>n|n| 当 m»>n2 2 2 2时,m|m|>0>n|n| ;当 n<mO 时,-n>-m>0,可得 n >m,故-n <-m,即 m|m|>n|n|，故选 B⑵取 a=2,b=4,c=3,d=2,则 d-a=0,c-b=- 1,此时 d-a>c-b ,故 A 中不等式不成立；取a=2,b=3,x=-1,则-二,——=2, 此时-<——做B 中不等式不成立；取a=,b=3,c=1,d=-3,则b c =3,a d =8,此时b c <a d ，故 C 中不等式不成立; ----- = ——< 0,故D 中不等式成立.故选D.例3 ［思路点拨］(1)首先将已知不等式同时除以a,化为关于-厂的不等式组，然后利用不等式的性质可 求得-的取值范围;(2)首先根据函数解析式明确条件中的两个不等式 ，令2a-b=mf(1)+ nf (-1),通过比较系数求得mn 的值，即可根据条件中两个代数式的取值范围确定2a-b 的取值范围.(1)A (2)-—［解析］(1) •••三个正数 a,b,c 满足 a < b+c < 2a,b < a+c < 2b, • 1W- +- < 2-< 1+-< 2 •-，即-2 •-W -1- Y --，与 1 <-+- < 2 相加，得 1- 2 •-W -- K 2--,解得 -故选 A.⑵由函数的解析式可知 0<a+b<2,-1<-a+b<1,即令2a-b=m(a+b)+n(a-b),即2a-b=(m+na+(m-n)b,比较系数得 解得 即 2a-b=-(a+b)*(a-b).而0<-(a+b)<1,-Y-(a-b)<-,所以-Y-(a+b)k(a-b)<-,即 2a-b € -- 变式题 (1)A (2)(-1,0)［解析］(1)设 a +3 B =入(a + 3 )+V ( a +2 3 )=(入 +v) a +(入 +2v) B .比较系数得解得即 a +3 3 =-1( a + 3 ) +2( a +2 3 )，而-1 W - a - 3 W 1,2< 2 a +4 3 < 6,所以 1Wa +3 3< 7.故a +3 3的取值范围是［1,7］.故选A.<0.又•••a>b,.・.a -b>0,.・ --------------- <0,即-1<ab<0,故 ab 的取值范围是(-1,0).⑵•••&-—<・_,•••&--- -一 v0,「.备用例题JiAOSHI EJC YONG LlTl【备选理由】例1将不等式比较大小与函数进行交汇；例2利用作差法比较大小，并与对数的运算性质相结合,是对探究点一比较大小方法的深化；例3考查不等式性质在实际生活中的应用.例1 ［配合例1使用］［2018 •武汉4月调研］记min{a,b,c}为a,b,c中的最小值若x,y为任意正实数，则M=min - -的最大值是()A 1+ 一B 2C2+ 一 D -［解析］D 设a=2x,b=-,c=y+-=^-则M=min - 一=min{ a,b,-+1 .令a=b=4,得a=b= ― (1)当 aJ \W b W或b W a W时,c=-+-A —=+—==，所以min • a,b—+ - =a或b,其最大值为；(2)当a>b》或b >a> 时,C=-+-W=+== 所以min ‘ a,b,-+-} =c，其最大值为.综上所述,M的最大值为，故选D例2 ［配合例1使用］［2019 •长沙联考］设a=ln-,b=lo 一-,则（）Aa+b<ab<0 B.ab<a+b<0Ca+b<0<ab D.ab< 0<a+b［解析］B 由题得a=ln-<ln 1=0,b=lo ->lo 1=0所以ab<O.a+b=ln-+lo -=-ln 2+—=1 n 2—— =ln2 • ----- <0,ab- (a+b)=ab-a-b= ln_ • lo _-1n_- lo _=-ln 2 • 一+ln 2 - 一=ln 2 -一- 一=ln2 • —-_ =ln 2 •二<0,所以ab<a+b,故选 B.例3 ［配合例3使用］已知6枝玫瑰与3枝康乃馨的价格之和大于24元，而4枝玫瑰与4枝康乃馨的价格之和小于20元，那么2枝玫瑰和3枝康乃馨的价格的比较结果是()A2枝玫瑰的价格高B3枝康乃馨的价格高C价格相同D-不确定［解析］A 设1枝玫瑰与1枝康乃馨的价格分别为x,y元，则6x+3y>24,4x+4y<20，得2x+y>8,x+y<5,因此2x-3y=5(2x+y)-8(x+y)>5X 8-8 X 5=0,因此2 枝玫瑰的价格高，故选A.第35讲一元二次不等式及其解法考试说明1 .会从实际情境中抽象出一元二次不等式模型2. 通过函数图像了解一元二次不等式与相应的二次函数、一元二次方程的联系3. 会解一元二次不等式，对给定的一元二次不等式，会设计求解的程序框图.【课前双基巩固】知识聚焦2. {x|x<x 1 或X>X2} {x|x 工X’} R {X|X 1VXVX2} ? ?对点演练1. (-出，-2］U ［4,+^)［解析］由x2-2x-8=(x-4)(x+2)>0,解得x<-2 或x>4,即不等式的解集为(-，- 2］U ［4,+x).2. - ［解析］由题意可得A= - ,B={x| 1<x<2}, AAP B=- .2 23. a<- 3或a>6 ［解析］因为方程3x +2ax+(a+6)=0有两个不相等的实数根，所以△ =(2a) -4X 3X (a+6)>0, 解得a<-3或a>6.4. (-5,3)［解析］原不等式等价于(x+5)(x-3)<0,解得-5<x<3,即该不等式的解集为(-5,3).5. - -［解析］由(x+1)(3-2x)>0,得(x+1)(2x-3)< 0,二不等式的解集为- -. 工2时，必须满6. (-2,2］［解析］原不等式可整理为(2-m)x+(4-2n)x+4>0.当m=2时，不等式为4>0该不等式恒成立当m解得-2vm<2.综上知实数m的取值范围是(-2,2］.【课堂考点探究】例1 ［思路点拨］通过解一元二次不等式得到集合A,解一元一次不等式得到集合B然后求A n B;(2)首先根据一元二次不等式的解集，结合根与系数的关系得a,b的值,再解不等式.I2 t(1)D (2)A ［解析］(1)由题意得A={x|x -5X+6》0}={x|x <2 或x>3},B={x| 2x-1>0}= - ,AA n B=2 2⑵•••不等式ax+bx+2>0 的解集为{x|- 1<x<2},二ax +bx+2=0 的两根为-1,2,且a<0,二-1+2=-_,(-1)x 2二,解得a=-1,b=1,则2x2+bx+a>0可化为2x2+x-1>0该不等式的解集为变式题或-故选A(1)(-1,-lg2)［解析］(1)由一元二次不等式f(x)<0的解集为亠一U 一知f(x)>0的解集为一-，则一<10乂,得不等式的解集为x € (-1,-lg 2 ).⑵解方程(x-a)(x+1)=0的两根为-1,a.①当a<-1,即-3<a<-1时，原不等式的解集为{x|x<a或x>-1};②当a=-1时，原不等式的解集为{x|x € R且x工-1};③当a>-1,即-1<a<3时，原不等式的解集为{x|x<- 1或x>a}.综上所述，当-3<a<-1时，原不等式的解集为{x|x<a或x>-1};当a=-1时，原不等式的解集为{x|x € R且X K -1};当-1<a<3时，原不等式的解集为{x|x<- 1或x>a}.例2 ［思路点拨］分a=0与a K 0两种情况讨论,结合二次函数的图像特征建立不等式组进行求解.2C ［解析］若a=0,则不等式等价于3>0,该不等式恒成立，满足条件；若a K0,要使ax+ax+a+3 >0对一切实数x恒成立，则解得a>0.综上可得实数a的取值范围是［0,+叼,故选C2 _________________________ __________ . . ____________________________ ___________________________________例3 ［思路点拨］可令f(x)=x +ax- 3a,由题意及二次函数图像可知，只要f (x)在-1和1处的函数值小于0即可;或将参数a分离岀来，转化为求函数的最值来解决.A ［解析］方法一:令f (x) =x2+ax-3a,则由题意及二次函数f(x)的图像知-即--解得a>-故选A.2方法二:由x+ax-3a<0,知a>_,由题意知当x € [-1,1]时,a> 一.令g(x)=—，当x=0 时,g(x)=O；当x€［-1,1］,且x 工0 时,g(x)=—= --- =---------- ,W g(x)max=g(i)=_.故a>,故选A.例4 ［思路点拨］将已知转化为关于a的不等式，然后利用一次函数的单调性求x的取值范围.2 2(-,2)U (4,+叼［解析］已知不等式等价于(x- 3)a+x - 6x+9>0,令g但)=(x-3)a+x-6x+9，由题意，知x +(a- 6)x+9- 3a>0对|a| < 1 恒成立，等价于g(a)=(x- 3)a+x-6x+9 当a€ ［-1,1］时的函数值恒大于0.当x=3 时,g(a)=O,不符合题意当x丰3时，由一次函数的单调性得- -- -解得x<2或x>4.故x的取值范围为(-g,2) U (4,+x).应用演练1. A ［解析］命题"ax -2 ax+3>0恒成立"是假命题，则ax - 2ax+3< 0有解.当a=0时,ax-2ax+3w 0不成立;当a^ 0时，要使ax2- 2ax+3< 0有解，则或a<0,解得a<0或a> 3.故选A2. D ［解析］•••对于满足K x< 4 的一切x,都有f (x)=ax-2x+2>0,「.a 工0,且a> ---- =2-- --- 对任意的1Wx w4恒成立，•.•-€-€ 1, —2 -- --- €-,二实数a的取值范围是- g，故选D3. (-g,1)U (3,+g)［解析］由题意，知对任意a€ ［-1,1］,f (x)=x+(a-4)x+4-2a>0 恒成立，等价于(x- 2)a+x - 4x+4>0 对任意a€ ［-1,1］恒成立.令g(a)=(x- 2)a+x -4x+4,当x=2 时,g(a)=0,不符合题意当X K 2 时，由一次函数的单调性得解得x<1或x>3.故x的取值范围是(-g ,1) U (3,+ g).例5 ［思路点拨］(1)由题意分Kt w 10,10<t w 15,15<t w20三种情况，分别求得日销售量，然后与相应的销售利润相乘可得F(t)的解析式；⑵结合(1)中的日销售利润函数分别求解对应的一元二次不等式即可.解：(1)由题意可得:2 2 2当1W t w 10 时，日销售量为10t+ (-t +20t )=-t +30t, 日销售利润为40 (-t +30t);2 2 2当10<t w 15 时，日销售量为-10t+ 200+(-t +20t )=-t +10t+200，日销售利润为40(-t +10t+ 200);当15<t w 20 时，日销售量为-10t+ 200+(-t +20t )=-t +10t+200，日销售利润为20(-t +10t+ 200).综上可得F(t)=2⑵当K t < 10 时由40(-t +30t)> 5000,得5< t < 10;2当10<t < 15 时，由40(-t +10t+200)> 5000,得10<t < 15;当15<t < 20 时,不等式20(-t 2+10t+ 200) > 5000 无解.故第5天至第15天产品甲给该公司带来的日销售利润不低于5000元.变式题解:(1)W=x&)- (16x+40)= ------------ - 16x+4360,10<x<100,即年利润W万元)关于年产量x(万件)的函数解析式为W=- ----------- 16x+4360(10<x<100).当WN760时，由- -解得x=50(万件).故年利润为2760万元时该公司一年内共生产电饭煲50万件.2QW= --------- - 16X+4360》2360,整理得x -125x+2500< 0,解得25<x< 100，又10<x<100，所以25<x<100.故为了让年利润W不低于2360万元,年产量x的取值范围是［25,100).备用例题I JiAOSlil 0CIYONG Lin ______________________________________________________________________________【备选理由】例1考查解含参数的一元二次不等式问题，需要对参数进行分类讨论；例2是一元二次不等式在给定区间上的存在性问题，能开阔视野、拓展思路，完善知识体系；例3考查另一种形式的一元二次不等式恒成立问题.2例1 ［配合例1使用］解关于x的不等式a(a-1)x-(2a-1)x+1>0，其中a€ R解:由题得(ax- 1)［(a- 1)x-1］>0.①当a<0 时,x € -x - u —g ;②当a=0 时,x € (-1，+g);③------------------------------ 当0<a<1时,x€④当a=1 时,x € (-g,1);⑤当a>i时,x € -K _ U OO .2例2 ［配合例3使用］若关于x的不等式x +ax- 2>0在区间［1,5］上有解，则实数a的取值范围为()A —°° B. -----C (1,+O) D. -O -一［解析］A 不等式x +ax-2>0可化为a ——-x.设f(x)=--x,x€ ［1,5］,由题意得a>f(x)mm.因为函数f(x)在［1,5］上是减函数，所以f (x)min=f(5)亠-5=- —，故选A例3 ［配合例2使用］［2018 •银川二中模拟］已知a1>a2>a3>0,则使得(1-a i x)2<1(i= 1,2,3)都成立的x的取值范围是()A -B —C -D -2 2［解析］B (1-a i x) <1? x-2a i x<0? x -—<0,其解集为—.又0<—J<—,故选 B.第36讲二元一次不等式(组)与简单的线性规划问题考试说明1 .会从实际情境中抽象出二元一次不等式组2. 了解二元一次不等式的几何意义，能用平面区域表示二元一次不等式组.3. 会从实际情境中抽象出一些简单的二元线性规划问题，并能加以解决.【课前双基巩固】知识聚焦1. 边界边界公共部分2. 不等式(组)一次解析式一次解集合最大值最小值最大值最小值对点演练1.4 ［解析］作岀不等式组表示的平面区域，如图中△ ABC及其内部所示，则&ABC==4.2.—［解析］作岀满足不等式组的平面区域，如图中阴影部分所示，由z=3x+2y得y二-x+_，因此将求z=3x+2y的最大值转化为求直线y=--x+-的纵截距的最大值.易知直线2x+y=4与x+2y=4的交点为C- -，由图知当直线y二-x+一经过点C时,z取得最大值，其最大值为3X-+2 X-=一.3.350 ［解析］设每周生产空调x台、彩电y台，则生产冰箱120-x-y台，总产值为z千元，依题意得目标函数z=4x+3y+2(120-x-y )=2x+y+240，且x,y 满足- -€ €行域如图中阴影部分内的整点.解方程组得-- 即其可€ €即M(10,90).让目标函数表示的直线2x+y+240=z在可行域上平移，可得z=2x+y+240在M(10,90)处取得最大值，且z max=2 X 10+90+240=350(千元）.4•- ［解析］画岀满足不等式组的平面区域，如图中阴影部分所示.易知当直线y=-x-_z 经过B--时,z 取得最大值，最大值为--2X -- —.2 2画岀可行域，如图中阴影部分所示，易求得点A(1,2),B(3,4).x +y 的几何意2 2义为可行域内的点到原点 o 的距离的平方.由图知，可行域内的点A 到原点的距离最小，所以x +y 的最2 9小值是1 +2 =5.6.1 ［解析］画岀不等式组表示的可行域如图中阴影部分所示，由z=y-ax ，得 y=ax+z,要使z 取最大值时 的最优解有无数个，则直线y=ax+z 必平行于y-x+ 1=0，所以a=1.【课堂考点探究】例1 ［思路点拨］(1)首先作岀满足条件的平面区域，然后观察区域的形状;(2)首先画岀不等式组表示的 平面区域，然后分析得岀直线y=kx+-将平面区域分为面积相等的两部分时所经过的定点，即可列方程求5.5 ［解析］由- (3,4)(1)C (2)- ［解析］⑴作岀不等式组表示的平面区域，如图中阴影部分所示，由图知平面区域是一个等 腰三角形，故选C. ⑵画岀不等式组表示的平面区域，如图中阴影部分所示，由图可知，直线y=kx —恒经过点A -，当直线 y=kx+_再经过BC 的中点D--时,平面区域被直线y=kx+-分为面积相等的两部分.将点D 的坐标代入 直线方程得-=-k+-,解得k=-. 变式题(1)A (2)m ：2［解析］(1)作岀不等式组表示的平面区域，如图中阴影部分所示.联立方程得A(1,0),所以平面区域的面积为-X 1 X 3亠,故选A(2)作岀_ 所表示的平面区域，如图中的阴影部分所示.易知直线x=1与x- 2y+1=0的交点坐 得B(2,3)，标为理1,1).若使原不等式组所表示的平面区域的形状为三角形，则需满足点A位于直线x+y=m下方,据此有1+1<m即m的取值范围为m2例2 ［思路点拨］(1)首先画岀约束条件表示的可行域，然后通过平移等值线来确定目标函数的最值.(2)作岀可行域，求岀顶点的坐标，根据最优解的可能情况求岀a的值,再验证a的值是否符合题意.(1)B (2)B［解析］⑴作岀约束条件表示的可行域，如图中阴影部分所示.由得A -.令z=x-4y,则y=-x--z,平移直线y=-x--z,由图可知，当直线y=-x--z经过点A时，直线y=x--z在y轴上的截距最小此时z 有最大值，为-4,故选B.(2)作岀约束条件表示的平面区域如图中阴影部分所示，易知A(2,0),B(1,1).若z=ax+y过点A时取得最大值4,则2a=4,解得a=2,此时目标函数为z=2x+y,即y=-2x+z.平移直线y=-2x+z,易知当直线经过A(2,0)时,y=- 2x+z在y轴上的截距最大，此时z的最大为4,满足条件.若z=ax+y过点B时取得最大值4,则a+1=4,解得a=3,此时目标函数为z=3x+y,即y=-3x+z.平移直线y=-3x+z,易知当直线经过A(2,0)时,y=- 3x+z在y轴上的截距最大，此时z的最大值为6,不满足条件.综上所述，a=2.故选B.变式题(1)B (2)C ［解析］(1)画岀约束条件表示的可行域(如图中阴影部分所示).由z=-2x-y得y=- 2x-z.平移直线y=-2x-z,由图可得，当直线y=-2x-z经过点A时,直线在y轴上的截距最大，此时z取得最小值.由-解得故点A(2,3),.・.z min=-2X 2-3=-7，故选B(2)作岀可行域，如图中厶ABC及其内部所示，并作直线l:2x-y=0,平移直线丨，易知当丨经过点A —时,z取得最小值，.•• 2X ------ =- 4,解得a=3，故选C例3 ［思路点拨］设运送甲种货物x件，乙种货物y件，可获利润为乙然后根据已知条件确定x,y满足的不等式组和目标函数，再画岀平面区域，平移等值线找到最优解.62 ［解析］设运送甲种货物x件，乙种货物y件,可获利润为乙则由题意得即€且z=8x+10y.作岀不等式组对应的平面区域如图中阴影部分内的整点.由z=8x+10y得y=-」+—,平移直线y二_x+—,由图可知当直线y=-_x+—经过点B时,直线在y轴上的截距最大，此时z最大.由得即B(4,3),故Z max=8X 4+10 X 3=62,即一次运输获得的最大利润为62元.目标函数为z=60x+25y,画岀可行变式题A ［解析］设总收视人次为z.依题意得域如图中阴影部分所示.由图易知，目标函数在点M(6,3)处取得最大值.故选A2 2例4 ［思路点拨］(i)(x-1)+ y的几何意义为可行域内的点到点(1,0)的距离的平方，据此可求岀z的最小值;(2)利用z=——=2 •—的几何意义，即平面区域内的点(x,y)与定点 -的连线的斜率的2倍求解.(1)C (2)C2 2［解析］(1)作岀不等式组表示的可行域，如图中阴影部分所示.(x-1) + y的几何意义为可行域内的点到点(1,0)的距离的平方，由图可得，点P(2,1)到点(1,0)的距离最小，此时z的值最小，最小值z min=(2-1) +1 =2, 故选C(2)作岀不等式组表示的平面区域，如图中阴影部分所示.目标函数z—=2 •二表示平面区域内的点与点 -的连线的斜率的2倍.由图可得，目标函数在点qi,2)处取得最大值，最大值Z max=—一=3,在点B(2,1)处取得最小值，最小值Z min = ------ =—--- =—. 故目标函数Z=—的取值范围是-，故选C 变式题(1)B (2)B2 2［解析］⑴由题意，作岀约束条件表示的可行域，如图中阴影部分所示.由方程x+y+6y-k=o,得2 2X +(y+3) =9+k,则此问题可转化为求可行域内的点到定点C(0,- 3)的距离最小时实数k的值.点C到直线x+2y+2=0的距离d=——=一==,易知点C到直线x+2y+2=0的距离即为点C到可行域内的点的距离的最小值,则有9+k==，解得k=-—.故选B.⑵由题意，作岀不等式组所表示的平面区域，如图中阴影部分所示.不等式kx-y+k < 1等价于 X——，- 的几何意义是平面区域内的点与点(-1,-1 )连线的斜率，记P(-1,-1),由题意知k< Z min.由图可知点P与B(1 ,0)连线的斜率最小，所以Z min=——=_所以实数k的取值范围是-^-，故选B.tMV备用例题JIAOSHI 0C YONG UM【备选理由】 例1需要先由已知条件确定不等式组中的参数 ，再求目标函数的最值，增加了解题难度 例2是已知目标函数的最值求参数问题；例3考查线性规划在实际问题中的应用，进一步强化应用意识 例4与例5为非线性目标函数的问题，考查斜率型目标函数与距离型目标函数的最值 .例1 ［配合例2使用］［2018 •杭州二中模拟］已知不等式组 为9,若点P(x,y)€ S,则z=2x+y 的最大值为 ( )A3 B 6C 9D 12［解析］C 作岀不等式组对应的平面区域，如图中阴影部分所示 则A(a,a),B(a,-a),所以平面区域的面积 S=- - a - 2a=9,解得a=3,此时A(3,3),B(3,- 3).由图可得当z=2x+y 过点A(3,3)时,z=2x+y 取得最大值9,故选 C例2 ［配合例2使用］［2018 •汕头二模］设变量x,y 满足约束条件 最小值为-4,则a 的值是()A 1B 0C- 1 D -表示的平面区域S 的面积 目标函数z=3x- 2y 的［解析］C 作岀约束条件所对应的可行域(如图中阴影部分所示).目标函数z=3x-2y可化为y二x-_z,平移直线y=»-J,由图可知，当直线经过点A时直线在y轴上的截距最大，此时z最小.由- -解得-•••A(a-1,a),「. 3(a-1)-2a=-4,解得a=-1,故选C.例3 ［配合例3使用］［2018 •南昌模拟］某公司计划明年用不超过6千万元的资金投资本地养鱼场和远洋捕捞队.对本地养鱼场的调研结果是平均年利润率为0. 3,对远洋捕捞队的调研结果是平均年利润率为0. 4,为确保本地的鲜鱼供应，市政府要求该公司对远洋捕捞队的投资不得高于对本地养鱼场的投资的2倍.根据调研数据，明年该公司投资这两个项目的利润之和最大为_________________ 千万元.［答案］2.2［解析］设该公司对本地养鱼场的投资金额为x千万元，对远洋捕捞队的投资金额为y千万元，利润之和目标函数z=0. 3x+0. 4y.画岀约束条件表示的可行域如图中阴影部分所示，由z=0. 3x+0. 4y得y=-z--x,由图可知，当直线y=-z--x经过点M(2,4)时,z取得最大值此时Z max=0. 3 X 2+0. 4X 4=2. 2,所以最大利润为2. 2千万元.则目标函数z=——的例4 ［配合例4使用］［2018宜昌三模］若实数x,y满足不等式组最大值是()A 1 B- 一［解析］B 画岀 - 表示的可行域，如图中阴影部分所示.将z=— 变形为z=1-—表示可 行域内的点与 理3,5）连线的斜率，由图知可行域内的点P 与点A 连线的斜率最小，目标函数在点P 处取得 最大值.由 即 P(0,1).则 Z ma = —二-,故选 B.例5 ［配合例4使用］［2018 •河南名校考前预测］已知实数x,y 满足-的取值范围为( )A[2, —] B — —C —D [4,10]2 2［解析］C 作岀- 表示的可行域，如图中阴影部分所示.（x-i ）+（y+i ）的几何意义为可行域 内的点（x,y ）与MU ）的距离的平方.由图可知，点M 到直线x- 2y+1=0的距离的平方，就是目标函数的最 2 2 小值，最小值为 ,点M 到C(0,2)的距离的平方，就是目标函数的最大值，最大值为1+3=10.所 2 2 以z=(x-1) +(y+1)的取值范围为— ，故选C 可得 2 2则z=(x-1)+(y+i)第37讲基本不等式考试说明1 .了解基本不等式的证明过程.2.会用基本不等式解决简单的最大(小)值问题.【课前双基巩固】知识聚焦1. (1) a>0,b>0 (2)a=b2. (1)2ab (2)23. ——两个正数的算术平均数不小于它们的几何平均数4()2 一(2)-对点演练1.2 ［解析］当x>0时,x+-> 2 -=2,当且仅当x=1时等号成立，则x+-的最小值为2.2. ---------------------------------------------------------------------------------------- - ［解析］•••正实数x,y 满足2x+3y=2,「. xy= x2x - 3y <- ------------------------------------------- 二，当且仅当2x=3y=1,即x=-,y=-时等号成立,即xy的最大值为-.2 __3. 81 m ［解析］设矩形菜园的长和宽分别为x m,y m,则x>0,y>0,由题意有2(x+y)=36,二x+y=8,「.矩形菜园的面积S=xy< --------- =—=81 (m),当且仅当x=y=9时取等号，二当菜园的长和宽都为9 m时，菜园的面2 积最大,为81 m .4.1-2 一［解析］J x<0,.・・f(x)= -------- =2xi+仁-- -+K-2 - —+1=1-2 一，当且仅当-2x=—,即x二一时，等号成立，「.f (x)的最大值为1- 2 .5.3 ［解析］设x+2=t则x+一=t+_-2.又由x> 2得t >4,而函数y=t+--2在［2,+^ )上是增函数，因此当t=4时,t+ _-2即x+一取得最小值，最小值为4+--2=3.6.9 ［解析］2a+_= _ - 一=5+—+—> 5+2 •=9,当且仅当一=一，即a=3,b=9 时取等号••• 2a，的最小值为9.【课堂考点探究】例1 ［思路点拨］(1)根据已知等式凑岀定值，然后利用基本不等式求最大值；(2)根据所求式子凑岀定值然后利用基本不等式求解.(1)- ⑵2 一+2 一［解析］(1) •/ x»,y>0,「. xy= X 2x X 3y< ---------------- =-，当且仅当2x=3y=3,即x=,y=1 时，等号成立，故xy的最大值是-.⑵2a+——+—=a+b+a-b+——+—,丁a>b»,「. a+b —>2 _,当且仅当a+b= _时取等号,a-b+一>2 _,当且仅当a-b= 一时取等号，联立_ 解得 ___ •••当___时,a+b+a-b+——+—>2 _+2 一,即2a+——+ —取得最小值2 一+2 一例2 ［思路点拨］(1)设数列｛a n｝的公比为q,由题意可得到关于mn的等式,则可利用常数代换法求岀-+-的最小值;(2)首先将已知等式变为一+—=1,然后采用常数代换法将a+b变换为(a+b)——展开后再利用基本不等式求最值.m n 4(1)A (2)2+ ［解析］(1)设数列｛a n｝的公比为q(q^ 0).根据题意，得a m=q ,a n=q ,a4=q ,m+2n 8由a m =，得q =q ,•- m+?n=8, •- ---- =1,又mn € N,---------- +------ —>-+2 —=1，当且仅当一=—，即卩m=4,n=2 时取等号(2)因为3a+b=2ab,所以一+—=1,又a>0,b>0,故a+b=(a+b) _ — =2+—+_> 2+ 一,当且仅当一=_时取等号即a+b的最小值为2+ 一例3 ［思路点拨］首先根据条件等式用a,b表示岀c,并代入一中，利用基本不等式通过求最值确定a,b 的关系，进而将a+b-c转化为关于b的式子，最后通过配方求解.C ［解析］根据题意得c=a2-ab+4b2,所以一=— ------ =_+一-1》2 _-1=3，当且仅当-J,即a=2b时取等2 2 2 2号，所以a+b-c=2b+b-4b +2b -4b =-6b +3b=-6 -一+_,所以当b=时,a+b-c 取得最大值-，故选C应用演练2 2 2 2 2 21. A ［解析］T 0< =••• 0<x ~,1-4x >0,则y=x (1-4x ) = X (4x ) X (1-4x ) ------- —匚,当且仅，等号成立，即y=x (1- 4x )的最大值为一，故选A— 2 2 当x= 士一时2. D ［解析］因为a=-［(a+b)+(a-b)］,所以a+—+一=(a+b) +—+-(a-b)—又因为-(a+b) +—>2 ，当且仅当-(a+b)=——时取等号，-(a-b)+—>2 -= 一,当且仅当-(a-b)=—时取等号，所以a—+—>3 一,当且仅当-即 -时取等号，故选D.3. C ［解析］由函数的解析式可得M1,1),则-+-=1(a>0,b>0),则a+b=(a+b) - - =2—+- >2+2 - •- =4,当且仅当a=b=2时等号成立.综上,a+b的最小值为4,故选C4. 8+4 ［解析］由题得-+-= - - • (2x+3y)=8—+—> 8+2 —• —=8+4 ，当且仅当一=—，即x=——,y=——时等号成立.5. 8 ［解析］Ta,b,c 均为正数，且abc=4(a+b),「. c= --- ,• a+b+c=a+b+ ------ =a+b+4 >2 • -+2 • -=8,当且仅当a=2,b=2时取等号,• a+b+c的最小值为8.例4 ［思路点拨］(1)首先利用导数与函数单调性的关系将问题转化为一个不等式恒成立问题，然后转化为求函数的最值问题，最后利用基本不等式求函数的最值；(2)首先利用基本不等式确定两个对数MN 中的真数的取值范围，由此得到MN的取值范围，然后计算岀Q的值，进而得到MN,Q的大小关系.(1)D (2)B ［解析］(1)函数f (x)的定义域为(0,+ V,f' (x)=4x+--a.由已知有f (x)> 0在定义域上恒成立, 所以4x+-a >0对于x € (0,+s)恒成立，即a< 4x+_恒成立,所以a< - .因为4x+_ >2 • -=4, 当且仅当x=-时等号成立，所以a < 4,故选D⑵•••f(a)=f(b),.・.|lg a|=| lg b|,「.lg a+lg b=0,即ab=1. J _= = ------- = ---- <—=—,••. Nlog 2 _= <-2. ---------------- >_乂，二Mlog ------ >-2.又•.•Q=n _=-2,二M>Q>故选B.变式题(1)A (2)- 懈析］(1)由题意得f' (x)=3ax +2bx+c.因为函数f (x)在R上单调递增，所以可得c>-，且a>0所以^>———> --------------------- =1,当且仅当c=b=3a时等号成立，所以——的最小值为1,故选A⑵易得函数f(x)=e x-e-x+x3+3x在R上单调递增，且为奇函数,又f (2a-1)+f (b-1)=0，即f (2a-1)=-f (b-1)，所以2a-1=1-b,即2a+b=2.所以一+——= ---------- -- ---------- +b+-=2(a+1)+b+—+--4 —+-= 一-［2(a+1)+b］ x-=- x —— ------ >-x (5+4)=-,当且仅当a=-,b=-时取等号.例5 ［思路点拨］(1)首先求岀运输到第x年年底该大货车运输累计收入与总支岀的差，然后令其大于0,即可得到结论;(2)利用利润=累计收入+销售收入-总支岀，可得年平均利润，再利用基本不等式即可得结论.解:(1)设大货车运输到第x年年底，该车运输累计收入与总支出的差为y万元，2 *则y=25x- ［6x+x(x-1 )］-50=-x +20x- 50(0<x< 10,x € N),由-x2+20x- 50>0，可得10-5 -<x< 10.••• 2<10-5 _<3,A大货车运输到第3年年底该车运输累计收入超过总支岀.⑵•/利润=累计收入+销售收入-总支岀，。

6-5 数学归纳法课时规范练(授课提示：对应学生用书第285页)A 组　基础对点练1．(2018·商丘期末)用数学归纳法证明：(n ＋1)(n ＋2)·…·(n ＋n )＝2n ×1×3×…×(2n －1)时，从“k 到k ＋1”左边需增加的代数式是 (k ＋1)(k ＋2)…(k ＋k )(4k ＋1) ．解析：从“k 到k ＋1”左边需增加的代数式是：(k ＋2)(k ＋3)·…·(k ＋k )(k ＋1＋k )(k ＋1＋k ＋1)－(k ＋1)·(k ＋2)·…·(k ＋k )＝(k ＋2)(k ＋3)·…·(k ＋k )·[(k ＋1＋k )(k ＋1＋k ＋1)－(k ＋1)]＝(k ＋1)(k ＋2)·…·(k ＋k )(4k ＋1)．2．(2018·杭州期末)设正项数列{a n }的前n 项和为S n ，若a 1＝1,2S n ＝a n ·a n ＋1(n ∈N *)．(1)求a 2，a 3以及数列{a n }的通项公式；(2)设b n ＝2－a n ，数列{b n }的前n 项和为T n .①求T n ；②证明：＋＋…＋≤2T n (n ∈N *)．1S 11S 21S n 解析：(1)∵a 1＝1,2S n ＝a n ·a n ＋1，∴2a 1＝a 1·a 2，即a 2＝2，∴2(a 1＋a 2)＝a 2·a 3，即a 3＝3.猜想a n ＝n ，证明如下：①当n ＝1时，显然成立，②假设当n ＝k 时成立，即a k ＝k ，则S k ＝.k k ＋1 2那么当n ＝k ＋1时，a k ＋1＝＝＝k ＋1，2S k a k k k ＋1 k故n ＝k ＋1时也成立，由①②可得a n ＝n 对于n ∈N *都成立，∴数列{a n }的通项公式为a n ＝n .(2)易知b n ＝n ，(12)①T n ＝＝1－.12(1－12n)1－1212n②由(1)可知S n ＝，n n ＋1 2∴＝＝2，1S n 2n n ＋1 (1n －1n ＋1)∴＋＋…＋1S 11S 21S n＝2(1－12＋12－13＋13－14＋…＋1n －1n ＋1)＝2.(1－1n ＋1)要证明＋＋…＋≤2T n ，1S 11S 21S n 只要证明2≤2，只要证≥，只要证n ＋1≤2n ，(1－1n ＋1)(1－12n )1n ＋112n ①当n ＝1时，不等式显然成立，②假设当n ＝k 时，不等式成立，即k ＋1≤2k ，那么当n ＝k ＋1时，k ＋2＝k ＋1＋1≤2k ＋1≤2k ＋1，即当n ＝k ＋1时不等式成立，由①②可得n ＋1≤2n 对于n ∈N *都成立，故＋＋…＋≤2T n (n ∈N *)．1S 11S 21S n 3．函数f (x )＝ln(x ＋1)－(a >1)．ax x ＋a (1)讨论f (x )的单调性；(2)设a 1＝1，a n ＋1＝ln(a n ＋1)，证明：<a n ≤.2n ＋23n ＋2解析：(1)f (x )的定义域为(－1，＋∞)，f ′(x )＝.x [x － a 2－2a ] x ＋1 x ＋a 2①当1<a <2时，若x ∈(－1，a 2－2a )，则f ′(x )>0，f (x )在(－1，a 2－2a )上是增函数；若x ∈(a 2－2a,0)，则f ′(x )<0，f (x )在(a 2－2a,0)上是减函数；若x ∈(0，＋∞)，则f ′(x )>0，f (x )在(0，＋∞)上是增函数．②当a ＝2时，f ′(x )≥0，当且仅当x ＝0时，f ′(x )＝0成立，f (x )在(－1，＋∞)上是增函数．③当a >2时，若x ∈(－1,0)，则f ′(x )>0，f (x )在(－1，0)上是增函数；若x ∈(0，a 2－2a )，则f ′(x )<0，f (x )在(0，a 2－2a )上是减函数；若x ∈(a 2－2a ，＋∞)，则f ′(x )>0，f (x )在(a 2－2a ，＋∞)上是增函数．(2)证明：由(1)知，当a ＝2时，f (x )在(－1，＋∞)上是增函数．当x ∈(0，＋∞)时，f (x )>f (0)＝0，即ln(x ＋1)>(x >0)．2x x ＋2又由(1)知，当a ＝3时，f (x )在[0,3)上是减函数．当x ∈(0,3)时，f (x )<f (0)＝0，即ln(x ＋1)<(0<x <3)．3x x ＋3下面用数学归纳法证明<a n ≤.2n ＋23n ＋2①当n ＝1时，由已知得<a 1＝1；23②假设当n ＝k 时结论成立，即<a k ≤.2k ＋23k ＋2当n ＝k ＋1时，a k ＋1＝ln(a k ＋1)>ln >＝.(2k ＋2＋1)2×2k ＋22k ＋2＋22k ＋3a k ＋1＝ln(a k ＋1)≤ln <＝.(3k ＋2＋1)3×3k ＋23k ＋2＋33k ＋3即当n ＝k ＋1时，有<a k ＋1≤，结论成立．2k ＋33k ＋3根据①②知对任何n ∈N *结论都成立．B 组　能力提升练1．(2018·南京期末)把圆分成n (n ≥3)个扇形，用4种颜色给这些扇形染色，每个扇形恰染一种颜色，并且要求相邻扇形的颜色互不相同，设共有f (n )种方法．(1)写出f (3)，f (4)的值；(2)猜想f (n )(n ≥3)，并用数学归纳法证明．解析：(1)n ＝3时，第一个有4种方法，第二个有3种方法，第三个有2种方法，可得f (3)＝24；n ＝4时，第一个有4种方法，第二个有3种方法，第三个与第一个相同有1种方法，第四个有3种方法，或第一个有4种方法，第二个有3种方法，第三个与第一个不相同有2种方法，第四个有2种方法，可得f (4)＝36＋48＝84.(2)当n ≥4时，首先，对于第1个扇形a 1，有4种不同的染法，由于第2个扇形a 2的颜色与a 1的颜色不同，所以对于a 2有3种不同的染法，类似地，对扇形a 3，…，a n －1均有3种染法．对于扇形a n ，用与a n －1不同的3种颜色染色，但是，这样也包括了它与扇形a 1颜色相同的情况，而扇形a 1与扇形a n 颜色相同的不同染色方法数就是f (n －1)，于是可得f (n )＝4×3n －1－f (n －1)，猜想f (n )＝3n ＋(－1)n ·3.①当n ＝3时，左边f (3)＝24，右边33＋(－1)3·3＝24，所以等式成立②假设n ＝k (k ≥3)时，f (k )＝3k ＋(－1)k ·3，则n ＝k ＋1时，f (k ＋1)＝4×3k －f (k )＝4×3k －[3k ＋(－1)k ·3]＝3k ＋1＋(－1)k ＋1·3，即n ＝k ＋1时，等式也成立．综上，f (n )＝3n ＋(－1)n ·3(n ≥3)．2．数列{a n }满足a n ＋1＝，a 1＝1.a n 2a n ＋1(1)证明：数列是等差数列；{1a n }(2)求数列的前n 项和S n ，并证明＋＋…＋>.{1a n }1S 11S 21S n n n ＋1解析：(1)证明：∵a n ＋1＝，a n 2a n ＋1∴＝，化简得＝2＋，1a n ＋12a n ＋1a n 1a n ＋11a n 即－＝2，故数列是以1为首项，2为公差的等差数列．1a n ＋11a n {1a n }(2)由(1)知＝2n －1，∴S n ＝＝n 2.1a n n 1＋2n －1 2法一　＋＋…＋＝＋＋…＋>＋＋…＋＝＋1S 11S 21S n 1121221n 211×212×31n n ＋1 (1－12)(12－13)＋…＋＝1－＝.(1n －1n ＋1)1n ＋1n n ＋1法二　(数学归纳法)当n ＝1时，＝1，＝，不等式成立．1S 1n n ＋112假设当n ＝k 时，不等式成立，即＋＋…＋>.1S 11S 21S k k k ＋1则当n ＝k ＋1时，＋＋…＋＋>＋，1S 11S 21S k 1S k ＋1k k ＋11 k ＋1 2又＋－＝1－＋－1＋＝－＝kk ＋11 k ＋1 2k ＋1k ＋21k ＋11 k ＋1 21k ＋21k ＋2k k ＋1 2>0，1 k ＋2 k ＋1 2∴＋＋…＋＋>，1S 11S 21S k 1S k ＋1k ＋1k ＋2∴原不等式成立．3．设函数f (x )＝x 2＋m ln(x ＋1)．(1)若函数f (x )是定义域上的单调函数，求实数m 的取值范围；(2)若m ＝－1，试比较当x ∈(0，＋∞)时，f (x )与x 3的大小；(3)证明：对任意的正整数n ，不等式e 0＋e －1×4＋e －2×9＋…＋e(1－n )n 2<成立．n n ＋3 2解析：(1)∵f ′(x )＝2x ＋＝，又函数f (x )在定义域上是单调函数，mx ＋12x 2＋2x ＋m x ＋1∴f ′(x )≥0或f ′(x )≤0在(－1，＋∞)上恒成立．若f ′(x )≥0在(－1，＋∞)上恒成立，即函数f (x )是定义域上的单调递增函数，则m ≥－2x 2－2x ＝－22＋在(－1，＋∞)上恒成立，由此可得m ≥；(x ＋12)1212若f ′(x )≤0在(－1，＋∞)上恒成立，即函数f (x )是定义域上的单调递减函数，则m ≤－2x 2－2x ＝－22＋在(－1，＋∞)上恒成立．(x ＋12)12∴y ＝－22＋在(－1，＋∞)上没有最小值，(x ＋12)12∴不存在实数m 使f ′(x )≤0在(－1，＋∞)上恒成立．综上所述，实数m 的取值范围是.[12，＋∞)(2)当m ＝－1时，函数f (x )＝x 2－ln(x ＋1)．令g (x )＝f (x )－x 3＝－x 3＋x 2－ln(x ＋1)，则g ′(x )＝－3x 2＋2x －＝－，1x ＋13x 3＋ x －1 2x ＋1显然，当x ∈(0，＋∞)时，g ′(x )<0，∴函数g (x )在(0，＋∞)上单调递减．又g (0)＝0，∴当x ∈(0，＋∞)时，恒有g (x )<g (0)＝0，即f (x )－x 3<0恒成立．故当x ∈(0，＋∞)时，f (x )<x 3.(3)证明：①当n ＝1时，左边＝e 0＝1，右边＝＝2，原不等式成立．1×42②设当n ＝k 时，原不等式成立，即e 0＋e －1×4＋e －2×9＋…＋e(1－k )k 2<，　k k ＋3 2则当n ＝k ＋1时，左边＝e 0＋e －1×4＋e －2×9＋…＋e(1－k )k 2＋e(1－k －1)(k ＋1)2<＋e －k (k ＋1)2，k k ＋3 2只需证明＋e －k (k ＋1)2<，　k k ＋3 2 k ＋1 k ＋4 2即证e －k (k ＋1)2<k ＋2，即证－k (k ＋1)2<ln(k ＋2)．由(2)知x 2－x 3<ln(x ＋1)(x ∈(0，＋∞))，即x 2(1－x )<ln(x ＋1)，令x ＝k ＋1，即有－k (k ＋1)2<ln(k ＋2)，∴当n ＝k ＋1时不等式成立．由①②知，原不等式成立．。