【强烈推荐】七年级相交线和平行线的证明(精华)

平行线与相交线的性质推导与证明平行线和相交线是几何中常见的概念，它们之间存在一些有趣的性质和定理。

本文将推导和证明平行线和相交线的性质，以及相关的定理。

1. 平行线的性质推导与证明在几何中，平行线是指在同一个平面内永远不会相交的两条直线。

接下来我们将推导平行线的性质，并给出相应的证明。

性质1：平行线具有传递性。

即若直线l1与l2平行，直线l2与l3平行，则直线l1与l3平行。

证明：设直线l1与l2平行，直线l2与l3平行。

可以假设直线l1与直线l3不平行，并且在某一点O处相交。

由于直线l1与直线l3不平行，所以在点O处有两条直线通过。

设通过点O的直线分别为m1和m2，其中直线m1与l1平行，直线m2与l3平行。

根据平行线的定义，直线m1与直线m2是平行的。

又根据平行线与相交线的性质，直线m1与直线l2平行，直线m2与直线l2平行。

因此，直线m1与直线l2、直线l2与m2平行。

然而，这与已知条件直线l1与l2平行，l2与l3平行产生矛盾。

因此，直线l1与l3必须平行。

于是我们证明了平行线的传递性。

2. 相交线的性质推导与证明相交线是指在同一个平面内相交于一点的两条非重合直线。

下面我们将推导相交线的性质，并给出相关的证明。

性质2：相交线的对顶角相等。

即相交线AB和CD形成的对顶角α与β相等。

证明：考虑平面内有两条相交线AB和CD，它们相交于点O。

接下来，我们需要证明∠AOC = ∠DOG，即角α = β。

通过点O分别作OA、OC和OD三条射线，构成△AOC和△COD。

根据△AOC和△COD的对应边分别平行，我们可以得出△AOC与△COD相似。

根据相似三角形的性质，两个相似三角形中对应角度相等。

因此，∠AOC = ∠COD，即角α = β。

因此，我们证明了相交线的对顶角相等的性质。

3. 平行线与相交线的定理在了解了平行线和相交线的性质之后，我们可以推导一些重要的定理，这些定理在几何证明中起到重要的作用。

平行线与相交线的性质和判定方法平行线和相交线是几何学中非常重要的概念。

它们的性质和判定方法不仅在数学中有广泛应用，而且在实际生活中也有很多实际意义。

本文将介绍平行线和相交线的性质，并详细说明判定两条线是否平行或相交的方法。

一、平行线的性质和判定方法平行线是指在同一个平面中永不相交的两条直线。

以下是平行线的性质和判定方法：1. 特殊角的对应角相等若两条平行线被一条与它们相交的直线切割成多个角，那么这些角的对应角（位于两条平行线的内部、外部但同侧的角）相等。

2. 平行线间的距离相等两条平行线之间的任意两个点到这两条平行线的距离相等。

3. 平行线的证明方法- 对于已知的平行线，可以使用证明方法来确认，如使用平行线的定义和定理进行推导和证明。

- 可以利用等角和同位角的性质，通过夹角相等或对应角相等来判断两条线是否平行。

二、相交线的性质和判定方法相交线是指在同一个平面上相交的两条直线。

以下是相交线的性质和判定方法：1. 相交线上的相邻角互补若两条相交的直线之间有三个角，那么其中的相邻角（位于两条直线之间的两个角）互补，即它们的和为180度。

2. 四条线的交叉有序性若四条线两两相交于不同的点，并且这些点按照一定的顺序排列，那么这四条线相交于一个共同的交点。

3. 相交线的证明方法- 相交线的证明方法可以使用平行线的性质，如果两条线不平行，则一定相交。

- 利用等角和同位角的性质，可以根据角的性质进行相交线的证明。

三、应用示例下面通过几个简单的示例来说明平行线和相交线的性质和判定方法：例1：判断线段AB是否平行于线段CD。

解：连接线段AB和CD的两个端点，如果这两条连接线段的直线平行于CD，则线段AB与CD平行。

例2：已知直线l和直线m分别与直线n相交，且∠1和∠2为同位角，证明直线l和直线m平行。

解：根据同位角的性质可得∠1和∠2互补，即∠1+∠2=180度。

又因为直线l和直线m分别与直线n相交，所以∠1和∠2为同位角，故直线l与直线m平行。

平行线与相交线的证明平行线与相交线是几何学中常见的概念，它们之间存在着一些有趣的性质和定理。

本文将探讨平行线与相交线之间的关系，并给出相关证明。

1.平行线的定义在平面几何中，两条直线如果在同一平面内无论延长多远都不会相交，那么它们被称为平行线。

常用符号表示为：∥。

2.相交线的定义两条直线在同一平面内相交于一点，则这两条直线被称为相交线。

3.平行线与相交线之间的性质（1）两条平行线分别与一条相交线相交，所得的对应角是相等的。

证明：设直线l和m为平行线，n为相交线，交于点A，如图所示。

A-------\| || n || |B-------C\要证明∠BAC=∠BCA，我们假设∠BAC=α，∠BCA=β。

由平行线l和m的性质可知，∠BAC与∠ACB是同位角，同位角相等，即α=∠ACB。

又∠BAC与∠BCA是内错角，内错角相等，即α=β。

综上所述，根据角的性质，得证∠BAC=∠BCA。

（2）两条平行线分别与一条相交线相交，所得的内错角之和等于180°。

证明：设直线l和m为平行线，n为相交线，交于点A，如图所示。

A-------\| || n || |B-------C\要证明∠BAC+∠BCA=180°，根据前述证明可知∠BAC=∠BCA=α。

根据角的定义，可知α+α=180°。

通过简单的运算得到2α=180°，即α=90°。

综上所述，根据角的性质，得证∠BAC+∠BCA=180°。

通过以上证明可以得出，平行线与相交线之间存在着一些重要的性质和定理，这些性质和定理在几何学中具有重要的应用。

深入理解这些性质和定理，有助于我们更好地理解和解决与平行线和相交线相关的问题。

总结：本文通过证明的方法，阐述了平行线与相交线的性质和定理。

通过证明我们可以得出两条平行线与一条相交线的角度关系和内错角之和等于180°的结论。

这些定理和性质在几何学中起着重要的作用，并且可以应用到实际问题中。

平行线的证明与性质一、平行线的断定方法1.平行：假如两条直线a与b不相交，那么这两条直线a与b互相平行，记作a//b．2.平行公理：经过直线外一点，有且只有一条直线与这条直线平行．3.平行公理推论：假如两条直线都与第三条直线平行，那么这两条直线也互相平行．即假如a//b，b//c，那么a//c．4.断定方法1：两条直线被第三条直线所截，假如同位角相等，那么这两条直线互相平行．简单说成：同位角相等，两直线平行．5.在同一平面内，两条不同的直线的位置关系只有2种，就是相交和平行．例1.〔1〕在同一平面内，以下说法正确的有〔〕①过两点有且只有一条直线；②两条不同的直线有且只有一个交点；③过一点有且只有一条直线与直线垂直；④过一点有且只有一条直线与直线平行．A．1个B．2个C．3个D．4个〔2〕以下各种说法，正确的选项是〔〕①在平面内的两条线段，假如没有公一共点，那么这两条线段平行；②假如两条射线平行，那么这两条射线没有公一共点；③假如两条直线没有公一共点，那么这两条直线平行；④在平面内的两条直线，不相交那么一定平行A．②③④B．②③C．①②D．②④答案：〔1〕B 〔2〕D例2.〔1〕如图，假设∠1=∠2，那么_________//_________；假设∠2=∠3，那么____∥_____；假设∠3=_________，那么l3//l4；假设∠4=_________，那么l1//l2．〔2〕l1.l2.l3被l4所截，假设要使l1//l3，那么添加的一个条件是〔〕A．∠1=∠2 B．∠2=∠3C．∠1=∠3 D．∠1=∠4〔3〕如图，直线MN分别交AB.CD于E.F，∠MFD=50°，EG平分∠MEB，那么当∠MEG=_________时，AB//CD．答案：〔1〕l3 l4；l1 l2；∠4；∠1〔2〕C〔3〕25°提示：当∠MEB＝∠MFD时，AB∥CD即∠1＝∠2＋∠3又EG平分∠MEB，∴∠2＝∠3∴2∠2＝∠1＝50°，∴∠2＝25°例3.〔1〕如图，∠2=3∠1，且∠1＋∠3=90°，试说明AB//CD．∵∠1＋∠2=180°，且∠2=3∠1，∴∠1＋3∠1=180°，∴∠1＝45°又∠1＋∠3=90°，∴∠3=45°∴∠1＝∠3，∴AB//CD．〔2〕如图，∠1=∠2，AF平分∠EAQ，BC平分∠ABN，怎样说明PQ//MN．解：∵AF平分∠EAQ，BC平分∠ABN，∴∠EAQ＝2∠1，∠EBN＝2∠2，又∠1＝∠2，∴∠EAQ＝∠EBN∴PQ∥MN〔3〕如图，直线A.B.c被直线D.e所截，∠1=∠2，∠3=∠4，那么直线a与直线c平行吗？为什么？解：直线a与直线c平行．理由如下：∵∠1＝∠2，∴a∥b又∠3＝∠4，∴b∥c∴a∥c(平行公理推论)二、平行线的断定方法1.断定方法2：两条直线被第三条直线所截，假如内错角相等，那么这两条直线平行.简单说成：内错角相等，两直线平行.2.断定方法3：两条直线被第三条直线所截，假如同旁内角互补，那么这两条直线平行.简单说成：同旁内角互补，两直线平行.例1.〔1〕如图，要使得AB//CD，必须具备的条件是________或者________或者__________.〔2〕如图，以下条件中，不能判断直线l1//l2的是〔〕A．∠1=∠3 B．∠2=∠3C．∠4=∠5 D．∠2＋∠4=180°〔3〕如图，以下判断错误的选项是〔〕A．∵∠1=∠2，∴l3//l4B．∵∠3=∠4，∴l3//l4C．∵∠1=∠3，∴l3//l4D．∵∠2=∠3，∴l1//l2〔4〕如图，∠1=∠2，那么在结论：①∠3=∠4 ②AB//CD ③AD//BC中〔〕A．三个都正确B．只有一个正确C．三个都不正确D．只有一个不正确〔5〕如图，①假如∠1=________，那么DE//AC；②假如∠1=________，那么EF//BC；③假如∠AED＋_________=180°，那么AC//ED；④假如∠2＋_______=180°，那么AB//DF.答案：〔1〕∠1=∠2，∠3=∠2，∠2＋∠4=180°〔2〕B 〔3〕C 〔4〕B〔5〕①∠C ②∠FED ③∠A ④∠AED例2.如图，∠B=∠C，∠B＋∠D=180°，试说明为什么BC//DG？解：因为∠B=∠C，∠B＋∠D=180°，所以∠C＋∠D=180°，所以BC//DG.例3.如图，∠B=∠C，∠1=∠D，试问OM//AB吗？为什么？解：OM//AB．理由如下：因为∠B=∠C，所以AB∥CD又∠1=∠D，所以OM//CD所以 AB∥OM.例4.如图，BE平分∠ABD，DE平分∠BDC，∠1＋∠2=90°，AB//CD吗？为什么？解：AB//CD．理由如下：因为BE平分∠ABD，DE平分∠BDC，所以∠ABD＝2∠1，∠BDC＝2∠2所以∠ABD＋∠BDC＝2〔∠1＋∠2〕又∠1＋∠2＝90°，所以∠ABD＋∠BDC＝180°所以AB∥CD.例5.如图，AC是∠BAD的平分线，∠1=∠3，∠2=∠4，试说明以下结论为什么成立？〔1〕AB//CD 〔2〕AC//DE解：〔1〕因为AC平分∠BAD，所以∠1＝∠2.又∠1＝∠3，所以∠2＝∠3.所以AB∥CD.〔2〕因为∠2＝∠3，∠2＝∠4.所以∠3＝∠4，所以AC∥DE.三、平行线的性质性质1 两条平行线被第三条直线所截，同位角相等；性质2 两条平行线被第三条直线所截，内错角相等；性质3 两条平行线被第三条直线所截，同旁内角互补.简单说成：两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补.例1.〔1〕如图，AB//CD，直线EF与AB.CD分别相交于G、H，∠AGE=60°，那么∠EHD的度数是〔〕A．30°B．60°C．120°D．150°〔2〕如图，直线l1//l2，AB⊥CD，∠1=34°，那么∠2的度数是________.〔3〕如图，∠1=∠2，∠3=80°，那么∠4等于〔〕A．80°B．70°C．60°D．50°〔4〕如图，是明明养的小乌龟上的一块花纹，DE//FG，BC//DE，EF//DC，DC//AB，那么∠B 与∠F的关系是_____________.答案：〔1〕C 〔2〕56°〔3〕A 〔4〕∠B=∠F例2.〔1〕如图，AB//EF//CD，EG//DB，图中与∠1相等的角〔∠1除外〕一共有〔〕A．6个B．5个C．4个D．3个〔2〕如图，是赛车跑道的一段示意图，其中AB//DE，测得∠B=140°，∠D=120°，那么∠C的度数为〔〕A．120°B．100°C．140°D．90°〔3〕在同一平面内有两个角，它们有一条边在同一直线上，另一边互相平行，那么这两个角的关系是〔〕A．相等B．互补C．相等且互补D．相等或者互补答案：〔1〕B 〔2〕B 〔3〕D例3.如图，AD⊥BC于D，EG⊥BC于G，且∠E=∠3，试说明AD平分∠BAC的理由.解：∵AD⊥BC，EG⊥BC，∴AD∥EG，∴∠E＝∠2，∠3＝∠1又∠E=∠3，∴∠1＝∠2∴AD平分∠BAC例4.，如图，∠1=∠2，∠A=∠F，试说明为什么∠C=∠D？解：∵∠A＝∠F，∴DF∥AC，∴∠C＝∠4∵∠1=∠2，∠1=∠3，∴∠2＝∠3，∴DB∥EC，∴∠D＝∠4又∠C＝∠4∴∠C＝∠D例5.如图，∠1＋∠2=180°，∠B=∠3，试判断∠AED与∠C的大小关系，并说明理由.解：∠AED＝∠C．理由如下：∵∠1＋∠2＝180°，∠1＋∠5＝180°∴∠2＝∠5，∴AB∥EF∴∠4＝∠3又∠B＝∠3，∴∠4＝∠B∴DE∥BC，∴∠AED＝∠C例6.如图，AD⊥AB，DE平分∠ADC，CE平分∠BCD，且∠1＋∠2=90°，那么BC⊥AB，说明理由.解：∵DE平分∠ADC，CE平分∠BCD∴∠1＝∠3，∠2＝∠4又∠1＋∠2＝90°∴∠1＋∠2＋∠3＋∠4＝180°即∠ADC＋∠BCD＝180°∴ AD∥BC又 AD⊥AB∴ BC⊥AB一、选择题1.以下说法正确的选项是〔〕A．不相交的两条直线是平行线B．互相平行的两条直线在同一平面内C．同一平面内，不相交的两条线段是平行线D．假设线段AB和线段CD无交点，那么它们一定平行2.直线l外点A，过点A作直线与l平行，那么这样的直线〔〕A．有两条B．不存在C．有且只有一条D．有一条或者不存在3.以下推理正确的选项是〔〕A．因为a∥d，b∥c，所以c//dB．因为a∥c，b//d，所以c∥dC．因为a∥b，a∥c，所以b//cD．因为a∥b，c//d，所以a∥c4.在同一平面内，直线a与b相交，直线c与b相交，那么a，c的位置关系是〔〕A．一定相交B．一定平行C．也可能平行，也可能相交D．上述都不对5.在同一平面内，以下说法：①过两点有且只有一条直线；②两条不一样的直线有且只有一个公一共点；③经过直线外一点有且只有一条直线与直线垂直；④经过直线外一点有且只有一条直线与直线平行，其中正确的个数为〔〕A．1个B．2个C．3个D．4个6.如下图立方体，以下说法正确的有〔〕①AA1∥BB1；②AA1∥CC1；③AA1∥DD1；④AA1∥A1B1．A．0个 B．1个C．2个 D．3个7.在同一平面内有三条直线，假设其中两条平行但与第三条直线不平行，那么它们的交点的个数为〔〕A．0个 B．1个C．2个 D．3个8.如下图，假如∠D=∠EFC，那么〔〕A．AD//BC B．EF//BCC．AB//DC D．AD//EF9.如下图，P是直线l外一点，直线l1，l2都过点P，假如l1//l，那么l2与l__________，根据____________．10.如下图，在∠AOB的内部有一点P，∠AOB=60°．(1)过点P作PC∥OA，PD∥OB；(2)量出∠CPD的度数，说出它与∠AOB的关系．11.假设直线a∥b，b∥c，c∥d，那么a∥d吗?为什么?对于n条直线l1，l2，l3，…，ln，假设l1∥l2，l2∥l3，…，ln－1∥ln，那么又可得出什么结论?BCCCCDCD〔1〕略〔2〕∠CPD=60°，∠CPD与∠AOB相等或者互补．10.解：∵a∥b，b∥c，∴a∥c，又c∥d，∴a∥d．同理l1∥l2∥l3∥…∥ln－1∥ln．作业1一、选择题1.如下图，以下条件中，能判断AB//CD的是〔〕A．∠BAD=∠BCD B．∠1=∠2C．∠3=∠4 D．∠BAC=∠ACD2.如下图，在以下给出的条件中，不能判断AB//DF的是〔〕A．∠A＋∠2=180° B．∠A=∠3C．∠1=∠4 D．∠1=∠A3.如下图，∠1=∠2，∠A=∠D，那么以下推理正确的选项是〔〕A．因为∠1=∠2，所以AB//CDB．因为∠1=∠2，所以BE//CFC．因为∠A=∠D，所以AB//CDD．因为∠1=∠2，所以∠1=∠2=∠3=∠4二、填空题4.如下图.〔1〕如图∠1=∠3，可推出_______//________，其理由是________________；〔2〕假如∠2=∠4，可推出_______//__________，其理由是________________；〔3〕假如∠B＋∠BAD=180°，那么可推出_______//__________，其理由是________________.5.如下图，请你填写上一个适当的条件：___________，使AD//BC.6.在同一平面内，假设直线a1⊥a2，a2//a3，a3⊥a4，a4//a5，…，a9⊥a10，那么a1与a10的位置关系为___________〔a1与a10不重合〕.三、综合题7.如下图，∠A=∠ACE，∠B=∠BDF，且∠A=∠B，那么CE//DF吗？8.如下图，点B在直线DE上，AB⊥CB，∠A=50°，∠CBD=40°，那么AC与BD是否平行？为什么？9.如下图，直线EF交直线AB，CD于点M，N，∠EMB=∠END，MG平分∠EMB，NH平分∠END．试探究MG与NH的位置关系，并说明理由.4.〔1〕AD//BC，内错角相等，两直线平行.〔2〕AB∥CD，内错角相等，两直线平行.〔3〕AD∥BC，同旁内角互补，两直线平行.5.∠ADB＝∠DBC或者∠DAB＋∠ABC＝180°.6.a1⊥a107.解：CE//DF．理由如下：因为∠A=∠ACE，∠B=∠BDF，且∠A=∠B，所以∠ACE＝∠BDF.因为∠ACE＋∠ECD＝∠BDF＋∠CDF＝180°，所以∠ECD＝∠CDF，所以CE//DF.8.解：平行，理由如下：∵AB⊥CB∴∠ABC=90°∵∠CBD=40°∴∠ABE=180°－∠ABC－∠CBD=180°－90°－40°=50°∵∠A=50°∴∠A=∠ABE∴AC//BD9.解：∵MG平分∠EMB∴∠EMG=∠EMB∵NH平分∠END∴∠ENH=∠END又∠EMB=∠END∴∠EMG=∠ENH∴MG//NH作业2一、填空题1.如图，直线a//b，∠1=70°，那么∠2=_______.2.在第1题中，假设a//b，那么∠1与∠3的关系是_________________.3.如图，l1//l2，那么∠1=________.4.如图，DE//BC，∠D=2∠DBC，∠1=2∠2，那么∠DEB=________.二、选择题5.如图，假设AD∥BC，那么有：①∠A＋∠B＝180°，②∠B＋∠C＝180°，③∠C＋∠D＝180°．以上结论正确的选项是〔〕A．①B．②C．③D．①③6.如图，CD//AB，OE平分∠DOB，假设∠D=50°，那么∠AOE为〔〕A．145°B．155°C．165°D．175°7.假设两条直线被第三条直线所截，那么一组同旁内角的平分线〔〕A．互相平行B．互相垂直C．重合D．相交三、综合题8.如图，AB//CD，∠B=∠D，试断定AD与BC的位置关系，并证明.9.有一条直的的等宽纸带，按图折叠时，纸带重叠局部中∠α是多少？10.如图，直线AC//BD，连结AB，直线AC.BD及线段AB把平面分成①、②、③、④四个局部，规定：线上各点不属于任何局部.当动点P落在某个局部时，连结PA.PB，构成∠PAC，∠APB，∠PBD三个角.〔提示：有公一共端点的两条重合的折射所组成的角是0°角〕〔1〕当动点P落在第①局部时，求证：∠APB=∠PAC＋∠PBD；〔2〕当动点P落在第②局部时，∠APB=∠PAC＋∠PBD是否成立〔直接答复成立或者不成立〕？〔3〕当动点P在第③局部时，全面探究∠PAC，∠APB，∠PBD之间的关系，并写出动点P的详细位置和相应的结论.选择其中一种结论加以证明.1.70°2.∠1＋∠3=180°3.60°4.40°DBD8.平行．理由如下：∵AB//CD，∴∠B+∠C＝180°∵∠B＝∠D∴∠D+∠C＝180°∴AD∥BC9.75°10.〔1〕解法一：如图1延长BP交直线AC于点E∵ AC∥BD, ∴∠PEA = ∠PBD. ∵∠APB = ∠PAE ＋∠PEA, ∴∠APB = ∠PAC ＋∠PBD.解法二：如图2过点P作FP∥AC,∴∠PAC = ∠APF.∵ AC∥BD，∴FP∥BD.∴∠FPB =∠PBD.∴∠APB =∠APF ＋∠FPB =∠PAC＋∠PBD.解法三：如图3，∵ AC∥BD，∴∠CAB ＋∠ABD = 180°即∠PAC ＋∠PAB ＋∠PBA ＋∠PBD = 180°.又∠APB ＋∠PBA ＋∠PAB = 180°,∴∠APB =∠PAC ＋∠PBD.〔2〕不成立.〔3〕(a)当动点P在射线BA的右侧时，结论是∠PBD=∠PAC＋∠APB.(b)当动点P在射线BA上，结论是∠PBD =∠PAC ＋∠APB.或者∠PAC =∠PBD ＋∠APB 或者∠APB = 0°，∠PAC =∠PBD〔任写一个即可〕.(c) 当动点P在射线BA的左侧时，结论是∠PAC =∠APB ＋∠PBD.选择(a) 证明：如图4，连接PA，连接PB交AC于M∵ AC∥BD,∴∠PMC =∠PBD.又∵∠PMC =∠PAM ＋∠APM,∴∠PBD =∠PAC ＋∠APB.选择(b) 证明：如图5∵点P在射线BA上，∴∠APB = 0°.∵ AC∥BD ,∴∠PBD =∠PAC.∴∠PBD =∠PAC ＋∠APB或者∠PAC =∠PBD＋∠APB或者∠APB = 0°，∠PAC =∠PBD.选择(c) 证明：如图6，连接PA，连接PB交AC于F ∵ AC∥BD ,∴∠PFA =∠PBD.∵∠PAC =∠APF ＋∠PFA,∴∠PAC =∠APB ＋∠PBD.励志赠言经典语录精选句；挥动**，放飞梦想。

初中数学平行线与相交线知识点汇总平行线与相交线是初中数学中的重要知识点，掌握了这些知识，可以帮助我们解决许多几何问题。

本文将对初中数学平行线与相交线的相关知识进行汇总。

首先，我们来说说平行线的概念。

在平面几何中，如果两条直线在同一个平面上，且它们没有交点，我们就称这两条直线是平行线。

平行线之间的距离始终相等，永远不会相交。

平行线的符号一般为“||”。

接下来，我们来了解一些关于平行线的性质。

首先是平行线的判定定理。

根据该定理，如果两条直线与一条直线相交，并且所成的相对内角或相对外角相等，那么这两条线就是平行线。

这个定理在实际问题中非常实用，可以通过观察角度的相等性来判断是否存在平行关系。

在平行线性质中，我们还有平行线的传递性。

也就是说，如果直线a与直线b平行，直线b与直线c平行，那么直线a与直线c也平行。

利用这个性质，我们可以通过已知的平行线关系推导出新的平行线关系。

除了平行线，相交线也是几何中重要的概念。

相交线是指两条直线在同一平面内同时存在交点的现象。

直线之间的交点被称为交点。

相交线的符号一般为“∩”。

了解了相交线的概念后，我们接下来考虑一些与相交线相关的性质。

首先是相交线的判定定理。

根据该定理，如果两条直线的内锐角之和为180度，那么这两条直线是相交线。

只要我们知道两条直线的内锐角之和为180度，就可以判定它们是相交线。

在相交线性质中，还有一条重要的定理，叫做同位角定理。

这个定理指出，如果一条直线与两条平行线相交，那么所成的内错角和外错角相等。

同位角定理在证明几何问题时经常被使用，是解决几何问题的有力工具。

平行线与相交线知识点的运用广泛。

在三角形中，比如我们需要证明两条边平行，我们可以通过找出一条辅助线，并观察角度关系来实现目标。

在求解相似三角形的问题时，我们也经常需要利用平行线与相交线的性质进行推导。

除了在几何中的应用，平行线与相交线的知识在实际生活中也有很多应用。

比如在建筑设计中，我们需要保证墙壁、地板等元素的平行与垂直关系，从而保证建筑的稳定性和美观性。

平行线与相交线的性质推导平行线与相交线是几何学中常见的概念，它们之间存在一些重要的性质关系。

在本文中，我们将推导并探讨平行线与相交线之间的性质。

1.平行线的性质首先，我们来研究平行线的性质。

平行线是指在同一个平面内永不相交的两条线。

根据平行线的定义，我们可以得出以下定理：定理1：如果两条直线分别与第三条直线相交，并且这两条交线都与第三条直线的某一边形成同侧内角，则这两条直线是平行线。

证明：假设有两条直线AB和CD与直线EF相交，且∠ABC和∠DEF同侧内角。

根据同侧内角和定理，我们知道这两条交线必定是平行线。

定理2：平行线具有传递性。

如果直线AB与直线CD平行，且直线CD与直线EF平行，那么直线AB与直线EF也平行。

证明：假设直线AB与直线CD平行，直线CD与直线EF平行。

由于两条平行线各自都与第三条直线相交，并且它们的同侧内角相等，根据同侧内角和定理，可以得出直线AB与直线EF是平行线。

2.相交线的性质接下来，我们来探讨相交线的性质。

相交线是指在同一个平面内相交的两条线。

根据相交线的定义，我们可以得出以下定理：定理3：相交线之间的对应角相等。

在平面内，如果两条直线AB 和CD相交于点O，那么∠AOB与∠COD对应角相等，∠BOC与∠AOD对应角相等。

证明：由于直线AB和CD相交于点O，我们可以得到斜线交错定理。

两对同位角∠AOB和∠BOC、∠COD和∠AOD对应角相等。

定理4：相交线之间的交错角互补。

在平面内，如果两条直线AB 和CD相交于点O，那么∠AOB与∠COD交错角互补，∠BOC与∠AOD交错角互补。

证明：根据交错角定义，由直线AB和CD相交于点O可得交错角∠AOB与∠COD、∠BOC与∠AOD交错角互补。

综上所述，平行线与相交线之间存在许多重要的性质关系。

通过了解和应用这些性质，我们可以更好地理解和解决几何学中涉及到平行线和相交线的问题。

在实际应用中，平行线和相交线的性质也被广泛应用于建筑、工程、地理测量等领域。

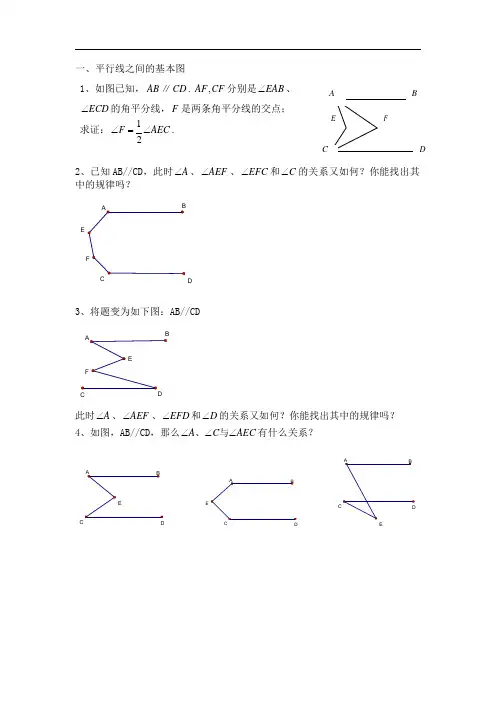
一、平行线之间的基本图1、如图已知， AB ∥ CD . AF , C F 分别是 ∠EAB 、∠ECD 的角平分线， F 是两条角平分线的交点；求证： ∠F = 1∠AEC .2D2、已知 AB//CD ，此时 ∠A 、 ∠AEF 、 ∠EFC 和 ∠C 中的规律吗？D3、将题变为如下图：AB//CDC D此时 ∠A 、 ∠AEF 、 ∠EFD 和 ∠D 的关系又如何？你能找出其中的规律吗？ 4、如图，AB//CD ，那么 ∠A 、∠C 与∠AEC 有什么关系？DDEC二、两组平行线的证明题【找出连接两组平行线的角】1.已知：如图，CD 平分∠ACB ，AC ∥DE ，∠DCE=∠FEB ，求证：EF 平分∠DEB ．CE B3、已知：如图 2-96,DE ⊥AO 于 E,BO ⊥AO,FC ⊥AB 于 C ，∠1=∠2,求证：DO ⊥AB.3、如图，已知 EF ⊥AB ，∠3=∠B ，∠1=∠2，求证：CD ⊥AB 。

4、已知 AD ⊥BC ，FG ⊥BC ，垂足分别为 D 、G ，且∠1=∠2，猜想∠BDE 与∠C 有怎样的 大小关系？试说明理由.AB 、 两点，三、两组平行线构造平行四边形 1．已知：如图，AB 是一条直线，∠C = ∠1，∠2 和∠D 互余，BE ⊥FD 于 G ． 求证：AB ∥CD ．2、如图，E 点为 DF 上的点，B 为 AC 上的点，∠1=∠2，∠C =∠D ，求证 DF ∥AC ．D EF1342A BC(第 22 题)3、如图，M 、N 、T 和 A 、B 、C 分别在同一直线上，且∠1=∠3，∠P=∠T ，求证：∠M=∠R 。

四、证特殊角1、AB ∥CD ，∠BAC 的平分线和∠ACD 的平分线交于点 E ，则∠AEC 的度数是．2、 AB ∥CD ，直线 EF 与 图 7CD 分别相交于 E 、 F 图 8EP 平分∠ AEF ， 过点 F 作 PF EP 垂足为 P ，若∠ PEF ＝30 0 ，则∠ PFC ＝DA3、如图，已知：DE ∥AC ，CD 平分∠ACB ，EF 平分∠DEC ，∠1 与∠2 互余，求证： DG ∥EF.4．已知：如图，AB ∥DE ，CM 平分∠BCE ，CN ⊥CM ．求证：∠B ＝2∠DCN ．5.如图已知直线 a ∥b ，AB 平分∠MAD ，AC 平分∠NAD ，DE ⊥AC 于 E ，求证：∠1=∠2．ANMEBDC4、求证：三角形内角之和等于 180°．五、寻找角之间的关系1、如图 2-97,已知：∠1=∠2，∠3=∠4，∠5=∠6.求证:AD ∥BC.2、已知，如图，BCE 、AFE 是直线，AB ∥CD ，∠1=∠2，∠3=∠4。