小学五年级多边形的面积计算公式汇总附练习题
- 格式：docx
- 大小：155.01 KB
- 文档页数：9
下载文档原格式
合集下载
人教版五年级上册《多边形的面积》知识点+练习
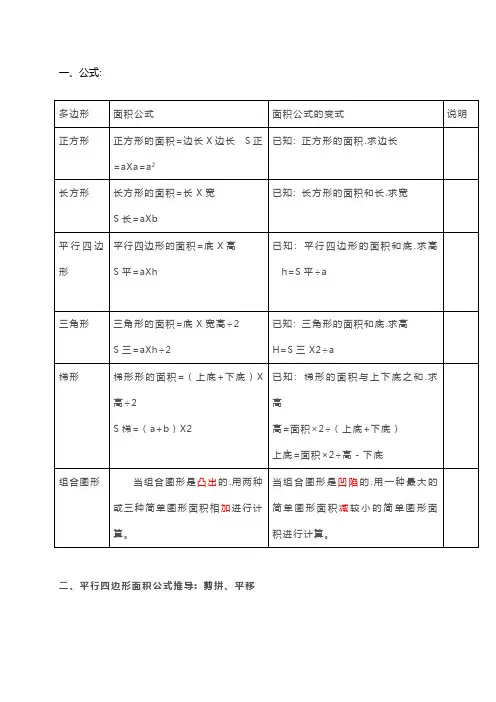
二、平行四边形面积公式推导: 剪拼、平移平行四边形可以转化成一个长方形；长方形的长相当于平行四边形的底；长方形的宽相当于平行四边形的高；长方形的面积等于平行四边形的面积.因为长方形面积=长×宽.所以平行四边形面积=底×高。
三、三角形面积公式推导: 旋转两个完全一样的三角形可以拼成一个平行四边形.平行四边形的底相当于三角形的底；平行四边形的高相当于三角形的高；平行四边形的面积等于三角形面积的2倍.因为平行四边形面积=底×高.所以三角形面积=底×高÷2四、梯形面积公式推导: 旋转两个完全一样的梯形可以拼成一个平行四边形。
平行四边形的底相当于梯形的上下底之和；平行四边形的高相当于梯形的高；平行四边形面积等于梯形面积的2倍.因为平行四边形面积=底×高.所以梯形面积=(上底+下底)×高÷2五、等底等高的平行四边形面积相等；等底等高的三角形面积相等；等底等高的平行四边形面积是三角形面积的2倍。
六、长方形框架拉成平行四边形.周长不变.面积变小。
七、组合图形面积计算: 必须转化成已学的简单图形。
当组合图形是凸出的.用虚线分割成几种简单图形.把简单图形面积相加计算。
当组合图形是凹陷的.用虚线补齐成一种最大的简单图形.用最大简单图形面积减几个较小的简单图形面积进行计算。
一、“认真细致”填一填: （17分）1.篮球场占地约420（）.2.65平方米=（）平方分米 3600平方米=（）公顷 286厘米=( )米2.一个三角形底5dm.高6dm.面积是（） dm2.与它等底等高的平行四边形面积是（）。
4.右图平行四边形的面积是15 cm2.阴影部分的面积是（）。
5.一个梯形的上底是24 cm.下底16 cm.高1 dm.面积是（）。
6.一个平行四边形的面积是60 cm2.如果它的高缩小3倍.底不变.面积是（）。
7、一堆木材堆成近似的梯形.最上层有5根.最底层有10根.每下一层都上一层多一根.这堆木材有（）层.它的面积是（）。
小学数学苏教版五年级上册正多边形面积、练习题
小学数学苏教版五年级上册正多边形面积、
练习题
正多边形是指边数相等且角数相等的多边形。
在数学中，计算
正多边形的面积是一个重要的概念。
本文将介绍小学数学苏教版五
年级上册中有关正多边形面积的知识和练题。
正多边形的面积计算方法
计算正多边形的面积有几种不同的方法，其中最常用的是使用
正多边形的边长和周长来计算。
下面是计算正多边形面积的公式：面积 = 面积公式
其中，边长表示正多边形的边长，周长表示正多边形的周长。
练题
1. 某学生绘制了一个边长为3厘米的正五边形，求该正五边形
的面积。
2. 一个正六边形的周长为30厘米，求该正六边形的面积。
3. 某正多边形的周长为40厘米，已知该正多边形的边数为8，求该正多边形的面积。
4. 若一个正多边形的边长为4厘米，面积为16平方厘米，求
该正多边形的周长。
5. 一个正多边形的面积为36平方厘米，边数为9，求该正多边形的周长。
请注意，以上练题仅作为练和巩固正多边形面积计算的知识点，实际应用中可能会有更复杂的情况。
总结
正多边形的面积计算是小学数学中的基础知识之一，帮助学生
加深对正多边形性质和计算的理解。
通过练题的实践，学生可以更
好地掌握正多边形面积计算的方法和技巧。
以上是小学数学苏教版五年级上册正多边形面积的相关知识和练习题。
希望本文对您有所帮助！。
五年级数学多边形的面积练习题
五年级数学多边形的面积练习题一、矩形的面积矩形是一种特殊的四边形，它的对边相等且平行。
计算矩形的面积很简单，只需知道矩形的长度和宽度，然后将两者相乘即可得到矩形的面积。
练习题：1.请计算长度为8cm，宽度为6cm的矩形的面积。
2.请计算长度为15m，宽度为12m的矩形的面积。
3.请计算长度为5.2cm，宽度为3.9cm的矩形的面积。
二、正方形的面积正方形是一种特殊的矩形，它的边长相等。
计算正方形的面积也很简单，只需将正方形的边长进行平方运算即可。
练习题：1.请计算边长为10cm的正方形的面积。
2.请计算边长为7m的正方形的面积。
3.请计算边长为4.5cm的正方形的面积。
三、三角形的面积三角形是一种三边形，其面积计算公式为底边乘以高，再除以2。
练习题：1.请计算底边为12cm，高为8cm的三角形的面积。
2.请计算底边为10m，高为5m的三角形的面积。
3.请计算底边为6.5cm，高为4.2cm的三角形的面积。
四、梯形的面积梯形是一种四边形，其两个底边平行，且其他两边不平行。
计算梯形的面积需要知道梯形的两个底边长度和高。
练习题：1.请计算上底为5cm，下底为11cm，高为6cm的梯形的面积。
2.请计算上底为8m，下底为15m，高为10m的梯形的面积。
3.请计算上底为3.5cm，下底为6cm，高为4.5cm的梯形的面积。
五、菱形的面积菱形是一种特殊的四边形，其两对边相等。
计算菱形的面积需要知道菱形的对角线长度。
练习题：1.请计算对角线1为8cm，对角线2为10cm的菱形的面积。
2.请计算对角线1为12m，对角线2为15m的菱形的面积。
3.请计算对角线1为3cm，对角线2为4.5cm的菱形的面积。
六、总结多边形的面积计算是数学中的基础知识，掌握了多边形面积的计算方法，可以帮助我们更好地理解和解决与面积相关的问题。
通过以上练习题的实践，相信大家对多边形的面积计算有了更深入的理解和掌握。
希望大家能继续进行练习，巩固和提升自己的数学能力。
五年级数学上册《多边形的面积》知识点汇总
五年级数学上册《多边形的面积》知识点汇总五年级数学上册《多边形的面积》知识点汇总（精选2篇）五年级数学上册《多边形的面积》知识点汇总篇11、公式：长方形：周长=(长+宽)×2 字母公式：c=(a+b)×2面积=长×宽字母公式：s=ab正方形：周长=边长×4 字母公式：c=4a面积=边长×边长字母公式：s=a平行四边形的面积=底×高字母公式： s=ah底=面积÷高高=面积÷底三角形的面积=底×高÷2 字母公式：s=ah÷2（底=面积×2÷高；高=面积×2÷底）梯形的面积=（上底+下底）×高÷2 字母公式： s=（a+b）h÷2 上底=面积×2÷高－下底下底=面积×2÷高－上底高=面积×2÷（上底+下底）2、单位换算的方法：大化小，乘进率；小化大，除以进率。
3、常用的单位间的进率长度单位：1千米=1000米 1米=10分米 1分米=10厘米 1厘米=10毫米面积单位：1平方千米=100公顷 1公顷=10000平方米1平方米=100平方分米 1平方分米=100平方厘米4、图形之间的关系：两个完全相同的三角形可以拼成一个平行四边形。
两个完全相同的梯形可以拼成一个平行四边形。
等底等高的平行四边形面积相等；等底等高的三角形面积相等。
等底等高的平行四边形面积是三角形面积的2倍。
如果一个三角形和一个平行四边形等面积，等底，则三角形的高是平行四边形的2倍。
如果一个三角形和一个平行四边形等面积，等高，则三角形的底是平行四边形的2倍。
5、把长方形框架拉成平行四边形，周长不变，面积变小了。
6、求组合图形面积的方法：（1）仔细观察，确定组合图形可以分割或添补成哪些可以计算面积的基本图形。
五年级数学上册求多边形面积公式和习题
1、长方形的面积=长×宽字母表示：S=ab长方形的长=面积÷宽 a=S÷b长方形的宽=面积÷长 b=S÷a2、正方形的面积=边长×边长字母表示：S=a23、平行四边形的面积=底×高字母表示：S=ah平行四边形的高=面积÷底 h=S÷a平行四边形的底=面积÷高 a=S÷h4、三角形的面积=底×高÷2 字母表示：S=ah÷2三角形的高=2×面积÷底 h=2S÷a三角形的底=2×面积÷高 a=2S÷h5、梯形的面积=（上底+下底）×高÷2字母表示：S=(a+b)·h÷2梯形的高=2×面积:（上底+下底) h=2S÷(a+b)梯形的上底=2×面积÷高一下底 a=2S÷h-b梯形的下底=2×面积÷高一上底 b=2S÷h-a1.求阴影部分的面积。
解:8×8÷2＝32(cm²)2.计算下面图形的面积。
解:14X5÷2=35(dm²)(14+18)X9÷2=144(dm²)35+144=179(dm²)3.求三角形的高。
解：6X8÷2=24(cm²)4.如图，直角三角形的面积时15cm²,一条直角边长6cm,另一条直角边长多少厘米?解：b=2S÷a= 2X15÷6=5(cm)答:另一条边长5厘米。
5.李大爷家要盖一间新房，新房一面墙的平面图如右图，如果每平方米要用90块砖，砌这面墙至少要用多少块砖?解：6X7.5=45(m²)6X2÷2=6(m²)(6+45)X90=4590(块)答:砌这面墙至少要用4590块砖。
小学五年级奥数专题讲座20多边形的面积(附答案)
小学五年级奥数专题讲座20多边形的面积(附答案)正方形面积=边长×边长=a2，长方形面积=长×宽=ab，平行四边形面积=底×高=ah，圆面积=半径×半径×π=πr2，扇形面积=半径×半径×π×圆心角的度数÷360°在实际问题中，我们遇到的往往不是基本图形，而是由基本图形组合、拼凑成的组合图形，它们的面积不能直接用公式计算。
在本讲和后面的两讲中，我们将学习如何计算它们的面积。
例1 小两个正方形组成下图所示的组合图形。
已知组合图形的周长是52厘米，DG=4厘米，求阴影部分的面积。
分析与解：组合图形的周长并不等于两个正方形的周长之和，因为CG部分重合了。
用组合图形的周长减去DG，就得到大、小正方形边长之和的三倍，所以两个正方形的边长之和等于（52-4）÷3=16（厘米）。
又由两个正方形的边长之差是4厘米，可求出大正方形边长=（16+4）÷2=10（厘米），小正方形边长=（16-4）÷2=6（厘米）。
两个正方形的面积之和减去三角形ABD与三角形BEF 的面积，就得到阴影部分的面积。
102+62-（10×10÷2）-（10+6）×6÷2=38（厘米2）。
例2如左下图所示，四边形ABCD与DEFG都是平行四边形，证明它们的面积相等。
分析与证明：这道题两个平行四边形的关系不太明了，似乎无从下手。
我们添加一条辅助线，即连结CE（见右上图），这时通过三角形DCE，就把两个平行四边形联系起来了。
在平行四边形ABCD中，三角形DCE的底是DC，高与平行四边形ABCD边DC上的高相等，所以平行四边形ABCD的面积是三角形DCE的两倍；同理，在平行四边形DEFG中，三角形DCE的底是DE，高与平行四边形DEFG 边DE上的高相等，所以平行四边形DEFG的面积也是三角形DCE的两倍。
五年级上册多边形面积练习题
五年级上册多边形面积练习题1. 矩形面积计算(1) 小明家的花坛是一个矩形，长是8米，宽是3米。
请计算花坛的面积。
解答：花坛的面积等于长乘以宽，即8米 × 3米 = 24平方米。
所以花坛的面积是24平方米。
(2) 书桌的长是1.2米，宽是0.6米。
请计算书桌的面积。
解答：书桌的面积等于长乘以宽，即1.2米 × 0.6米 = 0.72平方米。
所以书桌的面积是0.72平方米。
2. 正方形面积计算(1) 一块地的边长是5米，这块地是正方形，请计算地的面积。
解答：正方形的面积等于边长的平方，即5米 × 5米 = 25平方米。
所以地的面积是25平方米。
(2) 一块纸的边长是9厘米，这块纸是正方形，请计算纸的面积。
解答：正方形的面积等于边长的平方，即9厘米 × 9厘米 = 81平方厘米。
所以纸的面积是81平方厘米。
3. 三角形面积计算(1) 一个三角形的底边长是6米，高是4米。
请计算三角形的面积。
解答：三角形的面积等于底边长乘以高的一半，即(6米 × 4米) ÷ 2= 12平方米。
所以三角形的面积是12平方米。
(2) 一个三角形的底边长是8厘米，高是5厘米。
请计算三角形的面积。
解答：三角形的面积等于底边长乘以高的一半，即(8厘米 × 5厘米) ÷ 2 = 20平方厘米。
所以三角形的面积是20平方厘米。
4. 其他多边形面积计算(1) 一个梯形的上底长是10厘米，下底长是8厘米，高是6厘米。
请计算梯形的面积。
解答：梯形的面积等于(上底长 + 下底长)乘以高的一半，即[(10厘米 + 8厘米) × 6厘米] ÷ 2 = 54平方厘米。
所以梯形的面积是54平方厘米。
(2) 一个菱形的对角线长度分别为10厘米和8厘米，请计算菱形的面积。
解答：菱形的面积等于两条对角线的长度的乘积的一半，即(10厘米 × 8厘米) ÷ 2 = 40平方厘米。
五年级多边形面积练习题
五年级多边形面积练习题五年级多边形面积练习题在数学学科中，多边形是一个常见的几何图形。
它由多个边和角组成，是我们日常生活中经常能够看到的图形之一。
而计算多边形的面积是数学学习中的一个重要内容。
在五年级的数学课程中，学生们开始接触多边形的面积计算问题。
下面，我们将通过一些练习题来帮助学生们更好地理解多边形面积的计算方法。
练习题一：矩形的面积计算1. 一个矩形的长为8厘米，宽为5厘米，计算其面积。
解答：矩形的面积可以通过长乘以宽来计算。
所以，这个矩形的面积为8厘米乘以5厘米，即40平方厘米。
练习题二：正方形的面积计算2. 一个正方形的边长为6厘米，计算其面积。
解答：正方形的面积也可以通过边长的平方来计算。
所以，这个正方形的面积为6厘米的平方，即36平方厘米。
练习题三：三角形的面积计算3. 一个三角形的底边长为10厘米，高为4厘米，计算其面积。
解答：三角形的面积可以通过底边长乘以高再除以2来计算。
所以，这个三角形的面积为10厘米乘以4厘米再除以2，即20平方厘米。
练习题四：梯形的面积计算4. 一个梯形的上底长为6厘米，下底长为10厘米，高为8厘米，计算其面积。
解答：梯形的面积可以通过上底长、下底长和高来计算。
首先，计算上底长和下底长的平均值，即（6+10）/2=8厘米。
然后，将平均值乘以高，再除以2，即8厘米乘以8厘米再除以2，即32平方厘米。
练习题五：菱形的面积计算5. 一个菱形的对角线长分别为6厘米和8厘米，计算其面积。
解答：菱形的面积可以通过对角线长相乘再除以2来计算。
所以，这个菱形的面积为6厘米乘以8厘米再除以2，即24平方厘米。
通过以上的练习题，我们可以看到不同多边形的面积计算方法有所不同。
对于矩形和正方形，可以直接使用长度或边长的乘积来计算面积。
而对于三角形、梯形和菱形，则需要使用不同的公式来计算面积。
这些练习题可以帮助学生们巩固对多边形面积计算方法的理解，并且提高他们的计算能力。
在实际生活中，多边形的面积计算也有着广泛的应用。
小学五年级多边形的面积计算公式汇总
小学五年级多边形的面积计算公式汇总
多边形的面积计算公式：
1.长方形的面积为长乘以宽，用字母表示为 S=ab。
长方
形的长为面积除以宽，即 a=S÷b；长方形的宽为面积除以长，即 b=S÷a。
2.正方形的面积为边长的平方，用字母表示为 S=a²。
3.平行四边形的面积为底乘以高，用字母表示为 S=ah。
平行四边形的高为面积除以底，即 h=S÷a；平行四边形的底为面积除以高，即 a=S÷h。
4.三角形的面积为底乘以高除以2，用字母表示为S=ah÷2.三角形的高为2倍面积除以底，即 h=2S÷a；三角形的底为2
倍面积除以高，即 a=2S÷h。
5.梯形的面积为上底加下底乘以高除以2，用字母表示为S=(a+b)·h÷2.梯形的高为2倍面积除以上底加下底，即
h=2S÷(a+b)；梯形的上底为2倍面积除以高减去下底，即a=2S÷h-b；梯形的下底为2倍面积除以高减去上底，即b=2S÷h-a。
小学数学《正多边形的面积》练习题
小学数学《正多边形的面积》练习题题目一已知一个正六边形的边长为8cm，求该正六边形的面积。
解答一正六边形的面积计算公式为：面积= 3√3 × 边长² ÷ 2根据已知条件，可得到：面积= 3√3 × 8² ÷ 2计算得到的结果为：面积= 96√3 cm²题目二一个正五边形的面积为60 cm²，求该正五边形的边长。
解答二正五边形的面积计算公式为：面积 = 5 ×边长² × cot(π/5) ÷ 4根据已知条件，可得到：60 = 5 ×边长² × cot(π/5) ÷ 4通过计算，可得到方程的解为：边长² = 24 cot(π/5)求得边长的平方后，再开平方可得到边长的值。
题目三已知一个正三角形的面积为16√3 cm²，求该正三角形的边长。
解答三正三角形的面积计算公式为：面积= (√3 × 边长²) ÷ 4根据已知条件，可得到：16√3 = (√3 × 边长²) ÷ 4通过计算，可得到方程的解为：边长² = 64求得边长的平方后，再开平方可得到边长的值。
题目四一个正四边形的边长为10 cm，求该正四边形的面积。
解答四正四边形的面积计算公式为：面积 = 边长²根据已知条件，该正四边形的边长为10 cm，则可得到：面积 = 10²计算得到的结果为：面积 = 100 cm²以上是《正多边形的面积》练习题的解答。
希望对你有帮助！。
多边形的面积练习题及答案
多边形的面积练习题及答案练习题一：三角形面积计算题目：已知一个三角形的底边长为10厘米，高为6厘米，求该三角形的面积。
解答：根据三角形面积公式，面积 = (底边长× 高) / 2。
代入数值得面积= (10 × 6) / 2 = 30平方厘米。
练习题二：平行四边形面积计算题目：一个平行四边形的底边长为8厘米，高为5厘米，求该平行四边形的面积。
解答：平行四边形的面积公式为面积 = 底边长× 高。
代入数值得面积= 8 × 5 = 40平方厘米。
练习题三：梯形面积计算题目：一个梯形的上底长为4厘米，下底长为8厘米，高为6厘米，求该梯形的面积。
解答：梯形的面积公式为面积 = (上底 + 下底) × 高 / 2。
代入数值得面积= (4 + 8) × 6 / 2 = 18平方厘米。
练习题四：正多边形面积计算题目：一个正六边形的边长为5厘米，求该正六边形的面积。
解答：正六边形可以被划分为6个等边三角形，每个三角形的底边长等于正六边形的边长。
因此，每个三角形的面积= (5 × 5 ×sin(60°)) / 2。
正六边形的总面积= 6 × 每个三角形的面积 = 6× (5 × 5 × √3 / 4) = 75√3 / 2 ≈ 64.95平方厘米。
练习题五：不规则多边形面积估算题目：一个不规则多边形，已知其所有顶点的坐标，如何估算其面积？解答：可以通过将其划分为多个三角形，然后计算每个三角形的面积并求和。
如果顶点坐标已知，可以使用多边形面积公式，即根据顶点坐标计算多边形的面积。
练习题六：圆内接多边形面积计算题目：一个圆的半径为10厘米，求其内接正六边形的面积。
解答：圆内接正六边形的边长等于圆的半径。
因此，正六边形的面积= 6 × (半径× 半径× sin(60°)) / 2 = 6 × (10 × 10 ×√3 / 4) = 150√3 ≈ 259.81平方厘米。
人教版小学五年级数学上册第六单元《多边形的面积》练习二十二课件
练习题
8.图中每个小方格的面积为1cm2，计算阴 影部分面积。
近似转化成长方形 8×4 = 32（cm2）
阴影部分面积大约是 32cm2。
练习题
9.图中每个小方格的面积为1m2，请你估 计这个池塘的面积。
S =ah =12×8 =96（m2 ）
这个池塘的面积大约是96m2。（答案不唯一）
练习题
练习题
11*.学校校园里有一块长方形的地，想种上红 花、黄花和绿草。 请你也设计一种方案，用上我们学过的图 形，并求一求每种植物的种植面积。
（答案略）
人教版小学五年级数学上册
第六单元 多边形的面积
练习二十二
练习题
1.新丰小学有一块菜地，形状如下图。这块 菜地的面积是多少平方米？ S平行四边形+S三角形 =50×33+35×12÷2 =1650+210 =1860（m²） 答：这块菜地的面积是1860m²。
练习题
2.一面中国少年先锋队中队旗的面积是多少？
方法一：
30+30=60（cm） S=S长方形一S三角形
=80×60-60×20÷2
=4800-600 =4200（cm²）
你能想出几种算法？
答：一面中国少年先锋队中队旗的面积是4200m²。
练习题
方法二： S=S梯形×2
方法三： S=S正方形+S三角形×2
练习题
3.下面是一块正方形空心地砖，它实际占地 面积是多少？
答：它实际占地面积是731cm²。
练习题 4.在一块梯形的地中间有一个长方形的游泳池，其 余的地方是草地。草地的面积是多少平方米？
（70+40）×30÷2－30×15
= 110×30÷2－450
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
多边形的面积计算公式1、长方形的面积= 长×宽字母表示：S=ab长方形的长= 面积÷宽a=S÷b长方形的宽= 面积÷长b=S ÷a2 、正方形的面积= 边长×边长字母表示: S= a 23 平行四边形的面积= 底×高字母表示: S=ah平行四边形的高= 面积÷底h=S ÷a平行四边形的底= 面积÷高a=S ÷h4、三角形的面积= 底×高÷ 2字母表示: S=ah ÷2三角形的高= 2 ×面积÷底h=2S ÷a 三角形的底= 2 ×面积÷高a=2S ÷h5、梯形的面积= (上底+下底)×高÷ 2字母表示：S=(a+b) ·h ÷2梯形的高=2 ×面积÷(上底+ 下底) h=2S ÷(a+b) 梯形的上底=2 ×面积÷高—下底a=2S ÷h-b梯形的下底=2 ×面积÷高—上底b=2S ÷h-a1 平方千米=100 公顷1 公顷=10000 平方米1 平方米=100 平方分米1 平方米=10000 平方厘米1 米==10 分米=100 厘米《多边形的面积》同步试题一、填空1．完成下表。
考查目的：平行四边形、三角形和梯形的面积计算及变式练习。
答案：解析：直接利用公式计算这三种图形的面积，对于学生来说完成的难度不大。
对于已知平行四边形的面积和高求底、已知三角形的面积和底求高这两个变式练习，可引导学生进行比较，理解并强化三角形和梯形的类似计算中需要先将“面积× 识点。
2．下图是一个平行四边形，它包含了三个三角形，其中两个空白三角形的面积分别是 15 平方厘米和 25 平方厘米。
中间涂色三角形的面积是（ ）。
考查目的 ：等底等高的三角形和平行四边形的面积之间的关系。
答案 ： 40 平方厘米。
解析 ：引导学生仔细观察图形，得出涂色部分三角形与整个平行四边形存在等底等高 的关系，则该三角形的面积应为平行四边形面积的一半，据此进一步推导出涂色三角 形的面积和两个空白三角形的面积之和相等这一结论。
3．有一批圆木堆成梯形，最上面一层有 3 根，最下面一层有 8 根，相邻两层相差根，一共堆了 6 层，这堆圆木共有（ ）根。
考查目的 ：运用梯形的面积计算方法解决相关的实际问题。
答案 ： 33。
解析 ：根据“（顶层根数 +底层根数）×层数÷ 2 ”进行解答。
在此基础上，可引导学 生用不同的方法对结果加以验证，重点分析采用等差数列求和的方法即“（首项 项）×项数÷ 2”，这既是解决该题的基本数学模型，也能突出体现“数形结合”的 思想。
4．如图的小花瓶中， 1 个小正方形的面积是 1 平方厘米，那么整个花瓶的面积是（ 平方厘米。
考查目的 ：组合图形的面积计算。
答案 ： 5。
2”这一知+末解析：通过转化，小花瓶左右两侧的部分可以组合成两个小正方形，再加瓶身的部分即可。
也可采用计算的方法，由题意可得一个小正方形的边长为1 厘米，则花瓶两边三角形的面积之和为2× 1÷ 2× 2=2 （平方厘米），整个花瓶的面积为2+3=5 （平方厘米）。
5．下图中，已知AB=BC=CD=EF=FG=GH=1 dm 。
（1）平行四边形AEGC的面积和平行四边形（）的面积相等，是（）；（2）三角形AEC和三角形（）的面积相等，是（）；该三角形的面积和平行四边形（）的面积也相等；（3）梯形CDHE的面积是（），和平行四边形（）的面积相等。
考查目的：多边形的面积计算，相互之间的面积关系。
答案：（1）BFHD，4 dm2；（2）GEC，2 dm2；AEFB或BFGC、CGHD；（3）4 dm2，AEGC 或BFHD。
解析：综合考查学生运用所学知识解决问题的能力。
对于学生读图能力的培养具有很高的利用价值，在练习中，教师还应强调用字母表示多边形时的规范要求。
二、选择1．一个平行四边形相邻两条边分别是6 厘米、4 厘米，量得一条边上的高为5 厘米，这个平行四边形的面积是（）平方厘米。
A.24B.42C.20D.30考查目的：平行四边形的认识以及面积计算。
答案：C解析：根据平行四边形的特点，底边上的高一定小于另一条底边，所以高为 5 厘米对应的底为4 厘米，再根据面积公式计算。
在分析时，可让学生通过画图的方式得出类似结论并加以强化。
2．如图，四边形ABCD是一个梯形，由三个直角三角形拼成，它的面积是（）。
C.4 cm考查目的：对组合图形的分析，梯形的面积计算。
答案：D解析：重点是根据图形的特点确定这个直角梯形的上底和下底的长度。
由题意可知：左右两个三角形都是等腰直角三角形，所以AB=2.4 cm ，CD=1.6 cm ，梯形的高BC的长度为2.4+1.6=4 （cm），最后根据梯形的面积公式进行计算。
3．如图，4 个完全相同的正方形拼成一个长方形，对图中阴影部分三角形面积的大小关系表述正确的是（）。
A. 甲＞乙＞丙B. 乙＞甲＞丙C. 丙＞甲＞乙D. 甲＝乙＝丙考查目的：三角形的面积计算。
答案：D解析：三角形的面积=底×高÷ 2，而图中甲、乙、丙3 个三角形等底等高，所以面积都相等。
也可以引导学生探索3 个三角形与各自所在正方形的面积关系，发现每个三角形的面积都等于正方形面积的一半。
4．图中每个小方格表示 1 平方厘米，比较阴影部分的面积，（）图与其他三个图形A.1.92 2 B.16 2 2 D.8 2不相等。
答案：C解析 ：根据图示分别求出四个阴影部分的面积： A 图形的面积是 3 平方厘米； B 图形 的面积是 3平方厘米； C 图形的面积是 2.5 平方厘米； D 图形的面积是 3 平方厘米。
所以， C 图阴影部分的面积与其他三个不相等。
25．如图所示，每个小正方形的面积为 1 cm 2，请你估计一下，这个米老鼠图片的面积 约是（ ） cm 2。
A.15B.20C.35D.60考查目的 ：利用组合图形的面积计算解决实际问题。
答案 ： C解析 ：认真分析图形，弄清图形所占的方格数是解答此题的关键。
在分析讲解中，可引导学生说出自己的解题思路，鼓励不同的方法解答。
这里介绍一种：从上往下看， 小方格的个数约为 2+6+8+4 × 3+3+4=35 ，所以图形的面积约为 35 平方厘米。
三、解答1．模具厂车间里放着两块废弃的钢板（如图），请分别计算出面积。
（单位：答案 ：（ 1）（ 24+30 ）× 24÷2+20×30÷2=948 （平方厘米） 答：面积是 948 平方厘米。
2 ） 10 × 15- （7+10）× 4÷ 2=116 （平方厘米）厘米）考查目的 ：组合图形的面积计算。
答：面积是 116 平方厘米。
解析 ：通过观察图形可知，第一块钢板的面积是梯形和三角形的面积之和，第二块钢 板的面积是长方形的面积减去梯形的面积。
通过读图，找出相关的隐藏条件，再运用 公式进行计算。
2．图中已画出了一个三角形，请你在图上画出一个平行四边形，使平行四边形的面 积是三角形的 3 倍；再画出一个梯形，使梯形的面积和所画平行四边形的面积相等。
考查目的 ：平行四边形、三角形和梯形的面积。
答案 ：解析 ：因为等底等高的平行四边形面积是三角形面积的 2 倍，由图形可知，平行四边 形和三角形的高相等，要使平行四边形的面积是三角形的 3 倍，只要平行四边形的底 是三角形底的1.5 倍即可；在高相等的情况下，要使梯形的面积和平行四边形的面积 相等，只要梯形的上下底之和的一半等于平行四边形的底即可。
3．如图，梯形的面积是 450 cm 2，求阴影部分的面积。
考查目的 ：梯形的面积计算，三角形的面积计算。
2 答案 ： 450 × 2÷（ 5+25 ） =30（ cm ）， 30 × 25÷2=375 （ cm 2） 是 375 cm 2。
答：阴影部分的面积解析 ：由题意可知，阴影部分是一个三角形，且底已知，只要求出高即可运用公式计 算。
而梯形的面积和上、下底已知，可以求出高（也即阴影部分三角形4．如图，一个平行四边形的一边长 15 厘米，这条边上的高为 6 厘米，一条线段将此 平行四边形分成了两部分，它们的面积相差 18 平方厘米，求其中梯形的上底是多少 厘米？考查目的：平行四边形和梯形的面积计算。
答案：平行四边形的面积为15× 6=90（平方厘米），则梯形的面积为（90+18 ）÷2=54（平方厘米），其上底为54× 2÷ 6-15=3 （厘米）。
答：梯形的上底是3 厘米。
解析：先依据平行四边形的面积公式计算出整个图形的面积，将该面积加上18 平方厘米再除以2 就是梯形的面积，最后利用梯形的面积公式计算出上底的长。
5．每个小方格的面积为1 平方厘米，先估计下图中小鱼的面积大约是多少平方厘米，再用计算的方法加以验证。
考查目的：图形面积的估算，组合图形的面积计算。
答案：估算的结果和计算的方法都不唯一，这里只提供一种思路作为参考，具体如下：平方厘米）答：小鱼的面积是12 平方厘米。
解析：如上图所示，此图形是一个轴对称图形，只要计算出一半的面积即可求出总面积。
图中①②的面积均等于小正方形面积的一半；③④⑤的面积等于2 个小正方形面积的一半（即1 个小正方形的面积）；上述 5 个三角形的面积相加，再加上 2 个小正方形的面积就是小鱼图形一半的面积，进而可以求出总面积。