期末综合练习卷(2)(含答案)

四年级语文下册期末综合模拟试卷（二）（含答案）部编版(时间：90分钟 满分：100分)卷首寄语：亲爱的同学，转眼间一学期的学习生活就要结束了，相信你的语文水平有了很大的提高。

愿你能沉着冷静地答题，交上一份自己满意的试卷。

加油！第一部分 基础知识（55分）一、读下面语段，看拼音写词语，注意把字写得正确、美观。

（6分）2021年5月15日7时18分，中国火星探测器“天问一号”sh ǎn shu ò( )着c àn l àn( )的光芒，在j ì j ìng( )的火星乌托邦平原成功着陆，我国首次火星探测任务着陆火星取得圆满成功。

未来三个月，拥有“一身技艺”的“祝融号”火星车将在g ǎng w èi( )上y ī s ī b ù g ǒu( )地展开工作,它的成功k āi p ì了( )我们祖国崭新的未来。

二、我会读拼音，写词语。

(10分)li ǎn ji á ji é n àn h ū xi ào w ú y ōu w ú l ǜg ōng j ìng k ū long ji àn k āng w éi ch í zh ì x ù三、照样子，写词语。

（6分）如泣如诉（ABAC）白雪皑皑（ABCC）前俯后仰（带有反义词）见多识广（带有近义词）四、照样子，写字并组词。

（7分）末抹（涂抹）汤____( )各____( ) 旨____( )屈____( )卑____( )冈____( ) 扁____( )五、补充词语，并完成填空。

（8分）囊( )夜读铁杵成( ) 依山( )水高楼( )立左( )右盼鸡犬相( ) 不可一( )( )丝不动（1）以上词语中含有动物的词语是“___________”和“__________”，我还能写出两个含有动物的四字词语：___________、____________。

期末综合素质评价（二）时间：90 分钟满分：100分题号一二三四五总分得分一、仔细推敲，选一选。

(把正确答案的字母填在括号里)(每小题2分，共24 分)1. 下面的算式中，商小于1 的是( )。

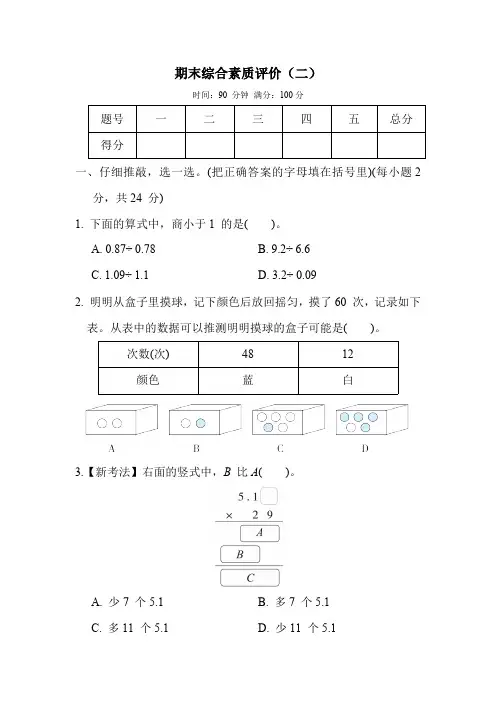
A. 0.87÷ 0.78B. 9.2÷ 6.6C. 1.09÷ 1.1D. 3.2÷ 0.092. 明明从盒子里摸球，记下颜色后放回摇匀，摸了60 次，记录如下表。

从表中的数据可以推测明明摸球的盒子可能是( )。

次数(次)4812颜色蓝白3.【新考法】右面的竖式中，B比A( )。

A. 少7 个5.1B. 多7 个5.1C. 多11 个5.1D. 少11 个5.14. 已知a×0.99 = b×1.01 = c×0.88(a、b、c都不为0)，则a、b、c三个数中最小的是( )。

A. aB. bC. cD. 无法确定5. 把两个三条边长分别是3 cm、4 cm、5 cm 的直角三角形拼成一个平行四边形，这个平行四边形的面积是( )cm2。

A. 12B. 15C. 20D. 246. 厦门园林博览苑以广阔的杏林湾水域为背景，自然形成多岛结构、众星拱月的“园在水上，水在园中”的景观特点，是我国独一无二的水上大观园。

为了吸引游客，园博苑管理员在门口的一块边长为9 m 的正方形花圃的四周摆放盆栽，每隔3 m 摆一盆(4 个角都摆)，一共要摆( )盆。

A. 11B. 12C. 13D. 147.【新角度】下列问题中，不能用“20÷a”来解决的是( )。

A. 一个数是20，另一个数是这个数的a倍，求另一个数是多少B. 一个平行四边形的面积是20 m2，底是a m，求高是多少米C. 有20 人，平均分成a组，求每组有多少人D. 一本练习本a元，求20 元可以买多少本8. 在同一幅方格图上，如果点A用数对表示为(1，5)，点B用数对表示为(1，1)，点C用数对表示为(3，1)，那么三角形ABC一定是( )三角形。

八年级数学期末综合素质检测卷（二）含答案一、选择题(每题3分，共30分)1．【教材P104习题T1变式】下列运算正确的是()A．a·a2＝a2B．(a5)3＝a8C．(ab)3＝a3b3D．a6÷a2＝a3 2．【教材P4练习T2改编】下列长度的三条线段，不能．．构成三角形的是() A．3，3，3 B．3，4，5 C．5，6，10 D．4，5，9 3．【教材P147习题T8变式】世界上最小的开花结果植物是澳大利亚的出水浮萍，这种植物的果实像一个微小的无花果，质量只有0.000 000 076 g．将数0.000 000 076用科学记数法表示为()A．7.6×10－9B．7.6×10－8C．7.6×109D．7.6×108 4．【教材P60练习T1拓展】在如图所示的4个图案中，属于轴对称图案的有()A．1个B．2个C．3个D．4个5．如果把分式xyx＋y中的x和y都扩大为原来的5倍，那么分式的值() A．扩大为原来的10倍B．扩大为原来的5倍C．不变D．缩小为原来的1 56．如图，在△ABC中，∠ABC，∠ACB的平分线BE，CD相交于点F，∠A＝60°，则∠BFC等于()A．100°B．110°C．120°D．150°(第6题)(第9题)(第10题)7．下列各式中，计算结果是x2＋7x－18的是()A．(x－1)(x＋18) B．(x＋2)(x＋9)C．(x－3)(x＋6) D．(x－2)(x＋9)8．已知y2＋10y＋m是完全平方式，则m的值是()A．25 B．±25 C．5 D．±59．如图，沿过点A的直线折叠这个直角三角形纸片的直角，使点C落在AB边上的点E处，折痕为AD.若BC＝24，∠B＝30°，则DE的长是() A．12 B．10 C．8 D．610．已知，如图，△ABC是等边三角形，AE＝CD，BQ⊥AD于Q，BE交AD于点P，下列说法：①∠APE＝∠C，②AQ＝BQ，③BP＝2PQ，④AE＋BD＝AB，其中正确的有()A．1个B．2个C．3个D．4个二、填空题(每题3分，共24分)11．若式子(x－4)0有意义，则实数x的取值范围是______________．12．【教材P117练习T2(3)变式】分解因式：xy－xy3＝________________．13．【教材P24练习T2改编】一个多边形的每个内角都是150°，这个多边形是________边形．14．如图，在△ABC和△DEF中，已知CB＝DF，∠C＝∠D，要使△ABC≌△EFD，还需添加一个条件，那么这个条件可以是____________．(第14题)(第15题)(第18题)15．【教材P56复习题T10改编】如图，在△ABC中，DE是AC的垂直平分线，AB＝4，△ABD的周长为12，则BC＝________.16．已知点P(1－a，a＋2)关于y轴的对称点在第二象限，则a的取值范围是____________．17．已知3x＋5y－5＝0，则8x×32y的值是________．18．如图，在平面直角坐标系中，点A，B分别在x轴和y轴上，∠BAO＝60°，在坐标轴上找一点P，使得△P AB是等腰三角形，则符合条件的P点共有________个．三、解答题(19～21题每题8分，22～24题每题10分，25题12分，共66分) 19．先化简后求值：(x＋3)2－(x－4)(x＋4)．其中x＝－2.20. 解方程：1－xx－2＝12－x－2.21．如图，已知EC＝AC，∠BCE＝∠DCA，∠A＝∠E.求证：∠B＝∠D.22．如图，在平面直角坐标系中，每个小正方形的边长都为1个单位长度，△ABC 的顶点都在格点上，点A的坐标为(－3，2)．请按要求完成下列问题：(1)把△ABC先向下平移7个单位长度，再向右平移7个单位长度，得到△A1B1C1，画出△A1B1C1；(2)画出△A1B1C1关于x轴对称的△A2B2C2；画出△A1B1C1关于y轴对称的△A3B3C3；(3)求△ABC的面积．23．如图，在△ABC中，AB＝BC，DE⊥AB于点E，DF⊥BC于点D，交AC 于点F.(1)若∠AFD＝155°，求∠EDF的度数；(2)若点F是AC的中点，求证：∠CFD＝12∠ABC.24．某商店老板第一次用1 000元购进了一批口罩，很快销售完；第二次购进时发现每只口罩的进价比第一次上涨了2.5元．老板用2 500元购进了第二批口罩，所购进口罩的数量是第一次购进口罩数量的2倍，同样很快销售完，两批口罩的售价均为每只15元．(1)第二次购进了多少只口罩？(2)商店老板第一次购进的口罩有3%的损耗，第二次购进的口罩有5%的损耗，商店老板销售完这些口罩后是盈利还是亏本？盈利或亏本多少元？25．(1)在等腰直角三角形ABC中，∠BAC＝90°，AB＝AC，点A，B分别是y 轴，x轴上的两个动点，直角边AC交x轴于点D，斜边BC交y轴于点E.①如图①，当点C的横坐标为－1时，求点A的坐标；②如图②，当点D恰好为AC中点时，连接DE，求证：∠ADB＝∠CDE.(2)如图③，点A在x轴上，且A(－4，0)，点B在y轴的正半轴上，分别以OB，AB为直角边在第一、二象限作等腰直角三角形BOD和等腰直角三角形ABC，且∠OBD＝90°，∠ABC＝90°，连接CD交y轴于点P，当点B在y轴的正半轴上运动时，BP的长度是否变化？若变化，请说明理由；若不变化，请求出BP的长．答案一、1.C 2.D 3.B 4.B 5.B 6.C7．D 8.A 9.C 10.C二、11.x ≠4 12.xy (1＋y )(1－y )13．十二 14.AC ＝ED (答案不唯一)15．8 16.－2＜a ＜1 17.32 18.6三、19.解：原式＝x 2＋6x ＋9－(x 2－42)＝x 2＋6x ＋9－x 2＋16＝6x ＋25，当x ＝－2时，原式＝6×(－2)＋25＝－12＋25＝13.20．解：方程两边同时乘(x －2)，得1－x ＝－1－2(x －2)，解得x ＝2.检验：当x ＝2时，x －2＝0，故此方程无实数根．21．证明：∵∠BCE ＝∠DCA ，∴∠BCE ＋∠ACE ＝∠DCA ＋∠ACE ，即∠ACB ＝∠ECD .在△ACB 和△ECD 中，⎩⎨⎧∠A ＝∠E ，AC ＝EC ，∠ACB ＝∠ECD ，∴△ACB ≌△ECD (ASA)．∴∠B ＝∠D .22．解：(1)如图所示，△A 1B 1C 1即为所求．(2)如图所示，△A 2B 2C 2，△A 3B 3C 3即为所求．(3)S △ABC ＝2×3－12×2×1－12×1×2－12×1×3＝6－1－1－32＝52.23．(1)解：∵∠AFD ＝155°，∴∠DFC ＝25°.∵DF ⊥BC ，DE ⊥AB ，∴∠FDC ＝∠AED ＝90°.∴∠C ＝180°－90°－25°＝65°.∵AB ＝BC ，∴∠A ＝∠C ＝65°.∴∠EDF ＝360°－65°－155°－90°＝50°.(2)证明：如图，连接BF .∵AB ＝BC ，且点F 是AC 的中点，∴BF ⊥AC , ∠ABF ＝∠CBF ＝12∠ABC .∴∠CFD ＋∠BFD ＝90°.∵FD ⊥BC ，∴∠CBF ＋∠BFD ＝90°.∴∠CFD ＝∠CBF .∴∠CFD ＝12∠ABC .24. 点方法：利润问题的相关公式及其数量关系：1．相关公式．售价＝进价×(1＋利润率)；售价＝标价×折扣；利润率＝利润进价×100%.2．基本数量关系．利润＝售价－进价；利润＝进价×利润率；销售额＝销售量×销售单价．进价×(1＋利润率)＝标价×折扣．解：(1)设第一次购进了x只口罩，则第二次购进了2x只口罩，依题意，得1 000x＝2 5002x－2.5，解得x＝100.经检验，x＝100是原方程的解，且符合题意．则2x＝2×100＝200.答：第二次购进了200只口罩．(2)[100×(1－3%)＋200×(1－5%)]×15－1 000－2 500＝805(元)．答：商店老板销售完这些口罩后盈利，盈利805元．25．(1)①解：如图①，过点C作CF⊥y轴于点F，则∠CAF＋∠ACF＝90°.∵∠BAC＝90°，即∠BAO＋∠CAF＝90°，∴∠ACF＝∠BAO.又∵∠AFC＝∠BOA＝90°，AC＝BA，∴△AFC≌△BOA(AAS)．∴AO＝CF＝1.∴点A的坐标是(0，1)．②证明：如图②，过点C作CG⊥AC，交y轴于点G.∵CG⊥AC，∴∠ACG＝90°.∴∠CAG＋∠AGC＝90°.∵∠AOD＝90°，∴∠ADO＋∠DAO＝90°.∴∠AGC＝∠ADO.又∵∠ACG＝∠BAD＝90°，AC＝BA，∴△ACG≌△BAD(AAS)．∴CG＝AD＝CD.∵∠BAC＝90°，AB＝AC，∴∠ACB＝45°.又∵∠ACG＝90°，∴∠DCE＝∠GCE＝45°.又∵CD＝CG，CE＝CE，∴△DCE≌△GCE(SAS)．∴∠CDE＝∠CGE.∴∠ADB＝∠CDE.(2)解：BP的长度不变化．如图③，过点C作CH⊥y轴于点H.∵∠ABC＝90°，∴∠CBH＋∠ABO＝90°.∵∠BAO＋∠ABO＝90°，∴∠CBH＝∠BAO.又∵∠CHB＝∠AOB＝90°，BC＝AB，∴△CBH≌△BAO(AAS)．∴CH＝BO，BH＝AO＝4.∵BD＝BO，∴CH＝BD.又∵∠CHP＝∠DBP＝90°，∠CPH＝∠DPB，∴△CPH≌△DPB(AAS)．∴BP＝HP＝12BH＝2.。

八上英语期末综合测试卷二（含答案）一、选择题(每小题1分, 共8分)1. —What’s your for the weekend?—I want to have a trip with my family.A. resolutionB. planC. job2. —How do you like the soap opera?—I think the soap opera is . We can learn nothing from it.A. seriousB. enjoyableC. meaningless3. —Do you think humans will live on the moon?—No. But I think it’s for humans to live under the sea.A. possibleB. impossibleC. probably4. There a soccer game between your class and my class tomorrow.A. is going to haveB. is going to beC. will have5. —What are you going to do for the coming winter holiday?—I’m going to skating because I like walking on the ice freely.A. pick upB. take upC. take down6.—Mom, can I leave the chores till tomorrow?—I’m afraid not. You can’t today’s work till tomorrow.A. put offB. turn downC. give awayD. look up7. —I’m awfully sorry for bringing you so much trouble.—9 / 9A. Never mind.B. It’s a pleasure.C. Of course not.D. You are welcome.8.—Karl Marx is a great thinker. Do you know ?—In 1818.A. where he was fromB. when he was bornC. how he learned foreign languages二、补全对话(每小题1分, 共5分)根据对话内容, 从方框内选择恰当的句子将对话补充完整。

苏教版四年级科学下册期末综合测试卷（二）含答案学校:___________姓名：___________班级：___________考号：___________一、选择题1．古希腊学者亚里士多德推测地球是球形的，他的根据是（）。

A．帆船进港，总是先看见船帆，后看见船身B．月食时，地球投射到月球的弧形阴影C．日月星辰东升西落2．许多年来，科学家一直认为环形山是由于（）形成的。

A．火山喷发B．流星体C．行星3．孔子遇见两个小孩在争辩，一个小孩说太阳刚升起时离我们最近，而到中午时离我们远，因为早晚太阳看起来大，中午小。

另一个则认为太阳刚升起来时离我们远，而到中午时离我们近，因为早晚冷而中午热，孔子觉得两人说的都有道理。

在这个故事里，一天中早晚和中午冷热的不同的原因是（）。

A．太阳和地球的距离不同B．太阳的高度不同C．天气特征不同4．蚕是以产卵的方式进行繁殖，而猫的繁殖方式则是（）。

A．产卵B．下蛋再进行孵化C．直接生出小猫5．满月到下一次满月的时间大约是（）。

A．一个月B．半个月C．一周6．月球的方位变化与月相的循环周期是（）。

A．24小时B．半个月C．一个月7．做实验时，如果洒出的酒精在酒精灯外燃烧，我们应该（）。

A．用湿抹布扑灭火焰B．用嘴吹灭火焰C．用水浇灭火焰8．从太空拍摄的地球照片，表面蓝色的部分是（）。

A．森林B．荒漠C．海洋9．下列星体是地球的卫星，也是距地球最近的一个天体是（）。

A．太阳B．火星C．月球10．（）年，人类发射了第一艘宇宙飞船。

A．1961B．1962C．196311．下列植物中通过叶繁殖后代的有（）。

A．蓟B．长寿花C．菊花D．落地生根12．目前，海洋污染日趋加剧，以海洋石油污染尤为严重。

石油泄漏的主要危害是（）。

二、填空题13．植物除了用种子繁殖，还可以用________器官繁殖。

14．影子形成的条件是______和________。

15．月球本身( )（填“会”或“不会”）发光。

北师大版2022-2023学年三年级下册数学期末综合检测卷（卷二）一、选一选1．下图是一张动物园的示意图，根据图中所标的位置，下面四种描述中正确的是（）。

A．狮虎山在大门的南面B．猴山在花坛的东南方向C．鹿苑在大象馆的北面，大象馆在鹿苑的南面D．从熊猫馆出发，先向北到达鹿苑，再向西北到达鸣禽馆2．有238支玫瑰，每8支扎成一束。

最多能扎成的花束数量（）。

A．比30束少B．比20束少C．比30束多3．从复式统计表中可以看出（）。

A．味酸奶的B．一月份比二月份情况好C．两个月情况呈上升趋势4．老师买来23盒羽毛球，每盒有12个，一共有多少个羽毛球？小明用下边的竖式计算出结果，箭头所指的这一步是在计算（）。

A．23盒羽毛球有276个B．2盒羽毛球有24个C．20盒羽毛球有240个5．35×16的结果比34×16的结果大（）。

A．1B．16C．34D．356．一本练习本的封面约是4（）。

A．平方米B．平方分米C．平方厘米7．一根铁丝正好可以围成一个边长是2厘米的正方形，把这根铁丝展开再围成一个长方形（无剩余），这个长方形的面积可能是（）平方厘米。

A．3B．7C．12D．15二、脱式计算8．脱式计算。

（1）150－120÷5（2）13×（36＋27）三、竖式计算9．列竖式计算（带有★的要验算）。

306÷3＝★950÷5＝10．列竖式计算。

39×42＝64×25＝82×56＝73×29＝18×84＝67×75＝四、口算和估算11．口算。

300×5＝13×3＝50÷5＝99÷3＝70×8＝200÷5＝48÷8＝125×10＝五、填空题12．日落时，妙想面向太阳，她的左面是()方。

13．36的3倍是()，从84里连续减去4，减()次正好得0。

人教版八年级数学上册期末综合检测试卷带答案一、选择题1．下列四个图形中，轴对称图形有（ ）个．A ．1B ．2C ．3D ．42．6月15日，莉莉在网络上查到了小区PM 2.5的平均浓度为0.000038克/立方米，0.000038用科学记数法表示为（ ） A ．43.810-⨯B ．43.810⨯C ．53.810-⨯D ．53.810⨯3．已知4=m x ，6n x =，则2-m n x 的值为（ ） A ．10 B ．83C ．32D ．234．若分式12x x +-有意义，则x 的取值范围是（ ） A ．x ≥2B ．x ≠2且x ≠－1C ．x ≠2D ．x ≠－15．下列因式分解正确的是（ ） A ．22(1)2x x x x -+=-+ B ．329(9)x x x x -=- C ．22324(1)a a a -=-++D ．2222(1)(1)-=+-x x x6．下列变形中，正确的是（ ） A ．1-=--a bb aB ．0.330.5252a b a ba b a b++=--C ．21111a a a -=-+ D ．22b bc a ac= 7．如图，AC BC =，下列条件不能判定．．．．△ACD 与△BCD 全等的是（ ）A ．AD BD =B ．ACD BCD ∠=∠C ．ADC BDC ∠=∠D ．点O 是AB 的中点8．若关于x 的方程4233x mx x--=--有增根，则m 的值为（ ） A ．3B ．0C ．1D ．任意实数9．勾股定理是人类早期发现并证明的重要数学定理之一，这是历史上第一个把数与形联系起来的定理，其证明是论证几何的发端．下面四幅图中，不能证明勾股定理的是（ ）A ．B ．C ．D ．10．如图，在等边△ABC 中，AC =3，点O 在AC 上，且AO =1．点P 是AB 上一点（可移动），连接OP ，以线段OP 为一边作等边△OPD ，且O 、P 、D 三点依次呈逆时针方向，当点D 恰好落在边BC 上时，则AP 的长是（ ）A ．1B ．2C ．3D ．4二、填空题11．若242x x -+的值为零，则x 的值为______．12．点P 1（4,m n -）与P 2（3,2m -）关于y 轴对称，则mn =______． 13．已知114ab-=，则aba b-的值是______． 14．已知3m a =，2n a =，则2m n a -的值为______．15．如图，在ABC ∆中，7AB cm =，5BC cm =，AC 的垂直平分线分别交AB ，AC 于点D ，E ，点F 是DE 上的任意一点，则BCF ∆周长的最小值是________cm ．16．已知关于x 的二次三项式29x kx ++ 是完全平方式，则常数k 的值为_____． 17．若14x x+=，则221x x ⎛⎫+ ⎪⎝⎭的值是_________．18．如图，直线PQ 经过Rt △ABC 的直角顶点C ，△ABC 的边上有两个动点D 、E ，点D 以1cm /s 的速度从点A 出发，沿AC →CB 移动到点B ，点E 以3cm /s 的速度从点B 出发，沿BC →CA 移动到点A ，两动点中有一个点到达终点后另一个点继续移动到终点．过点D 、E 分别作DM ⊥PQ ，EN ⊥PQ ，垂足分别为点M 、N ，若AC =6cm ，BC =8cm ，设运动时间为t ，则当t =__________ s 时，以点D 、M 、C 为顶点的三角形与以点E 、N 、C 为顶点的三角形全等．三、解答题19．分解因式 (1)224x y ；(2)a 2(x -y )+16(y -x )．20．先化简，再求值：2223111x x x x -⎛⎫-÷ ⎪--⎝⎭，其中x ＝2021． 21．如图，已知△ABC ≌△DEB ，点E 在AB 上，AC 与BD 交于点F ，AB ＝6，BC ＝3，∠C ＝55°，∠D ＝25°． （1）求AE 的长度； （2）求∠AED 的度数．22．如图，在ABC 中，C B ∠>∠，AD BC ⊥，AE 平分∠BAC ．(1)计算：若30B ∠=︒，60C ∠=°，求∠DAE 的度数； (2)猜想：若50C B ∠-∠=︒，则DAE =∠______； (3)探究：请直接写出∠DAE ，∠C ，∠B 之间的数量关系．23．某服装店老板到厂家选购A 、B 两种品牌的夏季服装，每袋A 品牌服装进价比B 品牌服装每袋进价多25元，若用4000元购进A 种服装的数量是用1500元购进B 种服装数量的2倍．(1)求A 、B 两种品牌服装每套进价分别是多少元？(2)若A 品牌服装每套售价为150元，B 品牌服装每套售价为100元，服装店老板决定一次性购进两种服装共100套，两种服装全部售出后，要使总的获利不少于3500元，则最少购进A品牌服装多少套？24．我们知道某些代数恒等式可用一些卡片拼成的图形面积来解释，例如：图A可以用来解释2()++=+，实际上利用一些卡片拼成的图形面积也可以对某些二次三项式进行因式a ab b a b分解．（1）图B可以解释的代数恒等式是；（2）现有足够多的正方形和矩形卡片（如图C），试画出．．一个用若干张1号卡片、2号卡片和3号卡片拼成的矩形（每两块纸片之间既不重叠，也无空隙，拼出的图中必须保留拼图的痕迹），使该矩形的面积为2223++a ab b23a ab b++，并利用你所画的图形面积对22进行因式分解．25．如图①，在等边△ABC中，点D、E分别是AB、AC上的点，BD=AE，BE与CD交于点O．（1）填空：∠BOC＝度；（2）如图②，以CO为边作等边△OCF，AF与BO相等吗？并说明理由；（3）如图③，若点G是BC的中点，连接AO、GO，判断AO与GO有什么数量关系？并说明理由．26．如图1，在平面直角坐标系xOy中，直线AB与x轴交于点A、与y轴交于点B，且∠ABO＝45°，A（－6，0），直线BC与直线AB关于y轴对称.(1)求△ABC的面积；(2)如图2，D为OA延长线上一动点，以BD为直角边，D为直角顶点，作等腰直角△BDE，求证：AB⊥AE；(3)如图3，点E是y轴正半轴上一点，且∠OAE＝30°，AF平分∠OAE，点M是射线AF上一动点，点N是线段AO上一动点，判断是否存在这样的点M，N，使OM＋NM的值最小？若存在，请写出其最小值，并加以说明.【参考答案】一、选择题 2．C 解析：C【分析】根据轴对称图形的定义，逐项判断即可求解． 【详解】解∶第一个图形不是轴对称图形， 第二个图形是轴对称图形， 第三个图形是轴对称图形， 第四个图形是轴对称图形， ∴轴对称图形有3个． 故选：C【点睛】本题主要考查了轴对称图形的定义，熟练掌握若一个图形沿着一条直线折叠后两部分能完全重合，这样的图形就叫做轴对称图形，这条直线叫做对称轴是解题的关键．3．C解析：C【分析】绝对值小于1的数也可以利用科学记数法表示，一般形式为10n a -⨯，与较大数的科学记数法不同的是其所使用的是负整数指数幂，指数n 由原数左边起第一个不为零的数字前面的0的个数所决定． 【详解】解：0.000038=53.810-⨯． 故选：C ．【点睛】此题主要考查了用科学记数法表示较小的数，一般形式为10n a -⨯，其中1≤|a |＜10，n 为由原数左边起第一个不为零的数字前面的0的个数所决定．4．B解析：B【分析】4=m x 根据幂的乘方，可得要求形式，根据同底数幂的除法，可得答案． 【详解】解：xm ＝4， 两边平方可得， x 2m ＝16，∴2-m n x ＝x 2m ÷xn ＝16÷683=，故选：B ．【点睛】题考查了同底数幂的除法，先利用了幂的乘方得出要求的形式，再利用同底数幂的除法得出答案．5．C解析：C【分析】根据分式有意义的条件：分母不等于0即可得出答案． 【详解】解：∴20x -≠， ∴2x ≠． 故选：C ．【点睛】本题考查了分式有意义的条件，掌握分式有意义的条件：分母不等于0是解题的关键．6．D解析：D【分析】根据因式分解的概念以及方法逐项判断即可．【详解】A 、22(1)2x x x x -+-+＝没有变为整式的积的形式，故A 选项错误； B 、32()()(9933)x x x x x x x -=-=+-，故B 选项错误；C 、()222413a a a -+=-+没有变为整式的积的形式，故C 选项错误； D 、22222(1)2(1)(1)x x x x -=-=+-，故D 选项正确， 故选：D ．【点睛】本题考查了因式分解的概念，把一个多项式在实数范围内化为几个整式的积，这种式子变形叫做多项式的因式分解，掌握因式分解的概念是解答本题的关键．7．A0c 时，等号右边的式子没有意义，选项错误，不符合题意；A【点睛】此题考查了分式的性质，涉及了平方差公式，解题的关键是熟练掌握分式的有关性质．8．C解析：C【分析】根据全等三角形的判定定理，逐项判断即可求解． 【详解】解：∵AC BC =，CD =CD ，∴A 、可以利用边边边判定△ACD 与△BCD 全等，故本选项不符合题意；B、可以利用边角边判定△ACD与△BCD全等，故本选项不符合题意；C、不能判定△ACD与△BCD全等，故本选项符合题意；∠=∠，可以利用边角边判定△ACD与△BCD全D、因为点O是AB的中点，所以ACD BCD等，故本选项不符合题意；故选：C【点睛】本题主要考查了全等三角形的判定定理，等腰三角形的性质，熟练掌握全等三角形的判定定理，等腰三角形的性质是解题的关键．9．C解题的关键．10．D边正方形面积，∴4×12ab+（b﹣a）2＝c2，∴整理得：a2+b2＝c2，即能证明勾股定理，故本选项不符合题意；D、∵四个小图形面积和=大正方形面积，∴ab+ b2+ a2+ ab=（a+b）2，∴a2+ 2ab +b2=（a+b）2，根据图形证明完全平方公式，不能证明勾股定理，故本选项符合题意；故选：D．【点睛】本题考查利用面积推导勾股定理与完全平方公式，掌握利用面积推导勾股定理与完全平方公式是解题关键．11．B解析：B【分析】如图，通过观察，寻找未知与已知之间的联系．AO=1，则OC=2．证明△AOP≌△COD求解即可．【详解】解：∵△ABC和△ODP都是等边三角形，∴∠C=∠A=∠DOP=60°，OD=OP，∴∠CDO+∠COD=120°，∠COD+∠AOP=120°，∴∠CDO=∠AOP，∴△ODC≌△POA（AAS），∴AP=OC，∴AP=OC=AC﹣AO=2．故选：B．【点睛】此题考查了等边三角形的性质和全等三角形的性质与判定，解决本题的关键是利用全等把所求的线段转移到已知的线段上．二、填空题12．2【分析】直接利用分式的值为零则分子为零分母不为零进而得出答案．【详解】解：∵分式242xx-+的值为零，∴24x-=0且x+2≠0，即24x-=0且x≠-2，解得：x=2．故答案为：2．【点睛】本题主要考查了分式的值为零的条件，正确掌握相关定义是解题关键． 13．-2【分析】根据关于y 轴对称的点的特点解答即可．【详解】∵点P 1（4,m n -）与P 2（3,2m -）关于y 轴对称， ∴n =-2，m -4=-3m 解得：n =-2，m =1 则mn =-2 故答案为：-2【点睛】此题主要考查了关于y 轴对称的点的特点；用到的知识点为：两点关于y 轴对称，横坐标互为相反数，纵坐标不变． 14．14-##-0.25【点睛】本题主要考查了分式的加减法，解题的关键是通分，得出4ab=，是解题关键． 【详解】a 法法则是解题的关键．16．12【分析】当点于重合时，的周长最小，根据垂直平分线的性质，即可求出的周长．【详解】∵DE 垂直平分AC ，∴点C 与A 关于DE 对称， ∴当点于重合时，即A 、D 、B 三点在一条直线上时，BF+CF解析：12【分析】当F 点于D 重合时，BCF ∆的周长最小，根据垂直平分线的性质，即可求出BCF ∆的周长．【详解】∵DE 垂直平分AC ，∴点C 与A 关于DE 对称，∴当F 点于D 重合时，即A 、D 、B 三点在一条直线上时，BF +CF=AB 最小，（如图）， ∴BCF ∆的周长为：BCF C BD CD BC ∆，∵DE 是垂直平分线， ∴AD CD =， 又∵7AB cm =，∴7cm BD AD BD CD ， ∴7512cm BCFC ∆，故答案为：12．【点睛】本题考查最短路径问题以及线段垂直平分线的性质：垂直平分线上的点到线段两端的距离相等，熟练掌握最短路径的求解方法以及垂直平分线的性质是解题的关键．17．±6【分析】利用完全平方公式的结构特征判断即可． 【详解】解：∵关于x 的二次三项式是完全平方式， ∴；，则常数k 的值为±6． 故答案为：±6．【点睛】此题考查了完全平方式，熟练掌握解析：±6【分析】利用完全平方公式的结构特征判断即可．【详解】解：∵关于x 的二次三项式29x kx ++是完全平方式， ∴()22693x x x ++=+；()22693x x x -+=-， 则常数k 的值为±6． 故答案为：±6．【点睛】此题考查了完全平方式，熟练掌握完全平方公式是解本题的关键．18．14【分析】根据即可求得其值．【详解】解：，故答案为：14．【点睛】本题考查了代数式求值问题，熟练掌握和运用代数式求值的方法是解决本题的关键． 解析：14 【分析】根据222211x x x x ⎛⎫=+- ⎪⎝⎫ ⎝⎭⎛+⎪⎭即可求得其值． 【详解】解：14x x+=， 221x x ⎛⎫∴+ ⎪⎝⎭ 212x x ⎛⎫=+- ⎪⎝⎭ 242=-=14 故答案为：14．【点睛】本题考查了代数式求值问题，熟练掌握和运用代数式求值的方法是解决本题的关键．19．1或或12【分析】由以点D 、M 、C 为顶点的三角形与以点E 、N 、C 为顶点的三角形全等．可知CE=CD ，而CE ，CD 的表示由E ，D 的位置决定，故需要对E ，D 的位置分当E 在BC 上，D 在AC 上时或当E 在解析：1或72或12 【分析】由以点D 、M 、C 为顶点的三角形与以点E 、N 、C 为顶点的三角形全等．可知CE =CD ，而CE ，CD 的表示由E ，D 的位置决定，故需要对E ，D 的位置分当E 在BC 上，D 在AC 上时或当E 在AC 上，D 在AC 上时，或当E 到达A ，D 在BC 上时，分别讨论．【详解】解：当E 在BC 上，D 在AC 上，即0＜t ≤83时，CE =（8-3t ）cm ，CD =（6-t ）cm ，∵以点D 、M 、C 为顶点的三角形与以点E 、N 、C 为顶点的三角形全等．∴CD =CE ，∴8-3t =6-t ，∴t =1s ，当E 在AC 上，D 在AC 上，即83＜t ＜143时，CE =（3t -8）cm ，CD =（6-t ）cm ，∴3t -8=6-t ，∴t =72s ， 当E 到达A ，D 在BC 上，即143≤t ≤14时，CE =6cm ，CD =（t -6）cm ，∴6=t -6，∴t =12s ，故答案为：1或72或12． 类，分别表示出每种情况下CD 和CE 的长．三、解答题20．(1)(2)（x ﹣y ）（a+4）（a ﹣4）【分析】（1）直接利用公式法分解因式即可；（2）先提提取公因式，然后运用公式法分解因式即可．（1）解： =；（2）a2（x ﹣y ）+16（解析：(1)(2)(2)x y x y +-(2)（x ﹣y ）（a +4）（a ﹣4）【分析】（1）直接利用公式法分解因式即可；（2）先提提取公因式，然后运用公式法分解因式即可．（1）解：224x y =(2)(2)x y x y +-；（2）a 2（x ﹣y ）+16（y ﹣x ）=a 2（x ﹣y ）-16（x ﹣y ）=（x ﹣y ）（a 2﹣16）＝（x ﹣y ）（a +4）（a ﹣4）．【点睛】题目主要考查利用提公因式法及公式法分解因式，熟练掌握因式分解的方法是解题关键．21．，【分析】先把括号里的通分，再相减，把除法转化为乘法、分解因式，然后约分，最后把x 的值代入化简后的代数式计算即可．【详解】解：当x ＝2021时，原式．【点睛】本题主要考查了22．（1）；（2）．【分析】（1）先根据全等三角形的性质可得，再根据线段的和差即可得； （2）先根据全等三角形的性质可得，再根据三角形的外角性质即可得．【详解】解：（1）∵，∴，∵，解析：（1）3AE =；（2）80AED ∠=︒．【分析】（1）先根据全等三角形的性质可得3BE BC ==，再根据线段的和差即可得； （2）先根据全等三角形的性质可得55DBE C ∠=∠=︒，再根据三角形的外角性质即可得．【详解】解：（1）∵,3ABC DEB BC ≅=，∴3BE BC ==，∵6AB =，∴633AE AB BE =-=-=；（2）∵ABC DEB ≅△△，∴55DBE C ∠=∠=︒，∵25D ∠=︒，∴552580AED DBE D ∠=∠+∠=︒+︒=︒．【点睛】本题考查全等三角形的性质等知识点，熟练掌握全等三角形的对应角和对应边相等是解题关键．23．(1)(2)25°(3)【分析】（1）先根据三角形内角和定理可计算出∠BAC=180°-∠B-∠C=60°，再利用角平分线定义得∠CAE=∠BAC=30°，接着由AD ⊥BC 得∠ADC=9殊到一般，（3）中的结论为一般性结论． 24．(1)A 品牌服装每套进价是100元，B 品牌服装每套进价是75元(2)最少购进A 品牌服装40套【分析】（1）设A 品牌服装每套x 元，则B 品牌服装每袋进价为（x ﹣25）元，由题意：用4000元购进准等量关系，正确列出分式方程；（2）找出数量关系，正确列出一元一次不等式． 25．（1）；（2）【详解】试题分析：（1）根据图所示，可以得到长方形长为2a ，宽为a+b ，面积为：2a （a+b ），或四个小长方形和正方形面积之和；（2）①根据题意，可以画出相应的图形然后完成因式解析：（1）2222()a ab a a b +=+；（2）()()22232a ab b a b a b ++=++【详解】试题分析：（1）根据图所示，可以得到长方形长为2a ，宽为a+b ，面积为：2a （a+b ），或四个小长方形和正方形面积之和；（2）①根据题意，可以画出相应的图形然后完成因式分解.试题解析：（1）()2222a ab a a b +=+（2）①根据题意，可以画出相应的图形，如图所示②因式分解为：()()22232a ab b a b a b ++=++26．（1）120；（2）相等，理由见解析；（3）AO=2OG ．理由见解析【分析】（1）证明△EAB ≌△DBC （SAS ），可得结论．（2）结论：AF=BO ，证明△FCA ≌△OCB （SAS ），可得结 解析：（1）120；（2）相等，理由见解析；（3）AO =2OG ．理由见解析【分析】（1）证明△EAB ≌△DBC （SAS ），可得结论．（2）结论：AF =BO ，证明△FCA ≌△OCB （SAS ），可得结论．（3）证明△AFO ≌△OBR （SAS ），推出OA =OR ，可得结论．【详解】解：（1）如图①中，∵△ABC 是等边三角形，∴AB =BC ，∠A =∠CBD =60°，在△EAB 和△DBC 中，AE BD A CBD AB BC =⎧⎪∠=∠⎨⎪=⎩， ∴△EAB ≌△DBC （SAS ），∴∠ABE =∠BCD ，∴∠BOD =∠BCD +∠CBE =∠ABE +∠CBE =∠CBA =60°，∴∠BOC =180°-60°=120°．故答案为：120．（2）相等．理由：如图②中，∵△FCO ，△ACB 都是等边三角形，∴CF =CO ，CA =CB ，∠FCO =∠ACB =60°，∴∠FCA =∠OCB ，在△FCA 和△OCB 中，CF CO FCA OCB CA CB =⎧⎪∠=∠⎨⎪=⎩， ∴△FCA ≌△OCB （SAS ），∴AF =BO ．（3）如图③中，结论：AO =2OG ．理由：延长OG 到R ，使得GR =GO ，连接CR ，BR ．在△CGO 和△BGR 中，GC GB CGO BGR GO GR =⎧⎪∠=∠⎨⎪=⎩， ∴△CGO ≌△BGR （SAS ），∴CO =BR =OF ，∠GCO =∠GBR ，AF =BO ，∴CO ∥BR ，∵△FCA ≌△OCB ，∴∠AFC =∠BOC =120°，∵∠CFO =∠COF =60°，∴∠AFO =∠COF =60°，∴AF ∥CO ，∴AF ∥BR ，∴∠AFO =∠RBO ，在△AFO 和△OBR 中，AF OB AFO RBO FO BR =⎧⎪∠=∠⎨⎪=⎩， ∴△AFO ≌△OBR （SAS ），∴OA =OR ，∵OR =2OG ，∴OA =2OG ．【点睛】本题属于三角形综合题，考查了等边三角形的判定和性质，全等三角形的判定和性质，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．27．（1）36；（2）证明见解析；（3）3，理由见解析.【分析】(1)根据直线与坐标轴的交点易得A,C 的坐标，从而得出AC=12，OB=6，根据三角形面积公式可求解；(2) 过E 作EF ⊥x 轴于点解析：（1）36；（2）证明见解析；（3）3，理由见解析.【分析】(1)根据直线与坐标轴的交点易得A,C 的坐标，从而得出AC=12，OB=6，根据三角形面积公式可求解；(2) 过E 作EF ⊥x 轴于点F ，延长EA 交y 轴于点H ，证△DEF ≌△BDO ，得出EF ＝OD ＝AF ，有EAF OAH OAB 45∠∠∠===︒，得出∠BAE ＝90°.(3)由已知条件可在线段OA 上任取一点N,再在AE 作关于OF 的对称点N ',当点N 运动时，´ON 最短为点O 到直线AE 的距离.再由OAE 30∠=︒，在直角三角形AO N '中,OM ON O N +='即可得解.【详解】解：（1）由已知条件得：AC=12，OB=6∴1126362ABC S =⨯⨯= （2）过E 作EF ⊥x 轴于点F ，延长EA 交y 轴于点H,∵△BDE 是等腰直角三角形，∴DE=DB, ∠BDE=90°,∴EDF BDO 90∠∠+=︒∵BOD 90∠=︒∴BDO DBO 90∠∠+=︒∴EDF DBO ∠∠=∵EF x ⊥轴，∴DEF BDO ≅∴DF=BO=AO,EF=OD∴AF=EF∴EAF OAH OAB 45∠∠∠===︒∴∠BAE ＝90°（3）由已知条件可在线段OA 上任取一点N,再在AE 作关于OF 的对称点N ',当点N 运动时，´ON 最短为点O 到直线AE 的距离,即点O 到直线AE 的垂线段的长，∵OAE 30∠=︒，OA=6，∴OM+ON=3【点睛】本题考查的知识点主要是直角三角形的性质及应用，轴对称在最短路径问题中的应用，弄懂题意，作出合理的辅助线是解题的关键.。

部编版二年级语文下册期末综合训练二时间：60分钟满分：100分班级：姓名：考号： .一、看拼音写词语，我会写得既正确又美观。

(10分)wēn nuǎn rè nɑo kǎo yā yǐn rén zhù mùxìnɡ yùn tián cài shānɡ diàn jīn pí lì jìn二、给加点字选择正确的读音，打“√”。

(4分)1．用“√”为加点字选择正确的读音。

(4分)(1)有虫子来的话，大象只要把他的大耳朵一扇．(shān shàn)，就能把他们赶跑。

(2)这糕的．(de dí)确应该叫“千人糕”啊！(3)彗星运动的时候，后面有一个扫．(sǎo sào)把样的尾巴，所以又叫“扫把星”。

(4)即使把杯子倒．(dǎo dào)过来，水也不会往下流。

三、按要求填空。

(6分)1．“特”的第三笔是__________，“特”可以组词：__________。

2．“钱”的部首是__________，含这个部首的字大多与__________有关。

我还能写出2个含有这个部首的字：__________、__________。

四、根据音节写同音字。

(8分)juéyù dì yì( )赛( )见兄( ) 容( )感( ) ( )室快( ) 回( )五、按要求写词语。

(6分)形容生气的词语：__________ __________ __________表示“笑”的词语：__________ __________ __________ 六、照样子，写一写。

(6分)例：(碧绿)的草地( )的阳光( )的浪花 ( )的枫树例：(捉)蜻蜓( )星星( )故事( )围巾七、用“\”画去不是同一类的词语。

(4分)1．教师魔术师饲养员叔叔2．陀螺七巧板作业本毽子3．博物馆少先队展览馆派出所4．脆生生黄澄澄酸溜溜甜津津八、我会选择合适的字词填空。

期末综合素质评价(二)一仔细推敲, 选一选。

(将正确答案的字母填在括号里) (每小题2 分, 共24 分)1. 下面各数中, 只读1 个零的是( ) 。

A. 509800B. 50009800C. 5009800D. 50980002. 爸爸今年35 岁, 估计下面( ) 选项最接近他的年龄。

A. 1800 个月B. 1800 周C. 1800 天D. 1800000 小时3. □48 是一个三位数, □48÷54, 要使商是两位数, □里有( )种填法。

A. 3B. 4C. 5D. 64. 如果下面线段表示的是0°到180°, 那么钟面上时针和分针所形成的较小角接近线段上( ) 点。

A. AB. BC. CD. D5. 已知a×b = 50, 下面算式( ) 的积不等于500。

A. a×b×10B. a×10×bC. a×2×b×5D. a×5×b×56. 【新考法】阅读浸润心灵, 学校开展全学科阅读活动, 四(1) 班购买12 套课外读物, 每套145 元, 一共需要多少元? 列式为145×12, 下面说法正确的是( ) 。

A. 箭头所指的这一步表示购买1 套的价钱B. 箭头所指的这一步表示购买2 套的价钱C. 箭头所指的这一步表示购买10 套的价钱D. 箭头所指的这一步表示购买12 套的价钱7. 如图, P 为直线a外一点, 点A、B、C为直线a上的三点, 已知PA = 3 cm, PB= 4 cm, PC= 6 cm, 则点P 到直线a的距离( ) 。

A. 等于3 cmB. 等于4 cmC. 等于6 cmD. 小于3 cm8. 下面可以用248÷62 解决的数学问题是( ) 。

A. 一个长方形的长是248 厘米, 宽是62 厘米, 它的面积是多少B. 爸爸买梨和苹果共248 千克, 其中苹果有62 千克, 梨买了多少千克C. 小轿车每小时行62 千米, 行248 千米需要多少小时D. 一套桌椅248 元, 62 套这样的桌椅多少钱9. 在同一平面内, 把两根小棒都摆成和第三根小棒垂直, 这两根小棒的位置关系是( ) 。

人教版四年级数学上册期末总复习综合测试卷（二）一、单选题1.与算式30×600积相等的是（）A. 30×300B. 60×300C. 15×2002.一个除法算式中，商是10，除数是20，余数最大是（）A. 9B. 19C. 213.已知∠1+∠2=∠3，∠1+∠2+∠3=180°，则∠3是（）A. 锐角B. 钝角C. 直角D. 平角4.小丽一步约走62厘米，她从学校到图书馆走了596步，学校离图书馆约有（）米．A. 300厘米B. 300米C. 360米5.把一张平行四边形卡片剪一刀分成两个图形，下面几种情况中不可能出现的是（）A. 两个三角形B. 两个梯形C. 一个平行四边形和一个梯形6.13□0000000≈13亿，□里最大可填（）A. 1B. 2C. 3D. 47.两个数相除商5余7，被除数，除数同时乘10，余数是（）A. 5B. 7C. 70D. 508.关于式子37□1698＜3756361，□里最大能填（）A. 6B. 5C. 49.比69999多一万的数是（）A. 70000B. 169999C. 7999910.如图．从某村走到公路，以下表达正确的是（）A. ①线路最短B. ②线路最短C. ③线路最短11.如图，以给出的点为端点，能画出（）条线段．A. 5B. 6C. 无数条12.一个面积为2公顷的果园．如果每5平方米种一棵果树，那么这个果园一共可以种果树（）棵．A. 400B. 4000C. 40000二、判断题13.一个三位数除以两位数，商一定是一位数或两位数．（）14.直线比射线长．（）15.从直线外一点到这条直线所画的线段中，垂直线段最短。

（）16.除数乘商加上余数所得的和，除以被除数，商是1。

（）17.一个因数的末尾有几个0，积的末尾就有几个0．（）三、填空题18.量出如图所示的角度，并判断是哪一种角．∠1＝________°，________角．19.在9□7865600的□里填上适当的数字，使它接近9亿，则□里可以填________；如果要使它接近10亿，则□里可以填________．20.如图，∠2是∠1的2倍，∠3是∠1的6倍，那么∠3﹣∠2＝________°．21.在一个除法算式中，被除数是除数的14倍，除数是商的5倍，这个除法算式可以是________．22.单位换算．70平方千米＝________平方米；6200000平方米＝________公顷．23.在同一平面内，两条直线都与第三条直线垂直，那么这两条直线________。