简单六方结构二维光子晶体能带的COMSOL模拟

Comsol软件在二维材料教学中的应用摘要：石墨烯是一种典型的二维材料，具有优良的光学和电学性能，光-物质响应能力强并且易于进行光电调控，在小型化、多功能化的光电子学器件研究中具有广阔应用前景。

为了进行石墨烯的理论与实验教学，首先需进行准确的光电特性建模。

目前，始终缺乏针对石墨烯精准、直观的光电仿真方法，导致教学内容晦涩难懂。

有限元分析软件Comsol Multiphysics具有多物理场综合仿真能力，可自主编译并且剖分精确，可为石墨烯的理论教学提供直观、易于理解的仿真手段。

本文通过研究石墨烯的光电特性，确定了准确的建模参数，之后利用Comsol进行了建模仿真，通过与公开实验数据对比验证了模型的正确性。

该建模方法可用于进行多种二维材料的教学演示。

关键词：Comsol软件，石墨烯，二维材料，仿真建模一、石墨烯特性石墨烯（graphene）是由单层碳原子以六角形式排列的蜂巢状晶格平面结构，2004年，英国科学家Andre Geim和Konstantin Novoselov利用机械剥离法成功制备出单层石墨烯，掀起了对二维材料的研究热潮[1]。

石墨烯每个碳原子都有六个电子，其中2个为内壳层电子，4个为外壳层价电子。

形成石墨烯晶格时，碳原子外壳层4个价电子中的3个电子按sp2杂化轨道分别与邻边三个碳原子构成平面共价键，用“σ”键表示，相比于钻石的sp3杂化轨道共价键，石墨烯具有更为坚固的轨道键，这决定了其卓越的机械性能。

共价键外的一个电子被称为‘π’电子，由于石墨烯的平面结构，其可以自由移动且具有超高迁移率，这一特性使石墨烯展示出了诸多奇异光电子学性质。

不同于其他半导体材料，石墨烯具有零带隙特性，如图1。

其特殊的能量-色散关系决定了石墨烯的超高电导率。

科学家们在理论上证明了石墨烯载流子迁移率可达到100000，实验中诸多研究者获得了超过15000的载流子迁移率。

这一数值超过硅材料的10倍，是目前已知载流子迁移率最高的物质，因此石墨烯也被称为“半金属”。

简单六方结构二维光子晶体能带的COMSOL模拟北京东之星应用物理研究所伍勇1.引言COMSOL携带的案例库里，其中一篇<Bandgap Analysis of a Photonic Crystal>(以下简称< Bandgap >)对砷化镓简单正方格子2D光子能带进行了完整计算和研究。

本文将程序用于简单六方结构，并将结果在此做一介绍。

2. 关于 Floquet (弗洛盖）波矢F k这是入门COMSOL光子晶体能带模拟的重要概念，在另一案例<Porous Absorber>中，在Floquet周期性边界条件一段写明：)dk(ie)dx(p)x(p由此我判断Floquet 波矢就是Bloch（布洛赫）波矢,但“帮助”文档中有：)sinancosa(sinkk21211F ，以正格子基矢21a,a表示（其文没有任何几何插图和物理说明），使我决定必须在六方格子中选择矩形单胞作为周期单元，以使计算机程序能够运行我的几何方案。

3.几何建模图1作为试探选择的几何模型，圆形柱代表以GaAs作为格点材料，在空气介质中周期性排列，形成二维六方结构人造晶体。

a 是晶格常数。

z 是z 方向的单位矢量形单胞六方格子光子晶体的矩图.1以上根据倒格子基矢定义计算出1b ，2b 及其分量。

由倒格子基矢1b ，2b ，构建长方格子的布里渊区也是长方结构如图2：a3aKMxk yk aa 1aa 32a i )a a (a a ab x222321321)a a (a a ab 3211322里渊区六方结构光子晶体的布图2.4.二维光子晶体主方程COMSOL 在< Bandgap > “模型开发器” [电磁波，频域] 写出方程形式如下：0)()(201E jk E rr ，在< Bandgap >中，下面目录 [波方程，电] 中直接简化为，20Ek )E (r 电磁波在光子晶体中的传播遵从麦克斯韦方程，上述方程可由麦克斯韦方程组出发导出介质中的麦克斯韦方程组)(D1)(B 30)(tB E2)(tD JH4E D，H B，EJ在电介质中一般认为自由电荷，自由电流密度（电导率）为零。

1.近来用COMSOL 计算光子晶体光纤的模场分布，可是不知道PML 的参数如何设置，以及边界条件怎么设置，计算出来的结果不对. 实验室老板催得急，算不出来特别郁闷，不想读的心思都有了。

请用过的人帮帮忙吧：）我也是用comsol 算光纤的，关于pml 层的设定问题，如果不考虑损耗的话，pml 层可以不设，你可以试一试就知道了，pml 对模场分布基本没有影响2. COMSOL Multiphysics 如何模拟带隙光子晶体光纤？要用COMSOL Multiphysics 模拟带隙光子晶体光纤，也就是要加入kz，可以用如下方法：（1）用平面波模式，将模型边界条件改为电场，输入一个表达式的名字，例如E1。

（2）定义该边界表达式E1，菜单“选项gt表达式gt边界表达式”，选择不同的边界，分别写入该边界上电场E1 的表达式，将所需的周期性边界方程写入COMSOL Multiphysics。

这样就能加入kz，3. 如何准确求光子晶体光纤的限制损耗即有效折射率的虚部我在模拟PCF 时，为了求其限制损耗即有效折射率的虚部，PCF 结构的外面加了PML，在但是在加了PML后，却发现光束不能约束在纤芯中了。

不知道哪里出了问题，还望各位高手给予指点，谢谢。

V W-d 8vpw-qT- 1attach219885/attach :T o1OB0j P 加了PML 后的结果如下：attach219886/attachbeautycatcher 发表于2009-10-21 07:31我也是初学，也在做一些光子晶体的方法。

目前还不懂帮你顶顶，大家多多讨论caoer 发表于2009-10-21 11:17有限元做光子？这个挺有新意，不过要注意是否适用mahui 发表于2009-11-5 09:59能说一下有限元做光子为什么不合适吗？不过用FDTD 做光子的还蛮多的Feit 发表于2009-11-5 12:22PML 的几何不对，应该是加个六边形的PML 才对吧：）fangany 发表于2009-11-8 13:29纤芯比外面的小，当然有可能找到外面的那个模式，多找几个模式或者将外面的区域减小应该就可以了shanyrain 发表于2009-11-8 20:35加个圆形的就可以了PML 要考虑模型的对称性，比如这个模型可以只计算1/4 或者1/6xwx000000 发表于2009-11-13 22:31楼主具体交流下怎么划分格点的？我算光子晶体光纤的模式，伪模很多阿，比如设neff1.5 附近寻找，200 个，设它就给找出200 个neff出来。

COMSOL使用步骤打开COMSOL光子晶体光纤模式仿真模块：双击图标，选择射频模块—垂直波—混合模波—模式分析。

10damper初始界面：所选用的COMSOL模块的初始界面。

一、圆孔型光子晶体光纤的建模选择左边绘图对象中的“椭圆形/圆形（以圆心）”图标点击图标并同时在键盘上按Shift键，以(0,0)为圆心画圆。

画好圆后双击此圆，可以设定圆的直径、圆心等参数。

这里设定直径为9um，此时的圆变得很小，我们可以通过工具栏上的“放大、缩小、缩放至视窗大小”按钮将圆缩放到界面适合的大小。

复制圆：选择Ctrl+C与Ctrl+V后会出现下面的小对话框，可以设定x或y轴位移将圆进行上下左右的移动。

这里设定y轴位移为10um。

复制后的界面如下图所示。

对于图两个圆中上面的圆同样进行“复制，粘贴”，位移中x、y轴都为0。

此时两个圆是重叠的。

选择左边绘图对象中的“旋转”图标，旋转60度。

旋转后的图如下所示。

同样进行旋转可得到第一层空气孔，如下图所示。

1复制上图中的标志为1的圆，设定其y轴位移为10um。

同样进行旋转可得到第二层空气孔。

重复上面步骤，便可以画出空气孔为圆形的光子晶体光纤的截面图。

这里我们仿真的是空气孔为五层的光子晶体光纤，第一层空气孔缺失，所以将截面图中的第一层空气孔去掉。

所得截面图如下所示。

纤芯直径为3um，光纤外直径为125um。

二、柚子型光子晶体光纤的建模画圆，这里我们设定的空气孔直径为36um。

选择左边绘图对象中的矩形/正方形(中心)图标。

建立一个具有一定宽度和长度的长方形。

将长方形旋转30度选择镜射图标选择联集，将两个长方形组合在一起复制联集后的长方形，再将原来的圆与长方形取联集。

2将上图中的长方形组合2，与左侧的长方形组合重合取差集，便可以得到一个柚子型的空气孔将图形沿y轴上移。

这里内包层直径为28um，空气孔直径36um，所以上移14+18=32um。

同样将空气孔进行旋转，得到下图。

将中间的柚子型去掉，加上圆形的纤芯和包层。

COMSOL⼆维膜层光学性能-吸收率仿真教学COMSOL⼆维膜层结构光学性能/吸收率仿真教学新建
1. 新建→模型向导→⼆维；
2. →选择物理场：光学→波动光学→电磁波，频域→增加→研究；
3. 选择研究：波长域→完成；
建模
4. ⼏何绘制多个长⽅形形成多层膜结构；
5. 必要的情况下可以在上下层加⼊空⽓层（真空层）；
边界条件
6. 添加“端⼝”，设置红外⼊射端⼝，在空⽓层边界上。

再添加“端⼝”，设置出射端⼝，另⼀端的空⽓层；
7. 模型两侧边界设置为“周期性边界条件”；
8. 对于膜层很薄的部分，可以设置为“过渡边界条件”，代替超薄层，厚度可在此条件下设置；
9. 进⾏⽹格化；
材料参数
10. 顶部⼯具栏：增加材料；
11. 可在右侧框内搜索要添加的材料，然后“增加到选择”；或者添加空材料，去选择⼀个域，然后材料属性⽬录下会出现做该仿真必要的参数，输⼊参数即可；研究：结果
12. 研究→波长域，设置波长范围及步长，点击“研究”；
13. 派⽣值→全局计算，表达式选“ewfd.Atotal” ；数据系列运算选“⽆”，计算；仿真图下⽅出现“表格”，得到“波长”与“吸收率”关系。

点击“表图”按钮，得到“吸收曲线”；
14. 派⽣值→全局计算，表达式选“ewfd.Atotal”；数据系列运算选“平均值”，计算；仿真图下⽅出现“表格”，得到“平均吸收率”值。

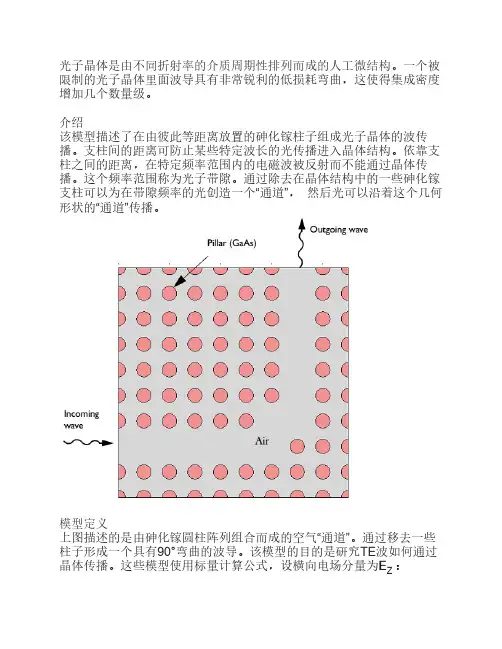
应用COMSOL对二维三角晶格光子晶体带隙仿真
张雁茗;逯贵祯
【期刊名称】《中国传媒大学学报：自然科学版》
【年(卷),期】2017(24)3
【摘要】介绍了一种使用COMSOL用数值计算方法仿真2D光子晶体色散图的方法,通过COMSOL将Z方向无限延伸的介质介质圆柱阵列形成的二维三角晶格光子晶体等效为二维平面进行仿真,并采用了独特的矩形结构作为该三角晶格光子晶体的单元晶格,相比传统的用正六边形作为单元晶格的方法,建模与设置Floquet 周期边界条件的过程更为简单。

成功仿真出了该光子晶体的色散图,并与参考文献中的结果进行了对比分析,带隙、色散曲线与文献中结果基本吻合,证明了这种仿真方法的正确性。

【总页数】3页(P31-33)
【关键词】光子晶体;光子带隙;色散图;三角晶格;COMSOL
【作者】张雁茗;逯贵祯
【作者单位】中国传媒大学
【正文语种】中文
【中图分类】O481.1
【相关文献】
1.二维三角晶格光子晶体的光子带隙分析 [J], 张晓娟
2.Ge基二维三角晶格光子晶体的光子带隙 [J], 刘建军;范志刚;肖昊苏;张旺;关春颖;
苑立波
3.柱体截面不同三角晶格二维光子晶体完全带隙的研究 [J], 廖兴展;林少光;张桂春
4.二维斜三角晶格光子晶体完全带隙研究 [J], 赵永林;闫珂柱;刘军;李开才
5.铜币形空气孔二维三角晶格光子晶体的完全光子带隙 [J], 李传起;范庆斌;杨梦婕;张秀容
因版权原因，仅展示原文概要，查看原文内容请购买。

简单六方结构二维光子晶体能带的COMSOL 模拟北京东之星应用物理研究所伍勇1.引言COMSOL 携带的案例库里，其中一篇<Bandgap Analysis of aPhotonic Crystal>(以下简称< Bandgap >)对砷化镓简单正方格子2D 光子能带进行了完整计算和研究。

本文将程序用于简单六方结构，并将结果在此做一介绍。

2. 关于 Floquet (弗洛盖） 波矢F k这是入门COMSOL 光子晶体能带模拟的重要概念，在另一案例<Porous Absorber>中，在Floquet 周期性边界条件一段写明：)d k (i e )d x (p )x (p ⋅-+=由此我判断Floquet 波矢就是Bloch （布洛赫）波矢,但“帮助”文档中有：)sin a n cos a (sin k k 21211F ααα ⨯+=，以正格子基矢21a ,a 表示（其文没有任何几何插图和物理说明），使我决定必须在六方格子中选择矩形单胞作为周期单元，以使计算机程序能够运行我的几何方案。

3.几何建模图1作为试探选择的几何模型，圆形柱代表以GaAs 作为格点材料，a 32=a i x 022π里渊区六方结构光子晶体的布图2.4.二维光子晶体主方程COMSOL 在< Bandgap > “模型开发器” [电磁波，频域] 写出方程形式如下： 0)()(0201=--⨯∇⨯∇-E j k E r r ωεσεμ， 在< Bandgap >中，下面目录 [波方程，电] 中直接简化为，020=-⨯∇⨯∇E k )E (r ε电磁波在光子晶体中的传播遵从麦克斯韦方程，上述方程可由麦克斯韦方程组出发导出介质中的麦克斯韦方程组)(D 1ρ=⋅∇ )(B 30=⋅∇ )(t B E 2∂∂-=⨯∇ )(t D J H 4∂∂+=⨯∇ E D ε=，H B μ=，E J σ=在电介质中一般认为自由电荷，自由电流密度（电导率）为零。

简单六方结构二维光子晶体能带的C O M S O L 模拟 北京东之星应用物理研究所伍勇1.引言COMSOL 携带的案例库里，其中一篇<BandgapAnalysisofaPhotonicCrystal>(以下简称<Bandgap>)对砷化镓简单正方格子2D 光子能带进行了完整计算和研究。

本文将程序用于简单六方结构，并将结果在此做一介绍。

2.关于Floquet (弗洛盖）波矢F k这是入门COMSOL 光子晶体能带模拟的重要概念，在另一案例<PorousAbsorber >中，在Floquet 周期性边界条件一段写明：)d k (i e )d x (p )x (p 由此我判断Floquet 波矢就是Bloch （布洛赫）波矢,但“帮助”文档中有：)sin a n cos a (sin k k 21211F ，以正格子基矢21a ,a 表示（其文没有任何几何插图和物理说明），使我决定必须在六方格子中选择矩形单胞作为周期单元，以使计算机程序能够运行我的几何方案。

3.几何建模图1作为试探选择的几何模型，圆形柱代表以GaAs 作为格点材料，在空气介质中周期性排列，形成二维六方结构人造晶体。

a 是晶格常数。

z ˆ 是z 方向的单位矢量 以上根据倒格子基矢定义计算出1b ，2b 及其分量。

由倒格子基矢1b ，2b ，构建长方格子的布里渊区也是长方结构如图2：4.二维光子晶体主方程COMSOL 在<Bandgap>“模型开发器”[电磁波，频域]写出方程形式如下：0)()(0201 E j k E r r ， 在<Bandgap>中，下面目录[波方程，电]中直接简化为，电磁波在光子晶体中的传播遵从麦克斯韦方程，上述方程可由麦克斯韦方程组出发导出介质中的麦克斯韦方程组E D ，H B ，E J在电介质中一般认为自由电荷，自由电流密度（电导率）为零。

本文档不考虑磁性质，0 ，0 J ，1 r传播模态电场函数COMSOL 表达为：)(t i e z z ik e )y ,x (E )t ,z ,y ,x (E 5 ，在周期结构中，它应具有Bloch 波的性质，不考虑衰减损耗。

comsol仿真实验报告一、实验目的本次实验旨在通过使用 COMSOL Multiphysics 软件对特定的物理现象或工程问题进行仿真分析，深入理解相关理论知识，并获取直观、准确的结果，为实际应用提供有效的参考和指导。

二、实验原理COMSOL Multiphysics 是一款基于有限元方法的多物理场仿真软件，它能够将多个物理场（如电场、磁场、热场、流体场等）耦合在一个模型中进行求解。

其基本原理是将连续的求解区域离散化为有限个单元，通过对每个单元上的偏微分方程进行近似求解，最终得到整个区域的数值解。

在本次实验中，我们所涉及的物理场及相关方程如下：（一）热传递热传递主要有三种方式：热传导、热对流和热辐射。

热传导遵循傅里叶定律：＄q ＝k\nabla T$，其中＄q$ 为热流密度，＄k$ 为热导率，＄＼nabla T$ 为温度梯度。

热对流通过牛顿冷却定律描述：＄q ＝ h(T T_{amb}）＄，其中＄h$ 为对流换热系数，＄T$ 为物体表面温度，＄T_{amb}＄为环境温度。

（二）流体流动对于不可压缩流体，其运动遵循纳维斯托克斯方程：＄＼rho(＼frac{＼partial ＼vec{u}｝｛＼partial t} ＋（＼vec{u}＼cdot\nabla)＼vec{u}）＝＼nabla p ＋＼mu\nabla^2\vec{u} ＋＼vec{f}＄其中＄＼rho$ 为流体密度，＄＼vec{u}＄为流体速度，＄p$ 为压力，＄＼mu$ 为动力粘度，＄＼vec{f}＄为体积力。

（三）电磁场麦克斯韦方程组是描述电磁场的基本方程：＄＼nabla\cdot\vec{D} ＝＼rho$＄＼nabla\cdot\vec{B} ＝ 0$＄＼nabla\times\vec{E} ＝＼frac{＼partial ＼vec{B}｝｛＼partial t}＄＄＼nabla\times\vec{H} ＝＼vec{J} ＋＼frac{＼partial ＼vec{D}｝｛＼partial t}＄其中＄＼vec{D}＄为电位移矢量，＄＼vec{B}＄为磁感应强度，＄＼vec{E}＄为电场强度，＄＼vec{H}＄为磁场强度，＄＼rho$ 为电荷密度，＄＼vec{J}＄为电流密度。

COMSOL多物理场模拟软件简单入门教程下面是COMSOL多物理场模拟软件的简单入门教程：
第一步，首先打开COMSOL多物理场模拟软件。

在启动界面上，选择
创建新模型。

第二步，选择您要模拟的物理场。

COMSOL提供了多个物理现象的模块，如传热模块、流体力学模块、电磁场模块等。

选择适合您模拟对象的
物理现象模块。

点击下一步。

第三步，定义几何模型。

在这一步中，您可以创建几何图形、导入CAD文件或使用现有几何形状。

您可以使用COMSOL的几何建模工具来创
建您想要的几何形状。

完成后，点击下一步。

第四步，设置物理场。

在这一步中，您可以设定边界条件、物理参量等。

COMSOL提供了丰富的物理场设置选项，您可以根据需要进行调整。

完成后，点击下一步。

第五步，设置网格。

COMSOL使用网格来离散化物理现象的模型。

您
可以选择自动生成网格或手动调整网格的细化程度。

完成后，点击下一步。

第六步，设置求解器。

COMSOL提供了多个求解器选项，根据您的模
型和要求选择合适的求解器。

完成后，点击下一步。

第七步，设置后处理。

COMSOL提供了多种可视化和后处理选项，如
绘制剖面图、动态模拟、导出数据等。

根据您的需求选择合适的后处理选项。

第八步，点击求解按钮。

COMSOL将自动求解您的模型，并显示结果。

您可以根据需要进一步优化和改进模型。

2019年第38卷第8期传感器与微系统（Transducer and Microsystem Technologies）DOI：10．13873/J．1000—9787（2019）08—0111—03基于COMSOL的光子晶体能带结构仿真计算*付子义1，王晨旭1，长谷川弘治2（1．河南理工大学电气工程与自动化学院，河南焦作454000；2．室兰工业大学情报电子工学系，日本室兰0500071）摘要：为更方便、快捷地求解光子晶体能带结构问题，基于有限元数值仿真软件COMSOL Multiphysics系数偏微分方程模块，重新建立了数学模型，直接从亥姆霍兹方程出发，结合布洛赫态，推导出光子晶体偏微分形式的本征方程，充分考虑了布洛赫波矢的传播情况，求解出相应的本征频率从而求解出能带，对一维和二维光子晶体能带结构分别进行仿真计算。

仿真计算结果与传统方法结果进行对比分析，验证了此方案的可行性。

关键词：光子晶体；偏微分方程；本征方程；能带结构；COMSOL Multiphysics中图分类号：TP391文献标识码：A文章编号：1000—9787（2019）08—0111—03Simulation computation of photonic crystals energyband structure based on COMSOL*FU Ziyi1，WANG Chenxu1，HASEGAWA Koji2（1．School of Electrical Engineering and Automation，Henan Polytechnic University，Jiaozuo454000，China；2．Information and Electronic Engineering，Muroran Institute of Technology，Muroran0500071/Hokkaido，Japan）Abstract：In order to solve the problem of photonic crystal band structure more conveniently and quickly，basedon the COMSOL Multiphysics coefficient partial differential equation（PDE）module of the finite elementnumerical simulation software，the mathematical model is reestablished．The partial differential form of the photoniccrystal is derived from the Helmholtz equation and combined with the Bloch state．The eigenfunction，and thepropagation of Bloch wave vector is taken into full consideration，the corresponding eigenfrequency is solved so asto solve the energy band．In this case，the energy band structure of one and two-dimensional photonic crystals issimulated respectively．The simulation results are compared with the results of traditional methods，and thefeasibility of the scheme is verified．Keywords：photonic crystals；partial differential equation（PDE）；eigenfunction；energy band structure；COMSOL Multiphysics0引言当电磁波在光子晶体［1，2］中传播时由于布拉格衍射的影响，会受到调制而形成能带结构，即光子能带（photonic band），光子能带之间可能出现的带隙，即光子带隙（pho-tonic band gap，PBG），频率处于光子能带里的电磁波可以在光子晶体中几乎无损地传播，但是出于光子带隙的电磁波，却不能在光子晶体中传播。

电机驱动器模型：2D发电机2D发电机简介本案例说明带有永久磁铁的转子做圆周运动时在定子线圈内如何产生电动势。

产生的电压由时间函数计算出来。

本模型也说明了材料参数，旋转速度和线圈的匝数对电压的影响。

转子的中心由退火处理过的中碳钢组成，中碳钢具有高的相对磁导率。

中心被几个由钐，钴做成的用来产生强磁场的永磁铁块包围。

定子由与转子中心相同的导磁材料制成，可将磁场限制在通过线圈的闭环中。

线圈缠绕在定子磁极上。

图 3-2是具不完整定子的发电机示意图，这样可看到线圈和转子。

图3-2: 发电机示意图，说明了转子，定子和定子线圈的构造。

在环路间线圈也是连接的，这样可产生最高的电压。

在COMSOL Multiphysics中建模本发电机的COMSOL Multiphysics 模型是关于发电机横截面的时间相关2D问题。

这是一个时变模型，其中转子中磁源的运动被认为是定子和转子几何体的边界条件。

因此，方程中没有罗伦兹项，偏微分方程为其中磁位能仅仅有z分量。

旋转运动利用移动网格应用模式建模，其中几何体包括了转子和部分气隙的中心部分旋转，相对于定子坐标轴有一个旋转变换。

变形网格的旋转由下列变换定义转子和定子是两个分离的几何对象，因此可使用装配几何体(详见COMSOL Multiphysics Modeling Guide413页的“使用装配” )。

这样有几个好处：转子和定子可自动耦合，部件可单独划分网格，并且允许两个几何体界面（称为裂缝）上的位能矢量不连续。

转子问题在一个旋转坐标系统中求解，在该坐标轴系统中转子是固定的（转子支架），但是定子问题是在相对定子（定子支架）固定的坐标系统中求解。

定子和转子中心部分的材料在磁通量B 和磁场H 存在非线性关系，称为B-H 曲线。

在COMSOL Multiphysics中，B-H 曲线通过一个插补函数引入；见图 3-3。

该函数可用在求解域设定中。

通常B-H 曲线由| B |相对于| H |给出，但是垂直波应用模式必须知道| H |对于| B |的关系。

收稿日期:2010-07-19作者简介:臧克宽(1981-),男,硕士,主要从事光子晶体激光器方面的研究;孙晓红,女,博士,郑州大学教授,主要从事光子晶体方面的研究.光电器件与材料基于comsol 软件的光子晶体通信器件模拟臧克宽,孙晓红,李大海,刘国斌(郑州大学河南激光与光电信息技术重点实验室,河南 郑州 450052)摘 要:利用comsol 软件对几种光子晶体通信器件的模拟,有光子晶体光纤、波导、分波器以及滤波器等器件,模拟结果很好,可以更直观地了解光子晶体器件的优越性,更为开发集成光通信器件提供了有益的参考.关键词:光子晶体;通信器件;comsol 模拟中图分类号:TN 929.11 文献标识码:A 文章编号:1673-1255(2010)05-0051-03S imulation of Optical Communication ApparatusBased on the Comsol SoftwareZANG Ke kuan,SUN Xiao hong,Li Da hai,LIU Guo bin(T he key L aboratory of L aser and Photo eletr icity I nf or mation T echnology of H e N an p r ovince,Zhengz hou 450052,China)Abstract:T he comsol software is used to simulate some integrated apparatus of the optical commuciaction such as photonic crystal fiber,w aveguide,w ave separater and filter.T he result of simulation is very good.T he advantages of photonic crystal dev ices can be more intuitively understood.It provides the useful information for the development of the apparatus of the optical commuciaction.Key words:optical crystal;com munication apparatus;comsol simulation 长期以来,人们一直希望能够突破电子在信息传输上的瓶颈限制,而让拥有极高信息容量和效率、极快响应能力、极强的互连能力和并行能力以及极大存储能力的光子来取代电子成为新型的信息载体.光子具有高传输速度、高密度及高容错性等优点,成为代替电子作为信息的载体.光子晶体(Pho tonic Crystal)概念的提出,加速了人们对光子作为信息载体的研究.由于光子在光子晶体中的行为类似于电子在天然晶体(从某种意义上来说可以叫做电子晶体)中的行为,固体物理中的许多概念都可用在光子晶体上,所以光子晶体的基本特征是具有光子禁.频率落在禁带中的电磁波是禁止传播的,因为带隙中没有任何态存在.光子晶体的另一个主要特征是光子局域[1-4].光子晶体的出现使自由地操纵和控制光的行为成为现实,人们能够按自己的需求,以人工的方式设计和制造光子器件,由于光子晶体能够控制光在其中的传播,所以它的应用十分广泛.其主导思想就是利用光子禁带或禁带结构中的缺陷态来改变光子晶体中某种电磁态的密度,以制作全新原理或以前所不能制作的高性能器件[5].1 光子晶体通信器件的模拟[6,7]1.1 光子晶体光纤如今,人们对光子晶体的应用研究得最多也是进展最快的领域莫过于对光子晶体光纤的研究.光子晶体光纤虽然和传统光纤的导光机制一样,但是却具有明显优于传统光纤的特性,诸如无截止单模、不同的色度色散、极好的非线性效应、双折射效应、第25卷第5期2010年10月光电技术应用EL ECT RO-O PT IC T ECHNO LOG Y APP LICAT I ONVo l.25,No.5October.2010较高的入射功率、非线性现象、易于实现多芯传输等,这些优良特性使其在未来的光通信领域将有着广阔的应用前景.图1是用comsol 软件简单模拟了光子晶体光纤的光场分布.图1 六角形结构光子晶体光纤的光场分布图从图中可以明显看到,光只会分布在光纤孔中,不会散射到其他区域.1.2 光子晶体波导传统的介电波导在传播电磁波是会在传输过程中损失能量,特别是在拐角处损失的能量更多,但是光子晶体波导可以改变这种情况.即光子晶体波导对直线和转角都有很高的效率.具有如此高效传播能力波波导使得人们不得不对其另眼相看.因此,对光子晶体波导的研究也成为光子晶体应用研究的一个主要领域.图2是用comsol 软件模拟的直线波导和弯折波导的光传播情况.图2 正方晶格光子晶体直波导传输图从模拟图2中可以清楚看到:不在禁带区域的光会出现很强的散射,传导模式不对会很快衰减,只有在范围内而又有很好的传导模式的光才能顺利传播,而且损耗极小.看以看到,与直波导相同,弯曲波导的传输率也可以接近100%,如图3所示.图3 直角弯折波导的光传播模拟图1.3 光分波器在通信电路中,分波器是很重要的器件,那么光分波器在全光路中必不可少,图4是T 字型光分波器的光场模拟图.可以看到,与图3中的直角弯折波导具有相似性,只是光能量分开传播,分开后的总能量与分开前的能量相差很小,效率可以高达96%.图4 T 字型光分波器的光场模拟图1.4 宽带带阻滤波器和极窄带选频滤波器利用光子晶体的光子频率禁带特性可以实现对光子极优良的滤波性能.这是由于光子晶体的滤波带宽可以做得比较大.钻石结构的光子晶体的滤波带宽可以做到中心频率的20%.而由S.Gupta 等人所提出的金属-介质复合型光子晶体可以将从低频(频率接近0Hz)直到红外波段的电磁波完全滤掉.这种大范围的滤波作用利用传统的滤波器是难以实现的.另外研究发现,当光子晶体中的某些单元被取消而造成缺陷时,就会使得光子晶体的光子频率禁带出现一些 可穿透窗口 .即光子频率禁带内的某些频率会毫无损失地穿过光子晶体,光子晶体的这一特性可以用来制作高品质的极窄带选频滤波器.经分析可以知道,为了得到窄的线宽,应该选择52光 电 技 术 应 用 第25卷合适的谐振腔和波导之间的距离.图5带阻滤波器结构传输图图6 归一化频率不同的两种频率的窄带滤波器传输图图6a 为频率在谐振频率处,图6b 传输频率仅仅偏离谐振频率1%,而传输率却降低为输入的2%多一点.可见此时的滤波器带宽相当窄.1.5 多组合滤波器当把多个谐振腔与波导组合后,会形成不同种类的滤波器.下面把两个波导两个谐振腔组合成一个二维光子晶体的三端口通道下路滤波器并用comsol 软件模拟光传播,如图7所示.图7 三端口通道下路滤波器的结构图与光传输图从图7可以清楚观察到,光波从A 端入射,传输到B 端的能量几乎为零了,所以下载到C 端的效率比较高.如果入射波端口改为C (此时此端口成为上传端口),能量将沿相反的方向传输从端口A 输出,而B 端口因为反射谐振腔的反射而几乎得不到能量.2 结 束 语文中基于comsol 软件对几种光子晶体通信器件的模拟,模拟结果非常好地体现光子晶体器件的优越性,并对模拟结果进行了简单分析,并提出多组合滤波器设计思路,为开发集成光通信器件提供了有益的参考.参考文献[1] John D Joannopoulos,St even G Johnson,Joshua NWinn,et al.Photonic Crystals:M olding the F low of Light [M ].2nd Edition.Princeton U niversity Press,2008.[2] Steven G Johnson,P hotonic Crystals:F rom T heory toPractice [M ].M assachusetts Institute of T echnolo gy,2001.[3] K azuaki Sakoda.Optical Properties of P hotonic Crystals[M ].Springer,2001.[4] E Yablonov itch.Inhibited Spontaneous Emissio n in Solid-State Physics and Electronics [J].Phys.Rev.Lett.1987,58:2059-2062[5] Z Zhang ,S Satpathy.Electromag netic w ave pr opagationin per iodic structures:Bloch wave solution of M ax well s equations[J].Phys.Rev.Lett.1990,65.[6] Y T anaka,T Asano,Y Akahane,et al.T heoretical investig ation of a two -dimensional photonic cryst al slab w ith taper ed air holes.Appl[J].Phys.Lett.2003,82(9).[7] K S Y ee.Numer ical solutio n to initial boundary valueproblems in -volving M ax well s equat ions in isotropic media[J].IEEE Irans.Antennas Propagate.1966.AP -14.[8] O Painter ,J Vuckovic,A Scherer.Defect modes of atwo-dimensio nal photonic crystal in an optically thin di electric slab[J].JOSA B,1999,275(16).53第5期 臧克宽等:基于comsol 软件的光子晶体通信器件模拟。

利用COMSOL仿真进行二维光子晶体的教学作者：邱伟彬林志立来源：《高教学刊》2019年第07期摘; 要：文章以COMSOL RF 模块为工具，进行半导体光电子学课程中的光子晶体的教学。

文中以介质光子晶体和色散材料光子晶体为例，给学生介绍了如何利用商用软件计算特定结构的光子晶体的能带结构，并且实现二维光场结构的可视化输出，使学生既掌握光子晶体能带结构的特点，又掌握如何使用商用软件来获得此能带结构。

关键词：COMSOL;光波导;仿真;商用软件中图分类号：G642 文献标志码：A 文章编号：2096-000X（2019）07-0084-03Abstract： In this paper， we use COMSOL RF module as a tool to teach photonic crystals in semiconductor optoelectronics course. Taking dielectric photonic crystals and dispersive materials photonic crystals as examples， this paper introduces how to use commercial software to calculate the band structure of photonic crystals with specific structures， and realize the visual output of two-dimensional optical field structure， so that students can not only grasp the characteristics of band structure of photonic crystals， but also grasp how to use commercial software to get the band structure.Keywords： COMSOL; optical waveguide; simulation; commercial software一、概述光子晶體是一直介电常数受到周期性调制的结构，类似于电子在晶体中的运动受到晶体中受到周期性势场限制而呈现的允带和禁带，光子在周期性介电常数分布的结构中传播时也出现允带和禁带，因此该晶体就被形象地称为光子晶体。