台风、触礁问题

海损案例触礁海损是指船舶在航行过程中因意外事故而导致船舶、货物、设备等受损的情况。

海损案例触礁，是指船舶在航行中因触礁而导致的海损案例。

触礁是一种常见的海上事故，一旦发生触礁，可能会导致船舶受损、货物损失、环境污染等严重后果。

下面将介绍一个海损案例触礁的具体情况，并对相关问题进行分析和探讨。

案例描述，某货轮在航行途中，因恶劣天气和导航失误，不慎触礁，导致船体受损严重，货物损失严重，同时还造成了海洋环境的污染。

事故发生后，船上的船员和相关部门迅速采取了应急措施，进行了人员疏散和紧急救援，并对货物进行了清点和保护。

同时，还组织了海洋环境清理工作，减少了环境污染的程度。

问题分析，触礁事故导致了船舶受损、货物损失和环境污染等问题，需要对相关责任进行认定和处理。

首先，需要对货轮的航行和导航情况进行调查和分析，确定触礁原因和责任归属。

其次，需要对货物损失进行评估和赔偿，保障货主的合法权益。

同时，还需要对海洋环境污染进行清理和修复，减少环境损害。

最后，还需要对事故中可能存在的人为失误和管理漏洞进行整改和改进，提高船舶安全管理水平，避免类似事故再次发生。

问题探讨，触礁事故的发生往往与恶劣天气、导航失误、人为疏忽等因素有关，需要加强船舶安全管理和风险防范。

在船舶航行过程中，应加强对天气和海况的监测和预警，及时调整航线和速度，避免恶劣天气对船舶造成影响。

同时，应加强对船员的培训和管理，提高其应急处理能力和危机意识，确保船舶安全运行。

另外，还需要加强对船舶设备和导航系统的维护和检修，确保其正常运行，减少因设备故障导致的事故发生。

结论，海损案例触礁是一种常见的海上事故，对船舶、货物和环境都会造成严重影响。

在处理触礁事故时，需要对相关责任进行认定和处理，保障相关权益。

同时，还需要加强船舶安全管理和风险防范，提高船舶安全运行水平，减少事故发生的可能性。

只有这样，才能确保船舶安全运行，保障海上交通安全和海洋环境保护。

第1篇一、面试背景某豪华游轮在航行过程中不幸触礁，导致船只受损，乘客和船员的生命财产安全受到威胁。

为了确保事件得到妥善处理，游轮公司决定组织一次应急处理面试，选拔具备专业能力和应急处理能力的人才加入应急处理团队。

以下为面试题目，字数超过2500字。

二、面试题目1. 请简要介绍您在应急处理方面的背景和经验。

2. 请描述一次您参与的应急处理事件，包括事件背景、您的角色、处理过程及结果。

3. 请谈谈您对游轮触礁事件应急处理的整体思路。

（1）在事件发生后，您认为首要任务是做什么？（2）如何确保乘客和船员的生命财产安全？（3）如何协调各方资源，确保救援工作顺利进行？4. 请列举几种可能的救援措施，并简要说明其优缺点。

（1）派遣救援船只进行救援（2）利用飞机进行空中救援（3）组织潜水员进行水下救援（4）利用无人机进行搜索和救援5. 请谈谈如何处理触礁事件中可能出现的医疗救助问题。

（1）如何快速评估伤员情况？（2）如何确保伤员得到及时有效的救治？（3）如何与外界医疗机构协调，为伤员提供更好的救治？6. 请谈谈如何处理触礁事件中的通信问题。

（1）如何确保与外界保持畅通的通信？（2）如何处理通信中断的情况？（3）如何协调救援队伍之间的通信？7. 请谈谈如何处理触礁事件中的心理辅导问题。

（1）如何为乘客和船员提供心理支持？（2）如何处理因触礁事件引发的心理创伤？（3）如何与专业心理辅导机构合作，为乘客和船员提供心理援助？8. 请谈谈如何处理触礁事件中的媒体应对问题。

（1）如何确保信息发布的准确性？（2）如何处理媒体采访？（3）如何协调与媒体的关系？9. 请谈谈如何处理触礁事件后的善后工作。

（1）如何对乘客和船员进行赔偿？（2）如何处理受损船只的修复工作？（3）如何预防类似事件再次发生？10. 请谈谈您在应急处理过程中，如何发挥团队协作精神？11. 请谈谈您在应急处理过程中，如何应对压力和挑战？12. 请谈谈您认为游轮触礁事件应急处理中最重要的是什么？13. 请谈谈您对游轮安全管理的看法。

海上航行五问题海上航行遇到的突发事件很多，但我们如何利用自己掌握的知识把它化险为夷呢？这就需要我们有足够的经验和丰富的知识。

下面，给大家举例说明，希望大家能够从中得到感悟。

一、诠释原委例1 某大草原上有一条笔直的公路，在紧靠公路相距40千米的A 、B 两地，分别有甲、乙两个医疗站，如图，在A 地北偏东45°、B 地北偏西60°方向上有一牧民区C ．一天，甲医疗队接到牧民区的求救电话，立刻设计了两种救助方案，方案I ：从A 地开车沿公路到离牧民区C 最近的D 处，再开车穿越草地沿DC 方向到牧民区C ．方案II ：从A 地开车穿越草地沿AC 方向到牧民区C ． 已知汽车在公路上行驶的速度是在草地上行驶速度的3倍．（1）求牧民区到公路的最短距离CD ．（2）你认为甲医疗队设计的两种救助方案，哪一种方案比较合理？并说明理由.（结果精确到0.1.1.731.41）析解：（1）设CD 为x 千米，由题意得， ∠CBD =30°，∠CAD =45°， ∴AD =CD =x在Rt △BCD 中，tan30°=xBD∴ BDAD +DB =AB =40 ∴40x += 解得 x ≈14.7∴ 牧民区到公路的最短距离CD 为14.7千米．（2）设汽车在草地上行驶的速度为v ，则在公路上行驶的速度为3v ， 在Rt △ADC 中，∠CAD =45°，∴ AC方案I 用的时间134333AD CD AD CD CDt v v v v +=+==方案II用的时间2ACt v== ∴2143CD t t v -=-， AD Ｂ北东例1题图∵4＞0 ∴ 21t t -＞0∴方案I 用的时间少，方案I 比较合理点评：在紧急非常情况下，要做出正确合理的判断只有知识丰富才有可能做到。

二、确定航行速度例2 如图，甲船在港口P 的北偏西60 方向，距港口80海里的A 处，沿AP 方向以12海里/时的速度驶向港口P ．乙船从港口P 出发，沿北偏东45 方向匀速驶离港口P ，现两船同时出发，2小时后乙船在甲船的正东方向．求乙船的航行速度．（精确到0.1海里/1.411.73） 析解：依题意，设乙船速度为x 海里/时，2小时后 甲船在点B 处，乙船在点C 处，作PQ BC ⊥于Q ，则 8021256BP =-⨯=海里，2PC x =海里．在Rt PQB △中，60BPQ ∠= ，1cos 6056282PQ BP ∴==⨯= ． 在Rt PQC △中，45QPC ∠= ，cos 4522PQ PC x ∴=== ．28=，x =．19.7x ∴≈．答：乙船的航行速度约为19.7海里/时．点评：构建方程模型是解答此类问题的一般规律。

船的触礁问题教学目标(一)教学知识点1.经历探索船是否有触礁危险的过程，进一步体会三角函数在解决问题过程中的应用.2.能够把实际问题转化为数学问题，能够借助于计算器进行有关三角函数的计算，并能对结果的意义进行说明.(二)能力训练要求发展学生的数学应用意识和解决问题的能力.教具重点1.经历探索船是否有触礁危险的过程，进一步体会三角函数在解决问题过程中的作用.2.发展学生数学应用意识和解决问题的能力.教学难点根据题意，了解有关术语，准确地画出示意图教学过程Ⅰ.创设问题情境，引入新课[师]直角三角形就像一个万花筒，为我们展现出了一个色彩斑澜的世界.我们在欣赏了它神秘的“勾股”、知道了它的边的关系后，接着又为我们展现了在它的世界中的边角关系，它使我们现实生活中不可能实现的问题，都可迎刃而解.它在航海、工程等测量问题中有着广泛应用，例如测旗杆的高度、树的高度、塔高等.下面我们就来看一个问题(多媒体演示).海中有一个小岛A，该岛四周10海里内有暗礁.今有货轮由西向东航行，开始在A岛南偏西55°的B处，往东行驶20海里后，到达该岛的南偏西25°的C处，之后，货轮继续往东航行，你认为货轮继续向东航行途中会有触礁的危险吗?你是如何想的?与同伴进行交流.下面就请同学们用锐角三角函数知识解决此问题.(板书：船有触礁的危险吗)Ⅱ.讲授新课[师]我们注意到题中有很多方位，在平面图形中，方位是如何规定的?[生]应该是“上北下南，左西右东”.[师]请同学们根据题意在练习本上画出示意图，然后说明你是怎样画出来的.[生]首先我们可将小岛A确定，货轮B在小岛A的南偏西55°的B处，C在B的正东方，且在A南偏东25°处.示意图如下.[师]货轮要向正东方向继续行驶，有没有触礁的危险，由谁来决定?[生]根据题意，小岛四周10海里内有暗礁，那么货轮继续向东航行的方向如果到A的最短距离大于10海里，则无触礁的危险，如果小于10海里则有触礁的危险.A到BC所在直线的最短距离为过A作AD⊥BC，D为垂足，即AD的长度.我们需根据题意，计算出AD的长度，然后与10海里比较.[师]这位同学分析得很好，能将实际问题清晰条理地转化成数学问题.下面我们就来看AD 如何求.根据题意，有哪些已知条件呢?[生]已知BC°＝20海里，∠BAD＝55°，∠CAD＝25°.[师]在示意图中，有两个直角三角形Rt△ABD和Rt△ACD.你能在哪一个三角形中求出AD 呢?[生]在Rt△ACD中，只知道∠CAD=25°，不能求AD.[生]在Rt△ABD中，知道∠BAD=55°，虽然知道BC＝20海里，但它不是Rt△ABD的边，也不能求出AD.[师]那该如何是好?是不是可以将它们结合起来，站在一个更高的角度考虑?[生]我发现这两个三角形有联系，AD是它们的公共直角边.而且BC是这两个直角三角形BD 与CD的差，即BC＝BD-CD.BD、CD的对角是已知的，BD、CD和边AD都有联系.[师]有何联系呢?[生]在Rt△ABD中，tan55°＝，BD=ADtan55°；在Rt△ACD中，tan25°＝，CD ＝ADtan25°.[生]利用BC＝BD-CD就可以列出关于AD的一元一次方程，即ADtan55°-ADtan25°＝20.[师]太棒了!没想到方程在这个地方帮了我们的忙.其实，在解决数学问题时，很多地方都可以用到方程，因此方程思想是我们初中数学中最重要的数学思想之一.下面我们一起完整地将这个题做完.[师生共析]解：过A作BC的垂线，交BC于点D.得到Rt△ABD和Rt△ACD，从而BD=ADtan55°，CD＝ADtan25°，由BD-CD＝BC，又BC＝20海里.得ADtan55°-ADtan25°＝20.AD(tan55°-tan25°)＝20，AD=≈20.79(海里).这样AD≈20.79海里>10海里，所以货轮没有触礁的危险.[师]接下来，我们再来研究一个问题.还记得本章开头小明要测塔的高度吗?现在我们来看他是怎样测的，并根据他得到的数据帮他求出塔的高度.多媒体演示想一想你会更聪明：如图，小明想测量塔CD的高度.他在A处仰望塔顶，测得仰角为30°，再往塔的方向前进50m至B处.测得仰角为60°.那么该塔有多高?(小明的身高忽略不计，结果精确到1 m)[师]我想请一位同学告诉我什么是仰角?在这个图中，30°的仰角、60°的仰角分别指哪两个角?[生]当从低处观测高处的目标时，视线与水平线所成的锐角称为仰角.30°的仰角指∠DAC，60°的仰角指∠DBC.[师]很好!请同学们独立思考解决这个问题的思路，然后回答.(教师留给学生充分的思考时间，感觉有困难的学生可给以指导)[生]首先，我们可以注意到CD是两个直角三角形Rt△ADC和Rt△BDC的公共边，在Rt△ADC 中，tan30°=，即AC＝在Rt△BDC中，tan60°=,即BC＝，又∵AB=AC-BC＝50 m，得-=50.解得CD≈43(m)，即塔CD的高度约为43 m.[生]我有一个问题，小明在测角时，小明本身有一个高度，因此在测量CD的高度时应考虑小明的身高.[师]这位同学能根据实际大胆地提出质疑，很值得赞赏.在实际测量时.的确应该考虑小明的身高，更准确一点应考虑小明在测量时，眼睛离地面的距离.如果设小明测量时，眼睛离地面的距离为1.6 m，其他数据不变，此时塔的高度为多少?你能画出示意图吗?[生]示意图如图所示，由前面的解答过程可知CC′≈43 m，则CD＝43+1.6＝44.6 m.即考虑小明的高度，塔的高度为44.6 m.[师]同学们的表现太棒了.现在我手里有一个楼梯改造工程问题，想请同学们帮忙解决一下.多媒体演示：某商场准备改善原来楼梯的安全性能，把倾角由40°减至35°，已知原楼梯长为4 m，调整后的楼梯会加长多少？楼梯多占多长一段地面?(结果精确到0.0l m)请同学们根据题意，画出示意图，将这个实际问题转化成数学问题，(先独立完成，然后相互交流，讨论各自的想法)[生]在这个问题中，要注意调整前后梯楼的高度是一个不变量.根据题意可画㈩示意图(如右图).其中AB表示楼梯的高度.AC是原楼梯的长，BC是原楼梯的占地长度；AD是调整后的楼梯的长度，DB是调整后的楼梯的占地长度.∠ACB是原楼梯的倾角，∠ADB是调整后的楼梯的倾角.转化为数学问题即为：如图，AB⊥DB，∠ACB＝40°，∠ADB＝35°，AC＝4m.求AD-AC及DC的长度.[师]这位同学把这个实际楼梯调整问题转化成了数学问题.大家从示意图中不难看出这个问题是前面问题的变式.我相信同学们一定能用计算器辅助很快地解决它，开始吧![生]解：由条件可知，在Rt△ABC中,sin40°＝，即AB＝4sin40°m，原楼梯占地长BC＝4cos40°m.调整后,在Rt△ADB中，sin35°＝，则AD＝m.楼梯占地长DB=m.∴调整后楼梯加长AD-AC＝-4≈0.48(m)，楼梯比原来多占DC＝DB-BC= -4cos40°≈0.61(m).Ⅳ.课时小结本节课我们运用三角函数解决了与直角三角形有关的实际问题，提高了我们分析和解决实际问题的能力.其实，我们这一章所学的内容属于“三角学”的范畴.请同学们阅读“读一读”，了解“三角学”的发展，相信你会对“三角学”更感兴趣.Ⅴ.课后作业习题1.6第1、2、3题.Ⅵ.活动与探究(2003年贵州贵阳)如图，某货船以20海里／时的速度将一批重要物资由A处运往正西方向的B处，经16小时的航行到达，到达后必须立即卸货.此时.接到气象部门通知，一台风中心正以40海里／时的速度由A向北偏西60°方向移动，距台风中心200海里的圆形区域(包括边界)均受到影响.(1)问：B处是否会受到台风的影响?请说明理由.(2)为避免受到台风的影响，该船应在多少小时内卸完货物?(供选用数据：≈1.4，≈1.7)[过程]这是一道需借助三角知识解决的应用问题，需抓住问题的本质特征.在转化、抽象成数学问题上下功夫.[结果](1)过点B作BD⊥AC.垂足为D.依题意，得∠BAC＝30°，在Rt△ABD中，BD= AB=×20×16=160＜200，∴B处会受到台风影响.(2)以点B为圆心，200海里为半径画圆交AC于E、F，由勾股定理可求得DE=120.AD=160.AE=AD-DE=160 -120，∴=3.8(小时).因此，陔船应在3.8小时内卸完货物.。

礁石和海问题初三数学问题:海中有一个小岛A，它的周围8海里范围内有暗礁，渔船跟踪鱼群由西向东航行，在B点测得小岛A在北偏东60°方向上，航行12海里到达D点，这时测得小岛A在北偏东30°方向上，如果渔船不改变航线继续向东航行，有没有触礁的危险?解:过A作AF⊥BD于F.设AF=x海里在Rt△ABF中,∠BAF=60°∴BF=AF·tan60°=√3X在Rt△ADF中，∠DAF=30°。

∴DF=AF·tan30°=√3/3X∵BF-DF=BD,即∴x=所以，没有触角的危险。

2.如图，海中有一小岛A，它的周围10海里内有暗礁，渔船由西向东航行．在B点测得小岛A在北偏东60°方向，再航行12海里到达D点，这时测得小岛A在北偏东30°方向．如果渔船不改变航向，继续向东航行，有没有触礁的危险？分析作AM⊥BD于M，首先证明BD=AD=12，在RT△ADM中求出AM与10比较，AM大于等于10海里没有危险，AM小于10有危险．解答解：如图作AM⊥BD于M．∵∠ABD=30°，∠ADM=60°，∠ADM=∠ABD+∠BAD，∴∠DBA=∠DAB=30°，∴DB=DA=12，在RT△ADM中，∵∠AMD=90°，AD=12，∠DAM=30°，∴DM=1212AD=6，AM=√33DM=6√33≈10.4＞10，∴渔船不改变航向，继续向东航行，没有触礁的危险．点评本题考查解直角三角形、方向角、特殊角的三角函数等知识，解题的关键是添加辅助线构造直角三角形，把实际问题转化为解直角三角形问题，属于中考常考题型．。

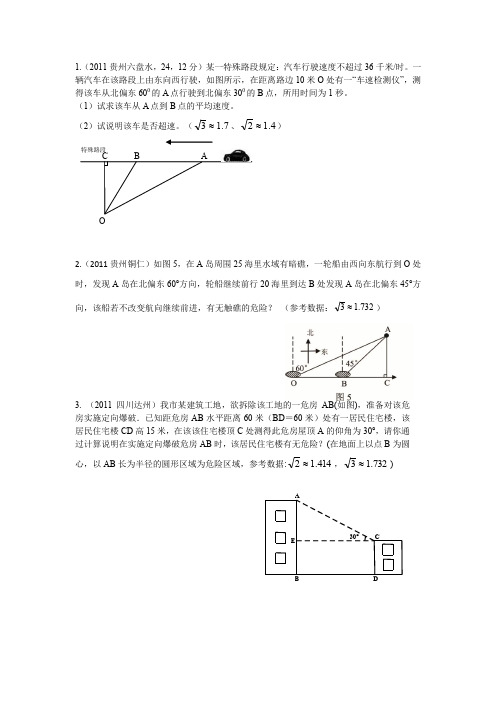
1.（2011贵州六盘水，24，12分）某一特殊路段规定：汽车行驶速度不超过36千米/时。

一辆汽车在该路段上由东向西行驶，如图所示，在距离路边10米O 处有一“车速检测仪”，测得该车从北偏东600的A 点行驶到北偏东300的B 点，所用时间为1秒。

（1）试求该车从A 点到B 点的平均速度。

（2）试说明该车是否超速。

（7.13≈、4.12≈）2.（2011贵州铜仁）如图5，在A 岛周围25海里水域有暗礁，一轮船由西向东航行到O 处时，发现A 岛在北偏东60°方向，轮船继续前行20海里到达B 处发现A 岛在北偏东45°方向，该船若不改变航向继续前进，有无触礁的危险？ （参考数据：）3. （2011四川达州）我市某建筑工地，欲拆除该工地的一危房AB(如图)，准备对该危房实施定向爆破．已知距危房AB水平距离60米（BD ＝60米）处有一居民住宅楼，该居民住宅楼CD 高15米，在该该住宅楼顶C 处测得此危房屋顶A 的仰角为30°，请你通过计算说明在实施定向爆破危房AB 时，该居民住宅楼有无危险？(在地面上以点B 为圆心，以AB 长为半径的圆形区域为危险区域，参考数据:414.12≈，732.13≈)32.713≈C B AO特殊路段30°EDCBA4. 如图,公路MN 和公路PQ 在点P 处交汇,且∠QPN=30°,点A 处有一所学校,AP=160米,假设拖拉机行驶时,周围100米以内会受到噪声的影响,那么拖拉机在公路MN 上沿PN 的方向行驶时 ,学校是否会受到噪声影响?请说明理由.5. 以申办2010年冬奥会,需改变哈尔滨市的交通状况,在大直街拓宽工程中, 要伐掉一棵树AB,在地面上事先划定以B 为圆心,半径与AB 等长的圆形危险区,现在某工人站在离B 点3米远的D 处测得树的顶点A 的仰角为60°,树的底部B 点的俯角为30°, 如图所示,问距离B 点8米远的保护物是否在危险区内?6.如图,某学校为了改变办学条件,计划在甲教学楼的正北方21米处的一块空地上(BD=21米),再建一幢与甲教学等高的乙教学楼(甲教学楼的高AB=20米),设计要求冬至正午时,太阳光线必须照射到乙教学楼距地面5米高的二楼窗口处, 已知该地区冬至正午时太阳偏南,太阳光线与水平线夹角为30°,试判断: 计划所建的乙教学楼是否符合设计要求?并说明理由.7. 一艘渔船正以30海里／小时的速度由西向东追赶鱼群，在A 处看见小岛C 在船的北偏东600方向，40分钟后，渔船行至B 处，此时看见小岛C 在船的北偏东300方向，已知以小岛C 为中心周围10海里以内为我军导弹部队军事演习的着弹危险区，问这艘渔船继续向东追赶鱼群，是否有进入危险区域的可能？NB30︒DA60︒CE 030060例3图南北北南西东CDBA第3题图 C B A 8.如图：某海域直径为30海里的圆形暗礁区中心有一哨所A ，值班人员发现有一轮船从哨所正西方向45海里的B 处向哨所驶来。

第1篇一、背景介绍近日，我国某海域发生一起严重海难事故，一艘载有20名乘客和船员的客轮在航行过程中遭遇暴风雨，不幸触礁沉没。

目前，已有8名乘客被救起，其余乘客和船员仍在沉船附近海域漂流。

我国政府高度重视此次事故，迅速启动应急预案，组织相关部门进行救援。

二、面试题目1. 请简要描述你在面对紧急救援任务时的心理状态，以及如何调整自己的情绪以确保救援工作的顺利进行。

2. 在救援现场，你作为救援队伍的一员，发现一名乘客身体虚弱，急需救治。

请问你将如何处理这一情况？3. 请结合实际情况，谈谈你对于海难救援现场的人员搜救、物资分配、通讯保障等方面的应对策略。

4. 在救援过程中，你发现部分乘客和船员情绪失控，恐慌情绪蔓延。

作为救援队伍的一员，你将如何安抚他们，确保救援工作的正常进行？5. 在救援现场，你发现一名乘客有特殊疾病，需要特殊药物和护理。

请问你将如何协调相关部门，确保患者得到及时救治？6. 请谈谈你在救援过程中遇到的困难，以及你是如何克服这些困难的。

7. 在救援现场，你发现一名乘客因受惊过度导致精神崩溃。

请问你将如何对其进行心理疏导？8. 请结合实际情况，谈谈你在救援过程中如何与团队成员进行有效沟通和协作。

9. 在救援结束后，你将如何总结此次救援经验，为今后类似救援任务提供借鉴？10. 请谈谈你对海难救援工作的认识，以及你认为我国在海难救援方面还存在哪些不足，应该如何改进？三、面试评分标准1. 思维清晰，能够迅速分析问题并提出解决方案。

（20分）2. 具备良好的心理素质，能够在紧急情况下保持冷静，有效调整情绪。

（20分）3. 能够妥善处理救援现场的各种突发情况，具备较强的应变能力。

（20分）4. 具备良好的团队协作精神，能够与团队成员高效沟通、共同完成任务。

（20分）5. 具备高度的责任感和使命感，关注救援工作的全局。

（20分）四、面试注意事项1. 面试过程中，考生应保持自信、从容的态度，充分展示自己的能力和素质。

船舶防台风措施船舶防台风措施船舶防台方式有两种：系泊防台和海上航行防台。

一、船舶系泊防台方式船舶处在港湾、江河和沿岸浅水区内，有地形的屏蔽，受到台风袭击的强度大为减弱。

因此，抗风浪能力差的船舶主要采取系泊防台方式。

在海上航行的船舶遇到台风，如果条件和时间许可，应尽量驶往适宜的港湾、江河、岛屿或沿岸浅水区进行系泊防台。

系泊防台有锚泊、系浮筒和靠码头三种方法，锚泊防台时，为增加锚的系留力和减少船舶的偏荡，一般抛双锚。

系浮筒防台，一般均应使用专门的抗台风浮筒，以求牢固平安。

除可供机动的水域狭窄，或港务部门对系泊有专门的规定者外，船舶一般应系单浮筒防台,必须使用锚链和浮筒相连，必要时还应加带系缆。

船舶系浮筒防台中如锚链负荷过大，可适当用车，谨慎行事。

在浪涌大的港口，船舶不能靠码头防台，而应到开敞的锚地锚泊。

二、船舶系泊防台前的检查台风季节来临前一个月，应做一次系统平安检查。

(1)系泊设备——锚具、锚链、起锚机、缆绳(防台应急缆绳)、制锚设备、备件等。

(2)操舵设备——操舵仪、传动装置、舵机、手舵装置、备件等。

(4)水密装置——水密门、窗、舷门、人孔盖、风斗、空气管、锚链孔等。

(5)排水设备——甲板排水孔、排水管系、排水泵、污水沟和锚链舱排水装置、主海水泵等。

(6)海损急救装置——海损急救物料、防水堵漏物品、抛绳枪等。

(7)救生设备——救生艇、救生筏、救生圈、救生衣、求救信号等。

(9)举行一次防台风应急演习。

三、在台风“威胁中〞的措施船舶于未来48小时内遭遇风力可能到达6级以上，应被认为已在台风“威胁中〞。

在此过程中，应做到以下几点。

(3)封闭一切露天甲板舱口，对通风筒、空气管等开口部位应进行适当封堵。

(4)全部水密门、舷门、舷窗除应急用外，应紧密关闭。

(5)清扫甲板，检查排水孔、沟，确保无堵塞。

(6)检查码头系缆，系缆数量应足够，全部系缆受力必须平均，并在磨擦处妥为衬垫。

系缆与船体摩擦处应包扎好，防止磨断。

勾股定理是否在(台风、噪声、触礁等)影响范围问题的解决方法勾股定理是否在（台风、噪声、触礁等）影响范围问题的解决方法新课程强调“人人学有价值的数学，人人学有用的数学。

”因此，数学学习必须加强与生活实际的联系，让学生感受到生活中处处有数学。

数学家华罗庚曾经说过：“宇宙之大，粒子之微，火箭之速，化工之巧，地球之变，日用之繁，无处不用数学。

”这是对数学与生活的精彩描述。

勾股定理作为一个重要知识点，是往年中考中必考的一个内容，而且这一知识点考查，也常结合在一些实际问题中出现。

例题1米，（1）教室（2学生思考：（1）“教室A 是否在大型货车的噪声污染范围内”看什么？怎样说明？（2）要求“教室A 受污染的时间是多少”应该先求什么？怎样求？ （通过问题，启发学生思维，培养学生文字语言、图形语言、符号语言的转译能力，提高数学思考、交流的能力，给后进生以深入学习的机会。

）解：（1）过点A 作AD 垂直于BC ，垂足为D160,300==∠AB ABC 米 ∴ 在ABD Rt ∆中能解得AD=80米<100米，所以受噪声影响，以点A 为圆心，100米为半径画圆弧分别交BC 与E ，F 两点 线段EF 即为受影响的路段。

（2）在AED Rt ∆中，由勾股定理求出ED=60米，EF=2ED=120米，1201012÷=秒答：教室受噪声影响的时间为12秒。

30︒教室A B 处C学生思考：（1）有无危险，怎样用图形语言结合符号语言表达？（2）怎样确定改变方向的地点？（3）怎样确定有危险的一段行程？（4）例题1与例题2在解题方法上有什么共同之处吗？请说明。

（在问题驱使下，引导学生发现两例题解法的共同点，在学生总结的过程中，不断培养学生的语言表达能力、归纳概括能力、提炼升华能力。

）练习2、如图10，某货船以20海里/时的速度将一批重要物资由A处运往正西方向的B处，经16小时的航行到达，到达后必须立即卸货。

此时，接到气象部门通知，一台风中心正以40海里/时的速度由A向北偏西60°方向移动，距台风中心200海里的圆形区域（包括边界）均会受到影响。