丹阳市高中数学第三章空间向量与立体几何3.1.2共面向量定理学案苏教版选修

第3章空间向量与立体几何3．1空间向量及其运算3．1.1 空间向量及其线性运算3．1.2 共面向量定理(教师用书独具)●三维目标1．知识与技能(1)了解空间向量与平面向量的联系与区别．(2)理解空间向量的线性运算及其性质．(3)理解共面向量定理．2．过程与方法(1)学生通过类比平面向量的学习过程了解空间向量的研究内容和方法，经历向量及其运算由平面向空间的推广，体验数学概念的形成过程．(2)通过类比平面向量基本定理，得出共面向量基本定理，并能利用共面向量基本定理证明向量共面，学会判定与证明向量共面及四点共面的方法．3．情感、态度与价值观逐步培养学生观察、分析、综合和类比能力，会准确地阐述自己的思路和观点，着重培养学生的认知能力．●重点难点重点：了解空间向量与平面向量的联系与区别，理解空间向量的线性运算及其性质．难点：共面向量定理的理解及应用．先回顾平面向量的定义及线性运算法则，类比得出空间向量的有关定义及运算法则，并通过空间图形进行严格的理论验证，从而突出教学重点．对于共面向量定理，完全可由平面向量基本定理类比得出，重在应用其证明共面问题，通过例题，体现向量法证明线线平行、线面平行的方法与步骤，从而突破教学难点．(教师用书独具)●教学建议本节内容是第三章《空间向量与立体几何》的第一节，由于是起始节，所以这节课中也包含了章引言的内容．章引言中提到了本章的主要内容和研究方法，即类比平面向量来研究空间向量的概念和运算．向量是既有大小又有方向的量，它能像数一样进行运算，本身又是一个“图形”，所以它可以作为沟通代数和几何的桥梁，在很多数学问题的解决中有着重要的应用．本章要学习的空间向量，将为解决三维空间中图形的位置关系与度量问题提供一个十分有效的工具．采用的教学方式是通过问题启发引导学生自主完成概念的探究过程，紧紧围绕教学重点展开教学，并从教学过程的每个环节入手，努力突破教学难点．●教学流程回顾平面向量的定义，类比得出空间向量的定义、几何表示、符号表示；找出空间向量与平面向量的区别与联系．⇒回顾平面向量的线性运算法则，得出空间向量的线性运算法则，并通过空间图形加以验证，得出空间向量线性运算满足的运算律．理解单位向量、共线向量、平行向量等概念，理解共线向量定理成立的条件及作用．⇒理解共面向量的定义，区分向量共面与直线共面的区别，理解共面向量定理的内涵，会用共面向量定理证明向量共面，从而证明立体几何问题如共面问题、线面平行问题等．⇒通过例1及变式训练，使学生掌握空间向量的线性运算法则，在常见的立体图形中，灵活的应用三角形和平行四边形法则进行空间向量的运算，实现利用给定向量表示某一向量的目的．⇒通过例2及变式训练，使学生体会共线向量定理的两个应用，正向可用来证明线线平行，逆用可用来求解字母参数，体会向量法解证立体几何问题的步骤与规律．⇒通过例3及变式训练，使学生体会共面向量定理的两个应用，正向可用来证明线面平行，四点共面，逆用可用来求解字母参数，体会向量法解证立体几何问题的步骤与规律．⇒通过易错易误辨析，体会零向量的特殊性，在分析向量间关系及向量运算时，应注意零向量的特殊性．⇒归纳整理，进行课堂小结，整体认识本节课所学知识．⇒完成当堂双基达标，巩固基本知识，形成基本能力.在空间，把既有大小又有方向的量叫做空间向量．已知空间四边形ABCD ，则AB →＋BC →＋CD →＋DA →＝0还成立吗？【提示】 成立．根据向量的加法法则，表示相加向量的有向线段依次首尾相接，其和为从第一个向量的首指向最后一个向量的尾，故AB →＋BC →＋CD →＋DA →＝AA →＝0.向量加法可以推广到有限个向量的和，并且可用口诀记忆：首尾首尾首指向尾．【问题导思】共线向量一定是同一直线上的向量吗？【提示】 共线向量不一定是同一直线上的向量，而是表示向量的有向线段只要可以平移到同一直线上即可，因此共线向量也叫平行向量．对空间任意两个向量a，b (a ≠0)，b 与a 共线的充要条件是存在实数λ，使b ＝λa .如果两个向量a 、b )，使得p ＝x a ＋y b .图3－1－1如图3－1－1，在长方体ABCD －A ′B ′C ′D ′中，化简下列各式，并在图中标出化简得到的向量：【思路探究】 观察各式涉及的向量在图形中的位置特点，将减法运算转化为加法运算，利用向量加法的三角形法则即可化简．【自主解答】(3)设M 是线段AC ′的中点，则12AD →＋12AB →－12＝12AD →＋12AB →＋12＝12(AD →＋AB →＋)＝12＝AM →.向量，AM →如图所示．1．进行向量的线性运算，实质是进行向量求和，解题时应抓住两条主线：一是基本“形”，通过作出向量，运用平行四边形法则或三角形法则求和；二是基于“数”，熟练掌握AB →＋BC →＝AC →及向量中点公式．2．用已知向量表示空间向量，实质是向量的线性运算的反复应用．图3－1－2如图3－1－2，在平行六面体ABCD －A 1B 1C 1D 1中，AA 1→＝a ，AB →＝b ，AD →＝c ，M ，N ，P 分别为AA 1，BC ，C 1D 1的中点，试用a ，b ，c 表示：(1)AC 1→；(2)AP →； (3)A 1N →；(4)MP →＋NC 1→.【解】 (1)AC 1→＝AB →＋BC →＋CC 1→＝b ＋c ＋a . (2)∵P 为D 1C 1→的中点， ∴D 1P →＝12D 1C 1→＝12AB →＝12b ，∴AP →＝AA 1→＋A 1D 1→＋D 1P →＝a ＋AD →＋12AB →＝a ＋c ＋12b .(3)A 1N →＝A 1A →＋AB →＋BN →＝－AA 1→＋b ＋12AD →＝－a ＋b ＋12c .(4)∵MP →＝MA 1→＋A 1D 1→＋D 1P → ＝12AA 1→＋AD →＋12AB → ＝12a ＋c ＋12b . NC 1→＝NC →＋CC 1→＝12AD →＋AA 1→＝12c ＋a .∴MP →＋NC 1→＝(12a ＋c ＋12b )＋(12c ＋a )＝32a ＋12b ＋32c .图3－1－3如图3－1－3，已知点E ，F ，G ，H 分别是空间四边形ABCD 的边AB ，BC ，CD ，DA 上的点，其中E ，H 是中点，F ，G是三等分点，且CF ＝2FB ，CG ＝2GD .试判断四边形EFGH 的形状．【思路探究】 证明向量EH →∥FG →且模不相等． 【自主解答】 ∵E ，H 分别是AB ，AD 的中点， ∴EH →＝AH →－AE →＝12AD →－12AB →＝12(AD →－AB →)＝12BD →. 又∵CF →＝2FB →，CG →＝2GD →， ∴CF →＝23CB →，CG →＝23CD →，∴FG →＝CG →－CF →＝23CD →－23CB →＝23(CD →－CB →)＝23BD →， ∴BD →＝32FG →，∴EH →＝34FG →，∴EH →∥FG →，|EH →|＝34|FG →|.又点F 不在直线EH 上，∴EH ∥FG ，且EH ≠FG ， ∴四边形EFGH 是梯形．1．证明EFGH 为梯形，必须证明两点：①EH →∥FG →； ②|EH →|≠|FG →|.2．利用向量共线可证空间图形中的两直线平行，为向量法证明立体几何问题奠定了基础．设e 1，e 2是空间两个不共线的向量，已知AB →＝e 1＋k e 2，BC →＝5e 1＋4e 2，DC →＝－e 1－2e 2，且A 、B 、D 三点共线，求实数k 的值． 【解】 ∵BC →＝5e 1＋4e 2，DC →＝－e 1－2e 2. ∴BD →＝BC →＋CD →＝(5e 1＋4e 2)＋(e 1＋2e 2)＝6e 1＋6e 2. ∵A ，B ，D 三点共线， ∴AB →＝λBD →.∴e 1＋k e 2＝λ(6e 1＋6e 2)．∵e 1，e 2是不共线向量，∴⎩⎪⎨⎪⎧1＝6λ ，k ＝6λ ，∴k ＝1.(2012·辽宁高考)如图3－1－4，直三棱柱ABC －A ′B ′C ′，点M ，N 分别为A ′B 和B ′C ′的中点．证明：MN ∥平面A ′ACC ′.图3－1－4【思路探究】 利用向量的线性运算得到向量MN →可以由平面A ′ACC ′内两个不共线的向量表示即可．【自主解答】 因为MN →＝MA ′→＋A ′N →，且点M ，N 分别为A ′B 和B ′C ′的中点，所以MN →＝12BA ′→＋12(A ′B ′→＋A ′C ′→)＝12(B ′A ′→＋AA ′→)＋12(A ′B ′→＋A ′C ′→)＝12AA ′→＋12A ′C ′→. 因为MN ⊄平面A ′ACC ′，所以MN ∥平面A ′ACC ′.1．判断三个向量共面，即利用向量的线性运算实现其中一个向量能用另外两个向量惟一表示．2．利用向量判断线面平行有两种方法：一是利用共线向量定理，找出平面内的一个向量与直线上的向量共线；二是利用共面向量定理，找出平面内不共线的两个向量能表示出直线上的向量．两种方法中注意说明直线不在平面内．已知非零向量e 1，e 2不共线，如果AB →＝e 1＋e 2，AC →＝2e 1＋8e 2，AD →＝3e 1－3e 2，求证：A ，B ，C ，D 四点共面． 【证明】 令λ(e 1＋e 2)＋μ(2e 1＋8e 2)＋ν(3e 1－3e 2)＝0， 则(λ＋2μ＋3ν)e 1＋(λ＋8μ－3ν)e 2＝0.∵e 1，e 2不共线，则⎩⎪⎨⎪⎧λ＋2μ＋3ν＝0，λ＋8μ－3ν＝0，解得λ＝－5，μ＝1，ν＝1是其中一组解， 则AB →＝15AC →＋15AD →，∴A 、B 、C 、D 四点共面.忽略零向量导致错误下列命题：①空间任意两个向量a ，b 不一定是共面的； ②a ，b 为空间两个向量，则|a |＝|b |⇔a ＝b ； ③若a ∥b ，则a 与b 所在直线一定平行； ④若a ∥b ，b ∥c ，则a ∥c . 其中错误命题的序号是________． 【错解】 ②【错因分析】 ①空间任意两个向量都是共面的．②向量的模相等时，两个向量不一定相等，还要看向量的方向．③当a ∥b 时，它们所在直线平行或重合．④当b ＝0时，a 与c 不一定平行．【防范措施】 向量的平行(共线)不具备传递性，即若a ∥b ，b ∥c ，不一定有a ∥c ，但当b 为非零向量时，向量平行(共线)具备传递性，即若b ≠0，则当a ∥b ，b ∥c 时，有a ∥c .【正解】 ①②③④1．空间向量是平面向量的拓广和延伸，空间向量的线性运算法则和运算律与平面向量具有可类比性，但空间向量比平面向量应用范围更广泛．2．共线向量定理是判定两向量共线的充要条件，利用共线向量定理可以解决两方面的问题：(1)判定两向量共线；(2)由两向量共线，求待定字母的值．3．共面向量定理是判断三向量共面的理论依据，依此可以证明三向量共面，从而证明四点共面与线面平行问题．1．在空间四边形ABCD 中，AB →＋BC →＋CD →＋DA →＝______. 【解析】 AB →＋BC →＋CD →＋DA →＝AC →＋CD →＋DA →＝AD →＋DA →＝0. 【答案】 02．在长方体ABCD －A 1B 1C 1D 1中，化简式子：DA →－DB →＋B 1C →－B 1B →＋CB 1→－CB →＝________. 【解析】 DA →－DB →＋B 1C →－B 1B →＋CB 1→－CB →＝BA →＋BC →＋BB 1→＝BD →＋BB 1→＝BD 1→. 【答案】 BD 1→3．有下列命题：①平行于同一直线的向量是共线向量；②平行于同一平面的向量是共面向量；③平行向量一定是共面向量；④共面向量一定是平行向量．其中正确的命题有________．【解析】 “共面向量一定是平行向量”不正确，即共面向量不一定共线．①②③均正确． 【答案】 ①②③图3－1－54．如图3－1－5，在空间四边形ABCD 中，E 、F 为AB 、CD 的中点，试证EF →，BC →，AD →共面． 【证明】 空间四边形ABCD 中，E 、F 分别是AB 、CD 上的点，利用多边形加法法则可得⎭⎬⎫EF →＝EA →＋AD →＋DF →，EF →＝EB →＋BC →＋CF →.①又E 、F 分别是AB 、CD 的中点，故有EA →＝－EB →，DF →＝－CF →.②将②代入①中，两式相加得2EF →＝AD →＋BC →. 所以EF →＝12AD →＋12BC →，即EF →与BC →、AD →共面．一、填空题1．下列命题中真命题的个数是________． ①空间中任两个单位向量必相等；②将空间中所有的单位向量移到同一起点，则它们的终点构成一个圆； ③若两个非零向量a ，b 满足a ＝k b ，则a ，b 同向； ④向量共面即它们所在的直线共面．【解析】 ①是假命题，单位向量模相等，但方向不一定相同，因此空间中任两个单位向量不一定相等； ②是假命题，将空间中所有的单位向量移到同一起点，则它们的终点构成一个球面； ③是假命题，当k >0时，a ，b 同向，当k <0时，a ，b 反向；④是假命题，表示共面向量的有向线段所在的直线可以“平移”(平行移动)到同一平面，但不一定共面． 【答案】 02．平行六面体ABCD －A 1B 1C 1D 1中，M 为AC 和BD 的交点，若A 1B 1→＝a ，A 1D 1→＝b ，A 1A →＝c ，则B 1M →＝________. 【解析】 B 1M →＝B 1B →＋BM →＝c ＋12BD →＝c ＋12B 1D 1→＝c ＋12b －12a ＝－12a ＋12b ＋c .【答案】 －12a ＋12b ＋c3．非零向量e 1、e 2不共线，若k e 1＋e 2与e 1＋k e 2共线，则k ＝________. 【解析】 若k e 1＋e 2与e 1＋k e 2共线，则k e 1＋e 2＝λ(e 1＋k e 2)，∴⎩⎪⎨⎪⎧k ＝λ，λk ＝1，∴k ＝±1.【答案】 ±14．空间四边形OABC 中，OA →＝a ，OB →＝b ，OC →＝c ，点M 在OA →上，且OM →＝2MA →，N 为BC 的中点，则MN →＝________.(用a ，b ，c 表示)【解析】 如图， MN →＝ON →－OM →＝12(OB →＋OC →)－23OA → ＝12(b ＋c )－23a ＝－23a ＋12b ＋12c .【答案】 －23a ＋12b ＋12c5．如图3－1－6，在正方体ABCD —A 1B 1C 1D 1中，下列各式中运算的结果为BD 1→的是________．图3－1－6①(A 1D 1→－A 1A →)－AB →；②(BC →＋BB 1→)－D 1C 1→； ③(AD →－AB →)－2DD 1→；④(B 1D 1→－A 1A →)＋DD 1→.【解析】 (A 1D 1→－A 1A →)－AB →＝AD 1→－AB →＝BD 1→，(BC →＋BB 1→)－D 1C 1→＝BC 1→＋C 1D 1→＝BD 1→. 【答案】 ①② 6．有四个命题：①若p ＝x a ＋y b ，则p 与a ，b 共面； ②若p 与a ，b 共面，则p ＝x a ＋y b ； ③若MP →＝xMA →＋yMB →，则P 、M 、A 、B 共面； ④若P 、M 、A 、B 共面，则MP →＝xMA →＋yMB →. 其中真命题是________(填序号)．【解析】 由共面向量定理知，①真；若p 与a ，b 共面，当a 与b 共线且p 与a 和b 不共线时，就不存在实数组(x ，y )使p ＝x a ＋y b 成立，故②假．同理③真，④假．【答案】 ①③7．在下列各式中，使P ，A ，B ，C 四点共面的式子的序号为________． ①OP →＝OA →－OB →－OC →； ②OP →＝17OA →＋14OB →＋12OC →；③PA →＋PB →＋PC →＝0； ④OP →＋OA →＋OB →＋OC →＝0； ⑤OP →＝12OA →－OB →＋32OC →.【解析】 根据四点共面的充要条件，易知①②④不适合，③⑤适合． 【答案】 ③⑤8．(2013·平遥高二检测)已知点G 是△ABC 的重心，O 是空间任一点，若OA →＋OB →＋OC →＝λOG →，则λ＝________.【解析】 如图，取AB 的中点D ， OG →＝OC →＋CG → ＝OC →＋23CD →＝OC →＋23·12(CA →＋CB →)＝OC →＋13[(OA →－OC →)＋(OB →－OC →)]＝13OA →＋13OB →＋13OC →. ∴OA →＋OB →＋OC →＝3OG →. 【答案】 3 二、解答题图3－1－79．如图3－1－7，已知平行六面体ABCD －A ′B ′C ′D ′，M 是线段CC ′的中点，G 是线段AC ′的三等分点，化简下列各式，并在图中标出化简得到的向量：(1)AB →＋BC →； (2)AB →＋AD →＋AA ′→； (3)AB →＋AD →＋12CC ′→；(4)13(AB →＋AD →＋AA ′→)．【解】 (1)AB →＋BC →＝AC →.(2)AB →＋AD →＋AA ′→＝AC →＋AA ′→＝AC →＋CC ′→＝AC ′→. (3)AB →＋AD →＋12CC ′→＝AB →＋BC →＋CM →＝AC →＋CM →＝AM →.(4)13(AB →＋AD →＋AA ′→)＝13AC ′→＝AG →. 向量AC →，AC ′→，AM →，AG →如图所示．10．如图3－1－8所示，四边形ABCD 、ABEF 都是平行四边形且不共面，M 、N 分别是AC 、BF 的中点，判断CE →与MN →是否共线．图3－1－8【解】 ∵M 、N 分别是AC 、BF 的中点，四边形ABCD 、ABEF 都是平行四边形， ∴MN →＝MA →＋AF →＋FN →＝12CA →＋AF →＋12FB →，MN →＝MC →＋CE →＋EB →＋BN →＝－12CA →＋CE →－AF →－12FB →，∴12CA →＋AF →＋12FB →＝－12CA →＋CE →－AF →－12FB →， ∴CE →＝CA →＋2AF →＋FB →＝2(MA →＋AF →＋FN →)＝2MN →， ∴CE →∥MN →，即CE →与MN →共线．图3－1－911．如图3－1－9，在多面体ABCDEF 中，四边形ABCD 是正方形，EF ∥AB ，AB ＝2EF ，H 为BC 的中点．求证：FH ∥平面EDB . 【证明】 因为H 为BC 的中点，所以FH →＝12(FB →＋FC →)＝12(FE →＋EB →＋FE →＋ED →＋DC →)＝12(2FE →＋EB →＋ED →＋DC →)．因为EF ∥AB ，CD ∥AB ，且AB ＝2EF ，所以2FE →＋DC →＝0，所以FH →＝12(EB →＋ED →)＝12EB →＋12ED →.因为EB →与ED →不共线，由共面向量定理知，FH →，EB →，ED →共面． 因为FH ⊄平面EDB ，所以FH ∥平面EDB .(教师用书独具)已知A 、B 、M 三点不共线，对于平面ABM 外的任一点O ，确定下列各条件下，点P 是否与A 、B 、M 一定共面． (1)OB →＋OM →＝3OP →－OA →； (2)OP →＝4OA →－OB →－OM →.【思路探究】 判断点P 是否在平面MAB 内，可先看MP →能否用向量MA →、MB →表示．当MP →能用MA →、MB →表示时，点P 位于平面MAB 内，否则点P 不在平面MAB 内．【自主解答】 (1)原式可变形为 OP →＝OM →＋(OA →－OP →)＋(OB →－OP →) ＝OM →＋PA →＋PB →，∴OP →－OM →＝PA →＋PB →， ∴PM →＝－PA →－PB →，∴P 与M 、A 、B 共面． (2)原式可变形为 OP →＝2OA →＋OA →－OB →＋OA →－OM →＝2OA →＋BA →＋MA →， ∴AP →＝－AO →－AB →－AM →，表达式中还含有AO →， ∴P 与A 、B 、M 不共面．1．解答本题中注意构造以P 、A 、B 、M 中某一点为起点，另三点为终点的三个向量来判断此三向量是否共面，若共面又共起点，此四点必共面，否则不共面．2．要证四点共面，可先作从同一点出发的三个向量，由向量共面推知点共面，应注意待定系数法的应用．已知A 、B 、C 三点不共线，对平面ABC 外的任一点M 满足OM →＝13OA →＋13OB →＋13OC →.(1)判断MA →、MB →、MC →三个向量是否共面； (2)判断点M 是否在平面ABC 内． 【解】 (1)∵OM →＝13OA →＋13OB →＋13OC →，∴13(OA →－OM →)＋13(OB →－OM →)＋13(OC →－OM →)＝0， ∴MA →＋MB →＋MC →＝0， ∴MA →＝－MB →－MC →，∴MA →、MB →、MC →三个向量是共面向量． (2)由(1)知MA →、MB →、MC →三个向量共面， 又有共同起点M ，所以M 、A 、B 、C 四点共面， 即点M 在平面ABC 内．3．1.3 空间向量基本定理 3．1.4 空间向量的坐标表示(教师用书独具)●三维目标 1．知识与技能(1)掌握空间向量基本定理，能恰当地选择基底，用基向量表示空间任一向量． (2)理解空间向量的正交分解，理解向量坐标的意义．(3)掌握向量加法、减法、数乘的坐标运算法则，会应用向量坐标进行线性运算，能判断向量共线． 2．过程与方法(1)由平面向量基本定理，类比得出空间向量基本定理，体会定理的条件及内涵；会在具体空间图形中，选取基底表示空间向量． (2)类比平面向量坐标运算法则，得出空间向量坐标运算法则，并运用这些法则进行向量坐标线性运算． (3)运用向量坐标进行向量共线的判定与应用． 3．情感、态度与价值观能过教师的引导，学生探究，激发学生求知欲望和学习兴趣，使学生具备探究、归纳、应用的能力，形成严谨的思维习惯． ●重点难点重点：用基底表示空间向量，向量线性运算的坐标表示． 难点：用基底表示空间向量．教学时，应采用类比思维的方法，先回顾平面向量基本定理及坐标表示，得出空间向量基本定理及坐标表示，降低问题的难度，在具体的常见几何体(正方体、三棱锥、棱柱)中，展示用基底表示空间向量的方法与过程，突出本节的重点，化解教学的难点．(教师用书独具)●教学建议空间向量基本定理是向量法研究立体几何问题的基石，是本章的重中之重，空间向量的坐标表示及坐标运算，是坐标法研究立体几何的工具．因此本节课是全章内容的工具性内容，为学生学习立体几何提供新角度、新手段、新方法．由于学生已学习了平面向量基本定理及坐标运算，因而本节宜采用类比教学法，多发挥学生自主探究能力，通过回顾→类比→完善→应用的环节获取新知识，应用新知识．除使用常规的教学手段外，还将使用多媒体投影和计算机辅助教学，增加教学的直观性和趣味性．●教学流程回顾平面向量基本定理，类比得出空间向量基本定理，强调基向量的不共面性，线性表示的惟一性，常见几何体中基底的一般选法，定义单位正交基，推导空间向量基本定理的推论 .⇒回顾平面向量的坐标表示，得出空间向量的坐标表示，理清向量坐标的实际意义，向量坐标与点坐标的关系．⇒回顾平面向量线性运算的坐标表示，得出空间向量的线性运算的坐标表示，向量坐标与起始点坐标的关系，共线向量的坐标条件．⇒通过例1及变式训练，让学生掌握基底的选取条件，即不共面向量，加深对基底概念的理解．⇒通过例2及变式训练，让学生掌握如何选取基向量，如何用基底表示某一向量，在具体操作中运用向量的线性运算法则．⇒通过例3及变式训练，让学生掌握向量坐标运算法则，掌握如何运用起点、终点坐标表示向量坐标．⇒通过例4及变式训练，让学生掌握向量共线的坐标条件的应用，由此判定向量共线或求值．⇒通过易错易误辨析，让学生分清向量共线与向量同向的区别，以免概念混淆，解题出错．⇒归纳整理，进行课堂小结，整体认识本节所学知识．⇒完成当堂双基达标，巩固基本知识，形成基本能力.p＝x e1＋y e2＋z e3.如果三个向量e1，e2，e3如果空间一个基底的三个基向量是两两互相垂直，那么这个基底叫做正交基底．特别地：当一个正交基底的三个基向量都是单位向量时，称这个基底为单位正交基底，通常用{i ，j ，k }表示．设O ，A ，B ，C 是不共面的四点，则对空间任意一点P ，都存在惟一的有序实数组(x ，y ，z )，使得OP ＝xOA →＋yOB →＋zOC →.【问题导思】空间直角坐标系中，点的坐标与向量坐标有何联系与区别？【提示】 在空间直角坐标系中，当起点为原点时，向量坐标就是其终点坐标；当起点不是原点时，向量坐标是终点坐标减去起点坐标．所以向量坐标不是点的坐标，而是终点坐标与起点坐标的差值．在空间直角坐标系中，设A (a 1，b 1，c 1)，B (a 2，b 2，c 2)，则AB →＝(a 2－a 1，b 2－b 1，c 2－c 1)；当空间向量a 的起点移至坐标原点时，其终点坐标就是向量a 的坐标．【问题导思】空间向量的坐标运算与几何运算相比较，有哪些好处？【提示】 坐标运算实际上是实数间的运算，运算起来更为简捷方便． 设a ＝(a 1，a 2，a 3)，b ＝(b 1，b 2，b 3)已知{e 1，e 2，e 3}是空间的一个基底，且OA →＝e 1＋2e 2－e 3，OB →＝－3e 1＋e 2＋2e 3，OC →＝e 1＋e 2－e 3，试判断{OA →，OB →，OC →}能否作为空间的一个基底？若能，试以此基底表示向量OD →＝2e 1－e 2＋3e 3；若不能，请说明理由．【思路探究】 判断{OA →，OB →，OC →}能否作为基底，关键是判断它们是否共面，一般假设其共面，利用共面向量定理分析；求OD →的表示式，设OD →＝pOA →＋qOB →＋zOC →，利用待定系数法求系数．【自主解答】 假设OA →、OB →、OC →共面，由向量共面的充要条件知存在实数x 、y 使OA →＝xOB →＋yOC →成立． ∴e 1＋2e 2－e 3＝x (－3e 1＋e 2＋2e 3)＋y (e 1＋e 2－e 3)＝(－3x ＋y )e 1＋(x ＋y )e 2＋(2x －y )e 3，∵{e 1，e 2，e 3}是空间的一个基底， ∴e 1，e 2，e 3不共面， ∴⎩⎪⎨⎪⎧－3x ＋y ＝1，x ＋y ＝2，2x －y ＝－1，此方程组无解，即不存在实数x 、y 使OA →＝xOB →＋yOC →， ∴OA →，OB →，OC →不共面．故{OA →，OB →，OC →}能作为空间的一个基底． 设OD →＝pOA →＋qOB →＋zOC →，则有2e 1－e 2＋3e 3＝p (e 1＋2e 2－e 3)＋q (－3e 1＋e 2＋2e 3)＋z (e 1＋e 2－e 3)＝(p －3q ＋z )e 1＋(2p ＋q ＋z )e 2＋(－p ＋2q －z )e 3 ∵{e 1，e 2，e 3}为空间的一个基底，∴⎩⎪⎨⎪⎧p －3q ＋z ＝2，2p ＋q ＋z ＝－1，－p ＋2q －z ＝3，解之得⎩⎪⎨⎪⎧p ＝17，q ＝－5，z ＝－30，∴OD →＝17OA →－5OB →－30OC →.1．判断三个向量能否作为基底，关键是判断它们是否共面，若从正面判断难以入手，可以用反证法结合共面向量定理或者利用常见的几何图形帮助，进行判断．2．求一向量在不同基底下的表示式(或坐标)，一般采用待定系数法，即设出该向量在新基底下的表示式(或坐标)，转化为在原基底下的表示式，对比系数．若{a ，b ，c }是空间的一个基底．试判断{a ＋b ，b ＋c ，c ＋a }能否作为空间的一个基底．【解】 假设a ＋b ，b ＋c ，c ＋a 共面，则存在实数λ，μ，使得a ＋b ＝λ(b ＋c )＋μ(c ＋a )成立，即a ＋b ＝μa ＋λb ＋(λ＋μ)c . ∵{a ，b ，c }是空间的一个基底， ∴a ，b ，c 不共面． ∴⎩⎪⎨⎪⎧μ＝1λ＝1λ＋μ＝0，此方程组无解．即不存在实数λ，μ，使得a ＋b ＝λ(b ＋c )＋μ(c ＋a )成立，∴a ＋b ，b ＋c ，c ＋a 不共面． 故{a ＋b ，b ＋c ，c ＋a }能作为空间的一个基底．图3－1－10如图3－1－10，四棱锥P －OABC 的底面为矩形，PO ⊥平面OABC ，设OA →＝a ，OC →＝b ，OP →＝c ，E ，F 分别是PC ，PB 的中点，试用a ，b ，c 表示：BF →，BE →，AE →，EF →.【思路探究】选取基向量→观察空间图形→利用线性运算→用基底表示向量【自主解答】 连结OB ，则BF →＝12BP →＝12(BO →＋OP →)＝12(－OA →－OC →＋OP →)＝ －12a －12b ＋12c . BE →＝BC →＋CE →＝－a ＋12CP →＝－a ＋12(CO →＋OP →)＝－a ＋12(－b ＋c )＝－a －12b ＋12c .AE →＝AP →＋PE →＝AO →＋OP →＋12PC →＝AO →＋OP →＋12(PO →＋OC →)＝－a ＋c ＋12(－c ＋b )＝－a ＋12b ＋12c .EF →＝12CB →＝12OA →＝－12a .1．空间中的任一向量均可用一组不共面的向量来表示，只要基底选定，这一向量用基底表达的形式是惟一的． 2．用基底来表示空间中的向量是用向量解决数学问题的关键，解题时注意三角形法则以及平行四边形法则的应用．图3－1－11如图3－1－11，在平行六面体ABCD －A ′B ′C ′D ′中，AB →＝a ，AD →＝b ，＝c ，M 是CD ′的中点，N 是C ′D ′的中点，用基底{a ，b ，c }表示以下向量：(1)AM →；(2)AN →.【解】 (1)AM →＝12(AC →＋)＝12(AB →＋AD →＋AD →＋)＝12(a ＋2b ＋c )＝12a ＋b ＋12c . (2)AN →＝12(＋)＝12[(AB →＋AD →＋)＋(AD →＋)]＝12(AB →＋2AD →＋2)＝12a ＋b ＋c .已知A ，B ，C 三点的坐标分别是(2，－1,2)，(4,5，－1)，(－2,2,3)，求适合下列条件的点P 的坐标．(1)OP →＝12(AB →－AC →)；(2)AP →＝12(AB →－AC →)．【思路探究】 利用向量的坐标等于终点的坐标减去起点的坐标求出AB →，AC →，然后进行坐标运算得到OP →，AP →，从而可确定点P 的坐标． 【自主解答】 AB →＝(2,6，－3)，AC →＝(－4,3,1)．(1)OP →＝12(AB →－AC →)＝12(6,3，－4)＝(3，32，－2)，则点P 的坐标为(3，32，－2)．(2)设点P 的坐标为(x ，y ，z )，则AP →＝(x －2，y ＋1，z －2)．由(1)知，AP →＝12(AB →－AC →)＝(3，32，－2)，则⎩⎪⎨⎪⎧ x －2＝3y ＋1＝32z －2＝－2，解得⎩⎪⎨⎪⎧x ＝5y＝12z ＝0，则点P 的坐标为(5，12，0)．1．牢记运算法则是正确进行向量线性运算的关键．2．涉及已知点的坐标进行向量运算时，注意利用终点的坐标减去起点的坐标得到向量的坐标，这是向量运算的前提．已知空间三点A (－2,0,2)，B (－1,1,2)，C (－3,0,4)，求AB →，AC →及2AB →＋3AC →. 【解】 AB →＝(－1,1,2)－(－2,0,2)＝(1,1,0)， AC →＝(－3,0,4)－(－2,0,2)＝(－1,0,2)，2AB →＋3AC →＝2(1,1,0)＋3(－1,0,2)＝(2,2,0)＋(－3，0,6)＝(－1,2,6)．已知A (1,0,0)，B (0,1,0)，C (0,0,2)，求满足DB ∥AC ，DC ∥AB 的点D 的坐标．【思路探究】 由已知条件DB ∥AC ，DC ∥AB ，转化为向量平行，用共线向量定理及空间向量平行的坐标表示，可求得D 点的坐标． 【自主解答】 设D (x ，y ，z )，则DB →＝(－x,1－y ，－z )，AC →＝(－1,0,2)， 由DB ∥AC ，设DB →＝λAC →，即(－x,1－y ，－z )＝(－λ，0,2λ)， 则⎩⎪⎨⎪⎧－x ＝－λ，1－y ＝0，－z ＝2λ，解得⎩⎪⎨⎪⎧x ＝λ，y ＝1，z ＝－2λ，得D (λ，1，－2λ)．∴DC →＝(－λ，－1,2＋2λ)，AB →＝(－1,1,0)． 又DC →∥AB →，设DC →＝μAB →，即(－λ，－1,2＋2λ)＝(－μ，μ，0)， 则⎩⎪⎨⎪⎧－λ＝－μ，－1＝μ，2＋2λ＝0.解得λ＝μ＝－1.∴点D 的坐标为(－1,1,2)．1．本例中，求点D 的坐标，主要是利用两向量平行的坐标条件，列出关于点D 的坐标的方程组，通过解方程组求得．2．两向量平行的充要条件有两个：①a ＝λb ，②⎩⎪⎨⎪⎧x 1＝λx 2y 1＝λy 2z 1＝λz 2，依此，既可以判定两向量共线，也可以通过两向量平行求待定字母的值．设a ＝(2,3,0)，b ＝(－3，－2,1)，计算2a ＋3b,5a －6b ，并确定λ，μ的值，使λa ＋μb 与向量b 平行． 【解】 ∵a ＝(2,3,0)，b ＝(－3，－2,1)，∴2a ＋3b ＝2(2,3,0)＋3(－3，－2,1)＝(4,6,0)＋(－9，－6,3)＝(－5,0,3)， 5a －6b ＝5(2,3,0)－6(－3，－2,1)＝(10,15,0)－(－18，－12,6)＝(28,27，－6)． ∵λa ＋μb ＝λ(2,3,0)＋μ(－3，－2,1)＝(2λ－3μ，3λ－2μ，μ)，且(λa ＋μb )∥b ， ∴2λ－3μ－3＝3λ－2μ－2＝μ1. ∴λ＝0，μ∈R ，即λ＝0，μ∈R 时，λa ＋μb 与b 平行.误解“两向量平行”和“两向量同向”已知向量a ＝(1,2,3)，b ＝(x ，x 2＋y －2，y )，并且a ，b 同向，求x ，y 的值．【错解】 由题意知a ∥b ，则x 1＝x 2＋y －22＝y3，可得⎩⎪⎨⎪⎧y ＝3x ①x 2＋y －2＝2x ②，把①代入②得x 2＋x －2＝0，解得x ＝－2或x ＝1.当x ＝－2时，y ＝－6；当x ＝1时，y ＝3.【错因分析】 “两向量同向”是“两向量平行”的充分不必要条件．错解忽略了“同向”这一条件的限制，扩大了范围． 【防范措施】 由于向量具有平移不变性，因此有关向量的平行问题与直线的平行是有区别的，并且两向量同向与向量平行也是不等价的，向量平行则两向量可能同向也可能反向，因此，解决这类问题时要特别注意限制条件．【正解】 由题意知a ∥b ，则x 1＝x 2＋y －22＝y3，可得⎩⎪⎨⎪⎧y ＝3x ①x 2＋y －2＝2x ②，把①代入②得x 2＋x －2＝0，解得x ＝－2或x ＝1.当x＝－2时，y ＝－6；当x ＝1时，y ＝3.当⎩⎪⎨⎪⎧ x ＝－2y ＝－6时，b ＝(－2，－4，－6)＝－2a ，向量a 与b 反向，不符合题意，故舍去．当⎩⎪⎨⎪⎧ x ＝1y ＝3时，b ＝(1,2,3)＝a ，向量a 与b 同向，故⎩⎪⎨⎪⎧x ＝1y ＝3.1．用基底表示空间几何体中一向量时，应结合立体图形，根据空间向量线性运算法则，写出要求的向量表达式． 2．建立空间直角坐标系后，空间向量都有惟一的坐标(x ，y ，z )，两向量间的线性运算也有相应的坐标运算法则．3．对于两向量a ＝(x 1，y 1，z 1)，b ＝(x 2，y 2，z 2)，a ∥b ⇔a ＝λb ⇔⎩⎪⎨⎪⎧x 1＝λx 2y 1＝λy 2z 1＝λz 2(b ≠0)，依此可以判定两向量平行或由两向量平行求待定字母的值.1．下列说法正确的是________．①任何三个不共线的向量都可构成空间的一个基底； ②不共面的三个向量就可构成空间的单位正交基底； ③单位正交基底中的基向量模为1，且互相垂直；④不共面且模为1的三个向量可构成空间的单位正交基底．【解析】 根据基底的有关概念可知：任何三个不共面的向量都可以构成一个基底，当这三个基向量是模为1且两两垂直的向量时，称此基底为单位正交基底，故有③正确，①②④错误．【答案】 ③图3－1－122．如图3－1－12，已知平行六面体OABC －O ′A ′B ′C ′中，OA →＝a ，OC →＝c ，＝b ，D 是四边形OABC 的中心，则OD →＝________.【解析】 结合图形，充分利用向量加、减的三角形法则和平行四边形法则，利用基向量a 、b 、c 表示OD →.仔细观察会发现OD →与OA →、OC →是共面向量，故它们三者之间具有线性关系，即可得到答案．【答案】 12a ＋12c3．已知a ＝(1，－2,1)，a ＋b ＝(－1,2，－1)，则b ＝______. 【解析】 设b ＝(x ，y ，z )，则a ＋b ＝(x ＋1，y －2，z ＋1)．∴⎩⎪⎨⎪⎧x ＋1＝－1，y －2＝2，z ＋1＝－1.∴⎩⎪⎨⎪⎧x ＝－2，y ＝4，z ＝－2.∴b ＝(－2,4，－2)． 【答案】 (－2,4，－2)4．设a ＝(1,5，－1)，b ＝(－2,3,5)．若(k a ＋b )∥(a －3b )，求k . 【解】 法一 ∵a ＝(1,5，－1)，b ＝(－2,3,5)．∴k a ＋b ＝k (1,5，－1)＋(－2,3,5)＝(k －2,5k ＋3，－k ＋5)．a －3b ＝(1,5，－1)－3(－2,3,5)＝(7，－4，－16)．∵(k a ＋b )∥(a －3b )． ∴k －27＝5k ＋3－4＝－k ＋5－16.∴k ＝－13.法二 ∵(k a ＋b )∥(a －3b )． ∴k a ＋b ＝λ(a －3b )．∴⎩⎪⎨⎪⎧k ＝λ，1＝－3λ，∴k ＝－13.一、填空题1．设命题p ：a ，b ，c 是三个非零向量，命题q ：{a ，b ，c }为空间的一个基底，则命题p 是命题q 的______条件(填“充分不必要”“必要不充分”“充要”“既不充分又不必要”)．【解析】 命题q 中，{a ，b ，c }为空间的一个基底，则根据基底的定义，可知a ，b ，c 为非零向量，且为不共面向量．故q ⇒p ，pD⇒/q ，所以命题p 是命题q 的必要不充分条件．【答案】 必要不充分2．设向量a ，b ，c 不共面，则下列可作为空间的一个基底的是________．①{a ＋b ，b －a ，a }； ②{a ＋b ，b －a ，b }； ③{a ＋b ，b －a ，c }; ④{a ＋b ＋c ，a ＋b ，c }．【解析】 因为只有③中三个向量不共面，所以可以作为一个基底． 【答案】 ③3．已知{i ，j ，k }为空间的一个基底，若a ＝i －j ＋k ，b ＝i ＋j ＋k ，c ＝i ＋j －k ，d ＝3i ＋2j －4k ，又d ＝α a ＋β b ＋γc ，则α＝________，β＝________，γ＝________.【解析】 由题意知：⎩⎪⎨⎪⎧α＋β＋γ＝3－α＋β＋γ＝2α＋β－γ＝－4，解之得：⎩⎪⎨⎪⎧α＝12β＝－1γ＝72.【答案】 12 －1 72图3－1－134．如图3－1－13，已知正方体ABCD —A ′B ′C ′D ′中，E 是底面A ′B ′C ′D ′的中心，a ＝12AA ′→，b ＝12AB →，c ＝13AD →，AE →＝x a ＋y b ＋z c ，则x ，y ，z 的值分别为x ＝________，y ＝________，z ＝________.【解析】 由题意知AA ′→，AB →，AD →为不共面向量，而AE →＝AA ′→＋A ′E →＝AA ′→＋12(A ′B ′→＋A ′D ′→)＝AA ′→＋12AB →＋12AD →＝2a ＋b ＋32c ，∴x ＝2，y ＝1，z ＝32.【答案】 2 1 325．已知A (3,2,1)，B (－4,5,3)，C (－1,2,1)，则2AB →＋5AC →的坐标为________． 【解析】 2AB →＋5AC →＝2(－7,3,2)＋5(－4,0,0) ＝(－14－20,6＋0,4＋0)＝(－34,6,4)． 【答案】 (－34,6,4)6．(2013·平遥高二检测)已知a ＝(λ＋1,0,2λ)，b ＝ (6,2μ－1,2)，a ∥b ，则λ与μ的值分别为________．。

322空间线面关系的判定(1)【学习目标】1 •能用向量语言表述线线，线面,面面的平行和垂直关系；2 •能用向量法证明线面的关系.【学习重点】空间线面关系的判定和运用.【学习难点】将几何中相关的量转化为坐标形式.【学习过程】一•知识要点1 •空间线线平行与垂直的向量表示设直线l i,丨2的方向向量分别是"a = ( x i, y i, z i) , I D = ( X2, y2, Z2)，贝U⑴ I 1丄l 2 孑丄" 孑• "= 0 _______________________ ；D D X1 y1 Z1⑵11 // 12 a // b X1 = Xx2, y1 = Xy 2,乙=^Z2(入€ R) = —= — ( X2 目2Z2X2 y2 Z2丰0) •2. 空间线面平行与垂直的向量表示设I 1 a , I2 a , l3 a, I2Q I3 =人且",","分别为I 1, I 2 , I 3 的方向向量，平面a的法向量分别为"•⑴ I 1 / a "=入" "丄" a" •"= 0;⑵ I 1 丄 a. I 1 // "或D Da1丄a2I II 1丄 a •D Da1 丄a33. 空间两平面的平行与垂直设I a ,直线I的方向向量为 "，平面a ,卩的法向量分别为n"和"•⑴ a 〃卩"/ " "丄卩；⑵ a 丄卩"丄" "丄卩.二•基础训练1 .已知"=(2 , 2m-3, n +2), "= (4 , 2m+1, 3n- 2) ，且D // D，贝U m= ______ , n = _____ .2•已知空间三点 A (x i ,屮,z i ) , B (X 2, y 2, Z 2), C (x 3, y 3, Z 3)，则例i .已知：直线 OAL 平面 a ，直线BDL 平面a , O B 为垂足.求证： OA/ BD例2 .证明：在平面内的一条直线，如果它和这个平面的一条斜线的射影垂直，那么它也 和这条斜线垂直（三垂线定理）.已知：如图，0B 是平面a 的斜线，0为斜足,为垂足，CD a , CDL 0A 求证：CDL OB 例 3.如图，直三棱柱 ABCAiBC 中，/ ACB 90。

3.1.2　共面向量定理学习目标　1.了解共面向量等概念.2.理解空间向量共面的充要条件．知识点一　共面向量能平移到同一平面内的向量叫做共面向量．知识点二　共面向量定理如果两个向量a ，b 不共线，那么向量p 与向量a ，b 共面的充要条件是存在有序实数组(x ，y )，使得p ＝x a ＋y b ，即向量p 可以由两个不共线的向量a ，b 线性表示．知识点三　空间四点共面的条件若空间任意无三点共线的四点，对于空间任一点O ，存在实数x ，y ，z 使得＝x ＋y OA → OB→ ＋z ，且x ，y ，z 满足x ＋y ＋z ＝1，则A ，B ，C ，D 四点共面．OC → OD→1．实数与向量之间可进行加法、减法运算．(×)2．空间中任意三个向量一定是共面向量．(×)3．若P ，M ，A ，B 共面，则＝x ＋y .(×)MP → MA → MB→类型一　向量共面的判定例1　给出以下命题：①用分别在两条异面直线上的两条有向线段表示两个向量，则这两个向量一定不共面；②已知空间四边形ABCD ，则由四条线段AB ，BC ，CD ，DA 分别确定的四个向量之和为零向量；③若存在有序实数组(x ，y )使得＝x ＋y ，则O ，P ，A ，B 四点共面；OP → OA → OB→ ④若三个向量共面，则这三个向量的起点和终点一定共面；⑤若a ，b ，c 三向量两两共面，则a ，b ，c 三向量共面．其中正确命题的序号是________．答案　③解析　①错，空间中任意两个向量都是共面的；②错，因为四条线段确定的向量没有强调方向；③正确，因为，，共面，OP→ OA → OB → ∴O ，P ，A ，B 四点共面；④错，没有强调零向量；⑤错，例如三棱柱的三条侧棱表示的向量．反思与感悟　共面向量不一定在同一个平面内，但可以平移到同一个平面内．判定向量共面的主要依据是共面向量定理．跟踪训练1　下列说法正确的是________．(填序号)①以三个向量为三条棱一定可以作成一个平行六面体；②设平行六面体的三条棱是，，，则这一平行六面体的对角线所对应的向量是AB→ AA 1—→ AD → ＋＋；AB→ AA 1—→ AD → ③若＝(P ＋)成立，则P 点一定是线段AB 的中点；OP → 12A → PB→ ④在空间中，若向量与是共线向量，则A ，B ，C ，D 四点共面；AB→ CD → ⑤若a ，b ，c 三向量共面，则由a ，b 所在直线所确定的平面与由b ，c 所在直线确定的平面是同一个平面．答案　④类型二　向量共面的证明例2　如图所示，若P 为平行四边形ABCD 所在平面外一点，点H 为PC 上的点，且＝PHHC ，点G 在AH 上，且＝m ，若G ，B ，P ，D 四点共面，求m 的值．12AGAH考点　空间向量的数乘运算题点　空间共面向量定理及应用解　连结BG .因为＝－，＝，AB → PB → PA → AB → DC → 所以＝－，DC → PB → PA → 因为＝＋，PC → PD → DC → 所以＝＋－＝－＋＋.PC → PD → PB → PA → PA → PB → PD → 因为＝，所以＝，PHHC 12PH → 13PC→ 所以＝(－＋＋)PH → 13PA → PB → PD → ＝－＋＋.13PA → 13PB → 13PD → 又因为＝－，AH → PH → PA → 所以＝－＋＋，AH →43PA → 13PB → 13PD → 因为＝m ，AG AH 所以＝m ＝－＋＋，AG → AH →4m 3PA → m 3PB → m 3PD → 因为＝－＋＝－＋，BG → AB → AG → PA → PB → AG → 所以＝＋＋.BG → (1－4m 3)PA → (m 3－1)PB → m 3PD→ 又因为G ，B ，P ，D 四点共面，所以1－＝0，m ＝.4m334即m 的值是.34反思与感悟　利用向量法证明向量共面问题，关键是熟练的进行向量的表示，恰当应用向量共面的充要条件，解题过程中注意区分向量所在的直线的位置关系与向量的位置关系．跟踪训练2　如图，在正方体ABCD －A 1B 1C 1D 1中，E ，F 分别为BB 1和A 1D 1的中点．证明：向量，，是共面向量．A 1B —→ B 1C —→ EF→证明　＝＋＋EF→ EB → BA 1—→ A 1F —→ ＝－＋12B 1B —→ A 1B —→ 12A 1D 1—→ ＝(＋)－12B 1B —→ BC → A 1B —→ ＝－.12B 1C —→ A 1B —→ 又，不共线，B 1C —→ A 1B—→ 由向量共面的充要条件知，，，是共面向量．A 1B —→ B 1C —→ EF→ 类型三　共面向量定理的应用例3　如图，在底面为正三角形的斜棱柱ABC-A 1B 1C 1中，D 为AC 的中点，求证：AB 1∥平面C 1BD .证明　记＝a ，＝b ，＝c ，则＝a ＋c ，AB → AC → AA 1—→ AB 1—→ DB→ ＝－＝a －b ，AB → AD→ 12＝＋＝b ＋c ，DC 1—→ DC → CC 1—→ 12所以＋＝a ＋c ＝，又与不共线，DB → DC 1—→ AB 1—→ DB → DC 1—→所以，，共面．AB 1—→ DB → DC 1—→ 又由于AB 1⊄平面C 1BD ，所以AB 1∥平面C 1BD .反思与感悟　在空间证明线面平行的又一方法是应用共面向量定理进行转化．要熟悉其证明过程和证明步骤．跟踪训练3　如图所示，已知斜三棱柱ABC-A 1B 1C 1，设＝a ，＝b ，＝c ，在面对AB → AC → AA 1—→ 角线AC 1上和棱BC 上分别取点M ，N ，使＝k ，＝k (0≤k ≤1)．AM → AC 1—→ BN → BC→求证：MN ∥平面ABB 1A 1.证明　＝k ·＝k (＋)＝k b ＋k c ，AM → AC 1—→ AA 1—→ AC→ 又∵＝＋＝a ＋k ＝a ＋k (b －a )＝(1－k )a ＋k b ，AN → AB → BN → BC→ ∴＝－＝(1－k )a ＋k b －k b －k c MN→ AN → AM → ＝(1－k )a －k c .又a 与c 不共线．∴与向量a ，c 是共面向量．MN→ 又MN ⊄平面ABB 1A 1，∴MN ∥平面ABB 1A 1.1．给出下列几个命题：①向量a ，b ，c 共面，则它们所在的直线共面；②零向量的方向是任意的；③若a ∥b ，则存在唯一的实数λ，使a ＝λb .其中真命题的个数为________．答案　1解析　①假命题．三个向量共面时，它们所在的直线或者在平面内或者与平面平行；②真命题．这是关于零向量的方向的规定；③假命题．当b ＝0时，则有无数多个λ使之成立．2．已知点M 在平面ABC 内，并且对空间任一点O ，＝x ＋＋，则x 的值为OM → OA → 13OB → 13OC→ ________．答案　13解析　由题意知，x ＋＋＝1，1313所以x ＝.133．下列命题中，正确命题的个数为________．①若a ∥b ，则a 与b 方向相同或相反；②若＝，则A ，B ，C ，D 四点共线；AB→ CD → ③若a ，b 不共线，则空间任一向量p ＝λa ＋μb (λ，μ∈R )．答案　0解析　当a ，b 中有零向量时，①不正确；＝时，A ，B ，C ，D 四点共面不一定共线，AB→ CD → 故②不正确；由p ，a ，b 共面的充要条件知，当p ，a ，b 共面时才满足p ＝λa ＋μb (λ，μ∈R )，故③不正确．4．已知A ，B ，C 三点不共线，O 为平面ABC 外一点，若由向量＝＋＋λ确OP → 15OA → 23OB → OC→ 定的点P 与A ，B ，C 共面，那么λ＝________.答案　215解析　∵P 与A ，B ，C 共面．∴＝α＋β，∴＝α(－)＋β(－)，即＝AP → AB → AC → AP → OB → OA → OC → OA → OP→ ＋α－α＋β－β＝(1－α－β)＋α＋β，OA → OB → OA → OC → OA → OA → OB → OC → ∴1－α－β＋α＋β＝1.因此＋＋λ＝1，解得λ＝.1523215共面向量定理的应用：(1)空间中任意两个向量a ，b 总是共面向量，空间中三个向量a ，b ，c 则不一定共面．(2)空间中四点共面的条件空间点P 位于平面MAB 内，则存在有序实数对x ，y 使得＝x ＋y ，①MP → MA → MB→ 此为空间共面向量定理，其实质就是平面向量基本定理，，实质就是平面MAB 内平MA→ MB → 面向量的一组基底．另外有＝＋x ＋y ，②OP → OM → MA → MB→ 或＝x ＋y ＋z (x ＋y ＋z ＝1)，③OP → OM → OA → OB→ ①②③均可作为证明四点共面的条件，但是①更为常用．一、填空题1．设a ，b 是两个不共线的向量，λ，μ∈R ，若λa ＋μb ＝0，则λ＝________，μ＝________.答案　0　0解析　∵a ，b 是两个不共线的向量，∴a ≠0，b ≠0，∴λ＝μ＝0.2．下列结论中，正确的是________．(填序号)①若a ，b ，c 共面，则存在实数x ，y ，使a ＝x b ＋y c ；②若a ，b ，c 不共面，则不存在实数x ，y ，使a ＝x b ＋y c ；③若a ，b ，c 共面，b ，c 不共线，则存在实数x ，y ，使a ＝x b ＋y c .答案　②③解析　要注意共面向量定理给出的是一个充要条件，所以第②个命题正确；但定理的应用又有一个前提：b ，c 是不共线向量，否则即使三个向量a ，b ，c 共面，也不一定具有线性关系，故①不正确；③正确．3．空间的任意三个向量a ，b,3a －2b ，它们一定是________．答案　共面向量解析　如果a ，b 是不共线的两个向量，由共面向量定理知，a ，b,3a －2b 共面；若a ，b 共线，则a ，b,3a －2b 共线，当然也共面．4.如图，平行六面体ABCD －A 1B 1C 1D 1中，E ，F 分别在B 1B 和D 1D 上，且BE ＝BB 1，DF ＝DD 1，若＝x ＋y ＋z ，则x ＋y ＋z ＝________.1323EF → AB → AD → AA1→答案　13解析　＝－＝＋－(＋)＝＋－－＝－＋.EF → AF → AE → AD → DF → AB → BE → AD → 23DD 1—→ AB → 13BB 1—→ AD → AB → 13AA 1—→ ∴x ＝－1，y ＝1，z ＝.∴x ＋y ＋z ＝.13135．i ，j ，k 是三个不共面的向量，＝i －2j ＋2k ，＝2i ＋j －3k ，＝λi ＋3j －5k ，且AB → BC → CD→ A ，B ，C ，D 四点共面，则λ的值为________．答案　1解析　若A ，B ，C ，D 四点共面，则向量，，共面，故存在不全为零的实数AB→ BC → CD → a ，b ，c ，使得a ＋b ＋c ＝0.AB → BC → CD → 即a (i －2j ＋2k )＋b (2i ＋j －3k )＋c (λi ＋3j －5k )＝0，∴(a ＋2b ＋λc )i ＋(－2a ＋b ＋3c )j ＋(2a －3b －5c )k ＝0.∵i ，j ，k 不共面，∴Error!∴Error!6.如图，在空间四边形OABC 中，＝a ，＝b ，＝c ，点M 在OA 上，且OA → OB → OC→ OM ＝2MA ，N 为BC 中点，则＝________.(用a ，b ，c 表示)MN→答案　－a ＋b ＋c231212解析　＝＋＋＝＋(－)＋＝a ＋(b －a )＋(－)MN → MA → AB → BN → 13OA → OB → OA → 12BC → 1312OC→ OB → ＝a ＋(b －a )＋(c －b )1312＝－a ＋b ＋c .2312127．平面α内有五点A ，B ，C ，D ，E ，其中无三点共线，O 为空间一点，满足＝＋x ＋y ，＝2x ＋＋y ，则x ＋3y ＝________.OA → 12OB → OC → OD → OB → OC → 13OD → OE→ 答案　76解析　由点A ，B ，C ，D 共面得x ＋y ＝，又由点B ，C ，D ，E 共面得2x ＋y ＝，联立方1223程组解得x ＝，y ＝，所以x ＋3y ＝.1613768．已知a ＝(－2,1,3)，b ＝(3，－4,2)，c ＝(7，λ，5)，若a ，b ，c 共面，则实数λ的值为________．答案　－12313解析　易得c ＝t a ＋μb ＝(－2t ＋3μ，t －4μ，3t ＋2μ)，所以Error!解得Error!故λ的值为－.123139．已知P ，A ，B ，C 四点共面且对于空间任一点O 都有＝2＋＋λ，则OP → OA → 43OB → OC→ λ＝________.答案　－73解析　因为P ，A ，B ，C 四点共面，所以＝x ＋y ＋z ，且x ＋y ＋z ＝1，所以2＋OP → OA → OB → OC→ ＋λ＝1，得λ＝－.437310．已知i ，j ，k 是不共面向量，a ＝2i －j ＋3k ，b ＝－i ＋4j －2k ，c ＝7i ＋5j ＋λk ，若a ，b ，c 三个向量共面，则实数λ＝________.答案　657解析　∵a ，b ，c 三向量共面，∴存在实数m ，n ，使得c ＝m a ＋n b ，即7i ＋5j ＋λk ＝m (2i －j ＋3k )＋n (－i ＋4j －2k )．∴Error!∴λ＝.65711．在以下命题中，不正确的命题的个数为________．①已知A ，B ，C ，D 是空间任意四点，则＋＋＋＝0；AB→ BC → CD → DA → ②|a |－|b |＝|a ＋b |是a ，b 共线的充要条件；③若a 与b 共线，则a 与b 所在直线平行；④对空间任意一点O 和不共线的三点A ，B ，C ，若＝x ＋y ＋z (其中OP → OA → OB → OC→ x ，y ，z ∈R )，则P ，A ，B ，C 四点共面．答案　3解析　＋＋＋＝＋＋＝＋＝0，①正确；AB→ BC → CD → DA → AC → CD → DA → AD → DA → 若a ，b 同向共线，则|a |－|b |<|a ＋b |，故②不正确；由向量平行知③不正确；由空间向量共面知④不正确．故共有3个命题不正确．二、解答题12.如图所示，已知矩形ABCD 和矩形ADEF 所在的平面互相垂直，点M ，N 分别在对角线BD ，AE 上，且BM ＝BD ，AN ＝AE .1313求证：向量，，共面．MN→ CD → DE →证明　因为M 在BD 上，且BM ＝BD ，13所以＝＝＋.MB → 13DB → 13DA → 13AB → 同理＝＋.AN → 13AD → 13DE → 所以＝＋＋MN → MB → BA → AN →＝＋＋(13DA → ＋13AB → )BA → (13AD → ＋13DE → )＝＋＝＋.23BA → 13DE → 23CD → 13DE → 又与不共线，根据向量共面的充要条件可知，，共面．CD → DE → MN → CD → DE → 13．已知非零向量e 1，e 2不共线，如果＝e 1＋e 2，＝2e 1＋8e 2，＝3e 1－3e 2，求证：AB → AC → AD → A ，B ，C ，D 共面．证明　方法一　令λ(e 1＋e 2)＋μ(2e 1＋8e 2)＋v (3e 1－3e 2)＝0，则(λ＋2μ＋3v )e 1＋(λ＋8μ－3v )e 2＝0.因为e 1，e 2不共线，所以Error!则Error!是其中一组解，则－5＋＋＝0，AB → AC → AD → 所以A ，B ，C ，D 共面．方法二　观察可得＋＝(2e 1＋8e 2)＋(3e 1－3e 2)＝5e 1＋5e 2＝5(e 1＋e 2)＝5，所以＝AC → AD → AB → AB → ＋.15AC → 15AD → 由共面向量知，，，共面．AB → AC → AD → 又它们有公共点A ，所以A ，B ，C ，D 四点共面．三、探究与拓展14．如图，在平行六面体ABCD-A 1B 1C 1D 1中，AE ＝3EA 1，AF ＝FD ，AG ＝GB ，过12E ，F ，G 三点的平面与对角线AC 1交于点P ，则AP ∶PC 1＝________.答案　316解析　设＝m ，AP → AC 1—→ 因为＝＋＋AC 1—→ AB → BB 1—→ B 1C 1—→＝＋＋AB → AA 1—→ AD →＝3＋＋2，AG → 43AE → AF → 所以＝3m ＋m ＋2m ，AP → AG → 43AE → AF → 又因为E 、F 、G 、P 四点共面，所以3m ＋m ＋2m ＝1，43所以m ＝，所以AP ∶PC 1＝3∶16.31915.如图所示，在平行六面体ABCD －A 1B 1C 1D 1中，O 是B 1D 1的中点，求证：，，B 1C —→ OD → 是共面向量．OC 1—→证明　设＝a ，C 1B 1—→ ＝b ，＝c ，C 1D 1—→ C 1C —→ ∵四边形B 1BCC 1为平行四边形，∴＝c －a ，B 1C —→又O 是B 1D 1的中点，∴＝(a ＋b )，C 1O —→ 12∴＝－(a ＋b )，OC 1—→ 12＝－＝b －(a ＋b )＝(b －a )．OD 1—→ C 1D 1—→ C 1O —→ 1212∵D 1D 綊C 1C ，∴＝c ，D 1D —→ ∴＝＋＝(b －a )＋c .OD → OD 1—→ D 1D —→ 12若存在实数x ，y ，使＝x ＋y (x ，y ∈R )成立，则B 1C —→ OD → OC 1—→ c －a ＝x ＋y [12(b －a )＋c ][－12(a ＋b )]＝－(x ＋y )a ＋(x －y )b ＋x c .1212∵a ，b ，c 不共线，∴Error!得Error!∴＝＋，又与不共线，B 1C → OD → OC 1—→ OD → OC 1—→ ∴，，是共面向量．B 1C → OD → OC 1—→。

§3.1.2 共面向量定理编写：陶美霞审核：赵太田一、知识要点1.共面向量定义：2.共面向量定理：如果两个向量,a b 不共线，那么向量p 与向量,a b 共面的充要条件是存在有序实数组(,)x y ，使得p xa yb =+。

二、典型例题例 1.如图所示，已知矩形ABCD 和矩形ADEF 所在平面相交于AD ，点,M N 分别在对角线,BD AE 上，且11,33BM BD AN AE ==，求证：MN CDE ∥平面。

例2.设空间任意一点O 和不共线三点,,A B C ，若点P 满足向量关系OP xOA yOB zOC =++ (其中1x y z ++=)。

试问：,,,P A B C 四点是否共面？思考：由()x y z OP xOA yOB zOC ++=++ ，你能得到什么结论？例3.已知四棱锥__P ABCD 的底面是平行四边形，M 是PC 的中点，求证：PA BMD ∥面。

三、巩固练习1.在四面体PABC 中，点,M N 分别为,PA PB 的中点，问：MN 与BC ，AC 是否共面？2.已知空间向量,,,a b c p ，若存在实数组1,11(,)x y z 和222(,,)x y z 满足111p x a y b z c =++，222p x a y b z c =++，且12x x ≠，试证明向量,,a b c 共面。

3.已知P 是ABCD 所在平面外一点，连,,,PA PB PC PD ，点E F G H 、、、分别是PAB ∆，,,PBC PCD PDA ∆∆∆的重心，求证：⑴E F G H 、、、共面；⑵EFGH ABCD 面∥面。

四、小结高二数学选修2-1教学案27FMNEAB DC五、课后作业1. ,a b 不共线时，a b +与a b -的关系是 ； A.共面B.不共面C.共线D.无法确定2.已知正方体__1111ABCD A B C D 的中心为O ，则在下列各结论中正确的共有 (写出序号)①OA OD +与11OB OC +是一对相反向量；②OB OC -与11OA OD -是一对相反向量； ③OA OB OC OD +++与1111OA OB OC OD +++是一对相反向量； ④1OA OA -与1OC OC -是一对相反向量。

（1）BMC（2）共面向量定理〖学习目标〗知识与技能：了解共面向量的含义，理解共面向量定理；利用共面向量定理证明有关线面平行和点共面的简单问题；过程与方法：运用类比的方法，自主探究向量共面的条件,并能灵活运用；情感态度与价值观：体会类比，化归的思想方法；领悟数学研究方法的模式化特点，感受理性思维的力量。

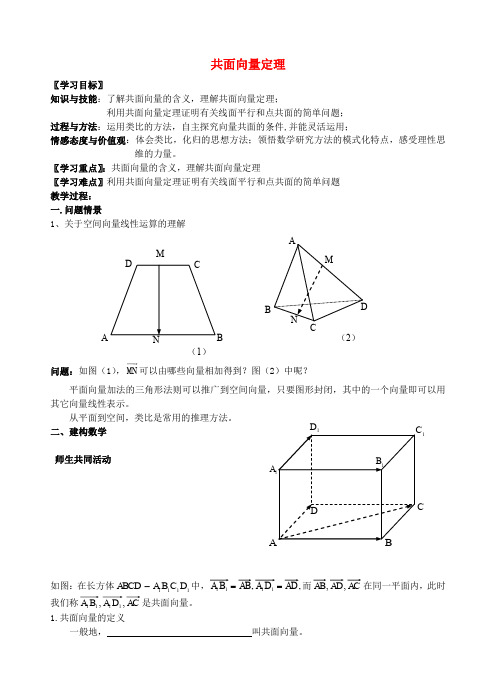
〖学习重点〗：共面向量的含义，理解共面向量定理〖学习难点〗利用共面向量定理证明有关线面平行和点共面的简单问题 教学过程： 一.问题情景1、关于空间向量线性运算的理解问题：如图（1），MN 可以由哪些向量相加得到？图（2）中呢？平面向量加法的三角形法则可以推广到空间向量，只要图形封闭，其中的一个向量即可以用其它向量线性表示。

从平面到空间，类比是常用的推理方法。

二、建构数学师生共同活动如图：在长方体1111D C B A ABCD -中，,,1111D A B A ==而,,在同一平面内，此时我们称AC D A B A ,,1111是共面向量。

1.共面向量的定义一般地， 叫共面向量。

ACA 1D类比1：共面向量与共线向量的定义在形式上有何相同之处?都是将向量问题转化为直线与直线或直线与平面之间的位置关系来研究.探究1：(1)我们已经知道空间中任意两个向量一定可以共面，那么空间中任意三个向量一定是共面向量吗？请举例说明．结论：空间中的任意三个向量不一定是共面向量． 例如：对于四面体ABCD ，AB 、AC 、AD 这三个向量就不是共面向量． (2)空间三个向量p ,b a ,具备怎样的条件时才是共面向量呢？2.共面向量的判定在平面向量中，向量b 与非零向量a 共线的充要条件是_______________________. 联想：空间任意一个向量与两个不共线向量b a ,共面时，它们之间存在怎样的关系呢？类比到空间向量，探究得到共面向量定理 如果两个向量,不共线，那么向量p 与向量,共面的充要条件类比2:空间共线向量定理和平面共线定理是相同的,那么,空间共面向量定理是否和平面向量的某个定理相联系呢?空间向量中的共面定理与平面向量基本定理不仅在形式上是相同的,而且在本质上也是一致的.这是因为任意两个空间向量b a ,都可以平移到同一个平面,当b a ,不共线时,可以作为基向量,向量与它们共面,也就是向量可以平移到这个平面,所以就能用,线性表示.三、数学运用问题:如图，已知两堵矩形墙壁ABCD 和ADEF 所在平面垂直于地面，有两只蚂蚁分别从D 、E 两点沿对角线BD,AE 向上爬，当它们分别爬到N M ,处时，此时.31,31AE AN BD BM ==它们惊奇的发现它们距离地面CDE 的高度一样，你能告诉它们这是为什么吗？分析：NFA MB证明：思考：你能用综合法来证明吗？试比较这两种方法的差异。

3.1.2 共面向量定理学习目标 1.了解共面向量等概念.2.理解空间向量共面的充要条件．知识点一 共面向量能平移到同一平面内的向量叫做共面向量． 知识点二 共面向量定理如果两个向量a ，b 不共线，那么向量p 与向量a ，b 共面的充要条件是存在有序实数组(x ，y )，使得p ＝x a ＋y b ，即向量p 可以由两个不共线的向量a ，b 线性表示． 知识点三 空间四点共面的条件若空间任意无三点共线的四点，对于空间任一点O ，存在实数x ，y ，z 使得OA →＝xOB →＋yOC →＋zOD →，且x ，y ，z 满足x ＋y ＋z ＝1，则A ，B ，C ，D 四点共面．1．实数与向量之间可进行加法、减法运算．(×) 2．空间中任意三个向量一定是共面向量．(×) 3．若P ，M ，A ，B 共面，则MP →＝xMA →＋yMB →.(×)类型一 向量共面的判定 例1 给出以下命题：①用分别在两条异面直线上的两条有向线段表示两个向量，则这两个向量一定不共面； ②已知空间四边形ABCD ，则由四条线段AB ，BC ，CD ，DA 分别确定的四个向量之和为零向量；③若存在有序实数组(x ，y )使得OP →＝xOA →＋yOB →，则O ，P ，A ，B 四点共面； ④若三个向量共面，则这三个向量的起点和终点一定共面； ⑤若a ，b ，c 三向量两两共面，则a ，b ，c 三向量共面． 其中正确命题的序号是________． 答案 ③解析 ①错，空间中任意两个向量都是共面的；②错，因为四条线段确定的向量没有强调方向； ③正确，因为OP →，OA →，OB →共面， ∴O ，P ，A ，B 四点共面； ④错，没有强调零向量；⑤错，例如三棱柱的三条侧棱表示的向量．反思与感悟 共面向量不一定在同一个平面内，但可以平移到同一个平面内．判定向量共面的主要依据是共面向量定理．跟踪训练1 下列说法正确的是________．(填序号) ①以三个向量为三条棱一定可以作成一个平行六面体；②设平行六面体的三条棱是AB →，AA 1—→，AD →，则这一平行六面体的对角线所对应的向量是AB →＋AA 1—→＋AD →；③若OP →＝12(P A →＋PB →)成立，则P 点一定是线段AB 的中点；④在空间中，若向量AB →与CD →是共线向量，则A ，B ，C ，D 四点共面；⑤若a ，b ，c 三向量共面，则由a ，b 所在直线所确定的平面与由b ，c 所在直线确定的平面是同一个平面． 答案 ④类型二 向量共面的证明例2 如图所示，若P 为平行四边形ABCD 所在平面外一点，点H 为PC 上的点，且PH HC ＝12，点G 在AH 上，且AGAH＝m ，若G ，B ，P ，D 四点共面，求m 的值．考点 空间向量的数乘运算 题点 空间共面向量定理及应用 解 连结BG .因为AB →＝PB →－P A →，AB →＝DC →，所以DC →＝PB →－P A →， 因为PC →＝PD →＋DC →，所以PC →＝PD →＋PB →－P A →＝－P A →＋PB →＋PD →. 因为PH HC ＝12，所以PH →＝13PC →，所以PH →＝13(－P A →＋PB →＋PD →)＝－13P A →＋13PB →＋13PD →.又因为AH →＝PH →－P A →， 所以AH →＝－43P A →＋13PB →＋13PD →，因为AGAH＝m ，所以AG →＝mAH →＝－4m 3P A →＋m 3PB →＋m 3PD →，因为BG →＝－AB →＋AG →＝P A →－PB →＋AG →， 所以BG →＝⎝⎛⎭⎫1－4m 3P A →＋⎝⎛⎭⎫m 3－1PB →＋m 3PD →. 又因为G ，B ，P ，D 四点共面， 所以1－4m 3＝0，m ＝34.即m 的值是34.反思与感悟 利用向量法证明向量共面问题，关键是熟练的进行向量的表示，恰当应用向量共面的充要条件，解题过程中注意区分向量所在的直线的位置关系与向量的位置关系． 跟踪训练2 如图，在正方体ABCD －A 1B 1C 1D 1中，E ，F 分别为BB 1和A 1D 1的中点．证明：向量A 1B —→，B 1C —→，EF →是共面向量．证明 EF →＝EB →＋BA 1—→＋A 1F —→＝12B 1B —→－A 1B —→＋12A 1D 1—→ ＝12(B 1B —→＋BC →)－A 1B —→＝12B 1C —→－A 1B —→. 又B 1C —→，A 1B —→不共线，由向量共面的充要条件知，A 1B —→，B 1C —→，EF →是共面向量． 类型三 共面向量定理的应用例3 如图，在底面为正三角形的斜棱柱ABC-A 1B 1C 1中，D 为AC 的中点， 求证：AB 1∥平面C 1BD .证明 记AB →＝a ，AC →＝b ，AA 1—→＝c ，则AB 1—→＝a ＋c ，DB →＝AB →－AD →＝a －12b ，DC 1—→＝DC →＋CC 1—→＝12b ＋c ，所以DB →＋DC 1—→＝a ＋c ＝AB 1—→，又DB →与DC 1—→不共线， 所以AB 1—→，DB →，DC 1—→共面．又由于AB 1⊄平面C 1BD ，所以AB 1∥平面C 1BD .反思与感悟 在空间证明线面平行的又一方法是应用共面向量定理进行转化．要熟悉其证明过程和证明步骤．跟踪训练3 如图所示，已知斜三棱柱ABC-A 1B 1C 1，设AB →＝a ，AC →＝b ，AA 1—→＝c ，在面对角线AC 1上和棱BC 上分别取点M ，N ，使AM →＝kAC 1—→，BN →＝kBC →(0≤k ≤1)．求证：MN ∥平面ABB 1A 1.证明 AM →＝k ·AC 1—→＝k (AA 1—→＋AC →)＝k b ＋k c ，又∵AN →＝AB →＋BN →＝a ＋kBC →＝a ＋k (b －a )＝(1－k )a ＋k b ，∴MN →＝AN →－AM →＝(1－k )a ＋k b －k b －k c ＝(1－k )a －k c .又a 与c 不共线． ∴MN →与向量a ，c 是共面向量． 又MN ⊄平面ABB 1A 1， ∴MN ∥平面ABB 1A 1.1．给出下列几个命题：①向量a ，b ，c 共面，则它们所在的直线共面； ②零向量的方向是任意的；③若a ∥b ，则存在唯一的实数λ，使a ＝λb . 其中真命题的个数为________． 答案 1解析 ①假命题．三个向量共面时，它们所在的直线或者在平面内或者与平面平行；②真命题．这是关于零向量的方向的规定；③假命题．当b ＝0时，则有无数多个λ使之成立． 2．已知点M 在平面ABC 内，并且对空间任一点O ，OM →＝xOA →＋13OB →＋13OC →，则x 的值为________． 答案 13解析 由题意知，x ＋13＋13＝1，所以x ＝13.3．下列命题中，正确命题的个数为________． ①若a ∥b ，则a 与b 方向相同或相反； ②若AB →＝CD →，则A ，B ，C ，D 四点共线；③若a ，b 不共线，则空间任一向量p ＝λa ＋μb (λ，μ∈R )． 答案 0解析 当a ，b 中有零向量时，①不正确；AB →＝CD →时，A ，B ，C ，D 四点共面不一定共线，故②不正确；由p ，a ，b 共面的充要条件知，当p ，a ，b 共面时才满足p ＝λa ＋μb (λ，μ∈R )，故③不正确．4．已知A ，B ，C 三点不共线，O 为平面ABC 外一点，若由向量OP →＝15OA →＋23OB →＋λOC →确定的点P 与A ，B ，C 共面，那么λ＝________. 答案215解析 ∵P 与A ，B ，C 共面．∴AP →＝αAB →＋βAC →，∴AP →＝α(OB →－OA →)＋β(OC →－OA →)，即OP →＝OA →＋αOB →－αOA →＋βOC →－βOA →＝(1－α－β)OA →＋αOB →＋βOC →， ∴1－α－β＋α＋β＝1.因此15＋23＋λ＝1，解得λ＝215.共面向量定理的应用：(1)空间中任意两个向量a ，b 总是共面向量，空间中三个向量a ，b ，c 则不一定共面． (2)空间中四点共面的条件空间点P 位于平面MAB 内，则存在有序实数对x ，y 使得MP →＝xMA →＋yMB →，①此为空间共面向量定理，其实质就是平面向量基本定理，MA →，MB →实质就是平面MAB 内平面向量的一组基底．另外有OP →＝OM →＋xMA →＋yMB →，②或OP →＝xOM →＋yOA →＋zOB →(x ＋y ＋z ＝1)，③①②③均可作为证明四点共面的条件，但是①更为常用．一、填空题1．设a ，b 是两个不共线的向量，λ，μ∈R ，若λa ＋μb ＝0，则λ＝________，μ＝________. 答案 0 0解析 ∵a ，b 是两个不共线的向量， ∴a ≠0，b ≠0，∴λ＝μ＝0.2．下列结论中，正确的是________．(填序号) ①若a ，b ，c 共面，则存在实数x ，y ，使a ＝x b ＋y c ； ②若a ，b ，c 不共面，则不存在实数x ，y ，使a ＝x b ＋y c ； ③若a ，b ，c 共面，b ，c 不共线，则存在实数x ，y ，使a ＝x b ＋y c . 答案 ②③解析 要注意共面向量定理给出的是一个充要条件，所以第②个命题正确；但定理的应用又有一个前提：b ，c 是不共线向量，否则即使三个向量a ，b ，c 共面，也不一定具有线性关系，故①不正确；③正确．3．空间的任意三个向量a ，b,3a －2b ，它们一定是________． 答案 共面向量解析 如果a ，b 是不共线的两个向量，由共面向量定理知，a ，b,3a －2b 共面；若a ，b 共线，则a ，b,3a －2b 共线，当然也共面．4.如图，平行六面体ABCD －A 1B 1C 1D 1中，E ，F 分别在B 1B 和D 1D 上，且BE ＝13BB 1，DF＝23DD 1，若EF →＝xAB →＋yAD →＋zAA 1→，则x ＋y ＋z ＝________.答案 13解析 EF →＝AF →－AE →＝AD →＋DF →－(AB →＋BE →)＝AD →＋23DD 1—→－AB →－13BB 1—→＝AD →－AB →＋13AA 1—→.∴x ＝－1，y ＝1，z ＝13.∴x ＋y ＋z ＝13.5．i ，j ，k 是三个不共面的向量，AB →＝i －2j ＋2k ，BC →＝2i ＋j －3k ，CD →＝λi ＋3j －5k ，且A ，B ，C ，D 四点共面，则λ的值为________． 答案 1解析 若A ，B ，C ，D 四点共面，则向量AB →，BC →，CD →共面，故存在不全为零的实数a ，b ，c ，使得aAB →＋bBC →＋cCD →＝0.即a (i －2j ＋2k )＋b (2i ＋j －3k )＋c (λi ＋3j －5k )＝0， ∴(a ＋2b ＋λc )i ＋(－2a ＋b ＋3c )j ＋(2a －3b －5c )k ＝0. ∵i ，j ，k 不共面， ∴⎩⎪⎨⎪⎧a ＋2b ＋λc ＝0，－2a ＋b ＋3c ＝0，2a －3b －5c ＝0.∴⎩⎪⎨⎪⎧a ＝c ，b ＝－c ，λ＝1.6.如图，在空间四边形OABC 中，OA →＝a ，OB →＝b ，OC →＝c ，点M 在OA 上，且OM ＝2MA ，N 为BC 中点，则MN →＝________.(用a ，b ，c 表示)答案 －23a ＋12b ＋12c解析 MN →＝MA →＋AB →＋BN →＝13OA →＋(OB →－OA →)＋12BC →＝13a ＋(b －a )＋12(OC →－OB →)＝13a ＋(b －a )＋12(c －b ) ＝－23a ＋12b ＋12c .7．平面α内有五点A ，B ，C ，D ，E ，其中无三点共线，O 为空间一点，满足OA →＝12OB →＋xOC →＋yOD →，OB →＝2xOC →＋13OD →＋yOE →，则x ＋3y ＝________.答案 76解析 由点A ，B ，C ，D 共面得x ＋y ＝12，又由点B ，C ，D ，E 共面得2x ＋y ＝23，联立方程组解得x ＝16，y ＝13，所以x ＋3y ＝76.8．已知a ＝(－2,1,3)，b ＝(3，－4,2)，c ＝(7，λ，5)，若a ，b ，c 共面，则实数λ的值为________． 答案 －12313解析 易得c ＝t a ＋μb ＝(－2t ＋3μ，t －4μ，3t ＋2μ)，所以⎩⎪⎨⎪⎧7＝－2t ＋3μ，5＝3t ＋2μ，λ＝t －4μ，解得⎩⎪⎨⎪⎧t ＝113，μ＝3113，λ＝－12313，故λ的值为－12313.9．已知P ，A ，B ，C 四点共面且对于空间任一点O 都有OP →＝2OA →＋43OB →＋λOC →，则λ＝________.答案 －73解析 因为P ，A ，B ，C 四点共面，所以OP →＝xOA →＋yOB →＋zOC →，且x ＋y ＋z ＝1，所以2＋43＋λ＝1，得λ＝－73.10．已知i ，j ，k 是不共面向量，a ＝2i －j ＋3k ，b ＝－i ＋4j －2k ，c ＝7i ＋5j ＋λk ，若a ，b ，c 三个向量共面，则实数λ＝________. 答案657解析 ∵a ，b ，c 三向量共面， ∴存在实数m ，n ，使得c ＝m a ＋n b ， 即7i ＋5j ＋λk ＝m (2i －j ＋3k )＋n (－i ＋4j －2k )． ∴⎩⎪⎨⎪⎧7＝2m －n ，5＝－m ＋4n ，λ＝3m －2n ，∴λ＝657.11．在以下命题中，不正确的命题的个数为________．①已知A ，B ，C ，D 是空间任意四点，则AB →＋BC →＋CD →＋DA →＝0； ②|a |－|b |＝|a ＋b |是a ，b 共线的充要条件； ③若a 与b 共线，则a 与b 所在直线平行；④对空间任意一点O 和不共线的三点A ，B ，C ，若OP →＝xOA →＋yOB →＋zOC →(其中x ，y ，z ∈R )，则P ，A ，B ，C 四点共面． 答案 3解析 AB →＋BC →＋CD →＋DA →＝AC →＋CD →＋DA →＝AD →＋DA →＝0，①正确； 若a ，b 同向共线，则|a |－|b |<|a ＋b |，故②不正确； 由向量平行知③不正确； 由空间向量共面知④不正确． 故共有3个命题不正确． 二、解答题12.如图所示，已知矩形ABCD 和矩形ADEF 所在的平面互相垂直，点M ，N 分别在对角线BD ，AE 上，且BM ＝13BD ，AN ＝13AE .求证：向量MN →，CD →，DE →共面．证明 因为M 在BD 上，且BM ＝13BD ，所以MB →＝13DB →＝13DA →＋13AB →.同理AN →＝13AD →＋13DE →.所以MN →＝MB →＋BA →＋AN →＝⎝⎛⎭⎫13DA →＋13AB →＋BA →＋⎝⎛⎭⎫13AD →＋13DE → ＝23BA →＋13DE →＝23CD →＋13DE →. 又CD →与DE →不共线，根据向量共面的充要条件可知MN →，CD →，DE →共面．13．已知非零向量e 1，e 2不共线，如果AB →＝e 1＋e 2，AC →＝2e 1＋8e 2，AD →＝3e 1－3e 2，求证：A ，B ，C ，D 共面．证明 方法一 令λ(e 1＋e 2)＋μ(2e 1＋8e 2)＋v (3e 1－3e 2)＝0， 则(λ＋2μ＋3v )e 1＋(λ＋8μ－3v )e 2＝0.因为e 1，e 2不共线，所以⎩⎪⎨⎪⎧λ＋2μ＋3v ＝0，λ＋8μ－3v ＝0，则⎩⎪⎨⎪⎧λ＝－5，μ＝1，v ＝1是其中一组解，则－5AB →＋AC →＋AD →＝0，所以A ，B ，C ，D 共面．方法二 观察可得AC →＋AD →＝(2e 1＋8e 2)＋(3e 1－3e 2)＝5e 1＋5e 2＝5(e 1＋e 2)＝5AB →，所以AB →＝15AC →＋15AD →.由共面向量知，AB →，AC →，AD →共面．又它们有公共点A ，所以A ，B ，C ，D 四点共面． 三、探究与拓展14．如图，在平行六面体ABCD-A 1B 1C 1D 1中，AE ＝3EA 1，AF ＝FD ，AG ＝12GB ，过E ，F ，G 三点的平面与对角线AC 1交于点P ，则AP ∶PC 1＝________.答案 316解析 设AP →＝m AC 1—→，因为AC 1—→＝AB →＋BB 1—→＋B 1C 1—→＝AB →＋AA 1—→＋AD →＝3AG →＋43AE →＋2AF →， 所以AP →＝3mAG →＋43mAE →＋2mAF →， 又因为E 、F 、G 、P 四点共面，所以3m ＋43m ＋2m ＝1， 所以m ＝319，所以AP ∶PC 1＝3∶16. 15.如图所示，在平行六面体ABCD －A 1B 1C 1D 1中，O 是B 1D 1的中点，求证：B 1C —→，OD →，OC 1—→是共面向量．证明 设C 1B 1—→＝a ，C 1D 1—→＝b ，C 1C —→＝c ，∵四边形B 1BCC 1为平行四边形，∴B 1C —→＝c －a ，又O 是B 1D 1的中点，∴C 1O —→＝12(a ＋b )， ∴OC 1—→＝－12(a ＋b )， OD 1—→＝C 1D 1—→－C 1O —→＝b －12(a ＋b )＝12(b －a )． ∵D 1D 綊C 1C ，∴D 1D —→＝c ，∴OD →＝OD 1—→＋D 1D —→＝12(b －a )＋c . 若存在实数x ，y ，使B 1C —→＝xOD →＋yOC 1—→ (x ，y ∈R )成立，则c －a ＝x ⎣⎡⎦⎤12(b －a )＋c ＋y ⎣⎡⎦⎤－12(a ＋b )＝－12(x ＋y )a ＋12(x －y )b ＋x c . ∵a ，b ，c 不共线，∴⎩⎪⎨⎪⎧ 12(x ＋y )＝1，12(x －y )＝0，x ＝1，得⎩⎪⎨⎪⎧x ＝1，y ＝1. ∴B 1C →＝OD →＋OC 1—→，又OD →与OC 1—→不共线， ∴B 1C →，OD →，OC 1—→是共面向量．。

3．1.2 共面向量定理[学习目标] 1.了解共面向量等概念.2.理解空间向量共面的充要条件．[知识链接]1．空间两向量共线，一定共面吗？反之还成立吗？ 答：一定共面，反之不成立．2．空间共面向量定理与平面向量基本定理有何关系？答：空间共面向量定理中，当向量a ，b 是平面向量时，即为平面向量基本定理． [预习导引] 1．共面向量能平移到同一平面内的向量叫做共面向量． 2．共面向量定理如果两个向量a ，b 不共线，那么向量p 与向量a ，b 共面的充要条件是存在有序实数组(x ，y )，使得p ＝x a ＋y b ，即向量p 可以由两个不共线的向量a ，b 线性表示． 3．空间四点共面的条件若空间任意无三点共线的四点，对于空间任一点O ，存在实数x 、y 、z 使得OA →＝xOB →＋yOC →＋zOD →，且x 、y 、z 满足x ＋y ＋z ＝1，则A 、B 、C 、D 共面．要点一 应用共面向量定理证明点共面例1 已知A 、B 、C 三点不共线，平面ABC 外的一点M 满足OM →＝13OA →＋13OB →＋13OC →.(1)判断MA →、MB →、MC →三个向量是否共面； (2)判断点M 是否在平面ABC 内． 解 (1)∵OA →＋OB →＋OC →＝3OM →， ∴OA →－OM →＝(OM →－OB →)＋(OM →－OC →)． ∴MA →＝BM →＋CM →＝－MB →－MC →. 又MB →与MC →不共线．∴向量MA →、MB →、MC →共面．(2)∵向量MA →、MB →、MC →共面且具有公共起点M ， ∴M 、A 、B 、C 共面．即点M 在平面ABC 内．规律方法 利用共面向量定理证明四点共面时，通常构造有公共起点的三个向量，用其中的两个向量线性表示另一个向量，得到向量共面，即四点共面．跟踪演练1 已知两个非零向量e 1、e 2不共线，如果AB →＝e 1＋e 2，AC →＝2e 1＋8e 2，AD →＝3e 1－3e 2，求证：A 、B 、C 、D 共面．证明 ∵AD →＋AC →＝5e 1＋5e 2＝5AB →，∴AB →＝15(AD →＋AC →)＝15AD →＋15AC →，又AD →与AC →不共线．∴AB →、AD →、AC →共面，又它们有一个公共起点A . ∴A 、B 、C 、D 四点共面．要点二 应用共面向量定理证明线面平行例2 如图，在底面为正三角形的斜棱柱ABCA 1B 1C 1中，D 为AC 的中点，求证：AB 1∥平面C 1BD .证明 记AB →＝a ，AC →＝b ，AA 1→＝c ，则 AB 1→＝a ＋c ，DB →＝AB →－AD →＝a －12b ，DC 1→＝DC →＋CC 1→＝12b ＋c ，所以DB →＋DC 1→＝a ＋c ＝AB 1→，又DB →与DC →1不共线， 所以AB 1→，DB →，DC 1→共面．又由于AB 1不在平面C 1BD 内，所以AB 1∥平面C 1BD .规律方法 在空间证明线面平行的又一方法是应用共面向量定理进行转化．要熟悉其证明过程和证明步骤．跟踪演练2 如图所示，已知斜三棱柱ABCA 1B 1C 1，设AB →＝a ，AC →＝b ，AA 1→＝c ，在面对角线AC 1上和棱BC 上分别取点M 、N ，使AM →＝kAC 1→，BN →＝kBC →(0≤k ≤1)．求证：MN ∥平面ABB 1A 1.证明 AM →＝k ·AC 1→＝k (AA 1→＋AC →)＝k b ＋k c ，又∵AN →＝AB →＋BN →＝a ＋kBC →＝a ＋k (b －a )＝(1－k )a ＋k b ， ∴MN →＝AN →－AM →＝(1－k )a ＋k b －k b －k c ＝(1－k )a －k c .又a 与c 不共线． ∴MN →与向量a ，c 是共面向量． 又MN 不在平面ABB 1A 1内， ∴MN ∥平面ABB 1A 1.要点三 向量共线、共面的综合应用例3 如图所示，已知四边形ABCD 是平行四边形，点P 是ABCD 所在平面外的一点，连结P A ，PB ，PC ，PD .设点E ，F ，G ，H 分别为△P AB ，△PBC ，△PCD ，△PDA 的重心．试用向量方法证明E ，F ，G ，H 四点共面．解 分别连结PE ，PF ，PG ，PH 并延长，交对边于点M ，N ，Q ，R ，连结MN ，NQ ，QR ，RM .∵E ，F ，G ，H 分别是所在三角形的重心，∴M ，N ，Q ，R 是所在边的中点，且PE →＝23PM →，PE →＝23PN →，PG →＝23PQ →，PH →＝23PR →.由题意知四边形MNQR 是平面四边形， ∴MQ →＝MN →＋MR →＝(PN →－PM →)－(PR →－PM →)＝32(PF →－PE →)＋32(PH →－PE →)＝32(EF →＋EH →)． 又MQ →＝PQ →－PM →＝32PG →－32PE →＝32EG →.∴EG →＝EF →＋EH →，由共面向量定理知，E ，F ，G ，H 四点共面．规律方法 选择恰当的向量表示问题中的几何元素，通过向量运算得出几何元素之间的关系，这是解决立体几何常用的方法．跟踪演练3 已知O 、A 、B 、C 、D 、E 、F 、G 、H 为空间的9个点(如图所示)，并且OE →＝kOA →，OF →＝kOB →，OH →＝kOD →，AC →＝AD →＋mAB →，EG →＝EH →＋mEF →.求证：(1)A 、B 、C 、D 四点共面，E 、F 、G 、H 四点共面； (2)AC →∥EG →； (3)OG →＝kOC →.证明 (1)由AC →＝AD →＋mAB →，EG →＝EH →＋mEF →知A 、B 、C 、D 四点共面，E 、F 、G 、H 四点共面．(2)∵EG →＝EH →＋mEF → ＝OH →－OE →＋m (OF →－OE →) ＝k (OD →－OA →)＋km (OB →－OA →) ＝kAD →＋kmAB →＝k (AD →＋mAB →)＝kAC →，∴AC →∥EG →.(3)由(2)知OG →＝EG →－EO →＝kAC →－kAO →＝k (AC →－AO →)＝kOC →，∴OG →＝kOC →.1．给出下列几个命题：①向量a ，b ，c 共面，则它们所在的直线共面； ②零向量的方向是任意的；③若a ∥b ，则存在惟一的实数λ，使a ＝λb .其中真命题的个数为________． 答案 1解析 ①假命题．三个向量共面时，它们所在的直线或者在平面内或者与平面平行；②真命题．这是关于零向量的方向的规定；③假命题．当b ＝0，则有无数多个λ使之成立． 2．已知两非零向量e 1，e 2不共线，设a ＝λe 1＋μe 2(λ，μ∈R 且λ，μ≠0)，则a 与e 1，e 2的关系为________． 答案 a 与e 1，e 2共面解析 若a ∥e 1，则存在实数t 使得a ＝t e 1， ∴t e 1＝λe 1＋μe 2，∴(t －λ)e 1＝μe 2， 则e 1与e 2共线，不符合题意． 同理，a 与e 2也不平行．由向量共面的充要条件知a 与e 1，e 2共面．3．已知点M 在平面ABC 内，并且对空间任意一点O ，有OM →＝xOA →＋13OB →＋13OC →，则x 的值为________． 答案 13解析 ∵OM →＝xOA →＋13OB →＋13OC →，且M ，A ，B ，C 四点共面，∴x ＋13＋13＝1，x ＝13.4．空间的任意三个向量a ，b,3a －2b ，它们一定是________． 答案 共面向量解析 如果a ，b 是不共线的两个向量，由共面向量定理知，a ，b,3a －2b 共面；若a ，b 共线，则a ，b,3a －2b 共线，当然也共面．共面向量定理的应用：(1)空间中任意两个向量a ，b 总是共面向量，空间中三个向量a ，b ，c 则不一定共面． (2)空间中四点共面的条件空间点P 位于平面MAB 内，则存在有序实数对x 、y 使得MP →＝xMA →＋yMB →，①此为空间共面向量定理，其实质就是平面向量基本定理，MA →，MB →实质就是面MAB 内平面向量的一组基底．另外有OP →＝OM →＋xMA →＋yMB →，② 或OP →＝xOM →＋yOA →＋zOB →(x ＋y ＋z ＝1)③①、②、③均可作为证明四点共面的条件，但是①更为常用．一、基础达标1．已知ABCD 为矩形，P 点为平面ABCD 外一点，且P A ⊥面ABCD ，G 为△PCD 的重心，若AG →＝xAB →＋yAD →＋zAP →，则x ＝________，y ＝________，z ＝________. 答案 13 23 13解析 ∵AG →＝AP →＋PG →＝AP →＋23[12(AD →－AP →)＋12(AD →＋AB →－AP →)]＝AP →＋13(AD →－AP →＋AD →＋AB →－AP →)＝13AP →＋23AD →＋13AB →. ∴x ＝13，y ＝23，z ＝13.2．在下列等式中，使点M 与点A ，B ，C 一定共面的是________． ①OM →＝2OA →－OB →－OC →； ②OM →＝15OA →＋13OB →＋12OC →；③MA →＋MB →＋MC →＝0； ④OM →＋OA →＋OB →＋OC →＝0. 答案 ③解析 若有MA →＝xMB →＋yMC →，则M 与点A 、B 、C 共面，或者OM →＝xOA →＋yOB →＋zOC →且x ＋y ＋z ＝1，则M 与点A 、B 、C 共面，①、②、④不满足x ＋y ＋z ＝1，③满足MA →＝xMB →＋yMC →，故③正确．3．已知P 和不共线三点A ，B ，C 四点共面且对于空间任一点O ，都有OP →＝2OA →＋OB →＋λOC →，则λ＝________. 答案 －2解析 P 与不共线三点A ，B ，C 共面，且OP →＝xOA →＋yOB →＋zOC →(x ，y ，z ∈R )，则有x ＋y ＋z ＝1.从而λ＝－2.4．设a ，b ，c 是不共面向量，m ＝2a －b ，n ＝b ＋c ，p ＝4a －5b －3c ，则向量m ，n ，p 的关系是________(填“共面”或“不共面”)． 答案 共面解析 因为p ＝2(2a －b )－3(b ＋c )＝2m －3n ，所以m ，n ，p 必共面．5．下列命题：①若p ＝x a ＋y b ，则p 与a ，b 共面；②若p 与a ，b 共面，则p ＝x a ＋y b ；③若MP →＝x ·MA →＋y ·MB →，则P 、M 、A 、B 四点共面；④若P 、M 、A 、B 四点共面，则MP →＝x ·MA →＋y ·MB →，其中正确的是________． 答案 ②④解析 ①与③中取x ＝0或y ＝0，则结论不一定成立．反之，②④正确．6．已知A 1B 1C 1ABC 是正三棱柱，D 是AC 上一点，若AB 1∥平面DBC 1，则D 在AC 上的位置是________． 答案 D 是AC 的中点解析 取BC 1的中点为O ，由AB 1∥平面DBC 1知，存在实数x ，y 满足AB 1→＝xDB →＋yDC 1→，又AB 1→＝AD →＋DO →＋OB 1→＝AD →＋DO →＋CO → ＝AD →＋DO →＋DO →－DC →＝AD →－DC →＋DB →＋DC 1→， 所以AD →＝DC →，即D 是AC 的中点．7．设A 、B 、C 及A 1、B 1、C 1分别是异面直线l 1、l 2上的三点，而M 、N 、P 、Q 分别是线段AA 1、BA 1、BB 1、CC 1的中点．求证：M 、N 、P 、Q 四点共面． 证明 因为NM →＝12BA →，NP →＝12A 1B 1→，所以BA →＝2NM →，A 1B 1→＝2NP →， 又因为PQ →＝12(BC →＋B 1C 1→)，(*)A 、B 、C 及A 1、B 1、C 1分别共线，所以BC →＝λBA →＝2λNM →，B 1C 1→＝ωA 1B 1→＝2ωNP →. 代入(*)式得PQ →＝12(2λNM →＋2ωNP →)，又NM →与NP →不共线．所以PQ →、NM →、NP →共面，所以M 、N 、P 、Q 四点共面． 二、能力提升8．平面α内有点A ，B ，C ，D ，E ，其中无三点共线，O 为空间一点，满足OA →＝12OB →＋xOC →＋yOD →，OB →＝2xOC →＋13OD →＋yOE →，则x ＋3y ＝________.答案 76解析 由点A ，B ，C ，D 共面得x ＋y ＝12，又由点B ，C ，D ，E 共面得2x ＋y ＝23，联立方程组解得x ＝16，y ＝13，所以x ＋3y ＝76.9.如图，在平行六面体ABCDA 1B 1C 1D 1中，AE ＝3EA 1，AF ＝FD ，AG ＝12GB ，过E 、F 、G 三点的平面与对角线AC 1交于点P ，则AP ∶PC 1的值为________． 答案316解析 设AP →＝mAC 1→，因为AC 1→＝AB →＋BB 1→＋B 1C 1→ ＝AB →＋AA 1→＋AD → ＝3AG →＋43AE →＋2AF →，所以AP →＝3mAG →＋43mAE →＋2mAF →，又因为E 、F 、G 、P 四点共面，所以3m ＋43m ＋2m ＝1，所以m ＝319，所以AP ∶PC 1＝3∶16.10．已知非零向量e 1，e 2不共线，如果AB →＝e 1＋e 2，AC →＝2e 1＋8e 2，AD →＝3e 1－3e 2.则A 、B 、C 、D 四点的位置关系为________． 答案 共面解析 令λ(e 1＋e 2)＋μ(2e 1＋8e 2)＋v (3e 1－3e 2)＝0. 则(λ＋2μ＋3v )e 1＋(λ＋8μ－3v )e 2＝0.∵e 1、e 2不共线，∴⎩⎪⎨⎪⎧λ＋2μ＋3v ＝0，λ＋8μ－3v ＝0，易知⎩⎪⎨⎪⎧λ＝－5μ＝1v ＝1是其中一组解，则－5AB →＋AC →＋AD →＝0，∴A 、B 、C 、D 共面．11．已知四边形ABCD 为正方形，P 是四边形ABCD 所在平面外一点，P 在平面ABCD 上的射影恰好是正方形的中点O ，Q 是CD 的中点，求下列各题中x ，y 的值． (1)OQ →＝PQ →＋xPC →＋yP A →； (2)P A →＝xPO →＋yPQ →＋PD →. 解 (1)如图所示∵OQ →＝PQ →－PO →＝PQ →－12(P A →＋PC →)＝PQ →－12P A →－12PC →，∴x ＝y ＝－12.(2)∵P A →＋PC →＝2PO →，∴P A →＝2PO →－PC →. 又PC →＋PD →＝2PQ →，∴PC →＝2PQ →－PD →. ∴P A →＝2PO →－(2PQ →－PD →)＝2PO →－2PQ →＋PD →. ∴x ＝2，y ＝－2.12．对于任意空间四边形ABCD ，E 、F 分别是AB 、CD 的中点．试判断：EF →与BC →、AD →的关系．解 如图所示．空间四边形ABCD 中，E 、F 分别是AB 、CD 的中点，利用多边形加法法则可得：EF →＝EA →＋AD →＋DF →，① EF →＝EB →＋BC →＋CF →，②又E 、F 分别是AB 、CD 的中点． 故有EA →＝－EB →，DF →＝－CF →，③ 将③代入①得EF →＝－EB →＋AD →－CF →，④ ②＋④得：2EF →＝AD →＋BC →，所以EF →＝12AD →＋12BC →，即EF →与BC →、AD →共面．三、探究与创新13.如图所示，在平行六面体ABCDA 1B 1C 1D 1中，O 是B 1D 1的中点，求证：B 1C →，OD →，OC 1→是共面向量． 证明 设C 1B 1→＝a ， C 1D 1→＝b ，C 1C →＝c ，∵四边形B 1BCC 1为平行四边形，∴B 1C →＝c －a ， 又O 是B 1D 1的中点， ∴C 1O →＝12(a ＋b )，∴OC 1→＝－12(a ＋b )，OD 1→＝C 1D 1→－C 1O →＝b －12(a ＋b )＝12(b －a )．∵D 1D 綊C 1C ，∴D 1D →＝c ， ∴OD →＝OD 1→＋D 1D →＝12(b －a )＋c .若存在实数x 、y ，使B 1C →＝xOD →＋yOC 1→(x ，y ∈R )成立，则 c －a ＝x ⎣⎡⎦⎤12(b －a )＋c ＋y ⎣⎡⎦⎤－12(a ＋b )＝－12(x ＋y )a ＋12(x －y )b ＋x c .∵a 、b 、c 不共线，∴⎩⎪⎨⎪⎧12(x ＋y )＝1，12(x －y )＝0，x ＝1，得⎩⎪⎨⎪⎧x ＝1，y ＝1. ∴B 1C →＝OD →＋OC 1→，又OD →与OC →1不共线． ∴B 1C →、OD →、OC 1→是共面向量．。

3.1空间向量及其运算3.1.1空间向量的线性运算教学目标：㈠知识目标：⒈空间向量；⒉相等的向量；⒊空间向量的加减与数乘运算及运算律；㈡能力目标：⒈理解空间向量的概念，掌握其表示方法；⒉会用图形说明空间向量加法、减法、数乘向量及它们的运算律；⒊能用空间向量的运算意义及运算律解决简单的立体几何中的问题．㈢德育目标：学会用发展的眼光看问题，认识到事物都是在不断的发展、进化的，会用联系的观点看待事物．教学重点：空间向量的加减与数乘运算及运算律．教学难点：应用向量解决立体几何问题．教学方法：讨论式．教学过程：Ⅰ.复习引入［师］在必修四第二章《平面向量》中，我们学习了有关平面向量的一些知识，什么叫做向量？向量是怎样表示的呢？［生］既有大小又有方向的量叫向量．向量的表示方法有：①用有向线段表示；②用字母a、b等表示；③用有向线段的起点与终点字母：AB．［师］数学上所说的向量是自由向量，也就是说在保持向量的方向、大小的前提下可以将向量进行平移，由此我们可以得出向量相等的概念，请同学们回忆一下．［生］长度相等且方向相同的向量叫相等向量.［师］学习了向量的有关概念以后，我们学习了向量的加减以及数乘向量运算：⒈向量的加法：⒉向量的减法：⒊实数与向量的积：实数λ与向量a的积是一个向量，记作λa，其长度和方向规定如下：(1)|λa|＝|λ||a|(2)当λ＞0时，λa与a同向；当λ＜0时，λa与a反向；当λ＝0时，λa ＝0.［师］关于向量的以上几种运算，请同学们回忆一下，有哪些运算律呢？ ［生］向量加法和数乘向量满足以下运算律加法交换律：a ＋b ＝b ＋a加法结合律：(a ＋b )＋c ＝a ＋（b ＋c ） 数乘分配律：λ(a ＋b )＝λa ＋λb［师］今天我们将在必修四第二章平面向量的基础上，类比地引入空间向量的概念、表示方法、相同或向等关系、空间向量的加法、减法、数乘以及这三种运算的运算率，并进行一些简单的应用．请同学们阅读课本P 26～P 27．Ⅱ.新课讲授［师］如同平面向量的概念，我们把空间中具有大小和方向的量叫做向量．例如空间的一个平移就是一个向量．那么我们怎样表示空间向量呢？相等的向量又是怎样表示的呢？［生］与平面向量一样，空间向量也用有向线段表示，并且同向且等长的有向线段表示同一向量或相等的向量．起点与重点重合的向量叫做零向量。

苏教版选修2《共面向量定理》教案及教学反思一、教学目标1.知识水平1.理解共面向量及其性质；2.理解二维向量组共面的判定方法；3.掌握平面向量定比分点公式的应用方法；4.掌握平面向量线性运算的基本性质及运算规则。

2.能力水平1.能判断二维向量组是否共面；2.能根据共面向量的特征求解未知向量；3.能够通过平面向量定比分点公式求解相关的几何问题；4.能熟练运用向量的基本性质进行向量的加减、数乘和点乘。

二、教学重点1.共面向量及其性质；2.二维向量组共面的判定方法；3.平面向量定比分点公式的应用方法。

三、教学难点1.平面向量定比分点公式的理解和应用；2.理解平面向量线性运算的基本性质及运算规则。

四、教学内容及教学方式1. 教学内容1.1 共面向量及其性质1.定义共面向量及其特征；2.两个共面向量的关系；3.三个以上共面向量的关系。

1.2 二维向量组共面的判定方法1.向量线性相关与共面的关系；2.二维向量组共面的判定方法。

1.3 平面向量定比分点公式的应用方法1.平面向量定比分点公式的公式推导；2.平面向量定比分点公式的应用。

2. 教学方式本节教学应以多样化和灵活性为原则，采用讲授、分组讨论和学生自主学习等教学方式相结合：1.讲授教师应首先讲解共面向量及其性质、二维向量组共面的判定方法和平面向量定比分点公式的应用方法，然后对基本公式和性质进行案例分析，让学生了解平面向量定比分点公式的应用范围和解题方法。

2.分组讨论教师可以将学生分成小组，让他们自行研究一些反映平面向量定比分点公式应用的典型问题，以讨论的形式进行交流。

教师可以组织合适的讨论形式，如小组探究、问题梳理、学生演示等，以培养学生解决实际问题的能力。

3.学生自主学习在讲解课程以外，可以对学生进行独立学习和探究，让他们自己寻找和解决有关课程的问题，从而增强学生的自学能力。

五、教学反思本节课程涉及内容较多，一开始学生可能感觉有些吃力，但授课过程中，教师通过多样化的教学和实例分析，增强了学生的学习意愿，有助于学生掌握有关知识，在短时间内学会并熟练应用。

3.1.2 共面向量定理双基达标 (限时20分钟)1．已知ABCD 为矩形，P 点为平面ABCD 外一点，且P A ⊥面ABCD ，G 为△PCD 的重心，若AG →＝xAB →＋yAD →＋zAP →，则x ＝________，y ＝________，z ＝________.解析 AG →＝AP →＋PG →＝AP →＋23[12(AD →－AP →)＋12(AD →＋AB →－AP →)] ＝AP →＋13(AD →－AP →＋AD →＋AB →－AP →) ＝13AP →＋23AD →＋13AB → ∴x ＝13，y ＝23，z ＝13. 答案 13 23 132．在下列等式中，使点M 与点A ，B ，C 一定共面的是________．①OM →＝2OA →－OB →－OC →②OM →＝15OA →＋13OB →＋12OC → ③MA →＋MB →＋MC →＝0④OM →＋OA →＋OB →＋OC →＝0解析 若有MA →＝xMB →＋yMC →，则M 与点A 、B 、C 共面，或者OM →＝xOA →＋yOB →＋zOC →且x ＋y ＋z ＝1，则M 与点A 、B 、C 共面，①、②、④不满足x ＋y ＋z ＝1，③满足MA →＝xMB →＋yMC →，故③正确．答案 ③3．如图所示，已知P 和不共线三点A ，B ，C 四点共面且对于空间任一点O ，都有OP →＝2OA→＋OB →＋λOC →，则λ＝________.解析 P 与不共线三点A ，B ，C 共面，且OP →＝xOA →＋yOB →＋zOC →(x ，y ，z ∈R )，则有x ＋y ＋z ＝1.从而λ＝－2.答案 －24．设a ，b ，c 是不共面向量，m ＝2a －b ，n ＝b ＋c ，p ＝4a －5b －3c ，则向量m ，n ，p ________(填“共面”或“不共面”)．解析 因为p ＝2(2a －b )－3(b ＋c )＝2m －3n ，所以m ，n ，p 必共面．答案 共面5．下列命题：①若p ＝x a ＋y b ，则p 与a ，b 共面；②若p 与a ，b 共面，则p ＝x a ＋y b ；③若MP →＝x ·MA →＋y ·MB →，则P 、M 、A 、B 四点共面；④若P 、M 、A 、B 四点共面，则MP →＝x ·MA →＋y ·MB →，其中正确的是________．解析 ①与③中取x ＝0或y ＝0，则结论不一定成立．反之，②④正确．答案 ②④6．设A 、B 、C 及A 1、B 1、C 1分别是异面直线l 1、l 2上的三点，而M 、N 、P 、Q 分别是线段AA 1、BA 1、BB 1、CC 1的中点．求证：M 、N 、P 、Q 四点共面．解 NM →＝12BA →，NP →＝12A 1B 1→，所以BA →＝2NM →，A 1B 1→＝2NP →，又因为PQ →＝12(BC →＋B 1C 1→)，(*) A 、B 、C 及A 1、B 1、C 1分别共线，所以BC →＝λBA →＝2λNM →，B 1C 1→＝ωA 1B 1→＝2ωNP →.代入(*)式得PQ →＝12(2λNM →＋2ωNP →) ＝λNM →＋ωNP →，所以PQ →、NM →、NP →共面，所以M 、N 、P 、Q 四点共面．综合提高（限时25分钟）7．已知A 1B 1C 1－ABC 是正三棱柱，D 是AC 上一点，若AB 1∥平面DBC 1，则D 在AC 上的位置是________．解析 取BC 1的中点为O ，由AB 1∥平面DBC 1知，存在实数x ，y 满足AB 1→＝xDB →＋yDC 1→，又AB 1→＝AD →＋DO →＋OB 1→＝AD →＋DO →＋CO →＝AD →＋DO →＋DO →－DC →＝AD →－DC →＋DB →＋DC 1→，所以AD →＝DC →，即D 是AC 的中点．答案 D 是AC 的中点8．平面α内有点A ，B ，C ，D ，E ，其中无三点共线，O 为空间一点，满足OA →＝12OB →＋xOC →＋yOD →，OB →＝2xOC →＋13OD →＋yOE →，则x ＋3y ＝________. 解析 由点A ，B ，C ，D 共面得x ＋y ＝12，又由点B ，C ，D ，E 共面得2x ＋y ＝23，联立 方程组解得x ＝16，y ＝13，所以x ＋3y ＝76. 答案 769.如图，在平行六面体ABCD －A 1B 1C 1D 1中，AE ＝3EA 1，AF＝FD ，AG ＝12GB ，过E 、F 、G 三点的平面与对角线AC 1交于点P ，则AP ∶PC 1的值为________．解析 设AP →＝mAC 1→，因为AC 1→＝AB →＋BB 1→＋B 1C 1→＝AB →＋AA 1→＋AD →＝3AG →＋43AE →＋2AF →， 所以AP →＝3mAG →＋43mAE →＋2mAF →， 又因为E 、F 、G 、P 四点共面，所以3m ＋43m ＋2m ＝1， 所以m ＝319，所以AP ∶PC 1＝3∶16. 答案 3∶1610.在正方体ABCD －A 1B 1C 1D 1中，M 是面对角线AC 的中点，N 是面对角线A 1B 上的点，若MN ∥平面B 1BCC 1，则点N 的位置为________．解析 设BN →＝λBA 1→，因为MN ∥平面B 1BCC 1，由共面向量定理知，存在实数x ，y ，使得MN →＝xBC →＋yBB 1→，①又MN →＝BN →－BM →＝λBA 1→－12(BC →＋BA →)＝λ(BB 1→＋BA →)－12(BC → ＋BA →)＝－12BC →＋λBB 1→＋(λ－12)BA →， 与①比较可知λ＝12，即点N 是面对角线A 1B 的中点． 答案 A 1B 的中点11.已知E 、F 、G 、H 分别是空间四边形ABCD 的边AB 、BC 、CD 、DA 的中点，设M 是EG 和FH 的交点，求证：对空间任一点O ，有OM →＝14(OA →＋OB →＋OC →＋OD →)． 证明 因为MA →＋MB →＝2ME →，MC →＋MD →＝2MG →，且ME →＋MG →＝0，所以MA →＋MB →＋MC →＋MD →＝0，OM →＋MA →＋OM →＋MB →＋OM →＋MC →＋OM →＋MD →＝4OM →，所以OM →＝14(OA →＋OB →＋OC →＋OD →)． 12．已知四边形ABCD 为正方形，P 是四边形ABCD 所在平面外一点，P 在平面ABCD 上的射影恰好是正方形的中点O ，Q 是CD 的中点，求下列各题中x ，y 的值．(1)OQ →＝PQ →＋xPC →＋yP A →；(2)P A →＝xPO →＋yPQ →＋PD →.解 (1)如图所示∵OQ →＝PQ →－PO →＝PQ →－12(P A →＋PC →)＝PQ →－12P A →－12PC →，∴x ＝y ＝－12. (2)∵P A →＋PC →＝2PO →，∴P A →＝2PO →－PC →.又PC →＋PD →＝2PQ →，∴PC →＝2PQ →－PD →.∴P A →＝2PO →－(2PQ →－OD →)＝2PO →－2PQ →＋PD →.∴x ＝2，y ＝－2.13．(创新拓展)设A ，B ，C 及A 1，B 1，C 1分别是异面直线l 1，l 2上的三点，而M ，N ，P ，Q 分别是线段AA 1，BA 1，BB 1，CC 1的中点，求证：M ，N ，P ，Q 四点共面．证明 由题意得，NM →＝12BA →，NP →＝12A 1B 1→，∴BA →＝2NM →，A 1B 1→＝2NP →.又A ，B ，C 及A 1，B 1，C 1分别共线， ∴BC →＝λBA →，B 1C 1→＝tA 1B 1→.又PQ →＝12(BC →＋B 1C 1→)，∴PQ →＝12(λBA →＋tA 1B 1→)＝12(2λNM →＋2tNP →)＝λNM →＋tNP →.∴PQ →，NM →，NP →共面．∴M ，N ，P ，Q 四点共面．。