当前位置：文档之家 › 数字逻辑 第三章习题讲解

数字逻辑 第三章习题讲解

  • 格式：ppt
  • 大小：234.00 KB
  • 文档页数：13

下载文档原格式

  / 13

合集下载

数字逻辑-习题以及习题答案

数字逻辑-习题以及习题答案

AD
F的卡诺图
ACD
G的卡诺图
根据F和G的卡诺图，得到：F G
湖南理工学院计算机与信息工程系通信教研室 陈进制作
第3章习题 3.4 在数字电路中，晶体三极管一般工作在什么状态？
答：在数字电路中，晶体三极管一般工作在饱和导通状态 或者截止状态。
湖南理工学院计算机与信息工程系通信教研室 陈进制作
第3章习题
111110
1100110
⊕ ⊕⊕⊕ ⊕
10 000 1
⊕ ⊕⊕⊕ ⊕⊕
10 101 01
⑵ (1100110)2 = 64+32+4+2 = (102)10 = (0001 0000 0010)8421码
(1100110)2 =( 101?0101 )格雷码
湖南理工学院计算机与信息工程系通信教研室 陈进制作
第2章习题
2.2 用逻辑代数的公理、定理和规则证明下列表达式：
⑴ AB AC AB AC
⑵ AB AB AB AB 1
⑶ AABC ABC ABC ABC
证⑴：AB AC
AB AC
A B A C
AA AC BA BC
证⑶：AABC
A A B C
AB AC
第1章习题 1.3 数字逻辑电路可分为哪两种类型？主要区别是什么？
答：数字逻辑电路可分为组合逻辑电路、时序逻辑电路两 种类型。 主要区别：组合逻辑电路无记忆功能， 时序逻辑电路有记忆功能。
湖南理工学院计算机与信息工程系通信教研室 陈进制作
第1章习题 1.6 将下列二进制数转换成十进制数、八进制数和十六进制数。
第2章习题 2.8 ⑴ ②求出最简或-与表达式。
两次取反法
圈0，求F 最简与或式。

《数字逻辑》第3章习题答案

《数字逻辑》第3章习题答案
习
题
【3-1】填空： (1) 逻辑代数中有三种最基本运算： 与 、 或 和 非 ，在此基础上又派生出五种基本运算， 分别为 与非 、 或非 、 异或 、 同或 、和 与或非 。 (2) 与运算的法则可概述为：有 0 出 0 ，全 1 出 1 ；类似地，或运算的法则为 有”1”出”1”， 全”0”出”0” 。 (3) 摩根定理表示为： A B = A B ； A B = A B 。 (4) 函数表达式 Y= AB C D ，则其对偶式为 Y ' = ( A B)C D 。 积的形式结果应为 M ( 0,1,2,4,5,8,9,10)。 (5) 函数式 F=AB+BC+CD 写成最小项之和的形式结果应为 m ((3,6,7,11,12,13,14,15))， 写成最大项之
0 0 1 1 1 1
1 1 0 0 1 1
0 1 0 1 0 1
1 1 0 0 1 0
【3-8】写出下列函数的反函数 F ，并将其化成最简与或式。 (1) F1 ( A D )( B C D)( AB C ) (2) F2 ( A B )( BCD E )( B C E )(C A) (3) F3 A B C A D (4) F4 ( A B)C ( B C ) D 解： (1) F1 AD C (2) F2 AB A C E (3) F3 AB AC A D (4) F4 BC C D ABD A B C 【3-9】用对偶规则，写出下列函数的对偶式 F ，再将 F 化为最简与或式。 (1) F1 AB B C A C (2) F2 A B C D (3) F3 ( A C )( B C D)( A B D) ABC (4) F4 ( A B )( A C )( B C )(C D) (5) F5 AB C CD BD C 解：题中各函数对偶函数的最简与或式如下： (1) F1 A BC AB C (2) F2 A B D A C D (3) F3 AC A BD (4) F4 A BC B C CD (5) F5 ABC D (6) F6 AB C D 【3-10】已知逻辑函数 F A B C , G=A⊙B⊙C，试用代数法证明： F G 。 解：

数字逻辑第3章答案

数字逻辑第3章答案

(最简与-或式)
F(A,B,C, D) ABC ABC
F(A,B,C, D) (A B C)(A B C) （最简或-与式）
（2）函数 F(A, B,C, D) BC D D (B C) (AD B) 的卡诺图如图 3 所示。
F(A,B,C, D) BC D D (B C) (AD B) BC D (B D C D)( AD B) BC D BCD
（2）
FA, B,C, D AB ABD (B CD)
A B ABD B CD (A B)(A B D) B CD AB AB AD BD B CD AB AD B CD AB(CD CD CD CD) AD(BC BC BC BC) B(ACD ACD ACD ACD ACD ACD ACD ACD) CD(AB AB AB AB) ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD m8 m9 m10 m11 m8 m10 m12 m14 m4 m5 m6 m7 m12 m13 m14 m15 m3 m7 m11 m15
(3) 正确。因为若 Y≠Z，则当 X=0 时，等式 X + Y = X + Z 不可能成立；当 X=1 时，等式 XY = XZ 不可能成立；仅当 Y=Z 时，才能使 X+Y = X+Z 和 XY = XZ 同时成立。

数字电路习题答案-第三章

数字电路习题答案-第三章
(2)写最简表达式
ABCD F
1000 1 1001 1 1010 Ø 1011 Ø 1100 Ø 1101 Ø 1110 Ø 1111 Ø
CD
AB
00
01
11
10
00
01
1
1
1
11
φ
φ
φ
φ
10
1
1
φ
φ
F = A + BD + BC=A · BD · BC (3)画逻辑电路，如下图所示：
D
&
B
&
C
所以，此时电路中存在功能冒险。
2.当 ABCD 从 1000 向 1101 变化时： 先判断是否有功能冒险，函数 F 的卡诺图如下图所
ABCD00 01 11 10 00 1
01 1
1
11 1 1 1 1
10 1 1 1
示： (1) F(1,0,0,0)=F(1,1,0,1)； (2) 有 2 个变量同时变化； (3) AC对应的卡诺圈中全部为“1”； 所以，此时电路中不存在功能冒险。 再判断是否有逻辑冒险：
10 1 1 Ø = ABC·CD·AB·AD
画逻辑电路，如下图所示：
C&
D
A&
B
A&
D
A B
&
C
&
F
3.9 人的血型有 A、B、AB、O 四种。输血时输血者的血型与受血者的血型必须符合图 P3.4 中箭头指示的授受关系。试设计一个逻辑电路，判断输血者与受血者的血型是否符合上述规 定。 解：设00代表血型A、01代表血型B、10代表血型AB、11代表血型O。输血者的血型用逻辑 变量WX表示，受血者的血型用YZ表示，则由图中所指示的授受关系，列真值表：

数字逻辑 第三章习题讲解

数字逻辑 第三章习题讲解

A=0
8421码= 2421码－ 0110（+ 1010） A = 1
AB C D
B3 A3B2 A2B1 A1B0 A0C0
74LS283
C4
S3 S2 S1 S0
Y8Y4Y2Y1
⑹ 8421码→ 2421码
十进 制整 数
8421 码
2421 码
d1 1d 0001 2421码=8421码
⑴ F=AB+CD+BCD+ACD ⑶ F=BD+BD+ABC+ACD
11 1 1
111 1 1
1
1
11
11
1
11
111
1 或非门：F3＝∏M(0,3,5,6)
F3＝∑m(1,2,4,7)
＝(A+B+C)(A+B+C)(A+B+C)(A+B+C)
另解，与非门： F3＝ABC ABC ABC ABC ＝AABAC BABBC CACBC ABC
（4）三变量的偶数电路（三变量中有偶数个1，输出为1；三变量有奇数个1，输出为0）
G1
Y0 Y1
Y2
Y3
D
A
Y4 Y5
C B Y6
B C Y7
⑹ Y0
Y1
Y2
Y3
C
A
Y4 Y5
B B Y6
A C Y7
⑸
Y0
Y1
Y2
Y3
Y4
&
C A Y5 F B B Y6
A C Y7
F
&
E D C
Y0
Y1
Y2
Y3

数字逻辑第3章习题参考解答

数字逻辑第3章习题参考解答

3.68
分析图 3-37 所示反相器的下降时间，设 RL=900Ω ，VL=2V。
解：该电路图可以等效为下列带开关的一阶电路图。当输出从高态转 为低态时，可以等效为开关 K 从位置 1 转到位置 2。
按照一阶电路三要素法的分析方法，对于电容上的电压分析如下： 初态：VH=4.45V 终态：VL=0.2V
VOUT VL VH VL (1 e t / )
由上式可以得出从 1.5V 到 3.5V 的上升时间为：
t ln VH 1.5 19ns VH 3.5
可以驱动。
I=（3.84-2.03）/0.487 = 3.72 < 4mA
可以驱动。
3.40 一个发光二极管导通时的电压降约为 2.0V，正常发光时需要约 5mA 的电流。当发光二极管如图 3－54（a）那样连接时，确定上拉电 阻的适当值。 解：根据 3.7.5 所给的条件，低态输出电平 VOLmax=0.37V。 对应等效 电路如下：
13 画出 NOR3 对应的电路图。 解：3 输入端或非门结构应为：上部 3 个 P 管串联，下部 3 个 N 管并 联，结构如图所示。
3.15 画出 OR2 所对应的电路图。 解：在 NOR2 电路的输出端后面级联一个 INV。
3.59 解：
画出图 X3.59 逻辑图所对应的电路图。
3.21 若输出低电平阈值和高电平阈值分别设置为 1.5V 和 3.5V，对 图 X3.21 所示的反相器特性，确定高态与低态的 DC 噪声容限。 解：由图中可以看到，输出 3.5V 对应的输入为 2.4V,输出 1.5V 对应 的输入为 2.5V； 所以，高态噪声容限为：3.5-2.5=1 V ;低态噪声 容限为：2.4-1.5=0.9 V。

数字逻辑第3章答案

数字逻辑第3章答案
(4) F A B[(C D)E G]
F， A B[(C D)E G]
5 (1) 如果已知 X + Y 和 X + Z 的逻辑值相同,那么 Y 和 Z 的逻
辑值一定相同。正确吗?为什么? (2) 如果已知 XY 和 XZ 的逻辑值相同,那么那么 Y 和 Z 的逻辑值
一定相同。正确吗?为什么? (3)如果已知 X + Y 和 X + Z 的逻辑值相同,且 XY 和 XZ 的逻辑
(1) F(A, B,C, D) BD AD CD CD ACD ABD
(2) F(A, B,C, D) (AB AB) C (AB AB) C
解答
G(A, B,C, D) AB BC AC (A B C) ABC
(1) 当 b a 时，令 a=1,b=0 能得到最简“与-或”表达式： F BC CD ACD （3 项）
(2) 当 a=1,b=1 时，能得到最简的“与-或”表达式：
F BC CD AC （3 项）
11 用列表法化简逻辑函数
F(A, B,C, D) m(0,2,3,5,7,8,10,11,13,15)
10
0
0
01 0 0 1 1
1
1
10 0 0 1 1
1
1
11 0 1 0 1
0
0
4 求下列函数的反函数和对偶函数： (1) F AB AB
(2) F A B A C C DE E
(3) F (A B)(C DAC)
(4) F A B CD E G
值相同，那么 Y = Z。正确吗?为什么? (4) 如果已知 X+Y 和 X·Y 的逻辑值相同,那么 X 和 Y 的逻辑值

数字电路 第三章习题答案课件

数字电路 第三章习题答案课件

解: 根据题意，该控制电路有三个输入A，B，C; 三个输出G， Y，R。G代表绿灯，Y代表黄灯，R代表红灯。状态赋值如下：1 表示水在电极之上，0表示水在电极之下; 0表示灯亮，1表示灯灭。 按照题意列出的真值表如下。由真值表画出的卡诺图：
3-11
G A B AB
Y AB C ABC RC
3-11
试用六个与非门设计一个水箱控制电路。图为水箱示意图。A、B、C是三个电极。 当电极被水浸没时，会有信号输出。水面在A，B间为正常状态，点亮绿灯G；水面在 B、C间或在A以上为异常状态，点亮黄灯Y；水面在C以下为危险状态．点亮红灯R。
3-4 试分析题示逻辑图的功能。图中G1，G0为控制端，A，B为输入端。要求写
出G1，G0四种取值下F的表达式。
3-5 列出题示逻辑图的真值表。图中T331为输出低电平有效的8421码译码器。
T33l为8421码的四线一十·线译码器，由于A3＝0， 便变成了三线一八线译码器。
Si Ai BiC Ai BiC Ai BiC Ai BiCi
S1S0 ( AB AB )
3-10
F S1 AB S0 AB S0 A B S0 AB S1S0 A B F F S1 AB S0 AB S0 AB S0 AB S1S0 AB
3-11
试用六个与非门设计一个水箱控制电路。图为水箱示意图。A、B、C是三个电极。 当电极被水浸没时，会有信号输出。水面在A，B间为正常状态，点亮绿灯G；水面在 B、C间或在A以上为异常状态，点亮黄灯Y；水面在C以下为危险状态．点亮红灯R。
X2X1X0 = Z2Z1Z0时，输出 F=0
X2X1X0 Z2Z1Z0时，输出 F=1
3-9 由八线一三线优先编码器74148和与非门构成的电路如下，试说明该电路的

第三章课后习题（1）参考答案

第三章课后习题（1）参考答案

第三章 课后习题（1）参考答案P1111、 试说明串行进位和并行进位方式的不同之处。

（P .61.） 答：串行进位中进位是逐级形成的，每一级的进位直接依赖于前一级的进位，延迟时间较长，但节省器件，成本低。

并行进位中，各位进位信号都有独自的进位形成逻辑，每位进位信号的产生时间都相同，与低位进位无关，可有效地减少进位延迟时间。

但这是以增加逻辑线路为代价的。

2、 用74181和74182芯片构成一个64位的ALU ，采用分级分组并行进位链。

画出逻辑框图，并注明输入、输出等。

参考（P .63. 图3-6）答：P .63. 图3-6 画出了一个16位的并行进位ALU 结构 （每个74181芯片处理4位，16位需要4片74181芯片，组间用1片74182芯片产生组间并行进位。

）64位ALU ，可采用4组图3-6 的结构，每组处理16位，再用1片74182，处理组间进位。

A 3~0B 3~0A 7~4B 7~4A 11~8B 11~8A 15~12B 15~12__ __Cn16位并行进位ALU结构A 15~0B 15~0A 31~16B 31~16A 47~32 B 47~32A 63~48B 63~48__ __Cn64位并行进位ALU结构3、 用变形补码计算[X]补+[Y]补，并指出是否溢出，说明是正溢还是负溢。

（P .66.） 答：（1）[X]补=00,110011 [Y]补=00,101101 [X]补+[Y]补 = 01,100000，正溢出 （2）[X]补=00,010110 [Y]补=00,100101 [X]补+[Y]补 = 00,111011 无溢出 （3）[X]补=00,1110011 [Y]补=11,101101 [X]补+[Y]补 = 11,100000，无溢出 （4）[X]补=11,001101 [Y]补=11,010011[X]补+[Y]补 = 10,100000，负溢出4、 用变形补码计算[X]补-[Y]补，并指出是否溢出。

《数字逻辑》第3章作业与习题_单选题第六小题已更正版本

《数字逻辑》第3章作业与习题_单选题第六小题已更正版本

。
20．如果某 TTL 与非门的输入低电平噪声容限 VNL=0.7V，输入低电平
ViL=0.2V，那么它的关门电平 Voff 为
。
21．对于或非门，只要有一个输入为高电平，则输出就为 电平，所以
对或非门多余输入端的处理不能接 电平。
22．对于 TTL 与非门，只要有一个输入为低电平，则输出就为 电平，
为
，按抗干扰能力强弱的顺序依次为
，按静态功耗低和高的顺序依次为
。
6. 假设 VGS(TH)为开启电压，一般在 1~3V 范围内，则 NMOS 管当
时
截止，当
时导通；PMOS 管当
时截止，当
时
导通。
7. CMOS 反相器是由
作为驱动管，
作为负载管形成了 电
路结构。
2）单选题
1．硅二极管导通和截止的条件是（ ）。
不形成
；在外电场作用下，
和
均能参与导电。
7． 半导体中载流子的两种运动方式指
运动和
运动。
8． 硅二极管的截止条件是
，导通条件是
。
9． 数字电路中的晶体三极管作为开关元件，主要工作在
和
。
10． 三种基本逻辑门是
、
、
。
11． 与门是可以实现
的电路。
12． 在 TTL 电路中，输入端悬空等效于逻辑 电平，但为了避免引入干
② 输出端能带同类门的输入端个数
③ 输出端能带同类门的个数
④ 输入端数
7．输出端可直接连在一起实现“线与”逻辑功能的门电路是（ ）。
① 与非门
② 或非门 ③ OC 门
④ 异或门
8．两输入变量 A、B 的逻辑门的输出、输入如图所示，根据输出波形 Y，该

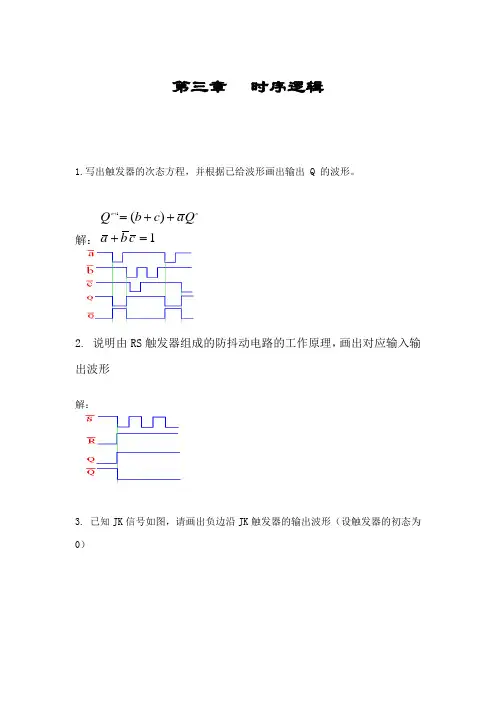
数字逻辑课后答案 第三章

数字逻辑课后答案 第三章

第三章 时序逻辑1.写出触发器的次态方程，并根据已给波形画出输出 Q 的波形。

解：2. 说明由RS 触发器组成的防抖动电路的工作原理，画出对应输入输出波形解：3. 已知JK 信号如图，请画出负边沿JK 触发器的输出波形（设触发器的初态为0）1)(1=+++=+c b a Qa cb Q nn4. 写出下图所示个触发器次态方程，指出CP 脉冲到来时，触发器置“1”的条件。

解：（1），若使触发器置“1”，则A 、B 取值相异。

（2），若使触发器置“1”，则A 、B 、C 、D 取值为奇数个1。

5.写出各触发器的次态方程，并按所给的CP 信号，画出各触发器的输出波形（设初态为0）解：6. 设计实现8位数据的串行→并行转换器。

B A B A D +=DC B A K J ⊕⊕⊕==Q AQ B Q D Q C Q E Q F Q7. 分析下图所示同步计数电路解：先写出激励方程，然后求得状态方程状态图如下：该计数器是五进制计数器，可以自启动。

8. 作出状态转移表和状态图，确定其输出序列。

解：求得状态方程如下故输出序列为：000119. 用D 触发器构成按循环码(000→001→011→111→101→100→000)规律工作的六进制同步计数器解：先列出真值表，然后求得激励方程PS NS 输出N0 0 0 0 0 1 00 0 1 0 1 1 0 0 1 1 1 1 1 0 1 1 1 1 0 1 0 1 0 1 1 0 0 0 1 0 0 0 0 0 1化简得：逻辑电路图如下：n Q 2n Q 1n Q 012+n Q 11+n Q 10+n Q n n n nn n n n n n nnQ Q Q Q Q Q Q Q Q Q Q Q Z 121002*********+==+==+++nnn nnn nnnn QQ Q D QQ Q D QQ Q Q D 121211121122+====+==+++10. 用D 触发器设计3位二进制加法计数器，并画出波形图。

数字电路与数字逻辑3组合逻辑电路习题解答

数字电路与数字逻辑3组合逻辑电路习题解答

3 33习 题1．解： CO =AB +BC +ACAC BC AB C B A ABC CO C B A ABC S +++++=+++=）（）（AC BC AB C B A ABC ）（+++=AC BC AB C AC BC AB B AC BC AB A ABC +++= A B AB C AC C A B C BC B A ABC +++= C B A C B A C B A ABC +++=真值表A B C S CO A B C S CO 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 1 0 1 0 1 0 1 0 1 1 0 0 1 011111111电路功能：一位全加器，A 、B 为两个加数，C 为来自低位的进位，S 是相加的和，CO 是进位。

2．解：处于工作状态的译码器C 、D 应输入的状态C D ① 0 0 ② 0 1 ③ 1 0 ④11逻辑功能：由74LS139构成的4线—16线译码器3．解：由图可见，74HC138的功能扩展输入端必须满足E 1＝1、032==E E 才能正常译码，因此E 1＝A 3＝1；542A A E =，即A 4＝1，A 5＝1； 0763=+=A A E ，即A 6＝0，A 7＝0。

所以，该地址译码器的译码地址范围为A 7A 6A 5A 4A 3A 2A 1A 0＝00111A 2A 1A 0＝00111000～3 3400111111，用十六进制表示即为38H ～3FH 。

输入、输出真值表如表P3.3-1所示。

表3.3-1 地址译码器的真值表4．解：由图写出逻辑函数并化简，得02460246L Y Y Y Y Y Y Y Y A BC ABC ABC ABC C ==+++=+++=5． 解：F AB B C A B C AB C ABC ABC =+=+++3 359．解：4选1数据选择器的逻辑表达式为： 301201101001D A A D A A D A A D A A Y +++=将A 1=A ，A 0=B ，D 0=1，D 1=C ，C D =2，D 3=C 代入得 ABC C B A BC A C B A C B A ABC C B A BC A B A Y ++++=+++=根据表达式可画出波形图：C ABL10．解：（1）写出逻辑函数表达式： C AB C B A BC A C B A C B A L ++++=（2）用卡诺图化简3 3611．解：567m m m ABC C B A ABC C AB AC AB L ++=+++=+=13． 解：D C B D C D D C A D C B D C C A F +++=++=)(0⋅+++=+++=CD D C D C A D C AB D C B D C D C A D C A令A 1=C ，A 0=D ，AB D =0，A D =1，D 2=1，D 3=0 连线图：14． 解：3 371。

数字电路逻辑设计课后习题答案第三章

数字电路逻辑设计课后习题答案第三章

3-1 分析题图3-1所示电路，写出电路输出Y 1和Y 2的逻辑函数表达式，列出真值表，说明它的逻辑功能。

解：由题图3-1从输入信号出发，写出输出Y 1和Y 2的逻辑函数表达式为1Y A B C =⊕⊕ ； 2()()Y A B C AB A B C A =⊕⋅⋅=⊕⋅+B将上式中的A 、 B 、C 取值000～111，分别求出Y 1和Y 2，可得出真值表如题解 表3-1所示。

题解 表3-1ABCA B ⊕()A B C ⊕⋅AB1Y2Y0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 1 0 1 0 0 1 0 0 1 1 1 1 0 0 1 1 0 0 1 0 0 1 0 1 0 1 1 1 0 0 1 1 1 0 0 0 1 0 1 111111综上，由题解 表3-1可以看出，该电路实现了一位全加器的功能。

其中，A 和B 分别是被加数及加数，C 为相邻低位来的进位数；Y1为本位和数，Y 2为相邻高位的进位数。

3-2 分析题图3-2所示电路，要求：写出输出逻辑函数表达式，列出真值表，画出卡诺图，并总结电路功能。

解：由题图3-2从输入信号出发，写出输出F 的逻辑函数表达式为()()F A B C D =:::将上式中的A 、 B 、C 、D 取值0000～1111，求出F ，可得真值表和卡诺图分别如题解 表3-2和题解 图3-1所示。

题解 表3-2A B C DA B : C D :F0 0 0 0 1 1 1 0 0 0 1 1 0 0 0 0 1 0 1 0 0 0 0 1 1 1 1 1 0 1 0 0 0 1 0 0 1 0 1 0 0 1 0 1 1 0 0 0 1 0 1 1 1 0 1 0 1 0 0 0 0 1 0 1 0 0 1 0 0 11 0 1 0 0 0 1 1 0 1 1 0 1 0 1 1 0 0 1 1 1 1 1 0 1 1 0 0 1 1 1 0 1 0 0 1 1 1 1 1 1 1综上，由题解 表3-2可以看出，当输入A 、 B 、C 、D 中含有偶数个“1”时，输出；否则，当输入A 、 B 、C 、D 中含有奇数个“1”时，输出。

数字逻辑准欧阳4版 题解3-4

数字逻辑准欧阳4版 题解3-4

F=AB C⊕D+AB C⊕D+AB C⊕D+AB C⊕D
=A⊕B C⊕D + A⊕B C⊕D =A⊕B ⊕ C⊕D
4.11 在输入不提供反变量的情况下，用与非门组成实现下 列函数的最简电路。 （1）F=AB+AC+BC （2）F=ABC+BCD+ACD+BCD 解：在输入不提供反变量的情况下，需尽可能将式中单 个反变量变换成公共的与非因子。
3.14 已知输入信号A和B的波形如图3.69(a)所示，试画出图 3.69(b)、(c)中两个触发器Q端的输出波形，设触发器初态为0。
1
0
1
0
1
1
Q
D=0
1
0
0
1
D=1
D=1
D=0
D=0
(b)
Q
T=0保持 T=1翻转 T=1翻转 T=1翻转 T=0保持
(c)
作业4
组合逻辑电路
“欧阳星明第四版” ，
F =（A B+AB）C +（A B+AB）C =A⊕B C +（A⊕B）C =A⊕B ⊕C （3）列出输出函数真值表 方法三：直接往电路中代数获得 真值表
A 0 0 0 0 1 1 1 1 B 0 0 1 1 0 0 1 1 C 0 1 0 1 0 1 0 1 F 1 0 0 1 0 1 1 0
(4) 输入是偶数个1时，输出F的值为1
习题四（pp.117 ）： 4.1, 4.2, 4.8, 4.9, 4.11, 4.12
4.1 分析图4.27所示的组合逻辑电路，说明电路功能，并画 出其简化逻辑电路图。 (1)根据逻辑电路图写出输出函数表达式 F=ABC· (A+B+C) (2)化简输出函数表达式 F=ABC+(A+B+C) =ABC+ABC (4)说明电路功能 (3)列出输出函数真值表

数字电子技术基础-第3章课后习题答案

数字电子技术基础-第3章课后习题答案

第3章集成逻辑门电路3-1 如图3-1a）～d）所示4个TTL门电路，A、B端输入的波形如图e）所示，试分别画出F1、F2、F3和F4的波形图。

A1A234a)b)c)d)F1F2F3F4BAe）图3-1 题3-1图解：从图3-1a）～d）可知，11F=，2F A B=+，3F A B=⊕，4F A B= ，输出波形图如图3-2所示。

F1F2F3F4AB图3-2题3-1输出波形图3-2 电路如图3-3a ）所示，输入A 、B 的电压波形如图3-3b ）所示，试画出各个门电路输出端的电压波形。

1A 23b)a)AB图3-3 题3-2图解：从图3-3a ）可知，1F AB =，2F A B =+，3F A B =⊕，输出波形如图3-4所示。

F 1F 2F 3AB图3-4 题3-2输出波形3-3在图3-5a ）所示的正逻辑与门和图b ）所示的正逻辑或门电路中，若改用负逻辑，试列出它们的逻辑真值表，并说明F 和A 、B 之间是什么逻辑关系。

b)a)图3-5 题3-3图解：（1）图3-5a ）负逻辑真值表如表3-1所示。

表3-1 与门负逻辑真值表F 与A 、B 之间相当于正逻辑的“或”操作。

（2）图3-5b ）负逻辑真值表如表3-2所示。

表3-2 或门负逻辑真值表F 与A 、B 之间相当于正逻辑的“与”操作。

3-4试说明能否将与非门、或非门和异或门当做反相器使用？如果可以，各输入端应如何连接？解：与非门、或非门和异或门经过处理以后均可以实现反相器功能。

1）与非门：将多余输入端接至高电平或与另一端并联； 2）或非门：将多余输入端接至低电平或与另一端并联；3） 异或门：将另一个输入端接高电平。

3-5为了实现图3-6所示的各TTL 门电路输出端所示的逻辑关系，请合理地将多余的输入端进行处理。

b)a)AB=A B=+A BC DABC D图3-6 题3-5图解：a ）多余输入端可以悬空，但建议接高电平或与另两个输入端的一端相连；b ）多余输入端接低电平或与另两个输入端的一端相连；c) 未用与门的两个输入端至少一端接低电平，另一端可以悬空、接高电平或接低电平；d ）未用或门的两个输入端悬空或都接高电平。

数字设计基础与运用第3章习题解答

数字设计基础与运用第3章习题解答

1第3章 时序逻辑基础习题33-1 解 该电路的状态图如图3-5输入序列： 1 1 1 0 0 1 0 1 状态序列：S 0 S 1 S 2 S 2 S 3 S 4 S 5 S 5 S 1输出序列： 0 0 0 0 0 1 1 0最后一位输入后电路处于S 1状态。

3-2解 该电路的状态表如表3-5所示，为米里型电路。

输入序列： 1 0 1 1 1 0 1 状态序列： A C C D B C C D 输出序列：0 0 0 0 1 0 0 最后一位输入后电路处于D 状态。

3-3 解 逻辑符号如图3-8所示，真值表如表3-6所示，工作波形如图3-9所示。

3-4 解 输出波形如图3-11所示。

3-5 解 Q端波形如图3-13所示。

3-19(a)、(b)、(c)所示。

3-9 解 Q3-10 解 Q1、Q0的输出波形如图3-23图3-22X图3-161J1KC1QQCPJKRSCLRPR图3-20233-11 解 8进制异步行波加法计数器电路如图3-24所示。

3-12解 4进制异步行波可逆计数器电路如图3-25所示。

3-13 解 5进制异步加法计数器电路如图3-26所示。

3-14 解 8进制同步减法计数器电路如图3-27所示。

3-15 解 4图3-24CLK 1D Q 0 Q 0 C1 1D Q 1 Q 1C1 1DQ 2Q 2C143-16 解 用7493构成的13进制和172进制计数器电路分别如图3-29和图3-30所示，因为13=(1101)2，172=16⨯10+12。

3-17 分别用74163构成8421BCD 和5421BCD 加法计数器，并画出全状态图。

解 8421BCD 加法计数器及全状态图如图3-31所示，采用同步清0方式变模。

5421BCD 加法计数器及全状态图如图3-32所示，采用预置方式变模。

根据5421BCD 码的编码规律，当Q D Q C Q B Q A =0100时，下一个CP 脉冲应置入1000；当Q D Q C Q B Q A =1100时，下一个CP 脉冲应置入0000。

数字电路 第三章习题答案PPT课件

数字电路 第三章习题答案PPT课件
根据题意画出的卡诺图。
FBCBC
F D 0 ( A 1 A 0 ) D 1 ( A 1 A 0 ) D 2 ( A 1 A 0 ) D 3 ( A 1 A 0 ) 令A 1 ： B , A 0C 得 D 1 ： D 2 1 , D 0 D 3 0
精选ppt课件2021
32
3-16 用74LS138三—八线译码器和与非门实现下列逻辑函数。
m (1,2,3,7)
Y 2 A B C A B C A B C A B Cm (2,3,4,5)
Y 3(A B )A ( C )A B A C A B AC
A B C A B C A B C AB Cm (0,1,5,7)
Y4ABC ABC m(0,7)
精选ppt课件2021
33
3-16 用74LS138三—八线译码器和与非门实现下列逻辑函数。
精选ppt课件2021
22
3-11
试用六个与非门设计一个水箱控制电路。图为水箱示意图。A、B、C是三个电极。 当 电极被水浸没时，会有信号输出。水面在A，B间为正常状态，点亮绿灯G；水面在B、 C间或在A以上为异常状态，点亮黄灯Y；水面在C以下为危险状态．点亮红灯R。
解: 根据题意，该控制电路有三个输入A，B，C; 三个输出G， Y，R。G代表绿灯，Y代表黄灯，R代表红灯。状态赋值如下：1 表示水在电极之上，0表示水在电极之下; 1表示灯亮，0表示灯灭。 按照题意列出的真值表如下。由真值表画出的卡诺图：
15
其他电路：
精选ppt课件2021
16
精选ppt课件2021
17
精选ppt课件2021
18
精选ppt课件2021
19
3-10 试用与非门设计一个逻辑选择电路。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

X>Y X=Y X<Y
•••
•••
+5V
X12 Y12 X13 Y13 X14 Y14 X15 Y15
3.26 使用一个MSI 4 位加法器设计下列十进制代码转换器 ⑸ 2421码→8421码
8421码=
2421码 + 0000 A=0 2421码－ 0110（+ 1010） A = 1
A B C
3.6分析图示电路的逻辑功能
a Z=D Y=C⊕D X=B⊕(C+Y) = B ⊕( C + C ⊕ D ) =B⊕(C+D) W=A⊕(B+C+D) 结论：a=16-b,a是b的16补码， 或称为二进制变补器（按位取 反加1）。
0(16) 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1
D
B3 A3 B2 A2 B1 A1 B0 A0 C0
74LS283
C4
S3 S2 S1 S0
Y8Y4Y2Y1
⑹ 8421码→ 2421码
十进 制整 数 0 1 2 3 4 5 6 7 8 9
8421 码
0000 0001 0010 0011 01
& F
D C B
=A(m2+m4+m6)+A(m6)
74LS138
G1 Y0 Y1 Y2 Y3 Y4 Y5 Y6 Y7
D C B
A B C
思考如何用一片74LS138实现该函数 : F=D(AC+BC+AB)=D(m31 +m32 + m33 +m37 )
⑷
A
D C B
G2A Y0 Y1 Y2 Y3 Y4 A Y5 B Y6 C Y7 G1 Y0 Y1 Y2 Y3 Y4 Y5 Y6 Y7 F Y0 Y1 Y2 Y3 Y4 Y5 Y6 Y7 &
（2）三变量非一致电路（三变量一致，输出为1；三变量不一致，输出为0） ABC 000 001 010 011 100 101 110 111 F2 0 1 1 1 1 1 1 0 C
AB
1 1 1
1
1 1
与非门：F2＝ AB ＋BC＋AC F2＝ABC＋ABC＝ABC（A＋B＋C）
＝A ABC＋B ABC＋C ABC
或非门：F2’＝(A+B+C)(A+B+C)=ABC＋ABC
F2＝∑m(1,2,3,4,5,6)
F2=(F2’)’=(A+B＋C)(A+B+C)
（3）三变量的奇数电路（三变量中有奇数个1，输出为1；三变量有偶数个1，输出为0）
ABC 000 001 010 011 100 101 110 111 F3＝∑m(1,2,4,7) F3 0 1 1 0 1 0 0 1 AB
⑸
Y0 Y1 Y2 Y3 Y4 Y5 Y6 Y7 & F
&
F
C B A
A B C
& G
D C B
A B C
⑹
C B A
A B C
E D C
A B C
Y0 Y1 Y2 Y3 Y4 Y5 Y6 Y7
&
G
3.22 至多用一个SSI器件和一个MSI器件(74LS138,74LS139, 74LS153,74LS151)实现下列功能. ⑴ F=XYZ+XYZ =m20 · Z+m23 · Z F= m30 +m37
3.12用二进制译码器74138或74139及与非门实现下列单输出 及多输出函数 ⑴ F = ∑m3(2,4,7) 解:F = ∑m3(2,4,7) =Y2+Y4+Y6 =Y2· Y4· Y6 ⑵ F = ΠM3(3,4,5,6,7) 解:F = ∏ M3(3,4,5,6,7) = ∑m3 (0,1,2) =Y0+Y1+Y2 =Y0· Y1· Y2
AGTB AGTB AEQB AEQB ALTB ALTB A0 B0 74LS85 A1 B1 A2 B2 A3 B3 AGTB AGTB AEQB AEQB ALTB ALTB A0 B0 74LS85 A1 B1 A2 B2 A3 B3
+5V
AGTB AGTB AEQB AEQB ALTB ALTB A0 B0 74LS85 A1 B1 A2 B2 A3 B3
ABC F3
000 001 010 011 100 101 110 111
F4＝∑m(0,3,5,6)
1 0 0 1 0 1 1 0
C
AB
1
1
1
1
与非门：F4＝ABC＋ABC＋ABC+ABC=A ⊙ B ⊙ C 或非门：F4＝∏M(1,2,4,7) ＝(A+B+C)(A+B+C)(A+B+C)(A+B+C)
WXYZ
0000 1111 1110 1101 1100 1011 1010 1001 1000 0111 0110 0101 0100 0011 0010 0001
b
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
ABCD
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
74138 Y0 Y1 Y2 Y3 Y4 Y5 Y6 Y7 74153
⑵F=XYZ+XYZ = m31 +m36
74151
Y X
& F
A B C0 C1 C2 C3
Z Y X F
A B C C0 C1 C2 C3 C4 C5 C6 C7
Y
F
Y
Z
Z
+5V
Z Y X
A B C
3.23
X0 Y0 X1 Y1 X2 Y2 X3 Y3
C
1 1 1
1
与非门：F3＝ABC＋ABC＋ABC+ABC=A⊕B ⊕C 或非门：F3＝∏M(0,3,5,6) ＝(A+B+C)(A+B+C)(A+B+C)(A+B+C)
另解，与非门： F3＝ABC ABC ABC ABC
＝AABAC BABBC CACBC ABC
（4）三变量的偶数电路（三变量中有偶数个1，输出为1；三变量有奇数个1，输出为0）
74LS138
Y0 Y1 Y2 Y3 Y4 Y5 Y6 Y7
74LS138
Y0 Y1 Y2 Y3 Y4 Y5 Y6 Y7
&
&
F
F
C B A
A B C
C B A
A B C
⑶
74LS138
A
G2A Y0 Y1 Y2 Y3 Y4 A Y5 B Y6 C Y7
F= ∑m4 (2,4,6,14) =ABCD+ABCD+ABCD+ABCD =A(BCD+BCD+BCD)+A(BCD)
2421 码
0000 0001 0010 0011 0100 1011 1100 1101 1110 1111