等腰梯形性质

等腰梯形的特点性质.
等腰梯形的性质：等腰梯形同一底上的两个内角相等。

两腰相等，两底平行，对角线相等。

等腰梯形中位线的长度是上下底边长度和的一半。

性质有哪些：
1、全等梯形同一底上的两个内角成正比。

2、两腰相等，两底平行，对角线相等。

3、由托勒密定理可以得全等梯形abcd，存有abxcd+bcxad=acxbd
4、等腰梯形对角线的平方等于腰的平方与上、下底积的乘积和。

bd=ac=ab+adxbc=cd+adxbc
5、全等梯形中位线的长度就是上下底边长度和的.一半。

6、等腰梯形是轴对称图形，只有一条对称轴，过上下两底中点的直线即为对称轴。

7、全等梯形的面积公式：s=(上底+下底)×低÷2。

8、特殊面积计算：当对角线垂直时：s=acxbd/2。

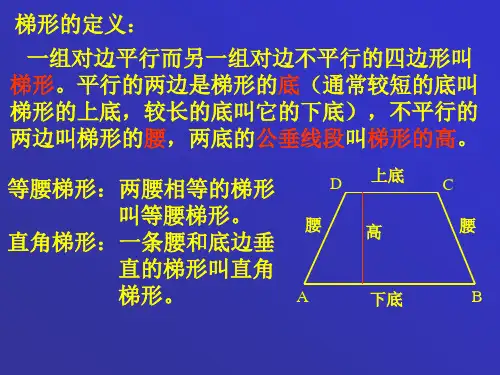
初中数学等腰梯形的性质知识点详解初中数学等腰梯形的性质知识点详解对于数学的学习中，下面是对等腰梯形的性质知识点的内容讲解，供大家参考学习。

等腰梯形的性质①两底平行，两腰相等②等腰梯形在同一底上的两个角相等③等腰梯形的两条对角线相等④等腰梯形是轴对称图形，只有一条对称轴，一底的垂直平分线是它的对称轴通过上面对数学中等腰梯形的性质知识点的内容讲解学习，相信同学们已经能很好的掌握了吧，希望同学们会从中学习的更好。

初中数学相关的角与性质知识点详解对于数学的学习中，下面是对相关的角与性质知识点的内容讲解，供大家参考学习。

相关的角与性质相关的角：1、对顶角：一个角的两边分别是另一个角的两边的反向延长线，这两个角叫做对顶角。

2、互为补角：如果两个角的和是一个平角，这两个角做互为补角。

3、互为余角：如果两个角的和是一个直角，这两个角叫做互为余角。

4、邻补角：有公共顶点，一条公共边，另两条边互为反向延长线的两个角做互为邻补角。

注意：互余、互补是指两个角的数量关系，与两个角的位置无关，而互为邻补角则要求两个角有特殊的位置关系。

角的性质1、对顶角相等。

2、同角或等角的余角相等。

3、同角或等角的补角相等。

通过上面对数学中相关的角与性质知识点的内容讲解学习，相信同学们已经能很好的掌握了吧，希望同学们会从中学习的更好。

初中数学菱形的定义与性质知识点详解下面是老师对数学中菱形的定义与性质相关知识讲解，希望给同学们的复习学习提供很好的帮助。

菱形的定义与性质1、定义：邻边相等的平行四边形是菱形。

2、性质：（1）菱形的四边形都相等。

（2）菱形的对角线互相垂直，并且每一条对角线平分一组对角，（3）菱形的面积等于对角线乘积的一半。

（4）菱形既是中心对称图形，又是轴对称图形，有2条对称轴。

相信上面对数学中菱形的定义与性质知识的讲解学习，同学们已经能很好的掌握了吧，希望同学们在考试中取得优异成绩。

初中数学梯形定义知识点详解下面是老师对数学中梯形定义相关知识讲解，希望给同学们的复习学习提供很好的帮助。

初中数学等腰梯形有哪些全等性质等腰梯形是一个重要的几何形状，在初中数学中学习它的全等性质可以帮助我们更好地理解和应用几何知识。

下面将介绍等腰梯形的全等性质，并解释它们的证明过程。

1. 全等性质1：等腰梯形的两个底角相等。

证明：设等腰梯形ABCD和A'B'C'D'的底边AB和A'B'相等，且底角∠DAB和∠D'A'B'相等。

我们需要证明∠DCB和∠D'C'B'也相等。

首先，连接AC和A'C'。

由于等腰梯形的底边平行，我们可以得知∠ADC和∠A'D'C'是对应角，它们相等。

又因为∠DAB和∠D'A'B'相等，所以∠DAC和∠D'A'C'也相等。

接下来，考虑三角形ADC和A'D'C'。

我们已经知道∠DAC和∠D'A'C'相等，底边AD和A'D'相等，且底边DC和C'D'相等。

根据第一个全等性质（SAS），我们可以得知三角形ADC和A'D'C'全等。

因此，∠DCB和∠D'C'B'也相等。

2. 全等性质2：等腰梯形的两个腿相等。

证明：设等腰梯形ABCD和A'B'C'D'的底边AB和A'B'相等，且腿BC和B'C'相等。

我们需要证明腿AD和A'D'也相等。

首先，连接AC和A'C'。

由于等腰梯形的底边平行，我们可以得知∠ADC和∠A'D'C'是对应角，它们相等。

又因为∠DAB和∠D'A'B'相等，所以∠DAC和∠D'A'C'也相等。

接下来，考虑三角形ADC和A'D'C'。

等腰梯形对角线的平方等于腰的平方与上、下底积的乘积和，等腰梯形是轴对称图形，只有一条对称轴，过上下两底中点的直线即为对称轴。

等腰梯形同一底上的两个内角相等。

两腰相等，两底平行，对角线相等。

等腰梯形的性质：
（1）两底边相互平行，并且两腰相等
（2）同一底上的底角相等
（3）等腰梯形对角线相等
几何表达举例：
（1）∵ABCD是等腰梯形
∴AD∥BC，AB=CD
（2）∵ABCD是等腰梯形
∴∠ABC=∠DCB
∠BAD=∠CDA
（3）∵ABCD是等腰梯形
∴AC=BD
等腰梯形的判定
1、一组对边相等且不平行，另一组对边平行的四边形是等腰梯形。

2、同一底上的两个角相等的梯形是等腰梯形。

3、对角线相等的梯形是等腰梯形。

4、两腰相等的梯形是等腰梯形
以下判定不作为定理使用：
5、对角线相等且能形成两个等腰三角形的四边形是等腰梯形。

6、对角互补的梯形是等腰梯形。

等腰梯形体积立方计算公式全文共四篇示例，供读者参考第一篇示例：等腰梯形是一种特殊的梯形，其两边边长相等，且上底和下底之间的距离也相等。

计算等腰梯形的体积是一个很常见的问题，通常使用立方计算公式来求解。

在本文中，我将介绍等腰梯形的定义、性质以及如何利用立方计算公式来找到等腰梯形的体积。

让我们来看看等腰梯形的定义。

等腰梯形是一种四边形，其中两条边长相等，被称为等边。

上底和下底之间的距离也相等，被称为梯形的高。

等腰梯形的性质包括：1. 对角线等长；2. 对角线互相垂直；3. 对角线平分角；4. 中点连线平行；5. 上底和下底的平行线段互等长。

接下来，让我们来看看如何计算等腰梯形的体积。

等腰梯形的体积计算公式为：V = (a + b) * h * H / 2，其中a为上底长，b为下底长，h为梯形的高，H为两底的间距。

如果我们有一个等腰梯形，上底长为5cm，下底长为8cm，梯形的高为6cm，两底的间距为3cm。

我们可以将这些值代入等腰梯形的体积计算公式中计算体积，其计算过程如下：V = (5 + 8) * 6 * 3 / 2V = 13 * 6 * 3 / 2V = 78 * 3 / 2V = 234 / 2V = 117这个等腰梯形的体积为117立方厘米。

在实际生活中，等腰梯形的体积计算常常用于建筑、制造业和工程等领域。

在建筑工程中，工程师可能需要计算某建筑物的梯形部分的体积来确定材料的用量，或者在制造业中，生产工人可能需要计算某个零件的体积来确定其重量和成本。

等腰梯形的体积计算是一种常见的数学问题，使用立方计算公式可以很容易地找到等腰梯形的体积。

通过掌握这些知识，我们可以更好地应用数学理论于实际生活中的问题解决，提高我们的数学素养和解决问题的能力。

希望本文能对您了解等腰梯形的体积计算有所帮助。

第二篇示例：等腰梯形是指四边形的两个对边（底边和顶边）长度相等的梯形，通常我们也称之为等腰梯形。

等腰梯形在几何学中具有重要意义，它的体积计算可以帮助我们更好地理解空间的立体形状。

等腰梯形的性质及证明第一章：等腰梯形的定义及基本性质1.1 等腰梯形的定义引导学生复习梯形的定义，引入等腰梯形的概念。

通过实物模型或图形，让学生观察并理解等腰梯形的特征。

1.2 等腰梯形的边长关系引导学生观察等腰梯形的两条腰和底边的关系。

证明等腰梯形的两条腰长相等。

1.3 等腰梯形的对角线性质引导学生观察等腰梯形的对角线。

证明等腰梯形的对角线互相平分。

第二章：等腰梯形的内角性质2.1 等腰梯形的内角和引导学生复习四边形的内角和定理。

证明等腰梯形的内角和为360度。

2.2 等腰梯形的对角线与内角的关系引导学生观察等腰梯形的对角线与内角的关系。

证明等腰梯形的对角线与内角相等。

第三章：等腰梯形的对称性质3.1 等腰梯形的轴对称性引导学生复习轴对称性的概念。

证明等腰梯形具有轴对称性。

3.2 等腰梯形的中心对称性引导学生复习中心对称性的概念。

证明等腰梯形具有中心对称性。

第四章：等腰梯形的角平分线性质4.1 等腰梯形的角平分线定义引导学生复习角平分线的定义。

引入等腰梯形的角平分线概念。

4.2 等腰梯形的角平分线性质引导学生观察等腰梯形的角平分线。

证明等腰梯形的角平分线互相平分。

第五章：等腰梯形的应用5.1 等腰梯形的面积计算引导学生复习梯形的面积计算公式。

推导等腰梯形的面积计算公式。

5.2 等腰梯形的应用实例给出等腰梯形的实际应用题目。

引导学生运用等腰梯形的性质和证明结果解决实际问题。

第六章：等腰梯形的判定6.1 等腰梯形的判定条件引导学生复习四边形的判定条件。

引入等腰梯形的判定条件，即两条腰相等。

6.2 等腰梯形的判定方法给出等腰梯形的判定方法。

通过实际例子，让学生学会运用判定方法判断一个四边形是否为等腰梯形。

第七章：等腰梯形的相似性质7.1 等腰梯形的相似性质引导学生复习相似图形的性质。

引入等腰梯形的相似性质，即对应角相等，对应边成比例。

7.2 等腰梯形的相似证明给出等腰梯形的相似证明方法。

通过实际例子，让学生学会运用相似性质证明两个等腰梯形相似。

等腰梯形的面积计算与性质等腰梯形是一种具有特殊性质的四边形，其两边平行，并且两对邻边长度相等。

在本文中，我们将讨论等腰梯形的面积计算方法以及其性质。

一、等腰梯形的面积计算要计算等腰梯形的面积，我们需要知道其两条平行边的长度以及高的长度。

假设等腰梯形的上底长为a，下底长为b，高为h。

等腰梯形的面积计算公式如下：面积 = (上底 + 下底) ×高 ÷ 2根据这个公式，我们可以将a、b和h的值代入，计算出等腰梯形的面积。

例如，如果上底长为5cm，下底长为8cm，高为6cm，那么根据面积计算公式，我们可以进行如下计算：面积 = (5 + 8) × 6 ÷ 2= 13 × 6 ÷ 2= 78 ÷ 2= 39cm²所以，该等腰梯形的面积为39平方厘米。

二、等腰梯形的性质除了面积计算，等腰梯形还有其他一些特殊性质：1. 等腰梯形的对角线相等：等腰梯形的两条对角线长度相等。

这是因为等腰梯形具有对称性，两条边平行且长度相等，所以对角线也相等。

2. 等腰梯形的内角性质：等腰梯形的内角有一些特殊性质。

两个腰之间的内角相等，两个底之间的内角相等，且这两个内角的和等于180度。

3. 等腰梯形的高线性质：等腰梯形的高线被平分，即将等腰梯形分成两个全等的直角三角形。

4. 等腰梯形的周长：等腰梯形的周长等于上底、下底和两腰的长度之和。

即周长 = 上底 + 下底 + 2 ×腰长。

通过对等腰梯形的面积计算和性质的了解，我们可以更好地理解和应用等腰梯形。

无论是在几何学中还是实际生活中，等腰梯形都有其特殊的应用。

这些应用包括建筑设计、制作家具、计算地表面积等等。

总结：等腰梯形是一种具有特殊性质的四边形，其面积计算可以使用面积计算公式进行。

除了面积计算，等腰梯形还有一些特殊性质，如对角线相等、内角性质、高线性质和周长计算。

通过对等腰梯形的研究和应用，我们可以更好地理解和利用这个几何形状。

等腰梯形的性质及证明第一章：等腰梯形的定义及基本性质1.1 等腰梯形的定义引导学生回顾梯形的定义，引入等腰梯形的概念。

通过实物模型或图形，让学生观察和描述等腰梯形的特征。

1.2 等腰梯形的边长关系引导学生测量和记录等腰梯形的上底、下底和斜边的长度。

分析等腰梯形上底和下底的长度关系，引导学生发现等腰梯形的两底边相等。

1.3 等腰梯形的对角线性质引导学生测量和记录等腰梯形的对角线长度。

分析等腰梯形对角线的长度关系，引导学生发现等腰梯形的对角线相等。

第二章：等腰梯形的角性质2.1 等腰梯形的底角性质引导学生观察等腰梯形的底角，并测量和记录底角的大小。

分析等腰梯形底角的大小关系，引导学生发现等腰梯形的底角相等。

2.2 等腰梯形的顶角性质引导学生观察等腰梯形的顶角，并测量和记录顶角的大小。

分析等腰梯形顶角的大小关系，引导学生发现等腰梯形的顶角相等。

第三章：等腰梯形的对称性质3.1 等腰梯形的轴对称性质引导学生观察等腰梯形的对称性，并画出对称轴。

分析等腰梯形的轴对称性质，引导学生发现等腰梯形是轴对称图形。

3.2 等腰梯形的中心对称性质引导学生观察等腰梯形的对称性，并画出中心对称点。

分析等腰梯形的中心对称性质，引导学生发现等腰梯形是中心对称图形。

第四章：等腰梯形的判定4.1 等腰梯形的判定条件引导学生回顾梯形的定义，引入等腰梯形的判定条件。

通过实例和图形，让学生判断和验证等腰梯形的判定条件。

4.2 等腰梯形的判定定理引导学生学习和理解等腰梯形的判定定理。

通过证明和实例，让学生掌握和应用等腰梯形的判定定理。

第五章：等腰梯形的应用5.1 等腰梯形的面积计算引导学生学习和理解等腰梯形的面积计算公式。

通过实例和练习，让学生应用面积计算公式计算等腰梯形的面积。

5.2 等腰梯形的实际应用引导学生思考和讨论等腰梯形在实际生活中的应用。

通过实例和问题，让学生解决实际问题，并应用等腰梯形的性质和判定。

第六章：等腰梯形的构造与应用6.1 等腰梯形的构造方法介绍使用直尺和圆规构造等腰梯形的方法。

等腰梯形所具备的条件等腰梯形是一种特殊的梯形，它具备以下条件：1. 平行边相等：等腰梯形的上下底边是平行的，且长度相等。

这意味着梯形的两条平行边的长度是相等的。

2. 对角线相等：等腰梯形的两条对角线的长度相等。

对角线是连接梯形的非相邻顶点的线段，因此等腰梯形的两条对角线长度相等。

3. 对角线互相垂直：等腰梯形的两条对角线互相垂直。

这意味着两条对角线的交点是一个直角。

4. 两组相等的内角：等腰梯形的上底角和下底角相等，且左斜边角和右斜边角相等。

这意味着梯形的两组内角的度数是相等的。

等腰梯形是一个特殊的四边形，它具备上述条件。

这些条件使得等腰梯形具有一些独特的性质和特点。

等腰梯形的平行边长度相等，这意味着梯形的上下底边的长度是相等的。

这样的性质使得等腰梯形在建筑设计中具有一定的应用价值。

例如，我们常见的楼梯就是由等腰梯形组成的，通过调整梯形的大小和角度，可以设计出美观、稳定的楼梯结构。

等腰梯形的对角线长度相等，这意味着梯形的两条对角线的长度是相等的。

这个性质在几何证明中经常被使用。

例如，在证明两个三角形相似或全等时，我们可以利用等腰梯形的对角线相等性质来推导出结论。

等腰梯形的两条对角线互相垂直，这意味着两条对角线的交点是一个直角。

这个性质在解决一些几何问题时非常有用。

例如，在求解等腰梯形的面积时，我们可以利用对角线垂直的性质将梯形分解为两个直角三角形，从而简化计算过程。

等腰梯形的两组内角相等。

这个性质在解决一些几何问题时也非常有用。

例如，在证明两个三角形相似或全等时，我们可以利用等腰梯形的内角相等性质来推导出结论。

总结起来，等腰梯形具备平行边相等、对角线相等、对角线互相垂直和两组内角相等四个条件。

这些条件使得等腰梯形具有一些特殊的性质和特点，对于几何学的研究和应用具有重要意义。

通过研究和应用等腰梯形的性质，我们可以更好地理解和解决与梯形相关的问题。