TSP问题的遗传算法求解

用于求解TSP问题的遗传算法改进一、TSP问题简介TSP问题，全称Traveling Salesman Problem，即旅行商问题。

所谓TSP问题是指，给定一些点和每一对点之间的距离，求出一条遍历每个点恰好一次的最短路径，该问题的解决方法对实际问题中的路径规划和优化有着很大的参考价值。

二、遗传算法的基本思想遗传算法，是模拟自然界中生物遗传进化过程的一种演化计算方法。

它通过模拟生物的繁殖、变异、适应性等生命过程来寻找问题的最优解。

其基本的过程如下：1. 初始化：随机生成一个初始群体，每个个体表示一种可能的解决方案。

2. 选择：根据适应度函数，选择一定数量的优秀个体作为繁殖的父亲。

3. 交叉：将所选父亲进行交叉操作，生成新的子代个体。

4. 变异：对于一部分子代个体，进行变异操作。

5. 替换：用新的子代个体替换掉一部分原有的个体，形成新一代群体。

6. 结束条件：当某种条件达到时结束算法，否则返回步骤二。

在TSP问题中，遗传算法的基本实现方法如下：1.初始化：随机生成一个初始群体，每个个体表示一个解决方案，其中每个基因表示一个城市的编号。

例如，假设有10个城市，则每个个体就是由这10个城市编号随机排列组成的，例如：1-2-5-8-4-3-7-9-6-10等。

2.适应度函数：对于每个个体，计算其总路程，将总路程作为适应度函数的值。

4.交叉：将所选父亲进行交叉操作，生成新的子代个体，交叉方式一般有：顺序交叉法、部分映射交叉法、环形交叉法、边交叉法等。

5.变异：对于一部分子代个体，进行变异操作，变异的方式一般是：交换变异、倒位变异、随机抽样变异等。

7.结束条件：当达到一定条件时结束算法，比如迭代次数达到上限或者群体的适应度达到一定的水平。

传统的遗传算法在求解TSP问题时，存在一些问题：1.收敛速度慢：由于集合了交叉、变异等算子，每一代都要进行大量的计算，所以收敛速度慢。

2.易受陷入局部最优解：由于遗传算法采用的是局部搜索策略，所以可能会陷入到局部最优解中。

实验六：遗传算法求解TSP问题实验2篇第一篇：遗传算法的原理与实现1. 引言旅行商问题（TSP问题）是一个典型的组合优化问题，它要求在给定一组城市和每对城市之间的距离后，找到一条路径，使得旅行商能够在所有城市中恰好访问一次并回到起点，并且总旅行距离最短。

遗传算法作为一种生物启发式算法，在解决TSP问题中具有一定的优势。

本实验将运用遗传算法求解TSP问题，以此来探讨和研究遗传算法在优化问题上的应用。

2. 遗传算法的基本原理遗传算法是模拟自然界生物进化过程的一种优化算法。

其基本原理可以概括为：选择、交叉和变异。

（1）选择：根据问题的目标函数，以适应度函数来评估个体的优劣程度，并按照适应度值进行选择，优秀的个体被保留下来用于下一代。

（2）交叉：从选出的个体中随机选择两个个体，进行基因的交换，以产生新的个体。

交叉算子的选择及实现方式会对算法效果产生很大的影响。

（3）变异：对新生成的个体进行基因的变异操作，以保证算法的搜索能够足够广泛、全面。

通过选择、交叉和变异操作，不断迭代生成新一代的个体，遗传算法能够逐步优化解，并最终找到问题的全局最优解。

3. 实验设计与实施（1）问题定义：给定一组城市和每对城市之间的距离数据，要求找到一条路径，访问所有城市一次并回到起点，使得旅行距离最短。

（2）数据集准备：选择适当规模的城市数据集，包括城市坐标和每对城市之间的距离，用于验证遗传算法的性能。

（3）遗传算法的实现：根据遗传算法的基本原理，设计相应的选择、交叉和变异操作，确定适应度函数的定义，以及选择和优化参数的设置。

（4）实验流程：a. 初始化种群：随机生成初始种群，每个个体表示一种解（路径）。

b. 计算适应度：根据适应度函数，计算每个个体的适应度值。

c. 选择操作：根据适应度值选择一定数量的个体，作为下一代的父代。

d. 交叉操作：对父代进行交叉操作，生成新的个体。

e. 变异操作：对新生成的个体进行变异操作，以增加搜索的多样性。

利⽤遗传算法求解TSP问题⼀、摘要TSP问题是指给定平⾯上N个点及每点的坐标，求⼀条路径，遍历所有的点并回到起点，使这条路径长度最⼩。

TSP问题是⼀个组合优化问题。

该问题可以被证明具有NPC计算复杂性。

因此，任何能使该问题的求解得以简化的⽅法，都将受到⾼度的评价和关注。

遗传算法是⼈⼯智能⽅法的⼀种，⽤于求解各种传统⽅法不⽅便求解或耗时很长的问题。

下⾯给出遗传算法求解TSP问题的步骤。

在传统遗传算法求解TSP的基础上，提出了⼀种新的编码⽅式，并且讨论了⼀种优化⽅法的可⾏性。

本次实验的程序⾸先在matlab上验证了基本的算法，然⽽由于matlab运⾏较慢，故⼜移植到C++平台上，经过测试，实验结果良好。

⼆、算法实现遗传算法的实现主要包括编码、选择、交叉、编译、将个体放⼊新种群这么⼏个步骤，经过很多代的编译求解，以逼近最优解。

下⾯讨论每⼀个步骤的实现，其中编码⽅式是我在考虑了传统编码⽅式不利于计算的缺点下，重新设计的⼀种全新的编码⽅式。

编码在传统TSP问题中，编码可以直接采⽤⼆进制编码或⾃然编码的形式，⽐如直接把城市转化成（2,5,4,1,3,6）的形式，表⽰从2到5到4到1到3到6最后回到起点。

但是在求解TSP问题时，如果直接采⽤此种编码⽅式，会导致在交叉或变异时出现冲突的情况。

如（2,5,4,1,3,6）和（3,5,6,1,2,4）交换后变成了（2,5,6,1,2,6）和（3,5,4,1,3,4），显然路径出现了冲突的现象，传统的解决⽅式是通过逐步调整的⽅法来消除冲突，但是这种⽅法增加了编码的复杂度，不利于问题的求解，根据问题的特点，提出了采⽤⼀种插⼊序号的编码⽅式。

假设6个城市（1,2,3,4,5,6）现在有编码（1,1,2,2,1,3），让第n个编码表⽰n放在第⼏个空格处。

那么⽣成路径的规则是⾸先取1放在第⼀个（1），然后取2放在第⼀个空格处（2，1），然后取3放在第⼆个空格处（2,3,1），然后取4放在第⼆个空格处（2,4,3,1）然后取5放在第⼀个空格处（5,2,4,3,1）最后取6放在第3个空格处（5,2,6，4,3,1）。

TSP问题的遗传算法求解一、问题描述假设有一个旅行商人要拜访N个城市，要求他从一个城市出发，每个城市最多拜访一次，最后要回到出发的城市，保证所选择的路径长度最短。

二、算法描述（一）算法简介遗传算法（GeneticAlgorithm）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，通过模拟自然进化过程搜索最优解。

遗传算法是从代表问题可能潜在的解集的一个种群（population）开始的，初代种群产生之后，按照适者生存和优胜劣汰的原理，逐代（generation）演化产生出越来越好的近似解，在每一代，根据问题域中个体的适应度（fitness）大小选择个体，并借助于自然遗传学的遗传算子（geneticoperators）进行组合交叉（crossover）和变异（mutation），产生出代表新的解集的种群。

这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境，末代种群中的最优个体经过解码（decoding），可以作为问题近似最优解。

（摘自百度百科）。

（二）遗传算子遗传算法中有选择算子、交叉算子和变异算子。

选择算子用于在父代种群中选择进入下一代的个体。

交叉算子用于对种群中的个体两两进行交叉，有Partial-MappedCrossover、OrderCrossover、Position-basedCrossover等交叉算子。

变异算子用于对种群中的个体进行突变。

（三）算法步骤描述遗传算法的基本运算过程如下：1.初始化：设置进化代数计数器t=0、设置最大进化代数T、交叉概率、变异概率、随机生成M个个体作为初始种群P2.个体评价：计算种群P中各个个体的适应度3.选择运算：将选择算子作用于群体。

以个体适应度为基础，选择最优个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代4.交叉运算：在交叉概率的控制下，对群体中的个体两两进行交叉5.变异运算：在变异概率的控制下，对群体中的个体两两进行变异，即对某一个体的基因进行随机调整6.经过选择、交叉、变异运算之后得到下一代群体P1。

用遗传算法求解TSP问题遗传算法（Genetic Algorithm——GA），是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型，它是由美国Michigan大学的J。

Holland教授于1975年首先提出的。

J.Holland 教授和它的研究小组围绕遗传算法进行研究的宗旨有两个：抽取和解释自然系统的自适应过程以及设计具有自然系统机理的人工系统。

遗传算法的大致过程是这样的:将每个可能的解看作是群体中的一个个体或染色体，并将每个个体编码成字符串的形式，根据预定的目标函数对每个个体进行评价,即给出一个适应度值。

开始时,总是随机的产生一些个体，根据这些个体的适应度，利用遗传算子-—选择（Selection）、交叉（Crossover)、变异（Mutation)对它们重新组合，得到一群新的个体.这一群新的个体由于继承了上一代的一些优良特性，明显优于上一代，以逐步向着更优解的方向进化.遗传算法主要的特点在于：简单、通用、鲁棒性强。

经过二十多年的发展，遗传算法已经在旅行商问题、生产调度、函数优化、机器学习等领域得到成功的应用。

遗传算法是一类可用于复杂系统优化的具有鲁棒性的搜索算法，与传统的优化算法相比,主要有以下特点：1、遗传算法以决策变量的编码作为运算对象.传统的优化算法往往直接决策变量的实际植本身,而遗传算法处理决策变量的某种编码形式，使得我们可以借鉴生物学中的染色体和基因的概念，可以模仿自然界生物的遗传和进化机理，也使得我们能够方便的应用遗传操作算子.2、遗传算法直接以适应度作为搜索信息，无需导数等其它辅助信息。

3、遗传算法使用多个点的搜索信息,具有隐含并行性。

4、遗传算法使用概率搜索技术，而非确定性规则。

遗传算法是基于生物学的,理解或编程都不太难。

下面是遗传算法的一般算法步骤:1、创建一个随机的初始状态初始种群是从解中随机选择出来的，将这些解比喻为染色体或基因，该种群被称为第一代，这和符号人工智能系统的情况不一样;在那里,问题的初始状态已经给定了。

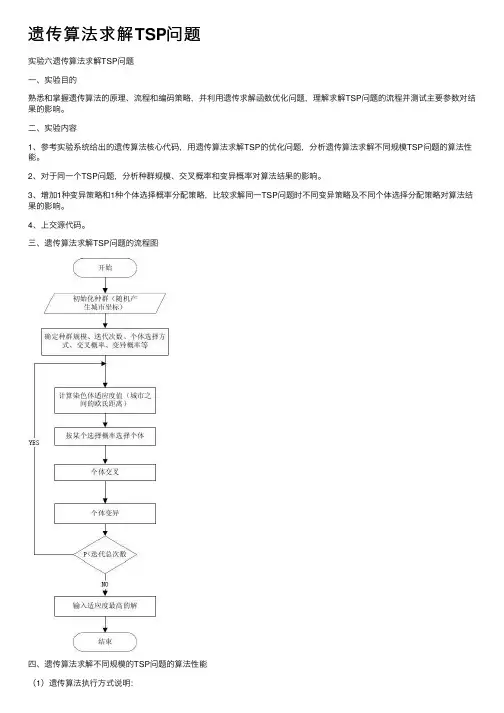
遗传算法求解TSP问题实验六遗传算法求解TSP问题⼀、实验⽬的熟悉和掌握遗传算法的原理、流程和编码策略，并利⽤遗传求解函数优化问题，理解求解TSP问题的流程并测试主要参数对结果的影响。

⼆、实验内容1、参考实验系统给出的遗传算法核⼼代码，⽤遗传算法求解TSP的优化问题，分析遗传算法求解不同规模TSP问题的算法性能。

2、对于同⼀个TSP问题，分析种群规模、交叉概率和变异概率对算法结果的影响。

3、增加1种变异策略和1种个体选择概率分配策略，⽐较求解同⼀TSP问题时不同变异策略及不同个体选择分配策略对算法结果的影响。

4、上交源代码。

三、遗传算法求解TSP问题的流程图四、遗传算法求解不同规模的TSP问题的算法性能（1）遗传算法执⾏⽅式说明：适应度值计算⽅法：当前路线的路径长度●个体选择概率分配⽅法：适应度⽐例⽅法●选择个体⽅法：轮盘赌选择●交叉类型：PMX交叉●变异类型: 两点互换变异（2）实验模拟结果：图1-1（3）分析由图1-1可知，遗传算法执⾏时间随着TSP问题规模的增⼤⽽增⼤，并且⼤致为线性增长。

五、不同参数下的计算结果对⽐最⼤迭代步数:100交叉概率：0.85变异概率：0.15如表1-1或3-1-0-9-2-4-8-5-7-6，注意到这是⼀圈，顺时针或者逆时针都可以。

当种群规模为10，20时，并没有找到最优解。

（2）交叉概率对算法结果的影响实验次数：15种群规模：25最⼤迭代步数:100变异概率：0.15实验结果：在该情况下，交叉概率过低将使搜索陷⼊迟钝状态，得不到最优解。

种群规模：25最⼤迭代步数:100交叉概率：0.85实验结果：⼜表1-3可知，当变异概率过⼤或过低都将导致⽆法得到最优解。

注：（2）（3）的实验数据与（1）的实验数据不同，详见附录。

六、不同变异策略和个体选择概率分配策略对算法结果的影响（1）两点互换变异与插⼊变异的⽐较：●试验次数（CASNUM）：10●城市数(POINTCNT):10●种群规模(POPSIZE)：100●最⼤迭代步数(GENERATIONS):100●交叉概率(PC)：0.85●变异概率(PM):0.15●选择个体⽅法：轮盘赌选择●交叉类型：PMX交叉●个体选择概率分配⽅法：适应度⽐例⽅法a.变异类型: 两点互换变异b.变异类型: 插⼊变异分析：两点互换变异20次模拟中，4次得到⾮最优解；⽽插⼊变异只有2次；插⼊变异的最好适应度平均值⽐两点互换变异⼩0.14755，最差适应度平均值和总的适应度平均值都⽐两点互换下，并且在Release下，运⾏时间前者⽐后者快218.3ms。

一、旅行商问题所谓旅行商问题(Travelling Salesman Problem , TSP)，即最短路径问题，就是在给定的起始点S到终止点T的通路集合中，寻求距离最小的通路，这样的通路成为S点到T点的最短路径。

在寻找最短路径问题上，有时不仅要知道两个指定顶点间的最短路径，还需要知道某个顶点到其他任意顶点间的最短路径。

遗传算法方法的本质是处理复杂问题的一种鲁棒性强的启发性随机搜索算法，用遗传算法解决这类问题，没有太多的约束条件和有关解的限制，因而可以很快地求出任意两点间的最短路径以及一批次短路径。

假设平面上有n个点代表n个城市的位置, 寻找一条最短的闭合路径, 使得可以遍历每一个城市恰好一次。

这就是旅行商问题。

旅行商的路线可以看作是对n 个城市所设计的一个环形, 或者是对一列n个城市的排列。

由于对n个城市所有可能的遍历数目可达(n- 1)!个, 因此解决这个问题需要0(n!)的计算时间。

假设每个城市和其他任一城市之间都以欧氏距离直接相连。

也就是说, 城市间距可以满足三角不等式, 也就意味着任何两座城市之间的直接距离都小于两城市之间的间接距离。

二、遗传算法1 遗传算法介绍遗传算法是由美国J.Holland教授于1975年在他的专著《自然界和人工系统的适应性》中首先提出的，它是一类借鉴生物界自然选择和自然遗传机制的随机化搜索算法。

通过模拟自然选择和自然遗传过程中发生的繁殖、交叉和基因突变现象，在每次迭代中都保留一组候选解，并按某种指标从解群中选取较优的个体，利用遗传算子(选择、交叉和变异)对这些个体进行组合，产生新一代的候选解群，重复此过程，直到满足某种收敛指标为止。

遗传算法在本质上是一种不依赖具体问题的直接搜索方法，是一种求解问题的高效并行全局搜索方法。

其假设常描述为二进制位串，位串的含义依赖于具体应用。

搜索合适的假设从若干初始假设的群体集合开始。

当前种群成员通过模仿生物进化的方式来产生下一代群体，如随机变异和交叉。

遗传算法解决TSP问题姓名:学号:专业:问题描叙TSP问题即路径最短路径问题，从任意起点出发（或者固定起点），依次经过所有城市，一个城市只能进入和出去一次，所有城市必须经过一次，经过终点再到起点，从中寻找距离最短的通路。

通过距离矩阵可以得到城市之间的相互距离，从距离矩阵中的到距离最短路径，解决TSP问题的算法很多，如模拟退火算法，禁忌搜索算法，遗传算法等等，每个算法都有自己的优缺点，遗传算法收敛性好，计算时间少，但是得到的是次优解，得不到最有解。

算法设计遗传算法属于进化算法的一种，它通过模仿自然界的选择与遗传的机理来寻找最优解.遗传算法有三个基本算子：选择、交叉和变异。

数值方法求解这一问题的主要手段是迭代运算。

一般的迭代方法容易陷入局部极小的陷阱而出现"死循环"现象，使迭代无法进行。

遗传算法很好地克服了这个缺点，是一种全局优化算法。

生物在漫长的进化过程中，从低等生物一直发展到高等生物，可以说是一个绝妙的优化过程。

这是自然环境选择的结果。

人们研究生物进化现象，总结出进化过程包括复制、杂交、变异、竞争和选择。

一些学者从生物遗传、进化的过程得到启发，提出了遗传算法。

算法中称遗传的生物体为个体，个体对环境的适应程度用适应值（fitness）表示。

适应值取决于个体的染色体，在算法中染色体常用一串数字表示，数字串中的一位对应一个基因。

一定数量的个体组成一个群体。

对所有个体进行选择、交叉和变异等操作，生成新的群体，称为新一代遗传算法计算程序的流程可以表示如下：第一步准备工作（1）选择合适的编码方案，将变量（特征）转换为染色体（数字串，串长为m）。

通常用二进制编码。

（2）选择合适的参数，包括群体大小（个体数M ）、交叉概率PC和变异概率Pm。

（3）确定适应值函数f （x）。

f（x）应为正值。

第二步形成一个初始群体（含M个个体）。

在边坡滑裂面搜索问题中，取已分析的可能滑裂面组作为初始群体。

第三步对每一染色体（串）计算其适应值fi，同时计算群体的总适应值。

用遗传算法解决TSP问题设计思路：1.初始化城市距离采用以城市编号（i,j=1代表北京，=2代表上海，=3代表天津，=4代表重庆，=5代表乌鲁木齐）为矩阵行列标的方法，输入任意两个城市之间的距离，用矩阵city表示，矩阵中的元素city(i,j)代表第i个城市与第j个城市间的距离。

2.初始化种群通过randperm函数，生成一个一维随机向量（是整数1，2，3，4，5的任意排列），然后将其赋给二维数组group的第一列，作为一个个体。

如此循环N次（本例生成了50个个体），生成了第一代种群，种群的每个个体代表一条路径。

3.计算适应度采用的适应度函数为个体巡回路径的总长度的函数。

具体为adapt(1,i)=(5*maxdis-dis) (1) 在式（1）中，adapt(1,i)表示第i个个体的适应度函数，maxdis为城市间的最大距离，为4077km,dis为个体巡回路径的总长度，这样定义的适应度，当路经越短时适应度值越大。

在适应度值的基础上，给出的计算个体期望复制数的表达式为adaptnum(1,i)=(N* adapt(1,i)/ sumadapt) (2) 其中，sumadapt为种群适应度之和。

4.复制采用优秀个体的大比例保护基础上的随机数复制法。

具体做法为在生成下一代个体时，先将最大适应度对应的路径个体以较大的比例复制到下一代，然后再用随机数复制法生成下一代的其他个体。

其中，有一个问题必须考虑，即若某一次生成的随机数过大，结果能复制一个或极少个样本。

为了避免这一情况，采用了限制措施，即压低了随机数的上限。

5.交叉采用的方法为按步长的单点交叉，为随机选择一对样本，再随机选择一个交叉点位置，按一定的步长进行交叉点的选择。

选择一个步长而不是将其设为1，是因为若某一位置处的城市代码因为进行了交叉而发生了改变，则其经过该处的两个距离都会改变。

这种交叉兼有遗传和变异两方面的作用，因为若交叉点处的城市编号都相同，则对两个个体而言交叉后样本无变化，否则样本有变化。

遗传算法解决旅行商(TSP)问题旅行商问题(traveling saleman problem,简称tsp)：已知N个城市之间的相互距离，现有一个推销员必须遍访这n个城市，并且每个城市只能访问一次，最后又必须返回出发城市。

如何安排他对这些城市的访问次序，可使其旅行路线的总长度最短？本程序使用MATLAB软件，利用遗传算法解决TSP问题。

程序使用如下：gatsp 为主程序，cityNum为城市个数，在此程序中可以设置为30、50和70。

Inn是种群个数，gnmax是最大迭代次数，pc是交叉概率，pm是变异概率。

算法程序运行结果如下：算法程序如下（不同的function需放在不同的.m文件中）：注：红色部分不属于算法内容，仅作间隔标致。

-------------------------------------------------------------------------------------------------------%主程序：%遗传算法求解tspfunction gaTSPCityNum=30;[dislist,Clist]=tsp(CityNum);inn=100; %初始种群大小gnmax=1000; %最大代数pc=0.9; %交叉概率pm=0.08; %变异概率%产生初始种群for i=1:inns(i,:)=randperm(CityNum);end[f,p]=objf(s,dislist);gn=1;while gn<gnmax+1for j=1:2:innseln=sel(s,p); %选择操作scro=cro(s,seln,pc); %交叉操作scnew(j,:)=scro(1,:);scnew(j+1,:)=scro(2,:);smnew(j,:)=mut(scnew(j,:),pm); %变异操作smnew(j+1,:)=mut(scnew(j+1,:),pm);ends=smnew; %产生了新的种群[f,p]=objf(s,dislist); %计算新种群的适应度%记录当前代最好和平均的适应度[fmax,nmax]=max(f);ymean(gn)=1000/mean(f);ymax(gn)=1000/fmax;%记录当前代的最佳个体x=s(nmax,:);drawTSP(Clist,x,ymax(gn),gn,0);gn=gn+1;%pause;endgn=gn-1;figure(2);plot(ymax,'r'); hold on;plot(ymean,'b');grid;title('搜索过程');legend('最优解','平均解');string1=['最终度',num2str(ymax(gn))];gtext(string1);End----------------------------------------------------------------- %交叉程序：function scro=cro(s,seln,pc);bn=size(s,2);pcc=pro(pc); %根据交叉概率决定是否进行交叉操作，1则是，0则否scro(1,:)=s(seln(1),:);scro(2,:)=s(seln(2),:);if pcc==1c1=round(rand*(bn-2))+1; %在[1,bn-1]范围内随机产生一个交叉位c2=round(rand*(bn-2))+1;chb1=min(c1,c2);chb2=max(c1,c2);middle=scro(1,chb1+1:chb2);scro(1,chb1+1:chb2)=scro(2,chb1+1:chb2);scro(2,chb1+1:chb2)=middle;for i=1:chb1while find(scro(1,chb1+1:chb2)==scro(1,i))zhi=find(scro(1,chb1+1:chb2)==scro(1,i));y=scro(2,chb1+zhi);scro(1,i)=y;endwhile find(scro(2,chb1+1:chb2)==scro(2,i))zhi=find(scro(2,chb1+1:chb2)==scro(2,i));y=scro(1,chb1+zhi);scro(2,i)=y;endendfor i=chb2+1:bnwhile find(scro(1,1:chb2)==scro(1,i))zhi=find(scro(1,1:chb2)==scro(1,i));y=scro(2,zhi);scro(1,i)=y;endwhile find(scro(2,1:chb2)==scro(2,i))zhi=find(scro(2,1:chb2)==scro(2,i));y=scro(1,zhi);scro(2,i)=y;endendendEnd----------------------------------------------------------------- %变异程序：function snnew=mut(snew,pm);bn=size(snew,2);snnew=snew;pmm=pro(pm); %根据变异概率决定是否进行变异操作，1则是，0则否if pmm==1c1=round(rand*(bn-2))+1; %在[1,bn-1]范围内随机产生一个变异位c2=round(rand*(bn-2))+1;chb1=min(c1,c2);chb2=max(c1,c2);x=snew(chb1+1:chb2);snnew(chb1+1:chb2)=fliplr(x);endend----------------------------------------------------------------- %适应度计算：function [f,p]=objf(s,dislist);inn=size(s,1); %读取种群大小for i=1:innf(i)=caldist(dislist,s(i,:)); %计算函数值，即适应度endf=1000./f';%计算选择概率fsum=0;for i=1:innfsum=fsum+f(i)^15;endfor i=1:innps(i)=f(i)^15/fsum;end%计算累积概率p(1)=ps(1);for i=2:innp(i)=p(i-1)+ps(i);endp=p';end----------------------------------------------------------------- %选着个体程序：function seln=sel(s,p);inn=size(p,1);%从种群中选择两个个体for i=1:2r=rand; %产生一个随机数prand=p-r;j=1;while prand(j)<0j=j+1;endseln(i)=j; %选中个体的序号endend-----------------------------------------------------------------%城市坐标：function [DLn,cityn]=tsp(n)if n==10city10=[0.4 0.4439;0.2439 0.1463;0.1707 0.2293;0.2293 0.761;0.5171 0.9414;0.8732 0.6536;0.6878 0.5219;0.8488 0.3609;0.6683 0.2536;0.6195 0.2634];%10 cities d'=2.691for i=1:10for j=1:10DL10(i,j)=((city10(i,1)-city10(j,1))^2+(city10(i,2)-city10(j,2))^ 2)^0.5;endendDLn=DL10;cityn=city10;endif n==30city30=[41 94;37 84;54 67;25 62;7 64;2 99;68 58;71 44;54 62;83 69;64 60;18 54;22 60;83 46;91 38;25 38;24 42;58 69;71 71;74 78;87 76;18 40;13 40;82 7;62 32;58 35;45 21;41 26;44 35;4 50];%30 cities d'=423.741 by D B Fogelfor i=1:30for j=1:30DL30(i,j)=((city30(i,1)-city30(j,1))^2+(city30(i,2)-city30(j,2))^ 2)^0.5;endendDLn=DL30;cityn=city30;endif n==50city50=[31 32;32 39;40 30;37 69;27 68;37 52;38 46;31 62;30 48;21 47;25 55;16 57;17 63;42 41;17 33;25 32;5 64;8 52;12 42;7 38;5 25; 10 77;45 35;42 57;32 22;27 23;56 37;52 41;49 49;58 48;57 58;39 10;46 10;59 15;51 21;48 28;52 33;58 27;61 33;62 63;20 26;5 6;13 13;21 10;30 15;36 16;62 42;6369;52 64;43 67];%50 cities d'=427.855 by D B Fogelfor i=1:50for j=1:50DL50(i,j)=((city50(i,1)-city50(j,1))^2+(city50(i,2)-city50(j,2))^ 2)^0.5;endendDLn=DL50;cityn=city50;endif n==75city75=[48 21;52 26;55 50;50 50;41 46;51 42;55 45;38 33;33 34;45 35;40 37;50 30;55 34;54 38;26 13;15 5;21 48;29 39;33 44;15 19;16 19;12 17;50 40;22 53;21 36;20 30;26 29;40 20;36 26;62 48;67 41;62 35;65 27;62 24;55 20;35 51;30 50;45 42;21 45;36 6;6 25;11 28;26 59;30 60;22 22;27 24;30 20;35 16;54 10;50 15;44 13;35 60;40 60;40 66;31 76;47 66;50 70;57 72;55 65;2 38;7 43;9 56;15 56;10 70;17 64;55 57;62 57;70 64;64 4;59 5;50 4;60 15;66 14;66 8;43 26];%75 cities d'=549.18 by D B Fogelfor i=1:75for j=1:75DL75(i,j)=((city75(i,1)-city75(j,1))^2+(city75(i,2)-city75(j,2))^ 2)^0.5;endendDLn=DL75;cityn=city75;endend----------------------------------------------------------------- %根据交叉概率决定是否进行交叉操作：function pcc=pro(pc);test(1:100)=0;l=round(100*pc);test(1:l)=1;n=round(rand*99)+1;pcc=test(n);end----------------------------------------------------------------- %计算城市距离矩阵：function F=caldist(dislist,s)distan=0;n=size(s,2);for i=1:n-1distan=distan+dislist(s(i),s(i+1));enddistan=distan+dislist(s(n),s(1));F=distan;----------------------------------------------------------------- %作图：function m=drawTSP(Clist,BSF,bsf,p,f)CityNum=size(Clist,1);for i=1:CityNum-1plot([Clist(BSF(i),1),Clist(BSF(i+1),1)],[Clist(BSF(i),2),Clist(B SF(i+1),2)],'ms-','LineWidth',2,'MarkerEdgeColor','k','MarkerFace Color','g');hold on;endplot([Clist(BSF(CityNum),1),Clist(BSF(1),1)],[Clist(BSF(CityNum), 2),Clist(BSF(1),2)],'ms-','LineWidth',2,'MarkerEdgeColor','k','Ma rkerFaceColor','g');title([num2str(CityNum),'城市TSP']);if f==0text(1.5,1.5,['第',int2str(p),' 步',' 最短距离为',num2str(bsf)]);elsetext(1,1,['最终搜索结果：最短距离 ',num2str(bsf)]);endhold off;pause(0.05)-----------------------------------------------------------------。

基于遗传算法求解TSP问题班级, 学号, 姓名摘要: 巡回旅行商问题（TSP）是一种组合优化方面旳问题, 从理论上讲, 使用穷举法不仅可以求解TSP问题, 并且还可以得到最优解。

不过, 运用穷举法所花费旳时间巨大旳, 当问题旳规模很大时, 穷举法旳执行效率较低, 不能满足及时旳需要。

遗传算法是计算机科学人工智能领域中用于处理最优化旳一种搜索启发式算法, 是进化算法旳一种。

该算法通过模拟生物学交叉、变异等方式, 是目前向最优解旳方向进化, 因此使用于TSP问题旳求解。

关键词: 人工智能；TSP问题；遗传算法本组组员: 林志青, 韩会雯, 赵昊罡本人分工：掌握遗传算法旳基本原理, 编写遗传算法中部分匹配交叉、循环交叉和循序交叉旳详细实现过程。

1 引言旅行商问题, 即TSP问题, 是一种最优解旳求解问题。

假设有n个都市, 并且每个都市之间旳距离已知, 则怎样只走一遍并获得最短途径为该问题旳详细解释。

对于TSP问题旳处理, 有穷举法、分支限界法等求解方式, 该文章重要简介遗传算法求解过程。

遗传算法简称GA, 在本质上是一种求解问题旳高效并行全局搜索措施。

遗传算法从任意一种初始化旳群体出发, 通过随机选择、交叉和变异等遗传操作, 使群体一代一代旳进化到搜索空间中越来越好旳区域, 直至抵达最优解。

在遗传算法中, 交叉操作为重要操作之一, 包括部分匹配交叉、循环交叉和次序交叉等。

2 算法原理与系统设计执行遗传算法, 根据需要设定对应旳交叉因子、变异因子和迭代次数, 并选择对应旳交叉算法,当程序图形显示并运算时会得到目前旳最优解, 判断与否获得最终旳最优解, 若已得到所需成果, 则停止运行, 否则继续执行。

详细流程图如下所示:部分匹配交叉（PMX）: 先随机生成两个交叉点, 定义这两点间旳区域为匹配区域, 并互换两个父代旳匹配区域。

如下图所示:父代A: 872 | 130 | 9546父代B: 983 | 567 | 1420互换后变为:temp A: 872 | 567 | 9546temp B: 983 | 130 | 1420对于 temp A.tempB中匹配区域以外出现旳数码反复, 要根据匹配区域内旳位置逐一进行替代。

TSP、MTSP问题遗传算法详细解读及python实现写在前⾯遗传算法是⼀种求解NPC问题的启发式算法，属于仿⽣进化算法族的⼀员。

仿⽣进化算法是受⽣物⾏为启发⽽发明的智能优化算法，往往是⼈们发现某种⽣物的个体虽然⾏为较为简单，但⽣物集群通过某种原理却能表现出智能⾏为。

于是不同的⼈研究不同的⽣物⾏为原理，受到启发⽽发明出新的仿⽣进化算法。

⽐如免疫优化算法，蚁群算法，模拟退⽕算法等，这些算法以后也会简单介绍。

本⽂的主题是遗传算法，该算法也是受到⽣物⾏为启发。

物竞天择，适者⽣存，优胜劣汰，是该优化算法的核⼼思想。

笔者在业务中需要⽤到遗传算法求解TSP问题，但是⽹上能查找到的资料对遗传算法的讲解不够通俗易懂，往往上来就是遗传变异交叉，对于我这样的初学者来说有点不知所云，于是不得不直接看源码，⼀⾏⼀⾏地理解代码的意思，才弄懂了原理。

这种⽅法对于初学者和编程基础薄弱者颇为困难，⽽且费时费⼒，苦不堪⾔。

同时，由于读者可能熟练掌握的是不同的语⾔，因此若代码是某⼀种语⾔编写的，那么掌握其他语⾔的读者很可能难以吸收，浪费了资源。

此外，⽹上关于TSP问题的资料很多，但是关于MTSP问题的资料却凤⽑麟⾓。

因此有了创作本⽂的意图，旨在⽤最通俗详尽的语⾔深⼊浅出地解释遗传算法解TSP、MTSP问题的原理及应⽤遗传算法解TSP问题原理⼀、TSP问题旅⾏商问题，即TSP问题（Traveling Salesman Problem）⼜译为旅⾏推销员问题、货郎担问题，是数学领域中著名问题之⼀。

假设有⼀个旅⾏商⼈要拜访n个城市，他必须选择所要⾛的路径，路径的限制是每个城市只能拜访⼀次，⽽且最后要回到原来出发的城市。

路径的选择⽬标是要求得的路径路程为所有路径之中的最⼩值。

想要求解出TSP问题的最优解，⽬前唯⼀的⽅法是穷举出所有的路径。

然⽽，路径的数量级是n!，也就是⽬标点数量的阶乘。

当n为14时，n!已经⼤于800亿。

当n更⼤，为30，40 时，更是天⽂数字，即使计算机⼀秒钟计算⼀亿次，其求解时间也远⼤于我们的寿命。

遗传算法解决旅⾏商问题（TSP）这次的⽂章是以⼀份报告的形式贴上来，代码只是简单实现，难免有漏洞，⽐如循环输⼊的控制条件，说是要求输⼊1，只要输⼊⾮0就⾏。

希望会帮到以后的同学(*＾-＾*)⼀、问题描述旅⾏商问题(Traveling-Salesman Problem,TSP)。

设有n个互相可直达的城市，某推销商准备从其中的A城出发，周游各城市⼀遍，最后⼜回到A城。

要求为该旅⾏商规划⼀条最短的旅⾏路线。

⼆、⽬的为了解决旅⾏商问题，⽤了遗传算法，模拟染⾊体的遗传过程，进⾏求解。

为了直观的更有⽐较性的观察到程序的运⾏效果，我这⾥程序⾥给定了10个城市的坐标，并计算出其任意两个的欧⽒距离，10个点的位置排布见图1。

程序的理想最优距离为20.485281，即绕三⾓形⼀圈，⽽且路程起点不固定，因为只要满⾜点围着三⾓形⼀圈即为最短距离，最优解。

所以问题转换为，求图中10 个点的不重复点的闭环序列的距离最⼩值。

图 1三、原理1、内部变量介绍程序总体围绕了遗传算法的三个主要步骤：选择--复制，交叉，变异。

给定了10个种群，即10条染⾊体，每条染⾊体都是除⾸位外不重复的点组成，⾸尾相同保证路线是闭合的，所以⼀条染⾊体包含11个点。

种群由⼀个结构体group表⽰，内含城市的序列int city[11]、种群的适应度double fit、该种群适应度占总群体适应度的⽐例double p，和为了应⽤赌轮选择机制的积累概率 double jlleigailv。

程序还包括⼀个始终记录所有种群中的最优解的城市序列数组groupbest[11]，记录最优解的适应度，即最⼤适应度的变量 double groupbestfit。

种群的最⼤繁衍代数设置为1000，⽤户能够输⼊繁衍代数，但必须在1000以内。

10个点的不同排列序列有10！种，即3628800中排列可能，其中各代之间可能产⽣重复，不同种群间也会出现重复，学⽣觉得1000左右应该能验证程序的性能了，就定为1000。

遗传算法求解TSP问题1、遗传算法前⼀篇遗传算法的基本内容在之前的博客已经应⽤过了之前遗传算法解决的是函数优化问题，即求解最⼤值或最⼩值问题；此次要解决的是组合优化问题中的TSP问题，即旅⾏商问题。

这边先介绍⼀下TSP问题TSP问题（Traveling Salesman Problem），即旅⾏商问题，⼜译为旅⾏推销员问题、货郎担问题，是数学领域中著名问题之⼀。

假设有⼀个旅⾏商⼈要拜访n个城市，他必须选择所要⾛的路径，路径的限制是每个城市只能拜访⼀次，⽽且最后要回到原来出发的城市。

路径的选择⽬标是要求得的路径路程为所有路径之中的最⼩值。

简单地说，TSP问题就是要找到图中的最短哈密尔顿回路，即全局最短路径。

然后遗传算法可以模仿⽣物进化，然后可以找到⼀个近似最优解，但其不⼀定是全局最优解。

2、实验原理1）产⽣初始种群；随机⽣成N个个体作为初始群体popm，随机选择⼀个种群；2）适应度函数；个体评价计算P（t）中各个个体的适应度，遗传算法在进化搜索中基本不利⽤外部信息,仅以适应度函数为依据,利⽤种群中每个个体的适应度值来进⾏搜索。

TSP的⽬标是路径总长度为最短3）选择运算；将使适应度较⼤(优良)个体有较⼤的存在机会，⽽适应度较⼩（低劣）的个体继续存在的机会也较⼩。

简单遗传算法采⽤赌轮选择机制4）交叉运算将交叉算⼦作⽤于群体；5）变异运算将变异算⼦作⽤于群体，并通过以上运算得到下⼀代群体P（t + 1）;6）终⽌条件输出解。

3、代码实现1.city.m：随机⽣成N个城市的坐标并保存2.plot_route.m：实现连点画图3.染⾊体的路程代价函数 mylength.m4.适应度函数fit.m5.交叉操作函数 cross.m6.变异函数 Mutation.m7.main函数3、结果分析调整参数并分析运⾏结果（1）对于city_25.mat⽂件中的城市序列，参数ITER=2000，m=2，Pc=0.8，Pm=0.05保持不变，调整种群个数M的值，观察其结果变化：M=50M=100M=500由运⾏结果可知当M=100时得到TSP的最短路径长度均⼩于M=50和M=500运⾏得出的最短路径长度。