17章部分习题解答

第17章勾股定理一．选择题（共10小题）1．已知Rt△ABC的三边分别为a、b、c，则下列结论不可能成立的是（）A．a2﹣b2＝c2B．∠A﹣∠B＝∠CC．∠A：∠B：∠C＝3：4：5 D．a：b：c＝7：24：252．有一个面积为1的正方形，经过一次“生长”后，在他的左右肩上生出两个小正方形，其中，三个正方形围成的三角形是直角三角形，再经过一次“生长”后，变成了下图，如果继续“生长”下去，它将变得“枝繁叶茂”，请你算出“生长”了2019次后形成的图形中所有的正方形的面积和是（）A．1 B．2018 C．2019 D．20203．如图，网格中每个小正方形的边长均为1，点A，B，C都在格点上，以A为圆心，AB为半径画弧，交最上方的网格线于点D，则CD的长为（）A．B．0.8 C．3﹣D．4．如图△ABC中，∠D＝90°，C是BD上一点，已知CB＝9，AB＝17，AD＝8，则DC的长是（）A．8 B．9 C．6 D．155．下列说法中，正确的个数有（）①已知直角三角形的面积为2，两直角边的比为1：2，则斜边长为；②直角三角形的最大边长为，最短边长为1，则另一边长为；③在△ABC中，若∠A：∠B：∠C＝1：5：6，则△ABC为直角三角形；④等腰三角形面积为12，底边上的高为4，则腰长为5．A．1个B．2个C．3个D．4个6．我国是最早了解勾股定理的国家之一．下面四幅图中，不能证明勾股定理的是（）A．B．C．D．7．如图，四边形ABCD中，∠ABC＝90°，AC＝BD，AC⊥BD，若AB＝4，AD＝5，则DC的长（）A．7 B．C．D．28．如图，某公司举行周年庆典，准备在门口长25米，高7米的台阶上铺设红地毯，已知台阶的宽为3米，则共需购买（）m2的红地毯．A．21 B．75 C．93 D．969．如图，某同学在做物理实验时，将一支细玻璃棒斜放入了一只盛满水的烧杯中，已知烧杯高8cm，玻璃棒被水淹没部分长10cm，这只烧杯的直径约是（）A．9cm B．8cm C．7cm D．6cm10．如图，公路AC，BC互相垂直，公路AB的中点M与点C被湖隔开，若测得AC＝12km，BC＝16km，则M，C两点之间的距离为（）A．13km B．12km C．11km D．10km二．填空题（共5小题）11．现有两根木棒的长度分别是40cm和50cm，若要钉成一个三角形木架，其中有一个角为直角，则所需木棒的最短长度为．12．已知一个三角形的三条边的长分别为、和，那么这个三角形的最大内角的大小为度．13．如图所示的网格是正方形网格，△ABC和△CDE的顶点都是网格线交点，那么∠BAC+∠CDE＝°．14．如图，在△ABC中，AB＝5，AC＝13，BC边上的中线AD＝6，则△ABD的面积是．15．如图，在△ABC中，AC＝BC＝13，AB＝24，D是AB边上的一个动点，点E与点A关于直线CD对称，当△ADE为直角三角形时，则AD的长为．三．解答题（共6小题）16．如图，正方形网格的每个小方格都是边长为1的正方形，△ABC的顶点都在格点上．（1）分别求出AB，BC，AC的长；（2）试判断△ABC是什么三角形，并说明理由．17．如图，是一个长8m，宽6m，高5m的仓库，在其内壁的A（长的四等分点）处有一只壁虎，B（宽的三等分点）处有一只蚊子，则壁虎爬到蚊子处的最短距离为多少米．18．如图，A、B两点都与平面镜相距4米，且A、B两点相距6米，一束光线由A射向平面镜反射之后恰巧经过B点，求B点到入射点的距离．19．如图，在正方形ABCD中，E是边AD的中点，点F在边DC上，且DF＝DC．试判断△BEF的形状，并说明理由．20．如图，已知∠ADC＝90°，AD＝8，CD＝6，AB＝26，BC＝24．（1）证明：△ABC是直角三角形．（2）请求图中阴影部分的面积．21．如图，在Rt△ABC中，AB＝3，BC＝4，动点P从点A出发沿AC向终点C运动，同时动点Q从点B出发沿BA向点A运动，到达A点后立刻以原来的速度沿AB返回．点P，Q 的运动速度均为每秒1个单位长度，当点P到达点C时停止运动，点Q也同时停止运动，连接PQ，设它们的运动时间为t（t＞0）秒．（1）设△CBQ的面积为S，请用含有t的代数式来表示S；（2）线段PQ的垂直平分线记为直线l，当直线l经过点C时，求AQ的长．参考答案一．选择题（共10小题）1．C．2．D．3．C．4．C．5．D．6．D．7．B．8．C．9．D．10．D．二．填空题（共5小题）11．30cm．12．9013．45°．14．15．15．17．三．解答题（共6小题）16．（1），，；（2）△ABC是直角三角形，理由如下：∵，AC2＝52＝25，∴AB2+BC2＝AC2，∴△ABC是直角三角形．17．①将正面和左面展开，过点B向底面作垂线，垂足为点C，则△ABC为直角三角形，∵AC＝×8+×6＝8m，BC＝5m，∴AB＝＝＝m．故壁虎爬到蚊子处的最短距离为m．②将正面和上面展开，则A到B的水平距离为6m，垂直距离为7m，此时的最短距离为m③将下面和右面展开，则A到B的水平距离为11m，垂直距离为2m，此时的最短距离为5m．综上所述，壁虎爬到蚊子处的最短距离为米．18．作出B点关于CD的对称点B′，连接AB′，交CD于点O，则O点就是光的入射点．因为B′D＝DB，所以B′D＝AC，∠B′DO＝∠OCA＝90°，∠B′＝∠CAO，所以△B′DO≌△ACO（ASA），则OC＝OD＝AB＝×6＝3米．连接OB．在Rt△ODB中，OD2+BD2＝OB2，所以OB2＝32+42＝52，即OB＝5（米），所以点B到入射点的距离为5米．19．【解答】证明：设正方形ABCD的边长为4x，∵E是边AD的中点，点F在边DC上，且DF＝DC，∴AE＝DE＝2x，DF＝x，CF＝3x，∴在Rt△EDF中，EF2＝ED2+DF2＝x2+（2x）2＝5x2；在Rt△AEB中，EB2＝EA2+AB2＝（2x）2+（4x）2＝20x2；在Rt△BCF中，BF2＝BC2+CF2＝（4x）2+（3x）2＝25x2；∴EF2+BE2＝BF2，∴△BEF是直角三角形．20．【解答】（1）证明：∵在Rt△ADC中，∠ADC＝90°，AD＝8，CD＝6，∴AC2＝AD2+CD2＝82+62＝100，∴AC＝10（取正值）．在△ABC中，∵AC2+BC2＝102+242＝676，AB2＝262＝676，∴AC2+BC2＝AB2，∴△ABC为直角三角形；（2）解：S阴影＝S Rt△ABC﹣S Rt△ACD＝×10×24﹣×8×6＝96．21．（1）如图1，当0＜t≤3时，BQ＝t，BC＝4，∴S＝×4×t＝2t；如图2，当3＜t≤5时，，AQ＝t﹣3，则BQ＝3﹣（t﹣3）＝6﹣t，∴S＝×4×（6﹣t）＝12﹣2t；（2）连接CQ，如图3，∵QP的垂直平分线过点C，∴CP＝CQ，∵AB＝3，BC＝4，∴AC＝＝＝5，∴42+t2＝（5﹣t）2，解得t＝；或42+（6﹣t）2＝（5﹣t）2，显然不成立；∴AQ＝3﹣＝．。

第十七章总需求—总供给模型1. 总需求曲线的理论来源是什么？为什么在IS—LM模型中，由P(价格)自由变动，即可得到总需求曲线？解答：(1)总需求是经济社会对产品和劳务的需求总量，这一需求总量通常以产出水平来表示。

一个经济社会的总需求包括消费需求、投资需求、政府购买和国外需求。

总需求量受多种因素的影响，其中价格水平是一个重要的因素。

在宏观经济学中，为了说明价格水平对总需求量的影响，引入了总需求曲线的概念，即总需求量与价格水平之间关系的几何表示。

在凯恩斯主义的总需求理论中，总需求曲线的理论来源主要由产品市场均衡理论和货币市场均衡理论来反映。

(2)在IS—LM模型中，一般价格水平被假定为一个常数(参数)。

在价格水平固定不变且货币供给为已知的情况下，IS曲线和LM曲线的交点决定均衡的收入(产量)水平。

现用图17—1来说明怎样根据IS—LM图形来推导总需求曲线。

图17—1分上下两个部分。

上图为IS—LM图。

下图表示价格水平和需求总量之间的关系，即总需求曲线。

当价格P的数值为P1时，此时的LM曲线LM(P1)与IS曲线相交于E1点，E1点所表示的国民收入和利率分别为y1和r1。

将P1和y1标在下图中便得到总需求曲线上的一点D1。

现在假设P由P1下降到P2。

由于P的下降，LM曲线移动到LM(P2)的位置，它与IS曲线的交点为E2点。

E2点所表示的国民收入和利率分别为y2和r2。

对应于上图中的点E2，又可在下图中找到D2点。

按照同样的程序，随着P的变化，LM曲线和IS曲线可以有许多交点，每一个交点都代表着一个特定的y和P。

于是就有许多P与y的组合，从而构成了下图中一系列的点。

把这些点连在一起所得到的曲线AD便是总需求曲线。

从以上关于总需求曲线的推导中可以看到，总需求曲线表示社会的需求总量和价格水平之间的反向关系。

即总需求曲线是向右下方倾斜的。

向右下方倾斜的总需求曲线表示，价格水平越高，需求总量越小；价格水平越低，需求总量越大。

第十七章 光的干涉一. 选择题 1．在真空中波长为的单色光，在折射率为n 的均匀透明介质中从A 沿某一路径传播到B ，若A ，B 两点的相位差为3，则路径AB 的长度为：（ D ） A.B.C. 3D./n解： πλπϕ32==∆nd 所以 n d /5.1λ=本题答案为D 。

$2．在杨氏双缝实验中，若两缝之间的距离稍为加大，其他条件不变，则干涉条纹将 （ A ）A. 变密B. 变稀C. 不变D. 消失解：条纹间距d D x /λ=∆，所以d 增大，x ∆变小。

干涉条纹将变密。

本题答案为A。

3．在空气中做双缝干涉实验，屏幕E上的P处是明条纹。

若将缝S2盖住，并在S1、S2连线的垂直平分选择题3图面上放一平面反射镜M，其它条件不变(如图)，则此时( B )A. P处仍为明条纹>B. P处为暗条纹C. P处位于明、暗条纹之间D. 屏幕E上无干涉条纹解对于屏幕E上方的P点，从S1直接入射到屏幕E 上和从出发S1经平面反射镜M反射后再入射到屏幕上的光相位差在均比原来增，因此原来是明条纹的将变为暗条纹，而原来的暗条纹将变为明条纹。

故本题答案为B。

4．在薄膜干涉实验中，观察到反射光的等倾干涉条纹的中心是亮斑，则此时透射光的等倾干涉条纹中心是（ B ）A. 亮斑B. 暗斑C. 可能是亮斑，也可能是暗斑 D. 无法确定解：反射光和透射光的等倾干涉条纹互补。

本题答案为B 。

、5．一束波长为的单色光由空气垂直入射到折射率为n 的透明薄膜上，透明薄膜放在空气中，要使反射光得到干涉加强，则薄膜最小的厚度为 ( B )A./4 B./ (4n ) C./2 D. / (2n )6．在折射率为n=的玻璃表面上涂以折射率n =的MgF 2透明薄膜，可以减少光的反射。

当波长为的单色光垂直入射时，为了实现最小反射，此透明薄膜的最小厚度为（ C ）A. B. C. D. 解：增透膜 6.904/min ==n e λnm 本题答案为C 。

第17章管理的创新职能17.1 复习笔记一、创新与创新管理1．作为管理基本职能的创新工作创新是一种思想及在这种思想指导下的实践，是一种原则以及在这种原则指导下的具体活动，是管理的一种基本职能。

（1）创新与管理创新的内涵①创新的定义是指产生新的思想和行为的活动，它一般包括设备的更新、产品的开发或工艺的改进等。

人们的创新活动也同样可以分成具体操作创新和管理创新。

②管理创新是指在探究人类创新活动规律的基础上，对管理活动改变的过程，是一种产生新的管理思想和新的管理行为的过程。

管理创新之所以能够成为管理活动的一个独立职能，原因在于：a．管理创新对任何组织来说都是一种重要的活动；b．与创新管理活动相对的，维持管理只是管理活动一个环节，管理工作离开了创新环节，管理是不完整，也是无效的（详见“创新管理与维持管理关系”部分）；c．管理创新也与其他管理职能一样，具有其内在逻辑性，是人类理性活动的一部分，这种活动既可以被人们所认知，也能够被实践。

③作为管理职能的创新，其主要内容包括计划创新（战略创新）、技术创新、组织创新、领导创新和环境创新等，它们构成创新管理活动的基本框架。

④从逻辑顺序上来考察，在特定时期内对某一社会经济系统（组织）的管理工作主要包括以下内容：a．设计系统的目标、结构和运行规划，启动并监视系统的运行，使之按预定的规则操作；b．分析系统运行中的变化，进行局部或全局的调整，使系统与内外环境保持动态一致。

（2）创新工作是重要的管理活动①创新是组织发展的基础，是组织获取经济增长的源泉；②创新是组织谋取竞争优势的利器；③创新是组织摆脱发展危机的途径。

（3）企业创新工作内在逻辑①企业家是指企业中能够承担风险和不确定性、发现市场机会和具有创新精神的管理者，它具有两个基本要件：创造利润和指向未来。

a．承担风险和不确定性是指他们能够克服在经营过程中的各种知识与理性的不完全性；b．发现市场机会是指他们能够发现市场机会和那些被市场低估的资源价值；c．创新是企业家的本质，熊彼特认为企业家就是创新者，正是通过创新来获得经济租金，企业家的创造活动包括创造新的产品、使用新的生产方法、开辟一个新的市场、获取新的供货来源以及实现新的组织形式。

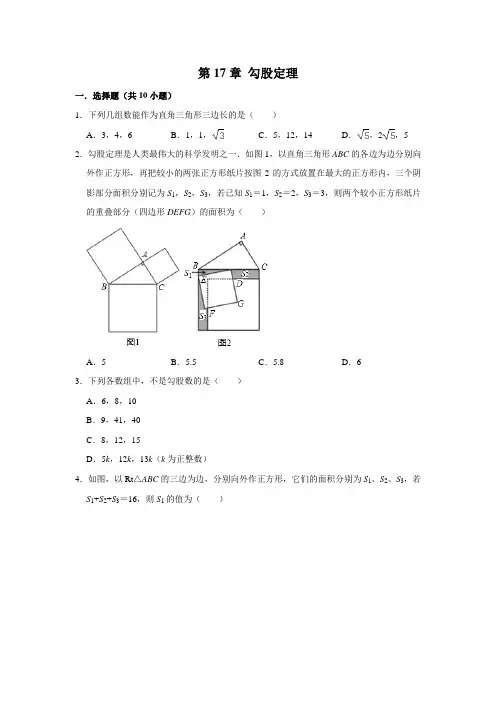
第17章勾股定理一．选择题（共10小题）1．下列几组数能作为直角三角形三边长的是（）A．3，4，6B．1，1，C．5，12，14D．，2，5 2．勾股定理是人类最伟大的科学发明之一．如图1，以直角三角形ABC的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大的正方形内，三个阴影部分面积分别记为S1，S2，S3，若已知S1＝1，S2＝2，S3＝3，则两个较小正方形纸片的重叠部分（四边形DEFG）的面积为（）A．5B．5.5C．5.8D．63．下列各数组中，不是勾股数的是（）A．6，8，10B．9，41，40C．8，12，15D．5k，12k，13k（k为正整数）4．如图，以Rt△ABC的三边为边，分别向外作正方形，它们的面积分别为S1、S2、S3，若S1+S2+S3＝16，则S1的值为（）A．7B．8C．9D．105．如图，数轴上的点A表示的数是﹣2，点B表示的数是1，CB⊥AB于点B，且BC＝2，以点A为圆心，AC为半径画弧交数轴于点D，则点D表示的数为（）A．B．+2C．﹣2D．26．如图，在△ABC中，D是BC上一点，已知AB＝13，AD＝12，AC＝15，BD＝5，则DC 的长为（）A．13B．12C．9D．87．如图，等腰△ABC中，AB＝AC＝10cm，BC＝12cm，D为BC上一点，连接AD，E为AD上一点，连接BE，若∠ABE＝∠BAE═∠BAC，则DE的长为（）A．cm B．cm C．cm D．1cm8．意大利著名画家达•芬奇用下图所示的方法证明了勾股定理．若设左图中空白部分的面积为S1，右图中空白部分的面积为S2，则下列表示S1，S2的等式成立的是（）A．S1＝a2+b2+2ab B．S1＝a2+b2+abC．S2＝c2D．S2＝c2+ab9．在△ABC中，AB＝AC＝10，BD是AC边上的高，DC＝2，则BD等于（）A．2B．4C．6D．810．如图，点O在线段AB上，AO＝2，OB＝1，OC为射线，且∠BOC＝60°，动点P以每秒2个单位长度的速度从点O出发，沿射线OC做匀速运动，设运动时间为t秒．当△ABP是直角三角形时，t的值为（）A．B．C．1或D．1或二．填空题（共5小题）11．如图，∠C＝∠ADB＝90°，AD＝1，BC＝CD＝2，则AB＝．12．如图，以AB为斜边的Rt△ABC的每条边为边作三个正方形，分别是正方形ABMN，正方形BCPQ，正方形ACEF，且边EF恰好经过点N．若S3＝S4＝5，则S1+S5＝．（注：图中所示面积S表示相应封闭区域的面积，如S3表示△ABC的面积）13．若点P（a，3）在第二象限，且到原点的距离是5，则a＝．14．图1是小慧在“天猫•双11”活动中购买的一张多档位可调节靠椅，档位调节示意图如图2所示，已知两支脚AB＝AC＝10分米，BC＝12分米，O为AC上固定连接点，靠背OD＝10分米．档位为Ⅰ档时，OD∥AB．档位为Ⅱ档时，OD'⊥AC．当靠椅由Ⅰ档调节为Ⅱ档时，靠背頂端D向后靠的水平距离（即EF）为分米．15．如图是高空秋千的示意图，小明从起始位置点A处绕着点O经过最低点B．最终荡到最高点C处，若∠AOC＝90°，点A与点B的高度差AD＝1米，水平距离BD＝4米，则点C与点B的高度差CE为米．三．解答题（共5小题）16．如图，图中数字代表正方形的面积，∠ACB＝120°，求正方形P的面积．（提示：直角三角形中，30°角所对的直角边等于斜边的一半）17．如图，在四边形ABCD中，AB＝1，AD＝，BD＝2，∠ABC+∠ADC＝180°，CD＝．（1）判断△ABD的形状，并说明理由；（2）求BC的长．18．如图所示，已知△ABC中，∠B＝90°，AB＝16cm，AC＝20cm，P、Q是△ABC的边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为ts．（1）则BC＝cm；（2）当t为何值时，点P在边AC的垂直平分线上？此时CQ＝；（3）当点Q在边CA上运动时，直接写出使△BCQ成为等腰三角形的运动时间．19．通过对《勾股定理》的学习，我们知道：如果一个三角形中，两边的平方和等于第三边的平方，那么这个三角形一定是直角三角形．如果我们新定义一种三角形﹣﹣两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形．（1）根据奇异三角形的定义，请你判断：等边三角形一定是奇异三角形吗？（填“是”或不是）；（2）若某三角形的三边长分别为1、、2，则该三角形是不是奇异三角形，请做出判断并写出判断依据；（3）在Rt△ABC中，两边长分别为a、c，且a2＝50，c2＝100，则这个三角形是不是奇异三角形？请做出判断并写出判断依据；探究：在Rt△ABC中，∠C＝90°，AB＝c，AC＝b，BC＝a，且b＞a，若Rt△ABC是奇异三角形，求a2：b2：c2．20．已知，DA，DB，DC是从点D出发的三条线段，且DA＝DB＝DC．（1）如图①，若点D在线段AB上，连接AC，BC，试判断△ABC的形状，并说明理由．（2）如图②，连接AC，BC，AB，且AB与CD相交于点E，若AC＝BC，AB＝16，DC ＝10，求CE和AC的长．参考答案一．选择题（共10小题）1．D．2．D．3．C．4．B．5．C．6．C．7．C．8．B．9．C．10．C．二．填空题（共5小题）11．3．12．5．13．﹣4．14．2．15．4.5．三．解答题（共5小题）16．解：如图，作AD⊥BC，交BC延长线于D，∵∠ACB＝120°，∴∠ACD＝60°，∠DAC＝30°；∴CD＝AC＝1，∴AD＝，在直角三角形ADB中，BD＝BC+CD＝3+1＝4，AD＝，根据勾股定理得：AB2＝AD2+BD2＝3+16＝19；∴正方形P的面积＝AB2＝19．17．解：（1）△ABD是直角三角形．理由如下：在△ABD中，∵AB2+AD2＝12+（）2＝4，BD2＝22＝4，∴AB2+AD2＝BD2，∴△ABD是直角三角形．（2）在四边形ABCD中，∵∠ABC+∠ADC＝180°，∴∠A+∠C＝180°，由（1）得∠A＝90°，∴∠C＝90°，在Rt△BCD中，∠C＝90°，BC2＝BD2﹣CD2＝22﹣（）2＝2，∴BC＝．18．解：（1）∵∠B＝90°，AB＝16cm，AC＝20cm ∴＝＝12（cm）．故答案为：12；（2）∵点P在边AC的垂直平分线上，∴PC＝P A＝t，PB＝16﹣t，在Rt△BPC中，BC2+BP2＝CP2，即122+（16﹣t）2＝t2解得：t＝．此时，点Q在边AC上，CQ＝（cm）；故答案为：13cm．（3）①当CQ＝BQ时，如图1所示，则∠C＝∠CBQ，∵∠ABC＝90°，∴∠CBQ+∠ABQ＝90°．∠A+∠C＝90°，∴∠A＝∠ABQ，∴BQ＝AQ，∴CQ＝AQ＝10，∴BC+CQ＝22，∴t＝22÷2＝11秒．②当CQ＝BC时，如图2所示，则BC+CQ＝24，∴t＝24÷2＝12秒．③当BC＝BQ时，如图3所示，过B点作BE⊥AC于点E，∴，∴＝．∴CQ＝2CE＝14.4，∴BC+CQ＝26.4，∴t＝26.4÷2＝13.2秒．综上所述：当t为11秒或12秒或13.2秒时，△BCQ为等腰三角形．19．解：（1）设等边三角形的边长为a，∵a2+a2＝2a2，∴等边三角形一定是奇异三角形；（2）∵，∴该三角形一定是奇异三角形；（3）当c为斜边时，b2＝c2﹣a2＝50，Rt△ABC不是奇异三角形；当b为斜边时，b2＝c2+a2＝150，∵50+150＝2×100，∴Rt△ABC是奇异三角形；∴a2+b2＝2c2，∴Rt△ABC是奇异三角形；拓展：Rt△ABC中，∠C＝90°，∴a2+b2＝c2，∵c＞b＞a，∴2c2＞b2+a2，2a2＜b2+c2，∵Rt△ABC是奇异三角形，∴2b2＝a2+c2，∴2b2＝a2+a2+b2，∴b2＝2a2，∴c2＝3c2，∴a2：b2：c2＝1：2：3．故答案为：是．20．解：（1）△ABC是直角三角形，理由：∵DA＝DB＝DC，∴∠A＝∠ACD，∠B＝∠BCD，∵∠A+∠ACD+∠B+∠BCD＝180°，∴∠ACD+∠BCD＝90°，∴∠ACB＝90°，∴△ABC是直角三角形；（2）∵DA＝DB，∴点D在线段AB的垂直平分线上，∵AC＝BC，∴点C在线段AB的垂直平分线上，∴CD垂直平分AB，∴∠AEC＝∠AED＝90°，∵AB＝16，DC＝10，∴AE＝8，AD＝CD＝10，∴DE＝＝6，∴CE＝CD﹣DE＝4，∴AC＝＝＝4．。

曼昆《经济学原理（微观经济学分册）》（第6版）第17章寡头课后习题详解跨考网独家整理最全经济学考研真题，经济学考研课后习题解析资料库，您可以在这里查阅历年经济学考研真题，经济学考研课后习题，经济学考研参考书等内容，更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验，从前辈中获得的经验对初学者来说是宝贵的财富，这或许能帮你少走弯路，躲开一些陷阱。

以下内容为跨考网独家整理，如您还需更多考研资料，可选择经济学一对一在线咨询进行咨询。

一、概念题1．寡头（oligopoly）（山东大学2003研；西北大学2004研）答：寡头亦称“寡头垄断”或“寡占”，指只有几个提供相似或相同产品的卖者的市场结构。

在寡头市场上，整个行业（或市场）的产品（或劳务）的一大部分是由少数几个企业（或卖者）供给的。

作为卖主的垄断寡头之间仍然存在着竞争，每个寡头都要考虑竞争对手对于自己的每一行动的反应。

一方面，如果有一卖主为争取更大的市场销售份额而降低商品价格，那么其他卖主势必也会降低价格，最终使各个卖主的原有市场份额保持不变，而使利润减少。

另一方面，如果有一卖主提高价格，那么其他卖主就不一定会提高价格，从而使提高价格的卖主丧失原来占有的市场份额。

由于垄断寡头能预计到这种结果，垄断寡头不会轻易提价。

因此，在卖方寡头市场上，商品价格一般比较稳定。

2．博弈论（game theory）答：博弈论也称为对策论，指研究人们在各种决策下如何行事的一般分析理论。

博弈论被应用于政治、外交、军事、经济等研究领域。

博弈就是决策者在某种竞争场合下做出的决策，或者说，参加竞争的各方为了自己的利益而采取的对付对方的策略。

博弈模型是人们对博弈现象的抽象。

博弈论就是分析博弈模型的方法和理论，它研究的典型问题是两个或两个以上的参加者（称为局中人）在某种对抗性或竞争性的场合下各自做出决策，使自己这一方得到尽可能最有利的结果。

博弈模型一般至少含有以下三个要素：①局中人。

第十七章习题与思考题17-1 何谓EH?电-液伺服执行机构或电液系统ELECTRONIC HYDRAULIC，简称EH。

17-2 DEH-Ⅲ的EH主要由哪几部分组成？DEH-Ⅲ的EH主要由伺服阀（电液转换器）、（阀）位移传感器、快速卸荷阀、油缸、截止阀、滤网、止回阀几部分组成。

17-3 DEH-Ⅲ的EH阀门是如何开启关闭的。

汽门开启由抗燃油压力来驱动，而关闭是靠操纵座上的弹簧力。

17-4 DEH-Ⅲ的EH执行机构有几种形式？DEH-Ⅲ的EH执行机构有二种基本形式，即开关型和控制型执行机构。

17-5 DEH执行机构的控制对象是如何划分的？在引进型600MW汽轮机液压控制系统中，按执行机构的控制对象一般可分为高压主汽阀执行机构(共2套)，高压调节汽阀执行机构(共4套)，中压调节汽阀执行机构(共4套)以及中压主汽阀执行机构(共2套)。

除中压主汽阀执行机构为开关型执行机构外，其余均为伺服(控制)型执行机构。

在引进型300MW汽轮机液压控制系统中，按执行机构的控制对象一般可分为高压主汽阀执行机构(共2套)，高压调节汽阀执行机构(共6套)，中压调节汽阀执行机构(共2套)以及中压主汽阀执行机构(共2套)。

除中压主汽阀执行机构为开关型执行机构外，其余均为伺服(控制)型执行机构。

在国产型300MW汽轮机(东汽型／上汽型)液压控制系统中，按执行机构的控制对象一般可分为高压主汽阀执行机构(共2套／2套)，高压调节汽阀执行机构(共4套／8套)，中压调节汽阀执行机构(共2套／4套)以及中压主汽阀执行机构(共2套／4套)。

除中压主汽阀执行机构为开关型执行机构外，其余均为伺服(控制)型执行机构。

在国产型200MW汽轮机液压控制系统中，按执行机构的控制对象可分为高压主汽阀执行机构(共2套)和中压主汽阀执行机构(共2套)，这两种执行机构为开关型执行机构。

另外还有高压调节汽阀执行机构(共4套)和中压调节汽阀执行机构(共4套)，这两种执行机构为伺服(控制)型执行机构。

八年级数学下册第17章 一元二次方程定向测评考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I 卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、关于x 的一元二次方程2420kx x +-=有实数根，则k 的取值范围是（ ）．A ．2k ≥-B ．2k ≤-且0k ≠C ．2k ≥-且0k ≠D ．2k ≤-2、下列是对方程2x 2﹣x +1＝0实根情况的判断，正确的是（ ）A ．有两个不相等的实数根B ．有一个实数根C ．有两个相等的实数根D ．没有实数根3、一元二次方程2234x x +=的根的情况是（ ）A ．有两个不相等的实数根B ．有两个相等的实数根C ．无实数根D ．只有一个实数根4、由于新冠疫情影响，某口罩加工厂改进技术，扩大生产，从今年10月份开始，平均每个月生产量的增长率为x ．已知今年10月份的生产量为800万个，12月的生产量为1152万个，则可列方程（ ）A ．800+800x 2＝1152B ．800（1+x ）2＝1152C ．800+800（1+x ）+800（1+x ）2＝1152D ．800+800（1+x ）＝11525、用配方法解一元二次方程2870x x -+=时，方程可变形为（ ）A ．2(4)7x -=B ．2(8)57-=xC ．2(4)9x -=D ．2(4)25x -=6、下列方程中，是关于x 的一元二次方程的为（ ）A ．2210x x +=B ．x 2-x -1=0C ．2320x xy -=D ．24-0y =7、关于x 的一元二次方程（a －1）x 2＋x ＋a 2－1＝0的一个根是0，则a 的值为（ ）A ．1B ．－1C ．1或－1D ．08、若a 是方程2310x x +-=的一个根，则2262020a a ++的值为（ ）A ．2020B ．2021-C ．2022D ．2021-9、用配方法解方程2250x x --=时，原方程应变形为（ ）A ．()216x +=B ．()216x -=C ．()229x +=D ．()229x -= 10、若1x =-是关于x 的一元二次方程20x mx m +-=的一个根，则m 的值为（ ）A ．1-B ．0C ．12D ．1第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、把2216x x -=化一般形式为________，二次项系数为________，一次项系数为______，常数项为_______．2、若k 为整数，关于x 的一元二次方程2(1)2(1)50k x k x k --+++=有实数根，则整数k 的最大值为__________．3、方程x (x ﹣5)＝7(x ﹣5)的解是_________．4、若关于x 的一元二次方程x 2－2x ＋m ＝0有一个根为1，则m 的值为_______．5、有3人患了流感，经过两轮传染后共有192人患流感，设每轮传染中平均一个人传染了x 人，则可列方程为____________．三、解答题（5小题，每小题10分，共计50分）1、解方程与化简：（1）解方程：2109x x -=-（2）化简：2221121a a a a a a -⎛⎫-÷ ⎪+++⎝⎭ 2、2020年，受新冠肺炎疫情影响，口罩紧缺，某网店以每袋8元（一袋十个）的成本价购进了一批口罩，二月份以一袋14元的价格销售了256袋，三、四月该口罩十分畅销，销售量持续走高，在售价不变的基础上，四月份的销售量达到400袋．（1）求三、四这两个月销售风的月平均增长率；（2）为回馈客户，该网店决定五月降价促销，经调查发现，在四月份销量的基础上，该口罩每袋降价1元，销售量就增加40袋，当口罩每袋降价多少元时，五月份可获利1920元？3、某服装厂批发应季T 恤衫，其单价y （元）与批发数量x （件）（x 为正整数）之间的函数关系如图所示．（1）直接写出y 与x 的函数关系式；（2）若每件T 恤衫的成本价是45元，当100500x <≤件（x 为正整数）时，服装厂如果想获得8000元利润，求一次批发多少件时所获利润为8000元？4、（问题提出）如果在一个平面内画出n 条直线，最多可以把这个平面分成几部分？（问题探究）为解决问题，我们经常采用一般问题特殊化的策略，先从最简单的情形入手，再逐次递进到复杂的情形，在探究的过程中，通过归纳得出一般性的结论，进而拓展应用．探究一：如图1，当在平面内不画（0条）直线时，显然该平面只有1部分，可记为()01f =．探究二：如图2，当在平面内画1条直线时，该平面最多被分成了2部分，比前一次多了1部分，可f=+=．记为()1112探究三：当在平面内画2条直线，若两条直线平行（如图3），该平面被分成3部分；若两条直线相交（如图4），交点将第2条直线分成2段，每一段将平面多分出1部分，因此比前一次多2部分，该平面被分成4部分．因此当在平面内画2条直线时，该平面最多被分成4部分，可记为()21124f=++=．我们获得的直接经验是：直线相交时，平面被分成的部分多．探究四：当在平面内画3条直线，若3条直线相交于一点（如图5），该平面被分成6部分；若3条直线的交点都不相同时（如图6），第3条直线与前两条直线有2个交点，该直线被2个交点分成了3段，每段将平面多分出1部分，所以比前一次多出3部分，该平面被分成7部分．因此当在平面内画f=+++=．我们获得的经验是：直线相交3条直线时，该平面最多被分成7部分，可记为()311237的交点个数越多，平面被分成的部分就越多，所以直接探索直线交点个数最多的情况即可．探究五：当在平面内画1条直线（如图7），第4条直线与前3条直线有3个交点，该直线被3个交点分成了4段，每段将平面多分出1部分，所以比前一次多出4部分，该平面被分成11部分．因此f=++++=．当在平面内画4条直线时，该平面最多被分成11部分，可记为()41123411（1）探究六：在平面内画5条直线，最多可以把这个平面分成几部分？（仿照前面的探究方法，写出解答过程，不需画图）．（2）（问题解决）如果在一个平面内画出n条直线，最多可以把这个平面分成______部分．（应用拓展）（3）如果一个平面内的10条直线将平面分成了50个部分，再增加3条直线，则该平面至多被分成______个部分．（4）如果一个平面被直线分成了466部分，那么直线的条数至少有______条．（5）一个正方体蛋糕切7刀（不移动蛋糕的位置，切只能竖着切），被分成的块数至多为______块．5、解方程：（1）x2＋8x－2＝0；（2）2(2x＋3)2－(2x＋3)－1＝0．-参考答案-一、单选题1、C【分析】根据一元二次方程的定义和根的判别式得到Δ＝42+8k≥0且k≠0，然后求出两不等式的公共部分即可；【详解】解：∵一元二次方程有实数根，∴Δ＝42﹣4×（-2）k≥0且k≠0，∴k≥-2且k≠0；故选：C【点睛】本题考查了根的判别式：一元二次方程ax2+bx+c＝0（a≠0）的根与Δ＝b2﹣4ac有如下关系：当Δ＞0时，方程有两个不相等的两个实数根；当Δ＝0时，方程有两个相等的两个实数根；当Δ＜0时，方程无实数根．2、C先求出根的判别式24b ac =-△的值，根据△>0有两个不相等实数根，△=0有两个相等实数根，△<0没有实数根作出判断即可．【详解】∵根的判别式224(4210b ac =-=--⨯⨯=，∴方程有两个相等的实数根．故选C ．【点睛】此题考查根据判别式判断一元二次方程根的情况，掌握根的判别公式为24b ac =-△是解答本题的关键．3、A【分析】根据根的判别式即可求出答案．【详解】解：原方程化为：22340x x +-=，∴()23424410∆=-⨯⨯-=＞，故选：A ．【点睛】本题考查一元二次方程，解题的关键是熟练运用一元二次方程的判别式，本题属于基础题型．4、B【分析】根据增长率公式即可得出答案．∵10月份的生产量为800万个，12月的生产量为1152万个，，经过了两个月，∴方程可为：2800(1)1152x +=．故选：B ．【点睛】本题考查一元二次方程的应用—增长率问题，经过n 次变化，增长率公式为(1)n a x b +=，其中x 为增长率，a 为起始值，b 为终值，掌握增长率公式是解题的关键．5、C【分析】先把常数项7移到方程右边，然后把方程两边加上42即可．【详解】方程变形为：x 2-8x =-7，方程两边加上42，得x 2-8x +42=-7+42，∴（x -4）2=9．故选C ．【点睛】本题考查了利用配方法解一元二次方程()200++=≠ax bx c a ：先把二次系数变为1，即方程两边除以a ，然后把常数项移到方程右边，再把方程两边加上一次项系数的一半，这样把方程变形为：（x -2b a ）2=244b ac a-． 6、B【详解】解：A 、分母中含有未知数，不是一元二次方程，故本选项不符合题意；B 、是一元二次方程，故本选项符合题意；C 、含有两个未知数，不是一元二次方程，故本选项不符合题意；D 、不含有未知数x ，不是x 的一元二次方程，故本选项不符合题意；故选：B【点睛】本题主要考查了一元二次方程的定义，熟练掌握含有一个未知数，且未知数的次数最高次数为2的整式方程称为一元二次方程是解题的关键．7、B【分析】根据一元二次方程的定义和一元二次方程的解的定义得出a -1≠0，a 2-1=0，求出a 的值即可．【详解】解：根据题意将x ＝0代入方程可得：a 2－1＝0，解得：a ＝1或a ＝－1，∵a －1≠0，即a ≠1，∴a ＝－1，故选：B ．【点睛】本题考查了对一元二次方程的定义，一元二次方程的解等知识点的理解和运用，注意根据已知得出a -1≠0且a 2-1=0，题目比较好，但是一道比较容易出错的题．8、C【分析】先根据一元二次方程根的定义得到231a a +=，再把2262020a a ++变形为22(3)2020a a ++，然后利用整体代入的方法计算．【详解】解：a是关于x的方程2310+-=的一个根，x x231a a∴+=，22∴++=++，a a a a2620202(3)2020=⨯+，212020=．2022故选：C．【点睛】本题考查了一元二次方程的解，解题的关键是能使一元二次方程左右两边相等的未知数的值是一元二次方程的解，利用整体代入的方法计算可简化计算．9、B【分析】根据配方法解一元二次方程的步骤首先把常数项移到右边，方程两边同时加上一次项系数一半的平方配成完全平方公式．【详解】解：2250--=x x移项得：225-=x x方程两边同时加上一次项系数一半的平方得：22151-+=+x x配方得：()216x-=．故选：B．【点睛】此题考查了配方法解一元二次方程的步骤，解题的关键是熟练掌握配方法解一元二次方程的步骤．配方法的步骤：配方法的一般步骤为：（1）把常数项移到等号的右边；（2）把二次项的系数化为1；（3）等式两边同时加上一次项系数一半的平方．10、C【分析】将1x =-代入方程20x mx m +-=得到关于m 的方程，然后解方程即可．【详解】解：将1x =-代入方程20x mx m +-=得：10m m --=，解得：m =12．故选：C ．【点睛】本题考查了一元二次方程根的定义，将已知方程的一个根代入方程得到新的方程是解答本题关键．二、填空题1、2x 2-6x -1=0 2 -6 -1【分析】先将方程移项化为一般形式()200++=≠ax bx c a ，即可求解． 【详解】解：将方程2216x x -=化成一般形式为22610x x --=，∴二次项系数为2，一次项系数为-6，常数项为-1．故答案为：①22610x x --=，②2，③-6，④-1．【点睛】本题主要考查了一元二次方程的一般形式，熟练掌握一元二次方程的一般形式是解题的关键． 2、3【分析】根据一元二次方程的二次项的系数不等于0、根的判别式求出k 的取值范围，由此即可得出答案．【详解】解：由题意得：[]2102(1)4(1)(5)0k k k k -≠⎧⎪⎨-+--+≥⎪⎩， 解得3k ≤，且1k ≠， k 为整数，∴整数k 的最大值为3，故答案为：3．【点睛】本题考查了一元二次方程根的判别式等知识点，熟练掌握一元二次方程根的判别式是解题关键．3、故答案为：【点睛】本题考查方程的解，解一元一次方程、解一元二次方程等知识，是重要考点，难度较易，掌握相关知识是解题关键．7．15=x ，27x =【分析】先移项，再将左边利用提公因式法因式分解，继而可得两个关于x 的一元一次方程，分别求解即可得出答案．【详解】解：(5)7(5)x x x -=-，(5)7(5)0x x x ∴---=，则(5)(7)0x x --=，50x ∴-=或70x -=，解得15=x ，27x =，故答案为：15=x ，27x =．【点睛】本题主要考查解一元二次方程的能力，解题的关键是熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法．4、1【分析】根据关于x 的方程x 2-2x +m =0的一个根是1，将x =1代入可以得到m 的值，本题得以解决．【详解】解：∵关于x 的方程x 2-2x +m =0的一个根是1，∴1-2+m =0，解得m =1，故答案为：1．【点睛】本题考查一元二次方程的解，解题的关键是明确题意，找出所求问题需要的条件．5、()3333192x x x +++=【分析】根据题意可得， 每轮传染中平均一个人传染了x 个人，经过一轮传染之后有33x +人感染流感，两轮感染之后的人数为192人，依此列出二次方程即可.【详解】解：设每轮传染中平均一个人传染了x 个人，依题可得：()3333192x x x +++=，故答案为：()3333192x x x +++=．【点睛】本题考查了由实际问题与一元二次方程，关键是得到两轮传染数量关系，从而可列方程求解．三、解答题1、（1）19x =，21x =（2）1a a - 【分析】（1）配方法解一元二次方程即可；（2）先根据分式的加减通分计算括号内的，同时将除法转化为乘法，进而根据分式的性质化简即可（1）解：配方，得21025925x x -+=-+()2516x -=开方，得54x -=±∴1459x =+=，2451x =-+=，（2） 解：原式()()()2111111a a a a +-⎛⎫=-÷ ⎪+⎝⎭+ 111a a a a -=÷++111a a a a +=⋅+- 1a a =- 【点睛】本题考查了配方法解一元二次方程，分式的化简，正确的计算是解题的关键．2、（1）25%（2）当口罩每袋降价2元时，五月份可获利1920元【分析】（1）设三、四这两个月销售量的月平均增长率为x ，根据题目已知条件列出方程即可求解；（2）设口罩每袋降价y 元，则五月份的销售量为()40040y +袋，根据题目已知条件得出()()148400401920y y --+=，解方程即可得出结果．（1）解：设三、四这两个月销售量的月平均增长率为x ，依题意，得：()22561400x +=，解得：10.2525%x ==，2 2.25x =-（不合题意，舍去）．答：三、四这两个月销售量的月平均增长率为25%；（2）解：设口罩每袋降价y 元，则五月份的销售量为()40040y +袋， 依题意，得：()()148400401920y y --+=，化简，得：24120y y +-=，解得：12y =，26y =-（不合题意，舍去）．答：当口罩每袋降价2元时，五月份可获利1920元．【点睛】本题主要考查的是一元二次方程的实际应用，根据题目意思正确的列出方程是解题的关键．3、（1）80y =（0100x ≤＜）；18520y x =-+（100500x ≤＜）；60y =（500x ＞）；（2）一次批发400件时,获得利润是8000元．【分析】（1）根据题意：分三段当0100x ≤＜且x 为整数时，当100500x ≤＜且x 为整数时，当500x ＞且x 为整数时，分别求函数关系式，即可求解；（2）利用每件利润乘以批发数量，列出方程，即可求解．【详解】解：（1）根据题意得：当0100x ≤＜且x 为整数时，80y =；当100500x ≤＜且x 为整数时，函数图象过点()()100,80,500,60 ， 设该段函数关系式为()0y kx b k =+≠∴1008050060k b k b +=⎧⎨+=⎩ ，解得：12085k b ⎧=-⎪⎨⎪=⎩ ， ∴该段函数关系式为18520y x =-+； 当500x ＞且x 为整数时，60y =；（2）当100500x ≤＜且x 为整数时，18520y x =-+∴()1458545800020y x x x ⎛⎫-=-+-= ⎪⎝⎭解得：12400x x ==，答：一次批发400件时,获得利润是8000元．【点睛】本题主要考查了一元二次方程的应用，列函数关系式，明确题意，准确得到等量关系是解题的关键． 4、（1）16（2）222n n ++ （3）86（4）30（5）29【分析】（1）根据题目给出的材料，仿照前面的探究方法，写出解答过程即可；（2）根据上面得出的结论，找到规律即可；（3）运用上面的规律，求出最多分成多少部分即可；（4）根据上面规律列出方程即可；（5）运用上面规律计算即可．（1）解：1条直线时，平面最多被分为1+1＝2部分；2条直线时，平面最多被分为1+1+2＝4部分；3条直线时，平面最多被分为1+1+2+3＝7部分；4条直线时，平面最多被分为1+1+2+3+4＝11部分；5条直线时，平面最多被分为1+1+2+3+4+5＝16部分故答案为：16（2）解：n条直线时：平面最多可分为：1+1+2+3+4+…+n＝1+（1+2+3+4+…+n）＝1+(1)2n n+＝222n n++（部分），故答案为：222n n++．（3）解：如果一个平面内的10条直线将平面分成了50个部分，再增加3条直线，该该平面至多被分成50+11+12+13=86（部分），故答案为：86（4）解：根据题意，224662n n++=，解得，130n=，231n=-（舍去），故答案为：30 （5）解：一个正方体蛋糕切7刀，分成的块数至多为2772292++=（块），故答案为：29【点睛】本题考查了直线、射线、线段，每两条直线都相交且三条直线不交于同一点，可得最多平面，一元二次方程的应用，通过计算、观察、发现规律是解题关键．5、（1）x1＝－4＋x2＝－4－；（2）x1＝－1，x2＝74 -．【分析】（1）通过移项配方，求出方程的解即可；（2）分解因式，即可得出两个一元一次方程，求出方程的解即可；【详解】解：（1）x2＋8x－2＝0，移项得：x2＋8x＝2，配方得：x2＋8x+16＝2+16，即（x+4）2＝18，∴x1＝－4＋x2＝－4－；（2）2(2x＋3)2－(2x＋3)－1＝0因式分解得：[(2x＋3)-1][2(2x＋3)+1]=0，即：（2x+2）（4x+7）=0，∴x1＝－1，x2＝74 ．【点睛】本题考查了解一元二次方程，掌握因式分解法以及配方法解方程是解题的关键．。

java2实用教程耿祥义张跃平编著(3版)习题解答1-17章完整版.doc第一章习题1．需3个步骤：1)用文本编辑器编写源文件2)使用javac编译源文件,得到字节码文件3)应用程序使用解释器运行；小应用程序使用浏览器运行。

2．应用程序必须有一个类含有public static void main(String args[])方法，含有该方法的类称为应用程序的主类。

小应用程序必须有一个类是java.applet.Applet类的子类，该类称做主类。

应用程序中可以没有public类，若有的话可以是应用程序中的任何一个类。

小应用程序的主类必须用public修饰。

3．java的源程序是由若干个书写形式互相独立的类组成的。

小应用程序的主类必须用public修饰。

应用程序中可以没有public类，若有的话可以是应用程序中的任何一个类。

一个java的源程序至多可以有一个public类。

Java源文件的名字可以和其中某个类的名字相同，扩展名是.java，但是，如果源程序中有public类，那么源文件的名字必须和这个public 类的名字相同，扩展名是.java。

4．属于操作，解答略。

第二章习题1．用来标识类名、变量名、方法名、类型名、数组名、文件名的有效字符序列称为标识符。

标识符由字母、下划线、美元符号和数字组成，并且第一个字符不能是数字字符2．关键字就是Java语言中已经被赋予特定意义的一些单词，不可以把关键字作为名字来用。

3．boolean ,char，byte，short，int，long，float，double。

4．b=x;5．数组b的长度为4b[0]=16．属于操作题，解答略。

7．属于操作题，解答略。

8．public class E{ public static void main (String args[ ]) { char cStart='α',cEnd='ω';for(char c=cStart;c<=cEnd;c++){ System.out.print(" "+c);}}}第三章习题1．你爱她2．beep!!3．public class Xiti3_3{ public static void main(String args[]){ double sum=0,a=1;int i=1;while(i<=20){ sum=sum+a;i++;a=a*i;}System.out.println("sum="+sum);}}4．public class Xiti4{ public static void main(String args[]){ int i,j;for(j=2;j<=100;j++){ for(i=2;i<=j/2;i++){ if(j%i==0)break;}if(i>j/2){ System.out.print(" "+j);}}}}5．class Xiti5{ public static void main(String args[]){ double sum=0,a=1,i=1;do { sum=sum+a;i++;a=(1.0/i)*a;}while(i<=20);System.out.println("使用do-while循环计算的sum="+sum);for(sum=0,i=1,a=1;i<=20;i++){ a=a*(1.0/i);sum=sum+a;}System.out.println("使用for循环计算的sum="+sum);}}6．class Xiti6{ public static void main(String args[]){ int sum=0,i,j;for(i=1;i<=1000;i++){ for(j=1,sum=0;j<i;j++){ if(i%j==0)sum=sum+j;}if(sum==i)System.out.println("完数:"+i);}}}7．public class E Xiti7{ public static void main(String args[]){ int m=8,item=m,i=1;long sum=0;while(i<=10){ sum=sum+item;i++;item=item*10+m;}System.out.println(sum);for(i=1,sum=0,item=m;i<=10;i++){ sum=sum+item;item=item*10+m;}System.out.println(sum);}}8．public class E{ public static void main(String args[]){ int n=1;long sum=0;while(true){ sum=sum+n;n++;if(sum>=8888)break;}System.out.println("满足条件的最大整数:"+(n-1));}}第四章习题1．用该类创建对象时。

机械设计习题解答第2章 机械设计总论一、填空题 1．当机械零件出现疲劳断裂时，应按 A 准则计算。

A ．强度； B.刚度； C.寿命； D.振动稳定性2.零件的工作安全系数为 B 。

A ．零件的极限应力比许用应力； B.零件的极限应力比工作应力C.零件的工作应力比许用应力；D.零件的工作应力比极限应力3.对大量生产、强度要求高、尺寸不大、形状不复杂的零件，应选择 D 。

A ．铸造； B.冲压； C.自由锻造； D.模锻二、是非题1.当零件可能出现塑性变形时，应按刚性准则计算。

（×）2．调质钢的回火温度越高，其硬度和强度将越低，塑性越好。

（√）3.机器的设计阶段是决定机器好坏的关键。

（√）4.疲劳破坏是引起大部分机械零件破坏的主要原因。

（√）5.随着工作时间的延长，零件的可靠度总是不变。

（×）第3章 机械零件的强度一、简答题1.弯曲疲劳极限的综合影响系数的含义是什么？它与那些因素有关？它对零件疲劳强度与静强度各有何影响？答：① 综合影响系数()D k σ的含义：在对称循环时，()D k σ是试件与零件疲劳极限的比值；在非对称循环时，()D k σ是试件与零件极限应力幅的比值。

② ()D k σ与零件的有效应力集中系数、尺寸系数、表面状态系数有关。

③ ()D k σ对零件的疲劳强度有影响，对零件的静强度没有影响。

2.零件的等寿命疲劳曲线与材料试件的等寿命疲劳曲线有何区别？零件和材料试件的失效形式是否总是相同的？为什么？答：① 零件的等寿命疲劳曲线相对于材料试件的等寿命疲劳曲线下移了一段距离。

② 在相同变应力作用下，两者的失效规律并不总是相同的，因为零件疲劳曲线中疲劳破坏的范围增大了。

3.试说明承受循环变应力的机械零件，在什么情况下可按静条件强度计算？在什么情况下按疲劳强度条件计算？答：承受循环变应力的机械零件，当应力循环次数310N ≤时，按静强度条件计算；当极限应力点与疲劳极限应力曲线中的屈服曲线相交时，也按静强度计算。

人教版九年级物理第17章练习题含答案17.1电流与电压和电阻的关系综合一、选择题1．下列探究实验中，需要控制电阻不变的是( )A．探究串联电路中的电流关系B．探究并联电路中的电压关系C．探究通过导体的电流与导体电阻的关系D．探究通过导体的电流与导体两端电压的关系2．某同学在探究“电流跟电压、电阻的关系”时，根据收集到的数据画出了如图所示的I-R图像，下列结论与图像相符的是A．电压一定时，电流随着电阻的增大而减小B．电阻一定时，电压随着电流的增大而增大C．电阻一定时，电流随着电压的增大而增大D．电压一定时，电阻随着电流的增大而减小3．小刚用图所示电路探究一段电路中电流跟电阻的关系，在此实验过程中，当A、B两点间的电阻由5Ω更换为10Ω后，为了探究上述问题，他应该采取的唯一操作是（）A．变阻器滑片不动B．将变阻器滑片适当向左移动C．将变阻器滑片适当向右移动D．适当增加电池的节数4．小红根据正确的测量数据绘制出电流与电阻（I—R）的图像，如图所示，其中正确的是（）A．B．C．D．5．关于电流与电压、电阻的关系，下列说法正确的是（）A．电阻一定时，电压随电流的增大而减小B．电阻一定时，电压随电流的增大而增大C．电压一定时，电流随电阻的增大而减小D．电压一定时，电阻随电流的增大而减小6．如图是“探究电流与电阻的关系”实验电路图。

先在A、B间接入5Ω的电阻，移动滑片，使电压表示数为2V,读出电流表示数。

接着断开开关，用10Ω的电阻替换5Ω的电阻，闭合开关后，电压表示数及下一步应进行的操作是A．大于2V，将滑片向左滑B ．小于2V ，将滑片向左滑C ．大于2V ， 将滑片向右滑D ．小于2V ,将滑片向右滑7．小帅用增加串联干电池数量的方法，分别做AB 两个电阻的电流与电压关系的实验，结果如图所示，则（ ）A ．A 电阻的阻值小于B 电阻的阻值B ．对同一电阻而言，电流与电压成正比C ．电压相同时，电阻越大，电流越大D ．电流相同时，电阻越大，电压越小8．如图所示的电路中，电阻阻值12R R <．闭合开关S 后，电阻1R 、2R 两端的电压分别为1U 、2U ，通过两个电阻的电流分别为1I 、2I ．下列判断中正确的是（ ）A ．12I I =B ．12I I >C ．12U U =D ．12U U >9．下列图象能正确表示导体中的电流与这段导体两端电压关系的是A．B．C．D．10．在“研究电流跟电压、电阻的关系”实验中，得到下表中一组实验数据，根据这组数据，可以得到的结论是A．导体电阻一定时，导体两端的电压跟通过导体的电流成正比B．导体电阻一定时，通过导体的电流跟导体两端的电压成正比C．导体两端的电压一定时，导体的电阻跟通过导体的电流成反比D．导体两端的电压一定时，通过导体的电流跟导体的电阻成反比二、解答题11．用图甲电路探究“电流跟电阻的关系”，电源电压恒为3V，滑动变阻器规格为“50Ω 2A”．（1）请用笔画线代替导线，将图甲中电压表接入电路，测R两端的电压___________；（2）滑片P移至阻值最大处，将5Ω电阻接入电路，闭合开关，移动滑片P发现，电压表有示数，电流表始终无示数，其原因可能是__________（只填序号）A．R短路B．R断路C．滑动变阻器短路（3）故障排除后，移动滑片P使电压表的示数如图乙所示，记下电压表的示数：（4）将5Ω电阻换成10Ω电阻，为保持电压表示数不变，滑片P应向________（选填“A”或“B”）端移动；（5）若每次实验均选用单个定值电阻连入电路，实验室有“15Ω，20Ω，30Ω，35Ω，50Ω”5个电阻，你认为能供继续实验的电阻最多还有认为表中有______个；（6）利用可选电阻继续实验，并得到结论：电压一定时，导体中的电流与导体的电阻成________比．12．如图甲为探究“电流与电压和电阻的关系”的实验电路图。

第17章同步电动机和同步调相机习题解答郑乃清王洪涛17-1 一台同步电动机在额定电压下运行，从电网吸收cos 0.8ϕ=超前的额定电流，已知该机的参数为：0.8, 0.5, 0d q a x x R **==≈，试求（1）励磁电动势0E *及功率角θ；（2）该机运行在什么励磁状态？解：方法一cos 0.8ϕ=超前，036.87ϕ=0sin 10.610.553.97cos 10.8q I x U arctgarctgU ϕψϕ****+⨯+⨯===⨯00053.9736.8717.1θψϕ=-=-=000cos sin 1cos17.110.8sin53.97 1.6d E U I x θψ****=+=⨯+⨯=00θ>，U&超前E &，电动机运行于过激状态。

方法二：设010U *=∠&，cos 0.8ϕ=超前，036.87ϕ= 0136.87I *=∠&00136.870.5 1.3617.1q UjI x j ***-=-∠⨯=∠-&&，该相量与E &同相位 017.1θ=00036.8717.153.97ψθϕ=+=+=sin 0.809dI I ψ**== 0() 1.360.809(0.80.5) 1.6q d d q E U jI x I x x *******=-+-=+⨯-=17-2 三相隐极同步发电机60kVA N S =，Y 接，380V N U =， 1.55t x =Ω，0a R ≈。

当电机过励cos 0.8N ϕ=滞后，37.5kVA S =时（1）作相量图，求0E 和θ；（2）原动机移去，不计损耗，作相量图，求I ；（3）改作电动机运行，em P 同（1）中数值，调节励磁使cos 1ϕ=，作相量图，求I 和0E 。

解：357(A)I ===cos 0.8ϕ=滞后，036.87ϕ= sin ()()sin t Ix U arctg acrtg arctg U ϕψθϕϕ+=+=57 1.552200.651.3822008arctg ⨯+⨯⎛⎫==⎪⨯⎝⎭00051.3836.8714.51θψϕ=-=-=()()20cos sin t E U U Ix ϕϕ=++()()()222200.82200.657 1.55282V =⨯+⨯+⨯=（2）10P =，00p ≈，20, 0P θ==0t E U Ix =+028222040(A)1.55t E U I x --=== （3）003282220sin sin14.5130085.3(W)1.55em t mE U P x θ⨯⨯==⨯= cos 1ϕ'=，I&与U &同相 em P 不变，cos I ϕ=常数，cos cos I I ϕϕ''=cos 570.845.6cos 1I I ϕϕ⨯'==='(A) ()22220()220 1.5545.6231(V)t E U Ix =+=+⨯=17-3 某工厂变电所变压器容量为2000kVA ，该厂电力设备消耗的总功率1200kW ，cos =0.65ϕ滞后。

第17章 量子物理基础17.1 夜间地面降温主要是由于地面的热辐射。

如果晴天夜里地面温度为-5°C ，按黑体辐射计算，每平方米地面失去热量的速率多大？解： 每平方米地面失去热量的速率即地面的辐射出射度2484W/m 2922681067.5=⨯⨯==-T M σ17.2 在地球表面，太阳光的强度是1.0⨯103W/m 2。

地球轨道半径以1.5⨯108 km 计，太阳半径以7.0⨯108 m 计，并视太阳为黑体，试估算太阳表面的温度。

解： ,44422T R I R M SE σππ==K 103.51067.5)107.6(100.1)105.1(348283211422⨯=⨯⨯⨯⨯⨯⨯==-σS E R I R T 17.3宇宙大爆炸遗留在宇宙空间的均匀背景辐射相当于3K 黑体辐射．求：（1）此辐射的单色辐射强度在什么波长下有极大值？ （2）地球表面接收此辐射的功率是多少？解：（1）根据公式λm T = b ，可得辐射的极值波长为λm = b/T = 2.897×10-3/3 = 9.66×10-4(m)．（2）地球的半径约为R = 6.371×106m ，表面积为 S = 4πR 2．根据公式：黑体表面在单位时间，单位面积上辐射的能量为 M = σT 4， 因此地球表面接收此辐射的功率是P = MS = 5.67×10-8×34×4π(6.371×106)2= 2.34×109(W)．17.4 铝的逸出功是eV 2.4，今有波长nm 200=λ（1 （2）截止电压； （3）铝的红限波长。

解：（1） AchA h E k -=-=λνeV 0.22.4106.1102001031063.6199834=-⨯⨯⨯⨯⨯⨯=--- （2）V 0.21/0.2/===e E U k c（3）A hc c==00νλnm 296m 1096.2106.12.41031063.6719834=⨯=⨯⨯⨯⨯⨯=--- 17.5 康普顿散射中入射X 射线的波长是λ = 0.70×10-10m ，散射的X 射线与入射的X 射线直．求：（1）反冲电子的动能E K ； （2）散射X 射线的波长；（3）反冲电子的运动方向与入射X 射线间的夹角θ． 解：（1）（2）根据康普顿散射公式得波长变化为21222sin 2 2.42610sin 24ϕπλΛ-∆==⨯⨯= 2.426×10-12(m)，散射线的波长为λ` = λ + Δλ = 0.72426×10-10(m)．反冲电子的动能为`k hchc E λλ=-34834810106.6310310 6.63103100.7100.7242610----⨯⨯⨯⨯⨯⨯=-⨯⨯= 9.52×10-17(J)． （3）由于/`tan /`hc hc λλθλλ==0.70.96650.72426==， 所以夹角为θ = 44°1`．17.6 求波长分别为71100.7-⨯=λm 的红光和波长1021025.0-⨯=λm 的X 射线光子的能量、动量和质量。