《28.1锐角三角函数_第3课时》

28．1锐角三角函数第3课时 特殊角的三角函数1. 3tan30°的值等于( ) A. 3 B ．3 3 C.33 D.322. 计算6tan45°－2cos60°的结果是( ) A ．4 3 B ．4 C ．5 3 D ．53．如图，在Rt △ABC 中，∠C ＝90°，AB ＝2BC ，则sin B 的值为( ) A.12 B.22 C.32D ．1第3题图 第5题图4．如果在△ABC 中，sin A ＝cos B ＝22，则下列最确切的结论是( ) A ．△ABC 是直角三角形B ．△ABC 是等腰三角形C ．△ABC 是等腰直角三角形D ．△ABC 是锐角三角形5．如图，当太阳光线与水平地面成30°角时，一棵树的影长为24 m ，则该树高为( )A ．8 3 mB ．12 3 mC ．12 2 m D. 12 m6．(1)3cos30°的值是____．(2)计算：sin30°·cos30°－tan30°＝____(结果保留根号)．(3)cos 245°＋tan30°·sin60°＝____．7．根据下列条件，求出锐角A 的度数．(1)sin A ＝32，则∠A ＝____；(2)cos A ＝12，则∠A ＝____； (3)cos A ＝22，则∠A ＝____；(4)cos A ＝32，则∠A ＝____． 8．如图是引拉线固定电线杆的示意图，已知CD ⊥AB ，CD ＝3 m ，∠CAD ＝∠CBD ＝60°，求拉线AC 的长．9.计算：(1)cos45°sin45°＋2sin60°tan60°－1tan30°＋tan45°； (2)sin45°＋cos30°3－2cos60°－sin60°(1－sin30°).10.已知α是锐角，且sin(α＋15°)＝32，计算8－4cos α－(π－3.14)0＋tan α＋⎝ ⎛⎭⎪⎫13－1的值．。

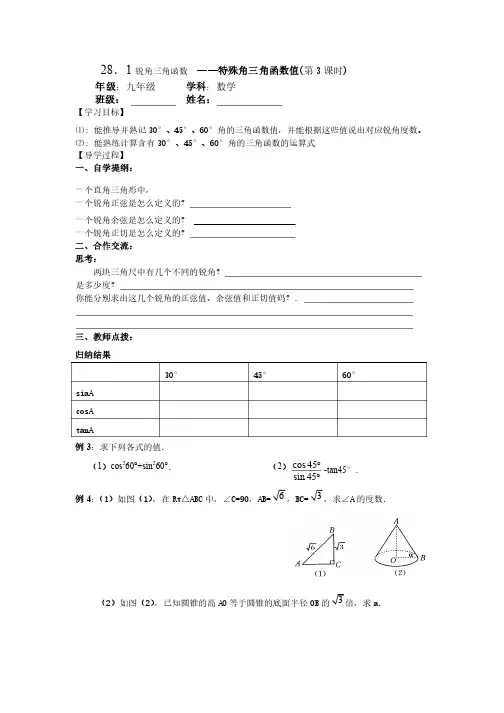
28．1锐角三角函数 ——特殊角三角函数值(第3课时)年级：九年级：九年级 学科：数学：数学班级： 姓名：【学习目标】⑴: 能推导并熟记3030°°、4545°°、6060°角的三角函数值，并能根据这些值说出对应锐角度数。

°角的三角函数值，并能根据这些值说出对应锐角度数。

⑵: 能熟练计算含有3030°°、4545°°、6060°角的三角函数的运算式°角的三角函数的运算式°角的三角函数的运算式【导学过程】一、自学提纲：一个直角三角形中，一个直角三角形中，一个锐角正弦是怎么定义的？一个锐角正弦是怎么定义的？一个锐角余弦是怎么定义的？一个锐角余弦是怎么定义的？一个锐角正切是怎么定义的？一个锐角正切是怎么定义的？二、合作交流：思考：两块三角尺中有几个不同的锐角？两块三角尺中有几个不同的锐角？ 是多少度？是多少度？ 你能分别求出这几个锐角的正弦值、余弦值和正切值码？．你能分别求出这几个锐角的正弦值、余弦值和正切值码？．三、教师点拨：归纳结果3030°° 4545°° 6060°° siaAcosAtanA例3：求下列各式的值．：求下列各式的值．（1）cos 260°60°+sin +sin 260°． （2）cos 45sin 45°°-tan45°．°． 例4：（1）如图（）如图（11），在Rt Rt△△ABC 中，∠中，∠C=90C=90C=90，，AB=6，BC=3，求∠，求∠A A 的度数．的度数．（2）如图（）如图（22），已知圆锥的高AO 等于圆锥的底面半径OB 的3倍，求a ．四、学生展示：1．已知：．已知：Rt Rt Rt△△ABC 中，∠中，∠C=90C=90C=90°，°，°，cosA=cosA=35 ，AB=15AB=15，则，则AC 的长是（的长是（ ））． A A．．3 B 3 B．．6 C 6 C．．9 D9 D．．12 2．下列各式中不正确的是（．下列各式中不正确的是（ ））． A A．．sin 260°+cos 26060°°=1 B =1 B．．sin30sin30°°+cos30+cos30°°=1C C．．sin35sin35°°=cos55=cos55°°D D．．tan45tan45°°>sin45>sin45°°3．计算2sin302sin30°°-2cos60-2cos60°°+tan45+tan45°的结果是（°的结果是（°的结果是（ ））． A A．．2 B 2 B．．3 C C．．2 D D．．14．已知∠．已知∠A A 为锐角，且cosA cosA≤≤12 ，那么（，那么（ ））A A．．0°<∠A ≤6060°°B ．6060°≤∠°≤∠°≤∠A<90A<90A<90°°C C．．0°<∠A ≤3030°°D ．3030°≤∠°≤∠°≤∠A<90A<90A<90°°5．在△．在△ABC ABC 中，∠中，∠A A 、∠、∠B B 都是锐角，且sinA=12， cosB=3 2 ，则△，则△ABC ABC 的形状是（的形状是（）） A A．直角三角形．直角三角形．直角三角形 B B B．钝角三角形．钝角三角形C ．锐角三角形．锐角三角形 D D D．不能．不能确定确定6．如图Rt Rt△△ABC 中，∠中，∠ACB=90ACB=90ACB=90°，°，°，CD CD CD⊥⊥AB 于D ，BC=3BC=3，，AC=4AC=4，设∠，设∠，设∠BCD=a BCD=a BCD=a，则，则tana•tana•的值为的值为（ ））． A ．34 B B．．43 C C．．35 D D．．457．当锐角a>60a>60°时，°时，°时，cosa cosa 的值（的值（ ））． A A．小于．小于12 B B．大于．大于12 C C．大于．大于3 2 D D．大于．大于1 8．在△．在△ABC ABC 中，三边之比为a ：b ：c=1c=1：：3：2，则sinA+tanA 等于（等于（ ））． A ．32313331.3..6222B C D +++9．已知梯形ABCD 中，腰BC 长为2，梯形对角线BD 垂直平分AC AC，若梯形的高是，若梯形的高是3，•则∠CAB 等于（等于（ ））A A．．3030°°B B．．6060°°C C．．4545°°D D．以上都不对．以上都不对．以上都不对1010．．sin 272°+sin 21818°的值是（°的值是（°的值是（ ））． A A．．1 B 1 B．．0 C 0 C．．12 D D．．3 2 1111．若（．若（3 tanA-3tanA-3））2+│2cosB-3 │=0=0，则△，则△，则△ABC ABC ABC（（ ））． A A．是直角三角形．是直角三角形．是直角三角形 B B B．是等边三角形．是等边三角形．是等边三角形C C．是含有．是含有6060°的任意三角形°的任意三角形°的任意三角形D D D．是顶角为钝角的等腰三角形．是顶角为钝角的等腰三角形．是顶角为钝角的等腰三角形三、填空题．三、填空题．1212．设．设α、β均为锐角，且sin α-cos β=0=0，则，则α+β=_______=_______．．1313．．cos 45sin 301cos60tan 452°-°°+°的值是的值是_____________________．．1414．．已知，等腰△等腰△ABC•ABC•ABC•的腰长为的腰长为43 ，•底为30•30•°，°，•则底边上的高为则底边上的高为__________________，，•周长为周长为__________________．．1515．在．在Rt Rt△△ABC 中，∠中，∠C=90C=90C=90°，已知°，已知tanB=5 2，则cosA=________cosA=________．．。

28.1 锐角三角函数(3)班级 姓名 座号 月 日主要内容:掌握特殊角三角函数值,能用它们进行计算,会由三角函数值说出相应锐角的大小 一、课堂练习:1.(课本83页)求下列各式的值: (1)12sin30cos30-o o(2)3tan30tan 452sin60-+o o o(3)cos6011sin 60tan 30++oo o 2cos60-oo2.(课本83页)在Rt ABC ∆中,90C ∠=o ,BC ,AC =求A ∠、B ∠的度数.3.已知α为锐角,且sin(10)α-︒=则α等于( )A.50oB.60oC.70oD.80o 4.如图,现有一扇形纸片,圆心角∠AOB 为120o ,弦AB 的长为侧面(接缝忽略不计),则该圆锥底面圆的半径为( ) A.23cm B.2π3cm C.32cm D.3π2cm二、课后作业:1.(课本85页)求下列各式的值:(1)sin 45o (2)12sin30cos30+o o(3)sin 45cos60sin 45⋅+o o o (4)2cos 45tan 60cos30+o o o2.如图,在平面直角坐标系中,点A 在第一象限内,点B 的坐标为(3,0),2OA =,60AOB ∠=o .(1)求点A 坐标；(2)若直线AB 交y 轴于点C ,求AOC ∆的面积.3.如图是一个中心对称图形,A 为对称中心,若90C ∠=o ,30B ∠=o ,1BC =,则BB '的长为( ) A.44.若A ∠是锐角,且3sin 4A =,则( )A.030A <∠<o oB.3045A <∠<o oC.4560A <∠<o oD.6090A <∠<o o 5.计算:1sin 60cos302⋅-=o o _______.6.在ABC ∆中,若sin cos 0A B 2||+(-=,则C ∠=_______.三、新课预习:1.用计算器求下列锐角三角函数值:(1)cos6317'≈o ______ (2)tan 27.35≈o _________ (3)sin35576'''≈o ________ 2.已知下列三角函数值,用计算器求其相应的锐角A (精确到0.01o ): (1)sin 0.9861A = (2)cos 0.8067A = (3)tan 0.189A =C'B 第3题参考答案一、课堂练习:1.(课本83页)求下列各式的值:(1)12sin30cos30-o o解:原式1122=-⨯1=-(2)3tan30tan452sin60-+o o o解:原式312=-+1=(3)cos6011sin60tan30++oo o2cos60-oo解:原式12=+=+22=-=解:原式2212⨯=-12=-12=-=2.(课本83页)在Rt ABC∆中,90C∠=o,BC,AC=求A∠、B∠的度数. 解:∵tan BCAAC===∴30A∠=o∴90903060B A∠=-∠=-=o o o o3.已知α为锐角,且sin(10)α-︒=则α等于( C)A.50oB.60oC.70oD.80o4.如图,现有一扇形纸片,圆心角∠AOB为120o,弦AB的长为侧面(接缝忽略不计),则该圆锥底面圆的半径为( A)A.23cm B.2π3cmC.32cm D.3π2cm二、课后作业:1.(课本85页)求下列各式的值:(1)sin45o(2)12sin30cos30+o o解:原式=+解:原式1122=+⨯⨯=1=+(3)sin45cos60sin45⋅+o o o(4)2cos45tan60cos30+o o o解:原式12=+解:原式2=+=2=2.如图,在平面直角坐标系中,点A 在第一象限内,点B 的坐标为(3,0),2OA =,60AOB ∠=o .(1)求点A 坐标；(2)若直线AB 交y 轴于点C ,求AOC ∆的面积. 解:(1)过点A 作 AD x ⊥轴于点D ,则1cos60212OD OA ==⨯=o,sin 602AD OA ==⨯=o ∴点A 坐标为(1(2)设直线AB 的关系式为y kx b =+∵直线AB 过点A (1)和点B (3,0)∴30k b k b ⎧+=⎪⎨+=⎪⎩解得k b ⎧=⎪⎪⎨⎪=⎪⎩∴直线AB的关系式为y x =+ 由0x =,得y =∴OC =∴112AOC S ∆==3.如图是一个中心对称图形,A 为对称中心,若90C ∠=o ,30B ∠=o ,1BC =,则BB '的长为( D )A.44.若A ∠是锐角,且3sin 4A =,则( C )A.030A <∠<o oB.3045A <∠<o oC.4560A <∠<o oD.6090A <∠<o o5.计算:1sin 60cos302⋅-=o o 14 .6.在ABC ∆中,若sin cos 0A B 2||+(-=,则C ∠=105o .三、新课预习:1.用计算器求下列锐角三角函数值: (1)cos6317'≈o . 04496 (2)tan 27.35≈o . 05172(3)sin35576'''≈o . 058712.已知下列三角函数值,用计算器求其相应的锐角A (精确到0.01o ): (1)sin 0.9861A = (2)cos 0.8067A = (3)tan 0.189A = 解:80.44A ∠≈o 解:36.23A ∠≈o 解:10.70A ∠≈oC'B 第3题。