全等三角形AAS和ASA练习题

①AB＝DE，②∠ACB＝∠F，③∠A＝∠D，④AC＝DF．选出两个作为条件，推出 ．并予以证明．（写出一种即可）
已知：，．
求证： ．
证明：
22.如图，在△AEC和△DFB中，∠E=∠F，点A，B，C，D在同一直线上，有 如下三个关系式：①AE∥DF，②AB=CD，③CE=BF。
（1）请用其中两个关系式作为条件，另一个作为结论，写出你认为正确的所有命题（用序号写出命题书写形式：“如果 ， ，那么 ”）；
C.△DCG≌△ECFD.△ADB≌△CEA
8.如图，在△ABC中，AB=AC，∠ABC．∠ACB的平分线BD，CE相交于O点，且
BD 交AC于点D，CE交AB于点E．某同学分析图形后得出以下结论：
①△BCD≌△CBE；②△BAD≌△BCD；③△BDA≌△CEA；④△BOE≌△COD；
⑤△ACE≌△BCE；上述结论一定正确的是（ ）
C.∠B=∠C，∠BAD=∠CADD.∠B=∠C，BD=DC
6.如图，已知 中， ， 是 高 和 的交点， ，则线段 的长度为（）.
A． B．4C． D．
7.如图，点B、C、E在同 一条直线上，△ABC与△CDE都是等边三角形，则下列结论不一定成立的是（ ）
A.△ACE≌△BCDB.△BGC≌△AFC
12.如图，AD=BC，AC=BD，则图中全等三角形有对.
13.如图，已知AB∥CF, E为DF的中点.若AB=9 cm,CF=5 cm,则BD的长度
为cm.
14. 如图，∠A =∠D，OA=OD,∠DOC=50°，则∠DBC=度.
15．如图， ，请你添加一个条件：，使 （只添一个即可）．
16.如图，Rt△ABC中，∠BAC=90°，AB=AC，分别过点B，C作过点A的直线的垂线BD，C E，垂足分别为点D,E.若BD=2，CE=3，则AE=，AD=.

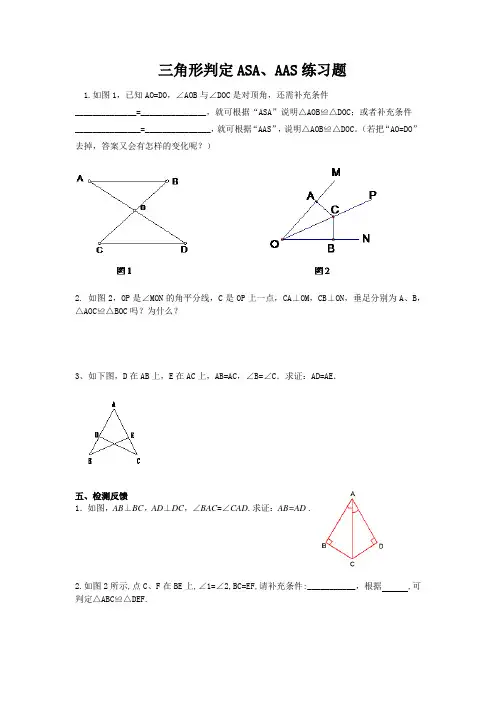
三角形判定ASA、AAS练习题
1.如图1，已知AO=DO，∠AOB与∠DOC是对顶角，还需补充条件
______________=_______________，就可根据“ASA”说明△AOB≌△DOC；或者补充条件
_______________=_______________，就可根据“AAS”，说明△AOB≌△DOC。

（若把“AO=DO”去掉，答案又会有怎样的变化呢？）
2. 如图2，OP是∠MON的角平分线，C是OP上一点，CA⊥OM，CB⊥ON，垂足分别为A、B，△AOC≌△BOC吗？为什么？
3、如下图，D在AB上，E在AC上，AB=AC，∠B=∠C．求证：AD=AE．
五、检测反馈
1．如图，AB⊥BC，AD⊥DC，∠BAC=∠CAD.求证：AB=AD .
2.如图2所示,点C、F在BE上,∠1=∠2,BC=EF,请补充条件:___________，根据 ,可判定△ABC≌△DEF.
3、如图，在△ABC中，∠C=2∠B,AD是△ABC的角平分线，∠1=∠B,求证AB=AC+AD
4、已知：如图，AB=DC，∠A=∠D．试说明：∠1=∠2．
5.如图，ΔABC中，D是AC上一点，BE∥AC，BE=AD，AE分别交BD、BC于点F、G．
⑴图中有全等三角形吗？请找出来，并证明你的结论．
⑵若连结DE，则DE与AB有什么关系？并说明理由．。

全等三角形AAS和ASA练习题全等三角形（三）AAS和ASA例1.在平行四边形ABCD中，AE=CF，证明AB=CD。

例2.在△ABE和△ACD中，AD=AE，∠ACD=∠ABE，证明BD=CE。

例 3.在△ABC和△ABD中，∠C=∠D，∠BAC=∠ABD，证明OC=OD。

例4.在四边形ABCD中，AB=CD，AD=BC，O是BD中点，过O点的直线分别交DA和BC的延长线于E，F，证明AE=CF。

例5.在△ABD和△BCE中，∠1=∠2=∠3，AB=AD，证明BC=DE。

例6.在四边形ABCD中，AB=DC，AD=BC，点F在AD 上，点E在BC上，AF=CE，EF的对角线BD交于O，请问O点有何特征？经典练】1.如果在△ABC和△A' B' C'中，∠A=∠A'，BC'=B'C'，∠C=∠C'，那么△ABC与△A' B' C'全等。

2.在△ABC和△DEF中，点C，F在BE上，∠1=∠2，BC=EF，那么如果再加上条件∠A=∠D，那么△ABC≌△DEF。

3.在△ABC和△A' B' C'中，哪些条件能够判断△ABC与△A' B' C'全等？①∠A=∠A'，∠B=∠B'，BC'=B'C'；②∠A=∠A'，∠B=∠B'，AC'=A'C'；③∠A=∠A'，∠B=∠B'，AC=BC'；④∠A=∠A'，∠B=∠B'，AB'=A'C'。

答案：C。

4.在△ABM和△CDN中，MB=ND，∠MBA=∠NDC，哪些条件不能判断△ABM≌△CDN？A.∠M=∠N；B。

AB=CD；C。

AM=CN；D。

AM∥CN。

答案：A。

5.在△ABC中，AB=AC，D是BC边上一点，E是AC边上一点，且DE∥AB，证明BD=CE。

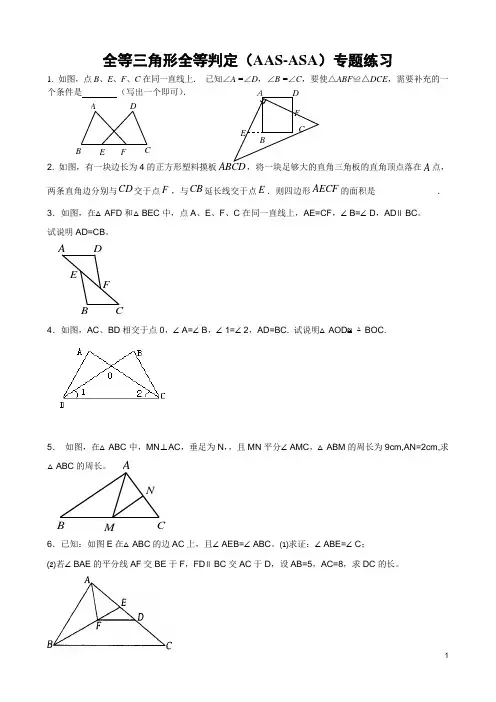
A N M CB AF E D C B A B E F C D全等三角形全等判定（AAS-ASA ）专题练习1. 如图，点B 、E 、F 、C 在同一直线上． 已知∠A =∠D ，∠B =∠C ，要使△ABF ≌△DCE ，需要补充的一个条件是 （写出一个即可）．2. 如图，有一块边长为4的正方形塑料摸板，将一块足够大的直角三角板的直角顶点落在A 点，两条直角边分别与CD 交于点F ，与CB 延长线交于点E ．则四边形AECF 的面积是 ．3．如图，在△AFD 和△BEC 中，点A 、E 、F 、C 在同一直线上，AE=CF ，∠B=∠D ，AD ∥BC 。

试说明AD=CB 。

4．如图，AC 、BD 相交于点0，∠A=∠B ，∠1=∠2，AD=BC. 试说明△AOD ≌△BOC.5． 如图，在△ABC 中，MN ⊥AC ，垂足为N ，，且MN 平分∠AMC ，△ABM 的周长为9cm,AN=2cm,求△ABC 的周长。

6．已知：如图E 在△ABC 的边AC 上，且∠AEB=∠ABC 。

⑴求证：∠ABE=∠C ；⑵若∠BAE 的平分线AF 交BE 于F ，FD ∥BC 交AC 于D ，设AB=5，AC=8，求DC 的长。

A B CD E7．如图，D 是AB 上一点，DF 交AC 于点E ，AE EC =，CF AB ∥．求证：AD CF =．8. 已知：如图 , FB=CE , AB ∥ED , AC ∥FD.F 、C 在直线 BE 上．求证：AB=DE , AC=DF ．9. 已知：如图 , AB ⊥BC 于B , EF ⊥AC 于G , DF ⊥BC 于D , BC=DF ．求证：AC=EF.10. 如图AC ⊥CD 于C , BD ⊥CD 于D , M 是AB 的中点 , 连结CM 并延长交BD 于点F 。

求证：AC=BF ．11. 如图 , E 、D 、B 、F 在同一条直线上 , AD ∥CB , ∠BAD=∠BCD , DE=BF ．求证：AE ∥CF.12. 如图在△ABC和△DBC中, ∠1=∠2 , ∠3=∠4 , P是BC上任意一点．求证：PA=PD.13. 已知：如图, AE=BF , AD∥BC , AD=BC.AB、CD交于O点．求证：OE=OF14.已知：如图AC∥BD , AE和BE分别平分∠CAB∠DBA ,CD过点E．求证AB＝AC＋BD15．一张矩形纸片沿对角线剪开，得到两张三角形纸片，再将这两张三角形纸片摆成如下右图形式，使点B、F、C、D在同一条直线上．（1）求证AB⊥ED；（2）若PB=BC，请找出图中与此条件有关的一对全等三角形，并给予证明．。

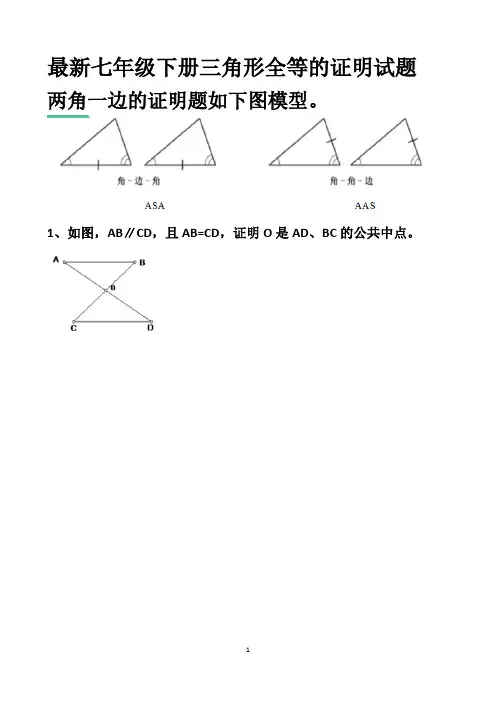
最新七年级下册三角形全等的证明试题两角一边的证明题如下图模型。

1、如图，AB∥CD，且AB=CD，证明O是AD、BC的公共中点。

2、如图，CA⊥OM，CB⊥ON，OC平分∠MON，证明（1）OA=OB（2）连接AB，证明AB⊥OC。

3、如图，∠B=∠C，AD=AE，证明BD=CE。

4、如图，AC平分∠BAD，AB⊥BC，AD⊥DC，证明CA平分∠BCD。

5、如图，AB∥DE，BF=CE，∠A=∠D，试着说明AC和DF的关系。

6、如图，AB=CD，∠A=∠D，证明∠1=∠2.7、如图，∠A=∠D，∠BCE=∠ACD，CB=CE，证明AB=ED。

8、如图，DE⊥AB，DF⊥AC，D是BC的中点，∠BDF=∠CDE，证明AB=AC。

9、如图，∠1=∠2，AB=AE，∠B=∠E，证明∠D=∠C。

10、如图，AB⊥BC，DC⊥BC，BE=CF，∠BED=∠ACF，证明AF⊥DE。

11、如图，CE、BD分别是三角形的两条高线，且AB=AC，证明∠CBD=∠BCE。

12、如图，BE=CF，∠A=∠D，AB∥DE，说明AC和DF的关系。

13、如图，∠C=∠D，∠ABD=∠BAC，证明DE=CE。

14、如图，AB∥CF，AD=CF，证明E是AC的中点。

15、如图，AF=CE，AD∥BC，DF∥BE，说明AB和CD关系。

16、如图，BE⊥CE，AD⊥CE，AC⊥BC，且AC=BC，说明线段BE、AD、DE之间的关系。

17、如图，∠A+∠C=180°,BD平分∠ABC，证明AD=CD。

18、如图，∠1=∠2，∠E=∠D，AE=AD，证明EC=BD。

19、如图，AD=BC，∠A=∠C，说明A、C的连线和B、D的连线的关系。

20、如图，∠1=∠2，∠D=∠E，AB=AC，证明BD=CE。

21、如图，BD平分∠ABC，∠A=∠C，证明A、C的连线和BD垂直。

22、如图，△ABD是以AB为斜边的等腰直角三角形，∠C与∠AEB互补，说明BE和AC的关系。

全等三角形判定练习(ASA、AAS、HL) 判定定理3、有两角及其夹边对应相等的两个三角形全等(ASA)在△ABC和△DFE中∠A=∠D （已知）AB=DE（已知）∠B=∠E（已知）∴△ABC≌△DEF（ASA）判定定理4、有两角及一角的对边对应相等的两个三角形全等(AAS)在△ABC和△DFE中∠A=∠D ,∠C=∠FAB=DE∴△ABC≌△DFE(AAS)判定定理5、直角三角形全等条件有：斜边及一直角边对应相等的两个直角三角形全等(HL) 在Rt△ABC和Rt△A′B′C′中AB=AB (直角边)BC = B′C′（斜边）∴Rt△ABC≌Rt△A′B′C′（HL）1 如图，∠E=∠B，∠1=∠2，EC=BC，求证：DE=AB。

2 已知：如图点C是AB的中点，CD∥BE，且∠D=∠E.求证：. CD=BE3 如图，DC=BC，∠B＝∠D=90°，求证：AB＝AD.ACB ED4 如图，AC⊥OB，BD⊥OA，AC与BD交于E点(1)如果OC=OD，求证：∠A=∠B。

(2)如果∠A=∠B ,OC=OD，求证：AC=BD。

(3)如果AO=BO,OC=OD，求证：∠A=∠B。

OBACDE5 如图.已知AC∥DF，且BE=CF、（1）请你只添加一个条件，使△ABC≌△DEF，你添加的条件是；．．（2）添加条件后，证明△ABC≌△DEF.6 如图，已知：点B、F、C、E在一条直线上，FB=CE，AC=DF．请从下列三个条件中选择一个合适．．．．的条件．．．，添加到已知条件中，使AB∥ED成立，并给出证明．供选择的三个条件（请从其中选择一个）：①AB=ED；②BC=EF；③∠ACB=∠DFE．7 如图，∠A=∠D，AB=CD，则△≌△，请证明8如图，O为AC中点，AB∥CD，证明AB=CDDOC BAAB EFC9 在ABC △中，D 是AB 上一点，DF 交AC 于点E ，DE FE =，AE CE =，AB 与CF 有什么位置关系？证明你的结论10 已知：如图∠B=∠E=90°AC=DF FB=EC ，证明：AB=DEAD BCFE11如图，已知AB=AC，AD=AE，BE与CD相交于O，证明：（1）ΔABE≌ΔACD（2）ΔDOB≌ΔEOC （3）ΔDBC≌ΔECB12 正方形ABCD 中, F 分别是AB 和AD 上的点，已知CE ⊥BF ，垂足为M ，证明BE=AFDMFEA。

全等三角形的判定办法SAS 专题练习之邯郸勺丸创作1.如图,AB=AC,AD=AE,欲证△ABD≌△ACE,可弥补条件( )A.∠1=∠2B.∠B=∠CC.∠D=∠ED.∠BAE=∠CAD2.能判定△ABC≌△A′B′C′的条件是（ ）A ．AB=A′B′,AC=A′C′,∠C=∠C′B. AB=A′B′, ∠A=∠A′,BC=B′C′C. AC=A′C′, ∠A=∠A′,BC=B′CD. AC=A′C′, ∠C=∠C′,BC=B′C3.如图,AB 与CD 交于点O,OA=OC,OD=OB,∠AOD=,按照_________可得到△AOD≌△COB,从而可以得到AD=_________．4.如图,已知BD=CD,要按照“SAS”判定△ABD≌△ACD,则还需添加的条件是.5.如图,AD=BC,要按照“SAS”判定△ABD≌△BAC,则还需添加的条件是6.如图,已知△ABC 中,AB=AC,AD 平分∠BAC,请弥补完整过程说明△ABD≌△ACD 的理由． 解：∵AD 平分∠BAC,∴∠________=∠_________(角平分线的定义).在△ABD 和△ACD 中,∵∴△ABD≌△ACD（ ）7.如图,AC 与BD 相交于点O,已知OA=OC,OB=OD, 第3题第4题第6题第5题求证:△AOB≌△COD证明：在△AOB和△COD中∵∴△AOB≌△COD( )第7题8.已知：如图,AB=CB,∠1=∠2 △ABD 和△CBD 全等吗？9.已知：如图,AB=AC,AD=AE ,∠1 =∠2 .试说明：△ABD ≌△ACE .10.已知：如图,△ABC中, AD⊥BC 于D,AD=BD, DC=DE,∠C=50°.求∠ EBD的度数.全等三角形的判定办法AAS、ASA专题练习1. 已知：如图, FB=CE , AB∥ED ,AC∥FD.F、C在直线BE上．求证：AB=DE , AC=DF．2.已知：如图, AB⊥BC于B , EF⊥AC于G ,DF⊥BC于D , BC=DF．求证：AC=EF.3. 已知：如图AC⊥CD于C , BD⊥CD于D , M是AB的中点 , 连结CM并延长交BD于点F.求证：AC=BF．4. 已知：如图 , E、D、B、F在同一条直线上 ,AD∥CB , ∠BAD=∠BCD , DE=BF．求证：AE∥CF.5.如图在△ABC和△DBC中, ∠1=∠2 , ∠3=∠4 ,P是BC上任意一点．求证：PA=PD.6.已知：如图, AE=BF , AD∥BC , AD=BC.AB、CD 交于O点．求证：OE=OF7.已知：如图AC∥BD , AE和BE辨别平分∠CAB∠DBA ,CD过点E．求证AB＝AC＋BD时间：二O二一年七月二十九日。

A B E F C 第1题 D全等三角形的判定(AAS-ASA)专题练习（优选.)龙江三中八年级数学分层教学专用练习题制卷人：田丽华审核人：刘海欣12.2三角形全等判定3-----AAS 或ASA 专题练习基础C 级1.如图，点B 、E 、F 、C 在同一直线上． 已知∠A =∠D ，∠B =∠C ，要使△ABF ≌△DCE ，需要补充的一个条件是（写出一个即可）．2.如图，已知BD=CD ，∠B =∠C ，要根据“AAS ”判定△ABD ≌△ACD ，则还需添加的条件是3.如图，AD=BC ，∠D =∠C ，要根据“ASA ”判定△ABD ≌△BAC ，则还需添加的条件是4.如图，AC 、BD 相交于点0，∠A=∠B ，∠1=∠2，AD=BC.试说明△AOD ≌△BOC.证明：∵∠A=∠B ，∠1=∠2 （已知）∴∠ADC=∠BCD （三角形内角和）∴∠ADC-∠1=∠BCD- ∠2即∠________=∠_________在△AOD 和△BOD 中，∵∴△AOD ≌△BOD （ ）5.如图，AC 与BD 相交于点O ，已知OA=OC ，∠A=∠C ，求证:△AOB ≌△COD证明：在△AOB 和△COD 中第2题 第5题第3题A F E D CB∵∴△AOB ≌△COD( )能力B 级1．如图，在△AFD 和△BEC 中，点A 、E 、F 、C 在同一直线上，AE=CF ，∠B=∠D ，AD ∥BC 。

试说明AD=CB 。

2.已知：如图 , ∠1=∠2 , ∠3=∠4求证：AC=AB ．3. 已知：如图 , FB=CE , AB ∥ED , AC ∥FD.F 、C 在直线 BE 上．求证：AB=DE , AC=DF ．综合A级1. 如图AC⊥CD于C , BD⊥CD于D , M是AB的中点 , 连结CM并延长交BD于点F。

求证：AC=BF．2. 如图在△ABC和△DBC中 , ∠1=∠2 , ∠3=∠4 ,P是BC上任意一点．求证：PA=PD.3.已知：如图 , AB⊥BC于B , EF⊥AC于G , DF⊥BC于D , BC=DF．求证：AC=EF.4.已知：如图AC∥BD , AE和BE分别平分∠CAB∠DBA ,CD过点E．求证：AB＝AC＋BD赠人玫瑰，手留余香。

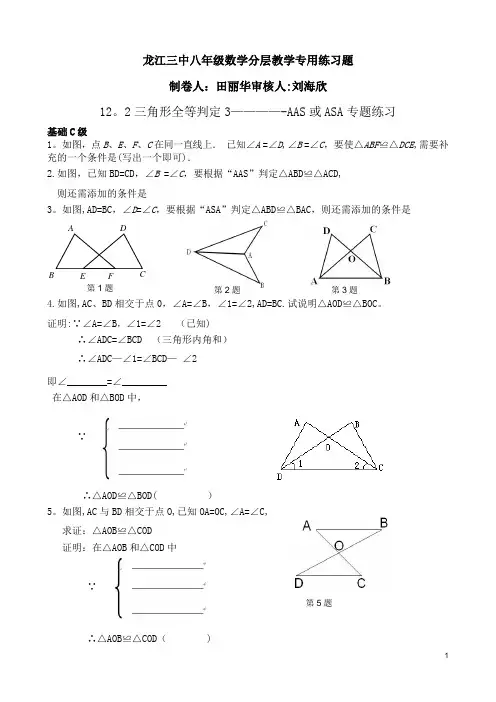
A B E F C 第1题 D龙江三中八年级数学分层教学专用练习题制卷人：田丽华审核人:刘海欣12。

2三角形全等判定3————-AAS 或ASA 专题练习基础C 级1。

如图，点B 、E 、F 、C 在同一直线上． 已知∠A =∠D ,∠B =∠C ，要使△ABF ≌△DCE ,需要补充的一个条件是(写出一个即可)．2.如图，已知BD=CD ，∠B =∠C ，要根据“AAS ”判定△ABD ≌△ACD,则还需添加的条件是3。

如图,AD=BC ，∠D =∠C ，要根据“ASA ”判定△ABD ≌△BAC ，则还需添加的条件是4.如图,AC 、BD 相交于点0，∠A=∠B，∠1=∠2,AD=BC.试说明△AOD≌△BOC。

证明:∵∠A=∠B ，∠1=∠2 （已知)∴∠ADC=∠BCD （三角形内角和）∴∠ADC —∠1=∠BCD — ∠2即∠________=∠_________在△AOD 和△BOD 中，∵∴△AOD ≌△BOD( ）5。

如图,AC 与BD 相交于点O,已知OA=OC,∠A=∠C,求证：△AOB ≌△COD证明：在△AOB 和△COD 中∵∴△AOB ≌△COD （ )第2题 第5题 第3题A F E D CB 能力B 级1．如图，在△AFD 和△BEC 中，点A 、E 、F 、C 在同一直线上，AE=CF,∠B=∠D，AD∥BC.试说明AD=CB 。

2。

已知:如图 ， ∠1=∠2 ， ∠3=∠4求证：AC=AB ．3。

已知:如图 ， FB=CE ， AB ∥ED , AC ∥FD 。

F 、C 在直线 BE 上．求证:AB=DE , AC=DF ．综合A级1。

如图AC⊥CD于C ， BD⊥CD于D , M是AB的中点 , 连结CM并延长交BD于点F。

求证：AC=BF．2。

如图在△ABC和△DBC中, ∠1=∠2 ，∠3=∠4 ,P是BC上任意一点．求证：PA=PD。

3.已知：如图, AB⊥BC于B ，EF⊥AC于G , DF⊥BC于D , BC=DF．求证：AC=EF.4.已知：如图AC∥BD ， AE和BE分别平分∠CA B∠DBA ，CD过点E．求证:AB＝AC＋BD。

14．(2016·福州)如图，∠1＝∠2，∠3＝∠4.求证：AC＝AD.
解 ： ∵∠3 ＝ ∠4 ， ∴ ∠ ABC ＝ ∠ABD. 在 △ABC 和 △ABD 中 ， ∠1＝∠2， ∴△ABC≌△ABD(ASA)，∴AC＝AD AB＝AB， ∠ABC＝∠ABD，
15．(习题变式)如图，点A，F，E，C在同一直线上，AB∥CD，∠ABE＝
1．如图，要测量池塘两岸相对的两点A，B的距离，可以在AB的垂线BF上 取两点C，D，使BC＝CD，再画出BF的垂线DE，使E与A，C在一条直线上， 这时测得DE的长就是AB的长，它的理论依据是( C A．SSS B．SAS C．ASA D．AAA )
2．如图，在四边形ABCD中，AB∥CD，若用“ASA”证明 ∠ACB＝∠CAD(或AD∥BC) △ABC≌△CDA，需添加条件_____________________________ ．
)
A．4个 B．3个
C．2个 D．1个
11．如图，在△ABC中，∠BAC＝90°，AB＝AC，分别过B，C两点作过 A的直线的垂线BD，CE，D，E为垂足，若BD＝4，CE＝3，则DE的长为 ____ 7 ．

12．如图，有一块边长为4的正方形塑料模板ABCD，将一块足够大的直角 三角板的直角顶点放在A点，两条直角边分别与CD交于点F，与CB的延长线 交于点E，则四边形 AECF的面积是______ 16 ．
八年级上册人教版数学
第十二章 全等三角形
12．2 三角形全等的判定
第3课时 用“ASA”或“AAS”证三角形全等
相等 夹边 1．_______ ASA 分别_________的两个三角形全等，可简写成 角边角 和它们的________ “____________”或“__________”． 练习1：如图，BD平分∠ABC和∠ADC，则△ABD≌△CBD，依据是 ( A ) A．ASA C．SAS

三角形全等AAS/ASA练习题一．解答题（共14小题）1．如图，AC＝AE，∠C＝∠E，∠1＝∠2．求证：△ABC≌△ADE．2．已知，如图，AB＝AE，AB∥DE，∠ECB＝70°，∠D＝110°，求证：△ABC≌△EAD．3．如图，D是AB上一点，DF交AC于点E，DE＝FE，FC∥AB，求证：△ADE≌△CFE．4．如图，∠A＝∠B，AE＝BE，点D在AC 边上，∠1＝∠2，AE和BD相交于点O．求证：△AEC≌△BED．5．如图，∠ACB＝90°，AC＝BC，AD⊥CE，BE⊥CE，垂足分别为D，E．求证：△ACD≌△CBE．6．如图，在Rt△ABC中，∠ACB＝90°，AC＝BC，过C点作直线l，点D，E在直线l上，连接AD，BE，∠ADC＝∠CEB ＝90°．求证：△ADC≌△CEB．7．已知：如图，点A、E、F、C在同一条直线上，AD∥CB，∠1＝∠2，AE＝CF．求证：△ADF≌△CBE．8．已知AB∥DE，BC∥EF，D，C在AF上，且AD＝CF，求证：△ABC≌△DEF．9．如图，AB＝AD，∠C＝∠E，∠1＝∠2，求证：△ABC≌△ADE．10．如图，AB＝AE，∠1＝∠2，∠C＝∠D．求证：△ABC≌△AED．12．如图（1），AB＝7cm，AC⊥AB，BD⊥AB垂足分别为A、B，AC＝5cm．点P在线段AB上以2cm/s的速度由点A向点B运动，同时，点Q在射线BD上运动．它们运动的时间为t（s）（当点P运动结束时，点Q运动随之结束）．（1）若点Q的运动速度与点P的运动速度相等，当t＝1时，△ACP与△BPQ是否全等，并判断此时线段PC和线段PQ的位置关系，请分别说明理由；（2）如图（2），若“AC⊥AB，BD⊥AB”改为“∠CAB＝∠DBA＝60°”，点Q的运动速度为xcm/s，其他条件不变，当点P、Q运动到某处时，有△ACP与△BPQ全等，求出相应的x、t的值．13．如图，△ABC中，∠ACB＝90°，AC＝6cm，BC＝8cm，点P从A点出发沿A﹣C路径向终点C运动；点Q从B点出发沿B﹣C﹣A路径向终点A运动．点P和Q分别以每秒1cm和3cm的运动速度同时开始运动，其中一点到达终点时另一点也停止运动，在某时刻，分别过P和Q作PE⊥l于E，QF⊥l于F．则点P运动时间为多少时，△PEC与△QFC全等？14．如图1，在长方形ABCD中，AB＝CD＝6cm，BC＝10cm，点P从点B出发，以2cm/s 的速度沿BC向点C运动，设点P的运动时间为t秒，且t≤5．（1）PC＝cm（用含t的代数式表示）．（2）如图2，当点P从点B开始运动的同时，点Q从点C出发，以vcm/s的速度沿CD 向点D运动，是否存在这样的v值，使得以A、B、P为顶点的三角形与以P、Q、C为顶点的三角形全等？若存在，请求出v的值；若不存在，请说明理由．三角形全等AAS/ASA练习题参考答案一．解答题（共14小题）1．；2．；3．；4．；5．；6．；7．；8．；9．；10．；11．；12．；13．；14．（10﹣2t）；。

三角形全等的判定练习一、三角形的全等性质：1 如图：△ ABC^A A B'，则有:AB= —, BC= —, CA =—/ A= ___ , / B= _ , / C= _ ,二、“SSS”判定的应用：1•完成下面的推理：如图，(1 )在厶ABC与厶A' B'中,AB A'B',2.如图：△ ADF ◎△ CBE，问AD 会平行CB吗？AE会等于CF吗？AC AC,• △ ABC^A A' B' (SSS・5 .如图，在△ ABC中，AB=AC , CD是厶ABC的中线，说明①厶ABD◎△ ACD。

②AD丄CB。

C 解: △A DF ◎△ CBE ( ____ )•I / A= __ (___••• AD// BC ( _______________ )△A DF ◎△ CBE ( ____ )•- AF=—( ____________________ )• AF-EF= B CA 2.女口图，AB=CD , AD=BC ,全等吗？AD会平行CB吗？解：在△ ADC与厶CBA中AD ,问：△ ADC与厶CBA ArB C6 .如图，△ ABD 和厶ABC , AC=AD , BC = BD , 那么△ ABD和厶ABC全等吗？即AE =—3.如图：△ ADB ◎△ ADC ,解: •/ △ ADB ADCAC AC,•=90•AD 丄CB=180问AD会垂直CB吗?4.如图：△ ABC ADE，问/ BAD= / CAE 吗?5.如图：△ ADF ◎△ CBE会等于CF吗？AE问AD会平行CB吗?A D•△ ADC ◎△ CBA( __ )•- / ____ = / _____ ( ___•AD// BC ( _______________________ )3.如图，C是BD和EF的中点，且BE=DF说明△BEC◎△ DFC。

4.女口图，在厶ADF 与厶BCE 中，AD=BC , DF=BE ,AE=CF，说明①厶ADF ◎△ CBE ,②AD // BC。

全等三角形的判定（SSS）1、如图1，AB=AD，CB=CD，∠B=30°，∠BAD=46°，则∠ACD的度数是( )A.120°B.125°C.127°D.104°2、如图2，线段AD与BC交于点O，且AC=BD，AD=BC，•则下面的结论中不正确的是( )A.△ABC≌△BADB.∠CAB=∠DBAC.OB=OCD.∠C=∠D3、在△ABC和△A1B1C1中，已知AB=A1B1，BC=B1C1，则补充条件____________，可得到△ABC≌△A1B1C1．4、如图3，AB=CD，BF=DE，E、F是AC上两点，且AE=CF．欲证∠B=∠D，可先运用等式的性质证明AF=________，再用“SSS”证明______≌_______得到结论．5、如图，已知AB=CD，AC=BD，求证：∠A=∠D．6、如图，AC与BD交于点O，AD=CB，E、F是BD上两点，且AE=CF，DE=BF.请推导下列结论：⑴∠D=∠B；⑵AE∥CF．7、已知如图，A、E、F、C四点共线，BF=DE，AB=CD.⑴请你添加一个条件，使△DEC≌△BFA；⑵在⑴的基础上，求证：DE∥BF.全等三角形的判定(SAS)1、如图1，AB∥CD，AB=CD，BE=DF，则图中有多少对全等三角形( )A.3B.4C.5D.62、如图2，AB=AC，AD=AE，欲证△ABD≌△ACE，可补充条件( )D CBA A.∠1=∠2 B.∠B=∠C C.∠D=∠E D.∠BAE=∠CAD3、如图3，AD=BC ，要得到△ABD 和△CDB 全等，可以添加的条件是( ) A.AB ∥CD B.AD ∥BC C.∠A=∠C D.∠ABC=∠CDA4、如图4，AB 与CD 交于点O ，OA=OC ，OD=OB ，∠AOD=________，•根据_________可得到△AOD ≌△COB ，从而可以得到AD=_________．5、如图5，已知△ABC 中，AB=AC ，AD 平分∠BAC ，请补充完整过程说明△ABD ≌△ACD 的理由． ∵AD 平分∠BAC ， ∴∠________=∠_________(角平分线的定义). 在△ABD 和△ACD 中，∵____________________________， ∴△ABD ≌△ACD （ ） 6、如图6，已知AB=AD ，AC=AE ，∠1=∠2，求证∠ADE=∠B.7、如图，已知AB=AD ，若AC 平分∠BAD ，问AC 是否平分∠BCD ？为什么？8、如图，在△ABC 和△DEF 中，B 、E 、F 、C ，在同一直线上，下面有4个条件，请你在其中选3个作为题设，余下的一个作为结论，写一个真命题，并加以证明. ①AB=DE ； ②AC=DF ； ③∠ABC=∠DEF ； ④BE=CF.9、如图⑴，AB ⊥BD ，DE ⊥BD ，点C 是BD 上一点，且BC=DE ，CD=AB ．⑴试判断AC 与CE 的位置关系，并说明理由．⑵如图⑵，若把△CDE 沿直线BD 向左平移，使△CDE 的顶点C 与B 重合，此时第⑴问中AC 与BE 的位置关系还成立吗？(注意字母的变化)全等三角形（三）AAS 和ASA【知识要点】1．角边角定理（ASA ）：有两角及其夹边对应相等的两个三角形全等.2．角角边定理（AAS ）：有两角和其中一角的对边对应相等的两个三角形全等.【典型例题】例1．如图，AB ∥CD ，AE=CF ，求证：AB=CD例2．如图，已知：AD=AE ，ABE ACD ∠=∠，求证：BD=CE.例3．如图，已知：ABD BAC D C ∠=∠∠=∠.，求证：OC=OD. 例4．如图已知：AB=CD ，AD=BC ，O 是BD 中点，过O 点的直线分别交DA 和BC 的延长线于E ，F.求证：AE=CF.例5．如图，已知321∠=∠=∠，AB=AD.求证：BC=DE.例6．如图，已知四边形ABCD 中，AB=DC ，AD=BC ，点F 在AD 上，点E 在BC 上，AF=CE ，EF 的对角线BD 交于O ，请问O 点有何特征？AABD C EO12 3AFDOBEC【经典练习】1.△ABC 和△C B A '''中，C B C B A A ''='∠=∠,'，C C '∠=∠则△ABC 与△C B A ''' .2．如图，点C ，F 在BE 上，,,21EF BC =∠=∠请补充一个条件，使△ABC ≌DFE,补充的条件是 .3．在△ABC 和△C B A '''中，下列条件能判断△ABC 和△C B A '''全等的个数有（ ） ①A A '∠=∠ B B '∠=∠，C B BC ''= ②A A '∠=∠，B B '∠=∠，C A C A ''=' ③A A '∠=∠ B B '∠=∠，C B AC ''= ④A A '∠=∠，B B '∠=∠，C A B A ''=' A ． 1个 B. 2个 C. 3个 D. 4个4．如图，已知MB=ND ，NDC MBA ∠=∠，下列条件不能判定是△ABM ≌△CDN 的是（ ）A ． N M ∠=∠ B. AB=CD C ． AM=CN D. AM ∥CN 5．如图2所示， ∠E =∠F =90°，∠B =∠C ，AE =AF ，给出下列结论：①∠1=∠2 ②BE=CF ③△ACN ≌△ABM ④CD=DN其中正确的结论是_________ _________。

全等三角形（三）AAS和ASA【知识要点】1．角边角定理（ASA）：有两角及其夹边对应相等的两个三角形全等.2．角角边定理（AAS）：有两角和其中一角的对边对应相等的两个三角形全等. 【典型例题】例1．如图，AB∥CD，AB=CD，求证：OE=OF例2．如图，已知：AD=AE，ABEACD∠=∠，求证：BD=CE. 例3．如图，已知：ABDBACDC∠=∠∠=∠.，求证：BC=AD. 例4．如图，已知321∠=∠=∠，AB=AD.求证：BC=DE.AAB D CEO123【经典练习】1.△ABC 和△C B A '''中，C B C B A A ''='∠=∠,'，C C '∠=∠则△ABC 与△C B A ''' .2．如图，点C ，F 在BE 上，,,21EF BC =∠=∠请补充一个条件，使△ABC ≌DFE,补充的条件是 .第2题 第4题3．在△ABC 和△C B A '''中，下列条件能判断△ABC 和△C B A '''全等的个数有（ ）①A A '∠=∠ B B '∠=∠，C B BC ''= ②A A '∠=∠，B B '∠=∠，C A C A ''=' ③A A '∠=∠ B B '∠=∠，C B AC ''= ④A A '∠=∠，B B '∠=∠，C A B A ''=' A ． 1个 B. 2个 C. 3个 D. 4个 4．如图，已知MB=ND ，NDC MBA ∠=∠，下列条件不能判定是△ABM ≌△CDN 的是（ ）A ． N M ∠=∠ B. AB=CD C ． AM=CN D. AM ∥CN 5．如图2所示， ∠E =∠F =90°，∠B =∠C ，AE =AF ，给出下列结论：①∠1=∠2 ②BE=CF ③△ACN ≌△ABM ④CD=DN其中正确的结论是_________ _________。

全等三角形的判定方法SAS专题练习1. 如图，AB=AC，AD=AE，欲证△ABD≌△ACE，可补充条件( )A.∠1=∠2B. ∠B=∠CC. ∠D =∠ED. ∠BAE=∠CAD2. 能判定△ABC≌△A′B′C′的条件是（）A．AB=A′B′，AC=A′C′，∠C =∠C′第1 题B. AB=A′B′，∠A=∠A′，BC=B′C′C. AC=A′C′，∠A=∠A′，BC=B′C第3 题D. AC=A′C′，∠C=∠C′，BC=B′C3. 如图，AB与CD交于点O，OA=O，C OD=O，B∠AOD=，根据_________可得到△AOD≌△COB，从而可以得到AD=_________．4. 如图，已知BD=C，D要根据“SAS”判定△ABD≌△ACD，第4 题需添加的条件是。

则还5. 如图，AD=BC，要根据“SAS”判定△ABD≌△BAC，需添加的条件是则还6. 如图，已知△ABC中，AB=AC，AD平分∠BAC，明△ABD≌△ACD的理由．程说请补充完整过解：∵AD平分∠BAC，第5 题∴∠________=∠_________(角平分线的定义).在△ABD和△ACD中，∵第6 题∴△ABD≌△ACD（）7. 如图，AC与BD相交于点O，已知OA=O，C OB=O，D:△AOB≌△COD求证证明：在△AOB和△COD中∵第7 题∴△AOB≌△COD( )8. 已知：如图，AB=CB，∠1=∠2 △ABD和△CBD全等吗？9. 已知：如图，AB=AC，AD=AE，∠1 = ∠2 。

试说明：△ABD≌△ACE。

10. 已知：如图，△ABC中，AD⊥BC 于D，AD=BD，DC=DE，∠C=50°。

求∠EBD的度数。

习全等三角形的判定方法AAS、ASA专题练1. 已知：如图, FB=CE , AB∥ED , AC∥FD.F、C 在直线B E 上．：AB=DE , AC=DF ．求证2.已知：如图, AB⊥BC 于B , EF⊥AC 于G , DF⊥BC 于D , BC=DF．：AC=EF .求证3. 已知：如图A C⊥CD 于 C , B D⊥CD 于D , M 是AB 的中点, 连结CM 并延长交BD 于点F。

用“ASA”或“AAS判断两个三角形全等1、有‗‗‗‗‗‗和它们的‗‗‗‗‗‗分别‗‗‗‗‗‗的两个三角形全等，可简写成“‗‗‗‗‗‗”或“‗‗‗‗‗‗”。

2、有‗‗‗‗‗‗和其中一角的对边分别相等的两个三角形全等，可简写成“‗‗‗‗‗‗”或“‗‗‗‗‗‗”。

3、三角分别相等的两个三角形‗‗‗‗‗‗全等。

4、如图所示，已知AB平分∠CAD，当∠1=∠2时，△ABC≌△ABD的依据是‗‗‗‗‗‗‗‗‗‗.5、如图，某同学把一块三角形的玻璃打碎成三块，现在他要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是带‗‗‗‗‗‗去配，依据是‗‗‗‗‗‗‗‗‗.6、如图，已知，EC=AC，∠BCE=∠DCA，∠A=∠E，求证：BC=DC.7、如图，已知：在△AFD和△CEB中，点A、E、F、C在同一直线上，AE=CF，∠B=∠D，AD∥BC.求证AD=CB.8、如图，AC与BD交于点O，∠A=∠D，请补充条件‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗，使△AOB≌△DOC.9、如图，∠ABC=∠DEF，AB=DE，要说明△ABC≌△DEF，（1）若以“SAS”为依据，还需添加的条件为‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗；（2）若以“ASA”为依据，还需添加的条件为‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗；（3）若以“AAS”为依据，还需添加的条件为‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗；10、如图所示，点D在△ABC的BC边上，DE与AC交于F，若∠1=∠2=∠3，AE=AC，则（） .A、△ABD≌△AFEB、△AFE≌△ADCC、△AFE≌DFCD、△ABC≌△ADE11、根据下列已知条件，能唯一画出△ABC的是（）.A 、AB=3，BC=4，CA=8 B、AB=4，BC=3，∠A=30°C、∠A=60°，∠B=45°，AB=4D、∠C=90°，AB=612、如图，有一块直角三角形纸片，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且点C与斜边AB的中点E正好重合，则∠CAB等于（）。

∴△ABF≌△ACF(SAS)，∴AB＝AC
AD =AE ，在△ABD和△ACE中， BD =CE AB =AC
∴△ABD≌△ACE，∴∠D＝∠E
18．(14分)两个大小不同的等腰直角三角板如图①放 置，图②是由它抽象出的几何图形，B，C，E在同一条 直线上，连接CD.求证：CD⊥BE.
6．(10分)如图，在△ABC中，∠ACB＝90°，AC＝ BC，BE⊥CE于点E，AD⊥CE于点D.求证： △BEC≌△CDA.
证明：∵∠ACB＝90°，BE⊥CE， AD⊥CE，∴∠BEC＝∠ADC＝90°， ∴∠BCE＋∠CBE＝90°，∠BCE＋∠ACD ＝90°，∴∠CBE＝∠ACD， 又∵AC＝BC，∴△BEC≌△CDA(AAS)
8．(8分)如图，已知：AB＝AD，AC＝AE，∠1＝ ∠2， 求证： (1)△ABC≌△ADE； (2)∠B＝∠D.
解：证明：(1)∵∠1＝∠2， ∴∠1＋∠EAC＝∠2＋∠EAC， 即∠BAC＝∠DAE， 又∵AB＝AD，AC＝AE， ∴△ABC≌△ADE (2)∵△ABC≌△ADE，∴∠B＝ ∠D
解：证△ABE≌△ACD(SAS)，得
∠ACD＝∠ABE＝45°，∴∠BCD
＝∠ACB＋∠ACD＝45°＋45°＝ 90°，即CD⊥BE.
9. 如图，已知AC平分∠BAD， ∠1=∠2，求证：AB=AD
2、如图:已知：AD为△ABC的中线，且CF⊥AD于点F，
BE⊥AD交AD的延长线于点E.求证：BE＝CF.
证明：∵AD为△ABC的中线， ∴BD＝CD.∵BE⊥AD，CF⊥AD， ∴∠BED＝∠CFD＝90°. 在△BED与△CFD中，
BED CFD 1 2 BD CD