高中数学 不等式恒成立问题 教案

教师： 学生： 时间: 2018年 2月 日 时段：高中 一、授课目的与考点分析：授课目的：在近些年的数学高考题及高考模拟题中经常出现恒成立问题，这样的题目一般综合性强，可考查函数、数列、不等式及导数等诸多方面的知识。

同时，培养学生分析问题、解决问题、综合驾驭知识的能力。

本人根据高考题及高考模拟题总结了四种常见的解决不等式恒成立问题的方法。

法一：转换主元法。

适用于一次型函数。

法二：化归二次函数法。

适用于二次型函数。

法三：分离参数法。

适用于一般初等函数。

法四：数型结合法。

二、授课内容 不等式恒成立问题1) 一、常见类型 1. 1.恒成立问题若不等式()f x A >在区间D 上恒成立,则等价于在区间D 上()min f x A > 若不等式()f x B <在区间D 上恒成立,则等价于在区间D 上()max f x B < 2 2. 能成立问题若在区间D 上存在实数x 使不等式()f x A >成立,则等价于在区间D 上()max f x A >； 若在区间D 上存在实数x 使不等式()f x B <成立,则等价于在区间D 上的()min f x B <.3 3. 恰成立问题若不等式()f x A >在区间D 上恰成立, 则等价于不等式()f x A >的解集为D ； 若不等式()f x B <在区间D 上恰成立, 则等价于不等式()f x B <的解集为D .二、 四种常见的方法法一：转换主元法。

适用于一次型函数。

法二：化归二次函数法。

适用于二次型函数。

法三：分离参数法。

适用于一般初等函数。

法四：数型结合法。

在近些年的数学高考题及高考模拟题中经常出现恒成立问题，这样的题目一般综合性强，可考查函数、数列、不等式及导数等诸多方面的知识。

同时，培养学生分析问题、解决问题、综合驾驭知识的能力。

在解综合性较强的恒成立问题时，有时一题多法。

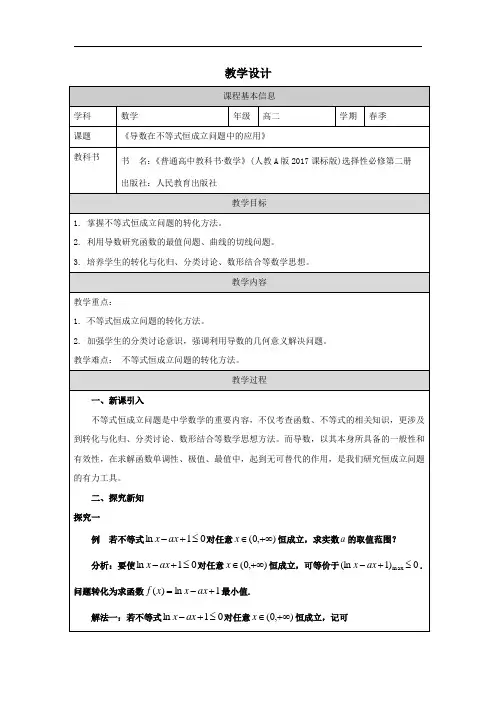
不等式的恒成立,能成立,恰成立等问题不等式恒成立问题的常规处理方式:常应用函数方程思想和“分离变量法”转化为最值问题，也可抓住所给不等式的结构特征，利用数形结合法）1).恒成立问题若不等式()A x f >在区间D 上恒成立,则等价于在区间D 上()min f x A >若不等式()B x f <在区间D 上恒成立,则等价于在区间D 上()max f x B < 2). 能成立问题若在区间D 上存在实数x 使不等式()A x f >成立,则等价于在区间D 上()max f x A >； 若在区间D 上存在实数x 使不等式()B x f <成立,则等价于在区间D 上的()m i n f x B <.3). 恰成立问题若不等式()A x f >在区间D 上恰成立, 则等价于不等式()A x f >的解集为D ； 若不等式()B x f <在区间D 上恰成立, 则等价于不等式()B x f <的解集为D .1.设常数a ＞0，若9x ＋a 2x ≥a ＋1对一切正实数x 成立，则a 的取值范围为___．2.已知f (x )＝2x x 2＋6.若对任意x >0，f (x )≤t 恒成立，求实数t 的范围． 3.当x>1时，不等式恒成立，则实数a 的取值范围是 A ．(－∞,2] B ．[2,+∞) C ．[3,+∞) D ．(－∞,3]4.若对任意恒成立，则的取值范围是_____5.若对任意x ＞0，x x 2＋3x ＋1≤a 恒成立，则a 的取值范围是________． 6.已知x ＞0，y ＞0，xy ＝x ＋2y ，若xy ≥m －2恒成立，则实数m 的最大值是________．7．已知x >0，y >0，2x +y =1，若2240x y m <+恒成立，则m 的取值范围是8.不等式)(322y x ay y x +≥+对任意R y x ∈,恒成立,则实数a 的最大值为.9.已知正实数满足,且恒成立,则的最大值是________.10. 若正实数,x y 满足244x y xy ++=，且不等式2(2)22340x y a a xy +++-≥恒成立，则实数a 的取值范围是 ．0x >1a ≤+a ,x y ln ln 0x y +=22(2)4k x y x y +≤+k。

高中数学恒成立问题教案
一、教学目标：
1. 理解恒成立问题的概念，并能够应用相关方法解决问题。

2. 掌握常见的恒成立问题解题技巧。

3. 提高分析问题和推理能力。

二、教学内容：
1. 恒成立问题的定义和性质。

2. 常见的恒成立问题的解法。

3. 实际问题中的恒成立问题应用。

三、教学重点：
1. 恒成立问题的理解和应用。

2. 常见恒成立问题的解法。

四、教学难点：
1. 理解恒成立问题的本质。

2. 能够灵活应用解题方法。

五、教学过程：
1. 概念引入（5分钟）：
教师简要介绍恒成立问题的概念和意义，引发学生的兴趣。

2. 例题讲解（15分钟）：
解释一个常见的恒成立问题，并指导学生解题思路和方法。

3. 学生练习（20分钟）：
让学生在教师的指导下，自行解决一些恒成立问题，并在课堂上相互讨论、交流解题思路。

4. 拓展练习（15分钟）：
提供一些更具挑战性的恒成立问题，让学生在课后自行解决。

5. 总结（5分钟）：
回顾本节课学习的内容，强调恒成立问题在数学分析中的重要性。

六、作业：
完成拓展练习题，并写一篇关于恒成立问题的小结。

七、教学反思：
本教案注重引导学生理解恒成立问题的本质，并通过实例讲解和练习巩固学习成果。

同时，引导学生在解题过程中思考，提高解决实际问题的能力。

学习过程一、复习预习考纲要求：1．理解导数和切线方程的概念。

2．能在具体的数学环境中，会求导，会求切线方程。

3．特别是没有具体点处的切线方程，如何去设点，如何利用点线式建立直线方程。

4．灵活应用建立切线方程与其它数学知识之间的内在联系。

5. 灵活应用导数研究函数的单调性问题二、知识讲解1.导数的计算公式和运算法那么几种常见函数的导数：0'=C (C 为常数)；1)'(-=n n nx x (Q n ∈)；x x cos )'(sin =； x x sin )'(cos -=；1(ln )x x '=； 1(log )log a a x e x'=， ()x x e e '= ； ()ln x x a a a '= 求导法那么：法那么1 [()()]()()u x v x u x v x ±'='±'．法那么2 [()()]()()()()u x v x u x v x u x v x '='+', [()]'()Cu x Cu x '=法那么3： '2''(0)u u v uv v v v -⎛⎫=≠ ⎪⎝⎭复合函数的导数：设函数()u x ϕ=在点x 处有导数()x u x ϕ'='，函数()y f u =在点x 的对应点u 处有导数()u y f u '='，那么复合函数(())y f x ϕ=在点x 处也有导数，且x u x u y y '''⋅= 或(())()()x f x f u x ϕϕ'='⋅'2.求直线斜率的方法〔高中范围内三种〕(1) tan k α=〔α为倾斜角〕； (2) 1212()()f x f x k x x -=-，两点1122(,()),(,())x f x x f x ； (3)0()k f x '= 〔在0x x =处的切线的斜率〕；3.求切线的方程的步骤：〔三步走〕〔1〕求函数()f x 的导函数()f x '；〔2〕0()k f x '= 〔在0x x =处的切线的斜率〕；〔3〕点斜式求切线方程00()()y f x k x x -=-；4.用导数求函数的单调性：〔1〕求函数()f x 的导函数()f x '；〔2〕()0f x '>，求单调递增区间；〔3〕()0f x '<，求单调递减区间；〔4〕()0f x '=，是极值点。

恒成立不等式的参数求解类型及方法对于恒成立不等式的参数问题，涉及知识面广，要求有较高的解题技巧.本文通过举例给同学们介绍恒成立不等式中参数问题的常见类型及解法.一、对于一次函数f (x )=kx +b ,若f (m )＞0,f (n )＞0,则当x ∈[m ,n ]时，恒有f (x )＞0.例1 已知P =(log 2x －1)(log a b )2+log 2x －6log 2x ·log a b +1(a ＞0,a ≠1)当x ∈[1,2]内任意取值时，P 的值恒为正，求b 的取值范围.解：P 可变形为P =[(log a b )2－6log a b ＋1]log 2x －(log a b )2＋1设t =log 2x ，则t ∈[0,1]P =f (t )=[(log a b )2－6log a b ＋1]t －(log a b )2＋1.于是，该问题就转化成当t ∈[0,1]时，f (t )＞0恒成立，求b 的取值范围.因为f (t )是一次函数，所以f (t )在[0，1]上恒为正，则有31log 102log 6)1(01)(log )0(2 b b f b f a a a -⇒⎩⎨⎧+-=+-= 故当a ＞1时，a 1＜b ＜3a ;当0＜a ＜1时，3a ＜b ＜a1. 二、不等式ax 2+bx +c ＞0对任意实数x 恒成立的充要条件是⎩⎨⎧⎩⎨⎧==0000 Δa c b a 或 不等式ax 2＋bx ＋c ＜0对任意实数x 恒成立的充要条件是⎩⎨⎧⎩⎨⎧==0000 Δa c b a 或 例2 不等式（a 2－1）x 2－(a －1)x －1＜0对x ∈R 恒成立，求a 的变化范围.解：（1）当a =1时，－1＜0，不等式恒成立；当a =－1时，不等式对x ∈R 不恒成立.（2）当a 2≠1时，有153153110)1(4)1(01222 a a a a a Δa -⇒⎪⎩⎪⎨⎧--⇒⎪⎩⎪⎨⎧-+-=- 综合（1）、（2）得153≤-a 三、若函数f (x )具有最大值，则f (x )≤a 恒成立的充要条件是max )(x f ≤a ;若函数f (x )具有最小值，则f (x )≥a 恒成立的充要条件是min)(x f ≥a .例3 设函数f (x )=ax 2－2x +2对于满足1＜x ＜4的一切x 都有f (x )＞0，求实数a 的取值范围. 解：原题化为⎪⎩⎪⎨⎧-⇔⎩⎨⎧+-22)1(24102241x x a x x ax x记max 2])1(2[x x M -= 令21)211(2)1(2)(22+--=-=x xx x t ∵1141 x∴当21,2,11===M x x x 时即 ∴a ＞.21 四、有一类对任意实数恒成立的不等式，具有明显的规律不变性，即规律不因数值的改变而变化，利用特殊情形表现这种不变性，可以解决一般性问题.例4 设a 、b ∈R ,不等式a cos x +b cos3x ≤1对任意实数x 恒成立，求b 的变化范围.解：由于x 的任意性，令a cos x +b cos3x ≤1中x =0得a +b ≤1 ①又令x =π得a +b ≥－1∴－1≤a +b ≤1 ② 又当12,12,3-≥+-≤-=b a b a x 即有时π 当121,12,32≤+-≤-≤+-=b a b a x 从而有有时π ∴－2≤－a ＋2b ≤2 ③②＋③得－3≤3b ≤3∴－1≤b ≤1五、根据恒成立不等式的特点，通过挖掘几何图形含意，利用函数图象的高低位置关系找出参数的变化范围.例5 不等式ax ≤)4(x x -在x ∈[0,3]内恒成立，求a 的变化范围.解：画出两个函数y =ax 与y =)4(x x -的图象.（如图）将x =3代入ax =)4(x x -,得a =33 ∴a ∈[33,＋∞].。

教师姓名韩贺凤单位名称巴州第一中学填写时间2020·8·15学科数学年级/册高一年级教材版本人教A版课题名称必修五第三章第二节3.2 解决一元二次不等式的恒成立问题难点名称根据实物，概括棱柱、棱椎、棱台的结构特征难点分析从知识角度分析为什么难对一元二次不等式恒成立的理解与一元二次不等式的解集二者之间的关联性。

从学生角度分析为什么难1、一元二次不等式的解法在教材中是利用二次函数的图像分析出来的，学生往往只重视结果，而忽视了它的形成过程。

2、一元二次不等式恒成立的理解不能与解法有机结合。

难点教学方法数形结合的思想方法教学环节教学过程导入从教材的一道例题的解法作为本节课的导入复习一元二次不等式的解法，教材例2：求不等式-x2+2x-3>0的解集知识讲解（难点突破）通过由简入难的螺旋思维形成过程，设计三道例题例1：已知关于x的不等式x2-x+a>0的解集是R，求a的取值范围。

分析：不等式的解集是R，意思是x取任何实数，都能使不等式成立，因此，二次函数y=x2-x+a的图像就要保证x为任何实数时，都要使y>0，所以，∆=1-4a<0,从而得到a>¼例2：已知关于x的不等式x2-ax+4≥0的解集是R，求a的取值范围分析：同样不等式的解集为R，意思是x取任何实数不等式都成立，因此，二次函数y=x2-ax+4的图像也就要保证x取任何实数都要使y≥0，所以，∆≤0，即：a2-16≤0,从而得到-4≤a≤4例3：已知关于x的不等式2ax2+ax-83<0对一切实数x都成立，求a的取值范围。

分析：不等式对一切实数x都成立，意思是不等式的解集为R，也就是实数x取任何值，不等式都成立，因此二次函数y=2ax2+ax- （a≠0)的图像就要保证x取任何实数都要使y<0，从而得到-3<a<0我们可以发现,题中并没有告诉a≠0，所以需检验a=0的情况，看是否也能保证题意成立。

《不等式恒成立问题》一、教学目标：（1）知识目标：利用二次函数、导数、均值不等式、三角函数和线性规划求最值。

（2）能力目标：掌握不等式恒成立问题的解法，熟练应用四大数学思想，提升解决问题的能力。

（3）情感目标：树立学好数学的信心，让学生体验到成功感，信心百倍地参加高考。

二、教学重点：利用二次函数相关知识解决此类问题。

三、教学难点：如何把不等式恒成立问题转换为二次函数求最值，即函数与方程思想的应用。

四、教学方法：通过例题讲解，引导学生思考、归纳和总结此类问题的解法，然后再练习习题。

五、教具准备：多媒体课件六、教学过程：高中数学的恒成立问题一直以来都是一个重点、难点，这类问题没有一个固定的思想方法去处理，在近些年的高考模拟题及数学高考题中屡见不鲜。

如何简单、准确、快速的解决这类问题并更好地认识把握，本节课通过举例来说明这类问题的一些常规处理方法。

12例1.若不等式x +ax +1≥0对于一切x x ∈(0,]成立，2则a 的最小值为（）A.0B.-25 D.-3C.-211由x ∈(0,]，∴a ≥-(x +).，法一:不等式可化为ax ≥-x 2-1Q (x +111∴(-x -)max )在(0,]上是减函数,x x 22法二：令f (x )=x +ax +1,对称轴为x =-a .2255=-∴a ≥-22x①a oy1x 2⎧a ⎪-≤0⎨2⇒a ≥0⎪⎩f (0)≥0②③ooyx =-yya 212x1⎧a -≥⎪⎪22⇒-1<a <0⎨⎪f (1)≥0⎪⎩2a 1⎧0<-<⎪⎪225⎨⇒-≤a ≤-1a 2⎪f (-)≥0⎪⎩2a2a2法三：验证法：令f (x )=x +ax +1,对称轴为x =-.212当a =0时，f (x )=x +1≥0在（0,]恒成立。

212当a =-2时，f (x )=x 2-2x +1=（x -1）在（0,]恒成立。

25551当a =-时，f (x )=x 2-x +1，对称轴x =，（0,]是f (x )的减区间，224211f ()=0，故f (x )≥0在（0,]恒成立。

不等式专题复习不等式恒成立和存在性问题教学设计一、教学目标确立依据（一）课程标准要求及解读1.课程标准要求（1）经历从实际情境中中抽象出一元二次不等式模型的过程；（2）通过函数图形了解一元二次不等式与相应函数、方程的关系（3）会用基本不等式解决简单的最大（小）值问题2.课程标准解读（1）不等式的考查主要以中档题为主，以选填题为主；（2）不等式的性质常与简易逻辑结合考查；（3）不等式的解法主要以一元二次不等式为主，兼顾其它（如简单的分式不等式、绝对值不等式、指对数不等式、与分段函数有关的不等式等），常与集合（选填题）、导数（解答题中对参数的分类讨论）结合；（4）线性规划问题难度不大；（5）基本不等式求最值是重点，要加强训练；（6）不等式的恒成立也应当重视。

（二）教材分析本章的主要内容是：不等式的性质、不等式的证明和一些简单不等式的解法；其中不等式的证明和不等式的解法是重点；不等式的性质及其证明中，不等式的证明是难点，掌握不等式的性质是学好本章的关键。

本节课的重点是不等式恒成立问题的探究，难点是用求函数（表达式）最值（取值范围）解决恒成立问题（三）学情分析1．认知分析：学生在初中已经学习了一元二次方程和二次函数，对不等式的性质有了初步的了解，在高中也学习了基本不等式，这为我们学习恒成立转化为函数（或二元变量）求最值打下了基础。

2．能力分析：高中学段的学生数学思维较初中来说更为严密，抽象思维能力也有了进一步的提升。

3．情感分析：学生对高考重点内容的学习有一定的兴趣和积极性，但在探究问题的能力以及合作交流等方面的发展不够均衡。

因此对于这个阶段的学生来说，对恒成立的学习有一定的基础和必要。

二、教学目标目标1：通过独立思考完成典型例题，梳理构建解题方法、解题步骤和注意问题，培养直观想象、逻辑推理、数学运算和数学抽象的核心素养目标2：通过小组合作探究完成变式练习，掌握不同的数学问题与不等式恒成立和存在性问题之间的等价转化，培养逻辑推理的核心素养目标3：通过独立思考完成目标检测，合理选择解决问题的方法，培养逻辑推理和数学运算的核心素养.三、评价设计目标1评价：学生通过独立思考，都能用基本三种方法中的一种解决简单的恒成立问题过程；目标2评价：通过小组讨论后的抢答展示，都能注意处理恒成立问题的细节目标3评价：学生通过独立思考，完成目标检测，60%的学生能正确解答，40%的学生通过学生讲解能意识到自己的错误并改正；四、教学过程一、“做”中“理”——问题导入，梳理知识师：通过前面的学习，发现同学们对不等式恒成立问题还存在思路不清晰，方法选择不恰当的情况。

教案不等式恒成立教案标题：不等式恒成立教学目标：1. 了解和理解不等式的概念和性质；2. 掌握解不等式的方法和技巧；3. 能够判断和证明不等式是否恒成立；4. 能够应用不等式恒成立的性质解决实际问题。

教学准备：1. 教师准备：教师备课笔记、教学课件、教学素材、练习题；2. 学生准备：课本、笔记本、笔、计算器。

教学过程：引入活动：1. 教师通过提问和讨论引导学生回顾不等式的概念和性质，例如“什么是不等式？不等式有哪些符号表示？不等式有哪些基本性质？”等。

知识讲解与示范：2. 教师结合教学课件，详细讲解不等式恒成立的概念和判断方法。

a. 解释什么是不等式恒成立，即对于给定的不等式，无论取任何满足条件的变量值，不等式都成立；b. 介绍判断不等式恒成立的基本方法，如代入法、变形法等；c. 通过具体的例子演示如何判断不等式是否恒成立。

练习与巩固：3. 学生进行个人或小组练习，解决一些简单的不等式恒成立的题目，巩固刚才所学的知识。

4. 教师在课堂上解答学生的问题，引导学生发现解题的关键点和方法。

拓展与应用：5. 学生通过课堂讨论或小组合作的方式，解决一些复杂的不等式恒成立的问题，培养学生的分析和推理能力。

6. 学生将所学的不等式恒成立的知识应用到实际问题中，例如通过不等式恒成立解决最优化问题、约束条件问题等。

总结与评价：7. 教师对本节课所学的内容进行总结，强调不等式恒成立的重要性和应用领域。

8. 学生进行自我评价，回顾自己在本节课中的学习情况和收获。

作业布置：9. 布置一些相关的课后作业，以巩固学生对不等式恒成立的理解和应用能力。

教学反思：教师根据本节课的教学情况和学生的反应，进行教学反思和调整，为下一节课的教学做好准备。

不等式恒成立问题教案教学目标：1．掌握解决不等式恒成立问题的基本方法：最值分析法、变量分离法、图像法等；能根据题目的构成特征，合理选择解题最优策略；2．在解决不等式恒成立问题的过程中，体验数形结合，函数与方程，分类讨论的数学思想方法；3．养成眼睛的思维习惯，提高分析解决问题的能力.教学重点: 处理不等式恒成立问题的基本方法．教学难点：不等式恒成立问题解法的合理选择．教学内容：一、复习二次不等式的恒成立问题二、例题分析例题1. 对于一切实数x，不等式恒成立，则实数的取值范围为 ．变式1：对于实数，不等式恒成立，则实数的取值范围为 ．变式2：对于实数，不等式恒成立，则实数的取值范围为 ．例题2. 若关于的不等式对任意在恒成立，则实常数的取值范围是.答案：巩固练习1：1. 在上定义运算：，若不等式对一切实数恒成立，则实数的取值范围是 _________________2．若函数在上有意义，则实数a的取值范围是______3. 已知关于的方程恒有解，求实数的取值范围。

例题3.：如果对任意实数x，不等式|x+1|≥kx恒成立，则实数k的范围是_______巩固练习2：2. 当x(1,2)时，不等式(x-1)2<log a x恒成立，求a的取值范围．3. 设函数，若对于任意，不等式恒成立，则实数的取值范围是．答案：三、知识回顾，方法总结；1．最值分析法2．分离变量法3．图像法四、结束语：数学常见恒成立,最值分析来考虑;变量分离和图像,往往也来共参与.五、教学反思1. 第三轮复习的内容可以参照二模的一些新题型，提高学生的学习兴趣2. 复习的内容偏重于基础，可以在思维上再加深一些难度。

3. 课上学生的含参问题的计算能力不强，需要在以后的教学过程中加以改进教学说明：不等式的恒成立问题是高考中常见的一类问题，解题方法比较多，需要让学生在复习过程中加以提炼。

所以我在第三轮复习时选择了这个课题让学生研究。

在教学过程中主要抓住了解不等式恒成立问题的一些基本类型加以复习巩固和课堂练习。

函数和不等式结的恒成立问题的解法“含参不等式恒成立问题”把不等式、函数、三角、几何等内容有机地结合起来，其以覆盖知识点多，综合性强，解法灵活等特点而倍受高考、竞赛命题者的青睐。

另一方面，在解决这类问题的过程中涉及的“函数与方程”、“化归与转化”、“数形结合”、“分类讨论”等数学思想对锻炼学生的综合解题能力，培养其思维的灵活性、创造性都有着独到的作用恒成立问题的基本类型：一、判别式法若所求问题可转化为二次不等式，则可考虑应用判别式法解题。

一般地，对于二次函数,有),0()(2R x a c bx ax x f ∈≠++=1）对恒成立; 0)(>x f R x ∈⎩⎨⎧<∆>⇔00a 2）对恒成立 0)(<x f R x ∈.00⎩⎨⎧<∆<⇔a 例1：若不等式的解集是R ，求m 的范围。

02)1()1(2>+-+-x m x m 例2 设函数f(x)＝ mx 2-mx-1．(1)若对于一切实数x ，f(x)＜0恒成立，求m 的取值范围；(2)对于x∈[1,3]，f(x)＜－m ＋5恒成立，求m 的取值范围二、最值法将不等式恒成立问题转化为求函数最值问题的一种处理方法，其一般类型有：1）恒成立a x f >)(min)(x f a <⇔2）恒成立a x f <)(max)(x f a >⇔例1、若时，不等式恒成立，求的取值范围。

[]2,2x ∈-23x ax a ++≥a 例2．设，当时，恒成立，求实数的取22)(2+-=mx x x f ),1[+∞-∈x m x f ≥)(m 值范围。

巩固．已知函数，若对任意，恒),1[,2)(2+∞∈++=x xa x x x f ),1[+∞∈x 0)(>x f 成立，求实数的取值范围。

a 练习2 已知，若恒成立，求a 的取值范围.a ax x x f -++=3)(22)(],2,2[≥-∈x f x 22210[0,1]x mx m x x m -++>∈练习1：若不等式对满足的所有实数都成立，求的取值范围。

“不等式恒成立问题”教学再设计高三数学两种主要课型是复习课与讲评课，解题教学是其重点，单纯求解应转变为解法拟定及具体实施，把能力培养置于首位。

于是，笔者对一节“不等式恒成立问题”教学设计进行了反思及再设计，并在后续教学中进行了尝试，取得了预期效果。

一、教学引入――预设练习，暴露问题1.设计意图考虑到学生已经具备一定解答问题知识方法，只是尚未系统化。

因此，在新教学设计中，将这节解题课转变成一节习题课，试图通过对学生前期解答剖析，来了解学生解题思路，对学生解题中暴露问题进行整理剖析，增加学生亲切感，更能引起重视，帮助学生由最近发展区靠近解题要点。

2.教学过程学生剖析预习作业错误原因，交流解题经验：（1）关于x不等式（a2+4a-5）x2-2（a+5）x+3>0对一切实数x恒成立，则实数a取值范围是________。

3.说明与反思高三教学中，新课较少，习题课增加。

本课即为一节有主题习题课。

然而一部分“懂而不会”高三学生，对习题课极不重视。

为解决这一问题，教师需在“备学生”上多下工夫。

本课设计以学生错误引入，让学生感受到内容重要性。

其中，作业（1）旨在巩固学生对常规问题解决及分类讨论能力，让学生在自我反思中发现二次项系数讨论重要性；作业（2）则是在学生解答中整理多种解法，一方面将解法归纳，另一方面通过解法对比体现解题过程中观察及思考重要性。

二、教学重点（一）重点突破，以“理”服人1.设计意图高三学生，由于已经学会了高中阶段数学知识，一些新知识方法常常会对其认知结构产生冲击，导致对新内容吸收较为困难。

所以切不能将教学内容强加于学生，那样学生从根本上不能掌握，也使学生对教师失去了信任。

苏霍姆林斯基曾说：“在人们心灵深处，都有一种根深蒂固需要，这就是希望感到自己是一个发明者、研究者、剖析者，而在孩子精神世界中，这种需要则特别强烈。

”因此，本课在教学重点环节处理，改变了过去教师传授讲解生硬方式，而是创设环境，给予学生表达自己想法空间，平等地与学生交流，让学生自然过渡到新方法运用中。

x yO6362+-=x y “一元一次不等式与一次函数”教案设计教 学 目 标知识与能力：通过做函数图象、观察函数图象，使学生进一步理解函数的概念，体会一元一次等式与一元一次函数的内在联系。

掌握用函数图象求一元一次不等式的解集的方法。

情感、态度、价值观：提供问题的策略化，发展学生的个性，发展学生的数学才能，感悟知识的价值。

教 学 重 点 难 点 教学重点：培养学生对函数图象的观察能力，进一步理解函数的概念。

用函数的知识求一元一次不等式的解集。

教学难点：对函数图象的理解和体会，一次函数图象与一元一次不等式一次函数的关系。

教 学 用 具小黑板或PPT 课件。

课 时安 排 1课时 学 习 任 务1．回顾什么叫一元一次函数？什么叫不等式？2．已知函数62+-=x y 的图象如图所示，根据图象回答： ⑴当x= 时，y=0，即方程062=+-x 的解为时，y ＞0，即不等式062＞+-x 的解集为 思考：⑵当x ＜0，即不等式062＜+-x 的解集为 ⑶当x 时，y 总结：当y=0时，正好是图象与 轴的交点 当y ＞0时，图象位于 轴 方 当y ＜0时，图象位于 轴 方四 总结1、本节课学习的数学知识是一次函数与一元一次不等式的关系 ⑴若方程0=+b ax （a 、b 为常数且a ≠0）的解为b ax -=，那么不等式0＞b ax +（或0＜b ax +）（a ≠0）的解集就是一次函数b ax y +=（a ≠0）函数值大于0（或小于0）时x 的取值范围。

⑵若解不等式ax+b ＞cx+d （或ax+b ＜cx+d ）（a 、b 、c 、d 为常数且a 、c 都不为0）则可化为最简一元一次不等式，再利用一次函数图象求解。

也可两边分别看成一次函数、利用图象求解。

2、本节课学习的数学方法——数形结合。

一元二次不等式恒成立的问题教学目标1. 会解决一元二次不等式恒成立的问题。

2. 进一步掌握一元二次不等式的解法。

3. 培养学生的分类讨论思想和数形结合思想。

教学重点：加强学生的分类讨论思想意识教学难点：提高学生利用数形结合的方法解决问题的能力教学过程：一、复习1．回顾一元二次不等式的解法，即“三个二次”之间的联系。

2．解一元二次不等式的步骤：一看（看是否标准型，非标准型须转化为标准型），二算（计算判别式及对应方程的解），三写（写出不等式的解集）。

3．解不等式(1)03532-2<-+x x (2)03-2<-+x x二、新授前面我们已经学习了一元二次不等式的解法，那现在看看一元二次不等式的 综合问题。

今天，我们就通过一个典型例题来研究不等式恒成立的问题。

典例：例、 关于的x 不等式04)2(2)2(2<--+-x a x a 对于一切实数x 恒成立，求实数a 的取值范围。

分析：（一）讨论系数① 当0)2(=-a 即2=a 时，原不等式变成常数不等式 。

② 当0)2(≠-a 时，原不等式是一元二次不等式。

（二）分类讨论①当0)2(=-a 即2=a 时，原不等式可化为04<-，∴2=a 时，不等式恒成立。

② 当0)2(≠-a 时，不等式04)2(2)2(2<--+-x a x a 是一个一元二次不等式，此时对应方程04)2(2)2(2=--+-x a x a 应满足⎩⎨⎧<∆<-002a （这一充要条件是通过借助函数4)2(2)2(y 2--+-=x a x a 的图像，在图像上找出x 时0y <取什么值，而得到的。

强调数形结合思想。

）练习：不等式012<--kx kx 的解集为全体实数，求k 的取值范围。

举一反三：（提问，学生思考）1. 若典例中的不等式变为04)2(2)2(2≤--+-x a x a 呢？2. 若典例中的不等式变为04)2(2)2(2>--+-x a x a 呢？3. 若典例中的不等式变为04)2(2)2(2≥--+-x a x a 呢？ （以上三个问题由学生来完成）三、小结通过典例，得到以下结论：不等式02<++c bx ax 对一切实数恒成立（解集为R ），则系数应满足的条件：⎩⎨⎧<-=∆<0402ac b a 或⎩⎨⎧<==00c b a （其他三种形式的不等式所得结论由学生自己归纳）。