大学物理(II)下册：05-波动(驻波)

大学物理波动与声学知识点汇总在大学物理的学习中，波动与声学是十分重要的部分。

它们不仅在物理学中有着基础且关键的地位，也在众多实际应用领域发挥着重要作用。

下面让我们一起来梳理一下这部分的重要知识点。

一、波动的基本概念波动是一种常见的物理现象，它是振动在介质中的传播过程。

（一）机械波的产生条件机械波的产生需要两个条件：一是要有做机械振动的物体，即波源；二是要有能够传播这种机械振动的介质。

（二）横波与纵波根据质点振动方向和波的传播方向的关系，波可以分为横波和纵波。

横波中质点的振动方向与波的传播方向垂直，例如电磁波。

纵波中质点的振动方向与波的传播方向平行，像声波就是典型的纵波。

（三）波长、波速和频率波长是指相邻两个同相点之间的距离。

波速是指波在介质中传播的速度，它由介质的性质决定。

频率则是波源振动的频率，等于单位时间内波源完成全振动的次数。

三者之间的关系为：波速＝波长×频率。

二、波动方程波动方程描述了波在空间和时间上的变化规律。

（一）简谐波的波动方程对于简谐波，其波动方程可以表示为：y ＝ A sin(ωt kx ＋φ) 或 y ＝A cos(ωt kx ＋φ) ，其中 A 为振幅，ω 为角频率，k 为波数，φ 为初相位。

（二）波动方程的物理意义波动方程反映了在不同时刻、不同位置处质点的位移情况。

通过波动方程，可以了解波的传播特性和质点的振动规律。

三、波的能量波在传播过程中伴随着能量的传递。

（一）能量密度能量密度是指单位体积内波所具有的能量。

（二）平均能量密度在一个周期内能量密度的平均值称为平均能量密度。

（三）能流和能流密度能流是指单位时间内通过垂直于波传播方向的某一面积的能量。

能流密度则是指通过垂直于波传播方向单位面积的能流，也称为波的强度。

四、波的干涉当两列波相遇时，会产生干涉现象。

（一）干涉的条件两列波的频率相同、振动方向相同、相位差恒定，才能产生稳定的干涉现象。

（二）干涉加强和减弱两列波在相遇点的相位差为2kπ（k 为整数）时，干涉加强；相位差为(2k ＋1)π 时，干涉减弱。

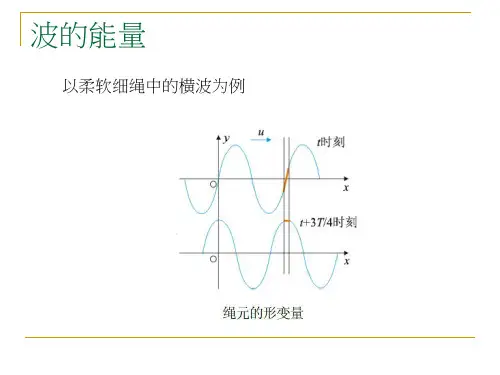
以柔软细绳中的横波为例
⏹波的能量密度w:波传播时,单位体积介质中所
储存的波的能量.
⏹波的能流密度I:波传播时,单位时间内通过垂
直于波的传播方向单位面积的
体积介质中所波的能量.
⏹对于简谐波,两者关系为:I=uw
简谐波的能量密度和能流密度
⏹机械波的平均能量密度和平均能流密度:
都与振幅平方成正比,与频率平方成正比.
⏹电磁波的平均能量密度和平均能流密度:
都与振幅平方成正比,与频率无关.
⏹在介质中任意一点,简谐机械波的动能与势能都是同相位振动的;在真空中传播的简谐电磁波的电场能和磁场能在任意一点都是同相位振动的.
波的叠加原理
当几列波在介质中某点相遇时,该点的振动位移是各列波单独存在时在该点引起的位移的叠加
波的叠加原理举例驻波(standing waves)
122cos cos x y y y A t u
ωω=+=1cos ()x y A t u ω=-2cos ()x y A t u
ω=+
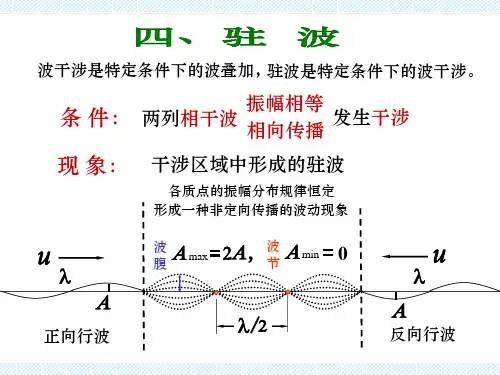
驻波
⏹形成驻波的条件:两列简谐波
✓频率相同;
✓振幅相同;
✓振动方向相同;
✓在同一媒介中相向传播,叠加而形成逐波.⏹驻波的现象:
✓相邻波节(或波腹)的间距为二分之一波长;✓相邻波节与波腹的间距为四分之一波长;
✓相邻两波节之间各点(称为一段)同相位振动;✓相邻两段的振动相位差为π.
驻波举例
位于A,B两点的两个简谐波源的振幅相同,频率都是100Hz,相位差为π.若A,B相距30m,波速为400m/s,求AB连线上因叠加而静止的各点的位置.
波的叠加原理举例驻波(standing waves)
拍(beats)。

大学物理波动的知识点总结一、波动的基本概念1.波动的定义波动是一种可以在介质中传播的能量或者信息的方式。

波动既可以是物质的波动，比如水波、声波等，也可以是场的波动，比如电磁波等。

根据波的传播方式和规律，波动可以分为机械波和电磁波。

2.波动的特点波动具有传播性、干涉性、衍射性和波粒二象性等特点。

波动的传播性表明波动能够沿着介质传播，干涉性指波动能够互相叠加，并产生干涉现象，衍射性说明波动能够弯曲传播并产生衍射现象，波粒二象性则是指波动既具有波动特征，也具有粒子特征。

3.波的基本要素波的基本要素包括振幅、频率、波长、波速等。

振幅是波动能量的大小，频率是波动的振动周期，波长是波动在空间中占据的长度，波速是波动在介质中的传播速度。

二、波动方程1.一维波动方程一维波动方程描述了一维波动在空间和时间上的变化规律。

一维波动方程的基本形式为：∂²u/∂t²=v²∂²u/∂x²其中u(x,t)表示波动的位移，v表示波速，t表示时间，x表示空间坐标。

2.二维波动方程二维波动方程描述了二维波动在空间和时间上的变化规律。

二维波动方程的基本形式为：∂²u/∂t²=v²(∂²u/∂x²+∂²u/∂y²)其中u(x,y,t)表示波动的位移，v表示波速，t表示时间，x和y表示空间坐标。

3.波动方程的解波动方程一般是偏微分方程，其解一般通过分离变量、叠加原理、傅里叶变换等方法求解。

对于特定的边界条件和初始条件，可以得到波动方程的具体解。

三、波动的性质1.反射和折射波动在介质表面的反射和折射是波动的基本性质之一。

反射是波动从介质边界反射回来的现象，折射是波动通过介质界面时改变传播方向的现象。

2.干涉和衍射干涉是波动相遇并相互叠加的现象，衍射是波动通过小孔或者障碍物后产生的弯曲传播的现象。

干涉和衍射都是波动的波动性质。

解析大学物理中的波动力学理论波动力学是大学物理课程中重要的一部分，涉及到波的传播、干涉、衍射、驻波等现象。

本文将对大学物理中的波动力学理论进行解析。

一、波动力学基础概念在开始介绍波动力学理论之前，有必要先说明一些基础概念。

波是一种能量传播的方式，它通过媒介传递能量，而不传递物质。

波的重要性源于其在自然界中广泛存在的现象，如光的传播、声音的传播等。

二、波的分类波可以分为机械波和电磁波两大类。

机械波是指需要介质进行传播的波，如水波、声波等；而电磁波是不需要介质进行传播的波，如光波、无线电波等。

本文将主要关注机械波的波动力学理论。

三、波动方程波动力学的核心是波动方程，通过该方程可以描述波的传播过程。

一维波动方程可以表示为:∂^2ψ/∂x^2 = (1/v^2) ∂^2ψ/∂t^2其中，ψ表示波的振幅，x表示位置，t表示时间，v表示波速。

四、波的传播波动力学理论告诉我们，波的传播方式可以分为纵波和横波。

纵波是指波动方向与振动方向平行的波，如声波；横波是指波动方向与振动方向垂直的波，如水波。

五、波的干涉和衍射波动力学理论还涉及到波的干涉和衍射现象。

干涉是指两个或多个波相遇时产生的干涉条纹现象，其实质是波的叠加。

典型的干涉现象包括双缝干涉和薄膜干涉。

衍射是波遇到障碍物时发生的弯曲现象，其实质是波在障碍物周围传播时受到阻碍而发生弯曲。

六、波的驻波驻波是指在一定条件下，两个同频率、相同振幅、但传播方向相反的波相互叠加形成的波动现象。

驻波具有节点和腹节点，节点处的振幅为零，腹节点处的振幅最大。

典型的驻波现象包括弦上的驻波和声管中的驻波。

七、波动力学的应用波动力学理论在实际生活中有广泛的应用。

例如，在音乐产生中，乐器发出的声音可通过波动力学理论解释；在光学中，通过衍射和干涉现象可以制造出各种精密的光学器件；在地震学中，可以通过地震波的传播来了解地球内部的结构等。

总结：通过对大学物理中的波动力学理论进行解析，我们了解到波的基础概念、分类、波动方程、传播方式以及干涉、衍射、驻波等现象。

⼤学物理——波动If you only do what you can do you’ll never be more than you are now.如果你只做你⼒所能及的事，你就没法进步。

⼤学物理 —— 波动留⽩⽬录1. 波动波动： 简称为波，振动或扰动在空间以⼀定的速度传播。

机械波： 机械振动或扰动在介质中的传播。

如声波、⽔波等。

电磁波： 变化电场和变化磁场在空间的传播。

如⽆线电波、光波等。

波动是振动状态的传播，不是介质的传播。

（机械波只能在介质中传播，电磁波不需要）简谐波： 简谐振动在空间的传播。

波的叠加性： ⼲涉和衍射。

2. 机械波的⼏个概念机械波产⽣的条件： 波源和弹性介质。

机械波的分类：横波： 质点振动⽅向与波的传播⽅向向垂直的波。

仅在固体中传播特征： 具有交替出现的波峰和波⾕。

横波： 质点振动⽅向与波的传播⽅向互相平⾏的波。

可以在固液⽓中传播特征：具有交替出现的密部和疏部。

图源知乎波线： 沿波传播的⽅向画⼀些带箭头的线。

波⾯： 波源在某⼀时刻的振动相位同时到达的各点所组成的⾯，也称同相⾯。

波前： 最前⾯的波⾯。

平⾯波和球⾯波在各向同性均匀介质中，波线和波⾯垂直。

相关物理量：波长： 同⼀波线上两个相邻、相位差为 2π 的质点之间的距离。

周期： 波前进⼀个波长的距离所需要的时间。

频率： 周期的倒数，单位时间内波所传播的完整波的数⽬。

波速： 单位时间振动传播的距离，级振动相位的传播速度。

1. 波的周期和频率和介质的性质⽆关，⼀般与波源的振动周期和频率相同。

2. 波速是相位传播的速度，也称相速度，⼤⼩取决于介质的性质，与波的频率⽆关。

3. 波长与波源和介质都有关，同⼀频率的波，在不同介质中传播时波长⼀般不同。

3. 平⾯简谐波平⾯波： 波阵⾯为平⾯的波，波源在⽆限远出。

时间上的⽅程：相位上的⽅程：4. 波的能量4.1 物质的弹性应⼒ ： 每单位⾯积的回复⼒线应变：物体长度的相对变化量应⼒与线应变成正⽐杨⽒模量：上式中的⽐例系数E。