知识点结构图

七年级数学（上）知识点人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章 有理数一． 知识框架二．知识概念1.有理数：(1)凡能写成)0p q ,p (pq ≠为整数且形式的数，都是有理数.正整数、0、负整数统称整数；正分数、负分数统称分数；整数和分数统称有理数.注意：0即不是正数，也不是负数；-a 不一定是负数，+a 也不一定是正数；π不是有理数；(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数2．数轴：数轴是规定了原点、正方向、单位长度的一条直线.3．相反数：(1)只有符号不同的两个数，我们说其中一个是另一个的相反数；0的相反数还是0；(2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数.4.绝对值：(1)正数的绝对值是其本身，0的绝对值是0，负数的绝对值是它的相反数；注意：绝对值的意义是数轴上表示某数的点离开原点的距离；(2) 绝对值可表示为：⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (a a ；绝对值的问题经常分类讨论； 5.有理数比大小：（1）正数的绝对值越大，这个数越大；（2）正数永远比0大，负数永远比0小；（3）正数大于一切负数；（4）两个负数比大小，绝对值大的反而小；（5）数轴上的两个数，右边的数总比左边的数大；（6）大数-小数 ＞ 0，小数-大数 ＜ 0.6.互为倒数：乘积为1的两个数互为倒数；注意：0没有倒数；若 a ≠0，那么a 的倒数是a 1；若ab=1⇔ a 、b 互为倒数；若ab=-1⇔ a 、b 互为负倒数.7. 有理数加法法则：（1）同号两数相加，取相同的符号，并把绝对值相加；（2）异号两数相加，取绝对值较大的符号，并用较大的绝对值减去较小的绝对值；（3）一个数与0相加，仍得这个数.8．有理数加法的运算律：（1）加法的交换律：a+b=b+a ；（2）加法的结合律：（a+b ）+c=a+（b+c ）.9．有理数减法法则：减去一个数，等于加上这个数的相反数；即a-b=a+（-b ）. 10 有理数乘法法则：（1）两数相乘，同号为正，异号为负，并把绝对值相乘；（2）任何数同零相乘都得零；（3）几个数相乘，有一个因式为零，积为零；各个因式都不为零，积的符号由负因式的个数决定.11 有理数乘法的运算律：（1）乘法的交换律：ab=ba ；（2）乘法的结合律：（ab ）c=a （bc ）；（3）乘法的分配律：a （b+c ）=ab+ac .12．有理数除法法则：除以一个数等于乘以这个数的倒数；注意：零不能做除数，无意义即0a . 13．有理数乘方的法则：（1）正数的任何次幂都是正数；（2）负数的奇次幂是负数；负数的偶次幂是正数；注意：当n 为正奇数时: (-a)n =-a n 或(a -b)n =-(b-a)n , 当n 为正偶数时: (-a)n =a n 或 (a-b)n =(b-a)n .14．乘方的定义：（1）求相同因式积的运算，叫做乘方；（2）乘方中，相同的因式叫做底数，相同因式的个数叫做指数，乘方的结果叫做幂；15．科学记数法：把一个大于10的数记成a ×10n 的形式，其中a 是整数数位只有一位的数，这种记数法叫科学记数法.16.近似数的精确位：一个近似数，四舍五入到那一位，就说这个近似数的精确到那一位.17.有效数字：从左边第一个不为零的数字起，到精确的位数止，所有数字，都叫这个近似数的有效数字.18.混合运算法则：先乘方，后乘除，最后加减.本章内容要求学生正确认识有理数的概念，在实际生活和学习数轴的基础上，理解正负数、相反数、绝对值的意义所在。

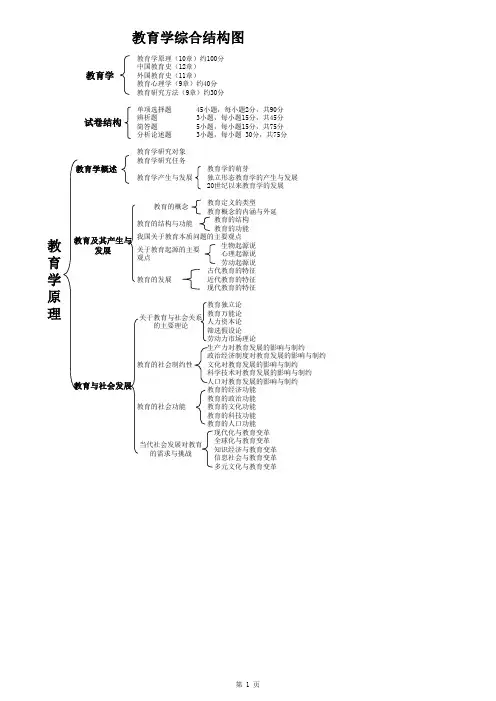
教育学研究对象教育学研究任务教育学的萌芽独立形态教育学的产生与发展20世纪以来教育学的发展教育定义的类型教育概念的内涵与外延教育的结构 教育的功能 生物起源说心理起源说 劳动起源说古代教育的特征近代教育的特征现代教育的特征教育独立论教育万能论人力资本论筛选假设论劳动力市场理论生产力对教育发展的影响与制约政治经济制度对教育发展的影响与制约文化对教育发展的影响与制约科学技术对教育发展的影响与制约人口对教育发展的影响与制约教育的经济功能教育的政治功能教育的文化功能教育的科技功能教育的人口功能现代化与教育变革全球化与教育变革 知识经济与教育变革 信息社会与教育变革多元文化与教育变革教育学综合结构图关于教育与社会关系的主要理论教育的社会制约性教育的社会功能 教育学教育学产生与发展教育学原理（10章）约100分中国教育史（12章）外国教育史（11章）教育学原理教育及其产生与发展教育的概念教育的结构与功能关于教育起源的主要观点教育的发展我国关于教育本质问题的主要观点 教育学概述教育心理学（9章）约40分教育研究方法（9章）约30分当代社会发展对教育的需求与挑战教育与社会发展单项选择题 45小题，每小题2分，共90分辨析题 3小题，每小题15分，共45分简答题 5小题，每小题15分，共75分分析论述题 3小题，每小题 30分，共75分试卷结构人的身心发展的主要特点人的身心发展特点对教育的制约关于影响人的身心发展的主要观点遗传素质及其在人的身心发展中的作用环境及其在人的身心发展中的作用个体个性化与个体社会化教育目的的概念关于教育目的的主要理论教育目的确立的依据我国的教育目的全面发展教育的构成培养目标的概念我国中小学培养目标教育制度的概念学制的概念与要素学制确立的依据各级学校系统各类学校系统现代教育制度改革课程的概念课程理论及主要流派学科课程与活动课程综合课程与分科课程必修课程与选修课程泰勒原理课程计划、课程标准与教材课程目标课程的范围与结构课程实施课程评价影响课程改革的主要因素20世纪60年代以来国外的主要课程改革当前我国基础教育课程改革教学的概念教学的主要作用与任务教学理论概述当代主要教学理论流派关于教学过程本质的主要观点教学过程中应处理好的几种关系教学设计教学模式概述当代国外主要教学模式当代我国主要教学模式教学原则的概念及确立依据中小学教学的基本原则教育学原理教学教学概述教学理论及主要流派教学过程教学模式教学原则中小学常用的教学方法教学工作的基本环节教育制度学校教育制度课程课程与课程理论课程类型课程改革课程编制学校教育在人的身心发展中的主导作用及有效发挥的条件教育目的与培养目标教育目的培养目标教育与人的发展人的身心发展特点及其对教育的制约人的身心发展的主要影响因素学校教育在人的身心发展中的作用教学组织形式的历史发展班级授课制教学组织形式的改革教学片评价的含义及其功能诊断性评价、形成性评价和终结性评价学业成就评价教学评价的改革德育概念德育任务道德教育、思想教育、政治教育和法制教育《小学德育纲要》与《中学德育大纲》德育过程的要素德育过程的规律说服教育法情感陶冶法实践锻炼法自我教育法、榜样示范法、品德评价法直接的道德教学间接的道德教育道德认识发展模式体谅模式价值澄清模式社会学习模式集体教育模式教师的概念与类别教师职业的产生与发展教师的地位与作用教师劳动的特点教师的专业素质教师专业发展的内涵与途径教师的权利与义务学生及学生观学生群体学生的权利与义务师生关系的特点与类型良好师生关系的建立学生师生关系德育概述我国学校德育的基本内容德育过程德育原则德育方法德育途径德育模式 德育教师与学生教师教育学原理教学教学组织原则教学评价及其改革集体教育与个别教育相结合；知行统一；正面引导与纪律约束相结合；发挥积极因素与克服消极因素相结合；严格要求与尊重信任相结合；照顾年龄特点与照顾个别特点相结合；教育影响的一致性；教育影响的连续性教育的起源学校的起源学在官府大学与小学国学与乡学家庭教育齐国的稷下学宫创办私学与编订“六经”“有教无类”与教育对象“学而优则仕”与教育目的教学内容教学方法道德教育论教师历史影响思孟学派“性善论”与教育作用“明人伦”与教育目的“大丈夫”的人格理想“深造自得”的教学思想荀况与“六经”的传授“性恶论”与教育作用以“大儒”为培养目标以儒经为教学内容“闻见知行”结合的学习过程与方法论教师墨家的教育思想道家的教育思想法家的教育思想《大学》《中庸》《学记》《乐记》《对贤良策》与三大文教政策论人性与教育作用论道德教育对谶纬神学的批判关于教育作用与培养目标论学习西晋的国子学南朝宋的“四馆”与总明观文教政策的探索与稳定政府教育管理机构和体制的确立中央和地方官学体系的完备私学发展学校教育发展的特点科举制度的萌芽与确立科举考试的程序、科目与方法科举制度与学校教育的关系科举制度的影响颜之推与《颜氏家训》论士大夫教育论家庭教育“性三品”说与教育作用关于人才培养和选拔的思想论尊师重道韩愈的教育思想封建国家教育体制的完善魏晋南北朝官学变革隋唐时期教育体系的完备科举制度的建立颜之推的教育思想私人讲学的兴起与传统教育思想的奠基儒学独尊与 读经做官教 育模式的初 步形成董仲舒的教育实践与教育思想王充的教育实践与教育思想“独尊儒术”文教政策的确立太学、郡国学与鸿都门学察举制度荀况的教育思想战国后期的教育论著私人讲学的兴起与诸子百家私学的发展“庶、富、教”、“性相近也，习相远也”与教育作用和地位孔丘的教育实践与教育思想孟轲的教育思想官学制度的建立与“六艺”教育的形成学校萌芽的传说西周的教育制度 “六艺”教育：礼、乐、射、御、书、数 中国教育史——古代教育科举制度的演变学校沦为科举附庸宋代“兴文教”政策北宋三次兴学与“三舍法”“苏湖教法”积分法、“六等黜陟法”、“监生历事”社学书院的产生与发展《白鹿洞书院揭示》与书院教育宗旨东林书院与书院讲会诂经精舍、学海堂与书院学术研究书院教育的特点私塾的发展与种类蒙学教材的发展、种类和特点朱熹与《四书章句集注》“明天理，灭人欲”与教育作用论“大学”和“小学”教育“朱子读书法”“致良知”与教育作用“随人分限所及”的教育原则论教学论儿童教育颜元与漳南书院；；；“实德实才”的培养目标“六斋”与“实学”的教育内容“习行”的教学方法理学教育思想和学校的改革与发展科举制度的演变与官学的改革书院的发展私塾与蒙学教材朱熹的教育思想王守仁的教育思想中国古代教育理学教育思想的批判与反思颜元的教育思想理学教育思想的批判黄宗羲的“公其非是于学校”洋务学堂的举办、类别和特点京师同文馆福建船政学堂幼童留美派遣留欧中体西用思想的形成和发展张之洞与《劝学篇》中体西用的历史作用和局限兴办学堂兴办学会与发行报刊创办京师大学堂改革科举制度维新运动中的教育改革主张《大同书》中的教育理想“开民智”“伸民权”与教育作用培养“新民”的教育目的论学制论师范教育、女子教育和儿童教育鼓民力、开民智、新民德的三育论“体用一致”的文化教育观“壬寅学制”和“癸卯学制”的颁布废科举，兴学堂建立教育行政体制确定教育宗旨留日教育“庚款兴学”与留美教育 制定教育方针颁布学制颁布课程标准“五育并举”的教育方针改革北京大学的教育实践教育独立思想平民教育思潮工读主义教育思潮职业教育思潮实用主义教育思潮勤工俭学运动科学教育思潮国家主义教育思潮学校教学改革与实验七项标准学制体系与特点近代教育的起步洋务学堂的兴办留学教育的起步“中体西用”思想与张之洞《劝学篇》教会学校在中国的兴办中国近代教育近代教育体系的建立维新派的教育实践“百日维新”中的教育改革康有为的教育思想梁启超的教育思想严复的教育思想清末新政时期的教育改革清末的留学教育近代教育体制改革教会教育的扩张与收回教育权运动新文化运动时期和20年代的教育思潮与教育改革运动蔡元培的教育思想与实践民国初年的教育改革1922年“新学制”党化教育“三民主义”教育宗旨“战时须作平时看”的教育方针大学院和大学区制的试行“戊辰学制”的颁行初等教育中等教育高等教育抗日战争时期的学校西迁训育制度中小学校的童子军训练高中以上学生的军训中学毕业会考苏维埃文化教育总方针抗日战争时期中国共产党的教育方针政策“民族的、科学的、大众的”文化教育方针干部在职培训干部学校教育“抗大”根据地的小学教育解放区中小学教育的正规化解放区高等教育的整顿与建设论教育本质“全人生指导”与青年教育职业教育的探索职业教育思想体系“四大教育”与“三大方式”“化农民”与“农民化”乡村建设和乡村教育理论乡村教育的实施儿童教育和“活教育”实验“活教育”思想体系“生活教育”理论体系杨贤江与马克思主义教育理论黄炎培的职业教育思想与实践晏阳初的乡村教育实验梁漱溟的乡村教育建设陈鹤琴的“活教育”探索现代教育 家的教育理论与实践陶行知的“生活教育”思想与实践“生活教育”实践：晓庄学校；山海工学团；“小先生制”；育才学校中国教育史——现代教育中国共产党领导下的革命根据地教育新民主主义教育方针的形成干部教育普通教育革命根据地教育的基本经验群众教育南京国民政府的教育教育宗旨与教育方针的变迁教育制度改革学校教育发展学校教育的管理措施古巴比伦的学校古巴比伦学校的教学内容与方法古代埃及的学校古代埃及学校的教学内容与方法婆罗门教育佛教教育教学内容丰富阶级性、等级性机构繁多教育方法简单，体罚盛行教师地位高斯巴达教育雅典教育智者派的教育活动智者派的教育贡献教育目的论德育论智育论苏格拉底方法灵魂论与教育教育作用论古罗马共和早期的教育古罗马共和后期的教育西塞罗的教育思想昆体良的教育思想奥古斯丁的教育思想基督教的教育形式、机构和教育内容基督教的教育思想宫廷学校骑士教育教育概况教育的特点及影响教育概况教育的特点及影响拜占廷与阿拉伯的教育拜占庭的教育阿拉伯的教育外国教育史——古代教育西欧中世纪教育新兴市民阶层的形成和城市学校的发展中世纪大学的形成与发展封建主贵族的世俗教育基督教教育古罗马的教育共和时期的罗马教育古罗马的教育思想帝国时期的罗马教育古希腊教育古风时代的教育古典时代的教育古希腊化时期的教育苏格拉底的教育思想柏拉图的教育思想——《理想国》亚里士多德的教育思想东方文明古国的教育古代东方文明古国教育发展的特点古代印度的教育古代埃及的教育古巴比伦的教育意大利人文主义教育北欧人文主义教育人文主义教育的基本特征路德派新教的教育主张与教育实践加尔文派新教的教育主张英国国教派的教育主张耶稣会的学校耶稣会学校的组织管理与教学方式教育概况教育思想：洛克、斯宾塞论教育教育概况教育思想：爱尔维修、狄德罗、拉夏洛泰论教育法国大革命时期的主要教育改革方案和教育主张教育概况教育思想：第斯多惠论教育教育概况教育思想：乌申斯基论教育教育概况教育思想：贺拉斯·曼论教育教育概况教育思想：福泽谕吉论教育论教育的目的和作用论教育适应自然的原则论普及教育和统一学制论学年制和班级授课制论教育原则论道德教育教育管理思想教育贡献及意义自然教育理论及其意义公民教育理论教育贡献及意义教育实践活动论教育目的论教育心理学化论教育要素建立初等学校各科教学法教育与生产劳动相结合教育实践活动教育思想的理论基础道德教育理论课程理论教学理论赫尔巴特教育思想的传播论教育的基本原理幼儿园教育理论对空想社会主义教育思想的批判论教育与社会的关系论教育与生产劳动论人的本质和个性形成论人的全面发展与教育的关系论教育与生产劳动相结合的意义外国教育史——近代教育西欧近代教育思想夸美纽斯的教育思想美国近代教育日本近代教育卢梭的教育思想裴斯泰洛齐的教育思想赫尔巴特的教育思想福禄培尔的教育思想文艺复兴与宗教改革时期的教育新教教育人文主义教育天主教教育马克思和恩格斯的教育思想欧美主要国家和日本的近代教育英国近代教育法国近代教育德国近代教育俄国近代教育新教育运动的形成和发展新教育运动中的著名实验进步教育运动始末进步主义教育运动的历史意义《巴尔福教育法》与教育行政管理体制的变化《费舍教育法》《哈多报告》《斯宾斯报告》《1944年教育法》“罗宾斯原则”《雷沃休姆报告》《1988年教育改革法》《费里教育法》统一学校运动与学制改革；中学课程的改革《阿斯蒂埃法》与职业技术教育的发展《郎之万一瓦隆教育改革方案》《教育改革法》《高等教育方向指导法》(《富尔法案》《法国学校体制现代化建议》(《哈比改革》)《课程宪章》德意志帝国与魏玛共和国时期的教育《改组和统一公立普通学校教育的总纲计划》《高等学校总纲法》中等教育的改革和发展初级学院运动；职业技术教育的发展《国防教育法》和20世纪60年代的教育改革20世纪70年代的教育改革：生计教育、“返回基础”20世纪初期至20年代末的教育改革与发展军国主义教育体制的形成和发展《教育基本法》和《学校教育法》20世纪七八十年代的教育改革建国初期的教育改革；教育管理体制改革的内容及成效；《统一劳动学校规程20世纪20年代的学制调整和教学改革实验；20世纪30年代教育的调整、巩固和发展第二次世界大战后的教育改革：1958年的教育改革、1966年的教育改革、1977年以后的教育改革。

建筑结构图基本知识点总结建筑结构图是建筑设计中非常重要的一部分，它是设计师将建筑设计理念和概念转化为具体的施工图纸的关键。

建筑结构图反映了建筑的结构形式、结构布局、材料选用等重要信息，是建筑施工的依据，对建筑质量和安全具有重要的影响。

建筑结构图包括平面图、立面图、剖面图、结构细部图等，这些图纸不仅仅是建筑施工的指导图，更是建筑设计师和结构工程师沟通交流的重要媒介。

因此，建筑结构图的编制需要建筑设计师和结构工程师的密切合作和协调。

下面将从建筑结构图基本知识点入手，对建筑结构图的基本内容、基本原则以及注意事项等方面进行总结，旨在为建筑设计师和结构工程师提供参考和指导。

一、建筑结构图的基本内容1. 平面图建筑平面图是建筑结构的布局图，它反映了建筑在平面上的形状和布局。

平面图是建筑结构图中最为基础的图形之一，它通常包括建筑的地面平面图、各层平面图以及特殊构件的布局图。

平面图中需要包括建筑的功能用途、出入口位置、内部空间布局等重要信息，同时也需要标注建筑结构的主要构件和位置，为建筑的立面和结构细部图提供参考。

2. 立面图建筑立面图是建筑结构的垂直展示图，它反映了建筑在立面上的形状和结构。

立面图是建筑结构图中的另一个基础图形，它通常包括建筑的正立面、背立面和侧立面等，立面图也是建筑外观设计的重要参考。

在立面图中需要标注建筑的各层标高、立面构件的材料和尺寸、窗户门洞的位置和尺寸等重要信息，为建筑的施工提供必要的参考。

3. 剖面图建筑剖面图是建筑结构的纵向展示图，它反映了建筑在剖面上的结构和布局。

剖面图是建筑结构图中的另一个基础图形，它通常包括建筑的纵向剖面、横向剖面等，剖面图也是建筑内部空间设计和构造原理的重要参考。

在剖面图中需要标注建筑的楼层高度、梁柱墙构件的布置、楼板地面的标高等重要信息，为建筑的施工提供必要的参考。

4. 结构细部图建筑结构细部图是建筑结构构件的详细图纸，它反映了建筑结构构件的连接形式和细节。

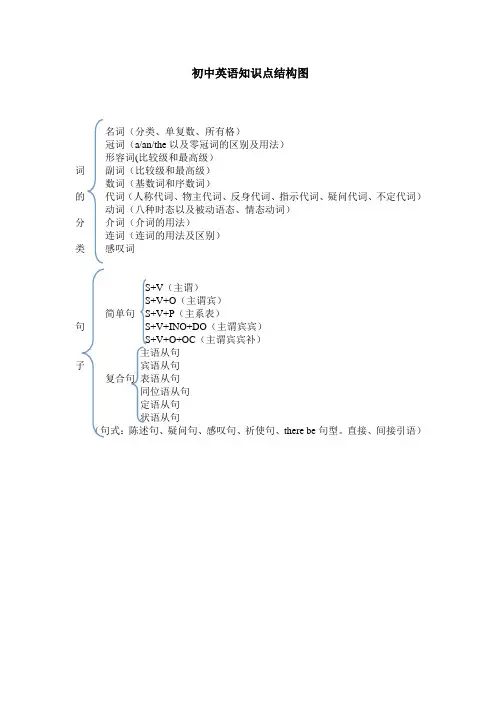
初中英语知识点结构图
名词（分类、单复数、所有格）
冠词（a/an/the以及零冠词的区别及用法）
形容词(比较级和最高级）
词副词（比较级和最高级）
数词（基数词和序数词）
的代词（人称代词、物主代词、反身代词、指示代词、疑问代词、不定代词）动词（八种时态以及被动语态、情态动词）
分介词（介词的用法）
连词（连词的用法及区别）
类感叹词
S+V（主谓）
S+V+O（主谓宾）
简单句S+V+P（主系表）
句S+V+INO+DO（主谓宾宾）
S+V+O+OC（主谓宾宾补）
主语从句
子宾语从句
复合句表语从句
同位语从句
定语从句
状语从句
（句式：陈述句、疑问句、感叹句、祈使句、there be句型。

直接、间接引语）。

;;=⇔⊆=⇔⊆=⇔⊆A B B A B A B A A B A B I A Bn-个A中元素有n个，则A的子集共有2n个，真子集有21集合间的运算2n R a +∈则2n n a n a ++≥平均值不等式2nnn a a n++≥当且仅当2,,)n 时取等号1111221n j n j n n n a b a b a b a b a b a b ++≤++≤+++,n Z 是∀,,nx 是区间1122)()()()n n n n q x q f x q f x q f x ++≤+++,,,1n i q R q +∈=∑）。

上凸函数不等号转向.1}n ma+仍是等比数列，其公比为)lim n n a ++=sin sin αtan tan 1tan tan α±2(AB x =，则a ⊥b2PP 所成比112222221cos ||||a b a b a ba b a b a ++⋅⋅==⋅+212()(x x y y =-+-空间向量的直角坐标运算律若123(,,a a a a =，12(,,b b b b =则①113(a b a b +=+，11(a b a b -=-123(,)()a a a R λλλλλ=∈，11a b a b ⋅=+②13//a ba b λλ⇔=，110a b a b ⊥⇔+若111(,,)A x y z 则2(AB x =-模长公式若12(,,a a a a =21||a a a a a =⋅=+空间向量的运算,,(OB OA AB a b BA OA OB a b OP a λλ=+=+=-=-=空间向量的加减与数乘OB OA AB =+=a +b ，AB OB OA =-，,(OP λ=a a b + c ⑶数乘分配律：λ(a + ) =λa +λb ．平行六面体向量的数乘积||||cos ,a b a b a b ⋅=⋅⋅<>空间向量数乘积的性质①||cos ,a e a a e ⋅=<>．②0a b a b ⊥⇔⋅=．③2||a a a =⋅．空间向量数量积运算律①()()()a b a b a b λλλ⋅=⋅=⋅②a b b a ⋅=⋅（交换律） ③()a b c a b a c ⋅+=⋅+⋅（分配律）④e a = a e =|a |cos ,a e⑤ab a b = 0⑥当a 与b 同向时，a b = |a ||b |；当a 与b 反向时，a b = |a ||b |.特别的a a = |a |2或||a a a =⋅⑦cos ,||||a ba b a b ⋅=Bα∈，则l αβ=且l，则A、B、C 。

总结知识点结构图知识点结构图的制作1. 确定主题：首先要确定知识点结构图的主题，即要总结的知识领域或内容。

主题可以是一个学科的知识体系，也可以是某一专题的重点知识点。

2. 收集知识点：收集和整理主题相关的知识点，可以通过查阅书籍、资料、网络搜索等方式获取知识点。

3. 确定知识点的层次结构：根据知识点的逻辑关系，确定知识点的层次结构，包括主要知识点、次要知识点和细节知识点。

4. 绘制结构图：根据知识点的层次结构，绘制知识点结构图。

可以使用思维导图、树状图等形式绘制知识点结构图。

知识点结构图的应用1. 知识总结：知识点结构图可以帮助我们系统地总结和整理知识，从整体上把握知识的结构和逻辑关系，有助于深入理解和掌握知识。

2. 学习导向：知识点结构图可以帮助我们明确学习的重点和难点，指导学习方向和方法，提高学习效率。

3. 复习备考：知识点结构图可以作为复习备考的工具，帮助我们快速回顾和记忆知识点，加强对知识的掌握。

4. 教学辅助：教师可以通过知识点结构图清晰地向学生展示知识点之间的逻辑关系，帮助学生理清知识结构，提高教学效果。

知识点结构图的制作和应用技巧1. 简洁清晰：知识点结构图要简洁清晰，避免过于复杂和繁琐，突出主要知识点和逻辑关系。

2. 逻辑严谨：知识点结构图应该按照知识点的逻辑关系进行排列，上下级知识点之间的关系要清晰明了。

3. 标注关键词：知识点结构图中可以标注关键词和关键概念，以便于记忆和理解。

4. 多层次显示：知识点结构图可以根据知识点的层次结构进行多层次显示，突出主次关系。

5. 多样化呈现：知识点结构图的制作可以根据个人喜好和需要选择不同的形式和颜色进行呈现，增加趣味性和美观性。

总之，知识点结构图是一种简单实用的学习工具，通过制作和应用知识点结构图，我们可以更清晰地理解和应用知识，提高学习效率和学习成绩。

希望上述总结的知识点结构图的制作和应用要点能够帮助大家更好地掌握知识，并在学习和工作中加以运用。

1 -七年级数学（上）知识点人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章 有理数一． 知识框架二．知识概念1.有理数：(1)凡能写成)0p q ,p (pq ≠为整数且形式的数，都是有理数.正整数、0、负整数统称整数；正分数、负分数统称分数；整数和分数统称有理数.注意：0即不是正数，也不是负数；-a 不一定是负数，+a 也不一定是正数；π不是有理数；(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数2．数轴：数轴是规定了原点、正方向、单位长度的一条直线.3．相反数：(1)只有符号不同的两个数，我们说其中一个是另一个的相反数；0的相反数还是0；(2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数.4.绝对值：(1)正数的绝对值是其本身，0的绝对值是0，负数的绝对值是它的相反数；注意：绝对值的意义是数轴上表示某数的点离开原点的距离；(2) 绝对值可表示为：⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (a a ；绝对值的问题经常分类讨论； 5.有理数比大小：（1）正数的绝对值越大，这个数越大；（2）正数永远比0大，负数永远比0小；（3）正数大于一切负数；（4）两个负数比大小，绝对值大的反而小；（5）数轴上的两个数，右边的数总比左边的数大；（6）大数-小数 ＞ 0，小数-大数 ＜ 0.6.互为倒数：乘积为1的两个数互为倒数；注意：0没有倒数；若 a ≠0，那么a 的倒数是a1；若ab=1⇔ a 、b 互为倒数；若ab=-1⇔ a 、b 互为负倒数.7. 有理数加法法则：（1）同号两数相加，取相同的符号，并把绝对值相加；（2）异号两数相加，取绝对值较大的符号，并用较大的绝对值减去较小的绝对值；（3）一个数与0相加，仍得这个数.8．有理数加法的运算律：（1）加法的交换律：a+b=b+a ；（2）加法的结合律：（a+b ）+c=a+（b+c ）.9．有理数减法法则：减去一个数，等于加上这个数的相反数；即a-b=a+（-b ）.2 -10 有理数乘法法则：（1）两数相乘，同号为正，异号为负，并把绝对值相乘；（2）任何数同零相乘都得零；（3）几个数相乘，有一个因式为零，积为零；各个因式都不为零，积的符号由负因式的个数决定.11 有理数乘法的运算律：（1）乘法的交换律：ab=ba ；（2）乘法的结合律：（ab ）c=a （bc ）；（3）乘法的分配律：a （b+c ）=ab+ac .12．有理数除法法则：除以一个数等于乘以这个数的倒数；注意：零不能做除数，无意义即0a .13．有理数乘方的法则：（1）正数的任何次幂都是正数；（2）负数的奇次幂是负数；负数的偶次幂是正数；注意：当n 为正奇数时: (-a)n =-a n 或(a -b)n =-(b-a)n , 当n为正偶数时: (-a)n =a n 或 (a-b)n =(b-a)n .14．乘方的定义：（1）求相同因式积的运算，叫做乘方；（2）乘方中，相同的因式叫做底数，相同因式的个数叫做指数，乘方的结果叫做幂；15．科学记数法：把一个大于10的数记成a ×10n 的形式，其中a 是整数数位只有一位的数，这种记数法叫科学记数法.16.近似数的精确位：一个近似数，四舍五入到那一位，就说这个近似数的精确到那一位.17.有效数字：从左边第一个不为零的数字起，到精确的位数止，所有数字，都叫这个近似数的有效数字.18.混合运算法则：先乘方，后乘除，最后加减.本章内容要求学生正确认识有理数的概念，在实际生活和学习数轴的基础上，理解正负数、相反数、绝对值的意义所在。