下载文档原格式
弹塑性矩阵推导（全面版）资料考虑材料的塑性，其增量形式的本构关系可表达为p d σ=(D-D )d ε (1)式(1)中，D 为弹性矩阵，p D 为塑性矩阵。
弹性矩阵D 的形式为422000333242000333224000333000000000000K G K GK G K G K GK G K GK GK G G G G ⎡⎤+--⎢⎥⎢⎥⎢⎥-+-⎢⎥⎢⎥=⎢⎥--+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦D (2) 体积模量3(12)E K μ=-，剪切模量2(1)EG μ=+。
在应变空间内，塑性矩阵可表达为1()T f fA ∂∂=∂∂p D D D σσ(3) 式中，()()T T p f f f fA B ∂∂∂∂=--∂∂∂∂D D σσσσ(4) f为屈服函数；p σ为塑性应力，p p =σD ε；1/2(()())T p T p T p f f f f B f f f ωθε∂∂⎧⎪∂∂⎪∂∂⎪'=⎨∂∂⎪∂∂∂⎪⎪∂∂∂⎩σσI σσσ(5) [111000]T '=I ；p ω为塑性功；p θ为塑性体应变；p ε为等效塑性应变；κ为反映加载历史的参数。
对于Drucker-Prager 模型，其屈服条件为10f I α== (6)1x y z I σσσ=++，22222221()2x yz xy yz zx J S S S S S S =+++++，α为材料常数。
f α∂''=∂I σ (7) 222Txyzxyyzzx S S S S S S '⎡⎤=⎣⎦S(8)()3f K αα∂'''==+∂DD I I σ(9) 2()()(3)9T T T f f A K K G ααα∂∂'''===+∂∂D I I σσ (10) 1()T f fA ∂∂=∂∂p D D D σσ22222222112123113211212311321121231131121121121(3)(3)999(9)(T TT T T TK K K GK G K G K G J m mn ml S m S m S m mn n nl S n S n S n ml nl l S l S l S l S m S n S l ααααααβββββββββββββ''=+++''''=++++=p D I I I I S SS211211222311221321231231231122231231132232113113113113212113223113)()()S S S S S S m S n S lS S S S S S m S n S l S S S S S ββββββββββββββββββββ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⋅⋅⎢⎥⎢⎥⋅⋅⎢⎥⋅⋅⎢⎥⎣⎦令43p K G =+，23q K G =- 弹塑性矩阵可表达为2112123113211212311321121231132112112112112112223112213123123123112223()(p m q mn q mlS mS m S m q mnp n q nl S n S n S nq ml q nl p l S l S l S l S m S n S l G S S S S S S m S n S lS S G βββββββββββββββββββββββ------------------=-=-----⋅-⋅----⋅-ep p D D D 21231132232113113113113212113223113)()S S S S m S n S lS S S S G S ββββββββββ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⋅⎢⎥----⋅-⋅-⎢⎥⎣⎦令1β=，2β=1112m S ββ=+，1222n S ββ=+，大型矩阵系统◆ELL系列ELL**V##(视频矩阵)ELL**A##(音频矩阵)ELL**RV##(环通视频矩阵)通道选择输入：8XN+64 最大256路输出：4XN+8 最大32路产品介绍：ELL系列视、音频主机采用大规模音视频切换专用芯片作为音频视频切换矩阵电路的多路多通道切换设备，溶合了先进的矩阵切换技术和计算机技术，可以给用户提供卓越的整体性能。
静力弹塑性分析(Pushover 分析)■ 简介Pushover 分析是考虑构件的材料非线性特点，分析构件进入弹塑性状态直至到达极限状态时结构响应的方法。
Pushover 分析是最近在地震研究及耐震设计中经常采用的基于性能的耐震设计(Performance-Based Seismic Design, PBSD)方法中最具代表性的分析方法。
所谓基于性能的耐震设计就是由用户及设计人员设定结构的目标性能(target performance)，并使结构设计能满足该目标性能的方法。
Pushover 分析前要经过一般设计方法先进行耐震设计使结构满足小震不坏、中震可修的规X 要求，然后再通过pushover 分析评价结构在大震作用下是否能满足预先设定的目标性能。
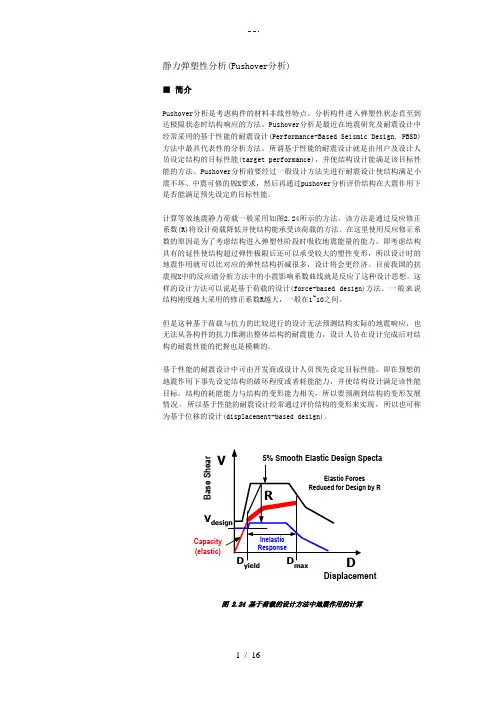
计算等效地震静力荷载一般采用如图2.24所示的方法。
该方法是通过反应修正系数(R)将设计荷载降低并使结构能承受该荷载的方法。
在这里使用反应修正系数的原因是为了考虑结构进入弹塑性阶段时吸收地震能量的能力，即考虑结构具有的延性使结构超过弹性极限后还可以承受较大的塑性变形，所以设计时的地震作用就可以比对应的弹性结构折减很多，设计将会更经济。
目前我国的抗震规X 中的反应谱分析方法中的小震影响系数曲线就是反应了这种设计思想。
这样的设计方法可以说是基于荷载的设计(force-based design)方法。
一般来说结构刚度越大采用的修正系数R 越大，一般在1~10之间。
但是这种基于荷载与抗力的比较进行的设计无法预测结构实际的地震响应，也无法从各构件的抗力推测出整体结构的耐震能力，设计人员在设计完成后对结构的耐震性能的把握也是模糊的。
基于性能的耐震设计中可由开发商或设计人员预先设定目标性能，即在预想的地震作用下事先设定结构的破坏程度或者耗能能力，并使结构设计满足该性能目标。
结构的耗能能力与结构的变形能力相关，所以要预测到结构的变形发展情况。
所以基于性能的耐震设计经常通过评价结构的变形来实现，所以也可称为基于位移的设计(displacement-based design)。
m i d a s C i v i lm i d a s C i v i lm i d a s C i v i l图2.8.38 基于位移设计法的结构抗震性能评价m i d a s C i v i l示。
m i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i l1n λ- : 前一步骤(n-1)的荷载因子1λ : 第1荷载步的荷载因子nstep : 总步骤数i : 等差增量步骤号当前步骤的外力向量如下。
0n n λ=⋅P P(10)(3) 第3阶段: 最终步骤的荷载增量(n nstep =) 最终荷载步骤(nstep )的外力向量如下、0nstep nstep λ=⋅P P ; 1.0nstep λ= (11)图2.8.43 自动调整荷载步长的例题(荷载因子结果)m i d a s C i v i l2. 点击步长控制选项 > 增量控制函数定义步长控制函数m i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lATC-40中对不同结构响应类型规定了谱折减系数的下限值(参见表2.8.7)。
弹塑性矩阵推导考虑材料的塑性，其增量形式的本构关系可表达为p d σ=(D -D )d ε (1)式(1)中，D 为弹性矩阵，p D 为塑性矩阵。
弹性矩阵D 的形式为422000333242000333224000333000000000000000K G K G K G K G K G K G K G K G K G G G G ⎡⎤+--⎢⎥⎢⎥⎢⎥-+-⎢⎥⎢⎥=⎢⎥--+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦D (2) 体积模量3(12)E K μ=-，剪切模量2(1)E G μ=+。
在应变空间内，塑性矩阵可表达为1()T f fA ∂∂=∂∂p D D D σσ(3) 式中，()()T T p f f f f A B ∂∂∂∂=--∂∂∂∂D D σσσσ(4)f为屈服函数；p σ为塑性应力，p p =σD ε；1/2(()())T p T pT p f f f f B f f f ωθε∂∂⎧⎪∂∂⎪∂∂⎪'=⎨∂∂⎪∂∂∂⎪⎪∂∂∂⎩σσI σσσ(5)[111000]T '=I ；p ω为塑性功；p θ为塑性体应变；p ε为等效塑性应变；κ为反映加载历史的参数。
当p κω=时当pκθ=时 当p κε=时对于Drucker-Prager 模型，其屈服条件为120f I J α== (6)1x y z I σσσ=++，22222221()2x y z xy yz zxJ S S S S S S =+++++，α为材料常数。
22f J α∂''=∂I σ (7)222Txyzxyyzzx S S S S S S '⎡⎤=⎣⎦S (8)22()32f K J J αα∂'''==+∂DD I I σ (9)222()()(3)92T T T f f A K K G J J ααα∂∂'''===+∂∂D I I σσ (10)1()T f f A ∂∂=∂∂p D D D σσ22222222222222112123113211212311321121231131121121121(3)(3)999(9)(9)(9)(T TT T T TK K K GJ J K G K G K G J K G J K G J m mn ml S m S m S m mnn nl S n S n S n ml nl l S l S l S l S m S n S l ααααααααβββββββββββββ''=++''''=++++++=p D I I I I S SS 211211222311221321231231231122231231132232113113113113212113223113)()()S S S S S S m S n S lS S S S S S m S n S lS S S S S ββββββββββββββββββββ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⋅⋅⎢⎥⎢⎥⋅⋅⎢⎥⋅⋅⎢⎥⎣⎦令43p K G =+，23q K G =- 弹塑性矩阵可表达为2112123113211212311321121231132112112112112112223112213123123123112223()(p m q mn q ml S m S m S mq mn p n q nl S n S n S n q ml q nl p l S l S l S l S m S n S l G S S S S S S m S n S lS S G βββββββββββββββββββββββ------------------=-=-----⋅-⋅----⋅-ep p D D D 21231132232113113113113212113223113)()S S S S m S n S l S S S S G S ββββββββββ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⋅⎢⎥----⋅-⋅-⎢⎥⎣⎦令122(9)K G J βα=+，229K Gβα=+，1112m S ββ=+，1222n S ββ=+，1332l S ββ=+ 2222222211222222111222299(9)(9)(9)(()(9)9x x x x K G S S S K G K G J K G J K G J S m K G J K Gαααααββαα⎡⎤=++⎣⎦++++==+=++p D22222221222222222221112122299(9)(9)(9)()((9)9(9)9()()y x x yx y K G S S S K G K G J K G J K G J K G J K GK G J K GS S mnαααααααααββββ⎡⎤=+++⎣⎦++++=+++++=++=p D2222222132222222221112133299(9)(9)(9)()((9)9(9)9()()z x x zx z K G S S S K G K G J K G J K G J S S K G J K GK G J K GS S mlαααααααααββββ⎡⎤=+⎣⎦++++=++++++=++=p D2221422111211211222222(9)(9)()()(9)(9)(9)xy x xyx xy G S S K G J K G J S S S S mK G K G J K G J ααββββααα⎡⎤=+⎣⎦++==+⋅=+++p D2221522111212312322222(9)(9)()()(9)(9)(9)yz x yzx yz G S S S K G J K G J S S S mK G K G J K G J ααββββααα⎡⎤=+⎣⎦++==+⋅=+++p D2221622111211311322222(9)(9)()()(9)(9)(9)zx x zxx zx G S S S K G J K G J S S S S mK G K G J K G J ααββββααα⎡⎤=+⎣⎦++==+⋅=+++p D222221222222222111212229(9)(9)(9)()((9)9(9)9()()x y y xx y S S K G K G J K G J K G J K G J K GK G J K GS S mnααααααααββββ⎡⎤=+⎣⎦++++=+++++=++=p D 2222222222222222122222299(9)(9)(9)(()(9)9y y y y K G S S K G K G J K G J K G J S S n K G J K Gαααααββαα⎡⎤=++⎣⎦++++=+=+=++p D2222222232222222221222133299(9)(9)(9))((9)9(9)9()()z y y Zy z K G S S S K G K G J K G J K G J S K G J K GK G J K GS S nlαααααααααββββ⎡⎤=+++⎣⎦++++=++++++=++=p D2222422122211211222222(9)(9)()()(9)(9)(9)xy y xyy xy G S S K G J K G J S S S nK G K G J K G J ααββββααα⎡⎤=+⎣⎦++==+⋅=+++p D2222522122212312322222(9)(9)()()(9)(9)(9)yz y yzy yz G S S K G J K G J S S S S nK G K G J K G J ααββββααα⎡⎤=+⎣⎦++==+⋅=+++p D2222622122211311322222(9)(9)()()(9)(9)(9)zx y zxy zx G S S K G J K G J S S S nK G K G J K G J ααββββααα⎡⎤=+⎣⎦++==+⋅=+++p D2222222312222222221112133299(9)(9)(9)()((9)9(9)9()()x z z xx z K G S S S K G K G J K G J K G J S S K G J K GK G J K GS S mlαααααααααββββ⎡⎤=+⎣⎦++++=++++++=++=p D222232222222222122213329(9)(9)(9)((9)9(9)9()()y z z yy z S S S K G K G J K G J K G J S K G J K GK G J K GS S nlααααααααββββ⎡⎤=+++⎣⎦++++=++++++=++=p D2222222233222222133222299(9)(9)(9)(()(9)9z z z z K G S S K G K G J K G J K G J S S l K G J K Gαααααββαα⎡⎤=+⎣⎦++++=+=+=++p D2223422133211211222222(9)(9)()()(9)(9)(9)xy z xyz xy G S S K G J K G J S S S S lK G K G J K G J ααββββααα⎡⎤=+⎣⎦++==+⋅=+++p D2223522133212312322222(9)(9)()()(9)(9)(9)yz z yzz yz G S S K G J K G J S S S lK G K G J K G J ααββββααα⎡⎤=+⎣⎦++==+⋅=+++p D2223622133211311322222(9)(9)()()(9)(9)(9)zx z zxz zx G S S S K G J K G J S S S lK G K G J K G J ααββββααα⎡⎤=+⎣⎦++==+⋅=+++p D2224122111211211222222(9)(9)(()9(9)(9)xy xy xx xy G S S K G J K G J S S S S mK GK G J K G J ααββββααα⎡⎤=+⎣⎦++==+⋅=+++p D2224222122211211222222(9)(9)(()9(9)(9)xy xy yy xy G S S S K G J K G J S S S nK GK G J K G J ααββββααα⎡⎤=+⎣⎦++==+⋅=+++p D2224322133211211222222(9)(9)(()9(9)(9)xy xy zz xy G S S S K G J K G J S S S lK GK G J K G J ααββββααα⎡⎤=+⎣⎦++==+⋅=+++p D222112244222()()(9)(9)xy xy S K G JK G J βαα⎡⎤===⎣⎦++p D1122232452222(9)(9)9xy yz xy yz S S S S S K G J K G J K G ββααα⎡⎤===⋅⎣⎦+++p D 1122132462222(9)(9)9xy zx xy zx S S S S K G J K G J K G ββααα⎡⎤===⋅⎣⎦+++p D 2225122111212312322222(9)(9)()()9(9)(9)yz yz xx yz G S S K G J K G J S S S mK GK G J K G J ααββββααα⎡⎤=+⎣⎦++==+⋅=+++p D2225222122212312322222(9)(9)()()9(9)(9)yz yz yy yz G S S S K G J K G J S S S S S nK GK G J K G J ααββββααα⎡⎤=+⎣⎦++==+⋅=+++p D2225322133212312322222(9)(9)()()9(9)(9)yz yz zz yz G S S K G J K G J S S S lK GK G J K G J ααββββααα⎡⎤=+⎣⎦++==+⋅=+++p D1122232542222(9)(9)9xy yz xy yz S S S S K G J K G J K G ββααα⎡⎤===⋅⎣⎦+++p D222123255222()()(9)(9)yz yz S K G JK G J βαα⎡⎤===⎣⎦++p D1132232562222(9)(9)9yz zx yz zx S S S S S K G J K G J K G ββααα⎡⎤===⋅⎣⎦+++p D2226122111211311322222(9)(9)()()9(9)(9)zx zx xx zx G S S K G J K G J S S S mK GK G J K G J ααββββααα⎡⎤=+⎣⎦++==+⋅=+++p D2226222122211311322222(9)(9)()()9(9)(9)zx zx yy zx G S S K G J K G J S S S nK GK G J K G J ααββββααα⎡⎤=+⎣⎦++==+⋅=+++p D2226322133211311322222(9)(9)()()9(9)(9)zx zx zz zx G S S S K G J K G J S S S S S lK GK G J K G J ααββββααα⎡⎤=+⎣⎦++==+⋅=+++p D1132122642222(9)(9)9zx xy zx xy S S S K G J K G J K G ββααα⎡⎤===⋅⎣⎦+++p D 1132232652222(9)(9)9zx yz zx yz S S S S S K G J K G J K G ββααα⎡⎤===⋅⎣⎦+++p D222113266222()()(9)(9)zxzx S S K G J K G J βαα⎡⎤===⎣⎦++p D。
