下载文档原格式
高一化学必修一知识点：铝三角铝是高中化学重要的金属，也是我们日常生活中经常用到的金属材料，今天小编要和大家分享的是高一化学必修一知识点：铝三角，希望能够帮助到大家好好学习并掌握这部分知识，赶快学习起来吧。
高一化学必修一知识点：铝三角铝是高中化学重要的金属，主要有铝、氧化铝、氢氧化铝。
高考化学中铝的考点主要集中的铝及其化合物的两性，即既可以与酸反应，也可以与碱反应。
点击图片可在新窗口打开铝三角主要体现了铝及其化合物的两性一、单质铝(Al)铝是一种活泼金属，具有金属的共性，能够与非金属、酸、某些盐反应，同时具有自己特有的性质，可以与碱反应。
铝极易失去最外层3个电子形成铝离子：Al-3e-=Al3+。
1.铝与非金属反应铝可以与大多数非金属单质反应，如氧气、氯气、硫、溴等，生成相应的氧化物或盐。
4Al+3O2点击图片可在新窗口打开2Al2O3;2Al+3S点击图片可在新窗口打开Al2S3;2Al+3Cl2点击图片可在新窗口打开2AlCl3;2.铝与酸反应这里所说的酸，主要指稀硫酸和稀盐酸，常温常压下，铝遇浓硫酸或浓硝酸会发生钝化，所以可用铝制容器盛装浓硫酸或浓硝酸。
注意钝化也属于化学变化。
2Al+6HCl=2AlCl3+3H2↑;2Al+3H2SO4=Al2(SO4)3+3H2↑;3.铝与强碱反应大多数金属不与碱反应，与强碱反应，是铝特有的性质，(锌也可以发生类似的反应，了解即可)2Al+2NaOH+2H2O==2Na AlO2+3H2↑;对应离子方程式：2Al+2OH-+2H2O==2AlO2-+3H2↑;该反应的本质是铝首先与水反应，生成氢氧化铝与氢气，2Al+6H2O=2Al(OH)3+3H2↑;然后，氢氧化铝与氢氧化钠反应，2Al(OH)3+2NaOH=2NaAlO2+4H2O。
在整个过程中，水是氧化剂，而氢氧化钠不是氧化剂。
在解答电子转移和电线桥双线桥法的题目中要注意。
4.铝热反应铝热反应是指铝在高温条件下还原金属氧化物，置换金属单质的一种反应，不是特指与铝与氧化铁的反应。
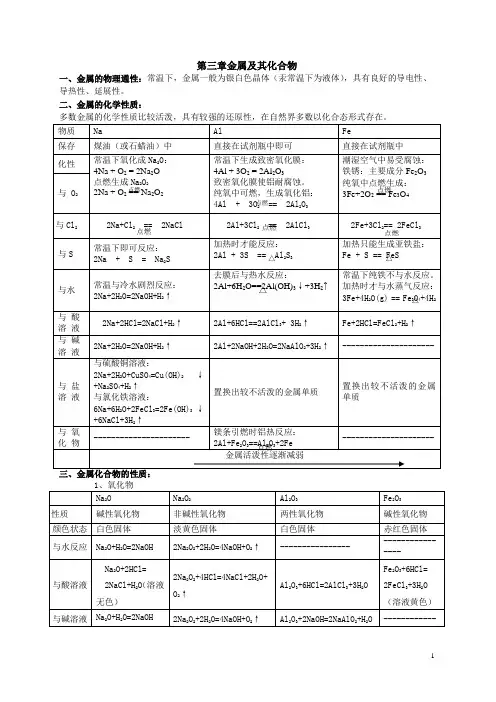
第三章金属及其化合物一、金属的物理通性：常温下，金属一般为银白色晶体（汞常温下为液体），具有良好的导电性、导热性、延展性。
二、金属的化学性质：多数金属的化学性质比较活泼，具有较强的还原性，在自然界多数以化合态形式存在。
四、金属及其化合物之间的相互转化1、铝及其重要化合物之间的转化关系，写出相应的化学反应方程式。
⑩NaAlO 2+HCl+H 2O=Al(OH)3↓+NaCl要求：1、掌握铝三角关系，能书写相关化学方程式 2、能识别和绘制铝三角相关的图象并能求解。
3、掌握相关铝及其化合物的计算。
2、铁及其重要化合物之间的转化关系，写出相应的化学反应方程式。
要求：1、掌握铁三角关系，能书写相关化学 方程式2、掌握相关铁及其化合物的计算。
3、钠及其化合物之间的相互转化，写出相应的化学反应方程式。
附：1、焰色反应：用于在火焰上呈现特殊颜色的金属或它们的化合物的检验。
注：观察钾焰色反应时，应透过蓝色钴玻璃，以便滤去杂质钠的黄光。
2、碳酸钠、碳酸氢钠：Na 2CO 3又叫纯碱，俗称苏打。
无水碳酸钠是白色粉末。
NaHCO 3俗称小苏打，也叫酸式碳酸钠。
它是白色粉末，在水中的溶解度比碳酸钠略小，水溶液呈微碱性，固体碳酸氢钠受热即分解。
NaHCO 3是发酵粉的主要成分，也用于制灭火剂、焙粉或清凉饮料等方面的原料，在橡胶工业中作发泡剂。
将碳酸钠溶液或结晶碳酸钠吸收CO 2可制得碳酸氢钠。
3、氧化铝、氢氧化铝 （1）Al 2O 3俗名矾土，是一种难熔又不溶于水的白色粉末。
它的熔点、沸点都高于2000度。
（2）氢氧化铝是典型的两性氢氧化物，它既能溶于强酸生成铝盐溶液，又能溶于强碱生成偏铝酸盐溶液。
氢氧化铝可用来制备铝盐，作吸附剂等的原料。
氢氧化铝凝胶有中和胃酸和保护溃疡面的作用，可用于治疗胃和十二指肠溃疡、胃酸过多等。
10、合金：钠 钾 黄色 紫色第四章非金属及其化合物一、本章知识结构框架硅及其化合物1、二氧化硅和二氧化碳比较二氧化硅二氧化碳类别酸性氧化物_酸性氧化物晶体结构原子晶体分子晶体熔沸点高低与水反应方程式不反应CO2+H2O H2CO3与酸反应方程式SiO2 + 4HF==SiF4↑+2H2O 不反应与烧碱反应方程式SiO2+2NaOH == Na2SiO3+H2O 少：2NaOH+CO2==Na2CO3+H2O 过：NaOH+CO2==NaHCO3与CaO反应方程式SiO2+CaO 高温CaSiO3CaO+CO2==CaCO3存在状态水晶、玛瑙、石英、硅石、沙子人和动物排放2、硅以及硅的化合物的用途物质用途硅单质半导体材料、光电池（计算器、人造卫星、登月车、探测器）SiO2饰物、仪器、光导纤维、玻璃硅酸钠矿物胶、具有粘性，能做木材的防火剂。
(名师选题)人教高中数学必修一第五章三角函数知识点归纳总结(精华版)单选题1、若sinα+cosαsinα−cosα=12，则tan (α+π4)的值为（ ） A ．−2B ．2C ．−12D ．12 答案：C分析：利用弦化切和两角和的正切展开式化简计算可得答案. 因为sinα+cosαsinα−cosα=12．所以tanα+1tanα−1=12，解得tanα=−3， 于是tan (α+π4)= tanα+tanπ41−tanαtanπ4=−3+11−(−3)=−12．故选：C.2、已知sinαcosα=12，则tanα+1tanα的值为（ ） A ．12B ．−12C ．−2D ．2答案：D解析：根据题中条件，由切化弦，将所求式子化简整理，即可得出结果. ∵sinαcosα=12， ∴tanα+1tanα=sinαcosα+cosαsinα=sin 2α+cos 2αsinαcosα=112=2，故选：D.3、设0<α<π，sinα+cosα=713，则1−tanα1+tanα的值为（ ）A ．177B ．717C ．−177D ．−717 答案：C分析：依题意可知π2<α<π，得到cosα−sinα<0，再利用正余弦和差积三者的关系可求得cosα−sinα的值，将所求关系式切化弦，代入所求关系式计算即可． 由sinα+cosα=713，平方得到1+sin2α=49169，∴sin2α=49169−1=−120169=2sinαcosα，0<α<π， ∴ π2<α<π，∴cosα<0，而sinα>0， ∴cosα−sinα<0； 令t =cosα−sinα(t <0)， 则t 2=1−sin2α，∴t 2=1−sin2α=1+120169=289169，t <0∴t =−1713∴ 1−tanα1+tanα=cosα−sinαcosα+sinα=137(cosα−sinα)=137×(−1713)=−177，故选：C ．4、若扇形周长为20，当其面积最大时，其内切圆的半径r 为（ ） A ．5−1sin1B ．1sin1+32C ．5sin11+sin1D ．5+51+sin1 答案：C分析：先根据扇形周长求解出面积取最大值时扇形的圆心角和半径，然后根据图形中的内切关系得到关于内切圆半径r 的等式，由此求解出r 的值.设扇形的半径为R ，圆心角为α，面积为S ，因为2R +αR =20， 所以S =12αR 2=(10−R )R ≤(10−R+R 2)2=25，取等号时10−R =R ，即R =5，所以面积取最大值时R =5,α=2， 如下图所示：设内切圆圆心为O ，扇形过点O 的半径为AP ，B 为圆与半径的切点， 因为AO +OP =R =5，所以r +rsin∠BPO =5，所以r +rsin1=5， 所以r =5sin11+sin1，故选：C.5、设函数f(x)=2sin (ωx +φ)−1(ω>0)，若对于任意实数φ，f(x)在区间[π4,3π4]上至少有2个零点，至多有3个零点，则ω的取值范围是（ ） A ．[83,163)B ．[4,163)C ．[4,203)D ．[83,203)答案：B分析：t =ωx +φ，只需要研究sint =12的根的情况，借助于y =sint 和y =12的图像，根据交点情况，列不等式组，解出ω的取值范围. 令f(x)=0，则sin (ωx +φ)=12 令t =ωx +φ，则sint =12则问题转化为y =sint 在区间[π4ω+φ,3π4ω+φ]上至少有两个，至少有三个t ，使得sint =12，求ω的取值范围.作出y =sint 和y =12的图像，观察交点个数，可知使得sint =12的最短区间长度为2π，最长长度为2π+23π，由题意列不等式的：2π≤(3π4ω+φ)−(π4ω+φ)<2π+23π 解得：4≤ω<163.故选：B小提示：研究y =Asin (ωx +φ)+B 的性质通常用换元法（令t =ωx +φ），转化为研究y =sint 的图像和性质较为方便.6、cos 2π12−cos 25π12=（ ） A ．12B ．√33C ．√22D ．√32 答案：D分析：由题意结合诱导公式可得cos 2π12−cos 25π12=cos 2π12−sin 2π12，再由二倍角公式即可得解. 由题意，cos 2π12−cos 25π12=cos 2π12−cos 2(π2−π12)=cos 2π12−sin 2π12 =cos π6=√32. 故选：D.7、已知函数f(x)=a 2x−6+3（a >0且a ≠1）的图像经过定点A ，且点A 在角θ的终边上，则sinθ−cosθsinθ+cosθ=（ ） A ．−17B ．0C ．7D ．17 答案：D分析：由题知A(3,4),进而根据三角函数定义结合齐次式求解即可. 解:令2x −6=0得x =3,故定点A 为A(3,4), 所以由三角函数定义得tanθ=43， 所以sinθ−cosθsinθ+cosθ=tanθ−1tanθ+1=43−143+1=17故选：D8、若y =f (x )的图像与y =cosx 的图象关于x 轴对称，则y =f (x )的解析式为（ ）A．y=cos(−x)B．y=−cosxC．y=cos|x|D．y=|cosx|答案：B分析：根据f(−x)、−f(x)、f(|x|)与|f(x)|的图象特征依次判断即可得到结果.对于A，y=cos(−x)=cosx，图象与y=cosx重合，A错误；对于B，∵y=f(x)与y=−f(x)图象关于x轴对称，∴y=−cosx与y=cosx图象关于x轴对称，B正确；对于C，当x≥0时，y=cos|x|=cosx，可知其图象不可能与y=cosx关于x轴对称，C错误；对于D，将y=cosx位于x轴下方的图象翻折到x轴上方，就可以得到y=|cosx|的图象，可知其图象与y= cosx的图象不关于x轴对称，D错误.故选：B.9、将一条闭合曲线放在两条平行线之间，无论这条闭合曲线如何运动，只要它与两平行线中的一条直线只有一个交点，就必与另一条直线也只有一个交点，则称此闭合曲线为等宽曲线，这两条平行直线间的距离叫等宽曲线的宽比．如圆所示就是等宽曲线．其宽就是圆的直径．如图所示是分别以A、B、C为圆心画的三段圆弧组成的闭合曲线Γ（又称莱洛三角形），下列关于曲线Γ的描述中，正确的有（）（1）曲线Γ不是等宽曲线；（2）曲线Γ是等宽曲线且宽为线段AB的长；（3）曲线Γ是等宽曲线且宽为弧AB的长；（4）在曲线Γ和圆的宽相等，则它们的周长相等；（5）若曲线Γ和圆的宽相等，则它们的面积相等．A．1个B．2个C．3个D．4个答案：B分析：若曲线Γ和圆的宽相等，设曲线Γ的宽为1，则圆的半径为1，根据定义逐项判断即可得出结论.2若曲线Γ和圆的宽相等，设曲线Γ的宽为1，则圆的半径为12，（1）根据定义，可以得曲线Γ是等宽曲线，错误； （2）曲线Γ是等宽曲线且宽为线段AB 的长，正确； （3）根据（2）得（3）错误；（4）曲线Γ的周长为3×16×2π=π，圆的周长为2π×12=π，故它们的周长相等，正确；（5）正三角形的边长为1，则三角形对应的扇形面积为π×126=π6，正三角形的面积S =12×1×1×√32=√34， 则一个弓形面积S =π6−√34， 则整个区域的面积为3(π6−√34)+√34=π2−√32， 而圆的面积为π(12)2=π4，不相等，故错误；综上，正确的有2个， 故选：B.小提示：本题主要考查新定义，理解“等宽曲线”得出等边三角形是解题的关键． 10、f(x)=−sinx−xcosx+x 2在[−π,π]的图象大致为（ ）A ．B ．C ．D ．答案：C分析：先由函数为奇函数可排除A ，再通过特殊值排除B 、D 即可.由f(−x)=−sin(−x)+xcosx+x2=−−sinx−xcosx+x2=−f(x)，所以f(x)为奇函数，故排除选项A.又f(π)=−sinπ−πcosπ+π2=−ππ2−1<0，则排除选项B,D故选：C填空题11、如图所示，一竖立在地面上的圆锥形物体的母线长为4，一只小虫从圆锥的底面圆上的点P出发，绕圆锥爬行一周后回到点P处，若该小虫爬行的最短路程为4√3，则这个圆锥的体积为___________.答案：128√2π81分析：作出该圆锥的侧面展开图，该小虫爬行的最短路程为PP′，由余弦定理求出cos∠P′OP=2π3，求出底面圆的半径r，从而求出这个圆锥的高，由此能求出这个圆锥的体积.作出该圆锥的侧面展开图，如图所示：该小虫爬行的最短路程为PP′，由余弦定理可得：cos∠P′OP=OP2+OP′2−PP′22OP·OP′=42+42−(4√3)22×4×4=−12∴cos∠P′OP=2π3.设底面圆的半径为r,则有2πr=2π3·4,解得r=43,所以这个圆锥的高为ℎ=√16−169=8√23，则这个圆锥的体积为V=13Sℎ=13πr2ℎ=13π×169×8√23=128√2π81.所以答案是：128√2π81.小提示：立体几何中的翻折叠（展开）问题要注意翻折（展开）过程中的不变量.12、自行车大轮48齿，小轮20齿，大轮转一周小轮转___________周．答案：125分析：通过两个车轮转动的齿数相同，计算即可得出结果.∵两个车轮转动的齿数相同，大轮有48齿，小轮有20齿，∴当大轮转动一周时，大轮转动了48个齿，∴小轮转动4820=125周.所以答案是：125.13、若cosα=−35,α为第二象限的角，则sin(π−α)=__________．答案：45分析：先根据同角三角函数的关系求出sinα，再结合诱导公式即可求出sin(π−α).∵cosα=−35,α为第二象限的角，∴sinα=√1−cos2α=45，∴sin(π−α)=sinα=45.所以答案是：45.小提示：本题考查同角三角函数的关系以及诱导公式的应用，属于基础题.14、若α∈(π2，π)，且cos2α−sinα=14，则tanα=_____.答案：−√33分析：根据同角平方和关系可解得sinα=12，进而根据角的范围可得α=5π6，进而可求.因为cos2α−sinα=14，所以4(1－sin2α)－4sinα－1=0即4sin 2α+4sin α－3=0 ，∴解得sin α=12或sin α=−32（舍去）．∵α∈(π2，π)，∴α=5π6，因此tan α=tan5π6=−√33． 所以答案是：−√33 15、已知cos(α+π6)=35，α∈(0，π2)，则cos(2α+7π12)=__．答案：−31√250分析：先求出cos(2α+π3)=−725，sin(2α+π3)=2425，再利用和差角公式即可求解. ∵cos(α+π6)=35，α∈(0，π2)． ∴(α+π6)∈(0，π2)，(2α+π3)∈(0，π)．cos(2α+π3)=2cos(α+π6)−1=2×(35)2−1=−725． ∴sin(2α+π3)=√1−cos(2α+π3)=2425．∴cos(2α+7π12)=cos(2α+π3+π4)=cos(2α+π3)cos π4−sin(2α+π3)sin π4 =−725×√22−2425×√22=−31√250． 所以答案是：−31√250. 解答题16、已知函数y =asin (2x −π3)+b (a >0).(1)求出该函数的单调递减区间；(2)当x ∈[0,π2]时，f (x )的最小值是−2，最大值是√3，求实数a ，b 的值.答案：(1)[k π+5π12,k π+11π12]，k ∈Z(2)a =2，b =−2+√3分析：(1)利用整体代入法即可求解y =asin (2x −π3)+b 的单调减区间；(2)结合x ∈[0,π2]，利用正弦函数的性质求出sin (2x −π3)的取值范围，然后结合已知条件求解即可. (1)结合已知条件和正弦函数性质，由2k π+π2≤2x −π3≤2k π+3π2，k ∈Z ，解得k π+5π12≤x ≤k π+11π12，k ∈Z ，故函数f (x )的单调递减区间为[k π+5π12,k π+11π12]，k ∈Z .(2)令t =2x −π3，∵0≤x ≤π2，∴−π3≤t ≤2π3，∴由正弦函数性质得，−√32≤sint =sin(2x −π3)≤1，故f (x )min =−√32a +b =−2，f (x )max =a +b =√3，由{−√32a +b =−2a +b =√3，解得{a =2b =−2+√3. 17、已知函数f (x )={cosx,−π⩽x <0,sinx,0⩽x ⩽π.（1）作出该函数的图象； （2）若f (x )=12，求x 的值；（3）若a ∈R ，讨论方程f (x )=a 的解的个数．答案：（1）图见解析；（2）x =−π3或π6或5π6；（3）当a >1或a <−1时，解的个数为0；当−1⩽a <0或a =1时，解的个数为1；当0⩽a <1时，解的个数为3． 分析：（1）根据正余弦函数的图象即可画出； （2）讨论x 的范围根据解析式即可求解；（3）方程f (x )=a 的解的个数等价于y =f (x )与y =a 的图象的交点个数，结合图象即可得出. （1）f (x )的函数图象如下：（2）当−π≤x <0时，f (x )=cosx =12，解得x =−π3，当0≤x ≤π时，f (x )=sinx =12，解得x =π6或5π6，综上，x =−π3或π6或5π6； （3）方程f (x )=a 的解的个数等价于y =f (x )与y =a 的图象的交点个数，则由（1）中函数图象可得，当a >1或a <−1时，解的个数为0；当−1⩽a <0或a =1时，解的个数为1；当0⩽a <1时，解的个数为3．18、已知函数f (x )=2cos 2x 2+√3sin x +a −1的最大值为1.(1)求函数f (x )的单调递减区间；(2)若x ∈[0，π2]，求函数f (x )的值域.答案：(1)[2kπ+π3,2kπ+4π3]，k ∈Z(2)[0,1]分析：(1)利用三角恒等变换化简函数解析式为y ＝A sin(ωx ＋φ)＋B 的形式，ωx ＋φ整体替换进行单调区间的求解；(2)求出ωx ＋φ整体范围，根据正弦型函数图像求其值域﹒（1）f (x )=2cos 2x 2+√3sin x +a −1 =cosx +√3sinx +a =2sin (x +π6)+a ．由f(x)max=2+a=1，解得a=−1．又f(x)=2sin(x+π6)−1，则2kπ+π2≤x+π6≤2kπ+3π2，k∈Z，解得2kπ+π3≤x≤2kπ+4π3，k∈Z，所以函数的单调递减区间为[2kπ+π3,2kπ+4π3]，k∈Z；（2）由x∈[0，π2]，则x+π6∈[π6，2π3]，所以12≤sin(x+π6)≤1，所以0≤2sin(x+π6)−1≤1，所以函数f(x)的值域为[0,1]．。
第三章铁金属材料第一节铁及其化合物.................................................................................................. - 1 - 第二节金属材料.......................................................................................................... - 6 - 第1课时合金...................................................................................................... - 6 -第2课时物质的量在化学方程式计算中的应用............................................ - 10 -第一节铁及其化合物1.基础知识一、铁单质1．铁元素在自然界中的存在形式铁在自然界中可以像陨铁中的铁那样以单质形态存在，但主要是以＋2价和＋3价化合物的形态存在于矿石中。
铁元素在地壳中的含量仅次于氧、硅和铝，居第四位。
2．铁单质的物理性质纯铁是一种银白色金属，有一定的延展性和导热性，能导电，其导电性不如铜和铝，熔、沸点较高，能被磁体吸引。
3．铁单质的化学性质(1)与非金属的反应(2)与酸反应离子反应方程式如下：Fe＋2H＋===Fe2＋＋H2↑(3)与水蒸气反应通常铁与冷水和热水均不反应，但铁可与水蒸气反应。
方法方法一方法二实验装置气体用小试管收集一试管气体，点燃，听到轻微噗声，证明生成了H2用火柴点燃肥皂泡，听到爆鸣声，证明生成了H2古代湿法炼铜反应原理： Fe ＋CuSO 4===Cu ＋FeSO 4。
4．铁的冶炼反应原理：C ＋O 2=====点燃CO 2， C ＋CO 2=====高温2CO ，Fe 2O 3＋3CO=====高温2Fe ＋3CO 2。
高中数学必修一第五章三角函数知识点归纳总结(精华版)单选题1、若sin (π7+α)=12，则sin (3π14−2α)=（ ） A ．35B ．−12C ．12D ．13答案：C分析：令θ=π7+α可得α=θ−π7，再代入sin (3π14−2α)，结合诱导公式与二倍角公式求解即可令θ=π7+α可得α=θ−π7，故sinθ=12，则sin (3π14−2α)=sin (3π14−2(θ−π7)) =sin (π2−2θ)=cos2θ=1−2sin 2θ=12故选：C2、若sin(π−α)+cos(−α)=15，α∈(0,π)，则tan (32π−α)的值为（ ） A ．−43或−34B ．−43C ．−34D ．34答案：C分析：根据同角三角函数的基本关系及诱导公式求解. 由sin(π−α)+cos(−α)=15可得：sinα+cosα=15，平方得：sin 2α+2sinαcosα+cos 2α=125 所以tan 2α+2tanα+1tan 2α+1=125，解得tanα=−43或tanα=−34， 又sinα+cosα=15，所以|sinα|>|cosα|， 故tanα=−43， 故选：C3、已知函数f(x)=cos 2ωx 2+√32sinωx −12(ω>0,x ∈R)，若函数f(x)在区间(π,2π)内没有零点，则ω的取值范围是（ ）A ．(0,512]B ．(0,56)C ．(0,512]∪[56,1112]D ．(0,512]∪(56,1112] 答案：C分析：先化简函数解析式，由π<x <2π得，求得πω+π6<ωx +π6<2πω+π6，利用正弦函数图象的性质可得2πω+π6≤π或{2πω+π6≤2ππω+π6≥π，求解即可. f(x)=cosωx+12+√32sinωx −12=√32sinωx +12cosωx =sin(ωx +π6)．由π<x <2π得，πω+π6<ωx +π6<2πω+π6， ∵函数f(x)在区间(π,2π)内没有零点，且πω+π6>π6， ∴2πω+π6≤π或{2πω+π6≤2ππω+π6≥π ， 解得0<ω⩽512或56⩽ω⩽1112，则ω的取值范围是(0,512]∪[56,1112].故选：C ．4、已知函数y =√2sin(x +π4)，当y 取得最小值时，tanx 等于（ ）A ．1B ．−1C ．√32D ．−√32答案：A分析：由正弦函数的性质，先求出当y 取得最小值时x 的取值，从而求出tanx . 函数y =√2sin(x +π4)，当y 取得最小值时，有x +π4=2kπ+3π2，故x =2kπ+5π4，k ∈Z ．∴tanx =tan (2kπ+5π4)=tan (π4)=1，k ∈Z ． 故选：A ．5、已知tanθ=2，则sin(π2+θ)−cos(π−θ)cosθ−sin(π−θ)=（ ）A ．2B ．-2C ．0D ．23 答案：B分析：根据tanθ=2，利用诱导公式和商数关系求解. 因为tanθ=2， 所以sin(π2+θ)−cos(π−θ)cosθ−sin(π−θ)，=2cosθcosθ−sinθ， =21−tanθ=−2，故选：B6、要得到函数y =sin (2x +π6)的图象，可以将函数y =cos (2x −π6)的图象（ ） A ．向右平移π12个单位长度B ．向左平移π12个单位长度C ．向右平移π6个单位长度D ．向左平移π6个单位长度 答案：A分析：利用诱导公式将平移前的函数化简得到y =sin (2x +π3)，进而结合平移变换即可求出结果.因为y =cos (2x −π6)=sin (2x −π6+π2)=sin (2x +π3)，而y =sin [2(x −π12)+π3]，故将函数y =cos (2x −π6)的图象向右平移π12个单位长度即可， 故选：A. 7、已知sinα=2√67，cos (α−β)=√105，且0<α<3π4，0<β<3π4，则sinβ=（ ）A ．9√1535B ．11√1035C ．√1535D ．√1035答案：A解析：易知sinβ=sin(α−(α−β))，利用角的范围和同角三角函数关系可求得cosα和sin (α−β)，分别在sin (α−β)=√155和−√155两种情况下，利用两角和差正弦公式求得sinβ，结合β的范围可确定最终结果. ∵sinα=2√67<√22且0<α<3π4，∴0<α<π4，∴cosα=√1−sin 2α=57. 又0<β<3π4，∴−3π4<α−β<π4，∴sin (α−β)=±√1−cos 2(α−β)=±√155. 当sin (α−β)=√155时，sinβ=sin(α−(α−β))=sinαcos (α−β)−cosαsin (α−β) =2√67×√105−57×√155=−√1535， ∵0<β<3π4，∴sinβ>0，∴sinβ=−√1535不合题意，舍去； 当sin (α−β)=−√155，同理可求得sinβ=9√1535，符合题意.综上所述：sinβ=9√1535.故选：A .小提示：易错点睛：本题中求解cosα时，易忽略sinα的值所确定的α的更小的范围，从而误认为cosα的取值也有两种不同的可能性，造成求解错误. 8、若tanθ=2，则sinθ(1−sin2θ)sinθ−cosθ=（ ）A ．25B ．−25C ．65D ．−65 答案：A分析：由二倍角正弦公式和同角关系将sinθ(1−sin2θ)sinθ−cosθ转化为含tanθ的表达式，由此可得其值. sinθ(1−sin2θ)sinθ−cosθ=sinθ(sin 2θ+cos 2θ−sin2θ)sinθ−cosθ=sinθ(sinθ−cosθ)2sinθ−cosθ=sin 2θ−sinθcosθsin 2θ+cos 2θ=tan 2θ−tanθtan 2θ+1=25．故选：A. 多选题9、若α是第二象限的角，则下列各式中成立的是（ ） A ．tanα=−sinαcosαB ．√1−2sinαcosα=sinα−cosαC ．cosα=−√1−sin 2αD ．√1+2sinαcosα=sinα+cosαE ．sinα=−√1−cos 2α 答案：BC解析：利用sin 2α+cos 2α=1,tanα=sinαcosα，结合三角函数在各个象限的符号，代入每个式子进行化简、求值.对A ，由同角三角函数的基本关系式，知tanα=sinαcosα，所以A 错；对B ，C ，D ，E ，因为α是第二象限角，所以sinα>0,cosα<0，所以sinα−cosα>0,sinα+cosα的符号不确定，所以√1−2sinαcosα=√(sinα−cosα)2=sinα−cosα，所以B ，C 正确；D ，E 错． 故选：BC.小提示：本题考查同角三角函数的基本关系、三角函数在各个象限的符号，考查运算求解能力. 10、下列各式中，值为12的是（ ）A ．cos 2π12−sin 2π12B ．tan22.5∘1−tan 222.5∘C ．2sin195°cos195°D ．√1+cos π62答案：BC分析：运用二倍角公式，结合诱导公式和特殊角的三角函数值的求法即可得到答案. 选项A ，cos 2π12−sin 2π12=cos (2×π12)=cos π6=√32，错误； 选项B ，tan22.5°1−tan 222.5°=12⋅2tan22.5°1−tan 222.5°=12tan45°=12，正确；选项C ，2sin195∘cos195∘=sin390∘=sin (360∘+30∘)=sin30∘=12，正确；选项D ，√1+cos π62=√1+√322=√2+√32，错误.故选：BC.11、（多选）已知θ∈(0,π)，sinθ+cosθ=15，则（ ）A ．θ∈(π2,π)B ．cosθ=−35 C ．tanθ=−34D ．sinθ−cosθ=75答案：ABD分析：已知式平方求得sinθcosθ，从而可确定θ的范围，然后求得sinθ−cosθ，再与已知结合求得sinθ,cosθ，由商数关系得tanθ，从而可判断各选项．因为sinθ+cosθ=15①，所以(sinθ+cosθ)2=sin 2θ+2sinθcosθ+cos 2θ=125，所以2sinθcosθ=−2425．又θ∈(0,π)，所以sinθ>0，所以cosθ<0，即θ∈(π2,π)，故A 正确．(sinθ−cosθ)2=1−2sinθcosθ=4925，所以sinθ−cosθ=75②，故D 正确．由①②，得sinθ=45，cosθ=−35，故B 正确．tanθ=sinθcosθ=−43，故C 错误． 故选：ABD ． 填空题12、当θ∈(0,π2)时，若cos (5π6−θ)=−12，则sin (θ+π6)的值为_________．答案：√32##12√3 分析：先由已知条件求出sin (5π6−θ)，然后利用诱导公式可求得结果. ∵θ∈(0,π2)，∴5π6−θ∈(π3,5π6)， ∴sin (5π6−θ)=√1−cos 2(5π6−θ)=√32， ∴sin (θ+π6)=sin [π−(5π6−θ)]=sin (5π6−θ)=√32． 所以答案是：√3213、已知sinα=2cosα，则sin 2α+2sinαcosα=______． 答案：85##1.6分析：根据题意，由同角三角函数关系可得tanα的值，而sin 2α+2sinαcosα1=sin 2α+2sinαcosαsin 2α+cos 2α，最后利用齐次式化成关于tanα的分式即可解.解：由sinα=2cosα，得tanα=sinαcosα=2， 则sin 2α+2sinαcosα1=sin 2α+2sinαcosαsin 2α+cos 2α=tan 2α+2tanαtan 2α+1=22+2×222+1=85.所以答案是：85.14、已知f (x )=sin (ωx +π3)(ω>0)，f (π6)=f (π3)，且f (x )在区间(π6,π3)上有最小值，无最大值，则ω=______.答案：143分析：由题意可得函数的图象关于直线x=π4对称，再根据f(x)在区间(π6,π3)上有最小值，无最大值，可得π4ω+π3=2kπ+3π2(k∈Z)，由此求得ω的值．依题意，当x=π6+π32=π4时，y有最小值，即sin(π4ω+π3)=−1，则π4ω+π3=2kπ+3π2(k∈Z)，所以ω=8k+143(k∈Z).因为f(x)在区间(π6,π3)上有最小值，无最大值，所以π3−π4≤T2=πω，即ω≤12，令k=0，得ω=143.所以答案是：143解答题15、已知函数f(x)=2sinxcosx−2√3sin2x+√3.(1)求函数f(x)的最小正周期及其单调递增区间；(2)当x∈[−π6,π6]，时，a−f(x)≤0恒成立，求a的最大值.答案：(1)最小正周期π，单调递增区间为[kπ−5π12,kπ+π12]，k∈Z(2)最大值为0分析：（1）根据正弦和余弦的二倍角公式以及辅助角公式即可化简f(x)为f(x)=2sin(2x+π3)，然后根据周期公式可求周期，整体代入法求单调增区间,（2）根据x的范围可求2x+π3∈[0,2π3]，进而可求f(x)的值域，故可求a的范围.（1）f(x)=2sinxcosx−2√3sin2x+√3=sin2x+√3cos2x=2sin(2x+π3)故函数f(x)的最小正周期T=2π2=π.由2kπ-π2≤2x+π3≤2kπ+π2得kπ−5π12≤x≤kπ+π12(k∈Z).∴函数f(x)的单调递增区间为[kπ−5π12,kπ+π12]，k∈Z.（2）∵x∈[−π6,π6]，∴2x+π3∈[0,2π3]，∴sin (2x +π3)∈[0,1]，f (x )=2sin (2x +π3)∈[0,2].由a −f (x )≤0恒成立，得a ≤(f (x ))min ，即a ≤0.故a 的最大值为0.。
学习笔记与氢氧化钠现象：产生白色沉淀，快速变成灰绿色，最终变成红褐色。
FeCl2+2NaOH==F e(O H)2↓+2NaCl4F e(O H)2+O2+2H2O==4F e(O H)3现象：产生红褐色沉淀FeCl3+3NaOH==F e(O H)3↓+ 3NaCl与KSCN溶液无现象产生血红色Fe3＋+3SCN-==Fe(SCN)3氧化（还原性）主要表现：还原性，举例：2FeCl2+Cl2 ==2FeCl3表现：氧化性，举例：2FeCl3+Fe==3FeCl2相互转化FeCl2FeCl3：2FeCl2+Cl2 ==2FeCl3FeCl3 FeCl2：2FeCl3+Fe==3FeCl2名称氢氧化亚铁氢氧化铁化学式F e(O H)2F e(O H)3颜色、状态白色固体红褐色固体水溶性难溶于水难溶于水与酸反应F e(O H)2+2HCl==FeCl2+2H2OF e(O H)2+2H＋==Fe2＋+2H2OF e(O H)3+3HCl==FeCl3+3H2OF e(O H)3+3H＋==Fe3＋+3H2O氢氧化亚铁露置空气中4F e(O H)2+O2+2H2O ==4F e(O H)33、铁三角二、本章典型题剖析1、滴加依次不同，试验现象不同（1）稀Na2CO3溶液与稀盐酸间的反应向Na2CO3溶液中逐滴加入稀盐酸，起先时无气体产生，达到肯定量后才有气泡冒出，由少到多的过程中依次发生下列反应：是NaOH。
若将1克该样品放入含有HCl 3.65克的盐酸中使其完全反应后，残酸再用50克2%的NaOH溶液恰好中和反应，蒸干溶液，所得固体的质量是多少克？解：所得固体是NaCl ，是5.85克［小结］本题数据众多，反应物不纯，过程困难。
若按常规方法，一步步分析计算，不但费时还易出错，若仔细分析就会发觉，最终所得固体物质NaCl中全部的Cl全来自于HCl中的Cl1、有5.1gMg–Al合金，投入500mL 2mol/L HCl中，金属完全溶解后，又加4mol/LNaOH 溶液VmL，得最多沉淀8.6g，则V等于A. 425mLB. 560mLC. 250mLD. 500mL2、铝三角转化及铝的图像问题(1) 向Al3＋的溶液中加入强碱(OH―)现象：先出现白色溶液后消逝方程式：Al3＋＋3OH―＝＝A l(O H)3↓A l(O H)3+OH― ==AlO2―+H2O图像：(2) 向强碱溶液中加入Al3＋现象：先没有沉淀后出现并不消逝方程式：Al3＋+4OH―==AlO2―+2H2O3AlO2―+Al3＋+6H2O==4A l(O H)3↓图像：(3) 向AlO2―溶液中加入H＋现象：先生成白色沉淀，然后白色沉淀渐渐溶解。
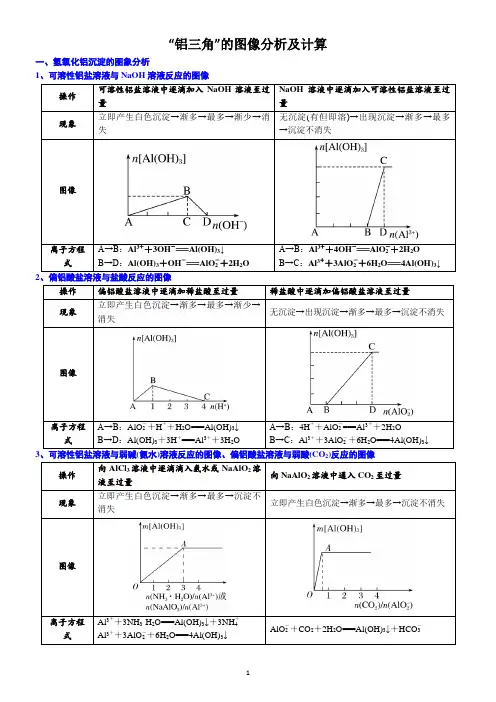
“铝三角”的图像分析及计算一、氢氧化铝沉淀的图象分析1、可溶性铝盐溶液与NaOH溶液反应的图像操作可溶性铝盐溶液中逐滴加入NaOH溶液至过量NaOH溶液中逐滴加入可溶性铝盐溶液至过量现象立即产生白色沉淀→渐多→最多→渐少→消失无沉淀(有但即溶)→出现沉淀→渐多→最多→沉淀不消失图像离子方程式A→B：Al3＋＋3OH－===Al(OH)3↓B→D：Al(OH)3＋OH－===AlO－2＋2H2OA→B：Al3＋＋4OH－===AlO－2＋2H2OB→C：Al3＋＋3AlO－2＋6H2O===4Al(OH)3↓2、偏铝酸盐溶液与盐酸反应的图像操作偏铝酸盐溶液中逐滴加稀盐酸至过量稀盐酸中逐滴加偏铝酸盐溶液至过量现象立即产生白色沉淀→渐多→最多→渐少→消失无沉淀→出现沉淀→渐多→最多→沉淀不消失图像离子方程式A→B：AlO－2＋H＋＋H2O===Al(OH)3↓B→D：Al(OH)3＋3H＋===Al3＋＋3H2OA→B：4H＋＋AlO－2===Al3＋＋2H2OB→C：Al3＋＋3AlO－2＋6H2O===4Al(OH)3↓3、可溶性铝盐溶液与弱碱(氨水)溶液反应的图像、偏铝酸盐溶液与弱酸(CO2)反应的图像操作向AlCl3溶液中逐滴滴入氨水或NaAlO2溶液至过量向NaAlO2溶液中通入CO2至过量现象立即产生白色沉淀→渐多→最多→沉淀不消失立即产生白色沉淀→渐多→最多→沉淀不消失图像离子方程式Al3＋＋3NH3·H2O===Al(OH)3↓＋3NH＋4Al3＋＋3AlO－2＋6H2O===4Al(OH)3↓AlO－2＋CO2＋2H2O===Al(OH)3↓＋HCO－34、可溶性铝盐、镁盐混合液与NaOH溶液反应的图像操作往等物质的量的AlCl3、MgCl2混合溶液中加入NaOH溶液至过量向MgCl2、AlCl3和盐酸的混合溶液(即将Mg、Al溶于过量盐酸所得的溶液)中逐滴滴入NaOH溶液至过量现象开始出现白色沉淀，后沉淀量增多，最后沉淀部分溶解先无沉淀，后出现白色沉淀，然后沉淀量增多，最后沉淀部分溶解图像离子方程式O→A：Al3＋＋3OH－===Al(OH)3↓Mg2＋＋2OH－===Mg(OH)2↓A→B：Al(OH)3＋OH－===AlO－2＋2H2OO→A：H＋＋OH－===H2OA→B：Al3＋＋3OH－===Al(OH)3↓Mg2＋＋2OH－===Mg(OH)2↓A→B：Al(OH)3＋OH－===AlO－2＋2H2O5、含不同阳离子的混合盐(或复盐)与碱的反应(1)向含MgCl2、AlCl3、盐酸、NH4Cl的混合溶液中，逐滴加入NaOH溶液至过量图像离子方程式O→A：H＋＋OH－===H2OA→B：Al3＋＋3OH－===Al(OH)3↓，Mg2＋＋2OH－===Mg(OH)2↓B→C：NH＋4＋OH－===NH3·H2OC→D：Al(OH)3＋OH－===AlO－2＋2H2O(2)把Ba(OH)2溶液逐滴加入到明矾溶液中至过量图像离子方程式O→A：2KAl(SO4)2＋3Ba(OH)2===2Al(OH)3↓＋3BaSO4↓＋K2SO4 A→B：2Al(OH)3＋K2SO4＋Ba(OH)2===BaSO4↓＋2KAlO2＋4H2O二、常见题型类型一图像认识1、向含有盐酸的AlCl3 溶液中慢慢滴入NaOH 溶液，生成沉淀W(g)与所加NaOH 溶液体积V的关系如下图，其中正确的是( )2、如图表示AlCl3溶液与NaOH溶液相互滴加过程中微粒的量的关系曲线，下列判断错误的是()A．①线表示Al3＋的物质的量的变化B．x表示AlCl3的物质的量C．③线表示Al(OH)3的物质的量的变化D．④线表示AlO－2的物质的量的变化3、下列实验操作对应的图像不正确的是()选项实验操作图像A 向MgCl2、AlCl3溶液中(各1 mol)，逐滴加入NaOH溶液B 向HCl、MgCl2、AlCl3、NH4Cl溶液中(各1 mol)，逐滴加入NaOH溶液C 向NaOH、NaAlO2溶液中(各1 mol)，逐滴加入HCl溶液D 向NaOH、Na2CO3混合溶液中(各1 mol)滴加稀盐酸类型二有关图像的计算1、向30mL1mol·L－1的AlCl3溶液中逐渐加入浓度为4mol·L－1的NaOH溶液，若产生0.78g白色沉淀，则加入的NaOH溶液的体积可能为()A．3mL B．7.5mL C．15mL D．17.5mL2、现有AlCl3和MgSO4混合溶液，向其中不断加入NaOH溶液，得到沉淀的量与加入NaOH溶液的体积如下图所示，原溶液中Cl－与SO2－4的物质的量之比为()A．1∶3 B．2∶3 C．6∶1 D．3∶13、向混有一定量盐酸的硫酸铝和硫酸镁混合溶液中，逐滴加入2mol/L的NaOH 溶液，所生成沉淀W g 与加入NaOH 溶液的体积V( mL)如图所示，则原混合溶液中c(Cl-)、c(Al3+)、c(Mg2+)之比为 ()A．1：3：1 B．1：2：1 C．1：1：2 D．1：1 ：14、某溶液中可能含有H＋、NH＋4、Mg2＋、Al3＋、Fe3＋、CO2－3、SO2－4、NO－3中的几种。
考点6铝三角的应用【考点定位】本考点考查铝三角的应用，涉及铝盐、偏铝酸盐及氢氧化铝之间的转化条件，特别注意铝盐与碱性溶液及偏铝酸盐与酸之间的反应，以及反应物的物质的量对反应原理的影响。
【精确解读】Al 3＋、Al(OH)3、AlO 2－之间的转化关系1．Al 3＋―→Al(OH)3（1）可溶性铝盐与少量NaOH 溶液反应：AlCl 3+3NaOH =Al(OH)3↓+3NaCl （2）可溶性铝盐与氨水反应：AlCl 3+3NH 3·H 2O =Al(OH)3↓+3NH 4Cl 2．Al(OH)3―→Al 3＋：Al(OH)3溶于强酸溶液：Al(OH)3+3HCl=AlCl 3+3H 2O3．Al 3＋―→AlO 2-：可溶性铝盐与过量的强碱反应：AlCl 3+4NaOH=NaAlO 2+3NaCl+2H 2O 4．AlO 2-―→Al 3＋：偏铝酸盐溶液与足量的盐酸反应：NaAlO 2+4HCl=AlCl 3+NaCl+2H 2O 5．AlO 2-―→Al(OH)3：偏铝酸钠溶液中加入少量盐酸：NaAlO 2+HCl+H 2O=Al(OH)3↓+NaCl 6．Al(OH)3―→AlO 2-：Al(OH)3溶于强碱溶液：Al(OH)3+NaOH=NaAlO 2+2H 2O特别注意：三种物质相互转化注意反应条件，特别是Al(OH)3既能溶于强酸，又能溶于强碱。
【精细剖析】1．两性化合物的概念指既能与酸反应，又能与碱反应的化合物。
与酸或碱反应生成的产物是盐和水的化合物才是两性化合物。
弱酸的铵盐、弱酸的酸式盐不属于两性化合物。
2．Al(OH)3的三种制备方法（1）用铝盐和氨水制备Al(OH)3，不选用强碱(如NaOH)溶液，是由于Al(OH)3溶于强碱溶液，而不溶于弱碱(如氨水)溶液。
（2）溶液中AlO 2-→Al(OH)3最好通入CO 2，而不是选用强酸，因为氢氧化铝溶于强酸，而不溶于较弱的酸。
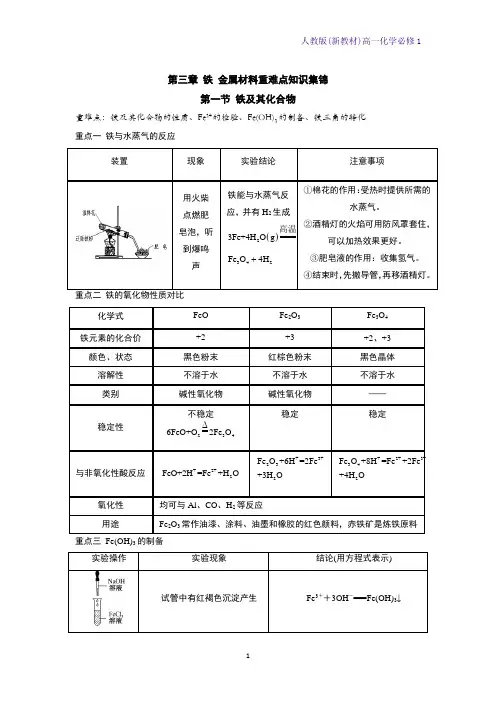
第三章 铁 金属材料重难点知识集锦第一节 铁及其化合物重难点：铁及其化合物的性质、Fe 3+的检验、Fe(OH)3的制备、铁三角的转化 重点一 铁与水蒸气的反应装置现象实验结论注意事项用火柴点燃肥皂泡，听到爆鸣声铁能与水蒸气反应，并有H 2生成()23243Fe+4H Fe H g O O 4+高温①棉花的作用：受热时提供所需的水蒸气。
②酒精灯的火焰可用防风罩套住，可以加热效果更好。
③肥皂液的作用：收集氢气。
④结束时，先撤导管，再移酒精灯。
重点二 铁的氧化物性质对比化学式 FeO Fe 2O 3 Fe 3O 4 铁元素的化合价 +2 +3 +2、+3 颜色、状态 黑色粉末 红棕色粉末 黑色晶体 溶解性 不溶于水 不溶于水 不溶于水 类别碱性氧化物 碱性氧化物 —— 稳定性不稳定234Δ6FeO+O 2Fe O稳定稳定与非氧化性酸反应+2+2FeO+2H =Fe +H O+3+232Fe O +6H =2Fe +3H O+2+3+342Fe O +8H =Fe +2Fe +4H O氧化性 均可与Al 、CO 、H 2等反应用途Fe 2O 3常作油漆、涂料、油墨和橡胶的红色颜料，赤铁矿是炼铁原料重点三 Fe(OH)3的制备实验操作实验现象结论(用方程式表示)试管中有红褐色沉淀产生Fe 3＋＋3OH －===Fe(OH)3↓试管中先生成白色沉淀，迅速变成灰绿色，最后变成红褐色Fe2＋＋2OH－===Fe(OH)2↓(白色)、4Fe(OH)2＋O2＋2H2O===4Fe(OH)3制备Fe(OH)2的注意问题(1)Fe2＋极易被氧化，所以FeSO4溶液要现制现用。
(2)为了防止Fe2＋被氧化，配制FeSO4溶液的蒸馏水和NaOH溶液要煮沸，尽可能除去O2。
(3)为了防止滴加NaOH溶液时带入空气，可将吸有NaOH溶液的长滴管伸入到FeSO4溶液的液面下，再挤出NaOH溶液。
(4)为防止Fe2＋被氧化，还可以向盛有FeSO4溶液的试管中加入少量的煤油或其他密度小于水而不溶于水的有机物，以隔绝空气。
