高三理科数学下册课后练习题2

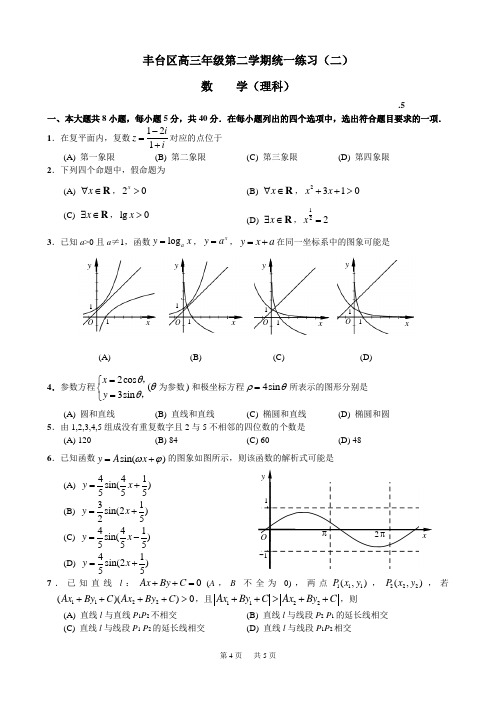
清华附中2006-2007高三下数学(理)统练2答案1-5 C D D D A 6-8 A D D9、四 10、?2 11、 2 12 、 43 13、3 14 83315、解：(1) 令⎩⎨⎧-==⎩⎨⎧=-=⇒⎪⎩⎪⎨⎧-=+⋅-=+=1001143cos 21),(22y x y x y x y x y x 或则π， )1,0()0,1(-=-=∴或 2分(2) )1,0(0),0,1(-=∴=⋅= 3分))32cos(,(cos )1)23(cos 2,(cos 2x x x x -=--=+ππ4分 2)234cos(122cos 1)32(cos cos ||222x x x x -+++=-+=+ππ 6分 )]23cos(2[cos 211)]234cos(2[cos 211x x x x --+=-++=ππ )32cos(211]2sin 232cos 212[cos 211π++=--+=x x x x 8分 35323320ππππ<+<⇒<<x x ， 45||2121)32cos(12<+≤⇒<+≤-∴b n x π 9分故25||22<+≤ 10分 16、 (1)63(注：第1、2次或第2、3次或三次均击中)；(2)162；(3)ξ 34… k… P27125 162625…233123()()55k k C --…17、方法一：(1) 证明：连结AC ，AC 交BD 于O ，连结EO ． ∵底面ABCD 是正方形，∴点O 是AC 的中点， 在PAC ∆中，EO 是中位线，∴PA⊂EO ⊄PA ⊂DC DC PD ⊥PDC ∆PC DE ⊥⊂DE DE BC ⊥⊥DE ⊂PB PB DE ⊥PB EF ⊥E EF DE = DF PB ⊥EFD ∠DBPD EF DE ⊥⊥,aBD a DC PD 2,===aBD PD PB 322=+=aDC PD PC 222=+=a PC DE 2221==PDBRt ∆a aa a PB BD PD DF 3632=⋅=⋅=EFDRt ∆233622sin ===a aDF DE EFD 3π=∠EFD 3πaDC =)2,2,0(),,0,0(),0,0,(a a E a P a A )0,2,2(aa (,0,),(,0,)22a aPA a a EG =-=-EG PA 2=⊂EG ⊄PA )0,,(a a B ),,(a a a -=(0,,)22a aDE =022022=-+=⋅a a DE PB DE PB ⊥PB EF ⊥EDE EF = ⊥PB ),,(000z y x λ=),,(),,(000a a a a z y x -=-λaz a y a x )1(,,000λλλ-===00011(,,)(,(),())2222a a FE x y z a a a λλλ=---=---PBEF ⊥0=⋅0)21()21(222=---+-a a a λλλ31=λ)32,3,3(a a a (,,)366a a aFE =--2(,,)333a a a FD =---03233222=+--=⋅a a a FD PB FD PB ⊥EFD ∠691892222a a a a =+-=⋅a a a a FE 6636369||222=++=aa a a 369499||222=++=2136666||||cos 2=⋅==a a a FD FE EFD 3π=∠EFD 3π3381122)2(12234341=⇒=-+=⇒≥-+=-a a a a a n n n3分(2) 假设存在的实数λ符合题意，则nn n n n n n a a a a 2222111λλλ--=+-+--- nn n 211212λλ+-=--=必是与n 无关的常数，则.1021-=⇒=+λλn7分 故存在实数λ= ?1，使得数列}21{n λ+为等差数列.(3) 由(2) 知数列}21{nn a -是公差d = 1的等差数列 12)1(11)1(21211+⋅+=⇒+=⨯-+-=-∴nn nn n a n n a a 9分 S n = n +2×2 + 3×22+ 4×23+…+(n +1)·2n +12S n = 2n +2×22 + 3×22 +…+n ·2n + (n +1)·2n +1⇒相减整理得： S n = n (2n +1+1) 12分附加．解：(1) 设)0,(),0,(),,(2100c F c F y x P -， 其中),(),()0,(,0000122y c x y x c PF b a c ---=--=-=则，).,(),()0,(00002y x c y x c PF --=-=从而.),(),(2202020220000021c y x y c x y x c y c x PF -+=+-=--⋅---=⋅ 2分 由于222122220202,c a PF c b a y x b -≤⋅≤-≤+≤所以，即.222122b PF a b ≤⋅≤- 3分又已知343421≤⋅≤-PF PF ， 4分 所以⎪⎩⎪⎨⎧==⇒⎪⎪⎩⎪⎪⎨⎧=-=-.34,4,34,34222222b a b a b从而椭圆的方程是.143422=+y x (2) 因为PCQ CQ CP F F CQ CP ∠+=⋅+||||,0||||(21的平分线平行，所以∠PCQ 的平分线垂直于x 轴.由).1,1(,1,1,,143422C y x x y y x ∴⎩⎨⎧==⎪⎩⎪⎨⎧==+解得 不妨设PC 的斜率为k ，则QC 的斜率为?k ，因此PC 和QC 的方程分别为)1(,1)1(--=+-=x k y x k y ，其中⎪⎩⎪⎨⎧=++-=≠.1434,1)1(,022y x x k y k 由消去y 并整理得(*).0163)1(6)31(222=--+--+k k x k k x k 9分 ∵C (1，1) 在椭圆上，∴x = 1是方程(*) 的一个根.从而222231163,31163k k k x k k k x Q P +-+=+--=同理， 10分从而直线PQ 的斜率为.313112231)13(22)(222=+--+-=--+=--=k k k k k k x x k x x k x x y y k Q P Q P Q P Q P PQ11分又知A (2，0) ，B (－1，－1) ， 所以,312101AB PQ AB k k k =∴=----=12分向量∴共线。

2018届嘉兴市高三数学下学期教学测试理科试题2（有答
案）
5 c 15题每题4分，共36分）
9．已知全集，集合，，则▲ ；▲ ．
10．在等差数列中，，，则差▲ ，▲ ．
11．若向量与满足，，．则向量与的夹角等于▲ ；
▲ ．
12．已知函数，则▲ ；若，则▲ ．
13．已知实数且，则的最小值是▲ ．
14．抛物线的焦点为，过点的直线与抛物线交于两点，线段的垂直平分线交轴于点，若，则点的横坐标为▲ ．
15．正方体的棱长为1，底面ABcD的对角线在平面内，则正方体在平面内的射影构成的图形面积的取值范围是▲ ．
三、解答题（本大题共5小题，共74分，解答应写出字说明、证明过程或演算步骤）
16．（本题满分14分）
三角形中，已知，其中，角所对的边分别为．
（Ⅰ）求角的大小；
（Ⅱ）求的取值范围．
17．（本题满分15分）
如图，在三棱锥中，平面，，，、、分别为、、的中点，、分别为线段、上的动点，且有．。

海淀区高三年级第二学期期末练习数 学 （理）参考答案及评分标准 ．5说明： 合理答案均可酌情给分，但不得超过原题分数.第Ⅰ卷（选择题 共40分）一、选择题（本大题共8小题,每小题5分,共40分）题号 1 2 3 4 5 6 7 8 答案BADCABAD第Ⅱ卷（非选择题 共110分）二、填空题（本大题共6小题,每小题5分, 有两空的小题，第一空3分，第二空2分，共30分） 9．1 10．< 11．2 ；10 12．48 13．2 14．；84.三、解答题(本大题共6小题,共80分) 15．（本小题满分13分）解：（Ⅰ）设等差数列{}n a 的公差为d ，由2446,10a a S +==，可得11246434102a d a d +=⎧⎪⎨⨯+=⎪⎩ ，………………………2分即1123235a d a d +=⎧⎨+=⎩，解得111a d =⎧⎨=⎩，………………………4分∴()111(1)n a a n d n n =+-=+-=， 故所求等差数列{}n a 的通项公式为n a n =.………………………5分 （Ⅱ）依题意，22n nn n b a n =⋅=⋅，∴12n n T b b b =+++231122232(1)22n n n n -=⨯+⨯+⨯++-⋅+⋅，………………………7分又2n T =2341122232(1)22n n n n +⨯+⨯+⨯++-⋅+⋅， …………………9分 两式相减得2311(22222)2n n n n T n -+-=+++++-⋅………………………11分()1212212n n n +-=-⋅-1(1)22n n +=-⋅-，………………………12分 ∴1(1)22n n T n +=-⋅+.………………………13分16．（本小题满分14分）（Ⅰ）证明：连结AC 交BD 于O ，连结OM ， ABCD 底面为矩形，O AC ∴为中点，………… 1分M N PC 、为侧棱的三等分点， CM MN ∴=，//OM AN ∴ ，………… 3分,OM MBD AN MBD ⊂⊄平面平面，//AN MBD ∴平面.………… 4分 （Ⅱ）如图所示，以A 为原点，建立空间直角坐标系A xyz -，则(0,0,0)A ，(3,0,0)B ，(3,6,0)C ，(0,6,0)D ，(0,0,3)P ，(2,4,1)M ，(1,2,2)N , (1,2,2),(0,6,3)AN PD ==-,………………………5分025cos ,335AN PDAN PD AN PD⋅+∴<>===⨯,………………………7分∴异面直线AN 与PD 25.………………………8分 （Ⅲ）侧棱PA ABCD ⊥底面,(0,0,3)BCD AP ∴=平面的一个法向量为,………………………9分 设MBD 平面的法向量为(,,)x y z =m ,(3,6,0),(1,4,1)BD BM =-=-，并且,BD BM ⊥⊥m m ,PAB CD MNzyPADM NO36040x y x y z -+=⎧∴⎨-++=⎩，令1y =得2x =，2z =-, ∴MBD 平面的一个法向量为(2,1,2)=-m.………………………11分2cos ,3AP AP AP ⋅<>==-m m m,………………………13分由图可知二面角M BD C --的大小是锐角, ∴二面角M BD C --大小的余弦值为23..………………………14分17． （本小题满分13分）解：（Ⅰ）设“4人恰好选择了同一家公园”为事件A . (1)分每名志愿者都有3种选择，4名志愿者的选择共有43种等可能的情况 . …………………2分 事件A 所包含的等可能事件的个数为3，…………………3分 所以，()431327P A ==. 即：4人恰好选择了同一家公园的概率为127.………………5分（Ⅱ）设“一名志愿者选择甲公园”为事件C ，则()13P C =..………………………6分4人中选择甲公园的人数X 可看作4次重复试验中事件C 发生的次数，因此，随机变量X 服从二项分布.X 可取的值为0，1，2，3，4..………………………8分()4412()()33i i iP X i C -==， 0,1,2,3,4i =..………………………10分 X0 1 23 4 P1681 32812481 881 181.………………………12分X 的期望为()14433E X =⨯=．.………………………13分18.（本小题满分13分）解法一：（Ⅰ）依题意得2()(2)e x f x x x =-，所以2()(2)e x f x x '=-， .………………………1分 令()0f x '=，得2x =±.………………………2分()f x '，()f x 随x 的变化情况入下表：x(,2)-∞-2-(2,2)-2(2,)+∞()f x ' － 0 + 0 －()f x极小值极大值………………………4分由上表可知，2x =()f x 的极小值点，2x ()f x 的极大值点.………………………5分（Ⅱ） 22()[(22)2]e ax f x ax a x a '=-+-+,.………………………6分由函数()f x 在区间(2,2)上单调递减可知：()0f x '≤对任意(2,2)x ∈恒成立，.………………………7分当0a =时，()2f x x '=-，显然()0f x '≤对任意(2,2)x ∈恒成立； .…………………8分当0a >时，()0f x '≤等价于22(22)20ax a x a ---≥，因为(2,2)x ∈，不等式22(22)20ax a x a ---≥等价于2222a x x a--≥,.………………………9分令2(),[2,2]g x x x x =-∈，则22()1g x x'=+，在[2,2]上显然有()0g x '>恒成立，所以函数()g x 在[2,2]单调递增， 所以()g x 在[2,2]上的最小值为(2)0g =，.………………………11分由于()0f x '≤对任意(2,2)x ∈恒成立等价于2222a x x a --≥对任意(2,2)x ∈恒成立，需且只需2min22()a g x a -≥，即2220a a-≥，解得11a -≤≤，因为0a >，所以01a <≤. 综合上述，若函数()f x 在区间(2,2)上单调递减，则实数a 的取值范围为01a ≤≤..………………………13分解法二：（Ⅰ）同解法一（Ⅱ）22()[(22)2]e ax f x ax a x a '=-+-+,.………………………6分由函数()f x 在区间(2,2)上单调递减可知：()0f x '≤对任意(2,2)x ∈恒成立， 即22(22)20ax a x a ---≥对任意(2,2)x ∈恒成立， (7)分当0a =时，()2f x x '=-，显然()0f x '≤对任意(2,2)x ∈恒成立；…………………8分当0a >时，令22()(22)2h x ax a x a =---，则函数()h x 图象的对称轴为21a x a-=，.………………………9分 若210a a-≤，即01a <≤时，函数()h x 在(0,)+∞单调递增，要使()0h x ≥对任意(2,2)x ∈恒成立，需且只需(2)0h ≥，解得11a -≤≤，所以01a <≤;..………………………11分若210a a->，即1a >时，由于函数()h x 的图象是连续不间断的，假如()0h x ≥对任意(2,2)x ∈恒成立，则有(2)0h ≥，解得11a -≤≤，与1a >矛盾，所以()0h x ≥不能对任意(2,2)x ∈恒成立.综合上述，若函数()f x 在区间(2,2)上单调递减，则实数a 的取值范围为01a ≤≤..………………………13分19．（本小题满分13分）解：（Ⅰ）由题意，抛物线2C 的方程为：24y x =，…………2分（Ⅱ）设直线AB 的方程为：(4),(0)y k x k k =-≠存在且. 联立2(4)4y k x y x=-⎧⎨=⎩，消去x ，得 24160ky y k --=，………………3分显然216640k ∆=+>，设1122(,),(,)A x y B x y ，则 124y y k += ①1216y y ⋅=- ②…………………4分 又12AM MB =，所以 1212y y =- ③…………………5分由①② ③消去12,y y ，得 22k =，故直线l 的方程为242,y x =-或242y x =-+ . (6)BM AF Py xO分（Ⅲ）设(,)P m n ，则OP 中点为(,)22m n， 因为O P 、两点关于直线(4)y k x =-对称，所以(4)221nm k n k m ⎧=-⎪⎪⎨⎪⋅=-⎪⎩，即80km n k m nk -=⎧⎨+=⎩，解之得2228181k m k k n k ⎧=⎪⎪+⎨⎪=-⎪+⎩， (8)分将其代入抛物线方程，得：222288()411k k k k -=⋅++，所以，21k =. ………………………9分联立 2222(4)1y k x x y ab =-⎧⎪⎨+=⎪⎩，消去y ，得：2222222222()8160b a k x k a x a k a b +-+-=.………………………10分由2222222222(8)4()(16)0k a b a k a k a b ∆=--+-≥，得 242222216()(16)0a k b a k k b -+-≥，即222216a k b k +≥，…………………12分将21k =，221b a =-代入上式并化简，得 2217a ≥，所以34a ，即234a ≥ 因此，椭圆1C 34 ………………………13分20．（本小题满分14分） 解：（Ⅰ）由题意可得:1()cos ,[0,]f x x x π=∈ ,………………………1分 2()1,[0,]f x x π=∈.………………………2分（Ⅱ）21,[1,0)()0,[0,4]x x f x x ⎧∈-=⎨∈⎩,………………………3分 221,[1,1)(),[1,4]x f x x x ∈-⎧=⎨∈⎩,………………………4分22121,[1,0)()()1,[0,1),[1,4]x x f x f x x x x ⎧-∈-⎪-=∈⎨⎪∈⎩,………………………5分当[1,0]x ∈-时，21(1)x k x -≤+1k x ∴≥-,2k ≥; 当(0,1)x ∈时，1(1)k x ≤+11k x ∴≥+1k ∴≥; 当[1,4]x ∈时，2(1)x k x ≤+21x k x ∴≥+165k ∴≥.综上所述，165k ∴≥………………………6分即存在4k =，使得()f x 是[1,4]-上的4阶收缩函数.………………………7分（Ⅲ）()2()3632f x x x x x '=-+=--,令'()0f x =得0x =或2x =.函数()f x 的变化情况如下：令()0f x =，解得0x =或3.………………………8分ⅰ）2b ≤时，()f x 在[0,]b 上单调递增，因此，()322()3f x f x x x ==-+，()1()00f x f ==.因为32()3f x x x =-+是[0,]b 上的2阶收缩函数， 所以，①()()21()20f x f x x -≤-对[0,]x b ∈恒成立；②存在[]0,x b ∈，使得()()21()0f x f x x ->-成立.………………………9分①即：3232x x x -+≤对[0,]x b ∈恒成立， 由3232x x x -+≤，解得：01x ≤≤或2x ≥，要使3232x x x -+≤对[0,]x b ∈恒成立，需且只需01b <≤..………………………10分②即：存在[0,]x b ∈，使得()2310x x x -+<成立.由()2310x x x -+<得：0x <3535x -+<<， 所以，需且只需35b ->351b -<≤..………………………11分ⅱ）当2b >时，显然有3[0,]2b ∈，由于()f x 在[0,2]上单调递增，根据定义可得：2327()28f =，13()02f =， 可得 2133273()232282f f ⎛⎫-=>⨯= ⎪⎝⎭，此时，()()21()20f x f x x -≤-不成立..………………………13分351b -<≤.注：在ⅱ）中只要取区间（1，2）内的一个数来构例均可，这里用32只是因为简单而已.。

高三理科数学试题参考答案CADDC ADACA BC 13.{}52x x x <≠且 14.6a ≥- 15. 9 16.①③④17答案：解：（Ⅰ）()1cos 22f x x x ωω=-π2sin 216x ω⎛⎫=-+ ⎪⎝⎭． 因为函数()f x 的最小正周期为π，且0ω>， 所以2ππ2ω=，解得1ω=． （Ⅱ）由（Ⅰ）得π()2sin 216f x x ⎛⎫=-+ ⎪⎝⎭． 因为2π03x ≤≤， 所以ππ7π2666x --≤≤， 所以π1sin 226x ⎛⎫-- ⎪⎝⎭≤2≤． 因此π0sin 216x ⎛⎫-+ ⎪⎝⎭≤≤3，即()f x 的取值范围为[]03，． 18解：(1)由3cos()cos 2A CB -+=及π()B AC =-+得 3cos()cos()2A C A C --+=，-------2分 3cos cos sin sin (cos cos sin sin )2A C A C A C A C +--=， 3sin sin 4A C =． 又由题知2b ac =及正弦定理得2sin sin sin B A C =， 故23sin 4B =，-------4分sin 2B =或sin 2B =-(舍去)， 于是π3B =或2π3B =．又由2b ac =知b a ≤或b c ≤， 所以π3B =．------------6分 由以上知：π3B =代入3cos()cos 2A C B -+=得：cos()1A C -=； 即3A C π==；因此ABC △为等边三角形，-------9分(2)因为ABC △为等边三角形,π83b B ==，． 所以ABC △的面积为21sin 2ABCS b B ∆==分 19．解：设1(1)n a a n d =+-，则1125,613,a d a d +=⎧⎨+=⎩解得11,2a d ==.………………4分 所以}{n a 的通项公式为1(1)221n a n n =+-⨯=-.…………………………………6分（2）解：依题意得2133n a n n b -==.……………………………………………………8分 因为21121393n n n n b b ++-==，所以}{n b 是首项为1133b ==，公比为9的等比数列，……10分 所以}{n b 的前n 项和3(19)3(91)198n n n T ⨯-==--.………………………………12分 20解：（1）21,3nn n a n b =-=。

2021年高三下学期统一练习（二）理科数学含解析一、选择题共8小题，每小题5分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.1. 复数的虚部为（A）3 （B）（C）4 （D）【答案】A，所以虚部为3，选A.2. 设向量a=(x,1), b=(4,x),且a,b方向相反，则x的值是（A）2 （B）-2 （C）（D）0【答案】B因为方向相反，所以设，则有，所以，解得，选B.3.展开式中的常数项是（A）6 （B）4 （C）-4 （D）-6【答案】A展开式的通项公式为，由，解得，所以常数项为，选A.4. 已知数列{a n}，则“{a n}为等差数列”是“”的（A）充要条件（B）必要而不充分条件（C）充分而不必要条件（D）既不充分又不必要条件【答案】C若{a n}为等差数列，一定有。

若，不妨取数列，0,0,0,2,0，满足，当数列不是等差数列，所以“{a n}为等差数列”是“”的充分而不必要条件，选C.5. 下列四个函数中，最小正周期为，且图象关于直线对称的是（A）（B）（C）（D）【答案】C因为函数的周期是，所以，解得，排除A,B.当时，为最大值，所以图象关于直线对称，选C.6. 在平面区域内任取一点，若满足的概率大于，则的取值范围是（A）（B）（C）（D）【答案】D其构成的区域D如图所示的边长为1的正方形，面积为S1=1，满足所表示的平面区域是以原点为直角坐标顶点，以b为直角边长的直角三角形，其面积为，所以在区域D内随机取一个点，则此点满足的概率,由题意令，解得,选D．7. 用5,6,7,8,9组成没有重复数字的五位数，其中两个偶数数字之间恰有一个奇数数字的五位数的个数是(A)18 (B) 36 (C) 54 (D) 72【答案】B从5、7、9三个奇数中任选一个放在6与8之间，可用中选法，而6与8可以交换位置有种方法，把6与8及之间的一个奇数看做一个整体与剩下的两个奇数全排列共有种方法，利用乘法原理可得两个偶数数字之间恰有一个奇数数字的五位数的个数是.选B．8. 已知偶函数f(x)（x∈R），当时，f(x)=-x(2+x)，当时，f(x)=(x-2)(a-x)（）.关于偶函数f(x)的图象G和直线:y=m（）的3个命题如下：①当a=4时，存在直线与图象G恰有5个公共点；②若对于，直线与图象G的公共点不超过4个，则a≤2；③，使得直线与图象G交于4个点，且相邻点之间的距离相等.其中正确命题的序号是(A) ①②(B) ①③(C) ②③(D) ①②③【答案】D①当a=4时，偶函数f（x）（x∈R）的图象如下：存在直线l，如y=0，与图象G恰有5个公共点；故①正确；②若对于，由于偶函数f（x）（x∈R）的图象如下：直线l与图象G的公共点不超过4个，则a≤2；故②正确；③，偶函数f（x）（x∈R）的图象如下：，使得直线l与图象G交于4个点，且相邻点之间的距离相等．故③正确；其中正确命题的序号是①②③．选D.第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分.9. 圆的半径是________。

F2021年高三下学期必答训练数学（理）试题（2） 含答案1.设集合{}[]{}12,2,0,2,xA x xB y y x =-<==∈，，则＝CA ．B ．C ．D ．2.设复数在复平面内的对应点关于虚轴对称，，则AA ．-5B ．5C ．D ． 3.已知命题：若 ，则；命题：若，则.在命题① ②；③；④中，真命题是CA . ①③ B.①④ C.②③ D.②④ 4.下列函数中，既是偶函数又在区间上单调递减的是C A. B. C. D.5．已知双曲线的一条渐近线的斜率为，则该双曲线的离心率为DA ．B ．C ．2D ． 6.已知为异面直线，⊥平面，⊥平面.直线满足⊥，⊥，则D A.∥且∥ B. ⊥且⊥C. 与相交，且交线垂直于D. 与相交，且交线平行于7．将5本不同的书摆成一排，若书甲与书乙必须相邻，而书丙与书丁不能相邻，则不同的摆法种数为BA ．48B ．24C ．20D ．128.已知在平面直角坐标系中有一个点列：()()()()12220,1,,,,,n n n P P x y P x y n N *∈.若点到点的变化关系为：，则=CA. B. C. D.二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分． （一）必做题（9－13题）9.不等式的解集为_________________10.若曲线上点P 处的切线平行于直线，则点P 的坐标是__________ 11.若2，，9成等差数列，则=_____________12．已知函数的图象经过点，则其反函数的解析式= ． 张参观券连号，那么不同的分法种数是_____________ 13.已知圆平面区域：，若圆心 ,且圆与 轴相切，则的最大值为______37________14．(坐标系与参数方程选做题) 在极坐标系中，直线被圆截得的弦长 为 .15．（几何证明选讲选做题）如图1，BE、CF分别为钝角△ABC的两条高，已知则BC边的长为．图115．依题意得，因△BEA∽△CFA得,所以．15..三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．16．(本小题满分12分)已知函数的最小正周期为.（1）求的值；（2）若，，求的值3648788451162139496612413415910288757145699398109977546196183120703612601 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 3080日期（AQI ）指数4012016020017．(本小题满分12分)图2是某市今年1月份前30天空气质量指数（AQI ）的趋势图.图2（1）根据该图数据在答题卷中完成频率分布表，并在图3中作出这些数据的频率分布直方图；（2）当空气质量指数（AQI ）小于100时，表示空气质量优良．某人随机选择当月1日至10日中的某一天到达该市，并停留2天，设是此人停留期间空气质量优良的天数，求的数学期望．（图中纵坐标1/300即，以此类推）图319．(本小题满分14分)已知为数列的前项和，（），且．（1）求的值；（2）求数列的前项和；（3）设数列满足，求证：．20．(本小题满分14分)在平面直角坐标系中，已知点，点在直线上，点满足，，点的轨迹为曲线.（1）求的方程；（2）设直线与曲线有唯一公共点，且与直线相交于点,试探究，在坐标平面内是否存在点，使得以为直径的圆恒过点？若存在，求出点的坐标，若不存在，说明理由.21．(本小题满分14分)已知函数，，其中,（e≈2.718）．（1）若函数有极值1，求的值；（2）若函数在区间上为减函数，求的取值范围；（3）证明：．37573 92C5 鋅28727 7037 瀷22923 598B 妋gB33554 8312 茒U40336 9D90 鶐34001 84D1 蓑.V`(。

数学大练习试题（理科）选择题（每小题5分，共50分）1．复数13z i =+，21z i =-，则复数12z z 的虚部为（ ）A ．2B ．2i -C ．2-D ．2i2．已知全集U R =，则正确表示集合{|(1)(2)0}M x R x x =∈-->和2{|0}N x R x x =∈+<的关系的韦恩（Venn ）图是（ ）3．2000辆汽车通过某一段公路时的时速的频率分布直方图如右图所示，时速在[50,60)的汽车大约有（ ） A ．300辆 B ．400辆C ．600辆D ．800辆4．“6x π=”是“1sin 2x =”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件5．已知某个几何体的三视图如图（主视图中的弧线是半圆），根据图中标出的尺寸，可得这个几何体的体积是（单位：cm3）（A ．πB ．2πC ．4πD ．8π6．2011案共有（ ）A ．240种B ．36种C ．24种D ．48种7．已知函数()sin(2)()4f x x x R π=+∈，为了得到函数()cos 2g x x =的图像，只需将AB C D俯视图2cm 左视图()y f x =的图像（ ）A ．向左平移8π个单位B ．向右平移8π个单位 C ．向左平移4π个单位D ．向右平移4π个单位8．已知函数42,1()31, 1xx x f x x -≤⎧=⎨->⎩，则下列式子成立的是（ ） A ．13()(1)()22f f f << B ．13(1)()()22f f f << C ．31()(1)()22f f f << D ．13()()(1)22f f f <<9．阅读右边所示的程序框图，运行相应的程序，输出的结果是（ ）A ．20B ．21C ．200D ．21010．设点P 为双曲线22112y x -=上的一点，1F ，2F 是该双曲线的左、右焦点，若12PF F ∆ 的面积为12，则12F PF ∠等于（ ）A ．4πB ．3πC ． 2πD ．23π二、填空题：本大题共5小题，每小题5分，共25分．将答案填写在题中的横线上． （一）必做题（11～14题）11．若55432543210(1)(1)(1)(1)(1)(1)x a x a x a x a x a x a -=++++++++++，则 12345a a a a a ++++= ．12．函数()1log (0,1)a f x x a a =+>≠的图像恒过定点A ，若点A 在直线20mx ny +-=上，其中0mn >，则11m n +的最小值为 ．13．在区间(0,1)内随机取两个数m ，n ，则关于x的一元二次方程20x m +=有实数根的概率为 ．14．直线0ax by c ++=与圆224x y +=相交于两点A 、B ，若222c a b =+，O 为坐标原点，则OA OB →→⋅= ．（二）选做题（考生只能从A 、B 、C 三小题中选做一题，若多做，则按所做的第一题评阅给分） 15．A ．（几何证明选讲选做题）已知PA 是圆O 的切线，切点为A ，PA = 2．AC 是圆O 的直径，PC 与圆O 交于点B ，PB = 1，则AB = ；B ．（不等式选讲选做题）已知关于x 的不等式|1|||x x k -+≤无解，则实数k 的取值范围是 ；C ．（坐标系与参数方程选做题）已知极坐标的极点在直角坐标系的原点O 处，极轴与x 轴的正半轴重合，曲线C 的参数方程为{2cos sin x y θθ==，直线l的极坐标方程为sin()4πρθ-=，则直线l 与曲线C 的交点个数为 ．三、解答题：共6道题，共75分．要求写出演算和推理过程． 16．（本小题满分12分）数列{}n a 满足11a =，1122n nn nn a a a ++=+（n N +∈）. （Ⅰ）证明：数列2n n a⎧⎫⎨⎬⎩⎭是等差数列；（Ⅱ）设(1)n nb nn a =+，求数列{}n b 的前n项和nS.17．（本小题满分12分）函数()s i n ()(0,0,)2f x A x A πωϕωϕ=+>><在区间5[,]66ππ-上的图象如图所示。

课时规范练36数学归纳法基础巩固组1.(2019福建三明三模)用数学归纳法证明不等式2n>(n+1)2(n∈N*)时,初始值n应等于()A.1B.4C.5D.62.用数学归纳法证明命题“当n是正奇数时,xn+yn能被x+y整除”,在第二步时,正确的证法是( )A.假设n=k(k∈N*),证明n=k+1时命题成立B.假设n=k(k是正奇数),证明n=k+1时命题成立C.假设n=2k+1(k∈N*),证明n=k+1时命题成立D.假设n=k(k是正奇数),证明n=k+2时命题成立3.(2019浙江丽水一模)已知n∈N*,用数学归纳法证明f(n)=1+4+7+…+(3n-2)=时.假设当n=k(k∈N*)时命题建立,证明当n=k+1时命题也建立,需要用到的f(k+1)与f(k)之间的关系式是( )A.f(k+1)=f(k)+3k-5B.f(k+1)=f(k)+3k-2C.f(k+1)=f(k)+3k+1D.f(k+1)=f(k)+3k+44.(2019江西吉安期末)下面是利用数学归纳法证明不等式2(√1×2+√2×3+…+√(n-1)·n)<n2(n≥2,且n∈N*)的部分过程: “……假设当n=k(k≥2)时,2(√1×2+√2×3+…+√(k-1)·k)<k2,故当n=k+1时,有,因为2√k·(k+1)=22+k<,故2(√1×2+√2×3+…+√(k-1)·k+√k·(k+1))<(k+1)2, ……”则横线处应该填()A.2(√1×2+√2×3+…+√(k-1)·k+√k·(k+1))<k2+2√k·(k+1),2k+1B.2(√1×2+√2×3+…+√(k-1)·k)<k2+2√k·(k+1),2k+1C.2(√1×2+√2×3+…+√(k-1)·k+√k·(k+1))<k2+2√k·(k+1),2k+2D.2(√1×2+√2×3+…+√<k2+2√k+25.用数学归纳法证明:“两两相交且不共点的n条直线把平面分为f(n)部分,则f(n)=1+.”证明第二步归纳递推时,用到f(k+1)=f(k)+ .6.(2019河南南阳期末)是否存在正整数m,使得对任意正整数n,f(n)=(2n+7)·3n+m都能被36整除?若存在,求出m的最小值,并用数学归纳法证明你的结论;若不存在,请阐明来由.7.证明:对任意的n∈N*,不等式32·54·76·…·2n+12n>√n+1成立.8.(2019江苏盐城期末)已知数列{an}各项均为正数,满足13+23+…+n3=.(1)求a1,a2,a3的值;(2)猜想数列{an}的通项公式,并用数学归纳法证明你的结论.综合提升组9.(2019浙江湖州一模)某个命题与正整数n有关,如果当n=k+1(k∈N*)时命题建立,那么可推得当n=k时命题也建立.现已知当n=2 019时该命题不建立,那么可推得( )A.当n=2 020时该命题不成立B.当n=2 020时该命题成立C.当n=2 018时该命题不成立D.当n=2 018时该命题成立10.设平面内有n条直线(n≥3),其中有且仅有两条直线相互平行,任意三条直线不外同一点.若用f(n)表示这n条直线交点的个数,则f(4)= ;当n>4时,f(n)= (用n表示).11.(2019江苏南京三模)对由0和1这两个数字构成的字符串,作如下规定:按从左向右的次序,当第一个子串“010”的最后一个0所在数位是第k(k∈N*,且k≥3)位,则称子串“010”在第k 位出现;再继续从第k+1位按从左往右的顺序找子串“010”,若第二个子串“010”的最后一个0所在数位是第k+m位(其中m≥3且m∈N*),则称子串“010”在第k+m位出现;……;云云不停地重复下去.如:在字符串11010101010中,子串“010”在第5位和第9位出现,而不是在第7位和第11位出现.记在n位由0,1构成的全部字符串中,子串“010”在第n位出现的字符串的个数为f(n).(1)求f(3),f(4)的值;(2)求证:对任意的正整数n,f(4n+1)是3的倍数.创新应用组12.将正整数作如下分组:(1),(2,3),(4,5,6),(7,8,9,10),(11,12,13,14,15),(16,17, 18,19,20,21),….分别计算各组包含的正整数的和如下,S1=1,S2=2+3=5,S3=4+5+6=15,S4=7+8+9+10=34,S5=11+12+13+14+15=65,S6=16+17+18+19+20+21=111,(1)求S7的值;(2)由S1,S1+S3,S1+S3+S5,S1+S3+S5+S7的值,试猜测S1+S3+…+S2n-1的结果,并用数学归纳法证明.13.(2019江苏无锡新吴区模拟)记[x ]r =x (x+1)…(x+r-1),x ∈R ,r ∈N *,并规定[x ]0=1, (1)分别求[3]2,[-3]2的值;(2)证明:[a+b ]r=∑k=0rC rk [a ]r-k [b ]k ,a ,b ∈R ,r ∈N *.参考答案课时规范练36数学归纳法1.D n=1时,左边=2,右边=4;n=2时,左边=4,右边=9;n=3时,左边=8,右边=16;n=4时,左边=16,右边=25;n=5时,左边=32,右边=36;n=6时,左边=64,右边=49,∴初始值n0至少应取6.故选D.2.D相邻两个正奇数相差2,故D选项正确.3.C因为用数学归纳法证明等式f(n)=1+4+7+…+(3n-2)=3n 2-n2时,假设n=k时,命题成立,f(k)=1+4+7+…+(3k-2)=3k2-k 2,则当n=k+1时,左端为f(k+1)=1+4+7+…+(3k+2)+[3(k+1)-2],需要用到的f(k+1)与f(k)之间的关系式是f(k+1)=f(k)+3k+1.故选C.4.A假设当n=k(k≥2)时,2(√1×2+√2×3+…+√)<k2,故当n=k+1时,有2(√1×2+√2×3+…+√+√<k2+2√.因为2√2√k2+k<2k+1,故2(√1×2+√2×3+…+√(k-1)·k+√k·(k+1))<(k+1)2.故选A.5.k+1当n=k(k≥2)时,有f(k)=1+k(k+1)2,当n=k+1时,f(k+1)=1+(k+1)(k+2)2,∴从k到k+1左端需增加的代数式1+(k+1)(k+2)2-1-k(k+1)2=k+12(k+2-k)=k+1,∴在证明第二步归纳推理的历程中,用到f(k+1)=f(k)+(k+1).6.解由f(n)=(2n+7)·3n+m,得f(1)=27+m,f(2)=99+m,∴27+m=36,99+m=3×36,由此猜想m=9.下面用数学归纳法证明,(1)当n=1时,显然成立.(2)假设n=k时,f(k)能被36整除,即f(k)=(2k+7)·3k+9能被36整除.当n=k+1时,[2(k+1)+7]·3k+1+9=3[(2k+7)·3k+9]+18(3k-1-1),由于3k-1-1是2的倍数,故18(3k-1-1)能被36整除.这就是说,当n=k+1时,f(n)也能被36整除.由(1)(2)可知对一切正整数n都有f(n)=(2n+7)·3n+9能被36整除,m的最小值为9.7.证明①当n=1时,左边=,右边=,因为,以是不等式建立.②假设当n=k时不等式建立,即…成立.则当n=k+1时,左边=32·54·76·…·2k+12k·2k+32k+2>√k+1·2k+32k+2=√(2k+3)24(k+1)=√4(k+1)2+4(k+1)+14(k+1)=√(k+1)+1+14(k+1)>√所以当n=k+1时,不等式也建立.由①②可得不等式恒建立.8.解(1)当n=1时,13=(a1·22) 2 ,又a n>0,所以a1=1,当n=2时,13+23=(a2·32)2,解得a2=2,当n=3时,13+23+33=(a3·42)2,解得a3=3.(2)猜想数列{a n}的通项公式为a n=n,①当n=1时,由(1)可知结论成立;②假设当n=k时,结论成立,即a k=k成立, 则n=k+1时,由13+23+…+k3=[a k(k+1)2]2与13+23+…+(k+1)3=[a k+1(k+2)2]2,所以(k+1)3=[a k+1(k+2)2]2−[a k(k+1)2]2=[a k+1(k+2)2]2−[k(k+1)2]2,所以a k+12(k+2)2=4(k+1)3+k2(k+1)2=(k+1)2(4k+4+k2)=(k+1)2(k+2)2.又a n>0,a k+1=k+1成立,根据①②猜想成立.9.A 由题意可知,原命题建立则逆否命题建立,P(n)对n=2 019不成立,P(n)对n=2 020也不成立,否则,n=2 020成立,由已知推得n=2 019也成立.与当n=2 019时该命题不建立抵牾.故选A.10.51(n+1)(n-2)f(3)=2,f(4)=f(3)+3=2+3=5,f(n)=f(3)+3+4+…+(n-1)=2+3+4+…+(n-1)=1(n+1)(n-2).211.(1)解在3位数字符串中,子串“010”在第三位出现有且只有1个,即010,∴f(3)=1.在4位数字符串中,子串“010”在第四位出现有2个,即0010与1010,∴f(4)=2.(2)证明当n≥5且n∈N*时,当最后3位是010时,前n-3个数位上,每个数位上的数字都有两种大概,即0和1,共有2n-3种可能.由于当最后3位是010时,若最后5位是01010,且前n-2位形成的字符串中子串“010”,是在第n-2位出现,此时不满足条件.∴f(n)=2n-3-f(n-2),n≥5且n∈N*.∵f(3)=1,∴f(5)=3.下面用数学归纳法证明f(4n+1)是3的倍数.①当n=1时,f(5)=3是3的倍数;②假设当n=k(k∈N*)时,f(4k+1)是3的倍数,那么,当n=k+1时,f [4(k+1)+1]=f (4k+5)=24k+2-f (4k+3)=24k+2-[24k -f (4k+1)]=3×24k +f (4k+1).∵f (4k+1)是3的倍数,且3×24k 也是3的倍数,∴f (4k+5)是3的倍数.即n=k+1时,f [4(k+1)+1]是3的倍数.综上,对于任意的正整数n ,f (4n+1)是3的倍数.12.解 (1)S 7=22+23+24+25+26+27+28=175.(2)S 1=1;S 1+S 3=16;S 1+S 3+S 5=81;S 1+S 3+S 5+S 7=256;猜测S 1+S 3+S 5+…+S 2n-1=n 4.证明如下:记M n =S 1+S 3+S 5+…+S 2n-1,①当n=1时,猜想成立.②假设当n=k 时,命题成立,即M k =S 1+S 3+S 5+…+S 2k-1=k 4.下面证明当n=k+1时,料想也建立.事实上,由题设可知Sn 是由1+2+3+…+(n -1)+1=+1开始的n 个一连自然数的和. 所以S n =n (n -1)2+1+n (n -1)2+2+…+n (n -1)2+n =n (n 2+1)2, 所以S 2k+1=(2k+1)[(2k+1)2+1]2=(2k+1)(2k 2+2k+1)=4k 3+6k 2+4k+1, 从而M k+1=M k +S 2k+1=k 4+4k 3+6k 2+4k+1=(k+1)4,所以猜想在n=k+1时也成立.综合①②可知猜想对任何n ∈N *都成立.13.(1)解 [3]2=3×4=12.[-3]2=-3×(-3+2-1)=6.(2)证明 使用数学归纳法证明.①r=1时,[a+b ]1=C 10[a ]1[b ]0+C 11[a ]0[b ]1=a+b 成立.②假设r=n 时成立,则[a+b ]n =∑k=0nC n k [a ]n-k [b ]k 成立,则r=n+1时,[a+b ]n+1=[a+b ]n [a+b ]1=(C n 0[a ]n +C n 1[a ]n-1[b ]1+…+C n n [b ]n )[a+b ]=(C n 0[a ]n+1+C n 1[a ]n [b ]1+…+C n n [a ][b ]n )+(C n 0[a ]n [b ]+C n 1[a ]n-1[b ]2+…+C n n [b ]n+1).根据C n k +C n k+1=C n+1k+1.∴[a+b ]n+1=C n 0[a ]n+1+C n+11[a ]n [b ]1+…+C n+1n+1[b ]n+1=∑k=0n+1C n+1k [a ]n+1-k [b ]k .假设成立,即r=n+1时命题建立.综上可得,[a+b]r=[a]r-k[b]k,a,b∈R,r∈N*.。

2021年高三下学期普通高考测试（二）数学理试题含答案一、选择题（本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．已知集合，集合，则（）．A．B．C．D．2．已知是复数，是虚数单位，若，则=（）．A．B．C．D．3．随机变量服从正态分布，若，则的值为（）．A．B．C．3 D．44．一个几何体的三视图如图，正视图和侧视图都是由一个半圆和一个边长为的正方形组成，俯视图是一个圆，则这个几何体的表面积是（）．A．B．C．D．5．在右图所示的程序框图中，输出的和的值分别为（）．A．3,21 B．3,22 C．4,21 D．4,226．设是定义在R上的周期为3的周期函数，如图表示该函数在区间上的图像，则=（）．A．3 B．2 C．1 D．07．若平面向量与的夹角是，且，则的坐标为（）．A．B．C．D．8．对于任意正整数，定义“”如下：当是偶数时，；当是偶数时，；且有．则如下四个命题：①；②；③的个位数是；④的个位数是．其中正确的命题有（）．A．个B．个C．个D．个二、填空题（本大题共7小题，考生作答6小题，每小题5分，满分30分．）（一）必做题（9～13题）9．曲线在点（0,0）处的切线方程是________________．10．双曲线的离心率是．11．_______________．12．某所学校计划招聘男教师名，女教师名，和须满足约束条件，则该校招聘的教师最多是名．13．已知全集，在中任取四个元素组成的集合记为，余下的四个元素组成的集合记为，，则集合的取法共有____________种．（二）选做题（14～15题，考生只能从中选做一题）14．（坐标系与参数方程选做题）直线的参数方程为（为参数），则直线的倾斜角是．15．（几何证明选讲选做题）如图，在梯形中，，，，点．分别在．上，且，若，则的长是．三．解答题（本大题共6小题，共80分．解答应写出文字说明．证明过程或演算步骤．）16．（本小题满分12分）设函数（1）求函数在区间上的值域（2）记内角的对应边分别为，若，且，求的值．17．（本小题满分12分）某中学一名数学教师对全班50名学生某次考试成绩分男生女生进行了统计（满分150分），得到右面频率分布表：其中120分（含120分）以上为优秀．（1）根据以上频率表的数据，完成下面的22列联表；（2）根据（1）中表格的数据计算，你有多大把握认为学生的数学成绩与性别之间有关系？（3）若从成绩在[130,140]的学生中任取3人，已知取到的第一个人是男生，求取到的另外2人中至少一名女生的概率．18．（本小题满分14分）如图，四棱锥中，0⊥，⊥，==平面DCDCPD．AD=，且//ADAB1BCD452CDABCD=AB,,∠（1）若点M是PD的中点，证明：;（2）若得面积为，求二面角的余弦值．19．（本小题满分14分）数列的前项和记为，对任意正整数，均有，且．求及数列的通项公式；令，求数列的前n项和．20．（本小题满分14分）已知曲线E上的任一点到点和点的距离之和为4．（1）求曲线E的方程；（2）已知点，设直线与曲线E交于B．D两点（B在第一象限），求四边形ABCD面积的最大值．21．（本小题满分14分）已知函数为实数，．（1）若，且函数的值域为，求；（2）设，，且函数为偶函数．证明：；（3）设的导函数是当时，证明：对任意实数，．24900 6144 慄21944 55B8 喸34192 8590 薐37318 91C6 釆23645 5C5D 屝40612 9EA4 麤a22390 5776 坶|lvk/22752 58E0 壠。