2020版高考数学总复习第二章函数第10讲指数与指数函数练习文新人教A版

第10课指数式与指数函数(本课时对应学生用书第页) 自主学习回归教材1.(必修1P60例1改编)计算：2(π-4)+π= .【答案】42(π-4)+π=|π-4|+π=4-π+π=4.2.(必修1P61例2改编)计算：1294⎛⎫⎪⎝⎭+(-9.6)0-2-3278⎛⎫⎪⎝⎭×232⎛⎫⎪⎝⎭= .【答案】3 2【解析】原式=32+1-49×94=32.3.(必修1P67练习1改编)若函数y=(a2-3a+3)·a x是指数函数，则实数a= .【答案】2【解析】由题意得a2-3a+3=1且a>0，a≠1，所以a=2.4.(必修1P52习题1改编)当x>0时，指数函数f(x)=(a-1)x，且(a-1)x<1恒成立，则实数a的取值范围是.【答案】(1，2)【解析】因为x>0时，(a-1)x<1恒成立，所以0<a-1<1，所以1<a<2.5.(必修1P52习题1改编)已知函数f(x)=a x+b(a>0且a≠1)的图象如图所示，则a+b= .(第5题)【答案】-2【解析】由图可知，此函数过点(2，0)和(0，-3)，则有a2+b=0，且1+b=-3，解得a=2，b=-4，所以a+b=-2.1.指数中的相关概念(1)n次方根正数的奇次方根是一个正数，负数的奇次方根是一个负数，0的奇次方根是0；正数的偶次方根是两个绝对值相等、符号相反的数，0的偶次方根是0，负数没有偶次方根.(2)方根的性质①当nna=a；②当nna=|a|=-0a aa a≥⎧⎨<⎩，，，.(3)分数指数幂的意义①mna n m a a>0，m，n都是正整数，n>1)；②-mna=1mna n m a(a>0，m，n都是正整数，n>1).2.指数函数的定义一般地，形如y=a x(a>0且a≠1)的函数叫作指数函数.3.指数函数的图象和性质a>10<a<1图象性质定义域R R值域(0，+∞) (0，+∞)过定点过点(0，1)，即x=0时，y=1 过点(0，1)，即x=0时，y=1单调性在R上是增函数在R上是减函数(1)在解决指数函数有关问题时，如果底数a大小不确定，则必须分“a>1”和“0<a<1”两种情况讨论.(2)画指数函数y=a x的图象，应抓住三个关键点：(1，a)，(0，1)，1-1a⎛⎫⎪⎝⎭，.(3)由于指数函数y=a x(a>0且a≠1)的图象均在x轴上方，故y>0，图象无限接近x轴，但不会相交，因此，x轴是指数函数的“渐近线”.【要点导学】要点导学各个击破指数幂的运算例1求下列各式的值.(1)(0.02723)+1-327125⎛⎫⎪⎝⎭-0.5729⎛⎫⎪⎝⎭+10-2；(2)214⎛⎫⎪⎝⎭+1-366323-2(1.03)0·36⎛⎝⎭.【思维引导】按照幂指数运算法则运算，分母含根式的进行分母有理化.【解答】(1)原式=9100+53-53+1100=110. (2)原式=116+(13--326)+222(32)(3)-(2)+-66-⎛⎫⎪ ⎪⎝⎭=116+6+5+26+36=81606+.【精要点评】指数幂化简与求值的原则及要求：(1)化简原则：①化根式为分数指数幂；②化负指数幂为正指数幂；③化小数为分数；④注意运算的先后顺序.(2)结果要求：①若题目以根式形式给出，则结果用根式表示；②若题目以分数指数幂的形式给出，则结果用分数指数幂的形式表示；③结果不能同时含有根式和分数指数幂，也不能既有分母又有负分数指数幂.变式 化简下列各式(a>0，b>0).(1)(2132a b )(-31132a b )÷156613a b ⎛⎫ ⎪⎝⎭； 34332323-8?24a a ba ab b ++÷31-2b a ⎛ ⎝3a 【思维引导】按照分数指数幂的运算性质求解，含根式的化成分数指数幂后再计算或化简.【解答】(1)原式=-9211115--326236ab++=-9a.(2)原式=413322333-842ab a a bb a +÷113313a -2b a×13a=1321123333a (a-8b)4b 2a b a ++÷113313a -2b a×13a=13a (13a -213b )131133aa -2b ×13a =a.【精要点评】若式子中既有分数指数幂、又有根式，则可先把根式化成分数指数幂，再根据幂的运算性质进行计算.在指数式运算中，注重运算顺序和灵活运用乘法公式.指数函数图象的应用例2已知函数f(x)=|2x-1|.(1)求f(x)的单调区间；(2)比较f(x+1)与f(x)的大小.【思维引导】(1)对于y=|2x-1|的图象，我们通过y=2x的图象翻折得到，在翻折指数函数图象时一定要注意渐近线也要随之翻折，作出f(x)的图象，数形结合求解.(2)在同一坐标系中分别作出f(x)，f(x+1)的图象，数形结合求解.【解答】(1)由f(x)=|2x-1|=2-101-20.xxxx⎧≥⎨<⎩，，，作出函数的图象如图(1)所示.因此函数f(x)在(-∞，0)上单调递减，在(0，+∞)上单调递增.(2)在同一坐标系中分别作出函数f(x)，f(x+1)的图象，如图(2)所示.由图象知，当|012x+-1|=|02x-1|时，x0=log223，根据图象可知，当x<log223时，f(x)>f(x+1)；当x=log223时，f(x)=f(x+1)；当x>log223时，f(x)<f(x+1).图(1)图(2)(例2)【精要点评】(1)指数型函数的图象与性质(单调性、最值、大小比较、零点等)的求解往往利用相应指数函数的图象，通过平移、对称变换得到其图象，然后数形结合使问题得解.(2)一些指数方程、不等式问题的求解，往往利用相应指数型函数图象数形结合求解.(3)函数y=a x，y=a|x|的关系：函数y=a x与y=|a x|是同一个函数的不同表现形式，函数y=a|x|与y=a x不同，前者是一个偶函数，其图象关于y轴对称，当x≥0时两函数图象相同.变式画出函数y=2|x|的图象，其图象有什么特征?根据图象指出其值域和单调区间.(变式)【解答】当x≥0时，y=2|x|=2x；当x<0时，y=2|x|=2-x=12x ⎛⎫⎪⎝⎭，所以函数y=2|x|的图象如图所示.由图象可知，y=2|x|的图象关于y轴对称，且值域是[1，+∞)，单调减区间是(-∞，0]，单调增区间是[0，+∞).指数函数的性质例3已知函数f(x)=2-4313ax x+⎛⎫⎪⎝⎭.(1)若a=-1，求函数f(x)的单调区间；(2)若函数f(x)有最大值3，求实数a的值；(3)若函数f(x)的值域为(0，+∞)，求实数a的值.【思维引导】(1)形如y=a g(x)的复合函数，由于底数为13，所以函数y=a g(x)的单调性和y=g(x)的单调性相反.(2)要借助“同增异减”这一性质分析，将问题归结为内层函数h(x)=ax2-4x+3有最小值-1，然后利用二次函数的知识加以解决.(3)由指数函数的值域知，h(x)=ax2-4x+3的值域为R.【解答】(1)当a=-1时，f(x)=2--4313x x+⎛⎫⎪⎝⎭，令g(x)=-x2-4x+3，由于g(x)在(-∞，-2)上单调递增，在(-2，+∞)上单调递减，而y=13t⎛⎫⎪⎝⎭在R上单调递减，所以f (x)在(-∞，-2)上单调递减，在(-2，+∞)上单调递增，即函数f(x)的单调增区间是(-2，+∞)，单调减区间是(-∞，-2).(2)令h(x)=ax2-4x+3，f(x)=()13h x⎛⎫⎪⎝⎭，由于f(x)有最大值3，所以h(x)应有最小值-1，因此必有3-4-1aaa>⎧⎪⎨=⎪⎩，，解得a=1，即当f(x)有最大值3时，实数a的值为1.(3)由指数函数的性质知，要使y=()13h x⎛⎫⎪⎝⎭的值域为(0，+∞).应使h(x)=ax2-4x+3的值域为R，因此只能a=0(若a≠0，则h(x)为二次函数，其值域不可能为R)，故a的值为0.【精要点评】求解与指数函数有关的复合函数问题时，首先要熟知指数函数的定义域、值域、单调性等相关性质，其次要明确复合函数的构成，涉及值域、单调区间、最值等问题时，都要借助“同增异减”这一性质分析判断，最终将问题归结为内层函数相关的问题加以解决.对于形如y=a g(x)的复合函数，关于单调区间有以下结论：当a>1时，函数y=a g(x)的单调性和y=g(x)的单调性相同；当0<a<1时，函数y=a g(x)的单调性和y=g(x)的单调性相反.变式若不等式2-23ax ax>13对一切实数x恒成立，求实数a的取值范围.【思维引导】将不等式2-23ax ax>2-2133ax ax转化为>3-1，然后利用指数函数的单调性，最后利用一元二次不等式恒成立的知识求解.【解答】原不等式即为2-23ax ax>3-1，则有ax2-2ax>-1，即ax2-2ax+1>0对一切实数恒成立.当a=0时，满足题意；当a>0时，Δ=(-2a)2-4a<0，即a2-a<0，解得0<a<1.综上，实数a的取值范围是[0，1).【精要点评】本题将13转化为3-1，从而将问题转化为同底数幂的大小问题.解决指数不等式的关键是根据指数函数的单调性进行转化，转化为代数不等式.指数函数的综合应用例4已知函数f(x)=11-12xa⎛⎫+⎪⎝⎭·x3(a>0且a≠1).(1)求函数f(x)的定义域；(2)讨论函数f(x)的奇偶性；(3)求实数a的取值范围，使f(x)>0在定义域上恒成立.【思维引导】对解析式较复杂的函数判断其奇偶性要适当变形，恒成立问题可通过求最值解决.【解答】(1)由a x-1≠0，得a x≠1，所以x≠0，所以函数f(x)的定义域为{x|x≠0}.(2)对于定义域内任意x，有f(-x)=-11-12xa⎛⎫+⎪⎝⎭(-x)3=11-2xxaa⎛⎫+⎪⎝⎭(-x)3=111-12xa⎛⎫--+⎪⎝⎭(-x)3=11-12xa⎛⎫+⎪⎝⎭x3=f(x)，所以f(x)是偶函数.(3)当a>1时，若x>0，由指数函数的性质知a x>1，所以a x-1>0，1-1xa+12>0.又x>0时，x3>0，所以x311-12xa⎛⎫+⎪⎝⎭>0，即当x>0时，f (x )>0.又由(2)知f (x )为偶函数，即f (-x )=f (x )， 则当x<0时，-x>0， 有f (-x )=f (x )>0成立.综上可知，当a>1时，f (x )>0在定义域上恒成立.当0<a<1时，f (x )=3(1)2(-1)x x a x a +. 当x>0时，1>a x>0，a x+1>0，a x -1<0，x 3>0，此时f (x )<0，不满足题意；当x<0时，-x>0，f (-x )=f (x )<0，也不满足题意. 综上，实数a 的取值范围是(1，+∞).【精要点评】(1)判断此类函数的奇偶性，常常需要对所给式子变形，以达到所需要的形式，另外，还可利用f (-x )±f (x )，()(-)f x f x 来判断奇偶性.(2)将不等式恒成立问题转化为求函数值域的问题，是解决恒成立问题的常用方法.变式 已知定义域为R 的函数f (x )=1-22x x b a +++是奇函数.(1)求实数a ，b 的值；(2)若对任意的t ∈R ，不等式f (t 2-2t )+f (2t 2-k )<0恒成立，求实数k 的取值范围. 【解答】(1)因为f (x )是奇函数，所以f (0)=0，即-12ba ++=0，解得b=1，从而有f (x )=1-212x x a +++. 又由f (1)=-f (-1)，知-214a ++=-1-121a ++，解得a=2.经检验a=2符合题意，故a=2，b=1.(2)由(1)知f (x )=1-2122x x +++=-12+121x+.由上式易知f (x )在(-∞，+∞)上为减函数.又f(x)是奇函数，从而不等式f(t2-2t)+f(2t2-k)<0，等价于f(t2-2t)<-f(2t2-k)=f(-2t2+k). 因为f(x)是减函数，所以t2-2t>-2t2+k，即对一切t∈R有3t2-2t-k>0，从而Δ=4+12k<0，解得k<-1 3.因此所求k的取值范围为1,3⎛⎫-∞-⎪⎝⎭.【精要点评】(1)解决恒成立问题时常转化为求最值来解决.(2)指数不等式的解法：对于不等式a f(x)>a g(x)(a>0且a≠1)，可利用指数函数的单调性求解.当0<a<1时，a f(x)>a g(x)⇔f(x)<g(x)；当a>1时，a f(x)>a g(x)⇔f(x)>g(x).1.(2015·海门中学模考改编)设函数f1(x)=12x，f2(x)=x-1，f3(x)=x2，则f1(f2(f3(2017)))= .【答案】1 2017【解析】f1(f2(f3(2 017)))=f1(f2(2 0172))=f1((2 0172)-1)=((2 0172)-112)=2 017-1.2.(2015·东北师大附中)设函数f(x)=|3x-1|，c<b<a且f(c)>f(a)>f(b)，在关系式①3c>3b；②3b>3a；③3c+3a>2；④3c+3a<2中，一定成立的是.(填序号)(第2题)【答案】④【解析】如图，作出y=|3x-1|的图象如图中实线部分所示，由c<b<a且f(c)>f(a)>f(b)，知3c<3b<3a且|3c-1|>|3a-1|>|3b-1|，转化为1-3c>3a-1>0，3c+3a<2，故填④.3.(2015·山东卷)已知函数f(x)=a x+b(a>0，a≠1)的定义域和值域都是[-1，0]，则a+b= .【答案】-3 2【解析】当a>1时，-1-1a ba b⎧+=⎨+=⎩，，无解；当0<a<1时，-1-1a ba b⎧+=⎨+=⎩，，解得b=-2，a=12，则a+b=12-2=-32.4.已知奇函数f(x)=-()1()m g xg x+的定义域为R，其中y=g(x)为指数函数且图象过点(2，9).(1)求函数y=f(x)的解析式；(2)若对任意的t∈[0，5]，不等式f(t2+2t+k)+f(-2t2+2t-5)>0恒成立，求实数k的取值范围. 【解答】(1)设g(x)=a x(a>0且a≠1)，则a2=9，所以a=3或a=-3(舍去)，所以g(x)=3x，f(x)=-313xxm+.又因为f(x)为定义在R上的奇函数，所以f(0)=0，即-111m+=0，所以m=1，所以f(x)=1-313xx +.(2)因为f(x)=1-313xx+=-31-231xx++=-1+231x+，所以f(x)为减函数.要使对任意的t∈[0，5]，f(t2+2t+k)+f(-2t2+2t-5)>0恒成立，即对任意的t∈[0，5]，f(t2+2t+k)>-f(-2t2+2t-5)恒成立.因为f(x)为奇函数，只需f(t2+2t+k)>f(2t2-2t+5)恒成立.又因为y=f(x)在R上单调递减，所以t2+2t+k<2t2-2t+5在t∈[0，5]时恒成立，所以k<t2-4t+5=(t-2)2+1在t∈[0，5]时恒成立.而当t∈[0，5]时，1≤(t-2)2+1≤10，所以k<1，即实数k的取值范围为(-∞，1).趁热打铁，事半功倍.请老师布置同学们完成《配套检测与评估》中的练习第19~20页.【检测与评估】第10课指数式与指数函数一、填空题1.(2015·海安中学期中)化简：()3232443·a··a b bba ba a>0，b>0)= .2.函数y=22-12x x⎛⎫⎪⎝⎭的值域是.3.若23-2x<0.53x-4，则x的取值范围是.4.若把y=f(x)的图象向左、向下分别平移2个单位长度，得函数y=2x的图象，则f(x)= .5.若102x=25，则10-x= .6.函数f(x)=1-e|x|的大致图象是.(填序号)①②③④(第6题)7.(2014·佛山模拟)已知不论a为何值，函数y=(a-1)2x-2a的图象恒过定点，则这个定点的坐标是.8.(2014·广州联考)已知函数f(x)=xα+1(α∈Q)的定义域为[-b，-a]∪[a，b]，其中0<a<b，且f(x)在区间[a，b]上的最大值为6，最小值为3，则f(x)在区间[-b，-a]上的最大值与最小值的和是.二、解答题9.(2014·合肥联考)已知定义域为R的奇函数f(x)满足f(x+1)=f(x-1)，且当x∈(0，1)时，f(x)=2-121xx .(1)求f(x)在区间[-1，1]上的解析式；(2)若存在x∈(0，1)，满足f(x)>m，求实数m的取值范围.10.若方程2a =|a x-1|(a >0，a ≠1)有两个实数解，求实数a 的取值范围.11.(2014·洛阳一模)已知函数f (x )=2-1a a (a x -a -x)(a >0且a ≠1).(1)判断f (x )的奇偶性； (2)讨论f (x )的单调性；(3)当x ∈[-1，1]时，f (x )≥b 恒成立，求实数b 的取值范围.三、 选做题(不要求解题过程，直接给出最终结果)12.已知函数f (x )=3x，且f (a +2)=18，g (x )=3ax-4x的定义域为[0，1]. (1)求g (x )的解析式；(2)求g (x )的单调区间，并判定函数的单调性； (3)求g (x )的值域.【检测与评估答案】第10课 指数式与指数函数1.ab 【解析】原式=1312322132·[()]·a b ab b ab a ⎛⎫ ⎪⎝⎭=1136322733·a b a ba b=a b .2. 12∞⎡⎫+⎪⎢⎣⎭， 【解析】g (x )=2x-x 2=-(x-1)2+1≤1，所以函数y=22-12x x ⎛⎫ ⎪⎝⎭的值域为12∞⎡⎫+⎪⎢⎣⎭，.3. (-∞，1) 【解析】原不等式等价于23-2x<24-3x ，所以3-2x<4-3x ，解得x<1.4.2x-2+2【解析】把y=f(x)的图象向左、向下分别平移2个单位长度，得函数y=2x的图象，即把y=2x的图象向右、向上分别平移2个单位长度，得函数y=f(x)的图象，即y=f(x)=2x-2+2.5.15【解析】由102x=25⇒(10x)2=25⇒10x=5⇒10-x=15.6.①【解析】函数f(x)=1-e|x|是偶函数，其图象关于y轴对称，又f(0)=0，故填①.7.1-1-2⎛⎫⎪⎝⎭，【解析】y=a12-2x⎛⎫⎪⎝⎭-2x，令2x-12=0，则y+2x=0，得x=-1，y=-12，所以这个定点的坐标为1-1-2⎛⎫ ⎪⎝⎭，.8.-5或9【解析】设h(x)=f(x)-1=xα，则由题意可知h(x)为奇函数或偶函数.当h(x)为奇函数时，由f(x)在区间[a，b]上的最大值为6，最小值为3，得h(x)在区间[-b，-a]上的最大值与最小值分别是-2，-5，从而f(x)在区间[-b，-a]上的最大值与最小值分别是-1，-4，其和为-5.当h(x)为偶函数时，由f(x)在区间[a，b]上的最大值为6，最小值为3，得h(x)在区间[-b，-a]上的最大值与最小值分别是5，2，从而f(x)在区间[-b，-a]上的最大值与最小值分别是6和3，其和为9.9.(1)当x∈(-1，0)时，-x∈(0，1).由f(x)为R上的奇函数，得f(-x)=--2-121xx+=1-221xx+=-f(x)，所以f(x)=2-121xx+，x∈(-1，0).又由f(x)为奇函数，得f(0)=0，f(-1)=-f(1)，在f(x+1)=f(x-1)中，令x=0，则f(-1)=f(1)，所以f(-1)=f(1)=0.故f (x )=2-1(-11)2101.x x x x ∈⎧⎪+⎨⎪=±⎩，，，，(2)因为x ∈(0，1)，所以f (x )=2-121x x +=21-221x x ++=1-221x+.又因为2x∈(1，2)，所以1-210213x⎛⎫∈ ⎪+⎝⎭，. 若存在x ∈(0，1)，满足f (x )>m ，则m<13.故实数m 的取值范围为1-3∞⎛⎫ ⎪⎝⎭，.10.当a>1时，函数y=|a x-1|的图象如图(1)所示，显然直线y=2a 与该图象只有一个交点，故a>1不合适；当0<a<1时，函数y=|a x -1|的图象如图(2)所示，要使直线y=2a 与该图象有两个交点，则0<2a<1，即0<a<12.图(1)图(2) (第10题)综上所述，实数a 的取值范围为102⎛⎫ ⎪⎝⎭，.11.(1)函数的定义域为R ，关于原点对称.又因为f (-x )=2-1a a (a -x -a x)=-f (x )，所以f (x )为奇函数.(2)当a>1时，2-1a a >0，y=a x 为增函数，y=a -x为减函数，从而y=a x-a -x为增函数， 所以f (x )为增函数.当0<a<1时，2-1a a <0，y=a x 为减函数，y=a -x为增函数，从而y=a x-a -x为减函数， 所以f (x )为增函数.故当a>0且a ≠1时，f (x )在定义域内单调递增. (3)由(2)知f (x )在区间[-1，1]上为增函数， 所以f (-1)≤f (x )≤f (1)，所以f (x )min =f (-1)=2-1a a (a -1-a )=-1，所以要使f (x )≥b 在[-1，1]上恒成立，只需b ≤-1. 故实数b 的取值范围是(-∞，-1].12.(1) 因为f (x )=3x，f (a+2)=18， 所以3a+2=18，得3a=2， 所以g (x )=2x-4x，x ∈[0，1]. (2) g (x )=2x-4x=2x-(2x )2， 设t=2x，因为x ∈[0，1]，所以t ∈[1，2]，所以g (t )=t-t 2=-21-2t ⎛⎫ ⎪⎝⎭+14，所以g (t )在[1，2]上单调递减. 因为t=2x为[0，1]上的增函数， 所以g (x )在[0，1]上为减函数.(3) 因为g(x)在[0，1]上为减函数，所以g(1)≤g(x)≤g(0)，即g(x)∈[-2，0]. 故g(x)的值域为[-2，0].。

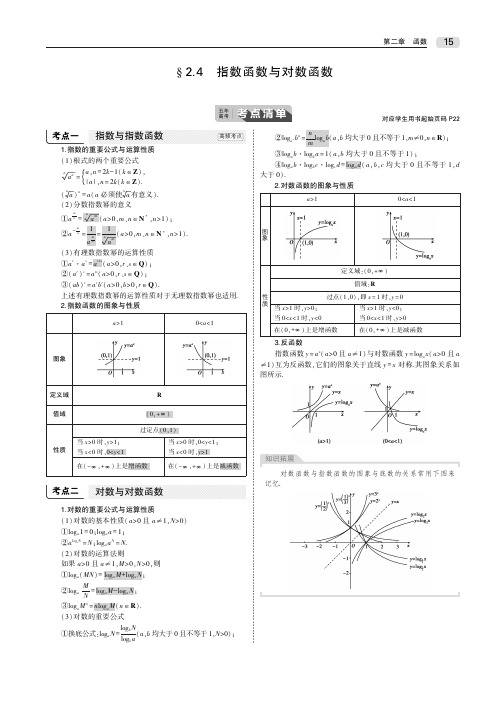
2023年高考数学总复习第二章函数概念与基本初等函数第5节指数与指数函数考试要求1.了解指数函数模型的实际背景；2.理解有理指数幂的含义，了解实数指数幂的意义，掌握幂的运算；3.理解指数函数的概念及其单调性，掌握指数函数图像通过的特殊点，会画底数为2，3，10，12，13的指数函数的图像；4.体会指数函数是一类重要的函数模型.1.根式的概念及性质(1)概念：式子na 叫作根式，其中n 叫作根指数，a 叫作被开方数.(2)性质：(na )n ＝a (a 使na 有意义)；当n 为奇数时，na n ＝a ，当n 为偶数时，na n ＝|a |，a ≥0，a ，a <0.2.分数指数幂规定：正数的正分数指数幂的意义是a mn ＝na m (a >0，m ，n ∈N +，且n >1)；正数的负分数指数幂的意义是a －mn ＝1na m(a >0，m ，n ∈N +，且n >1)；0的正分数指数幂等于0；0的负分数指数幂没有意义.3.指数幂的运算性质实数指数幂的运算性质：a r a s ＝a r ＋s ；(a r )s ＝a rs ；(ab )r ＝a r b r ，其中a >0，b >0，r ，s ∈R .4.指数函数及其性质(1)概念：函数y ＝a x (a >0，且a ≠1)叫作指数函数，其中指数x 是自变量，函数的定义域是R ，a 是底数.(2)指数函数的图像与性质a >10<a <1图像定义域R 值域(0，＋∞)性质过定点(0，1)，即x ＝0时，y ＝1当x >0时，y >1；当x <0时，0<y <1当x <0时，y >1；当x >0时，0<y <1在(－∞，＋∞)上是增函数在(－∞，＋∞)上是减函数1.画指数函数y ＝a x (a >0，且a ≠1)的图像，应抓住三个关键点：(1，a )，(0，1)，12.指数函数y ＝a x (a >0，且a ≠1)的图像和性质跟a 的取值有关，要特别注意应分a >1与0<a <1来研究.3.在第一象限内，指数函数y ＝a x (a >0，且a ≠1)的图像越高，底数越大.1.思考辨析(在括号内打“√”或“×”)(1)4（－4）4＝－4.()(2)分数指数幂a mn 可以理解为mn 个a 相乘.()(3)函数y ＝2x －1是指数函数.()(4)函数y ＝a x2＋1(a >1)的值域是(0，＋∞).()2.(易错题)若函数f (x )＝(a 2－3)·a x 为指数函数，则a ＝________.3.(易错题)函数y ＝21x －1的值域是________.4.函数f (x )＝a x －1＋2(a >0且a ≠1)的图像恒过定点________.5.(2021·贵阳一中月考)3213－76＋814×42－－2323________.6.已知a 35－13，b 35－14，c ＝3234，则a ，b ，c 的大小关系是________.考点一指数幂的运算1.计算：823－－780＋4（3－π）4＋[(－2)6]12＝________.2.[(0.06415)－2.5]23－3338－π0＝________.3.(2021·沧州七校联考1412·（4ab －1）3（0.1）－1·（a 3·b －3）12(a >0，b >0)＝________.4.已知f (x )＝3x ＋3－x ，f (b )＝4，则f (2b )＝________.考点二指数函数的图像及应用例1(1)已知实数a ，b 满足等式2022a ＝2023b ，下列等式一定不成立的是()A.a ＝b ＝0B.a <b <0C.0<a <bD.0<b <a(2)若函数f (x )＝|2x －2|－b 有两个零点，则实数b 的取值范围是________.训练1(1)函数f (x )＝a x －b 的图像如图所示，其中a ，b 为常数，则下列结论正确的是()A.a >1，b <0B.a >1，b >0C.0<a <1，b >0D.0<a <1，b <0(2)如果函数y ＝|3x －1|＋m 的图像不经过第二象限，则实数m 的取值范围是________.考点三解决与指数函数性质有关的问题角度1比较指数式的大小例2(1)设a＝0.60.6，b＝0.61.5，c＝1.50.6，则a，b，c的大小关系是() A.a<b<c B.a<c<bC.b<a<cD.b<c<a(2)若e a＋πb≥e－b＋π－a，下列结论一定成立的是()A.a＋b≤0B.a－b≥0C.a－b≤0D.a＋b≥0角度2解简单的指数方程或不等式例3(1)已知实数a≠1，函数f(x)4x，x≥0，2a－x，x<0，若f(1－a)＝f(a－1)，则a的值为________.(2)若2x2＋114x－2，则函数y＝2x的值域是()A.18，2 B.18，2C.－∞，18 D.[2，＋∞)角度3指数函数性质的综合应用例4(1)不等式4x－2x＋1＋a>0，对任意x∈R都成立，则实数a的取值范围是________.(2)已知定义域为R的函数f(x)＝－12＋12x＋1，则关于t的不等式f(t2－2t)＋f(2t2－1)<0的解集为________.训练2(1)(2021·郑州调研)已知函数f(x)＝4x－12x，a＝f(20.3)，b＝f(0.20.3)，c＝f(log0.32)，则a，b，c的大小关系为()A.c<b<aB.b<a<cC.b<c<aD.c<a<b(2)若函数f (x )2＋2x ＋3，19，则f (x )的单调递增区间是______.(3)函数y ＋1在区间[－3，2]上的值域是________.1.若函数f (x )＝a x (a >0，且a ≠1)f (－1)＝()A.1B.2C.3D.32.(2021·成都诊断)不论a 为何值，函数y ＝(a －1)2x －a2恒过定点，则这个定点的坐标是()113.(2022·哈尔滨质检)函数y ＝a x －1a(a >0，且a ≠1)的图像可能是()4.(2020·天津卷)设a ＝30.7，b 0.8，c ＝log 0.70.8，则a ，b ，c 的大小关系为()A.a ＜b ＜cB.b ＜a ＜cC.b ＜c ＜aD.c ＜a ＜b5.(2021·衡水中学检测)当x∈(－∞，－1]时，不等式(m2－m)·4x－2x<0恒成立，则实数m的取值范围是()A.(－2，1)B.(－4，3)C.(－3，4)D.(－1，2)6.(2020·新高考山东卷)基本再生数R0与世代间隔T是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数，世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段，可以用指数模型：I(t)＝e rt描述累计感染病例数I(t)随时间t(单位：天)的变化规律，指数增长率r与R0，T近似满足R0＝1＋rT.有学者基于已有数据估计出R0＝3.28，T＝6.据此，在新冠肺炎疫情初始阶段，累计感染病例数增加1倍需要的时间约为(ln2≈0.69)()A.1.2天B.1.8天C.2.5天D.3.5天7.化简：（a23·b－1）－12·a－12·b136a·b5(a>0，b>0)＝________.8.设偶函数g(x)＝a|x＋b|在(0，＋∞)上单调递增，则g(a)与g(b－1)的大小关系是____________.9.已知函数f(x)，a≤x<0，x2＋2x，0≤x≤4的值域是[－8，1]，则实数a的取值范围是________.10.已知定义域为R的函数f(x)＝－2x＋b2x＋1＋2为奇函数.(1)求b的值；(2)任意t∈R，f(t2－2t)＋f(2t2－k)<0恒成立，求k的取值范围.11.已知函数f(x)＝4x＋m2x是奇函数.(1)求实数m的值；(2)设g(x)＝2x＋1－a，若函数f(x)与g(x)的图像有公共点，求实数a的取值范围.12.若关于x的方程|a x－1|＝2a(a>0，且a≠1)有两个不相等的实根，则a的取值范围是()A.0，12(1，＋∞) B.0，12C.12，1 D.(1，＋∞)13.(2022·邯郸模拟)设f(x)|2x－1|，x≤2，－x＋5，x>2，若互不相等的实数a，b，c满足f(a)＝f(b)＝f(c)，则2a＋2b＋2c的取值范围是()A.(16，32)B.(18，34)C.(17，35)D.(6，7)14.已知定义在R上的函数f(x)＝2x－12|x|.(1)若f(x)＝32，求x的值；(2)若2t f(2t)＋mf(t)≥0对任意t∈[1，2]恒成立，求实数m的取值范围.。

第十节函数模型及其应用知识回顾1．几类函数模型2.三种函数模型的性质1.【2019年浙江丽水高一上学期期末考试数学试卷统测】某种放射性元素的原子数N随时间t的变化规律是N=N0eλt，其中N0，λ是正的常数．当N=2N0时，t=________ ．ln⁡2【答案】1λ【解析】【解答】某种放射性元素的原子数N随时间t的变化规律是N=N0eλt，其中N0，λ是正的常数．当N= 2N0时，则N=N0eλt=2N0≠0，化为：eλt=2，ln⁡2．解得t=1λ故答案为1λln⁡2．【分析】由题意可得：N =N 0e λt =2N 0≠0，化为：e λt =2，化为对数式即可得出． 【备注】【点评】本题考查了指数式化为对数式，考查了推理能力与计算能力，属于基础题．2．某市生产总值连续两年持续增加．第一年的增长率为p ，第二年的增长率为q ，则该市这两年生产总值的年平均增长率为________． 答案p ＋1q ＋1－1解析 设年平均增长率为x ，则(1＋x )2＝(1＋p )(1＋q )， ∴x ＝1＋p1＋q －1.3．某公司租地建仓库，已知仓库每月占用费y 1与仓库到车站的距离成反比，而每月车载货物的运费y 2与仓库到车站的距离成正比．据测算，如果在距离车站10千米处建仓库，这两项费用y 1，y 2分别是2万元和8万元，那么要使这两项费用之和最小，仓库应建在离车站________千米处． 答案 5解析 由题意得，y 1＝k 1x ，y 2＝k 2x ，其中x >0，当x ＝10时，代入两项费用y 1，y 2分别是2万元和8万元，可得k 1＝20，k 2＝45，y 1＋y 2＝20x ＋45x ≥220x ·45x ＝8，当且仅当20x ＝45x ，即x ＝5时取等号．4.某厂有许多形状为直角梯形的铁皮边角料，如图，为降低消耗，开源节流，现要从这些边角料上截取矩形铁片(如图中阴影部分)备用，当截取的矩形面积最大时，矩形两边长x ，y 应为________． 答案 15,12解析 由三角形相似得24－y 24－8＝x 20，得x ＝54(24－y )，∴S ＝xy ＝－54(y －12)2＋180，∴当y ＝12时，S 有最大值，此时x ＝15.5．加工爆米花时，爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”．在特定条件下，可食用率p 与加工时间t (单位：分钟)满足函数关系p ＝at 2＋bt ＋c (a 、b 、c 是常数)，如图记录了三次实验的数据．根据上述函数模型和实验数据，可以得到最佳加工时间为________分钟．答案 3.75解析 根据图表，把(t ，p )的三组数据(3,0.7)，(4,0.8)，(5,0.5)分别代入函数关系式，联立方程组得⎩⎪⎨⎪⎧0.7＝9a ＋3b ＋c ，0.8＝16a ＋4b ＋c ，0.5＝25a ＋5b ＋c ，消去c 化简得⎩⎪⎨⎪⎧7a ＋b ＝0.1，9a ＋b ＝－0.3，解得⎩⎪⎨⎪⎧a ＝－0.2，b ＝1.5，c ＝－2.0.所以p ＝－0.2t 2＋1.5t －2.0＝－15(t 2－152t ＋22516)＋4516－2＝－15(t －154)2＋1316，所以当t ＝154＝3.75时，p 取得最大值，即最佳加工时间为3.75分钟.6．(多选)某工厂生产一种溶液，按市场要求杂质含量不得超过0.1%，而这种溶液最初的杂质含量为2%，现进行过滤，已知每过滤一次杂质含量减少13，则使产品达到市场要求的过滤次数可以为(参考数据：lg2≈0.301，lg 3≈0.477)( ) A ．6 B ．9 C ．8 D ．7 答案 BC解析 设经过n 次过滤，产品达到市场要求， 则2100×⎝⎛⎭⎫23n ≤11 000，即⎝⎛⎭⎫23n ≤120， 由n lg 23≤－lg 20，即n (lg 2－lg 3)≤－(1＋lg 2)，得n ≥1＋lg 2lg 3－lg 2≈7.4，故选BC.课中讲解考点一.函数图像刻画变化过程例1．小明骑车上学，开始时匀速行驶，途中因交通堵塞停留了一段时间，后为了赶时间加快速度行驶．与以上事件吻合得最好的图象是( )解析：选C 小明匀速行驶时，图象为一条直线，且距离学校越来越近，故排除A.因交通堵塞停留了一段时间，与学校的距离不变，故排除D.后来为了赶时间加快速度行驶，故排除B.故选C.变式1．如图，四个容器高度都相同，将水从容器顶部一个孔中以相同的速度注入其中，注满为止．用下面对应的图象表示该容器中水面的高度h 和时间t 之间的关系，其中不正确的个数为( )A．1B．2C．3 D．4解析：选A将水从容器顶部一个孔中以相同的速度注入其中，容器中水面的高度h和时间t之间的关系可以从高度随时间的变化率上反映出来．图①应该是匀速的，故下面的图象不正确；②中的变化率应该是越来越慢的，正确；③中的变化率是先快后慢再快，正确；④中的变化率是先慢后快再慢，也正确，故只有①是错误的．例2．设甲、乙两地的距离为a(a>0)，小王骑自行车匀速从甲地到乙地用了20分钟，在乙地休息10分钟后，他又匀速从乙地返回到甲地用了30分钟，则小王从出发到返回原地所经过的路程y和其所用的时间x的函数图象为()答案 D解析y为“小王从出发到返回原地所经过的路程”而不是位移，故排除A，C.又因为小王在乙地休息10分钟，故排除B，故选D.变式2．某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x(单位：千元)对年销售量y(单位：t)的影响．根据近8年的年宣传费x i和年销售量y i(i＝1,2，…，8)数据得到下面的散点图．则下列哪个作为年销售量y关于年宣传费x的函数模型最适合()A．y＝ax＋b B．y＝a＋b xC．y＝a·b x D．y＝ax2＋bx＋c答案 B解析根据散点图可知，选择y＝a＋b x最适合．考点二.应用所给的模型解决实际问题例1.候鸟每年都要随季节的变化而进行大规模迁徙，研究某种候鸟的专家发现，该种候鸟的飞行速度 v （单位：m ⋅s −1）与其耗氧量 Q 之间的关系为 v =a +blog 3⁡Q10（其中 a 、b 是常数）．据统计，该种鸟类在静止时的耗氧量为 30 个单位，而其耗氧量为个 90 单位时，飞行速度为 1m ⋅s −1．若这种候鸟为赶路程，飞行的速度不能低于 2m ⋅s −1，求其耗氧量至少要多少个单位． 【答案】270 个单位【解析】由题意，知 {a +blog 3⁡3010=0a +blog 3⁡9010=1，即 {a +b =0a +2b =1，解得 {a =−1b =1，所以 v =−1+log 3⁡Q 10， 要使飞行速度不能低于 2m ⋅s −1，则有 v ⩾2，即 −1+log 3⁡Q 10⩾2，即 log 3⁡Q10⩾3，解得 Q10⩾27，即 Q10⩾270，所以耗氧量至少要 270 个单位．变式1.数据显示，某 IT 公司 2018 年上半年五个月的收入情况如下表所示：月份 2 3 4 5 6月收入（万元）1.42.565.311121.3根据上述数据，在建立该公司 2018 年月收入 y （万元）与月份 x 的函数模型时，给出两个函数模型 y =x 12 与 y =2x 3供选择．(1) 你认为哪个函数模型较好，并简单说明理由； 【答案】函数 y =2x 3这一模型较好【解析】画出散点图由图可知点 (2,1.4)；(3,2.56)；(4,5.31)；(5,11)；(6,21.3) 基本上是落在函数 y =2x 3的图像的附近，因此用函数 y =2x 3这一模型较好．(2) 试用你认为较好的函数模型，分析大约从第几个月份开始，该公司的月收入会超过 100 万元？（参考数据 lg⁡2=0.3010，lg⁡3=0.4771） 【答案】大约从第 9 月份开始 【解析】当2x 3>100 时，2x >300，∴lg⁡2x >lg⁡300即 xlg⁡2>2+lg⁡3∴x >2+lg⁡3lg 2=2+0.47710.3010≈8.23故大约从第 9 月份开始，该公司的月收入会超过 100 万元． 当2x 3>100 时，2x >30028=256<300；29=512>300故大约从第 9 月份开始，该公司的月收入会超过 100 万元．例2.为了预防流感，某学校对教室用药熏消毒法进行消毒．已知药物释放过程中，室内每立方米空气中的含药量y (毫克)与时间t (小时)成正比；药物释放完毕后，y 与t 的函数关系式y ＝⎝⎛⎭⎫116t －a(a 为常数)，如图所示，根据图中提供的信息，回答下列问题：①从药物释放开始，每立方米空气中的含药量y (毫克)与时间t (小时)之间的函数关系式为________________________________________________________________________．②据测定，当空气中每立方米的含药量降低到0.25毫克以下时，学生方可进教室，那么从药物释放开始，至少需要经过________小时后，学生才能回到教室． 答案 ①y ＝⎩⎪⎨⎪⎧10t ，0≤t ≤0.1，⎝⎛⎭⎫116t －0.1，t >0.1②0.6解析 ①设y ＝kt ，由图象知y ＝kt 过点(0.1,1)， 则1＝k ×0.1，k ＝10，∴y ＝10t (0≤t ≤0.1)． 由y ＝⎝⎛⎭⎫116t －a过点(0.1,1)，得1＝⎝⎛⎭⎫1160.1－a ， 解得a ＝0.1，∴y ＝⎝⎛⎭⎫116t －0.1(t >0.1)．②由⎝⎛⎭⎫116t －0.1≤0.25＝14，得t ≥0.6. 故至少需经过0.6小时学生才能回到教室．变式2.拟定甲、乙两地通话m 分钟的电话费(单位：元)由f (m )＝1.06(0.5[m ]＋1)给出，其中m >0，[m ]是不超过m 的最大整数(如[3]＝3，[3.7]＝3，[3.1]＝3)，则甲、乙两地通话6.5分钟的电话费为______元． 答案 4.24解析 ∵m ＝6.5，∴[m ]＝6， 则f (6.5)＝1.06×(0.5×6＋1)＝4.24. 考点三.构建函数模型解决实际问题1.二次函数模型例1.某企业为打入国际市场，决定从A ，B 两种产品中只选择一种进行投资生产，已知投资生产这两种产品的有关数据如下表(单位：万美元)：预计m ∈[6,8]，另外，年销售x 件B 产品时需上交0.05x 2万美元的特别关税，假设生产出来的产品都能在当年销售出去．(1)写出该厂分别投资生产A ，B 两种产品的年利润y 1，y 2与生产相应产品的件数x 1，x 2之间的函数关系式，并指明定义域；(2)如何投资才可获得最大年利润？请你做出规划．[解] (1)由题意得y 1＝10x 1－(20＋mx 1)＝(10－m )x 1－20(0≤x 1≤200且x 1∈N)，y 2＝18x 2－(40＋8x 2)－0.05x 22＝－0.05x 22＋10x 2－40＝－0.05(x 2－100)2＋460(0≤x 2≤120且x 2∈N)． (2)∵6≤m ≤8，∴10－m ＞0， ∴y 1＝(10－m )x 1－20为增函数． 又0≤x 1≤200，x 1∈N ，∴当x 1＝200时，生产A 产品的最大利润为(10－m )×200－20＝1 980－200m (万美元)． ∵y 2＝－0.05(x 2－100)2＋460(0≤x 2≤120，且x 2∈N)， ∴当x 2＝100时，生产B 产品的最大利润为460万美元． (y 1)max －(y 2)max ＝(1 980－200m )－460＝1 520－200m . 易知当6≤m ＜7.6时，(y 1)max ＞(y 2)max .即当6≤m ＜7.6时，投资生产A 产品200件可获得最大年利润；当m ＝7.6时，投资生产A 产品200件或投资生产B 产品100件，均可获得最大年利润； 当7.6＜m ≤8时，投资生产B 产品100件可获得最大年利润．变式1. 某城市对一种售价为每件160元的商品征收附加税，税率为R %(即每销售100元征税R 元)，若每年销售量为⎝⎛⎭⎫30－52R 万件，要使附加税不少于128万元，则R 的取值范围是( ) A ．[4,8] B ．[6,10] C ．[4%,8%] D ．[6%,10%]答案 A解析 根据题意，要使附加税不少于128万元，需⎝⎛⎭⎫30－52R ×160×R %≥128， 整理得R 2－12R ＋32≤0，解得4≤R ≤8，即R ∈[4,8]．2. 指对数函数模型例2.某公司为激励创新，计划逐年加大研发资金投入．若该公司2016年全年投入研发资金130万元，在此基础上，每年投入的研发资金比上一年增长12%，则该公司全年投入的研发资金开始超过200万元的年份是( )(参考数据：lg 1.12≈0.05，lg 1.3≈0.11，lg 2≈0.30) A ．2018年 B ．2019年 C ．2020年D ．2021年变式2.某食品的保鲜时间y (单位：小时)与储藏温度x (单位：℃)满足函数关系y ＝e kx ＋b (e ＝2.718…为自然对数的底数，k ，b 为常数)．若该食品在0 ℃的保鲜时间是192小时，在22 ℃的保鲜时间是48小时，则该食品在33 ℃的保鲜时间是( )A ．16小时B ．20小时C ．24小时D ．28小时[解析] (1)设第n (n ∈N *)年该公司全年投入的研发资金开始超过200万元． 根据题意得130(1＋12%)n －1＞200， 则lg[130(1＋12%)n －1]＞lg 200， ∴lg 130＋(n －1)lg 1.12＞lg 2＋2， ∴2＋lg 1.3＋(n －1)lg 1.12＞lg 2＋2， ∴0.11＋(n －1)×0.05＞0.30，解得n ＞245，又∵n ∈N *，∴n ≥5，∴该公司全年投入的研发资金开始超过200万元的年份是2020年．故选C. (2)由已知得192＝e b ，① 48＝e 22k ＋b ＝e 22k ·e b ，②将①代入②得e 22k ＝14，则e 11k ＝12，当x ＝33时，y ＝e 33k ＋b ＝e 33k ·e b ＝⎝⎛⎭⎫123×192＝24，所以该食品在33 ℃的保鲜时间是24小时．故选C. [答案] (1)C (2)C3. 对勾函数模型例3 某汽车运输公司购买了一批豪华大客车投入营运，据市场分析，每辆客车营运的总利润y (万元)与营运年数x 的关系如图所示(抛物线的一段)，则为使其营运年平均利润最大，每辆客车营运年数为________．答案 5解析 根据图象求得y ＝－(x －6)2＋11， ∴年平均利润yx＝12－⎝⎛⎭⎫x ＋25x ， ∵x ＋25x ≥10，当且仅当x ＝5时等号成立．∴要使平均利润最大，客车营运年数为5.变式3.某地区要建造一条防洪堤，其横断面为等腰梯形，腰与底边夹角为60°(如图)，考虑防洪堤坚固性及石块用料等因素，设计其横断面要求面积为9 3 平方米，且高度不低于 3 米．记防洪堤横断面的腰长为x 米，外周长(梯形的上底线段BC 与两腰长的和)为y 米．要使防洪堤的上面与两侧面的水泥用料最省(即横断面的外周长最小)，则防洪堤的腰长x ＝________米．答案 2 3解析 由题意可得BC ＝18x －x2(2≤x <6)，∴y ＝18x ＋3x 2≥218x ×3x2＝6 3. 当且仅当18x ＝3x2(2≤x <6)，即x ＝23时等号成立．4. 分段函数模型例4.某市营业区内住宅电话通话费用为前 3 分钟 0.20 元，以后每分钟 0.10 元（前 3 分钟不足 3 分钟按 3 分钟计，以后不足 1 分钟按 1 分钟计）．(1) 在直角坐标系内，画出一次通话在 6 分钟内（包括 6 分钟）的话费 y （元）关于通话时间 t （分钟）的函数图象； 【答案】见解析 【解析】如下图所示．(2) 如果一次通话t分钟（t>0），写出话费y（元）关于通话时间t（分钟）的函数关系式（可用[t]表示不小于t的最小整数）．【答案】y={0.2,0<t⩽30.2+[t−3]×0.1,t>3【解析】由(1)知，话费y与时间t的关系是分段函数．当0<t⩽3时，话费y为0.2元；当t>3时，话费y应为(0.2+[t−3]×0.1)元．所以y={0.2,0<t⩽30.2+[t−3]×0.1,t>3．变式4.在扶贫活动中，为了尽快脱贫（无债务）致富，企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙，并约定从该店经营的利润中，首先保证企业乙的全体职工每月最低生活费的开支3600元后，逐步偿还转让费（不计息）．在甲提供的资料中：①这种消费品的进价为每件14元；①该店月销量Q（百件）与销量价格P（元）的关系如图所示；①每月需各种开支2000元．(1) 当商品的价格为每件多少元时，月利润扣除职工最低生活费的余额最大？并求最大余额；【答案】当P=19.5元时，月利润余额最大，为450元【解析】设该店月利润余额为L元，则由题设得L=Q(P−14)×100−3600−2000①由销量图易得Q={−2P+50,14⩽P⩽20−32P+40,20<P⩽26，代入①式得L={(−2P+50)(P−14)×100−5600,14⩽P⩽20(−32P+40)(P−14)×100−5000,20<P⩽26当14⩽P⩽20时，L max=450元，此时P=19.5元；当20<P⩽26时，L max=12503元，此时P=613元．故当P=19.5元时，月利润余额最大，为450元．(2) 企业乙只依靠该店，最早可望在几年后脱贫？【答案】最早可望在20年后脱贫【解析】设可在n年后脱贫，依题意有12n×450−50000−58000⩾0，解得n⩾20．即最早可望在20年后脱贫．课后习题一．单选题1．(2018·北京石景山联考)小明在如图1所示的跑道上匀速跑步，他从点A出发，沿箭头方向经过点B跑到点C，共用时30 s，他的教练选择了一个固定的位置观察小明跑步的过程，设小明跑步的时间为t(s)，他与教练间的距离为y(m)，表示y与t的函数关系的图象大致如图2所示，则这个固定位置可能是图1中的()A．点M B．点NC．点P D．点Q解析：选D假设这个位置在点M，则从A至B这段时间，y不随时间的变化改变，与函数图象不符，故A选项错误；假设这个位置在点N，则从A至C这段时间，A点与C点对应y的大小应该相同，与函数图象不符，故B选项错误；假设这个位置在点P，则由函数图象可得，从A到C的过程中，会有一个时刻，教练到小明的距离等于经过30 s时教练到小明的距离，而点P不符合这个条件，故C选项错误；经判断点Q符合函数图象，故D选项正确，选D.2．(2019·洛阳模拟)某校为了规范教职工绩效考核制度，现准备拟定一函数用于根据当月评价分数x(正常情况下0≤x≤100，且教职工平均月评价分数在50分左右，若有突出贡献可以高于100分)计算当月绩效工资y(元)．要求绩效工资不低于500元，不设上限，且让大部分教职工绩效工资在600元左右，另外绩效工资越低或越高时，人数要越少．则下列函数最符合要求的是()A．y＝(x－50)2＋500 B．y＝10x25＋500C ．y ＝11 000(x －50)3＋625D ．y ＝50[10＋lg(2x ＋1)]解析：选C 由题意知，拟定函数应满足：①是单调递增函数，且增长速度先快后慢再快；②在x ＝50左右增长速度较慢，最小值为500.A 中，函数y ＝(x －50)2＋500先减后增，不符合要求；B 中，函数y ＝10x25＋500是指数型函数，增长速度是越来越快，不符合要求；D 中，函数y ＝50[10＋lg(2x ＋1)]是对数型函数，增长速度是越来越慢，不符合要求；而C 中，函数y ＝11 000(x －50)3＋625是由函数y ＝x 3经过平移和伸缩变换得到的，符合要求．故选C.3．(2019·邯郸名校联考)某企业准备投入适当的广告费对甲产品进行促销宣传，在一年内预计销售量y (万件)与广告费x (万元)之间的函数关系为y ＝1＋3x x ＋2(x ≥0)．已知生产此产品的年固定投入为4万元，每生产1万件此产品仍需再投入30万元，且能全部售完. 若每件甲产品售价(元)定为“平均每件甲产品所占生产成本的150%”与“年平均每件甲产品所占广告费的50%”之和，则当广告费为1万元时，该企业甲产品的年利润为( )A ．30.5万元B ．31.5万元C ．32.5万元D ．33.5万元解析：选B 由题意，产品的生产成本为(30y ＋4)万元，销售单价为30y ＋4y ×150%＋xy ×50%，故年销售收入为z ＝⎝⎛⎭⎫30y ＋4y ×150%＋xy ×50%·y ＝45y ＋6＋12x .∴年利润W ＝z －(30y ＋4)－x ＝15y ＋2－x 2＝17＋45x x ＋2－x 2(万元)．∴当广告费为1万元时，即x ＝1，该企业甲产品的年利润为17＋451＋2－12＝31.5(万元)．故选B. 4．一种放射性元素的质量按每年10%衰减，这种放射性元素的半衰期(剩余质量为最初质量的一半所需的时间叫作半衰期)是(精确到0.1，已知lg 2≈0.301 0，lg 3≈0.477 1)( ) A ．5.2 B ．6.6 C ．7.1 D ．8.3 答案 B解析 设这种放射性元素的半衰期是x 年， 则(1－10%)x ＝12，化简得0.9x ＝12，即x ＝log 0.912＝lg12lg 0.9＝－lg 22lg 3－1≈－0.301 02×0.477 1－1≈6.6(年)．故选B. 5．某单位为鼓励职工节约用水，作出了以下规定：每位职工每月用水不超过10 m 3的，按每立方米m 元收费；用水超过10 m 3的，超过部分加倍收费．某职工某月缴水费16m 元，则该职工这个月实际用水为( ) A ．13 m 3 B ．14 m 3 C ．18 m 3 D ．26 m 3答案 A解析 设该职工用水x m 3时，缴纳的水费为y 元，由题意得y ＝⎩⎪⎨⎪⎧mx ，0<x ≤10，10m ＋x －10·2m ，x >10，则10m ＋(x －10)·2m ＝16m ，解得x ＝13.6.(2020·青岛模拟)某厂有许多形状为直角梯形的铁皮边角料，如图，为降低消耗，开源节流，现要从这些边角料上截取矩形铁片(如图中阴影部分)备用，当截取的矩形面积最大时，矩形两边长x ，y 应为( )A ．x ＝15，y ＝12B ．x ＝12，y ＝15C ．x ＝14，y ＝10D ．x ＝10，y ＝14答案 A解析 由三角形相似得24－y 24－8＝x 20，得x ＝54(24－y )，所以S ＝xy ＝－54(y －12)2＋180，所以当y ＝12时，S 有最大值，此时x ＝15.检验符合题意．二．多选题7．(多选)在一次社会实践活动中，某数学调研小组根据车间持续5个小时的生产情况画出了某种产品的总产量y (单位：千克)与时间x (单位：小时)的函数图象，则以下关于该产品生产状况的正确判断是( )A ．在前三小时内，每小时的产量逐步增加B ．在前三小时内，每小时的产量逐步减少C ．最后一小时内的产量与第三小时内的产量相同D ．最后两小时内，该车间没有生产该产品 答案 BD解析 由该车间5小时来某种产品的总产量y (千克)与时间x (小时)的函数图象，得前三小时的年产量逐步减少，故A 错误，B 正确；后两小时均没有生产，故C 错误，D 正确．三．填空题 8．(2019·唐山模拟)某人计划购买一辆A 型轿车，售价为14.4万元，购买后轿车每年的保险费、汽油费、车检费、停车费等约需2.4万元，同时汽车年折旧率约为10%(即这辆车每年减少它的价值的10%)，试问，大约使用________年后，用在该车上的费用(含折旧费)达到14.4万元．解析：设使用x 年后花费在该车上的费用达到14.4万元，依题意可得，14.4(1－0.9x )＋2.4x ＝14.4. 化简得x －6×0.9x ＝0. 令f (x )＝x －6×0.9x ，易得f (x )为单调递增函数，又f (3)＝－1.374＜0，f (4)＝0.063 4＞0，所以函数f (x )在(3,4)上有一个零点． 故大约使用4年后，用在该车上的费用达到14.4万元． 答案：49.某地区要建造一条防洪堤，其横断面为等腰梯形ABCD ，腰与底边夹角为60°(如图)，考虑防洪堤坚固性及石块用料等因素，设计其横断面面积为93平方米，且高度不低于3米．记防洪堤横断面的腰长为x 米，外周长(梯形的上底线段BC 与两腰长的和)为y 米．要使防洪堤横断面的外周长不超过10.5米，则其腰长x 的取值范围为________．解析：根据题意知，93＝12(AD ＋BC )h ，其中AD ＝BC ＋2×x 2＝BC ＋x ，h ＝32x ，所以93＝12(2BC ＋x )32x ，得BC ＝18x －x2，由⎩⎨⎧h ＝32x ≥3，BC ＝18x －x2＞0，得2≤x ＜6.所以y ＝BC ＋2x ＝18x ＋3x2(2≤x ＜6)，由y ＝18x ＋3x2≤10.5，解得3≤x ≤4.因为[3,4] ⊆[2,6)，所以腰长x 的取值范围为[3,4]． 答案：[3,4]10．(2019·皖南八校联考)某购物网站在2019年11月开展“全部6折”促销活动，在11日当天购物还可以再享受“每张订单金额(6折后)满300元时可减免100元”．某人在11日当天欲购入原价48元(单价)的商品共42件，为使花钱总数最少，他最少需要下的订单张数为________． 答案 3解析 为使花钱总数最少，需使每张订单满足“每张订单金额(6折后)满300元时可减免100元”，即每张订单打折前原金额不少于500元．由于每件原价48元，因此每张订单至少11件，又42＝11×3＋9，所以最少需要下的订单张数为3.11．某市用37辆汽车往灾区运送一批救灾物资，假设以v km/h 的速度直达灾区，已知某市到灾区公路线长400 km ，为了安全起见，两辆汽车的间距不得小于⎝⎛⎭⎫v 202 km ，那么这批物资全部到达灾区的最少时间是______ h ．(车身长度不计) 答案 12解析 设全部物资到达灾区所需时间为t h ，由题意可知，t 相当于最后一辆车行驶了⎣⎡⎦⎤36×⎝⎛⎭⎫v 202＋400 km 所用的时间，因此，t ＝36×⎝⎛⎭⎫v 202＋400v ＝36v 400＋400v≥236v 400×400v＝12， 当且仅当36v 400＝400v ，即v ＝2003时取等号．故这些汽车以2003 km/h 的速度匀速行驶时，所需时间最少，最少时间为12 h.四．解答题12.某城市现有人口总数为 100 万，如果年自然增长率为 1.2%，试解答下面的问题： (1) 写出 x 年后该城市的人口总数 y （万人）与年数 x （年）的函数关系式； 【答案】y =100×(1+1.2%)x ,x ∈N ∗【解析】1 年后该城市人口总数为 y =100+100×1.2%=100×(1+1.2%)；2 年后该城市人口总数为 y =100×(1+1.2%)+100×(1+1.2%)×1.2%=100×(1+1.2%)2；3 年后该城市人口总数为 y =100×(1+1.2%)3；…； x 年后该城市人口总数为 y =100×(1+1.2%)x ,x ∈N ∗．(2) 计算 10 年以后该城市人口总数（精确到 0.1 万）； 【答案】112.7 万【解析】10 年后该城市人口总数为 y =100×(1+1.2%)10=100×1.01210≈112.7（万）．(3) 计算大约多少年以后该城市人口总数将达到 120 万（精确到 1 年）． 【答案】16 年【解析】令 y =120，则有 100×(1+1.2%)x =120，解方程可得 15<x <16． 故大约 16 年后该城市人口总数将达到 120 万．13.某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压 p （千帕）是气球的体积 V （立方米）的反比例函数，其图象如图所示．（千帕是一种压强单位）(1) 写出这个函数的解析式；【答案】p=96V【解析】设p与V的函数的解析式为p=k，把点A(1.5,64)代入，解得k=96．V∴这个函数的解析式为p=96．V(2) 当气球的体积为0.8立方米时，气球内的气压是多少千帕？【答案】120千帕【解析】把V=0.8代入p=96，p=120，V当气球的体积为0.8立方米时，气球内的气压是120千帕．(3) 当气球内的气压大于144千帕时，气球将爆炸，为了安全起见，气球的体积应不小于多少立方米？立方米【答案】气球的体积应不小于23，【解析】由p=144时，V=23∴p⩽144时，V⩾2，3当气球内的气压大于144千帕时，气球将爆炸，为了安全起见，气球的体积应不小于2立方米314.如图所示，已知边长为8米的正方形钢板有一个角被锈蚀，其中AE=4米，CD=6米．为合理利用这块钢板，在五边形ABCDE内截取一个矩形BNPM，使点P在边DE上．设MP=x米，PN=y米，将y表示成x的函数，求该函数的解析式及定义域．【答案】y=−12x+10，定义域为[4,8]【解析】作PQ⊥AF于Q，∴PQ=(8−y)米，EQ=(x−4)米．又△EPQ∼△EDF，∴EQPQ =EFFD，即x−48−y=42．∴y=−12x+10，定义域为[4,8]．15.大西洋鲑鱼每年都要逆流而上，游回产地产卵，研究鲑鱼的科学家发现鲑鱼的游速可以表示为函数v=1 2log3⁡O100，单位是m/s，其中O表示鱼的耗氧量的单位数，(1) 当一条鱼的行氧量是2700个单位时，它的游速是多少？【答案】当一条鱼的行氧量是2700个单位时，它的游速是32(m/s)【解析】由题意得v=12log3⁡2700100=32(m/s)当一条鱼的行氧量是2700个单位时，它的游速是32(m/s)．(2) 计算一条鱼静止时耗氧量的单位数．【答案】当一条鱼静止时耗氧量的单位数是100【解析】当一条鱼静止时，即v=0，则0=12log3⁡O100，解得O=100当一条鱼静止时耗氧量的单位数是100．。

§2.7指数与指数函数课标要求1.理解有理数指数幂的含义，了解实数指数幂的意义，掌握指数幂的运算性质.2.通过实例，了解指数函数的实际意义，会画指数函数的图象.3.理解指数函数的单调性、特殊点等性质，并能简单应用．知识梳理1．根式(1)一般地，如果x n ＝a ，那么x 叫做a 的n 次方根，其中n >1，且n ∈N *.(2)式子na 叫做根式，这里n 叫做根指数，a 叫做被开方数．(3)(na )n ＝a .当n 为奇数时，na n ＝a ，当n 为偶数时，n a n ＝|a |a ，a ≥0，－a ，a <0.2．分数指数幂正数的正分数指数幂：m na ＝na m (a >0，m ，n ∈N *，n >1)．正数的负分数指数幂：m n a＝1m na＝1na m(a >0，m ，n ∈N *，n >1)．0的正分数指数幂等于0,0的负分数指数幂没有意义．3．指数幂的运算性质a r a s ＝a r ＋s ；(a r )s ＝a rs ；(ab )r ＝a r b r (a >0，b >0，r ，s ∈R )．4．指数函数及其性质(1)概念：一般地，函数y ＝a x (a >0，且a ≠1)叫做指数函数，其中指数x 是自变量，定义域是R .(2)指数函数的图象与性质a >10<a <1图象定义域R 值域(0，＋∞)性质过定点(0,1)，即x ＝0时，y ＝1当x>0时，y >1；当x <0时，0<y <1当x <0时，y >1；当x >0时，0<y <1增函数减函数常用结论1．指数函数图象的关键点(0,1)，(1，a )12.如图所示是指数函数(1)y ＝a x ，(2)y ＝b x ，(3)y ＝c x ，(4)y ＝d x 的图象，则c >d >1>a >b >0，即在第一象限内，指数函数y ＝a x (a >0，且a ≠1)的图象越高，底数越大．自主诊断1．判断下列结论是否正确．(请在括号中打“√”或“×”)(1)4(－4)4＝－4.(×)(2)2a ·2b ＝2ab .(×)(3)指数函数y ＝a x 与y ＝a －x (a >0，且a ≠1)的图象关于y 轴对称．(√)(4)若a m <a n (a >0，且a ≠1)，则m <n .(×)2．已知函数y ＝a ·2x 和y ＝2x ＋b 都是指数函数，则a ＋b 等于()A ．不确定B ．0C ．1D ．2答案C解析由函数y ＝a ·2x 是指数函数，得a ＝1，由y ＝2x ＋b 是指数函数，得b ＝0，所以a ＋b ＝1.3．已知关于x 的不等式－4≥3－2x ，则该不等式的解集为()A ．[－4，＋∞)B ．(－4，＋∞)C ．(－∞，－4)D ．(－4,1]答案A 解析不等式－4≥3－2x ，即34－x ≥3－2x ，由于y ＝3x 是增函数，所以4－x ≥－2x ，解得x ≥－4，所以原不等式的解集为[－4，＋∞)．4．(2023·福州质检)3(－4)3＋120.254＝________.答案5解析3(－4)3＋120.254＝－4＋1＋0.5×16＝5.题型一指数幂的运算例1计算：－2×2310227-⎛⎫ ⎪⎝⎭－2×(2＋π)02；(2)23×331.5×612.解(1)原式＝128116⎛⎫ ⎪⎝⎭－2×236427-⎛⎫⎪⎝⎭－2＝14232⎡⎤⎛⎫⎢⎥ ⎪⎝⎭⎢⎥⎣⎦－2×23334⎡⎤⎛⎫⎢⎥ ⎪⎝⎭⎢⎥⎣⎦－2＋916＝94－2×916－2＋916＝94－98－2＋916＝－516.(2)原式＝11132623233(23)2⎛⎫⨯⨯⨯⨯⨯ ⎪⎝⎭1111133362623-+++=⨯⨯＝6×3＝18.思维升华(1)指数幂的运算首先将根式、分数的分数指数幂统一为整数的分数指数幂，以便利用法则计算，还应注意：①必须同底数幂相乘，指数才能相加．②运算的先后顺序．(2)运算结果不能同时含有根号和分数指数，也不能既有分母又含有负指数．跟踪训练1(多选)下列计算正确的是()A.12(－3)4＝3－3B ．2115113366221()(3)9(0,0)3a a b a b a a b ⎛⎫-÷=->> ⎪⎝⎭C.39＝33D ．已知x 2＋x －2＝2，则x ＋x －1＝2答案BC解析对于A ，12(－3)4＝1234＝143123=3＝33≠3－3，所以A 错误；对于B ，2115211115113366326236221()(3)93a b a b a b a b +-+⎛⎫-÷=-⋅ ⎪⎝⎭＝－9a (a >0，b >0)，所以B 正确；对于C ，391163=9=3＝33，所以C 正确；对于D ，因为(x ＋x －1)2＝x 2＋2＋x －2＝4，所以x ＋x －1＝±2，所以D 错误．题型二指数函数的图象及应用例2(1)(多选)已知实数a ，b 满足等式3a ＝6b ，则下列可能成立的关系式为()A ．a ＝bB ．0<b <aC ．a <b <0D ．0<a <b答案ABC解析由题意，在同一平面直角坐标系内分别画出函数y ＝3x 和y ＝6x 的图象，如图所示，由图象知，当a ＝b ＝0时，3a ＝6b ＝1，故选项A 正确；作出直线y ＝k ，当k >1时，若3a ＝6b ＝k ，则0<b <a ，故选项B 正确；作出直线y ＝m ，当0<m <1时，若3a ＝6b ＝m ，则a <b <0，故选项C 正确；当0<a <b 时，易得2b >1，则3a <3b <2b ·3b ＝6b ，故选项D 错误．(2)若函数f(x)＝|2x－2|－b有两个零点，则实数b的取值范围是________．答案(0,2)解析在同一平面直角坐标系中画出y＝|2x－2|与y＝b的图象，如图所示．∴当0<b<2时，两函数图象有两个交点，从而函数f(x)＝|2x－2|－b有两个零点．∴实数b的取值范围是(0,2)．思维升华对于有关指数型函数的图象问题，一般是从最基本的指数函数的图象入手，通过平移、伸缩、对称变换得到．特别地，当底数a与1的大小关系不确定时应注意分类讨论．跟踪训练2(多选)已知函数f(x)＝a x－b(a>0，且a≠1，b≠0)的图象不经过第三象限，则a，b 的取值范围可能为()A．0<a<1，b<0B．0<a<1,0<b≤1C．a>1，b<0D．a>1,0<b≤1答案ABC解析若0<a<1，则函数y＝a x的图象如图所示，要想f(x)＝a x－b的图象不经过第三象限，则需要向上平移，或向下平移不超过1个单位长度，故－b>0或－1≤－b<0，解得b<0或0<b≤1，故A，B正确；若a>1，则函数y＝a x的图象如图所示，要想f(x)＝a x－b的图象不经过第三象限，则需要向上平移，故－b>0，解得b<0，即C正确，D错误．题型三指数函数的性质及应用命题点1比较指数式的大小例3(2024·海口模拟)已知a＝1.30.6，b0.4，c，则()A．c<b<a B．a<b<cC ．c <a <bD ．b <c <a 答案D解析a ＝1.30.6>1.30＝1，b 0.4，c ，因为指数函数y 是减函数，所以＝1，所以b <c <1，所以b <c <a .命题点2解简单的指数方程或不等式例4已知p ：a x <1(a >1)，q ：2x ＋1－x <2，则p 是q 的()A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件答案B解析∵a x <1，当a >1时，y ＝a x 是增函数，∴p ：{x |x <0}．对于不等式2x ＋1<x ＋2，作出函数y ＝2x ＋1与y ＝x ＋2的图象，如图所示．由图象可知，不等式2x ＋1<x ＋2的解集为{x |－1<x <0}，∴q ：{x |－1<x <0}．又∵{x |－1<x <0}⊆{x |x <0}，∴p 是q 的必要不充分条件．命题点3指数函数性质的综合应用例5已知函数f (x )＝8x ＋a ·2xa ·4x (a 为常数，且a ≠0，a ∈R )是奇函数．(1)求a 的值；(2)若∀x ∈[1,2]，都有f (2x )－mf (x )≥0成立，求实数m 的取值范围．解(1)f (x )＝1a ·2x ＋12x ，因为f (x )是奇函数，所以f (－x )＝－f (x )，即1a ·12x ＋2x xx 0，即1a ＋1＝0，解得a ＝－1.(2)由(1)知a ＝－1，所以f (x )＝12x －2x ，x ∈[1,2]，所以122x －22x ≥所以m ≥12x ＋2x ，x ∈[1,2]，令t ＝2x ，t ∈[2,4]，设y ＝12x ＋2x ，则y ＝t ＋1t ，t ∈[2,4]，由于y ＝t ＋1t 在[2,4]上单调递增，所以m ≥4＋14＝174.所以实数m 的取值范围是174，＋思维升华(1)利用指数函数的性质比较大小或解方程、不等式，最重要的是“同底”原则，比较大小还可以借助中间量．(2)求解与指数函数有关的复合函数问题，要明确复合函数的构成，涉及值域、单调区间、最值等问题时，要借助“同增异减”这一性质分析判断．跟踪训练3(1)(多选)(2023·重庆模拟)已知函数f (x )＝e x －1e x ＋1，则下列结论正确的是()A ．函数f (x )的定义域为RB ．函数f (x )的值域为(－1,1)C ．函数f (x )是奇函数D ．函数f (x )为减函数答案ABC解析因为e x >0，所以e x ＋1>0，所以函数f (x )的定义域为R ，故A 正确；f (x )＝e x －1e x ＋1＝1－2e x ＋1，由e x >0⇒e x ＋1>1⇒0<1e x ＋1<1⇒－2<－2e x ＋1<0⇒－1<1－2e x ＋1<1，所以函数f (x )的值域为(－1,1)，故B 正确；因为f (－x )＝e －x－1e －x ＋1＝1e x －11e x ＋1＝1－e x1＋ex ＝－f (x )，所以函数f (x )是奇函数，故C 正确；因为函数y ＝e x ＋1是增函数，所以y ＝e x ＋1>1，所以函数y ＝2e x ＋1是减函数，所以函数y ＝－2e x ＋1是增函数，故f (x )＝e x －1e x ＋1＝1－2e x ＋1是增函数，故D 不正确．(2)(2023·银川模拟)函数f (x )＝a x (a >0，且a ≠1)在区间[1,2]上的最大值比最小值大a2，则a 的值为________．答案32或12解析当a >1时，函数f (x )在区间[1,2]上单调递增，由题意可得，f (2)－f (1)＝a 2－a ＝a2，解得a ＝32或a ＝0(舍去)；当0<a <1时，函数f (x )在区间[1,2]上单调递减，由题意可得，f (1)－f (2)＝a －a 2＝a2，解得a ＝12或a ＝0(舍去)，综上所述，a ＝32或a ＝12.课时精练一、单项选择题1．下列结论中，正确的是()A ．若a >0，则4334·a a ＝a B ．若m 8＝2，则m ＝±82C ．若a ＋a －1＝3，则1122a a-+＝±5D.4(2－π)4＝2－π答案B解析对于A ，根据分数指数幂的运算法则，可得443325334412a a aa +⋅==，当a ＝1时，2512a ＝a ；当a ≠1时，2512a≠a ，故A 错误；对于B ，m 8＝2，故m ＝±82，故B 正确；对于C ，a ＋a －1＝3，则21122a a -⎛⎫+ ⎪⎝⎭＝a ＋a －1＋2＝3＋2＝5，因为a >0，所以1122a a -+＝5，故C 错误；对于D ，4(2－π)4＝|2－π|＝π－2，故D 错误．2．已知函数f (x )＝a x －a (a >1)，则函数f (x )的图象不经过()A ．第一象限B ．第二象限C ．第三象限D ．第四象限答案B解析y ＝a x (a >1)是增函数，经过点(0,1)，因为a >1，所以函数f (x )的图象需由函数y ＝a x (a >1)的图象向下平移超过1个单位长度得到，所以函数f (x )＝a x －a 的图象如图所示．故函数f (x )的图象不经过第二象限．3．已知a ＝31.2，b ＝1.20，c 0.9，则a ，b ，c 的大小关系是()A ．a <c <bB ．c <b <aC ．c <a <bD ．b <c <a答案D解析因为b ＝1.20＝1，c 0.9＝30.9，且y ＝3x 为增函数，1.2>0.9>0，所以31.2>30.9>30＝1，即a >c >b .4．(2023·新高考全国Ⅰ)设函数f (x )＝2x (x －a )在区间(0,1)上单调递减，则a 的取值范围是()A ．(－∞，－2]B ．[－2,0)C ．(0,2]D ．[2，＋∞)答案D解析函数y ＝2x 在R 上是增函数，而函数f (x )＝2x (x－a )在区间(0,1)上单调递减，则函数y ＝x (x －a )－a 24在区间(0,1)上单调递减，因此a2≥1，解得a ≥2，所以a 的取值范围是[2，＋∞)．5．(2023·潍坊模拟)“关于x 的方程a (2|x |＋1)＝2|x |没有实数解”的一个必要不充分条件是()A ．a ≤12B ．a >1C ．a ≤12或a ≥1D ．a <12或a ≥1答案C解析a (2|x |＋1)＝2|x |，因为2|x |＋1>0，所以a ＝2|x |2|x |＋1＝1－12|x |＋1，因为2|x |≥20＝1，所以2|x |＋1≥2,0<12|x |＋1≤12，12≤1－12|x |＋1<1，要使a (2|x |＋1)＝2|x |没有实数解，则a <12或a ≥1，由于a <12或a ≥1不能推出a ≤12，故A 不成立；由于a <12或a ≥1不能推出a >1，故B 不成立；由于a <12或a ≥1⇒a ≤12或a ≥1，且a ≤12或a ≥1不能推出a <12或a ≥1，故C 正确；D 为充要条件，不符合要求．6．(2024·辽源模拟)已知函数f (x )＝2x －2－x ＋1，若f (a 2)＋f (a －2)>2，则实数a 的取值范围是()A ．(－∞，1)B ．(－2,1)C ．(－∞，－2)∪(1，＋∞)D ．(－1,2)答案C解析令g (x )＝2x －2－x ，定义域为R ，且g (－x )＝－g (x )，所以函数g (x )是奇函数，且是增函数，因为f (x )＝g (x )＋1，f (a 2)＋f (a －2)>2，则g (a 2)＋g (a －2)>0，即g (a 2)>－g (a －2)，又因为g (x )是奇函数，所以g (a 2)>g (2－a )，又因为g (x )是增函数，所以a 2>2－a ，解得a <－2或a >1，故实数a 的取值范围是(－∞，－2)∪(1，＋∞)．二、多项选择题7．已知函数f (x )＝|2x －1|，实数a ，b 满足f (a )＝f (b )(a <b )，则()A ．2a ＋2b >2B ．∃a ，b ∈R ，使得0<a ＋b <1C ．2a ＋2b ＝2D ．a ＋b <0答案CD解析画出函数f (x )＝|2x －1|的图象，如图所示．由图知1－2a ＝2b －1，则2a ＋2b ＝2，故A 错误，C 正确；由基本不等式可得2＝2a ＋2b >22a ·2b ＝22a ＋b ，所以2a ＋b <1，则a ＋b <0，故B 错误，D 正确．8．已知函数f (x )＝m －e x 1＋e x是定义域为R 的奇函数，则下列说法正确的是()A ．m ＝12B ．函数f (x )在R 上的最大值为12C ．函数f (x )是减函数D ．存在实数n ，使得关于x 的方程f (x )－n ＝0有两个不相等的实数根答案AC 解析因为函数f (x )＝m －e x 1＋e x 是定义域为R 的奇函数，所以f (0)＝m －e 01＋e 0＝0，解得m ＝12，此时f (x )＝12－e x 1＋e x，则f (－x )＝12－e －x 1＋e －x ＝12－11＋e x＝12－1＋e x －e x 1＋e x＝12－1＋e x 1＋e x ＝e x 1＋e x －12＝－f (x )，符合题意，故A 正确；又f (x )＝12－e x 1＋e x ＝12－e x ＋1－11＋ex ＝11＋e x －12，因为e x >0，所以e x ＋1>1，则0<11＋ex <1，所以－12<f (x )<12，即f (x )－12，B 错误；因为y ＝e x 是增函数，y ＝e x >0，且y ＝1x在(0，＋∞)上单调递减，所以f (x )＝11＋e x －12是减函数，故C 正确；因为f (x )是减函数，所以y ＝f (x )与y ＝n 最多有1个交点，故f (x )－n ＝0最多有一个实数根，即不存在实数n ，使得关于x 的方程f (x )－n ＝0有两个不相等的实数根，故D 错误．三、填空题9．013623290.125[(2)]8-⎛⎫-+-+ ⎪⎝⎭＝________.答案81解析原式＝13131326322112(23)2⎛⎫⨯- ⎪⨯⎝⎭⎛⎫-++⨯ ⎪⎝⎭＝2－1＋8＋(23×32)＝81.10．(2023·福州模拟)写出一个同时具备下列性质的函数f (x )＝________.①f (x ＋1)＝f (x )f (1)；②f ′(x )<0.答案e －x (答案不唯一)解析∵f (x ＋1)＝f (x )f (1)是加变乘，∴考虑指数函数类型，又f ′(x )<0，∴f (x )是减函数，∴f (x )＝e －x 满足要求．11．已知函数f (x )＝24313ax x -+⎛⎫ ⎪⎝⎭有最大值3，则a 的值为________．答案1解析令g (x )＝ax 2－4x ＋3，则f (x )(x )，∵f (x )有最大值3，∴g (x )有最小值－1，1，解得a ＝1.12．(2024·宁波模拟)对于函数f (x )，若在定义域内存在实数x 0满足f (－x 0)＝－f (x 0)，则称函数f (x )为“倒戈函数”．设f (x )＝3x ＋m －1(m ∈R ，m ≠0)是定义在[－1,1]上的“倒戈函数”，则实数m 的取值范围是________．答案－23，解析∵f (x )＝3x ＋m －1是定义在[－1,1]上的“倒戈函数”，∴存在x 0∈[－1,1]满足f (－x 0)＝－f (x 0)，∴03x -＋m －1＝03x -－m ＋1，∴2m ＝0033x x ---＋2，构造函数y ＝0033x x ---＋2，x 0∈[－1,1]，令t ＝03x ，t ∈13，3，则y ＝－1t－t ＋2＝2在13，1上单调递增，在(1,3]上单调递减，∴当t ＝1时，函数取得最大值0，当t ＝13或t ＝3时，函数取得最小值－43，∴y ∈－43，0，又∵m ≠0，∴－43≤2m <0，∴－23≤m <0.四、解答题13．如果函数y ＝a 2x ＋2a x －1(a >0，且a ≠1)在区间[－1,1]上的最大值是14，求a 的值．解令a x ＝t ，则y ＝a 2x ＋2a x －1＝t 2＋2t －1＝(t ＋1)2－2.当a >1时，因为x ∈[－1,1]，所以t ∈1a ，a ，又函数y ＝(t ＋1)2－2在1a ，a 上单调递增，所以y max ＝(a ＋1)2－2＝14，解得a ＝3或a ＝－5(舍去)；当0<a <1时，因为x ∈[－1,1]，所以t ∈a ，1a ，又函数y ＝(t ＋1)2－2在a ，1a 上单调递增，则y max －2＝14，解得a ＝13或a ＝－15(舍去)．综上，a ＝3或a ＝13.14．已知定义域为R 的函数f (x )＝a －2x b ＋2x是奇函数．(1)求a ，b 的值；(2)判断f (x )的单调性；(3)若存在t ∈[0,4]，使f (k ＋t 2)＋f (4t －2t 2)<0成立，求实数k 的取值范围．解(1)因为函数f (x )是定义在R 上的奇函数，所以f (0)＝0，即a －1b ＋1＝0，所以a ＝1，又因为f (－x )＝－f (x )，所以a －12x b ＋12x ＝－a －2x b ＋2x ，将a ＝1代入，整理得2x －1b ·2x ＋1＝2x －1b ＋2x，当x ≠0时，有b ·2x ＋1＝b ＋2x ，即(b －1)(2x －1)＝0，又因为当x ≠0时，有2x －1≠0，所以b －1＝0，所以b ＝1.经检验符合题意，所以a ＝1，b ＝1.(2)由(1)知，函数f (x )＝1－2x 1＋2x ＝－(1＋2x )＋21＋2x ＝－1＋21＋2x ，因为y ＝1＋2x 为增函数，且1＋2x >0，则函数f (x )是减函数．(3)因为存在t ∈[0,4]，使f (k ＋t 2)＋f (4t －2t 2)<0成立，且函数f (x )是定义在R 上的奇函数，所以不等式可转化为f (k ＋t 2)<f (2t 2－4t )，又因为函数f (x )是减函数，所以k ＋t 2>2t 2－4t ，所以k >t 2－4t ，令g (t )＝t 2－4t ＝(t －2)2－4，由题意可知，问题等价转化为k >g (t )min ，又因为g (t )min ＝g (2)＝－4，所以k >－4，即实数k 的取值范围为(－4，＋∞)．15．(2023·深圳模拟)已知αa ＝(cos α)sin α，b ＝(sin α)cos α，c ＝(cos α)cos α，则()A ．b >c >aB ．c >b >aC ．c >a >bD ．a >b >c 答案A 解析已知α0<cos α<sin α<1，因为y ＝(cos α)x 在(0,1)上单调递减，故c ＝(cos α)cos α>(cos α)sin α＝a ；因为幂函数y ＝x cos α在(0,1)上单调递增，故c ＝(cos α)cos α<(sin α)cos α＝b ，故b >c >a .16．(2023·徐州模拟)正实数m ，n 满足e 1－2m ＋2－2m ＝e n －1＋n ，则n m ＋1n的最小值为________．答案5 2解析由e1－2m＋2－2m＝e n－1＋n，得e1－2m＋(1－2m)＝e n－1＋(n－1)，令f(x)＝e x＋x，则原等式为f(1－2m)＝f(n－1)，显然函数f(x)为增函数，于是1－2m＝n－1，即2m＋n＝2，而m>0，n>0，因此nm＋1n＝nm＋2m＋n2n＝nm＋mn＋12≥2nm·mn＋12＝52，当且仅当nm＝mn，即m＝n＝23时取等号，所以当m＝n＝23时，nm＋1n取得最小值52.。