初中数学辅导2013中考总结复习冲刺专题：多种函数交叉综合问题

中考函数的交点问题汇总
函数的交点是指两个或多个函数在坐标系内的交点。

具体来说，是指当两个或多个函数的图像在坐标系内相交时，它们的交点所对应的横坐标和纵坐标的值。

2. 如何求解函数的交点？
求解函数的交点需要通过解方程来求出交点的坐标。

具体方法有以下几种：
①将两个函数相减，得到一个方程，然后解方程求出交点坐标。

②将两个函数分别表示为y=f(x)和y=g(x)，然后将两个方程联立，解方程组求出交点坐标。

③可以利用图像来估算交点的大致坐标，然后通过代入方程的
方法来求出精确的坐标。

3. 函数的交点有哪些应用？
函数的交点在实际生活中有很多应用，主要涉及到以下几个方面：
①在数学中，函数的交点是研究函数性质的重要基础之一，如
求函数的极值、拐点等。

②在物理学中，函数的交点可以用来求解物体的速度、加速度
等物理量。

③在经济学中，函数的交点可以用来研究市场供需关系、成本
收益等经济问题。

④在工程学中，函数的交点可以用来研究材料力学、机械运动
等问题。

总之，函数的交点具有广泛的应用价值，是数学研究和实际应用中的重要问题之一。

中考数学难点：多种函数“混合”综合型问题
一次函数、反比例函数以及二次函数是初中数学需要掌握的函数知识内容，也是中考必考的热门知识板块。

纵观近几年全国各地中考试题，我们发现二次函数基本上与一次函数结合的综合问题较多；二次函数与反比例函数基本不会涉及；一次函数与反比例函数的综合问题时一个“冷门”中考考点。

经典例题1：
解题反思：
此题考查了反比例函数与一次函数的交点，涉及的知识有：一次函数与坐标系的交点，待定系数法确定反比例函数解析式，坐标与图形性质以及反比例函数的性质，熟练掌握函数的性质是解本题的关键．
经典例题2：
解题反思：
本题考查了二次函数的性质，反比例函数图象上点的坐标特征，熟练掌握反比例函数图象上点的坐标特征是解题的关键．
经典例题3：
解题反思：
本题主要考查了运用待定系数法求反比例函数及一次函数的解析式、求反比例函数及一次函数图象的交点、三角形的中线平分三角形的面积、相似三角形的判定与性质、三角形外角的性质、直角三角形两锐角互余等知识，在解决问题的过程中，用到了分类讨论、数形结合、割补法等重要的数学思想方法，应熟练掌握．
经典例题4：
解题反思：
此题考查了待定系数法求二次函数、一次函数的解析式，二次函数的性质以及三角形面积、线段长度问题．此题难度适中，解题的关键是运用方程思想与数形结合思想．
经典例题5：
解题反思：
（1）此题主要考查了二次函数综合题，考查了分析推理能力，考查了分类讨论思想的应用，考查了数形结合思想的应用，考查了从已知函数图象中获取信息，并能利用获取的信息解答相应的问题的能力．
（2）此题还考查了函数解析式的求法，以及二次函数的最值的求法，要熟练掌握．（3）此题还考查了三角形的面积的求法，要熟练掌握．。

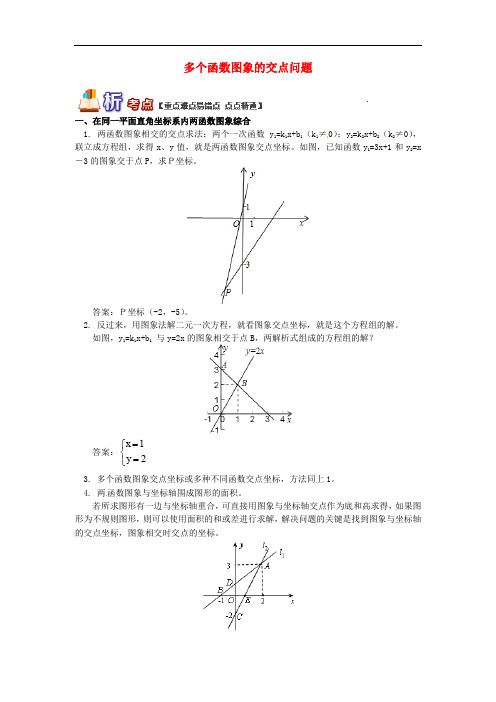
多个函数图象的交点问题一、在同一平面直角坐标系内两函数图象综合1. 两函数图象相交的交点求法：两个一次函数 y1=k1x+b1（k1≠0）；y2=k2x+b2（k2≠0），联立成方程组，求得x、y值，就是两函数图象交点坐标。

如图，已知函数y1=3x+1和y2=x －3的图象交于点P，求Ｐ坐标。

答案：Ｐ坐标（-2，-5）。

2. 反过来，用图象法解二元一次方程，就看图象交点坐标，就是这个方程组的解。

如图，y1=k1x+b1与y=2x的图象相交于点B，两解析式组成的方程组的解？答案：12 xy=⎧⎨=⎩3. 多个函数图象交点坐标或多种不同函数交点坐标，方法同上1。

4. 两函数图象与坐标轴围成图形的面积。

若所求图形有一边与坐标轴重合，可直接用图象与坐标轴交点作为底和高求得，如果图形为不规则图形，则可以使用面积的和或差进行求解，解决问题的关键是找到图象与坐标轴的交点坐标，图象相交时交点的坐标。

答案：两函数图象与坐标轴围成图形的面积为11 5。

5. 讨论两函数值比较大小问题时，可利用两函数交点坐标求得：如：①如果y1>y2，则x>1；②如果y1＝y2，则x=1；③如果y1<y2，则x<1。

二、利用全等三角形和解方程的方法求坐标1. 利用全等三角形求得坐标系内某点的坐标，进而求得过相关点的函数解析式；2. 使用解方程的思想解决计算类问题。

总结：1. 求方程组的解是解交点坐标的关键。

2. 在比较大小时注意哪个图象位置在上方，哪个函数值相应的就大。

例题1 直线y=－2x+m与直线y=2x－1的交点在第四象限，则m的取值范围是（）A. m＞－1B. m＜1C. －1＜m＜1D. －1≤m≤1解析：联立两直线解析式求出交点坐标，再根据交点在第四象限列出不等式组求解即可。

答案：解：联立221y x my x-+⎧⎨-⎩＝＝，解得1412mxmy+⎧=⎪⎪⎨-⎪=⎪⎩，∵交点在第四象限，∴1412mm+⎧>⎪⎪⎨-⎪<⎪⎩①②，解不等式①得，m＞－1，解不等式②得，m＜1，所以，m的取值范围是－1＜m＜1。

中考数学--------四大考试题型解题方法指导针对中考数学，分别从选择题解题技巧、填空题解法指导、压轴题突破方法、填空题解题方法等四个方面进行详细讲解。

一、中考数学选择题的解法技巧1、排除法。

是根据题设和有关知识，排除明显不正确选项，那么剩下唯一的选项，自然就是正确的选项，如果不能立即得到正确的选项，至少可以缩小选择范围，提高解题的准确率。

排除法是解选择题的间接方法，也是选择题的常用方法。

2、特殊值法。

即根据题目中的条件，选取某个符合条件的特殊值或作出特殊图形进行计算、推理的方法。

用特殊值法解题要注意所选取的值要符合条件，且易于计算。

此类问题通常具有一个共性：题干中给出一些一般性的条件，而要求得出某些特定的结论或数值。

在解决时可将问题提供的条件特殊化。

使之成为具有一般性的特殊图形或问题，而这些特殊图形或问题的答案往往就是原题的答案。

利用特殊值法解答问题，不仅可以选用特别的数值代入原题，使原题得以解决而且可以作出符合条件的特殊图形来进行计算或推理。

3、通过猜想、测量的方法，直接观察或得出结果。

这类方法在近年来的中考题中常被运用于探索规律性的问题，此类题的主要解法是运用不完全归纳法，通过试验、猜想、试误验证、总结、归纳等过程使问题得解。

二、中考数学填空题解法指导中考数学填空题与选择题同属客观性试题的填空题，具有客观性试题的所有特点，即题目短小精干，考查目标集中明确，答案唯一正确，答卷方式简便，评分客观公正等。

但是它又有本身的特点，即没有备选答案可供选择，这就避免了选择项所起的暗示或干扰的作用，及考生存在的瞎估乱猜的侥幸心理，从这个角度看，它能够比较真实地考查出学生的真正水平。

考查内容多是“双基”方面，知识复盖面广。

但在考查同样内容时，难度一般比选择题略大。

中考填空题主要题型：一是定量型填空题，二是定性型填空题，前者主要考查计算能力的计算题，同时也考查考生对题目中所涉及到数学公式的掌握的熟练程度，后者考查考生对重要的数学概念、定理和性质等数学基础知识的理解和熟练程度。

中考数学复习：多种函数交叉综合问题考试卷型中考是九年义务教育的终端显示与成果展现，中考是一次选拔性考试，其竞争较为猛烈。

为了更有效地关心学生梳理学过的知识，提高复习质量和效率，在中考中取得理想的成绩，下文为大伙儿预备了中考数学复习的内容。

初中数学所涉及的函数无非也就一次函数，反比例函数以及二次函数。

二次函数差不多上只会考和一次函数的综合问题，二次函数与反比例函数差不多可不能涉及。

因此如何把握好一次函数与反比例函数的综合问题就成为了又一重点。

这类题目本身并可不能太难，专门少作为压轴题显现，一样差不多上作为一道中档次题目来考察考生关于一次函数以及反比例函数的把握。

因此在中考中面对这类问题，一定要做到幸免失分。

一次函数、反比例函数以及二次函数是初中数学需要把握的函数知识内容，也是中考必考的热门知识板块。

纵观近几年全国各地中考试题，我们发觉二次函数差不多上与一次函数结合的综合问题较多;二次函数与反比例函数差不多可不能涉及;一样说来，“教师”概念之形成经历了十分漫长的历史。

杨士勋（唐初学者，四门博士）《春秋谷梁传疏》曰：“师者教人以不及，故谓师为师资也”。

这儿的“师资”，事实上确实是先秦而后历代对教师的别称之一。

《韩非子》也有云：“今有不才之子……师长教之弗为变”其“师长”因此也指教师。

这儿的“师资”和“师长”可称为“教师”概念的雏形，但仍说不上是名副事实上的“教师”，因为“教师”必须要有明确的传授知识的对象和本身明确的职责。

一次函数与反比例函数的综合问题时一个“冷门”中考考点。

三种函数交叉类型题目一样并可不能太难，一样差不多上作为一道中档次题目来考察考生关于函数图像与性质的把握情形，或结合几何图形等压轴题显现。

因此，在中考中面对这类问题，只要完全把握好函数差不多知识内容及图像与性质，便可轻松应对，幸免失分。

单靠“死”记还不行,还得“活”用,姑且称之为“先死后活”吧。

让学生把一周看到或听到的新奇事记下来,摒弃那些假话套话空话,写出自己的真情实感,篇幅可长可短,并要求运用积存的成语、名言警句等,定期检查点评,选择优秀篇目在班里朗读或展出。

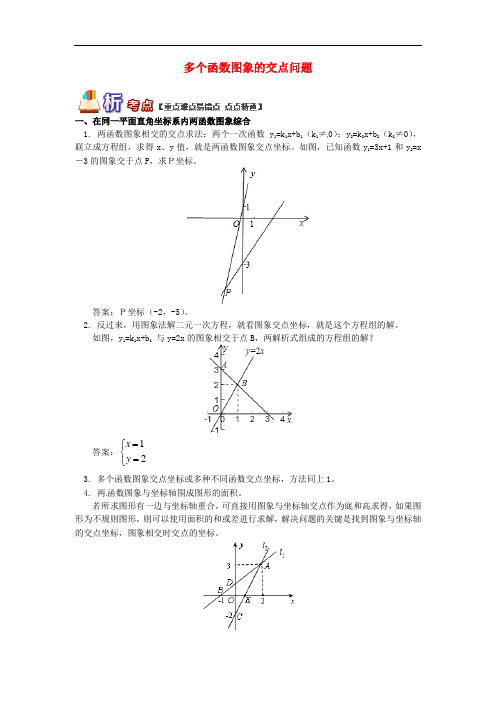
多个函数图象的交点问题一、在同一平面直角坐标系内两函数图象综合1. 两函数图象相交的交点求法：两个一次函数 y1=k1x+b1（k1≠0）；y2=k2x+b2（k2≠0），联立成方程组，求得x、y值，就是两函数图象交点坐标。

如图，已知函数y1=3x+1和y2=x －3的图象交于点P，求Ｐ坐标。

答案：Ｐ坐标（-2，-5）。

2. 反过来，用图象法解二元一次方程，就看图象交点坐标，就是这个方程组的解。

如图，y1=k1x+b1与y=2x的图象相交于点B，两解析式组成的方程组的解？答案：12 xy=⎧⎨=⎩3. 多个函数图象交点坐标或多种不同函数交点坐标，方法同上1。

4. 两函数图象与坐标轴围成图形的面积。

若所求图形有一边与坐标轴重合，可直接用图象与坐标轴交点作为底和高求得，如果图形为不规则图形，则可以使用面积的和或差进行求解，解决问题的关键是找到图象与坐标轴的交点坐标，图象相交时交点的坐标。

答案：两函数图象与坐标轴围成图形的面积为11 5。

5. 讨论两函数值比较大小问题时，可利用两函数交点坐标求得：如：①如果y1>y2，则x>1；②如果y1＝y2，则x=1；③如果y1<y2，则x<1。

二、利用全等三角形和解方程的方法求坐标1. 利用全等三角形求得坐标系内某点的坐标，进而求得过相关点的函数解析式；2. 使用解方程的思想解决计算类问题。

总结：1. 求方程组的解是解交点坐标的关键。

2. 在比较大小时注意哪个图象位置在上方，哪个函数值相应的就大。

例题1 直线y=－2x+m与直线y=2x－1的交点在第四象限，则m的取值范围是（）A. m＞－1B. m＜1C. －1＜m＜1D. －1≤m≤1解析：联立两直线解析式求出交点坐标，再根据交点在第四象限列出不等式组求解即可。

答案：解：联立221y x my x-+⎧⎨-⎩＝＝，解得1412mxmy+⎧=⎪⎪⎨-⎪=⎪⎩，∵交点在第四象限，∴1412mm+⎧>⎪⎪⎨-⎪<⎪⎩①②，解不等式①得，m＞－1，解不等式②得，m＜1，所以，m的取值范围是－1＜m＜1。

例说融合三类函数的综合问题 【专题综述】将一次函数、二次函数、反比例函数融合在同一问题中，构成综合型试题，是近几年中考中的热点考题.本文从近几年的中考题中撷取数例略加解析，供参考. 【方法解读】 一、寻找函数例1 下列函数中，当0x >时，y 随x 的增大而减小的是() (A)2y x = (B)113y x =- (C)2y x=-(D)22y x =- 分析 根据正比例函数，一次函数，反比例函数以及二次函数的增减性对各选项分析 判断后，利用排除法求解.解(A)20k =>，y 随x 增大而增大，故此选项错误; (B)103k =>，y 随x 增大而增大，故此选项错误; (C)20k =-<，图象位于二、四象限，在每一个分支，y 随x 增大而增大，故此选项错误;(D)20a =-<，抛物线的开口向下，对称轴为直线0x =，在对称轴的左侧(即0x <)，y 随x 增大而增大，在对称轴的右侧(即0x >)，y 随x 增大而减小，故此选项正确. 故选D.点评本题主要考查了函数的增减性.需要特别注意，反比例函数需要分象限讨论增减性;二次函数要考虑对称轴，对称轴的左右两边的增减性不同. 二、选择图象例2 二次函数2y ax bx c =++的图象在平面直角坐标系中的位置如图1所示，则一次函数y ax b =+与反比例函数cy x=在同一平面直角坐标系中的图象可能是()分析 根据二次函数图象开口方向，确定出a 的取值，利用“左同右异”或对称轴确定出b ，再根据抛物线图象与y 轴的交点确定出c 的取值，然后确定出一次函数图象与反比例函数图象的情况，即可得解. 解由二次函数图象开口向下，知0a <.又因为抛物线的对称轴在y 轴的右侧，故可得0b >. 再由抛物线图象与y 轴的正半轴相交，得0c >.所以，一次函数y ax b =+的图象经过第一、二、四象限，与y 轴的正半轴相交;反比例函数cy x=的图象位于第一三象限:于是，只有C 选项图象符合，故选C.点评 本题主要考查的是二次函数、一次函数、反比例函数的性质，掌握相关性质是解的关键. 三、判断正误例3 一次函数y ax b =+(0)a ≠、二次函数2y ax bx =+和反比例函数ky x=在同一 直角坐标系中的图象如图2所示，A 点的坐标为(2,0)-，则下列结论中，正确的是() (A)2b a k =+ (B)a b k =+ (C)0a b >>(D)0a k >>分析 由一次函数图象所在的象限可以确定a 、b 的符号，且直线与抛物线均经过点A ,所以把点A 的坐标代入一次函数或二次函数可以求得2b a =,k 的符号可以根据双曲线所在的象限进行判定.求出二次函数2y ax bx =+的顶点坐标为(1,)a --，将1x =-代入反比例函数ky x=中，求出其函数值，此时利用反比例函数与二次函数的图象位置即可确定出a 与k 大小.解 将(2,0)A -代入一次函数y ax b =+中得，20,2a b b a -+=∴=.因为一次函数y ax b =+图象过一、二、三象限，所以0a >,0b >.由图2知，双曲线位于第一、三象限，0,22k a k a ∴>∴+>，即2b a k <+，故A 选项错误.0,0,k b b k b >>∴+>,又2,2,b a b k a a b k =∴+>∴=+不成立，故B 选项错误. 0,0,2,0a b b a b a >>=∴>>，故C 选项错误.抛物线2y ax bx =+的对称轴为直线2122b ax a a=-=-=-. 当1x =-时，设此时二次函数的值为1y ，则2214444ac b a y a a a -==-=-.设反比例函数的值为2y ，则2y k =-.由图象可知，当1x =-时反比例函数的图象在二次函数图象的上方，且都在x 轴的下方，所以120y y <<，即0,0a k a k -<-<∴>>，故本选项正确. 所以正确选项为D.点评 本题综合考查了一次函数、二次函数以及反比例函数的图象与性质.解题的关键是会读图，从图中提取有用的信息. 四、求函数式例4 如图3，已知正比例函数和反比例函数的图象都经过点(3,3)A . (1)求正比例函数和反比例函数的解析式.(2)把直线OA 向下平移后与反比例函数的图象交于点(6,)B m ，求m 的值和这个一次函数的解析式.(3)第(2)问中的一次函数的图象与x 轴、y 轴分别交于点C 、D ，求过A 、B 、D 三点的二次函数的解析式.(4)在第(3)问的条件下，二次函数的图象上是否存在点E ，使四边形OECD 的面积1S 与四边形OABD 的面积S 满足123S S =?若存在，求点E 的坐标;若不存在，请说明理由. 分析 (1)用待定系数法解答.(2)将(6,)B m 代入反比例函数中，即可求得m 的值;再用待定系数法即可求出解解析式.(3) A 、B 坐标已求出，D 点坐标可根据一次函数解析式求得，借助二次函数的一般解析式用待定系数法即可求解.(4)画出图形，求出相应线段长.将不规则四边形面积转化为矩形面积与三角形面积的差或和即可解决.解 (1)易求出函数的解析式分别为9,y x y x==. (2)因为点(6,)B m 在9y x =的图象上，所以369,2m m ==,则点3(6,)2B . 设一次函数解析式为1(0)y kx b k =+≠.因为1y kx b =+的图象是由y x =平移得到的，所以1k =，即1y x b =+又因为1y x b =+的图象过点3(6,)2B ，所以1362b =+，解得192b =-，所以一次函数解析式为92y x =-. (3)因为一次函数92y x =-的图象交y 轴于点D ，所以D 的坐标为9(0,)2-.设二次函数的解析式为2y ax bx c =++(0)a ≠ 将点(3,3)A ，3(6,)2B ，9(0,)2D -代入得9333366292a b c a b c c ⎧⎪++=⎪⎪++=⎨⎪⎪=-⎪⎩，解得12492a b c ⎧=-⎪⎪=⎨⎪⎪=-⎩这个二次函数的解析式为219422y x x =-+- (4)因为直线92y x =-交x 轴于点C ，所以点C 的坐标是9(,0)2.如图4所示，过点A 作//AF x 轴，交y 轴于点F ，过点B 作//BH y 轴，交AF 于点H .则AOF ABH BHFD S S S S ∆∆=--梯形1315113=()6333222222⨯+⨯-⨯⨯-⨯⨯ 814= 假设存在点(,)E m n ，使122732S S ==.因为四边形CDOE 的顶点E 只能在x 轴上方，故0n >，连结OE ，CE ，则OCD OCE S S S ∆∆=+11991922222n =⨯⨯+⨯⨯ 81984n =+ ∴81927842n +=，解得32n = 因为(,)E m n 在二次函数的图象上， 则21934222m m -+-=，解得12m =，26m =.当6m =时，点3(6,)2E 与点B 重合，这时CDOE 不是四边形，故6m =舍去. 所以，存在这样的点E ，它的坐标为3(2,)2.点评 此题将初中阶段三个主要函数结合起来，考查了用待定系数法求函数解析式、函数与坐标的关系以及不规则图形面积的求法等知识点，综合性较强。

《中考压轴题》专题13：函数之一次函数、反比例函数和二次函数问题一、选择题1.函数y=ax 2+1与a y x =（a≠0）在同一平面直角坐标系中的图象可能是【】A ．B ．C ．D ．2.二次函数2y ax b =+（b ＞0）与反比例函数a y x=在同一坐标系中的图象可能是【】A. B. C. D.3.函数a y x=与y=ax 2（a≠0）在同一平面直角坐标系中的图象可能是【】A. B. C. D.4.已知反比例函数k y x =的图像如图所示，则二次函数22y 2kx 4x k =-+的图像大致为【】A. B. C. D.5.已知反比例函数k y x =的图像如图所示，则二次函数22y 2kx 4x k =-+的图像大致为【】A. B. C. D.6.在平面直角坐标系中，函数y=x 2﹣2x （x≥0）的图象为C 1，C 1关于原点对称的图象为C 2，则直线y=a （a 为常数）与C 1、C 2的交点共有【】A.1个B.1个或2个C.个或2个或3个D.1个或2个或3个或4个7.函数k y x=与y=﹣kx 2+k （k≠0）在同一直角坐标系中的图象可能是【】A. B. C.D.8.已知a ≠0，在同一直角坐标系中，函数y ax =与2y ax =的图象有可能是【】A. B. C. D.9.一次函数()y ax b a 0=+≠、二次函数2y ax bx =+和反比例函数()k y k 0x=≠在同一直角坐标系中图象如图，A 点为（－2，0）。

则下列结论中，正确的是【】A ．b 2a k =+B ．a b k =+C ．a b 0>>D ．a k 0>>10.若正比例函数y=mx （m ≠0），y 随x 的增大而减小，则它和二次函数y=mx 2+m 的图象大致是【】11.如图，已知抛物线21y x 4x =-+和直线2y 2x =.我们约定：当x 任取一值时，x 对应的函数值分别为y 1、y 2，若y 1≠y 2，取y 1、y 2中的较小值记为M ；若y 1=y 2，记M=y 1=y 2.下列判断：①当x ＞2时，M=y 2；②当x ＜0时，x 值越大，M 值越大；③使得M 大于4的x 值不存在；④若M=2，则x=1.其中正确的有【】A ．1个B ．2个C ．3个D ．4个12.二次函数的图象如图所示，反比例函数与一次函数在同一平面直角坐标系中的大致图象是【】A ．B ．C ．D ．13.二次函数y=ax 2+bx+c （a ≠0）的图象如图所示，则函数a y x=与y=bx+c 在同一直角坐标系内的大致图象是【】A ．B ．C ．D ．二解答题1.如图①，双曲线kyx（k≠0）和抛物线y=ax2+bx（a≠0）交于A、B、C三点，其中B（3，1），C（﹣1，﹣3），直线CO交双曲线于另一点D，抛物线与x轴交于另一点E．（1）求双曲线和抛物线的解析式；（2）抛物线在第一象限部分是否存在点P，使得∠POE+∠BCD=90°？若存在，请求出满足条件的点P的坐标；若不存在，请说明理由；（3）如图②，过B作直线l⊥OB，过点D作DF⊥l于点F，BD与OF交于点N，求DNNB的值．2.已知抛物线l：y=ax2+bx+c（a，b，c均不为0）的顶点为M，与y轴的交点为N，我们称以N为顶点，对称轴是y轴且过点M的抛物线为抛物线l的衍生抛物线，直线MN为抛物线l的衍生直线．（1）如图，抛物线y=x2﹣2x﹣3的衍生抛物线的解析式是，衍生直线的解析式是；（2）若一条抛物线的衍生抛物线和衍生直线分别是y=﹣2x2+1和y=﹣2x+1，求这条抛物线的解析式；（3）如图，设（1）中的抛物线y=x2﹣2x﹣3的顶点为M，与y轴交点为N，将它的衍生直线MN先绕点N旋转到与x轴平行，再沿y轴向上平移1个单位得直线n，P是直线n上的动点，是否存在点P，使△POM 为直角三角形？若存在，求出所有点P的坐标；若不存在，请说明理由．3.在平面直角坐标系中，一次函数y=kx+b 的图象与x 轴、y 轴分别相交于A （﹣3，0），B （0，﹣3）两点，二次函数y=x 2+mx+n 的图象经过点A ．（1）求一次函数y=kx+b 的解析式；（2）若二次函数y=x 2+mx+n 图象的顶点在直线AB 上，求m ，n 的值；（3）当﹣3≤x≤0时，二次函数y=x 2+mx+n 的最小值为﹣4，求m ，n 的值．4.在平面直角坐标系中,抛物线()2y x k 1x k =+--与直线y kx 1=+交于A,B 两点，点A 在点B 的左侧.（1）如图1，当k 1=时，直接写出．．．．A ，B 两点的坐标；（2）在（1）的条件下，点P 为抛物线上的一个动点，且在直线AB 下方，试求出△ABP 面积的最大值及此时点P 的坐标；（3）如图2，抛物线()()2y x k 1x k k >0=+--与x 轴交于C ，D 两点（点C 在点D 的左侧）.在直线y kx 1=+上是否存在唯一一点Q ，使得∠OQC=90°？若存在，请求出此时k 的值；若不存在，请说明理由.5.给定直线l ：y=kx ，抛物线C ：y=ax 2+bx+1．（1）当b=1时，l 与C 相交于A ，B 两点，其中A 为C 的顶点，B 与A 关于原点对称，求a 的值；（2）若把直线l 向上平移k 2+1个单位长度得到直线r ，则无论非零实数k 取何值，直线r 与抛物线C 都只有一个交点．①求此抛物线的解析式；②若P 是此抛物线上任一点，过P 作PQ ∥y 轴且与直线y=2交于Q 点，O 为原点．求证：OP=PQ ．6.已知：直线y=ax+b 与抛物线2y ax bx c =-+的一个交点为A （0，2），同时这条直线与x 轴相交于点B ，且相交所成的角β为45°．（1）求点B 的坐标；（2）求抛物线2y ax bx c =-+的解析式；（3）判断抛物线2y ax bx c =-+与x 轴是否有交点，并说明理由．若有交点设为M ，N （点M 在点N 左边），将此抛物线关于y 轴作轴反射得到M 的对应点为E ，轴反射后的像与原像相交于点F ，连接NF ，EF 得△DEF ，在原像上是否存在点P ，使得△NEP 的面积与△NEF 的面积相等？若存在，请求出点P 的坐标；若不存在，请说明理由．7.如图，在△ABC中，4AB=5AC，AD为△ABC的角平分线，点E在BC的延长线上，EF⊥AD于点F，点G在AF上，FG=FD，连接EG交AC于点H．若点H是AC的中点，则AGFD的值为．8.某体育用品商店试销一款成本为50元的排球，规定试销期间单价不低于成本价，且获利不得高于40%．经试销发现，销售量y（个）与销售单价x（元）之间满足如图所示的一次函数关系．（1）试确定y与x之间的函数关系式；（2）若该体育用品商店试销的这款排球所获得的利润Q元，试写出利润Q（元）与销售单价x（元）之间的函数关系式；当试销单价定为多少元时，该商店可获最大利润？最大利润是多少元？（3）若该商店试销这款排球所获得的利润不低于600元，请确定销售单价x的取值范围．9.大学生小张利用暑假50天在一超市勤工俭学，被安排销售一款成本为40元/件的新型商品，此类新型商品在第x 天的销售量p 件与销售的天数x 的关系如下表：x （天）123...50p （件）118116114 (20)销售单价q （元/件）与x 满足：当1≤x ＜25时q=x+60；当25≤x≤50时1125q 40x=+．（1）请分析表格中销售量p 与x 的关系，求出销售量p 与x 的函数关系．（2）求该超市销售该新商品第x 天获得的利润y 元关于x 的函数关系式．（3）这50天中，该超市第几天获得利润最大？最大利润为多少？10.如图，已知直线AB ：y kx 2k 4=++与抛物线21y x 2=交于A 、B 两点，（1）直线AB 总经过一个定点C ，请直接写出点C 坐标；（2）当1k 2=-时，在直线AB 下方的抛物线上求点P ，使△ABP 的面积等于5；（3）若在抛物线上存在定点D 使∠ADB ＝90°，求点D 到直线AB 的最大距离.11.某校八年级学生小丽、小强和小红到某超市参加了社会实践活动，在活动中他们参与了某种水果的销售工作．已知该水果的进价为8元/千克，下面是他们在活动结束后的对话．小丽：如果以10元/千克的价格销售，那么每天可售出300千克．小强：如果每千克的利润为3元，那么每天可售出250千克．小红：如果以13元/千克的价格销售，那么每天可获取利润750元．【利润=（销售价-进价） 销售量】（1）请根据他们的对话填写下表：销售单价x（元/kg）101113销售量y（kg）（2）请你根据表格中的信息判断每天的销售量y（千克）与销售单价x（元）之间存在怎样的函数关系．并求y（千克）与x（元）（x＞0）的函数关系式；（3）设该超市销售这种水果每天获取的利润为W元，求W与x的函数关系式．当销售单价为何值时，每天可获得的利润最大？最大利润是多少元？12.如图，抛物线y=ax 2+bx+c 关于y 轴对称，它的顶点在坐标原点O ，点B （2，43-）和点C （﹣3，﹣3）两点均在抛物线上，点F （0，34-）在y 轴上，过点（0，34）作直线l 与x 轴平行．（1）求抛物线的解析式和直线BC 的解析式．（2）设点D （x ，y ）是线段BC 上的一个动点（点D 不与B ，C 重合），过点D 作x 轴的垂线，与抛物线交于点G ．设线段GD 的长度为h ，求h 与x 之间的函数关系式，并求出当x 为何值时，线段GD 的长度h 最大，最大长度h 的值是多少？（3）若点P （m ，n ）是抛物线上位于第三象限的一个动点，连接PF 并延长，交抛物线于另一点Q ，过点Q 作QS ⊥l ，垂足为点S ，过点P 作PN ⊥l ，垂足为点N ，试判断△FNS 的形状，并说明理由；（4）若点A （﹣2，t ）在线段BC 上，点M 为抛物线上的一个动点，连接AF ，当点M 在何位置时，MF+MA 的值最小，请直接写出此时点M 的坐标与MF+MA 的最小值．13.如图，直线y=﹣3x+3与x 轴、y 轴分别交于点A 、B ，抛物线()2y a x 2k =-+经过点A 、B ，并与x 轴交于另一点C ，其顶点为P ．（1）求a ，k 的值；（2）抛物线的对称轴上有一点Q ，使△ABQ 是以AB 为底边的等腰三角形，求Q 点的坐标；（3）在抛物线及其对称轴上分别取点M 、N ，使以A ，C ，M ，N 为顶点的四边形为正方形，求此正方形的边长．14.如图，在平面直角坐标系中，O 为坐标原点，抛物线过2y ax bx c(a 0)=++≠过O 、B 、C 三点，B 、C 坐标分别为（10，0）和（185，245-），以OB 为直径的⊙A 经过C 点,直线l 垂直于x 轴于点B.（1）求直线BC 的解析；（2）求抛物线解析式及顶点坐标；（3）点M 是⊙A 上一动点（不同于O ，B ），过点M 作⊙A 的切线，交y 轴于点E ，交直线l 于点F ，设线段ME 长为m ，MF 长为n ，请猜想m n ⋅的值，并证明你的结论；（4）点P 从O 出发，以每秒1个单位速度向点B 作直线运动，点Q 同时从B 出发，以相同速度向点C 作直线运动，经过t(0<t)秒时恰好使△BPQ 为等腰三角形，请求出满足条件的t 值.15.在平面直角坐标系中，我们不妨把横坐标与纵坐标相等的点称为“梦之点”，例如点（﹣1，﹣1），（0，0），），…都是“梦之点”，显然，这样的“梦之点”有无数个．（1）若点P （2，m ）是反比例函数ny x=（n 为常数，n≠0）的图象上的“梦之点”，求这个反比例函数的解析式；（2）函数y=3kx+s ﹣1（k ，s 是常数）的图象上存在“梦之点”吗？若存在，请求出“梦之点”的坐标；若不存在，请说明理由；（3）若二次函数y=ax 2+bx+1（a ，b 是常数，a ＞0）的图象上存在两个不同的“梦之点”A （x 1，x 1），B （x 2，x 2），且满足﹣2＜x 1＜2，|x 1﹣x 2|=2，令t=b 2﹣2b+15748，试求出t 的取值范围．16.已知抛物线()25k 2y x k 2x 4+=-++和直线()()2y k 1x k 1=+++．（1）求证：无论k 取何实数值，抛物线总与x 轴有两个不同的交点；（2）抛物线于x 轴交于点A 、B ，直线与x 轴交于点C ，设A 、B 、C 三点的横坐标分别是x 1、x 2、x 3，求x 1•x 2•x 3的最大值；（3）如果抛物线与x 轴的交点A 、B 在原点的右边，直线与x 轴的交点C 在原点的左边，又抛物线、直线分别交y 轴于点D 、E ，直线AD 交直线CE 于点G （如图），且CA•GE=CG•AB ，求抛物线的解析式．17.如图①，直线l ：y=mx+n （m ＞0，n ＜0）与x ，y 轴分别相交于A ，B 两点，将△AOB 绕点O 逆时针旋转90°，得到△COD ，过点A ，B ，D 的抛物线P 叫做l 的关联抛物线，而l 叫做P 的关联直线．（1）若l ：y=﹣2x+2，则P 表示的函数解析式为；若P ：y=﹣x 2﹣3x+4，则l 表示的函数解析式为．（2）求P 的对称轴（用含m ，n 的代数式表示）；（3）如图②，若l ：y=﹣2x+4，P 的对称轴与CD 相交于点E ，点F 在l 上，点Q 在P 的对称轴上．当以点C ，E ，Q ，F 为顶点的四边形是以CE 为一边的平行四边形时，求点Q 的坐标；（4）如图③，若l ：y=mx ﹣4m ，G 为AB 中点，H 为CD 中点，连接GH ，M 为GH 中点，连接OM ．若OM=，直接写出l ，P 表示的函数解析式．18.如图，直线y=x ﹣4与x 轴、y 轴分别交于A 、B 两点，抛物线21y x bx c 3=++经过A 、B 两点，与x 轴的另一个交点为C ，连接BC ．（1）求抛物线的解析式及点C 的坐标；（2）点M 在抛物线上，连接MB ，当∠MBA+∠CBO=45°时，求点M 的坐标；（3）点P 从点C 出发，沿线段CA 由C 向A 运动，同时点Q 从点B 出发，沿线段BC 由B 向C 运动，P 、Q 的运动速度都是每秒1个单位长度，当Q 点到达C 点时，P 、Q 同时停止运动，试问在坐标平面内是否存在点D ，使P 、Q 运动过程中的某一时刻，以C 、D 、P 、Q 为顶点的四边形为菱形？若存在，直接写出点D 的坐标；若不存在，说明理由．19.如图，抛物线y=-x2+bx+c交x轴于点A，交y轴于点B，已知经过点A，B的直线的表达式为y=x+3．（1）求抛物线的函数表达式及其顶点C的坐标；（2）如图①，点P（m，0）是线段AO上的一个动点，其中-3＜m＜0，作直线DP⊥x轴，交直线AB于D，交抛物线于E，作EF∥x轴，交直线AB于点F，四边形DEFG为矩形．设矩形DEFG的周长为L，写出L 与m的函数关系式，并求m为何值时周长L最大；（3）如图②，在抛物线的对称轴上是否存在点Q，使点A，B，Q构成的三角形是以AB为腰的等腰三角形？若存在，直接写出所有符合条件的点Q的坐标；若不存在，请说明理由．20.如图，已知直线l的解析式为1y x12=-，抛物线y=ax2＋bx＋2经过点A（m，0），B（2，0），D51,4⎛⎫⎪⎝⎭三点．（1）求抛物线的解析式及A点的坐标，并在图示坐标系中画出抛物线的大致图象；（2）已知点P（x，y）为抛物线在第二象限部分上的一个动点，过点P作PE垂直x轴于点E,延长PE与直线l交于点F，请你将四边形PAFB的面积S表示为点P的横坐标x的函数，并求出S的最大值及S最大时点P的坐标；（3）将（2）中S最大时的点P与点B相连，求证：直线l上的任意一点关于x轴的对称点一定在PB所在直线上．21.今年5月1日起实施《青海省保障性住房准入分配退出和运营管理实施细则》规定：公共租赁住房和廉租住房并轨运行（以下简称并轨房），计划10年内解决低收入人群住房问题．已知第x年（x为正整数）投入使用的并轨房面积为y百万平方米，且y与x的函数关系式为1y x56=-+．由于物价上涨等因素的影响，每年单位面积租金也随之上调．假设每年的并轨房全部出租完，预计第x年投入使用的并轨房的单位面积租金z与时间x满足一次函数关系如下表：时间x（单位：年，x为正整数）12345…单位面积租金z（单位：元/平方米）5052545658…（1）求出z与x的函数关系式；（2）设第x年政府投入使用的并轨房收取的租金为W百万元，请问政府在第几年投入使用的并轨房收取的租金最多，最多为多少百万元？22.如图，抛物线y=14x2+bx+c与x轴交于A（5，0）、B（﹣1，0）两点，过点A作直线AC⊥x轴，交直线y=2x于点C；（1）求该抛物线的解析式；（2）求点A关于直线y=2x的对称点A′的坐标，判定点A′是否在抛物线上，并说明理由；（3）点P是抛物线上一动点，过点P作y轴的平行线，交线段CA′于点M，是否存在这样的点P，使四边形PACM是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．23.如图，过A（1，0）、B（3，0）作x轴的垂线，分别交直线y=4﹣x于C、D两点．抛物线y=ax2+bx+c经过O、C、D三点．（1）求抛物线的表达式；（2）点M为直线OD上的一个动点，过M作x轴的垂线交抛物线于点N，问是否存在这样的点M，使得以A、C、M、N为顶点的四边形为平行四边形？若存在，求此时点M的横坐标；若不存在，请说明理由；（3）若△AOC沿CD方向平移（点C在线段CD上，且不与点D重合），在平移的过程中△AOC与△OBD 重叠部分的面积记为S，试求S的最大值．24.如图，在平面直角坐标系中，抛物线与x轴交于点A（﹣1，0）和点B（1，0），直线y=2x﹣1与y轴交于点C，与抛物线交于点C、D．（1）求抛物线的解析式；（2）求点A到直线CD的距离；（3）平移抛物线，使抛物线的顶点P在直线CD上，抛物线与直线CD的另一个交点为Q，点G在y轴正半轴上，当以G、P、Q三点为顶点的三角形为等腰直角三角形时，求出所有符合条件的G点的坐标．25.二次函数y=ax2+bx+c的图象经过点（﹣1，4），且与直线1y x12=-+相交于A、B两点（如图），A点在y轴上，过点B作BC⊥x轴，垂足为点C（﹣3，0）．（1）求二次函数的表达式；（2）点N是二次函数图象上一点（点N在AB上方），过N作NP⊥x轴，垂足为点P，交AB于点M，求MN的最大值；（3）在（2）的条件下，点N在何位置时，BM与NC相互垂直平分？并求出所有满足条件的N点的坐标．26.如图，在平面直角坐标系中，抛物线2y ax bx 3=++与x 轴交于点A （﹣4，0），B （﹣1，0）两点．（1）求抛物线的解析式；（2）在第三象限的抛物线上有一动点D ．①如图（1），若四边形ODAE 是以OA 为对角线的平行四边形，当平行四边形ODAE 的面积为6时，请判断平行四边形ODAE 是否为菱形？说明理由．②如图（2），直线1y x 32=+与抛物线交于点Q 、C 两点，过点D 作直线DF ⊥x 轴于点H ，交QC 于点F ．请问是否存在这样的点D ，使点D 到直线CQ 的距离与点C 到直线DF ：2？若存在，请求出点D 的坐标；若不存在，请说明理由．27．如图，已知一次函数11y x b 2=+的图象l 与二次函数22y x mx b =-++的图象'C 都经过点B （0,1）和点C ，且图象'C 过点A （52-，0）.（1）求二次函数的最大值；（2）设使21y y >成立的x 取值的所有整数和为s ，若s 是关于x 的方程131x 0a 1x 3⎛⎫++= ⎪--⎝⎭的根，求a 的值；（3）若点F 、G 在图象'C 上，长度为5的线段DE 在线段BC 上移动，EF 与DG 始终平行于y 轴，当四边形DEFG 的面积最大时，在x 轴上求点P ，使PD+PE 最小，求出点P 的坐标.28．如图，已知直线y 3x 3=-+与x 轴交于点A ，与y 轴交于点C ，抛物线2y ax bx c =++经过点A 和点C ，对称轴为直线l ：x 1=-，该抛物线与x 轴的另一个交点为B ．（1）求此抛物线的解析式；（2）点P 在直线l 上，求出使△PAC 的周长最小的点P 的坐标；（3）点M 在此抛物线上，点N 在y 轴上，以A 、B 、M 、N 为顶点的四边形能否为平行四边形？若能，直接写出所有满足要求的点M 的坐标；若不能，请说明理由．29．如图，抛物线y=x2+bx+c与直线y=x﹣1交于A、B两点．点A的横坐标为﹣3，点B在y轴上，点P是y轴左侧抛物线上的一动点，横坐标为m，过点P作PC⊥x轴于C，交直线AB于D．（1）求抛物线的解析式；=2S△BPD；（2）当m为何值时，S四边形OBDC（3）是否存在点P，使△PAD是直角三角形？若存在，求出点P的坐标；若不存在，说明理由．30．已知：直线l：y=﹣2，抛物线y=ax2+bx+c的对称轴是y轴，且经过点（0，﹣1），（2，0）．（1）求该抛物线的解析式；（2）如图①，点P是抛物线上任意一点，过点P作直线l的垂线，垂足为Q，求证：PO=PQ．（3）请你参考（2）中结论解决下列问题：（i）如图②，过原点作任意直线AB，交抛物线y=ax2+bx+c于点A、B，分别过A、B两点作直线l的垂线，垂足分别是点M、N，连结ON、OM，求证：ON⊥OM．（ii）已知：如图③，点D（1，1），试探究在该抛物线上是否存在点F，使得FD+FO取得最小值？若存在，求出点F的坐标；若不存在，请说明理由．31．如图，已知抛物线23y ax x c 2=-+与x 轴相交于A 、B 两点，并与直线1y x 22=-交于B 、C 两点，其中点C 是直线1y x 22=-与y 轴的交点，连接AC ．（1）求抛物线的解析式；（2）证明：△ABC 为直角三角形；（3）△ABC 内部能否截出面积最大的矩形DEFG ？（顶点D 、E 、F 、G 在△ABC 各边上）若能，求出最大面积；若不能，请说明理由．32．对某一个函数给出如下定义：若存在实数M 0>，对于任意的函数值y ，都满足M y M -≤≤，则称这个函数是有界函数，在所有满足条件的M 中，其最小值称为这个函数的边界值．例如，下图中的函数是有界函数，其边界值是1．（1）分别判断函数()1y x 0x=>和()y x 14x 2=+-<≤是不是有界函数？若是有界函数，求其边界值；（2）若函数()y x 1a x b b a =-+≤≤>，的边界值是2，且这个函数的最大值也是2，求b 的取值范围；（3）将函数()2y x 1x m m 0=-≤≤≥，的图象向下平移m 个单位，得到的函数的边界值是t ，当m 在什么范围时，满足3t 14≤≤33．如图，抛物线2y x bx c =-++与x 轴交于A(-1，0)，B(5，0）两点，直线3y x 34=-+与y 轴交于点C ，，与x 轴交于点D.点P 是x 轴上方的抛物线上一动点，过点P 作PF ⊥x 轴于点F ，交直线CD 于点E.设点P 的横坐标为m.（1）求抛物线的解析式；（2）若PE =5EF ，求m 的值；（3）若点E /是点E 关于直线PC 的对称点、是否存在点P ，使点E /落在y 轴上？若存在，请直接写出相应的点P 的坐标；若不存在，请说明理由.34．某公司销售一种进价为20元/个的计算机，其销售量y （万个）与销售价格x （元/个）的变化如下表：价格x （元/个）…30405060…销售量y （万个）…5432…同时，销售过程中的其他开支（不含造价）总计40万元．（1）观察并分析表中的y 与x 之间的对应关系，用所学过的一次函数，反比例函数或二次函数的有关知识写出y （万个）与x （元/个）的函数解析式．（2）求出该公司销售这种计算器的净得利润z （万个）与销售价格x （元/个）的函数解析式，销售价格定为多少元时净得利润最大，最大值是多少？（3）该公司要求净得利润不能低于40万元，请写出销售价格x （元/个）的取值范围，若还需考虑销售量尽可能大，销售价格应定为多少元？35．如图，直角梯形ABCO的两边OA，OC在坐标轴的正半轴上，BC∥x轴，OA=OC=4，以直线x=1为对称轴的抛物线过A，B，C三点.（1）求该抛物线线的函数解析式.=+，它与x轴的交于点G，在梯形ABCO的一边上取点P.（2）已知直线l的解析式为y x m①当m=0时，如图1，点P是抛物线对称轴与BC的交点，过点P作PH⊥直线l于点H，连结OP，试求△OPH的面积.=-时，过P点分别作x轴、直线l的垂线，垂足为点E，F.是否存在这样的点P，使以P，E，F ②当m3为顶点的三角形是等腰三角形？若存在，求出点P的坐标；若不存在，请说明理由.36．某公司经营杨梅业务，以3万元/吨的价格向农户收购杨梅后，分拣成A、B两类，A类杨梅包装后直接销售，B类杨梅深加工再销售．A类杨梅的包装成本为1万元/吨，根据市场调查，它的平均销售价格y （单位∶万元/吨）与销售数量x（x≥2）（单位∶吨）之间的函数关系式如图，B类杨梅深加工总费用s（单位:万元）与加工数量t（单位∶吨）之间的函数关系是s＝12＋3t，平均销售价格为9万元/吨．（1）直接写出A类杨梅平均销售价格y与销售量x这间的函数关系式;（2）第一次，该公司收购了20吨杨梅，其中A类杨梅x吨，经营这批杨梅所获得的毛利润为w万元（毛利润＝销售总收人－经营总成本）.①求w关于x的函数关系式;②若该公司获得了30万元毛利润，问∶用于直销的A类杨梅有多少吨？（3）第二次该公司准备投人132万元资金，请设计－种经营方案，使公司获得最大毛利润，并求出最大毛利润．37．如图，直角梯形ABCO的两边OA，OC在坐标轴的正半轴上，BC∥x轴，OA=OC=4，以直线x=1为对称轴的抛物线过A，B，C三点.（1）求该抛物线线的函数解析式.=+，它与x轴的交于点G，在梯形ABCO的一边上取点P.（2）已知直线l的解析式为y x m①当m=0时，如图1，点P是抛物线对称轴与BC的交点，过点P作PH⊥直线l于点H，连结OP，试求△OPH的面积.=-时，过P点分别作x轴、直线l的垂线，垂足为点E，F.是否存在这样的点P，使以P，E，F ②当m3为顶点的三角形是等腰三角形？若存在，求出点P的坐标；若不存在，请说明理由.38.已知函数23y kx 2x 2=-+（k 是常数）（1）若该函数的图像与x 轴只有一个交点，求k 的值；（2）若点()M 1,k 在某反比例函数的图像上，要使该反比例函数和二次函数23y kx 2x 2=-+都是y 随x 的增大而增大，求k 应满足的条件以及x 的取值范围；（3）设抛物线23y kx 2x 2=-+与x 轴交于()()12x ,0,B x A ,0两点，且12x x <，2212x x 1+=，在y 轴上，是否存在点P ，使△ABP 是直角三角形？若存在，求出点P 及△ABP 的面积；若不存在，请说明理由。

初中三年数学重点考点梳理(分册整理)帮你理清思路，满分干
货!
（一）线段、角的计算与证明问题
中考简答题一般分为两三部分。

第一部分基本是简单题和中级题，旨在考察基础。

第二部分第二部分往往是开始拉分的难题。

（二）列方程（组）解决应用问题
中考中，方程是初中数学最重要的部分，所以也是中考的必考内容。

从近几年的中考来看，结合时事的考试比较多，所以考生需要有一些真实的生活经历。

（三）阅读理解问题
阅读理解是中考的一个亮点。

阅读理解往往是给一个材料或者介绍一个超类的知识或者给出某个题目的解答，然后给出问题的条件。

（四）多种函数交叉综合问题
初中接触的函数主要有一次函数、二次函数和反比例函数。

这类题目本身并不太难，很少作为压轴题目出现。

一般以中级题目出现，测试学生对函数的掌握程度。

（五）动态几何
从历年中考来看，动态几何经常作为期末题目出现，得分率也是最低的。

动态几何一般分为两类，一类是代数综合，在坐标系中，运动的直线一般是用多个函数求解的。

另一个是几何综合题，在梯形、矩形、三角形中设置动点，测试学生的综合分析能力。

（六）图形位置关系
在中学数学中，图形位置关系主要包括点、线、三角形、矩形和正方形及其关系。

中考时会包含在函数、坐标系、几何的题中，其中最重要的是三角形的各种问题。

函数与一次函数（提高）1、如图，边长分别为 1 和 2 的两个等边三角形，开始它们在左边重合，大三角形固定不动，然后把小三角形自左向右平移直至移出大三角形外停止．设小三角形移动的距离为 x，两个三角形重叠面积为 y，则 y 关于 x 的函数图象是（）2、如图，点A的坐标为（﹣，0），点B在直线y=x上运动，当线段AB最短时点B的坐为（）A．（﹣，﹣）B．（，）C．（，）D．（0，0）3、在平面直角坐标系中，四边形OABC是矩形，点B的坐标为（4，3）.平行于对角线AC 的直线 m 从原点 O 出发，沿 x 轴正方向以每秒1个单位长度的速度运动，设直线 m 与矩形 OABC 的两边分别交于点 M，N，直线 m 运动的时间为 t（秒）．设△OMN 的面积为S，则能反映 S 与 t 之间函数关系的大致图象是（）A B C D4、已知点P在直线上，点Q在直线上，则代数式.5、如图，直线与x轴、y轴分别交于A、B两点，把△A0B绕点A顺时针旋转 90°后得到△AO′B′，则点B′的坐标是．6、直线与双曲线交于两点,则的值为___________.7、如图，一次函数的图象与轴，轴交于A，B两点，与反比例函数的图象相交于 C，D 两点，分别过 C，D 两点作轴，轴的垂线，垂足为E，F，连接CF，DE．有下列四个结论：① ；② 相似于；③△DCE≌△CDF；④其中正确的结论是．（把你认为正确结论的序号都填上）8、如图 1，点A的坐标为（－1，0），点B在直线y＝2x－4 上运动，当线段 AB 最短时，点 B 的坐标是_______．图 19、如图，一次函数y1=k1x+b（k1≠0）的图象与反比例函数y2=k2x+b（k2≠0）的图象交于A，B两点，观察图象，当 y1＞y2时，x 的取值范围是．x 2 (x≤2)，210、若直线y＝m(m为常数)与函数y＝ 4(x＞2) 的图象恒有三个不同的交点，则常数 mx的取值范围是．11、一次函数图象一定经过第象限.。