(完整版)通信原理第二章课后答案

习题解答2-1、什么是调制信道？什么是编码信道？说明调制信道和编码信道的关系。

答：所谓调制信道是指从调制器输出端到解调器输入端的部分。

从调制和解调的角度来看，调制器输出端到解调器输入端的所有变换装置及传输媒质，不论其过程如何，只不过是对已调制信号进行某种变换。

所谓编码信道是指编码器输出端到译码器输入端的部分。

从编译码的角度看来，编码器的输出是某一数字序列，而译码器的输入同样也是某一数字序列，它们可能是不同的数字序列。

因此，从编码器输出端到译码器输入端，可以用一个对数字序列进行变换的方框来概括。

根据调制信道和编码信道的定义可知，编码信道包含调制信道，因而编码信道的特性也依赖调制信道的特性。

2-2、什么是恒参信道？什么是随参信道？目前常见的信道中，哪些属于恒参信道？哪些属于随参信道？答：信道参数随时间缓慢变化或不变化的信道叫恒参信道。

通常将架空明线、电缆、光纤、超短波及微波视距传输、卫星中继等视为恒参信道。

信道参数随时间随机变化的信道叫随参信道。

短波电离层反射信道、各种散射信道、超短波移动通信信道等为随参信道。

2-3、设一恒参信道的幅频特性和相频特性分别为：其中，0K 和d t 都是常数。

试确定信号)(t s 通过该信道后的输出信号的时域表示式，并讨论之。

解：传输函数d t j je K e H H ωωϕωω-==0)()()(冲激响应)()(0d t t K t h -=δ输出信号)()()()(0d t t s K t h t s t y -=*=结论：该恒参信道满足无失真条件，故信号在传输过程中无失真。

2-4、设某恒参信道的传输特性为d t j eT H ωωω-+=]cos 1[)(0，其中，d t 为常数。

试确定信号)(t s 通过该信道后的输出信号表达式，并讨论之。

解：输出信号为： dt K H ωωϕω-==)()(0)(21)(21)()(2121)(21]cos 1[)(00)()(00000T t t T t t t t t h e e e e e e e e T H d d d T t j T t j t j t j T j T j t j t j d d d d d d --++-+-=++=++=+=+--------δδδωωωωωωωωωω讨论：此信道的幅频特性为0cos 1)(T H ωω+=，相频特性为ωωϕd t -=)(，相频特性与ω成正比，无想频失真；K H ≠)(ω，有幅频失真，所以输出信号的失真是由信道的幅频失真引起的，或者说信号通过此信道只产生幅频失真。

WORD 格式可编辑第二章习题习题 2.1设随机过程 X(t ) 可以表示成：X (t) 2cos(2 t ),t式中，是一个离散随机变量，它具有如下概率分布：P(=0)=0.5 ，P(= /2)=0.5试求 E[ X( t )] 和 R X (0,1) 。

解：E[ X( t )]= P(=0)2 cos(2 t ) +P( =/2)2cos(2 t)=cos(2 t) sin 2 t cos t2习题 2.2设一个随机过程 X( t ) 可以表示成：X (t ) 2cos(2 t), t判断它是功率信号还是能量信号？并求出其功率谱密度或能量谱密度。

解：为功率信号。

R X ( )lim T1 T / 2X ( t ) X (t) dtTT / 2lim T1T / 2t)* 2 cos 2(t)dtTT / 22 cos(22cos(2) ej 2te j 2 tP ( f )R X ( ) e j 2fd(e j 2 te j 2 t )e j 2fd( f 1)( f 1)习题 2.3设有一信号可表示为：X (t)4exp( t) ,t 0{0, t<0试问它是功率信号还是能量信号？并求出其功率谱密度或能量谱密度。

解：它是能量信号。

X( t ) 的傅立叶变换为：X ( )x(t)e j tdt4e t e j tdt 4e(1 j )tdt41 j216则能量谱密度2=4G(f)= X ( f )j142 f21习题 2.4X(t )=x 1 cos2 tx 2 sin 2 t ，它是一个随机过程，其中x 1 和 x 2是相互统计独立的高斯随机变量，数学期望均为0，方差均为2。

试求：(1) E[ X(t )] ， E[ X 2(t ) ] ；(2) X( t )的概率分布密度； (3) R X (t 1 ,t 2 )解：(1) E X tE x 1 cos2 t x 2 sin 2 t cos 2 t E x 1 sin 2 t E x 2 0P X ( f )因为x 1和x 2相互独立，所以E x 1 x 2E x 1E x 2。

现代通信原理课后习题答案第⼆章2.40 ⼆进制对称信道中的误⽐特率P e为0.2，若输⼊信道的符号速率为2000符号/s，求该信道的信道容量。

解：2000×(1-0.2)=1600 (b/s)2.41 已知某语⾳信道带宽为4kHz，若接收端的信噪⽐S/N =60dB，求信道容量。

若要求该信道传输56000b/s的数据，则接收端的信噪⽐最⼩应为多少？解：dB=10 lgN 60 = 10 lg S/N →S/N = 106C = wlog2 (1+S/N)=4×103log2(1+106) = 8 × 104 (bps)5.6 × 104 = 4 × 103log2(1+S/N)log2(1+S/N) = 14 → 1+S/N = 214→S/N = 214－12.42 若⿊⽩电视机的每幅图像含有3×105个像素，每个像素都有16个等概率出现的亮度等级，如果信道的输出信噪⽐为S/N = 40dB、信道带宽为1.4MHz，则该信道每秒可传送多少幅图像？解：每幅图的信息量：3×105×log216 = 1.2×106（b）40dB = 10log2 S/N →S/N = 104C = wlog2（1 + S/N）= 1.4×106log2（1+104）≈1.862×107（bps）1.862×107/1.2×106 = 15.5 (幅/s)第三章3.50 ⽤10KHz的单频正弦信号对1MHz的载波进⾏调制，峰值频偏为2KHz。

试求：（1）该调频信号的带宽。

（2）若调制信号的幅度加倍，再求该调频信号的带宽。

解：（1）B FM = 2 × ( 2+10 ) = 24 ( KHz)（2）B FM = 2 ×（2 + 2×10）= 44 （KHz）3.51 幅度1V的10MHz载波受到幅度1V、频率为100Hz的正弦信号调制，最⼤频偏为500Hz。

5－10 某线性调制系统的输出信噪比为20dB，输出噪声功率为 ，由发射机输出端到解调器输入端之间总的传输损耗为100dB，910W试求：（1）DSB/SC时的发射机输出功率；（2）SSB/SC时的发射机输出功率。

，解调器输入信号功率为Si,解：设发射机输出功率为ST/Si=100(dB).则传输损耗K= ST（1）DSB/SC的制度增益G=2，解调器输入信噪比相干解调时：Ni=4No因此，解调器输入端的信号功率：发射机输出功率：（2）SSB/SC制度增益G=1，则解调器输入端的信号功率发射机输出功率：6-1设二进制符号序列为 1 1 0 0 1 0 0 0 1 1 1 0，试以矩形脉冲为例，分别画出相应的单极性码波形、双极性码波形、单极性归零码波形、双极性归零码波形、二进制差分码波形及八电平码波形。

解：各波形如下图所示：6-8已知信息代码为 1 0 1 0 0 0 0 0 1 1 0 0 0 0 1 1，求相应的AMI码及HDB3码，并分别画出它们的波形图。

解：6-11设基带传输系统的发送滤波器、信道及接收滤波器组成总特性为H(ω)，若要求以2/Ts波特的速率进行数据传输，试检验图P5-7各种H(ω)是否满足消除抽样点上码间干扰的条件？ω(a)(c) (d)解：无码间干扰的条件是：⎪⎪⎩⎪⎪⎨⎧>≤=⎪⎪⎭⎫⎝⎛+=∑ssisseqTTTTiHHπωπωπωω2)((a)⎪⎪⎩⎪⎪⎨⎧>=≤=ssTBTHπωππωω21)(则 sT B 21=，无码间干扰传输的最大传码率为：s s B T T B R 212max <== 故该H (ω)不满足消除抽样点上码间干扰的条件。

(b ) ⎪⎪⎩⎪⎪⎨⎧>=≤=ssT B T H πωππωω0231)(则 sT B 23=，无码间干扰传输的最大传码率为：s s B T T B R 232max >== 虽然传输速率小于奈奎斯特速率，但因为R Bmax 不是2/T s 的整数倍，所以仍然不能消除码间干扰。

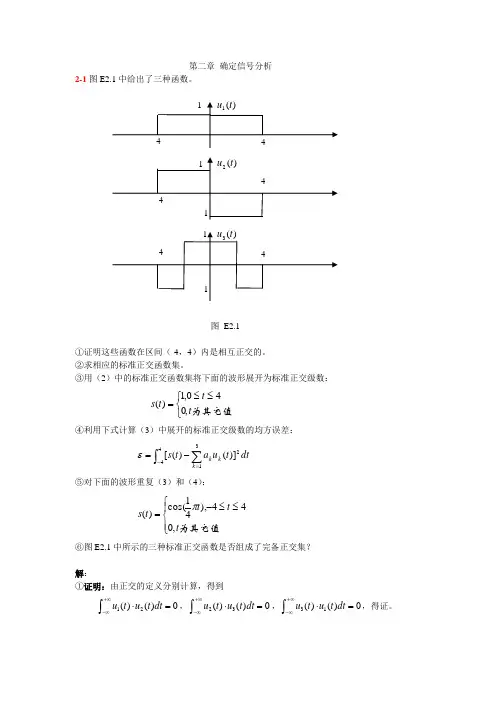
第二章 确定信号分析2-1图E2.1中给出了三种函数。

图 E2.1①证明这些函数在区间（-4，4）内是相互正交的。

②求相应的标准正交函数集。

③用（2）中的标准正交函数集将下面的波形展开为标准正交级数：⎩⎨⎧≤≤=为其它值t t t s ,040,1)(④利用下式计算（3）中展开的标准正交级数的均方误差： ⎰∑-=-=44231])()([dt t u a t s k k k ε⑤对下面的波形重复（3）和（4）：⎪⎩⎪⎨⎧≤≤-=为其它值t t t t s ,044),41cos()(π ⑥图E2.1中所示的三种标准正交函数是否组成了完备正交集？解：①证明：由正交的定义分别计算，得到12()()0u t u t dt +∞-∞⋅=⎰，23()()0u t u t dt +∞-∞⋅=⎰，31()()0u t u t dt +∞-∞⋅=⎰，得证。

②解：424()8,k C u t dt k -== =1,2,3⎰，对应标准正交函数应为()(),1,2,3k k q t t k ==因此标准正交函数集为123123{(),(),()}(),()()}q t q t q t t t t =③解：用标准正交函数集展开的系数为4()(),1,2,3k k a s t q t dt k =⋅ =⎰，由此可以得到4110()()a s t t dt ===⎰4220()()a s t t dt ===⎰4330()()0a s t t dt ==⎰。

所以，121211()()()()()22s t t t u t u t ==-④解：先计算得到312111()()()()()()022k k k t s t a u t s t u t u t ε==-=-+=∑ ⑤解：用标准正交集展开的系数分别为441141()())04a s t t dt t dt π--===⎰⎰，44224011()()cos()cos()044a s t t dt t dt t dt ππ--==-=⎰⎰⎰，433422442()()111cos()))444a s t t dtt dt t dt t dt ππππ----= =-+- =⎰⎰⎰⎰。

第二章（信道）习题及其答案【题2－1】设一恒参信道的幅频特性和相频特性分别为0()()d H K t ωϕωω⎧=⎨=-⎩其中，0,d K t 都是常数。

试确定信号()s t 通过该信道后的输出信号的时域表达式，并讨论之。

【答案2－1】 恒参信道的传输函数为：()0()()d j t j H H e K e ωϕωωω-==，根据傅立叶变换可得冲激响应为：0()()d h t K t t σ=-。

根据0()()()i V t V t h t =*可得出输出信号的时域表达式：000()()()()()()d d s t s t h t s t K t t K s t t δ=*=*-=-讨论：题中条件满足理想信道（信号通过无畸变）的条件：()d d H ωωφωωτττ⎧=⎨⎩常数（）＝－或＝ 所以信号在传输过程中不会失真。

【题2－2】设某恒参信道的幅频特性为[]0()1cos d j t H T e ωω-=+，其中d t 为常数。

试确定信号()s t 通过该信道后的输出表达式并讨论之。

【答案2－2】 该恒参信道的传输函数为()0()()(1cos )d j t j H H e T e ωϕωωωω-==+，根据傅立叶变换可得冲激响应为：0011()()()()22d d d h t t t t t T t t T δδδ=-+--+-+根据0()()()i V t V t h t =⊗可得出输出信号的时域表达式：0000011()()()()()()()2211 ()()()22d d d d d d s t s t h t s t t t t t T t t T s t t s t t T s t t T δδδ⎡⎤=⊗=⊗-+--+-+⎢⎥⎣⎦=-+--+-+讨论：和理想信道的传输特性相比较可知，该恒参信道的幅频特性0()(1cos )H T ωω=+不为常数，所以输出信号存在幅频畸变。

其相频特性()d t ϕωω=-是频率ω的线性函数，所以输出信号不存在相频畸变。

思考题1-1 什么是通信？常见的通信方式有哪些？1-2 通信系统是如何分类的？1-3 何谓数字通信？数字通信的优缺点是什么？1-4 试画出模拟通信系统的模型，并简要说明各部分的作用。

1-5 试画出数字通信系统的一般模型，并简要说明各部分的作用。

1-6 衡量通信系统的主要性能指标是什么？对于数字通信具体用什么来表述？1-7 何谓码元速率?何谓信息速率?它们之间的关系如何?习题1-1 设英文字母E出现的概率=0.105，X出现的概率为＝0.002，试求E和X的信息量各为多少？1-2 某信源的符号集由A、B、C、D、E、F组成，设每个符号独立出现，其概率分别为1/4、1/4、1/16、1/8、1/16、1/4，试求该信息源输出符号的平均信息量。

1-3 设一数字传输系统传送二进制信号，码元速率RB2=2400B，试求该系统的信息速率Rb2=？若该系统改为传送16进制信号，码元速率不变，则此时的系统信息速率为多少？1-4 已知某数字传输系统传送八进制信号，信息速率为3600b/s，试问码元速率应为多少？1-5 已知二进制信号的传输速率为4800b/s，试问变换成四进制和八进制数字信号时的传输速率各为多少（码元速率不变）？1-6 已知某系统的码元速率为3600kB，接收端在l小时内共收到1296个错误码元，试求系统的误码率=？1-7 已知某四进制数字信号传输系统的信息速率为2400b/s，接收端在0.5小时内共收到216个错误码元，试计算该系统=？l-8 在强干扰环境下，某电台在5分钟内共接收到正确信息量为355Mb，假定系统信息速率为1200kb/s。

（l）试问系统误信率=？（2）若具体指出系统所传数字信号为四进制信号，值是否改变？为什么？（3）若假定信号为四进制信号，系统传输速率为1200kB，则＝？习题答案第一章习题答案1-1 解：1-2 解：1-3 解：1-4 解：1-5 解：1-6 解：1-7 解：1-8 解：思考题2-1 什么是狭义信道？什么是广义信道？（答案）2-2 在广义信道中，什么是调制信道？什么是编码信道？2-3 试画出调制信道模型和二进制无记忆编码信道模型。