第二章MATLAB的基本使用方法共59页文档
- 格式:ppt
- 大小:328.50 KB
- 文档页数:57


MATLAB基本使用说明最近在学习使用matlab,将一些自己常用的功能整理一下,以备以后查阅。
同时发表在此,供大家参考评议引言:Matlab的名字源于matrix laboratory,是在linpack和eispack基础之上发展起来的,用于科学计算和数据可视化的高级编程软件。
由于其在linpack和eispack基础之上发展出来的,所以它最擅长的是科学计算,准确的说是矩阵处理。
在matlab里每一个数据都是当初一个matrix来进行处理的。
同时matlab提供了很强大的可视化功能,便于观察数据的特征。
但由于matlab最擅长的是数据处理,所以所有的可视化基本上都是基于数据处理的。
(当然它现在引入了符号处理等,但这不是它所擅长的。
曾比较过matlab和mathematics的符号处理功能,发现matlab的效率极低)。
把matlab定义为高级编程语言,可能需要解释一下。
高级不用说,matlab的层次确实比C,C++等的层次都要高,而且提供了极其丰富的库函数。
说它是编程语言,是因为它还提供了很强大的编程环境,很多实际问题都需要在其基础上编程得到。
而且matlab的工具箱就是很多.m文件构成的。
另外,现在的matlab有很多工具箱,能够各种各样的功能,其中常见的有SIMULINK工具箱,图像处理工具箱等。
这里暂时不涉及这些。
基本操作:打开matlab最先看到的是matlab的workspace,在这里能够完成各种简单操作和处理些简单问题。
其中常用的基本操作有:特殊变量:Matlab自定义了一些特殊变量,这些在实际使用中如能灵活使用会带来很大方便。
ans:默认的输出结果变量beep:发出“叮叮”声pi:pi的值eps:matlab支持的最小正数Inf:无穷大,可以当做值进行比较的NaN:not a numberi,j:复数单位realmin:最小实数realmax:最大实数bitmax:最大正整数(还有很多类似)nargin:函数输入的变量个数nargout:函数输出的变量个数varagin:可变函数的输入参数varagout:可变函数的输出参数(这四个灵活运用于编程可是程序适用性更强)矩阵处理:Matlab提供了各种矩阵处理。

MATLAB的基本使用教程MATLAB是一种强大的数学计算软件,广泛应用于科学、工程和技术领域。
它提供了丰富的功能和工具,能够快速、有效地处理和分析各种数学问题。
本文将介绍MATLAB的基本使用方法,帮助初学者快速入门。
一、MATLAB的安装与启动1、下载和安装MATLAB软件:在MathWorks官方网站上下载适合自己操作系统的MATLAB软件,并根据安装提示进行安装。
安装完成后,会生成一个MATLAB的启动图标。
2、启动MATLAB:双击MATLAB的启动图标,或者在命令行中输入"matlab"命令,即可启动MATLAB。
二、MATLAB的基本操作1、工作环境:MATLAB提供了一个强大的集成开发环境(IDE),可以在其中编写和运行代码。
在MATLAB的界面中,包括主窗口、命令窗口、变量窗口、编辑器等。
2、命令窗口:在命令窗口中可以输入和执行MATLAB命令。
可以直接在命令窗口中输入简单的计算,例如输入"2+3"并按下回车键,即可输出计算结果。
3、脚本文件:MATLAB可以编写和运行脚本文件,将一系列命令组织起来,并按顺序执行。
在编辑器中编写MATLAB代码,并将文件保存为.m扩展名的脚本文件。
然后在命令窗口中输入脚本文件的文件名(不带扩展名),按下回车键即可执行脚本文件中的代码。
4、变量和赋值:在MATLAB中,可以创建和操作各种类型的变量。
例如,可以使用"="符号将一个值赋给一个变量,例如"A=5"。
在后续的计算和分析中,可以使用这个变量,例如输入"B=A+3",结果B 将被赋值为8。
5、矩阵和向量:MATLAB中的基本数据结构是矩阵和向量。
可以使用方括号[]来创建矩阵和向量,并使用逗号或空格来分隔不同的元素。
例如,"[1,2,3]"表示一个包含3个元素的行向量。
6、矩阵运算:MATLAB提供了丰富的矩阵运算符和函数,可以对矩阵进行各种运算。


Matlab的基本用法读取图像:用imread函数读取图像文件,文件格式可以是TIFF、JPEG、GIF、BMP、PNG等。
比如>> f = imread('chestxray.jpg');读进来的图像数据被保存在变量f中。
尾部的分号用来抑制输出。
如果图片是彩色的,可以用rgb2gray转换成灰度图:>> f = rgb2gray(f);然后可以用size函数看图像的大小>> size(f)如果f是灰度图像,则可以用下面的命令把这个图像的大小赋给变量M和N>> [M, N] = size(f);用whos命令查看变量的属性>> whos f显示图像:用imshow显示图像imshow(f, G)其中f是图像矩阵,G是像素的灰度级,G可以省略。
比如>> imshow(f, [100 200])图像上所有小于等于100的数值都会显示成黑色,所有大于等于200的数值都会显示成白色。
pixval命令可以用来查看图像上光标所指位置的像素值。
pixval例如>> f = imread('rose_512.tif');>> whos f>> imshow(f)如果要同时显示两幅图像,可以用figure命令,比如>> figure, imshow(g)用逗号可以分割一行中的多个命令。
imshow的第二个参数用一个空的中括号:>> imshow(h, [])可以使动态范围比较窄的图像显示更清楚。
写图像。
用imwrite写图像imwrite(f, 'filename')文件名必须包括指明格式的扩展名。
也可以增加第三个参数,显式指明文件的格式。
比如>> imwrite(f, 'patient10_run1.tif', 'tif')也可以写成>> imwrite(f, 'patient10_run1.tif')还可以有其他参数,比如jepg图像还有质量参数:>> imwrite(f, 'filename.jpg', 'quality', q)q是0到100之间的一个整数。




MATLAB基本的使用方法1.基本概念-MATLAB的核心是矩阵和向量计算,用户可以通过使用矩阵和向量进行数值计算、数据处理和建模。
-MATLAB提供了大量的内置函数和工具箱,可以进行各种数学和科学计算,如线性代数、统计分析、信号处理、图像处理等。
-MATLAB还具有强大的绘图功能,可以生成高质量的二维和三维图形。
2.MATLAB环境-命令窗口是和MATLAB交互的主要途径,可以直接输入和运行MATLAB命令。
3.基本操作-MATLAB中的变量可以通过使用赋值操作符(=)进行定义和赋值。
例如,a=10;定义了一个变量a,并赋值为10。
-MATLAB支持各种数学运算,如加法、减法、乘法、除法、幂运算等。
可以直接在命令窗口中输入运算式来进行计算。
-可以使用分号(;)来分隔多个命令,使其在一行中连续执行。
- MATLAB支持各种逻辑判断和流程控制,如if语句、for循环、while循环等。
通过逻辑判断和循环可以实现复杂的算法和程序。
4.矩阵和向量操作-MATLAB中的矩阵可以通过方括号([])来定义,矩阵的每个元素之间用空格或逗号隔开,每一行用分号(;)分隔。
- 可以使用内置函数来生成特殊矩阵,如单位矩阵(eye)、零矩阵(zeros)等。
-MATLAB支持各种矩阵运算,如加法、减法、乘法、除法、转置、逆、行列式、特征值等。
-向量是一种特殊的矩阵,只有一列或一行。
可以使用方括号或空格来定义向量。
5.数据处理和分析-MATLAB提供了大量用于数据处理和分析的函数和工具箱,可以进行数据清洗、变换、过滤、拟合、建模等操作。
- 可以使用内置函数读取和写入各种文件格式的数据,如文本文件、Excel文件、图像文件等。
-MATLAB还支持各种统计分析方法,如描述统计、假设检验、方差分析、回归分析等。
6.图形可视化-MATLAB具有强大的绘图功能,可以生成各种类型的图形,如折线图、散点图、柱状图、等高线图、三维曲面图等。

matlab系统使用方法Matlab是一种广泛应用于科学计算和工程设计的强大软件工具。
它提供了一种方便且高效的编程环境,使用户能够进行数据分析、可视化、算法开发和模型建立等。
本文将介绍Matlab的一些基本使用方法,帮助读者快速入门并掌握这个工具的基本技巧。
我们需要了解Matlab的界面。
当我们打开Matlab时,会出现一个称为Command Window的窗口,它是与Matlab交互的主要界面。
在Command Window中,我们可以输入命令或表达式,并立即看到结果。
此外,Matlab还提供了其他窗口,如Editor窗口用于编写和编辑代码,Workspace窗口用于管理变量,Figure窗口用于显示图形等。
接下来,让我们学习一些Matlab的基本操作。
首先是变量的定义和赋值。
在Matlab中,我们可以使用等号“=”来定义一个变量,并通过赋值运算符“=”为其赋值。
例如,如果我们要定义一个变量x并将其赋值为5,可以输入“x = 5”。
在Command Window中按下回车键后,变量x的值将被存储起来,并可以在后续的计算中使用。
除了基本的数值操作外,Matlab还提供了许多内置的函数和工具箱,用于处理不同类型的数据。
例如,如果我们想计算一个向量的平均值,可以使用Matlab提供的mean函数。
只需输入“mean(vector)”即可计算出向量的平均值。
Matlab还具有强大的矩阵操作功能。
我们可以使用矩阵来存储和处理数据。
在Matlab中,矩阵可以通过一对方括号来定义。
例如,我们可以使用以下命令定义一个3x3的矩阵A:A = [1, 2, 3; 4, 5, 6; 7, 8, 9]在以上命令中,分号用于分隔行,逗号用于分隔列。
定义完成后,矩阵A将被存储在内存中,并可以通过变量名进行调用。
Matlab还支持各种数学运算和函数,如加减乘除、幂运算、三角函数等。
我们可以直接在Command Window中输入表达式进行计算。
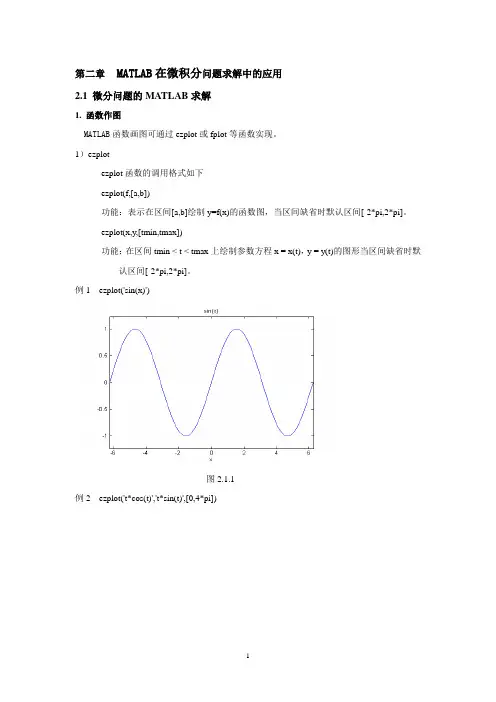
第二章 MATLAB在微积分问题求解中的应用2.1 微分问题的MATLAB求解1. 函数作图MATLAB函数画图可通过ezplot或fplot等函数实现。
1)ezplotezplot函数的调用格式如下ezplot(f,[a,b])功能:表示在区间[a,b]绘制y=f(x)的函数图,当区间缺省时默认区间[-2*pi,2*pi]。
ezplot(x,y,[tmin,tmax])功能:在区间tmin < t < tmax上绘制参数方程x = x(t),y = y(t)的图形当区间缺省时默认区间[-2*pi,2*pi]。
例1 ezplot('sin(x)')图2.1.1例2 ezplot('t*cos(t)','t*sin(t)',[0,4*pi])图2.1.22) fplotfplot 函数的调用格式如下fplot(fun,lims)功能:绘制函数fun在区间lims上的图形。
例3fplot('tan(x)',[-pi/4 pi/4])图2.1.32 极限的符号运算极限是高等数学中基本概念之一,在微积分中,很多概念是用极限定义的,例如导数和定积分。
因此,掌握极限的运算对学好高等数学是极为重要的。
在MATLAB中,极限的求解可由limit 函数来实现,limit 函数的格式及功能见表2.2.1。
表2.2.1 1limit 函数的格式及功能因为数列()n x f n =实际上就是定义在正整数集合上的函数,因此数列的极限可看成x →+∞时的特殊函数的极限;多元函数的极限可化为累次极限实现。
例1 求下列数列的极限1)lim n n→∞ 2)n →∞ 3)lim 3sin 3n n n π→∞ 4)1123lim 32n n n n n ++→∞-- 5))n →∞6)1lim()1n n n n →∞-+ 7)2(1)lim 1n n n →∞-+ 8)lim(1)n n →∞- 9)lim(2)nn →∞-解:syms n ar1=limit(sqrt(n^2+a^2)/n,n,inf,'left') 输出 r1 =1 r2=limit(sqrt(n^2+3)-sqrt(n^2-3),n,inf,'left') 输出r2 =0 r3=limit(3^n*sin(pi/3^n),n,inf,'left') 输出r3 =pir4=limit((2^n-3^(n+1))/(3^n-2^(n+1)),n,inf,'left') 输出r4 =-3 r5=limit(sin(pi*sqrt(n^2+1)),n,inf,'left') 输出r5 =1 .. 1 r6=limit(((n-1)/(n+1))^n,n,inf,'left') 输出r6 =exp(-2) r7=limit((n-1)^2/(n+1),n,inf,'left') 输出r7 =Infr8=limit((-1)^n,n,inf,'left') 输出r8 =-1 .. 1 r9=limit((-2)^n,n,inf,'left') 输出r9 =NaN 例2 求下列函数的极限 1)0sin()sin()limh x h x h →+- 2)3113lim()11x x x →--- 3)01lim sin x x x→ 4)3lim 2x tx →-5)0lim x x x-→ 6)lim (1)3x x t x →-∞+ 7)123lim()21x x x x +→∞+- 8)11lim sin 1x x x →- 9)lim sin x x x →∞解: syms x h tf1=limit((sin(x+h)-sin(x))/h,h,0) 输出f1 =cos(x) f2=limit(1/(1-x)-3/(1-x^3),x,1) 输出 f2 =-1 f3=limit(x*sin(1/x)) 输出 f3 =0 f4=limit(t/(x-2),3) 输出f4 =t f5=limit(abs(x)/x,x,0,'left') 输出f5 =-1f6=limit((1+t/(-3*x))^(-x),x,inf,'left') 输出f6 =exp(1/3*t) f7=limit(((2*x+3)/(2*x+1))^(x+1),x,inf) 输出f7 =exp(1) f8=limit(x*sin(1/(x-1)),x,1) 输出f8 =-1 .. 1 f9=limit(x*sin(x),x,inf) 输出f9 =NaN 例3 求下列函数的极限1)(,)(0,0)lim x y → 2)(,)lim y x y →解: syms x y;p1=limit(limit((2-sqrt(x*y+4))/(x*y),x,0),y,0) 输出p1 =-1/4 p2=limit(limit(log(x+exp(y))/sqrt(x^2+y^2),x,1),y,0) 输出p2 =log(2) 3. 一阶微商的计算由导数的定义可知,一切导数的问题,都可以用极限的方法求得,例如上面例2中的第1题。
MATLAB的基本使用教程详解MATLAB(Matrix Laboratory,矩阵实验室)是一种用于数值计算和可视化的编程环境。
它提供了强大的数值计算功能、丰富的数学函数库、快捷的可视化工具和易于使用的编程语言。
以下是关于MATLAB基本使用的一些教程:1. 安装和启动MATLAB:- 访问MATLAB官方网站下载并安装MATLAB。
- 安装完成后,在桌面上找到MATLAB图标并点击启动。
2. 创建一个新的MATLAB文件:- 在MATLAB界面,点击“新建”按钮,选择“新建图形”,或者使用快捷键Ctrl+N。
3. 基本的MATLAB命令:- 在命令窗口中输入命令并按Enter键执行。
例如,输入`1+2`并按Enter 键,将显示结果`3`。
- 可以使用括号对表达式进行组包。
例如,输入`(1+2)*3`并按Enter键,将显示结果`9`。
- 在MATLAB中,可以使用逗号将多个命令分开执行。
例如,输入`a = 1,b = 2,c = a+b`,将依次执行这三个命令并显示结果。
4. 变量和数组:- 在MATLAB中,可以使用`a = 1`的形式创建一个变量a并将其值设为1。
- 数组是一种可以存储多个相同类型数据的数据结构。
例如,可以使用`A = [1,2,3;4,5,6]`创建一个包含两行三列的数组。
5. 数学函数:- MATLAB提供了丰富的数学函数库,例如可以使用`sin(pi/2)`计算sin(π/2)的值。
- 可以同时使用多个函数对同一组输入参数进行操作。
例如,可以使用`c = a*b; d = log(a/b); e = sin(a)+cos(b)`同时对变量a、b进行多种操作。
6. 控制结构:- 可以使用`if`、`else`和`end`关键字创建条件语句。
例如,输入`if a > b, a = b; end`将使a的值等于b的值(如果a大于b)。
- 可以使用`for`循环遍历数组或向量。
matlab基本用法目录:一、说明二、数据类型及基本输入输出三、流程控制四、循环五、数组、数组运算和矩阵运算六、M脚本文件和M函数文件、函数句柄七、文件八、数据和函数的可视化一、说明matlab作为数学软件有其强大的图形用户界面操作、数据和函数的可视化和数值计算功能,且自带很多现有的函数和工具包。
而本文只涉及一些比较系统的基本操作,在最后附带介绍一些基本的数据和函数的可视化命令。
建议要用的时候再利用matlab自带的帮助文档来搜索有用的函数和工具包。
matlab的函数和命令都是比较人性化的,比如想要搜索读取fits文件的函数,搜索fits就能够搜到fitsread函数;需要将读出的fits数据重新做图,搜索image就可以找到imagesc函数。
从书和别人的文档都只能学到有限的比较系统的操作,看帮助文档能发现更多的东西并整理出自己的使用方法。
二、数据类型及基本输入输出1、数据类型,声明及赋初值matlab中存储的数据类型(class)有以下几种:而实际上matlab不需要对变量做声明,当它发现一个新的变量名时,将默认将其为双精度浮点类型(double)并分配内存空间。
(这比C和 Fortran方便了许多,但在完成大运算量的程序时就显得浪费存储空间了)当需要把变量a从double转为其他类型的时候,比如要转为int16型,可以使用以下命令:a=int16(a)当需要创建一个字符型变量x并对其赋初值时,用以下格式:x='字符串';注意:(1)在命令后加“;”表示不在command window中显示结果,而对上例来说如果不加“;”则会显示所赋字符串内容。
(2)所有的命令必须在英文输入状态下,如果使用中文输入状态下全角的“;”,将被处理为非法字符。
其中logical,cell和structure 为逻辑,元胞和构架数组类型,将在后面的数组部分提到;function handle为函数句柄类型,将在后面的“M脚本文件和M函数文件、函数句柄”部分提到;java类供JAVA API应用程序接口使用,本文不进行说明。
MATLAB基本使⽤⽅法基本使⽤⽅法⼀、简单数学运算(⼀)计算器使⽤⽅法a)直接输⼊法0.5*pi*5^2b)存储变量法a=0.5*pi*5^2注意:1)空格不处理2)遵守四则运算法则3)多重括号,从⾥向外运算4)⼩括号代表运算级别,中括号⽣成向量和数组,花括号⽣成单元数组(⼆)数学运算符(三)标点符号的使⽤>> a = [1,2,3;4,5,6;7,8,9] ⼆、常⽤命令和快捷键三、数据类型(⼀)整数>>x = int8(50)>>class(x)>>y = 50>>class(y)注意:1)MATLAB默认数据类型为双精度型,定义其它变量类型时需要指定类型2)整型除法运算时,系统先以双精度进⾏运算,将结果转为整型3)不同整型数据不能运算4)运算结果超出上限或下限,结果取值上限或下限>>x = int8(100)>>y = int8(90)>>z = x + y(⼆)浮点数单精度和双精度浮点数>>a = single(10.01)>>b = double(10.01)>>class(a)>>class(b)>>eps(‘single’)>>eps(‘double’)>>realmin(‘single’)>>realmax(‘single’)>>realmin(‘double’)>>realmax(‘double’)(三)复数>> a = 1 + 2i>> b = complex(1,2)>> c1 = int8([1;2;3;4])>> c2 = int8([5;6;7;8])>> c3 = complex(c1,c2)>> d1 = 1 + 0i>> d2 = complex(8,0)>> d3 = complex(9)>> isreal(d1)>> isreal(d2)>> isreal(d3)(四)逻辑变量1:真; 0:假>> a = [true, false, true, true, false] >> b1 = magic(3)>> b2 = b1 > 5>> b3 = sparse(b2)>> d1 = islogical(b1)>> d2 = islogical(b2)>> d3 = islogical(b3)>> A = rand(5)>> B = A>0.5>> A(B) = 0>> A = magic(4)>> B = isprime(A)>> A(~B) = 0(五)数据类型之间的运算双精度(double)数据可以和其它数据类型运算,结果为其它数据类型,⽽不是double数据。