一维数组的四个算法

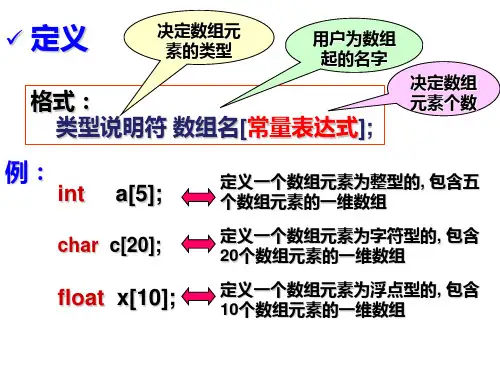
一维数组及数组的常见操作一维数组是一组相同类型的数据元素集合，存储在连续的内存空间中。

常见的一维数组操作包括：1. 声明数组：指定数组的类型和名称，例如：int[] arr;2. 创建数组：使用new关键字创建数组对象，并指定数组的长度，例如：arr = new int[5];3. 初始化数组：为数组元素赋初始值，可以通过循环遍历给数组元素逐个赋值，或者直接在声明数组时进行显示初始化，例如：int[] arr = {1, 2, 3, 4, 5};4. 访问数组元素：通过索引值来访问数组的元素，索引从0开始到数组长度-1，例如：int x = arr[3];5. 修改数组元素：通过索引值来修改数组的元素，例如：arr[2] = 10;6. 获取数组的长度：使用length属性获取一维数组的长度，例如：int length = arr.length;7. 遍历数组：使用循环遍历数组的所有元素，例如：for(inti=0; i<arr.length; i++) { System.out.println(arr[i]); }8. 搜索数组：可以使用循环遍历或者二分查找算法来搜索数组中的元素；9. 数组排序：可以使用各种排序算法对数组进行排序，例如冒泡排序、插入排序、选择排序、快速排序等；10. 数组拷贝：可以使用循环遍历或者System.arraycopy()方法将一个数组的元素复制到另一个数组；11. 数组的扩容：由于一维数组的长度在创建后固定不变，当需要添加新元素时，通常需要创建一个新数组，并将原数组的元素拷贝到新数组中；12. 数组的删除：可以通过创建新数组，并将原数组中需要保留的元素拷贝到新数组中，来实现删除数组元素的目的。

这些是一维数组的一些常见操作，还有其他一些操作和算法可以实现更复杂的功能。

1.6编程基础之一维数组01:与指定数字相同的数的个数总时间限制:1000ms内存限制:65536kB描述输出一个整数序列中与指定数字相同的数的个数。

输入输入包含三行：第一行为N，表示整数序列的长度(N <= 100)；第二行为N个整数，整数之间以一个空格分开；第三行包含一个整数，为指定的数字m。

输出输出为N个数中与m相同的数的个数。

样例输入样例输出02:陶陶摘苹果总时间限制:1000ms内存限制:65536kB描述陶陶家的院子里有一棵苹果树，每到秋天树上就会结出10个苹果。

苹果成熟的时候，陶陶就会跑去摘苹果。

陶陶有个30厘米高的板凳，当她不能直接用手摘到苹果的时候，就会踩到板凳上再试试。

现在已知10个苹果到地面的高度，以及陶陶把手伸直的时候能够达到的最大高度，请帮陶陶算一下她能够摘到的苹果的数目。

假设她碰到苹果，苹果就会掉下来。

输入包括两行数据。

第一行包含10个100到200之间（包括100和200）的整数（以厘米为单位）分别表示10个苹果到地面的高度，两个相邻的整数之间用一个空格隔开。

第二行只包括一个100到120之间（包含100和120）的整数（以厘米为单位），表示陶陶把手伸直的时候能够达到的最大高度。

输出包括一行，这一行只包含一个整数，表示陶陶能够摘到的苹果的数目。

样例输入样例输出来源NOIP2005复赛普及组第一题03:计算书费总时间限制:1000ms内存限制:65536kB描述下面是一个图书的单价表：计算概论28.9 元/本数据结构与算法32.7 元/本数字逻辑45.6元/本C++程序设计教程78 元/本人工智能35 元/本计算机体系结构86.2 元/本编译原理27.8元/本操作系统43 元/本计算机网络56 元/本JAVA程序设计65 元/本给定每种图书购买的数量，编程计算应付的总费用。

输入输入一行，包含10个整数(大于等于0，小于等于100)，分别表示购买的《计算概论》、《数据结构与算法》、《数字逻辑》、《C++程序设计教程》、《人工智能》、《计算机体系结构》、《编译原理》、《操作系统》、《计算机网络》、《JAVA程序设计》的数量（以本为单位）。

一维数组的赋值一维数组是一种常见的数据结构，可以存储一组相同类型的数据。

在编程中，给一维数组赋值是一项基本操作。

本文将介绍一维数组的赋值方法及其相关应用。

一、直接赋值法直接赋值法是最简单的一种给一维数组赋值的方法。

只需将要赋给数组的值逐个写入数组元素中即可。

例如，要给一个长度为5的整型数组赋值为1、2、3、4、5，可以使用如下代码：int[] arr = {1, 2, 3, 4, 5};这样就完成了整型数组arr的赋值。

需要注意的是，直接赋值法只适用于静态数组，即数组的长度在编译时已确定。

二、循环赋值法循环赋值法是一种常用的给一维数组赋值的方法。

通过使用循环结构，可以方便地给数组的每个元素赋值。

例如，要给一个长度为10的整型数组赋值为0到9的连续整数，可以使用如下代码：int[] arr = new int[10];for (int i = 0; i < arr.length; i++) {arr[i] = i;}这样就完成了整型数组arr的赋值。

循环赋值法适用于动态数组，即数组的长度在运行时才确定。

三、随机赋值法随机赋值法是一种给一维数组赋予随机值的方法。

通过使用随机数生成器，可以给数组的每个元素赋予不同的随机值。

例如，要给一个长度为5的整型数组赋予0到100之间的随机整数，可以使用如下代码：import java.util.Random;int[] arr = new int[5];Random random = new Random();for (int i = 0; i < arr.length; i++) {arr[i] = random.nextInt(101);}这样就完成了整型数组arr的赋值。

需要注意的是，随机赋值法需要使用Random类来生成随机数。

四、读取外部数据赋值法读取外部数据赋值法是一种给一维数组赋予外部数据的方法。

通过读取文件或从网络获取数据，可以将外部数据赋给数组的元素。

一维数组最短路径在计算机科学中，最短路径是一个重要的问题，在很多应用中都有广泛的应用。

而在一维数组中寻找最短路径也是一个常见的问题。

本文将介绍一维数组最短路径的相关概念及算法，帮助读者理解并解决这一问题。

一维数组是一个线性的数据结构，可以通过索引访问其中的元素。

而在一维数组中寻找最短路径，可以理解为在数组中找到从起点到终点的最短的访问路径。

这个问题可以抽象为一个图论问题，将数组中的元素看作是图中的节点，数组中的索引之间的关系看作是图中的边。

在一维数组中寻找最短路径的常见算法有多种，下面将介绍其中的两种：动态规划和迪杰斯特拉算法。

动态规划算法是一种通过将问题分解为子问题并记录子问题的解来解决复杂问题的方法。

在一维数组中寻找最短路径时，可以使用动态规划算法来解决。

具体步骤如下：1. 定义一个数组dp，dp[i]表示从起点到达第i个位置的最短路径长度。

2. 初始化dp数组，将所有的元素设置为无穷大。

3. 设置起点的最短路径为0，即dp[0] = 0。

4. 从起点开始遍历数组，对于每个位置i，更新其最短路径长度。

具体更新方法为：dp[i] = min(dp[i], dp[j] + 1)，其中j是i之前的位置。

5. 遍历完整个数组后，最终的最短路径长度即为dp数组的最后一个元素的值。

迪杰斯特拉算法是一种用于解决带权图中单源最短路径问题的算法。

在一维数组中寻找最短路径时，也可以使用迪杰斯特拉算法来解决。

具体步骤如下：1. 定义一个数组dist，dist[i]表示从起点到达第i个位置的最短路径长度。

2. 初始化dist数组，将所有的元素设置为无穷大。

3. 设置起点的最短路径为0，即dist[0] = 0。

4. 创建一个优先队列，用于选择下一个要访问的位置。

5. 将起点加入优先队列。

6. 进行循环，直到优先队列为空。

在每次循环中，从优先队列中选择一个距离起点最近的位置，更新其相邻位置的最短路径长度。

具体更新方法为：dist[i] = min(dist[i], dist[j] + weight[i])，其中j是与i相邻的位置，weight[i]是i到j的路径权重。

试设计一个算法,将一维数组a[n]的元素a[0]~a[n-1]循环右移k位,并要求只用一个元素试设计一个算法，将数组A中的元素A[0]至A[n-1]循环右移k位，并要求只用一个元素大小的附加存储，元素移动或交换次数为O(n).分析：我们看这个数组123456，循环右移2位。

先将数组逆序，654321，交换3次，然后交换前两个，564321，然后右面四个数字逆序，则561234，交换2次，正好是6次，并且在交换数据的时候，只使用了一个附加存储空间，正好满足题意。

#include <stdio.h> #include <stdlib.h> #include<iostream> #define maxsize 20 int arr[maxsize];using namespace std;void exchange_tool(int* arr, int len){ int i;int temp;for (i = 0; i<(len + 1) / 2; i++) { temp = *(arr + i); *(arr + i) = *(arr + len - i); *(arr + len - i) = temp;}}void rotate(int*arr, int n, int m){ m = m%n;exchange_tool(arr, n);exchange_tool(arr, m);exchange_tool(arr + m, n - m);}int main(){ int n, k, i;while (1) {cout << "数组长度？" << endl; cin >> n;cout << "右循环几位？" << endl;cin >> k;cout << "输入数字：" << endl;for (i = 0; i < n; i++) { cin >> *(&arr[i]); }rotate(arr, n, k);for (i = 0; i < n-1; i++) {cout << arr[i] << " "; }cout << arr[i] << endl;cout << endl;}return 0;}其中有2个地方要注意1. for(i=0;i<(len+1)/2;i++)，正好可以避开奇数和偶数的判断，大家自己琢磨一下。

一维数组快速填充算法-回复一维数组快速填充算法是一种用于将一维数组按照特定规则填充数据的算法。

它可以非常高效地将一维数组填充为指定的值，加快数据处理的速度。

在本文中，我将一步一步回答关于一维数组快速填充算法的问题，并详细介绍其原理和实现方法。

首先，我们需要清楚地了解什么是一维数组。

一维数组是一种最简单的数据结构，它由相同类型的元素组成，并按照一定的顺序排列。

一维数组通常用于存储大量的数据，例如存储学生的考试成绩、员工的工号等。

在计算机科学领域，我们经常需要对一维数组进行操作，而一维数组快速填充算法就是其中的一种。

接下来，我将介绍一维数组快速填充算法的原理。

该算法的主要思想是通过循环遍历数组的每个元素，将指定的值填充到数组中。

这种填充方式有多种实现方法，例如可以使用普通的循环语句、递归函数或者库函数。

这些方法各有优劣，主要取决于具体的应用场景和性能需求。

然后，让我们来看一下一维数组快速填充算法的具体实现方法。

以下是一种基于循环的填充算法：1. 首先，我们需要定义一个一维数组。

可以使用编程语言提供的数组数据类型，或者使用指针和动态内存分配来创建数组。

例如，在C语言中可以使用int类型的数组来存储整数数据。

2. 接下来，我们需要定义一个变量来存储填充的值。

这个值可以是任何与数组元素类型兼容的数据，例如整数、字符或者自定义的数据类型。

3. 然后，我们使用一个循环语句遍历数组的每个元素，并将填充的值赋给数组元素。

循环的次数通常与数组的长度相同，可以使用数组的长度属性或者计算得到。

4. 最后，我们输出或使用填充后的数组。

可以将数组的值打印到控制台上，或者将其传递给其他函数进行进一步处理。

该算法的时间复杂度为O(n)，其中n是数组的长度。

这是因为我们需要遍历数组的每个元素，将填充的值复制到数组中。

如果使用递归函数来实现填充算法，时间复杂度可能更高，取决于递归的深度和执行效率。

虽然一维数组快速填充算法非常简单，但在实际应用中却具有重要的意义。

一维数组比大小的方法引言概述：在计算机编程中，一维数组是一种常见的数据结构，它由一系列元素组成，这些元素按照顺序排列在内存中。

在处理一维数组时，经常需要比较数组中的元素的大小。

本文将介绍一维数组比大小的方法，包括如何比较数组中的最大值和最小值，以及如何按照升序或降序排列数组元素。

正文内容：1. 比较数组中的最大值和最小值1.1 使用循环遍历数组，将第一个元素设为最大值和最小值的初始值。

1.2 依次比较数组中的每个元素，更新最大值和最小值。

1.3 最终得到数组中的最大值和最小值。

2. 按照升序排列数组元素2.1 使用冒泡排序算法，比较相邻的元素，如果前一个元素大于后一个元素，则交换它们的位置。

2.2 重复进行上述比较和交换操作，直到整个数组按照升序排列。

2.3 冒泡排序的时间复杂度为O(n^2)，适用于小规模的数组排序。

3. 按照降序排列数组元素3.1 使用选择排序算法，找到数组中的最大值，并将其与数组的第一个元素交换位置。

3.2 在剩余的元素中找到最大值，并将其与数组的第二个元素交换位置。

3.3 重复进行上述选择最大值和交换操作，直到整个数组按照降序排列。

3.4 选择排序的时间复杂度为O(n^2)，同样适用于小规模的数组排序。

4. 比较数组中的相邻元素4.1 使用循环遍历数组，比较相邻的元素。

4.2 如果前一个元素大于后一个元素，则进行相应的操作。

4.3 可以根据需求，比较相邻元素的大小并进行相应的处理，例如交换位置或进行其他操作。

5. 使用数组排序方法5.1 大多数编程语言提供了现成的数组排序方法，例如Java中的Arrays.sort()。

5.2 这些方法使用高效的排序算法，如快速排序或归并排序，可以快速且准确地对数组进行排序。

5.3 使用数组排序方法可以简化代码，并提高排序效率。

总结：通过本文的介绍，我们了解了一维数组比大小的方法。

可以通过比较数组中的最大值和最小值来获取数组的范围，也可以按照升序或降序排列数组元素。

一维数组应用实验过程中遇到的问题及解决一、实验目的本次实验的主要目的是通过实践操作，了解一维数组的基本概念、应用场景和操作方法，提高自己的编程能力和解决问题的能力。

通过对比分析不同算法的优缺点，为今后的学习和工作打下坚实的基础。

二、实验内容1. 一维数组的基本概念和操作方法2. 一维数组在实际问题中的应用3. 不同算法在处理一维数组时的性能对比三、实验过程及遇到的问题及解决1. 一维数组的基本概念和操作方法在我们开始实验之前，首先需要了解一维数组的基本概念。

简单来说，一维数组就是一个由相同数据类型组成的有序序列。

在计算机中，我们可以用数组来存储多个相同的数据，这样可以节省内存空间，提高程序运行效率。

那么，如何操作一维数组呢？我们可以通过以下几种方式来实现：(1)初始化一维数组：在声明数组时，我们需要指定数组的数据类型和大小。

例如，我们可以创建一个整型数组，包含5个元素：```cppint arr[5];```(2)给数组赋值：我们可以通过下标的方式给数组的每个元素赋值：```cpparr[0] = 1;arr[1] = 2;arr[2] = 3;arr[3] = 4;arr[4] = 5;```(3)访问数组元素：我们可以通过下标的方式访问数组的任意一个元素：```cppint first_element = arr[0]; // first_element的值为1```(4)遍历数组：我们可以使用循环结构来遍历数组的所有元素：```cppfor (int i = 0; i < 5; i++) {cout << arr[i] << " "; // 输出数组的所有元素}```2. 一维数组在实际问题中的应用在实际问题中，一维数组有很多应用场景。

例如，我们可以用一维数组来表示一个人的成绩：```cppint scores[5] = {90, 80, 70, 60, 50}; // 表示5个人的成绩，分别用0-4的索引表示```我们还可以用一维数组来模拟掷骰子的过程：```cppint dice[6]; // 用一维数组表示6个面的点数(1-6)for (int i = 0; i < 6; i++) {dice[i] = rand() % 6 + 1; // 随机生成1-6之间的整数作为骰子的点数}```3. 不同算法在处理一维数组时的性能对比在实验过程中，我们还尝试了不同的算法来处理一维数组。

定义一维整型数组输入五个数从大到小排序输出次最大值1.引言1.1 概述概述部分的内容编写如下：引言部分的概述主要是对文章的主题进行一个简要介绍，给读者一个整体的了解。

本文的主题是关于定义一维整型数组，输入五个数，并按照从大到小的顺序进行排序，并输出次最大值。

接下来，将对文章的结构进行介绍，以及明确文章的目的。

在本文中，我们将介绍如何定义一维整型数组，并利用该数组来存储用户输入的五个整数。

然后，我们将通过某种排序算法，将这五个数按照从大到小的顺序进行排序。

最后，我们将输出排序结果中次最大的数值。

通过本文的阅读，读者将掌握如何操作一维整型数组，以及如何进行排序和输出最大值的操作。

这将有助于读者加深对数组的理解和应用，并提高解决问题的能力。

接下来，我们将进入正文部分，具体介绍一维整型数组的定义、输入五个数、排序和输出次最大值的步骤和方法。

1.2文章结构1.2 文章结构本文主要包括以下几个部分：2.1 定义一维整型数组：介绍如何定义一个一维整型数组，并说明数组的作用和意义。

2.2 输入五个数：介绍如何通过用户输入从键盘获取五个整数，并将它们存储到定义的数组中。

2.3 从大到小排序：详细讲解如何使用排序算法对数组进行从大到小的排序。

可以介绍常用的排序算法，例如冒泡排序、快速排序等，以及它们的原理和具体实现。

2.4 输出次最大值：最后，介绍如何从排序后的数组中获取次大的值，并将其输出。

可以提供一个函数或者方法来实现这个功能，并给出具体的代码示例。

通过以上几个步骤，我们可以将用户输入的五个数按照从大到小的顺序排列，并输出其中的次大值。

读者通过本文可以了解到如何使用一维数组和排序算法来实现这个功能，提升对数组和排序算法的理解和应用能力。

在结论部分，我们将对整个过程进行总结，并对代码的执行效率和结果进行分析，评估算法的优劣和可行性。

目的部分的内容应该描述本篇文章的目的和意义。

可以如下编写："1.3 目的本篇文章旨在介绍如何定义一维整型数组，并通过输入五个数并进行从大到小排序的操作，输出次最大值。

python 一维数组有损压缩算法一维数组的有损压缩算法用于减小数组的数据量，以节省存储空间。

有损压缩意味着在压缩数据时，会损失一些信息，但通常会尽量减小数据的损失，以在保持可接受数据质量的同时减小数据大小。

以下是一些用于一维数组的常见有损压缩算法：
1. 差分编码（Differential Encoding）：差分编码算法将数组中的元素与前一个元素之间的差异编码为新的值。

这可以用于数组中包含递增或递减的连续数值，以减小数据的大小。

2. 运行长度编码（Run-Length Encoding，RLE）：RLE 算法将连续重复的值替换为一个值和重复次数的组合。

这对于包含大量相同值的数组非常有效。

3. 哈夫曼编码（Huffman Coding）：哈夫曼编码通常用于编码符号流，但也可以用于一维数组。

它根据符号频率创建可变长度的编码，将高频率的值用短编码表示，低频率的值用长编码表示。

4. 差分脉冲编码调制（DPCM）：DPCM 用于连续信号的压缩。

它通过将信号样本与预测值之间的差异编码来减小数据量。

5. 小波变换（Wavelet Transform）：小波变换是一种在信号处理和图像压缩中常用的有损压缩技术。

它通过将信号或数组变换为不同频率成分的系数来减小数据量。

这些算法可以单独使用或组合使用，具体取决于数据的特性和应用需求。

需要注意的是，有损压缩会导致数据的信息损失，因此在某
些应用中，特别是对数据完整性要求很高的情况下，可能需要谨慎使用有损压缩算法。

VB常用算法算法1 交换2个变量的值算法思想：若交换两个变量的值，必须引入第三个新的变量进行传递。

交换a，b的值： t=a：a=b：b=t或者t=b：b=a：a=t算法2 产生随机数算法思想：生成一个[a,b]区间的整数公式为Int(Rnd*(b-a+1))+a1.自动生成[0，100]之间的随机数: Int(Rnd*101)2.自动生成2位随机整数: Int(Rnd*90+10)例：自动产生10个100~999之间的随机整数，并放到数组a中Dim a(10 ) as integerFor i=1 to 10a(i) =Int(Rnd*900)+100Next i算法3判断一个数是否能被另一个数整除算法思想：可以用整除的定义（余数为0）或X除以Y等于X整除Y等表达式进行判断。

条件表达式可以为：X mod Y=0或X＼Y=X/Y或Int(X/Y)=X/Y如果以上条件表达式为True，则表示X能被Y整除。

例题：统计0—100之间能被3整除的数的个数、累加和及其平均值。

s=0n=0For i=0 To 100If i mod 3=0 Thens=s+in=n+1End IfNext iPrint n,s,s/n算法4 求阶乘和累加和算法思想：使用循环语句，并用一个变量存放累加的中间及最终结果。

注:(1)累加求和时变量初值为0。

(2)计算阶乘时变量初值为1。

(3)统计计个数（计数）时可用一个变量作为统计个数的累加变量，每次加1即可。

(4)求平均值算法思想是先求和，再除以个数。

(5)条件求和（或计数）：在循环语句中加入If－End If判断语句。

1.求1 ~n个自然数的阶乘s=1For i=1 to ns=s*iNext i2.求1 ~n个自然数的累加和s=0For i=1 to ns=s+iNext i例题：计算1到10之间所有整数的累加和以及10！。

n=10sum= 0prod= 1For i=1 To 10sum=sum+ iprod=prod* iNext iPrint sum,prod例题：统计1—100之间能被3和7整除的数的个数、并求它们的累加和。

一维数组是一种常见的数据结构，它可以用来存储一组有序的数据。

在计算机编程领域，一维数组通常被用来表示一系列的数值或者其他类型的数据。

本文将介绍如何利用一维数组来计算斐波那契数列的前20项。

斐波那契数列是由意大利数学家斐波那契在13世纪提出的一个数列，它的定义如下：数列的第一项和第二项都是1，从第三项开始，每一项都是前两项的和。

即F(1)=1，F(2)=1，F(n)=F(n-1)+F(n-2)，其中n>2。

计算斐波那契数列的前20项可以用多种方法，其中一种方法是利用一维数组来存储数列的每一项。

下面将介绍如何使用一维数组来计算斐波那契数列的前20项。

1. 创建一个长度为20的一维数组fibonacci，用来存储斐波那契数列的前20项。

数组的第一个和第二个元素分别赋值为1，表示数列的前两项。

2. 使用一个循环来计算数列的后18个项。

在每一次循环中，将数组的第i个元素赋值为数组的第i-1个元素和第i-2个元素的和。

具体的代码如下所示：```int fibonacci[20];fibonacci[0] = 1;fibonacci[1] = 1;for (int i = 2; i < 20; i++) {fibonacci[i] = fibonacci[i-1] + fibonacci[i-2];}```3. 完成上述步骤后，数组fibonacci中存储的就是斐波那契数列的前20项。

可以将数组的内容打印出来，以验证计算的正确性。

以下是打印数组内容的代码：```for (int i = 0; i < 20; i++) {cout << fibonacci[i] << " ";}```通过上述方法，我们成功利用一维数组计算出了斐波那契数列的前20项。

这种方法的优点是简单易懂，代码量少，而且计算效率高。

一维数组的存储结构也符合斐波那契数列的定义，因此很适合用来存储数列的每一项。

vba 一维数组排序详解VBA（Visual Basic for Applications）是一种高级宏语言，它主要用于在Microsoft Office软件中编写自定义的宏和自动化任务。

其中一个常见的任务是对一维数组进行排序。

在本文中，我们将详细介绍VBA中一维数组排序的方法，并提供示例代码和指导意义。

一维数组是由相同数据类型的多个元素组成的线性数据结构。

在VBA中，我们可以使用一维数组来存储和操作大量相似的数据。

但是，有时我们需要对数组中的元素进行排序，以便更方便地查找和处理数据。

下面是VBA中一维数组排序的几种常见方法：1. 冒泡排序（Bubble Sort）：冒泡排序是一种简单而常见的排序算法。

它通过不断比较相邻的元素，并交换位置，将较大（或较小）的元素逐渐“冒泡”到数组的一端。

具体步骤如下：- 从数组的第一个元素开始，依次比较相邻的元素。

- 如果当前元素大于（或小于）后一个元素，则交换它们的位置。

- 重复上述步骤，直到没有交换操作发生。

示例代码：```vbaSub BubbleSort(arr() As Variant)Dim i As LongDim j As LongDim temp As VariantFor i = LBound(arr) To UBound(arr) - 1For j = LBound(arr) To UBound(arr) - 1 - i If arr(j) > arr(j + 1) Thentemp = arr(j)arr(j) = arr(j + 1)arr(j + 1) = tempEnd IfNext jNext iEnd Sub```2. 快速排序（Quick Sort）：快速排序是一种高效的排序算法，它通过分割和递归的方法，将数组逐步划分为较小和较大的部分，然后对各个部分进行排序。

具体步骤如下：- 选择一个基准元素（通常选择第一个或最后一个元素）。

总结一维数组知识点1. 数组的声明和初始化在大多数编程语言中，声明和初始化数组的方法类似，需要指定数组的类型和大小。

在C语言中，可以使用以下方式声明和初始化一个整型数组：int arr[5] = {1, 2, 3, 4, 5};在Java语言中，可以使用以下方式声明和初始化一个整型数组：int[] arr = {1, 2, 3, 4, 5};在Python语言中，可以使用以下方式声明和初始化一个整型数组：arr = [1, 2, 3, 4, 5]无论使用何种语言，声明和初始化数组都是一个基本的操作，程序员需要根据具体的需求选择合适的方式来完成数组的声明和初始化。

2. 数组的访问和操作一维数组中的元素可以通过索引来进行访问和操作。

在大多数编程语言中，数组的索引都是从0开始的，即第一个元素的索引为0，第二个元素的索引为1，依此类推。

可以使用以下方式来访问和操作数组中的元素：int x = arr[2]; // 访问数组中索引为2的元素arr[3] = 10; // 修改数组中索引为3的元素的值为10可以使用循环结构来遍历数组中的所有元素：for (int i = 0; i < arr.length; i++) {System.out.println(arr[i]);}程序员需要熟练掌握数组的访问和操作方法，并能够灵活运用在实际的编程中。

3. 数组的排序和搜索在实际的程序中，经常需要对数组进行排序和搜索操作。

排序可以让数组中的元素按照一定的规则进行排列，从而方便后续的操作。

常见的排序算法有冒泡排序、选择排序、插入排序、快速排序、归并排序等。

程序员需要根据具体的情况选择合适的排序算法来对数组进行排序。

搜索则是查找数组中是否包含某个元素或者查找某个元素的位置。

常见的搜索算法有线性搜索、二分搜索、哈希搜索等。

程序员需要了解不同的搜索算法的工作原理和适用场景，灵活运用到实际的程序中。

4. 数组的内存分配和优化数组是在内存中连续储存的数据结构，因此在使用数组时需要注意内存分配和优化的问题。