仿射变换用于从图像中提取目标块

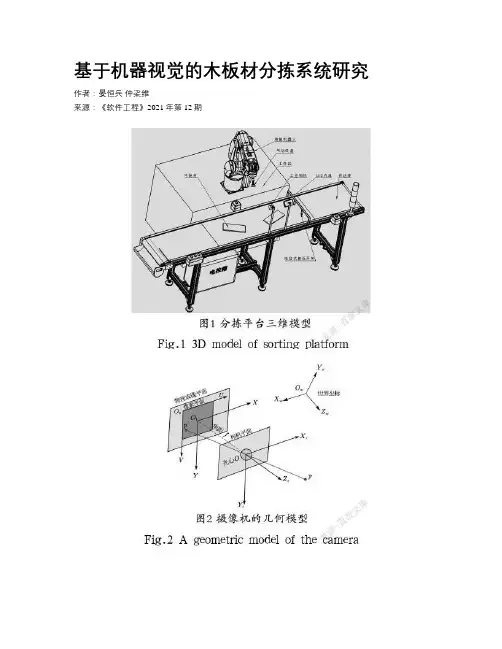
基于机器视觉的木板材分拣系统研究作者：晏恒兵仲梁维来源：《软件工程》2021年第12期摘要：木板材作為一种支撑社会发展的重要原材料，被广泛应用于建筑装修业和家具制造业，为了合理利用有限的木材资源，对其进行有效的检测至关重要。

改进的Faster R-CNN （“两阶段”检测）算法对木板材活节、死节、孔洞、裂纹等四类缺陷检测的平均精度分别为99.84%、94.24%、91.28%、90.06%，平均精度均值为93.86%，并根据木板材缺陷类型对其进行等级划分。

利用机器视觉引导技术，分拣机器人能够自动定位放置在传送带上的木板材，并依据木板材等级对其进行分拣作业。

本文还基于C++语言、Qt框架搭建了用于支撑系统运行的软件平台。

关键词：机器视觉;木板材分拣;机器人分拣;深度学习中图分类号：TP302.7 文献标识码：AAbstract： Wood panel， as an important raw material to support social development， is widely used in building， decorating and furniture manufacturing industry. To make the most of limited wood resources， it is very important to detect wood panel effectively. The improved Faster R-CNN （Faster Region-based Convolutional Neural Network， a "two-stage" detection） algorithm has an average precision of 99.84%， 94.24%， 91.28%， and 90.06% for detecting wood panel live knots， dead knots， holes， and cracks， respectively. The mean average precision is 93.86%，and wood panels are classified by defect types. BY using machine vision guidance technology，sorting robots automatically locate the wood panels placed on the conveyor belt， and sort them according to the grade of the wood panels. A software platform for system operation is built based on C++ language and Qt framework.Keywords： machine vision; wood panel sorting; robot sorting; deep learning1 引言（Introduction）长期以来，我国在基础设施上的投入逐年递增，木材需求也在不断增加。

仿射变换跟影射变换1.引言1.1 概述本文将介绍两种常见的几何变换方式：仿射变换和影射变换。

这两种变换方式在计算机视觉、图形学和图像处理领域中得到广泛的应用。

仿射变换是一种线性变换，其保持直线的性质。

在仿射变换中，平行线仍然保持平行，不会相交或者改变其相对位置关系。

此外，仿射变换也保持了物体的平直性和距离比例。

在实际应用中，我们常常用仿射变换来描述物体之间的平移、旋转、缩放和倾斜关系。

影射变换则是一种更为一般化的几何变换方式。

与仿射变换不同的是，影射变换可以改变直线的性质。

在影射变换中，我们可以看到平行线相交的情况，并且物体之间的距离比例也可能会改变。

影射变换提供了更大的灵活性，可以描述更为复杂的物体变换关系。

本文将会深入探讨仿射变换和影射变换的定义、特点以及它们在实际应用中的差异和共同点。

通过对它们的对比和分析，我们将能够更好地理解和应用这两种变换方式。

在下一节中，我们将开始介绍仿射变换的定义和特点。

1.2 文章结构文章结构部分将详细介绍本文的整体结构安排，包括各个章节的内容概述和相互之间的联系。

本文将围绕仿射变换和影射变换展开讨论，分为引言、正文和结论三个部分。

在引言部分，我们将对本文的主题进行概述，简要介绍仿射变换和影射变换的背景和基本概念，并阐明为何选择这两个主题进行研究。

同时，我们还会介绍本文的结构和目标，为读者提供整体的导引。

接下来的正文部分将详细探讨仿射变换和影射变换。

在2.1节中，我们将先对仿射变换进行定义，介绍其基本概念和数学表达式。

然后，在2.1.2节中，我们将进一步探讨仿射变换的特点，包括线性性、保直线性、保平行性等。

在2.2节中，我们将转向影射变换的讨论。

同样地，我们首先给出影射变换的定义和基本表达式，然后在2.2.2节中探讨其特点，例如保面积性质、保角性质和保相似性质等。

最后，在结论部分，我们将总结仿射变换和影射变换的主要内容和特点。

我们将强调它们之间的关联和差异，并探讨它们在实际应用中的重要性。

何为仿射变换（AffineTransformation）变换模型是指根据待匹配图像与背景图像之间⼏何畸变的情况，所选择的能最佳拟合两幅图像之间变化的⼏何变换模型。

可采⽤的变换模型有如下⼏种:刚性变换、仿射变换、透视变换和⾮线形变换等，如下图：其中第三个的仿射变换就是我们这节要讨论的。

仿射变换(Affine Transformation)Affine Transformation是⼀种⼆维坐标到⼆维坐标之间的线性变换，保持⼆维图形的“平直性”（译注：straightness，即变换后直线还是直线不会打弯，圆弧还是圆弧）和“平⾏性”（译注：parallelness，其实是指保⼆维图形间的相对位置关系不变，平⾏线还是平⾏线，相交直线的交⾓不变。

）。

c和d的区别可以看下图：仿射变换可以通过⼀系列的原⼦变换的复合来实现，包括：平移（Translation）、缩放（Scale）、翻转（Flip）、旋转（Rotation）和剪切（Shear）。

仿射变换可以⽤下⾯公式表⽰：这个矩阵乘法的计算如下：具体到⼆维的仿射变换的计算如下：⼏种典型的仿射变换如下：平移变换 Translation将每⼀点移动到(x+tx, y+ty)，变换矩阵为：平移变换是⼀种“刚体变换”，rigid-body transformation，就是不会产⽣形变的理想物体。

效果：缩放变换（Scale）将每⼀点的横坐标放⼤（缩⼩）⾄sx倍，纵坐标放⼤（缩⼩）⾄sy倍，变换矩阵为：变换效果如下：剪切变换（Shear）变换矩阵为：相当于⼀个横向剪切与⼀个纵向剪切的复合效果：旋转变换（Rotation）⽬标图形围绕原点顺时针旋转theta弧度，变换矩阵为：效果：组合旋转变换，⽬标图形以(x, y)为轴⼼顺时针旋转theta弧度，变换矩阵为：相当于两次平移变换与⼀次原点旋转变换的复合：先移动到中⼼节点，然后旋转，然后再移动回去。

这个转换矩阵也可以下⾯这样描述。

第一章测试1.图像是对物体的一种完全的、精确的描述。

（）A:对B:错答案:B2.根据图像的连续性，可以分为（）。

A:模拟图像B:物理图像C:数字图像D:虚拟图像答案:AC3.我们平时常用的PS技术属于图像处理中的（）。

A:图像到图像的处理B:图像到非图像的处理C:目标检测D:图像分类答案:A4.数字图像处理系统包括（）。

A:图像处理器B:输出设备C:存储器D:图像传感器答案:ABCD5.使用CT图像判断患者是否感染新冠肺炎属于图像处理中的（）。

A:图像分类B:目标跟踪C:图像语义分割D:目标检测答案:A6.数字图像坐标系中坐标原点在图像的（）。

A:右上角B:左下角C:右下角D:左上角答案:D7.我们日常生活中所说的黑白照片实际上是指（）。

A:都不是B:灰度图像C:二值图像D:彩色图像答案:B8.手机指纹、人脸解锁技术使用了图像处理中的生物特征识别技术。

（）A:对B:错答案:A9.图像生成技术生成的是实际存在的物理图像。

（）A:错B:对答案:A10.常见的数字图像处理技术的前沿应用有（）。

A:目标检测B:图像风格化C:图像生成D:图像分类答案:ABCD第二章测试1.图像的数字化不包括以下哪个步骤（）。

A:采样B:光电转换C:量化D:滤波答案:D2.一般来说，采样间距越大，图像数据量越少，质量越差。

（）A:错B:对答案:B3.扫描仪分辨率的单位是：（）。

A:dpiB:厘米C:像素D:bit答案:A4.目前非特殊用途的图像通常采用的量化等级是：（）。

A:3bitB:8bitC:16bitD:4bit答案:B5.量化是将各个像素所含的位置信息离散化后，用数字来表示。

（）A:对B:错答案:B6.如果图像的量化等级在____个灰度级以下，会发生伪轮廓现象。

（）。

A:2B:4C:8D:256答案:C7.索引色模式图像数据区保存的是：（）。

A:坐标值B:RGB值C:调色板D:颜色索引值答案:D8.真彩色模式图像数据区保存一个像素需要：（）。

图像配准中仿射变换参数优化方案一、图像配准技术概述图像配准技术是图像处理领域中的一项重要技术，它涉及将两幅或多幅图像按照一定的几何关系对齐，以便于进行后续的分析和处理。

在实际应用中，图像配准技术广泛应用于医学成像、遥感图像分析、计算机视觉等领域。

图像配准的关键在于如何准确地确定图像之间的几何变换关系，其中仿射变换是一种常用的几何变换形式。

1.1 仿射变换的定义仿射变换是一种二维图像变换方法，它能够保持图像中的直线、平行线和点的共线性不变。

仿射变换可以用一个6参数的矩阵来表示，包括平移、旋转、缩放和剪切等变换。

在图像配准中，通过优化这些参数，可以使两幅图像在几何上尽可能地对齐。

1.2 仿射变换的应用场景仿射变换在图像配准中的应用场景非常广泛，例如：- 医学成像：在进行CT、MRI等医学图像分析时，需要将不同时间点或不同角度拍摄的图像进行配准，以便进行病变的跟踪和分析。

- 遥感图像：在遥感图像处理中，需要将不同时间或不同传感器获取的图像进行配准，以便于进行地表变化检测和分析。

- 计算机视觉：在机器视觉和自动驾驶系统中，需要对摄像头捕获的图像进行配准，以实现物体的识别和跟踪。

二、仿射变换参数优化的重要性在图像配准过程中，仿射变换参数的优化是实现高精度配准的关键。

参数优化的目标是最小化两幅图像之间的差异，这通常通过定义一个代价函数来实现，该函数衡量了图像之间的相似度或差异度。

2.1 代价函数的选择代价函数的选择对参数优化的效果有着直接的影响。

常见的代价函数包括：- 均方误差(MSE)：计算两幅图像对应像素点的灰度值差的平方和，常用于灰度图像的配准。

- 互相关(Cross-Correlation)：计算两幅图像的局部区域之间的相似度，常用于特征不明显的图像配准。

- 归一化互相关(Normalized Cross-Correlation, NCC)：在互相关的基础上进行归一化处理，提高了配准的鲁棒性。

2.2 参数优化算法参数优化算法是实现仿射变换参数优化的核心，常用的算法包括：- 梯度下降法：通过计算代价函数的梯度来迭代更新参数，直至找到最小值。

C++ OpenCV 求两个轮廓之间的仿射变换在图像处理和计算机视觉领域，求两个轮廓之间的仿射变换是一个常见的问题。

通过对两个对象的轮廓进行比较和匹配，我们可以得到它们之间的相似度，并且可以根据它们之间的差异来进行一些后续处理，比如目标跟踪、物体识别等应用。

在 C++ OpenCV 中，我们可以利用一些图像处理的库函数来实现对两个轮廓之间的仿射变换。

接下来，我将介绍如何在 C++ OpenCV 中实现求两个轮廓之间的仿射变换，包括获取轮廓、计算仿射变换矩阵和应用仿射变换等步骤。

1. 获取轮廓我们需要从图像中获取两个对象的轮廓。

在 OpenCV 中，我们可以利用 findContours 函数来实现轮廓的获取。

该函数需要输入一个二值化的图像作为参数，然后返回一个包含所有轮廓信息的std::vector 对象。

```cppstd::vector<std::vector<cv::Point>> contours;cv::findContours(binaryImage, contours, CV_RETR_EXTERNAL,CV_CH本人N_APPROX_SIMPLE);```在上面的代码中，binaryImage 是经过预处理后的二值化图像，CV_RETR_EXTERNAL 和 CV_CH本人N_APPROX_SIMPLE 分别表示提取外部轮廓和使用简单的逼近方法。

contours 是一个包含所有轮廓信息的容器。

2. 计算仿射变换矩阵一旦获取了两个对象的轮廓，接下来就需要计算它们之间的仿射变换矩阵。

在 OpenCV 中，我们可以利用函数 getAffineTransform 来实现这一步。

```cppcv::Mat M = cv::getAffineTransform(obj1, obj2);```在上面的代码中，obj1 和 obj2 分别是两个对象的轮廓点集，M 是一个 2x3 的仿射变换矩阵。

仿射变换详解warpAffine今天遇到一个问题是关于仿射变换的，但是由于没有将仿射变换的具体原理型明白，看别人的代码看的很费解，最后终于在师兄的帮助下将原理弄明白了，我觉得最重要的是理解仿射变换可以看成是几种简单变换的复合实现，具体实现形式即将几种简单变换的变换矩阵M相乘，这样就很容易理解啦定义：仿射变换的功能是从二维坐标到二维坐标之间的线性变换，且保持二维图形的“平直性”和“平行性”。

仿射变换可以通过一系列的原子变换的复合来实现，包括平移，缩放，翻转，旋转和剪切。

这类变换可以用一个3*3的矩阵M来表示，其最后一行为（0，0，1）。

该变换矩阵将原坐标为（x,y)变换为新坐标（x',y')，即OpenCV中相应的函数是：void warpAffine(InputArray src, OutputArray dst, InputArray M, Size dsize,int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, constScalar& borderValue=Scalar())¶Parameters:∙src –input image.∙dst –output image that has the size dsize and the same type as src .∙M – transformation matrix，最重要的东东了，本文中着重讲M的构造∙dsize –size of the output image.ansformation ( ).∙borderMode – pixel extrapolation method (see borderInterpolate()); when borderM ode=BORDER_TRANSPARENT , it means that the pixels in the destination image correspon ding to the “outliers” in the source image are not modifi ed by the function.∙borderValue –value used in case of a constant border; by default, it is 0.下面介绍一些典型的仿射变换：（1）平移，将每一点移到到（x+t , y+t)，变换矩阵为(2)缩放变换将每一点的横坐标放大或缩小s x倍，纵坐标放大（缩小）到s y倍，变换矩阵为（3）旋转变换原点：目标图形围绕原点顺时针旋转Θ 弧度，变换矩阵为(4) 旋转变换：目标图形以（x , y ）为轴心顺时针旋转θ弧度，变换矩阵为相当于两次平移与一次原点旋转变换的复合，即先将轴心（x,y)移到到原点，然后做旋转变换，最后将图片的左上角置为图片的原点,即有的人可能会说为什么这么复杂呢，那是因为在opencv的图像处理中，所有对图像的处理都是从原点进行的，而图像的原点默认为图像的左上角，而我们对图像作旋转处理时一般以图像的中点为轴心，因此就需要做如下处理如果你觉得这样很麻烦，可以使用opencv中自带的Mat getRotationMatrix2D(Point2f center, double angle, double scale)函数获得变换矩阵M，center:旋转中心angle：旋转弧度，一定要将角度转换成弧度scale:缩放尺度它得到的矩阵是：其中α = scale * cos( angle ) , β = scale* sing( angle ) , ( center.x , center.y ) 表示旋转轴心但是不得不说opencv的文档以及相关书籍中都把这个矩阵写错了，如下：建议大家自己通过下式验证一下，即首先将轴心(x,y)移到原点，然后做旋转平绽放变换，最后再将图像的左上角转换为原点没有去研究该函数的源码，不晓得源码中到底怎么写的，但是在别人的博客中看到这个函数貌似需要修正opencv中还有一个函数：Mat getAffineTransform(InputArray src, InputArray dst)¶它通过三组点对就可以获得它们之间的仿射变换，如果我们在一组图像变换中知道变换后的三组点，那么我们就可以利用该函数求得变换矩阵，然后对整张图片进行仿射变换还有一种与仿射变换经常混淆的变换为透视变换，透视变换需要四组点对才能确定变换矩阵，由于仿射变换保持“平直性”与“平行性”，因此只需要三组点对，而透视变换没有这种约束，故需要四组点对warpPerspective函数主要作用：对图像进行透视变换，就是变形函数的调用形式：C++:void warpPerspective(InputArray src, OutputArray dst, InputArray M, Size dsize,int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, constScalar& borderValue=Scalar())参数详解：InputArray src：输入的图像OutputArray dst：输出的图像InputArray M：透视变换的矩阵Size dsize：输出图像的大小int flags=INTER_LINEAR：输出图像的插值方法，combination of interpolation methods (INTER_LINEAR or INTER_NEAREST) and the optionalflag WARP_INVERSE_MAP, that sets M as the inverse transformation ( )int borderMode=BORDER_CONSTANT：图像边界的处理方式const Scalar& borderValue=Scalar()：边界的颜色设置，一般默认是0函数原理：透视变换(Perspective Transformation)是将图片投影到一个新的视平面(Viewing Plane)，也称作投影映射(Projective Mapping)。