圆柱绕流的流场特性及涡脱落规律研究

圆柱绕流的数值模拟一、问题简介我们考虑一个固定的无限长圆柱体，其直径为10mm，空气以均匀的速度由远处而来绕过圆柱，气流会在圆柱后发展为复杂的流动。

这是一个经典的流体力学问题，随雷诺数的增加，柱体后的流动形态会由对称向不对称转变，并产生卡门涡街。

我对不同雷诺数下的流动进行了数值模拟，并对计算所得流场进行了比较和分析。

二、文献综述圆柱绕流作为最为常见的钝体绕流现象，演绎出了大量的流体控制工程技术和理论研究课题。

这类问题常见的有风掠过建筑物，气流对电线的作用，海流冲击海底电缆，河水对桥墩的冲击，气流经过冷凝器中的排管、空中加油机的油管以及飞行器上的柱体等等，具有很高的工程实践意义。

同时圆柱绕流又是流体力学的经典问题，其蕴含了丰富的流动现象和深刻的物理机理，长久以来一直是众多理论分析、实验研究及数值模拟的研究对象。

流体绕圆柱体流动时，过流断面收缩，流速沿程增加，压强沿程减小，由于黏性力的存在，就会在柱体周围形成附面层的分离，形成圆柱绕流。

在圆柱绕流问题中，流体边界层的分离与脱落、剪切层的流动和变化、尾迹区域的分布和变动，以及它们三者之间的相互作用等因素，使得该问题成为了一项复杂的研究课题。

圆柱绕流的流动状态主要由雷诺数(Re)决定,根据不同的Re范围，流动会经历多种流动状态，在我们流体力学的教材上，就可以查到不同雷诺数下圆柱绕流的形态变化，而下表更加完整详细。

表一在使用CFD方法对圆柱绕流进行求解时，早期使用求解二维定常N-S方程的方法来模拟绕流流场。

然而，由于圆柱尾部涡脱落的存在，绕流流场随时间在不断改变，具有非定常特性，因此就需要求解非定常N-S方程。

目前，在低雷诺数层流条件下，多以求解二维非定常N-S方程来研究圆柱绕流。

但随着雷诺数的增加，绕流流场中沿展向的三维特性越来越显著，如果还使用二维计算模型求解流场，必然不能正确的解析流场结构，获得正确的流场参数。

所以在大雷诺数条件下就需要求解三维的N-S方程。

二维圆柱绕流摘要:采用有限体积法求解二维N -S 方程，对雷诺数1,10,100的二维圆柱非定常流场进行了数值模拟，对比各雷诺数下其流动情况发现，在Re=1时，圆柱上下游的流线前后对称，此Re 数范围的绕流称为斯托克斯区；随着Re 的增大，圆柱上下游的流线逐渐失去对称性。

当Re=10时，沿圆柱表面流动的流体在到达圆柱顶点（90度）附近就离开了壁面，分离后的流体在圆柱下游形成一对固定不动的对称漩涡（附着涡），涡内流体自成封闭回路而成为“死水区”；随着Re 的增大，死水区逐渐拉长圆柱前后流场的非对称性逐渐明显，此Re 数范围称为对称尾流区。

圆柱下游流场不再是定常的，圆柱后缘上下两侧有涡周期性地轮流脱落，形成规则排列的涡阵，这种涡阵称为卡门涡街。

1. 圆柱绕流研究圆柱绕流是一个经典的流体力学问题，流体绕圆柱体流动时，过流断面收缩，流速沿程增加，压强沿程减小，由于粘性力的存在，，就会在柱体周围发生边界层的分离，形成圆柱绕流。

圆柱绕流现象比较复杂，因此，对圆柱绕流研究具有重要的基础理论意义。

研究圆柱绕流问题在工程实际中也具有非常重要的意义。

如水流对桥梁、海上钻井平台支柱、海上输运管线、桩基码头等的作用中，风对塔设备、化工塔设备，高空电缆等的作用中，都有着重要的工程应用背景。

因此，对圆柱绕流进行深入研究，对其流动机理进行分析，不仅具有理论意义，还有明显的社会经济效益。

2. 数值方法因为本文主要求解雷诺数Re=1,10,100时的圆柱绕流情况，需要求解二维非定常不可压的N—S 方程组：本文采用有限体积法对上述微分方程进行离散，然后用SIMPLE 算法对离散方程进行求解，计算中时间推进采用二阶隐式格式，空间离散采用三阶精度的QUICK 格式。

控制方程如下：0jju x ∂=∂ (1) 1()()ji j i j j j ju u p u u t x u x x νρ∂∂∂∂∂+=-+∂∂∂∂∂ (2) 3. 网格划分及模拟工况3.1计算网格计算的区域大小为上游边界距圆柱圆心为2.5D ，下游边界距圆柱圆心10D ，顶部和底部边界距圆柱圆心2.5D ，如图1所示。

133 科技创新导报 Science and Technology Innovation Herald 工 程 技 术墩柱周围水流问题研究中,传统的测量方法是点测量,[1]因而无法获得全场的同步信息。

近年来,随着图像处理技术和信号分析理论的迅猛发展,实验设备的数字化给流体力学的研究领域注入了新的活力。

[2]利用这些新型技术手段不仅能够直观地记录流动现象,还能够比以往更为准确地揭示流动的规律,这些技术已然成为水流问题研究过程中的重要的手段。

[3]本文在分析面流场时采用了粒子图像测速技术,[4]对圆柱型桥墩模型绕流的流场特性进行了分析。

1 实验装置介绍1.1试验仪器设备参数试验是在大连理工大学海岸及近海国家重点实验室的P I V 水槽进行。

水槽长22m,宽0.4m。

在测量中运用PIV(粒子成像技术)和ADV(声学多普勒流速仪)两种仪器结合的方法。

PIV流速测量系统为美国TSI公司生产。

A D V 为n o r t e k 公司产的Vectrino+。

1.2试验方案设计实验用圆柱直径为6cm,取0.1、0.15、0.25m /s 三种来流速度,激光取样频率为15Hz。

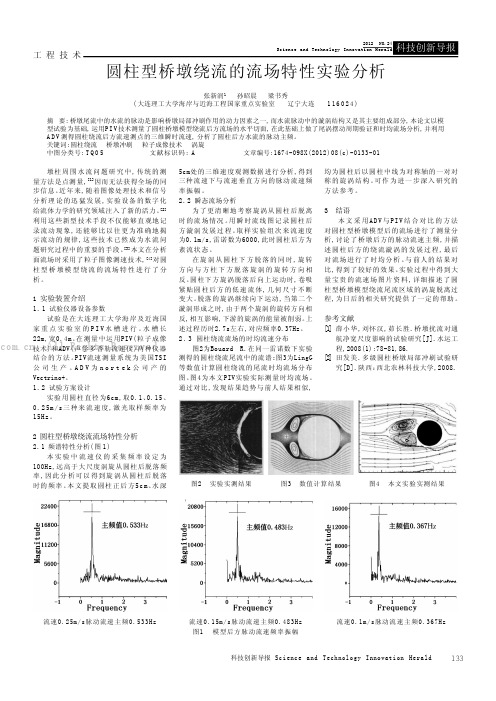
2 圆柱型桥墩绕流流场特性分析2.1频谱特性分析(图1)本实验中流速仪的采集频率设定为100Hz,远高于大尺度涡旋从圆柱后脱落频率,因此分析可以得到旋涡从圆柱后脱落时的频率。

本文提取圆柱正后方5c m、水深5cm处的三维速度观测数据进行分析,得到三种流速下与流速垂直方向的脉动流速频率振幅。

2.2瞬态流场分析为了更清晰地考察旋涡从圆柱后脱离时的流场情况。

用瞬时流线图记录圆柱后方漩涡发展过程。

取样实验组次来流速度为0.1m/s,雷诺数为6000,此时圆柱后方为紊流状态。

在旋涡从圆柱下方脱落的同时,旋转方向与方柱下方脱落旋涡的旋转方向相反。

圆柱下方旋涡脱落后向上运动时,卷吸紧贴圆柱后方的低速流体,几何尺寸不断变大。

脱落的旋涡继续向下运动,当第二个漩涡形成之时,由于两个旋涡的旋转方向相反,相互影响,下游的旋涡的能量被削弱。

亚临界雷诺数下串列双圆柱与方柱绕流的数值模拟摘要：本文运用Fｌｕｅｎｔ软件中的RNＧk-ε模型对亚临界雷诺数下二维串列圆柱和方柱绕流问题进行了数值研究，通过结果对比,分析了雷诺数、柱体形状对柱体绕流阻力、升力以及涡脱频率的影响。

一般而言,Rｅ数越大,方柱的阻力越大，圆柱体则不然；而Rｅ越大,两种柱体的升力均越大。

相对于圆柱,同种条件下，方柱受到的阻力要大；相反地，方柱涡脱落频率要小。

Ｒe越大，串列柱体的Sr数越接近于单圆柱体的Ｓr数。

关键字：圆柱绕流、升力系数、阻力系数、斯特劳哈尔数在工程实践中，如航空、航天、航海、体育运动、风工程及地面交通等广泛的实际领域中,绕流研究在工程实际中具有重大的意义。

当流体流过圆柱时, 由于漩涡脱落，在圆柱体上产生交变作用力。

这种作用力引起柱体的振动及材料的疲劳,损坏结构，后果严重。

因此,近些年来，众多专家和学者对于圆柱绕流问题进行过细致的研究，特别是圆柱所受阻力、升力和涡脱落以及涡致振动问题。

沈立龙等[1］基于RNG ｋ⁃ε模型,采用有限体积法研究了亚临界雷诺数下二维圆柱和方柱绕流数值模拟,得到了圆柱和方柱绕流阻力系数Ｃ与Ｓｔｒｏｄuhal 数随雷诺数的变化规律。

姚熊亮等［２］采用计算流体软件CFX中LES模型计算了二维不可压缩均匀流中孤立圆柱及串列双圆柱的水动力特性。

使用非结构化网格六面体单元和有限体积法对二维Ｎ-S方程进行求解。

他们着重研究了高雷诺数时串列双圆柱在不同间距比时的压力分布、阻力、升力及Sｒ数随Re数的变化趋势。

费宝玲等［3]用ＦＬUENT软件对串列圆柱绕流进行了二维模拟，他们选取间距比L/Ｄ(Ｌ为两圆柱中心间的距离，D为圆柱直径)2、3、４共３个间距进行了数值分析。

计算均在Re= ２0０的非定常条件下进行。

计算了圆柱的升阻力系数、尾涡脱落频率等描述绕流问题的主要参量,分析了不同间距对圆柱间相互作用和尾流特征的影响。

圆柱绕流的一个重要特征是流动形态取决于雷诺数。

二维圆柱绕流摘要:采用有限体积法求解二维N-S 方程，对雷诺数1,10,100的二维圆柱非定常流场进行了数值模拟，对比各雷诺数下其流动情况发现，在Re=1时，圆柱上下游的流线前后对称，此Re 数范围的绕流称为斯托克斯区；随着Re 的增大，圆柱上下游的流线逐渐失去对称性。

当Re=10时，沿圆柱表面流动的流体在到达圆柱顶点（90度）附近就离开了壁面，分离后的流体在圆柱下游形成一对固定不动的对称漩涡（附着涡），涡内流体自成封闭回路而成为“死水区”；随着Re 的增大，死水区逐渐拉长圆柱前后流场的非对称性逐渐明显，此Re 数范围称为对称尾流区。

圆柱下游流场不再是定常的，圆柱后缘上下两侧有涡周期性地轮流脱落，形成规则排列的涡阵，这种涡阵称为卡门涡街。

1. 圆柱绕流研究圆柱绕流是一个经典的流体力学问题，流体绕圆柱体流动时，过流断面收缩，流速沿程增加，压强沿程减小，由于粘性力的存在，，就会在柱体周围发生边界层的分离，形成圆柱绕流。

圆柱绕流现象比较复杂，因此，对圆柱绕流研究具有重要的基础理论意义。

研究圆柱绕流问题在工程实际中也具有非常重要的意义。

如水流对桥梁、海上钻井平台支柱、海上输运管线、桩基码头等的作用中，风对塔设备、化工塔设备，高空电缆等的作用中，都有着重要的工程应用背景。

因此，对圆柱绕流进行深入研究，对其流动机理进行分析，不仅具有理论意义，还有明显的社会经济效益。

2. 数值方法因为本文主要求解雷诺数Re=1,10,100时的圆柱绕流情况，需要求解二维非定常不可压的N —S 方程组：本文采用有限体积法对上述微分方程进行离散，然后用SIMPLE 算法对离散方程进行求解，计算中时间推进采用二阶隐式格式，空间离散采用三阶精度的QUICK 格式。

控制方程如下：0j ju x ∂=∂ (1)1()()j i j i j j j ju u p u u t x u x x νρ∂∂∂∂∂+=-+∂∂∂∂∂ (2)3. 网格划分及模拟工况3.1计算网格计算的区域大小为上游边界距圆柱圆心为2.5D ，下游边界距圆柱圆心10D ，顶部和底部边界距圆柱圆心2.5D ，如图1所示。

毕业论文题目圆柱扰流的流动稳定性分析学院专业姓名学号指导教师完成时间教务处制独立完成与诚信声明本人郑重声明：所提交的毕业设计（论文）是本人在指导教师的指导下，独立工作所取得的成果并撰写完成的，郑重确认没有剽窃、抄袭等违反学术道德、学术规范的侵权行为。

文中除已经标注引用的内容外，不包含其他人或集体已经发表或撰写过的研究成果。

对本文的研究做出重要贡献的个人和集体，均已在文中作了明确的说明并表示了谢意。

本人完全意识到本声明的法律后果由本人承担。

毕业设计（论文）作者签名：指导导师签名：签字日期：签字日期：毕业设计（论文）版权使用授权书本人完全了解华北水利水电大学有关保管、使用毕业设计的规定。

特授权华北水利水电大学可以将毕业设计的全部或部分内容公开和编入有关数据库提供检索，并采用影印、缩印或扫描等复制手段复制、保存、汇编以供查阅和借阅。

同意学校向国家有关部门或机构送交毕业设计原件或复印件和电子文档（涉密的成果在解密后应遵守此规定）。

毕业设计（论文）作者签名：导师签名：签字日期：签字日期：目录摘要 (III)Abstract (IV)图目录 (V)表目录 (XI)符号说明 (XII)第一章绪论 (1)1.1 前言 (1)1.2 文献回顾 (1)1.3研究动机 (4)第二章实验设备、仪器与方法 (4)2.1 实验设备 (4)2.1.1水循环系统之设备 (4)2.1.2 测试段 (5)2.1.3 动量注入尾流系统 (5)2.1.4 流场可视化系统于雷射光页烟线流场观察 (6)2.2 实验仪器 (7)2.2.1 流场影像撷取系统 (7)2.2.2 流速量测系统 (7)2.2.3 讯号撷取系统 (8)2.3 实验不准度 (9)2.4 实验方法 (9)第三章实验结果与讨论 (10)3.1 未注入动量之圆柱后尾流流场分析 (10)3.2 稳定注入动量之圆柱后尾流流场分析 (11)3.3 往复注入动量之圆柱后尾流流场分析 (12)3.4 稳定吸入动量之圆柱后尾流流场分析 (13)第四章结论与建议 (16)4.1 结论 (16)4.2 建议 (17)参考文献 (18)圆柱扰流的流动稳定性分析摘要本实验研究的对象为单一圆柱尾流，再以流体动量干扰此尾流场。