2013-2014学年福州市第一学期九年级期末质检_数学试卷

第1页 （共3页）2013-2014学年度第一学期期末调研测试九年级数学试卷评分标准一、选择题（本大题共12小题，每题3分，共36分。

下列各题的备选答案中，只有一个是正确的，请将正确答案的序号填入下表中相应题号下的空格内）题 号 1 2 3 4 5 6 7 8 9 10 11 12 答 案CACDABDBBDAC二、填空题（本大题共8小题，每题4分，共32分。

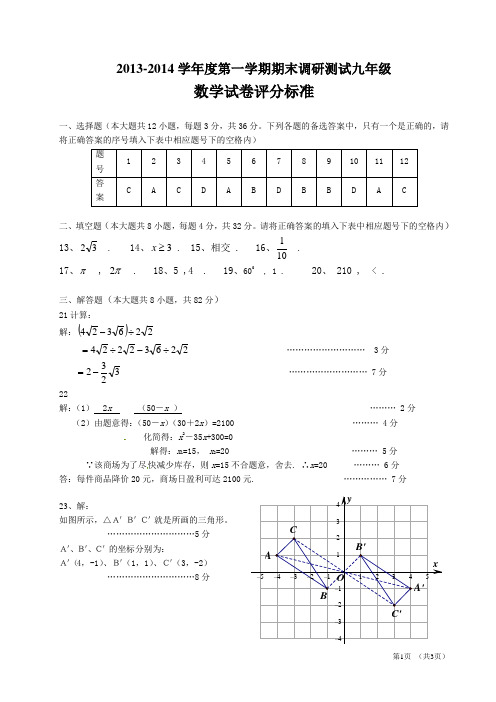
请将正确答案的填入下表中相应题号下的空格内）13、32 . 14、3≥x . 15、相交 . 16、101. 17、π , π2 . 18、5 ,4 . 19、600 , 1 . 20、 210 , < .三、解答题（本大题共8小题，共82分） 21计算：解：()226324÷-22632224÷-÷= ……………………… 3分3232-= ……………………… 7分 22解：（1） 2x （50－x ） ……… 2分 （2）由题意得：（50－x ）（30＋2x ）=2100 ……… 4分化简得：x 2－35x +300=0解得：x 1=15， x 2=20 ……… 5分 ∵该商场为了尽快减少库存，则x =15不合题意，舍去. ∴x =20 ……… 6分 答：每件商品降价20元，商场日盈利可达2100元. …………… 7分 23、解：如图所示，△Ａ＇Ｂ＇Ｃ＇就是所画的三角形。

…………………………5分Ａ＇、Ｂ＇、Ｃ＇的坐标分别为：Ａ＇（4，-1）、Ｂ＇（1，1）、Ｃ＇（3，-2）…………………………8分yx12345–1–2–3–4–51234–1–2–3–4OABC A'B'C'第2页 （共3页） 24、解：（1）∵ 方程有实数根 ∴⊿=22-4（k +1）≥0 …………… 2分 解得 k ≤0 …………… 4分∴ K 的取值范围是k ≤0 …………… 5分（2）∵21x x 和是一元二次方程0122=+++k x x 的实数根∴221-=+x x , 121+=k x x …… 6分 ∴()122121+--=-+k x x x x ………… 7分 由已知12121-<-+x x x x ，得 ()112-<+--k 解得 k ＞-2 ………… 8分又由（1）k ≤0 ∴ -2＜k ≤0 ……… 9分 ∵ k 为整数 ∴k 的值为-1和0. …………… 10分 25、 解：（1）因为5006.03= … 2分 所以在这个问题中，样本容量是50. … 4分（2）因为 1761410350=----， … 5分所以成绩在28-32这一组的频数17 … 6分 补全频数分布直方图如图所示。

第8题图2013～2014学年度第一学期期末质量检测试卷·九年级数学试卷·考生注意：1.本卷共八大题，计23小题，满分150分；2.答题前请将密封线内的项目填写清楚；3.考试过程中允许考生进行剪、拼、折叠等实验，但不得使用计算器哟！一、选择题（本题共10小题，每小题4分，满分40分）每一个小题都给出代号为A 、B、C 、D 的四个结论，其中只有一个是正确的，把正确结论的代号写在题后的括号内.每一小题：选对得4分，不选、选错或选出的代号超过一个的(不论是否写在括号内)一律得0分.1．下列根式中，不是．．最简二次根式的是（ ）．A B C D 2 ）．A ．1到2之间；B ．2到3之间；C ．3到4之间；D ． 4到5之间.3．下列汽车标志图形中，是中心对称图形的是（ ）．A ．B ．C ．D ．4．用配方法解一元二次方程01182=+-x x ，则方程可变形为（ ）．A ．()542=-x ；B ．()542=+x ；C ．()582=+x ；D ．()582=-x .5．下列成语所描述的事件是必然事件的是（ ）．A ．瓮中捉鳖；B ．拔苗助长；C ．守株待兔；D ．杯水车薪.6．已知关于x 的一元二次方程012)2(2=++-x x m 有两个不相等的实数解，则m 的取值范围是（ ）．A ．3->m ；B ．3<m ；C ．3<m 且2≠m ；D ．3->m且2≠m .7．小颍的哥哥在合肥工作，今年春节期间，她想让哥哥买几本复习资料带回家，于是发手机短信给哥哥，可一时记不清哥哥的手机号码后三位数的顺序，只记得是0、1、4三个数，则小颍给哥哥一次发短信成功的概率是（ ）．A ．91B ．61C ．31D ．218．如图，∠AOB ＝90°，∠B ＝30°，△A′OB′可以看作是由△AOB 绕点O 顺时针旋转α角度得到的，若使得点A′ 在AB 上，则旋转角α的大小可以是（ ）．第9题图 第10题图 A ．30° B ．45° C ．60； D ．90°9．已知函数y =x 2-2x -2的图象如图所示，根据其中提供的信息，可求得使y ≥1成立的x 的取值范围是（ ）．A ．-1≤x ≤3；B ．-3≤x ≤1；C ． x ≥-3；D ． x ≤-1或x ≥3.10．现有30％圆周的一个扇形彩纸片，该扇形的半径为40cm ，小红同学为了在庆祝澳门回归十周年联欢晚会上表演节目，她打算剪去部分扇形纸片后，利用剩下的纸片制作成一 个底面半径为10cm 的圆锥形纸帽(接缝处不重叠)，那么剪去的扇形纸片的圆心角为（ ）．A ． 9°B ．18°C ．63°D ．72°二、填空题（本题共4小题，每小题5分，满分20分） 11．在我们刚刚学过的九年级数学下册课本第14页，用“描点法”画一个函数图象时，列了如下表格：根据表格上的信息回答问题：该二次函数在x =9时，y = ．12．如图所示，矩形中长和宽分别为10cm 和6cm ，则阴影部分的面积为 ．13．如图，四边形EFGH 是由四边形ABCD 经过旋转得到的．如果用有序数对（2，1）表示方格纸上A 点的位置，用（1，2）表示B 点的位置，那么四边形ABCD 旋转得到四边形EFGH 时的旋转中心用有序数对表示是 ．14．如图，电路图上有四个开关A 、B 、C 、D 和一个小灯泡，闭合开关D 或同时闭合开关A 、B 、C ，都可以使小灯泡发光，任意闭合其中两个开关，则小灯泡发光的概率为 ．第14题图 第13题图 第12题图第17题图15．计算：320－45－51+(5－2)(5+2) ．16．解方程：2(3)4(3)0x x x -+-=．四、（本题共2小题，每小题8分，满分16分） 17．下面各图均为6⨯的正方形网格，点A B C 、、在格点上．试确定格点D ，并画出以A 、B 、C 、D 为顶点的四边形，使其为中心对称图形，画出两种不同的情况．18．如图：等腰△ABC，以腰AB 为直径作⊙O 交底边BC 于P ，PE ⊥AC ，垂足为E .求证：PE 是⊙O 的切线．C 第18题图19．如图，直角梯形OABC 中，O 为坐标原点，OC OA =，点C 的坐标是(08)，，以点B为顶点的抛物线2y ax bx c =++经过原点和x 轴上的点A ．求抛物线的解析式．20．无为县某乡镇改变农业生产模式为养殖螃蟹，为了加大投入，提高产出，某农户去年养殖了10亩螃蟹，亩产120kg ，今年初该农户扩大了养殖面积，并且改进了养殖方法，已知养殖面积的增长率是亩产量的增长率的2倍，今年螃蟹的总产量为3600kg ，求螃蟹亩产量的增长率．六、（本题满分12分） 21．在学习概率知识后，小明和小军共同做游戏，他们准备了四张形状、大小、颜色完全一样的卡片，分别在这四张卡片上面写上2、3、2、3四个数，放进一个盒子里摇匀，随机抽取一张记下数字，放回摇匀再随机抽取一张.游戏规定：若两次得到的数字的乘积是无理数，则小明得1分，否则小军得1分.请你为他们算一算这个游戏是否公平？若不公平，让你只改变其中一张卡片上的数字（数字可以改为任意实数)，使游戏公平，但卡片数量、抽取方式以及游戏的规则都不变（只写出一种改变即可，不必再计算）．第19题图22．观察下列各式，通过分母有理化（把分母中的根号化去），把不是最简二次根式的化成最简二次根式：121212)12)(12()12(1121-=--=-+-⨯=+， 同理可得：23231-=+，34341-=+，……（1）从中你发现了什么规律，试用含n 的式子表示出来．（2）并利用这一规律计算：)12010)(200920101341231121(+++⋯⋯++++++ 的值．（3）分母有理化：1231-+．23．如图⑴，△ABC中，AB=AC=8，∠BAC=120°，D为BC上任意一点(不包括B、C)，连接AD可得△ABD，将△ABD绕点A逆时针旋转120°，可形成四边形ADCF.（1）如图⑴，试确定△ABC周长与四边形ADCF周长的大小关系，并作简要说明．（2）试判断点D在何处时，四边形ADCF的周长最小（不需要说明理由）？并求出此时的四边形ADCF的周长.（下图供答题使用）．（3）四边形ADCF能否为等腰梯形？若能，在下图中画出所有情况的图形，并直接写出∠BAD的度数；若不能，请说明理由．BAC DF第23⑴题图第23⑵题图第23⑶题备用图第23⑶题图。

2013-2014学年度第一学期九年级期末质量检查考试数学试卷考试时间：120分钟；命题人：游宝发学校:___________姓名：___________班级：___________考号：___________ 注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上一、选择题1．下列式子中，属于最简二次根式的是（A ）（B （C ） （D 2．下列图形中，中心对称图形有【 】A ．1个B ．2个C ．3个D ．4个 3．已知一元二次方程2x x 1 0+-=，下列判断正确的是（ ） A.方程有两个相等的实数根 B.方程有两个不相等的实数根C.方程无实数根D.方程根的情况不确定4．一根水平放置的圆柱形输水管道横截面如图所示，其中有水部分水面宽0.8米，最深处水深0.2米，则此输水管道的直径是A ．0.5B ．1C ．2D ．45．已知⊙O 1和⊙O 2相切，两圆的圆心距为9cm ，⊙1O 的半径为4cm ，则⊙O 2的半径为（ ） A ．5cm B ．13cm C ．9 cm 或13cm D ．5cm 或13cm 6．已知圆锥的母线长为5，底面半径为3，则圆锥的表面积．．．为（ ） A ．15π B ．24π C ．30π D ．39π 7．下列事件是随机事件的为A 、度量三角形的内角和，结果是180︒B 、经过城市中有交通信号灯的路口，遇到红灯C 、爸爸的年龄比爷爷大D 、通常加热到100℃时，水沸腾 8．如果将抛物线2y x =向左平移2个单位，那么所得抛物线的表达式为A.22y x =+B.22y x =-C.2(2)y x =+D.2(2)y x =-9．如图，在平面直角坐标系中，抛物线2y 1x 2=经过平移得到抛物线21x 2y 2x =-，其对称轴与两段抛物线所围成的阴影部分的面积为A ．2B ．4C ．8D ．1610．如图，已知边长为2的正三角形ABC 顶点A 的坐标为（0,6），BC 的中点D 在y 轴上，且在A 的下方，点E 是边长为2，中心在原点的正六边形的一个顶点，把这个正六边形绕中心旋转一周，在此过程中DE 的最小值为A.3B.34-C.4D.326- 二、填空题11x 的取值范围是____________. 12．如果关于x 的方程220xx m -+=（m 为常数）有两个相等实数根，那么m ＝______．13．两块完全一样的含30°角的三角板重叠在一起，若绕长直角边中点M 转动，使上面一块的斜边刚好过下面一块的直角顶点，如图，∠A ＝30°，AC ＝10，则此时两直角顶点C 、C ′间的距离是_______． 14．如图，AB 为⊙O 的直径，点P 为其半圆上任意一点（不含A 、B ），点Q 为另一半圆上一定点，若∠POA 为x°，∠PQB 为y°，则y 与x 的函数关系是 . 15．如图，一条抛物线m x y +=241（m<0）与x 轴相交于A 、B 两点（点A 在点B 的左侧）．若点M 、N 的坐标分别为（0，—2）、（4，0），抛物线与直线MN 始终有交点，线段AB 的长度的最小值为 ．三、解答题16．计算：（1）)323(235a bb a ab b ÷-⋅（2） 17．解方程：0822=--x x18．如图，在正方形网络中，△ABC 的三个顶点都在格点上，点A 、B 、C 的坐标分别为（－2，4）、（－2，0）、（－4，1），结合所给的平面直角坐标系解答下列问题：（1）画出△ABC 关于原点O 对称的△A 1B 1C 1； （2）平移△ABC，使点A 移动到点A 2（0，2），画出平移后的△A 2B 2C 2并写出点B 2、C 2的坐标； （3）△A 1B 1C 1与△A 2B 2C 2成中心对称，写出其对称中心的坐标． 19．某人定制了一批地砖，每块地砖(如图(1)所示)是边长为0.5米的正方形ABCD.点E 、F 分别在边BC 和CD 上，△CFE 、△ABE 和四边形AEFD 均由单一材料制成，制成△CFE 、△ABE 和四边形AEFD 的三种材料的价格依次为每平方米30元、20元、10元.若将此种地砖按图(2)所示的形式铺设，则中间的阴影部分组成正方形．．．EFGH.已知烧制该种地砖平均每块需加．工费．．0.35元，要使BE 长尽可能小，且每块地砖的成本价为4元(成本价=材料费用+加工费用)，则CE 长应为多少米？解：设 CE ＝x ，则S △CFE ＝ ，S △ABE ＝ S 四边形AEFD ＝ (用含x 的代数式表示，不需要化简)。

2013－2014学年度第一学期期末考试初三数学试题卷（全卷共五个大题，满分150分，考试时间120分钟）参考公式：抛物线的2(0)y ax bx c a =++≠顶点坐标为24(,)24b ac b a a--，对称轴公式为2b x a=-。

一、选择题：（本大题10个小题，每小题4分，共40分）在每个小题的下面，都给出了代号为A 、B 、C 、D 的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑（或将正确答案的代号填入答题卷中对应的表格内）. 1．在3，－1，0这四个数中，最小的数是（ ） A. 3 B. －1 C. 02．下列图形是轴对称图形的是（ ）3．计算23(2)x 的结果是（ ）A ．66x B. 58x C. 56x D. 68x4．如图，ABC ∆为O 的内接三角形，50ACB ∠=︒，则ABO ∠的度数等于（ ） A.40° B.50° C.60° D.25° 5110,60E ︒∠=︒，则∠A. 30°B. 40°C. 50°D. 60° 6．下列调查适合全面调查（即：普查）的是（ ） A.了解全国每天丢弃的塑料袋的数量 B.了解某种品牌的彩电的使用寿命 C.调查“神州9号”飞船各零部件的质量 D.了解浙江卫视“中国好声音”栏目的收视率7．若x = 2是关于x 的一元二次方程280x ax -+=的一个解，则a 的值是（ ） A ．2 B. 5 C. －6 D. 68．地铁1号线是贯穿渝中区和沙坪坝区的重要交通通道，1号线的开通极大的方便了市民的出行，小王下班后从渝中区较场口乘坐地铁回沙坪坝，他从公司出发，先匀速步行至较场口地铁站，等了一会儿，小王搭乘地铁1号线到达沙坪坝站，下面能反映在此过程中小王到沙坪坝的距离y 与时间x 的函数关系的大致图象是（ ）9．如图，以下各图都是由同样大小的图形①按一定规律组成，其中第①个图形中共有1个完整菱形，第②个图形中共有5个完整菱形，第③个图形中共有13个完整菱形，……，则第⑦个图形中完整菱形的个数为（ ）A.83B.84C.85D.8610．二次函数2(0)y ax bx c a =++≠的图象如图所示， 则下列结论中，正确的是（ ） A.0abc >B.24ac b > C.20a b -=D.420a b c ++>二、填空题：（本大题６个小题，每小题４分，共24分）请将每小题的答案直接填在答题卡（卷）中对应的横线上.11．据统计，重庆市2011年全市地方财政收入超过29000000万元，将数29000000用科学记数法表示为 . 12．已知ABC ∆∽DEF ∆，ABC ∆的周长为2，DEF ∆的周长为4，则ABC ∆与DEF ∆的面积之比为 . 13．在体育中招考试的跳绳项目考试中，我校两个小组共8位同学的成绩分别如下：（单位：个/分钟）154、187、173、205、197、177、185、188，则这组数据的中位数是 . 14．已知扇形的圆心角为120°，半径为9cm ，则扇形的面积为 cm 2.（结果保留π） 15．在一个不透明的盒子里装有5个分别写有数字－2，－1，0，1，2的小球，它们除数字不同外其余全部相同. 现从盒子里随机取出一个小球，将该小球上的数字作为a 的值，将该数字加3作为b 的值，则（a ，b ）使得关于x 的不等式组3(2)0,0x a x x b --≥⎧⎨-+>⎩恰好有3个整数解的概率是 .16．甲、乙两车在一个环形跑道内进行耐力测试，两车从同一地点同时起步后，乙车速超过甲车速，在第8分钟时甲车提速，在第12分钟时甲车追上乙车并且开始超过乙，在第17分钟时，甲车再次追上乙车. 已知在测试中甲、乙两车均是匀速行驶，那么如果甲车不提速，乙车首次超过甲车是在第 分钟.三、解答题：（本大题4个小题，每小题6分，共24分）解答时每小题必须给出必要的演算过程或推理步骤，请将解答书写在答题卡（卷）中对应的位置上． 17．计算：120131(5)()(1)|4|2π--++---18．如图，AD = BC ，,12A B ∠=∠∠=∠，求证：PA = PB.19．解方程：42233x x x-+=--.20．如图，在ABC ∆中，60,C AD BC ∠=︒⊥，垂足为D，若2AD BD CD ==，求ABC ∆的周长（结果保留根号）.四、解答题：（本大题4个小题，每小题10分，共40分）解答时每小题必须给出必要的演算过程或推理步骤，请将解答书写在答题卡（卷）中对应的位置上．21．先化简22144(1)11x x x x -+-÷--，再从不等式组203(1)21x x x +>⎧⎨-≤-⎩的解集中选取一个合适的整数解作为x 的值代入求值.22．如图，一次函数y ax b =+的图象与反比例函数ky=交于A ，B 两点，与y 交于C ，与x 轴交于点D ，已知OA =（1）求反比例函数和一次函数的解析式；（2）求AOB ∆的面积. 23．重庆市物价局发出通知，从2011年2月18日起降低部分抗生素药品和神经系统类药品最高零售价格，共涉及162个品种，某药房对售出的抗生素药品A 、B 、C 、D 、E 的销量进行统计，绘制成如下统计图：（1）补全折线统计图；（2）计算2月份售出各类抗生素销量的极差为 ；（3）2月份王老师到药房买了抗生素类药D 、E 各一盒，若D 中有两盒是降价药，E 中有一盒是降价药，请用画树状图或列表法求出他买到两盒都是降价药的概率。

2013-2014学年度第一学期阶段性测试九年级数学（北师大版）本试题分第1卷（选择题）和第II卷（非选择题）两部分，第1卷共2页，满分为36分；第II卷共6页，满分为84分．本试题共8页，满分为120分．考试时间为120分钟．答卷前，请考生务必将自己的姓名、准考证号、座号、考试科目涂写在答题卡上，并同时将考点、姓名、准考证号、座号填写在试卷规定的位置，考试结束后，将本试卷和答题卡一并交回，本考试不允许使用计算器．第1卷（选择题共36分）注意事项：第1卷为选择题，每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑：如需改动，用橡皮擦干净后，再选涂其他答案标号．答案写在试卷上无效，一、选择题（本大题共12个小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的．）I．点A(-3，4)所在象限为A.第一象限 B．第二象限 C．第三象限 D．第四象限2．-个正比例函数的图象经过点（2，-1），那么这个正比例函数的表达式为3．若直线则直线不经过A．第一象限 B．第二象限 C．第三象限 D.第四象限4．某反比例函数的图象经过点（一l，6），下列各点也在该函数图象上的是A.(一3,2)B.(3,2)C.(2,3)D.f6,1)5．如图，已知AB为圆O的直径，点C在圆O上,∠C=15o,则∠BOC的度数为A. 150B. 300C. 450D. 6006．下列二次函数的图象中，开口向上的有：A． 1个 B．2个 C．3个 D．4个7．已知二次函数的图象如图所示，则下列结论正确的是A. a>0 B．b<0C. c<0D. b2-4ac>08．如图，4为反比例函数图象上一点，ABIx轴于点召，若则后的值为A.6 B． 3 D．无法确定9．如图，在4x4的正方形网格中，cosa的值为10.油箱中存油20升，油从油箱中均匀流出，流速为0.2升／分钟，则油箱中剩余油量Q（升）与流出时间“分钟）的函数关系是A.Q=0.2tB.Q=20-0.2tC.卢0.2QD. t=20-0.2Q11．有下列四个命题：①直径是弦；②经过三个点一定可以作圆；③三角形的外心到三角形各顶点的距离都相等；④平分弦的直径垂直于弦．其中正确的有A．4个 B．3个 C. 2个 D. 1个12．如图，的半径为2，点A的坐标为直线AB为的切线，曰为切点．则曰点的坐标为第1I卷（非选择题共84分）注意事项：1．第1I卷为非选择题，请考生用蓝、黑色钢笔（签字笔）或圆珠笔直接在试卷上作答． 2．答卷前，请考生先将考点、姓名、准考证号、座号填写在试卷规定的位置．二、填空题（本大题共6个小题，每小题3分，共1 8分j巴答案填在题中横线上．）13. cos600=14．如图，AB为的直径，点C在上，∠A=300，则∠B的度数为15.一次函数y=(k-2)x+b的图象如图所示，则K的取值范围是____．16.已知：线段AB=3cm，半径分别是lcm和4cm，则的位置关系是17.抛物线y= kx2 -3x -3的图象和x轴有交点，则K的取值范围是18.如图，把矩形纸片OABC放入平面直角坐标系中，使OA，OC分别落在x轴、y轴上，连接AC，将矩形纸片OABC沿AC折叠，使点B落在点D的位置，若B(1，2)，则点D的横坐标是三、解答题（本大题共9个小题，共66分．解答应写出文字说明，证明过程或演算步骤．）19.（本小题满分6分）20．（本小题满分6分）若反比例函数与一次函数，y=2x-4的图象都经过点A(a，2)．(1)求a的值．(2)求反比例函数的解析式；21.（本小题满分6分）如图，已知AB是求AB的长．22．（本小题满分7分）如图，热气球的探测器显示，从热气球A看一栋大楼顶部B的俯角为300，看这栋大楼底部C的俯角为600.热气球A的高度为240米，求这栋大楼的高度．23．（本小题满分7分）某商店以每件60元的价格购进一批商品，若以单价80元销售，每月可售出300件，调查表明；单价每上涨1元，该商品每月的销量就减少10件．(l)请写出每月销售该商品的利润y（元）与单价上涨x（元）的函数关系式：(2)单价定为多少元时，每月销售该商品的利润最大？最大利润为多少？24.（本小题满分8分）已知的直径AB的长为4cm，C是上一点，过点C作的切线交AB的延长线于点P，求BP的长．25.（本小题满分8分）如图，已知在(l)求图中阴影部分的面积；(2)若用阴影扇形OBD围成一个圆锥侧面，请求出这个圆锥的底面圆的半径^第25题圈26．（本小题满分9分）如图，直线y= - 2x+2与x轴、y轴分别交于A、B两点，将△OAB绕点D逆时针方向旋转900后得到△OCD.(1)填空：点C的坐标是(__ __，_ _)，点D的坐标是(_ __，_ )；(2)设直线CD与AB交于点M，求线段BM的长；27.（本小题满分9分）如图所示，抛物线与x轴交于A、B两点，直线BD的函数表达式为抛物线的对称轴l与冉线BD交于点C、与x轴交于点E.(1)求A、B、C三个点的坐标．(2)点P为线段AB上的一个动点（与点A 、点B不重合），以点A为圆心、以AP为半径的圆弧与线段AC交于点M，以点B为圆心、以BP为半径的圆弧与线段BC交于点N，分别连接AN、BM、MN.①求证：AN=BM．②在点P九年级数学试题参考答案与评分标准运动的过程中，四边形AMNB的面积有最大值还是有最小值？并求出该最大值或最小值．。

2013年福州市初中毕业班质检数学模拟试卷及参考答案数 学 试 卷（完卷时间：120分钟 满分：150分）一．选择题（每小题4分，满分40分;请在答题卡的相应位置填涂） 1．－2的相反数是（ ）A ．2B ．－2C ．21 D ．21-2．地球距离月球表面约为383900千米，那么这个数据用科学记数法表示为（ ）A ．410839.3⨯B ．510839.3⨯C ．610839.3⨯D ．41039.38⨯ 3．如图，下列几何体中主视图、左视图、俯视图都相同的是（ ）A ．半圆B ．圆柱C ．球D ．六棱柱 4．如图，直线a ∥b ，直线c 与a 、b 均相交，如果︒=∠501，那么∠2的度数是（ ）A ．︒50B ．︒100C ．︒130D ．︒150 5．下列计算正确的是（ ）A ．632a a a =⋅ B ．ba b a 22)(=C ．623)(ab ab =D ．426a a a =÷ 6．“a 是实数，0≥a ”这一事件是（ ）A ．必然事件B ．不确定事件C ．不可能事件D ．随机事件7．一条排水管的截面如图所示，已知排水管的截面圆半径10=OB ，截面圆圆心O 到水面的距离OC 是6，则水面宽AB 是（ ） A ．8 B ．10 C ．12 D ．16 8．下列四边形中，对角线不可能．．．相等的是（ ） A ．直角梯形 B ．正方形 C ．等腰梯形 D ．长方形12abc（第4题）（第7题）9．如图，直线233+-=x y 与x 轴、y 轴分别交于A 、B 两点，把△AOB 绕点A 顺时针旋转︒60后得到△B O A ''的坐标是（ ）A ．（4，32）B ．（32，4）C ．（3，3）D ．（232+，32）10．方程0132=-+x x 的根可看作是函数3+=x y 的图象与函数xy 1=的图象交点的横坐标，那么用此方法可推断出方程013=--x x 的实数根0x 所在的范围是（ ）A ．010<<-xB ．100<<xC ．210<<xD ．320<<x 二．填空题（共5小题，每题4分，满分20分;请将正确答案填在答题卡相应位置） 11．分解因式：=-92x ____________. 12．已知23=a ，则=a ____________.13．从分别标有1到9序号的9张卡片中任意抽取一张，抽到序号是4的倍数的概率是____________. 14．已知1-=x 是一元二次方程02=++n mx x的一个根，则222n mn m +-的值为____________. 15．如图，︒=∠30AOB ，n 个半圆依次外切，它们的圆心都在射线OA 上并与射线OB 相切，设半圆1C 、 半圆2C 、半圆3C ……、半圆n C 的半径分别是1r 、 2r 、3r ……、n r ，则=20112012r r ____________.三、解答题（满分90分;请将正确答案及解答过程填在答题卡相应位置，作图或添辅助线用铅笔画完，再用黑色签字笔描黑） 16．（每小题7分，共14分） （1）计算：10)21()14.3(8211---++-（2）先化简，再求值：)2()1(2-++x x x ，其中2=x 。

2013-2014学年度第一学期期末考试九年级数学试题注意事项：本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共120分，考试时间120分钟.第Ⅰ卷（选择题 共45分）一、选择题（本大题共15小题，每小题3分，共45分，在每小题给出的四个选项中，只有一项符合题目要求，请将正确答案填在后面的表格中．．．） 1．一元二次方程0)1(=-x x 的解是 A.0=xB.1=xC.0=x 或1=xD.0=x 或1-=x2．下面四个几何体中，俯视图为四边形的是3．抛物线()212y x =-+的对称轴为A ．直线1x =B ．直线1x =-C ．直线2x =D ．直线2x =- 4．如图，在8×4的矩形网格中，小正方形的边长都是1，若△ABC 的三个顶点在图中相应的格点上，则tan ∠ACB 的值为A ．1B ．13C ．12D ．25．如图，在□ABCD 中，添加下列条件不能判定□ABCD 是菱形的是 A. AB =BCB. AC ⊥BDC. BD 平分∠ABCD. AC =BD6．用配方法将2611y x x =-+化成2()y a x h k =-+的形式为 A ．2(3)2y x =++ B ．2(3)2y x =-- C ．2(6)2y x =-- D ．2(3)2y x =-+7．若3是关于方程x 2－5x ＋c ＝的一个根，则这个方程的另一个根是A ．－2B ．2C ．－5D ．58．由若干个相同的小立方体搭成的几何体的三视图如图所示， 则搭成这个几何体的小立方体的个数是A ．3B ．4C ．5D ．6A B C D主视图 左视图 俯视图DAB CDO B 1 C 1D 19．某校安排三辆车，组织九年级学生团员去敬老院参加学雷锋活动，其中小亮与小菲都可以从这三辆车中任选一辆搭乘，则小亮与小菲同车的概率为A ．13B ．19C ．12D ．2310．如图，一个小球由地面沿着坡度i =1∶2的坡面向上前进了10 m ，此时小球距离地面的高度为A ．5 mB ．52mC ．54mD ．310m 11．某商店购进一种商品，单价为30元．试销中发现这种商品每天的销售量P （件）与每件的销售价x （元）满足关系：1002P x =-.若商店在试销期间每天销售这种商品获得200元的利润，根据题意，下面所列方程正确的是A ．(30)(1002)200x x --=B ．(1002)200x x -=C ．(30)(1002)200x x --=D ．(30)(2100)200x x --= 12．若点（－3，y 1）、（－2，y 2）、（1，y 3）在反比例函数xy 2=的图象上，则下列结论正确的是A ．y 1> y 2> y 3B ．y 2> y 1> y 3C ．y 3> y 1> y 2D ．y 3> y 2> y 1 13．如图所示，在平面直角坐标系中，菱形MNPO 的顶点P 坐标是（3，4），则顶点M 、N 的坐标分别是A ．M (5，0)，N (8，4)B ．M (4，0)，N (8，4)C ．M (5，0)，N (7，4)D ．M (4，0)，N (7，4)14．如图，边长为1的正方形ABCD 绕点A 逆时针旋转45º得到正方形AB 1C 1D 1，边B 1C 1与CD 交于点O ，则四边形AB 1OD 的 周长是A ． 2B ．2 2C ．1＋ 2D ．315．如图，点A ，B 的坐标分别为（1, 4）和（4, 4）,抛物线n m x a y +-=2)(的顶点在线段AB 上运动，与x 轴交于C 、D 两点（C 在D 的左侧），点C 的横坐标最小值为3-，则点D 的横坐标最大值为A ．3B．5 C ．8 D ．9第10题图一、选择题答题表：第Ⅱ卷（非选择题，共75分）二、填空题（本大题共6小题，每小题3分，共18分，把答案填写在题中横线上）16．反比例函数y ＝kx的图象经过点P(－4，3)，则k 的值为 ．17．有一箱规格相同的红、黄两种颜色的小塑料球共1000个．为了估计这两种颜色的球各有多少个，小明将箱子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回箱子中，多次重复上述过程后．发现摸到红球的频率约为0.6，据此可以估计红．球．的个数约为 ． 18．如图，热气球的探测器显示，从热气球看一栋高楼的顶部B的仰角为45°，看这栋高楼底部C 的俯角为60°，热气球与高楼的水平 距离AD 为50m ，则这栋楼的高度为___________.19．如果关于x 的方程220x x m -+=（m 为常数）有两个相等实数根，那么m ＝_________．20．如同，矩形纸片ABCD 中，AB ＝2cm ，点E 在BC 上，且AE＝EC .若将纸片沿AE 折叠，点B 恰好与AC 上的点'B 重合，则AC ＝ cm.21．如图，已知二次函数c bx x y ++=2的图象经过点（-1，0），（1，-2），当y 随x 的增大而增大时，x 的取值范围是 ．（第21题）cA E BCFD7小题，共57分，解答应写出文字说明和运算步骤）22．（本小题7分）完成下列各题：（1）解方程：1042=+x x（2）计算：26tan 30cos45︒︒-︒． 23．（本小题7分）完成下列各题： （1）在□ABCD 中，E 、F 分别是AB 、CD 的中点，连接AF 、CE ．求证：四边形AECF 是平行四边形（2）已知：如图，在Rt △ABC 中，∠C =90°，∠ABC =60°，AC ，D 为CB 延长线上一点，且BD =2AB ．求AD 的长．24．（本小题8分）我市某楼盘准备以每平方米6000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，房地产开发商为了加快资金周转，对价格经过两次下调后，决定以每平方米4860元的均价开盘销售.（1）求平均每次价格下调的百分率.（2）某人准备以开盘价均价购买一套100平方米的住房，开发商给予以下两种优惠方案以供选择：①打9.8折销售；②不打折，一次性送装修费每平方米80元，试问哪种方案更优惠？25．（本小题8分）端午节吃粽子是中华民族的传统习俗，一超市为了吸引消费者，增加销售量，特此设计了一个游戏，其规则是：分别转动如图所示的两个可以自由转动的转盘各一次，每次指针落在每一字母区域的机会均等（若指针恰好落在分界线上则重转），当两个转盘的指针所指字母都相同时，消费者就可以获得一次八折优惠价购买粽子的机会．（1）用树状图或列表的方法表示出游戏可能出现的所有结果；（2）若一名消费者只能参加一次游戏，则他能获得八折优惠价购买粽子的概率是多少？转盘1转盘226．（本小题9分）对于抛物线243y x x=-+.（1）它与x轴交点的坐标为，与y轴交点的坐标为，顶点坐标为；（2）在坐标系中利用描点法画出此抛物线；（3）利用以上信息解答下列问题：若关于x的一元二次方程2430x x t-+-=（t为实数）在1-＜x＜72的范围内有解，则t的取值范围是．27．（本小题9分）如图，在直角坐标系中，O 为坐标原点. 已知反比例函数ky x=（k>0）的图象经过点A (2，m )，过点A 作AB ⊥x 轴于点B ，且△AOB 的面积为12.（1）求k 和m 的值；（2）点C （x ，y ）在反比例函数ky x=的图象上，求当 1≤x ≤3时函数值y 的取值范围； （3）过原点O 的直线l 与反比例函数ky x=的图象交于P 、 Q 两点，试根据图象直接写出线段PQ 长度的最小值.BOA28．（本小题9分）已知直角坐标系中菱形ABCD 的位置如图，C ，D 两点的坐标分别为（4，0），（0，3）.现有两动点P ，Q 分别从A ,C 同时出发，点P 沿线段AD 向终点D 运动，点Q 沿折线CBA 向终点A 运动，设运动时间为t 秒. （1）填空：菱形ABCD 的边长是 ；面积是 ；高BE 的长是 ； （2）若点P 的速度为每秒1个单位，点Q 的速度为每秒2个单位.当点Q 在线段BA 上时，求△APQ 的面积S 关于t九年级数学试题参考答案一、选择题：（每小题3分）C D A B D D B A A B A C A B C 二、填空题：（每小题3分）16. -12 17. 600 18. 50+ 19. 1 20. 4 21. x ＞21三、解答题：22．（1）解：244104x x ++=+2(2)14x +=…………………………..1分2x +=分2x =-∴12x =-+22x =-分（2）解：26tan 30cos45︒︒-︒26=⨯分32=-12= ………………………………………………7分23．（1）证明：∵四边形ABCD 是平行四边形∴AB=CD ，AB ∥CD ……………………………………1分 ∵E 、F 分别是AB 、CD 的中点∴AE =CF ，且AE ∥CF ………………………………..2分 ∴四边形AECF 是平行四边形…………………………..3分（2）解：在Rt △ABC 中，∠C =90°，∠ABC =60°，AC ， ∴ 2sin 60ACAB ==︒，BC =1．……………………5分 ∵ D 为CB 延长线上一点，BD =2AB ，∴ BD =4，CD =5． …………………………………6分∴AD =．……………………7分24．解：（1）设平均每次下调的百分率x ，则6000（1－x ）2=4860……………………………………3分 解得：x 1=0.1 x 2=1.9（舍去）……………………….…..4分∴平均每次下调的百分率10%..........................................................5分（2）方案①可优惠：4860×100×（1－0.98）=9720元………6分 方案②可优惠：100×80=8000元……………………………….7分∴方案①更优惠………………………………………………8分25．解: （1）解法一：--------------4分 --------------6分 解法二:分（2）∵共有6种结果，两个转盘的指针所指字母都相同时的结果只有一种，∴P （字母相同）=16-----------------------------8分 26．解：（1）它与x 轴交点的坐标为(1,0),(3,0)，与y 轴交点的坐标为(0,3)，顶点坐标为(2,1)-； ………………………………………3分（2）列表：分图象如图所示． 分 （3）t 的取值范围是18t -≤<．……………………9分……数学试题 第 11 页 （共 8 页）27．解：（1）∵A (2，m ) ， ∴OB =2 ，AB =m∴S △AOB =21•OB •AB =21×2×m =21 ∴m =21.............................................................................................................2分 ∴点A 的坐标为（2，21），把A （2，21）代入y=x k ，得21=2k ∴k =1 …………………………………………………………………………4分（2）∵当x =1时，y =1；当x =3时，y =31………………………………….6分 又∵反比例函数y =x1在x >0时，y 随x 的增大而减小 ∴当1≤x ≤3时，y 的取值范围为31≤y ≤1………………………………..7分 （3）由图象可得，线段PQ 长度的最小值为22……………………….9分28．解：（1）5 , 24, 524…………………………………3分 （2）①由题意，得AP =t ，AQ =10-2t. …………………………………………4分如图1,过点Q 作QG ⊥AD ，垂足为G ，由QG ∥BE 得△AQG ∽△ABE ……………………………5分 ∴BA QA BE QG =, ∴QG =2548548t -, …………………………6分 ∴t t QG AP S 5242524212+-=⋅=(25≤t ≤5). ……7分 ∵6)25(25242+--=t S (25≤t ≤5). ∴当t =25时，S 最大值为6.…………………9分。

学校：____________ 班级：_____________ 姓名：_____________ 座号：_____________---------------密----------------------封-----------------------线-----------------------内---------------------不-----------------------准--------------------------答----- -----------------------题-------------------------------2013～2014学年度第一学期期末联合调研测试九 年 级 数 学亲爱的同学，诚信是我们中华民族的传统美德。

诚信应考，是责任感的体现；诚信应考，是人格魅力的体现。

当你手捧着充满“诚信”的答卷，面对老师，面对父母时，他们一定会因你拥有的人格魅力而骄傲，同时，你也会为自己感到自豪。

亲爱的同学，相信在本场考试中，你的数学知识水平和探究能力一定会有很好的发挥。

特别提醒你要仔细审题。

祝你取得好成绩！并请你注意：1.答卷前，请你用钢笔（圆珠笔）将自己的校名、班级、姓名、座号填在密封线内。

2.答卷时，请按题目的要求作答。

3.试卷共6页，考试时间90分钟，满分150分。

题号 一题36分 二题32分 三题 82分 总分 21题 7分 22题 7分 23题 8分 24题 10分 25题 12分 26题12分 27题 12分 28题 14分 得分一、选择题（本大题共12小题，每题3分，共36分。

下列各题的备选答案中，只有一个是正确的，请将正确答案的序号填入下表中相应题号下的空格内）题号 1 2 3 4 5 6 7 8 9 10 11 12 答案1、下列二次根式中，最简二次根式是（ ）A.51B. 5.0C. 5D. 50 2、“a 是实数, ||0a ≥”这一事件是 （ ）A. 必然事件B. 不确定事件C. 不可能事件D. 随机事件 3、方程x x 22=的根为（ ）A. 2=xB. 0=xC.2021==x x ，D. 2021-==x x ， 4、如图，⊙O 的半径OC 垂直弦AB 于D ，若AB=8，OD=3 则⊙O 的直径为（ ）A.5B. 6C. 8D. 105、抛物线()21-=x y 的顶点坐标是( ) A ．（1，0） B ．（－1，0）C ．（－2，1）D ．（2，－1）6、已知正六边形的边心距为3，则它的周长是（ ） A. 6 B. 12 C.36 D. 3127、二次函数2)1(2+-=x y 的最小值是（ ） A. -2 B. -1 C. 1 D. 28、如图，小圆的半径为7，大圆的半径为9，则圆环的面积为（ ） A.17π B.32π C. 49πD. 80πD OB第4题AC 79第8题2013-2014学年度第一学期期末调研测试 九年级 数学9、下列图形中，是中心对称图形的是( )A ．B ．C ．D ．10、如图所示，将矩形纸片先沿虚线AB 按箭头方向向右．．对折，接着将对折后的纸片沿虚线CD 向下对折，然后剪下一个小三角形，再将纸片打开，则打开后的展开图是（ ）A ．B ．C ．D ．11、若114<<a ，则()()22114-+-a a 化简后为（ ）A. 7B. -7C. 152-aD. 无法确定12、已知抛物线()02≠++=a c bx ax y 在平面直角坐标系中的位置如图所示，则下列结论中正确的是( )A ． 0>aB ． 0<bC ． 0>cD ． 0<++c b a 二、填空题（本大题共8小题，每题4分，共32分。

福州市2013—2014学年第一学期九年级期末质量检测数学试卷参考答案及评分标准一、选择题(每小题4分，共40分)1．B 2．D 3．A 4．C 5．B 6．C 7．A 8．A 9．D 10．D二、填空题(每小题4分，共20分)：11．x ≥1 12． 1 6 13．1 14．100 15．7； 21 4(正确一个得2分) 三、解答题：(满分90分)16．(每小题7分，共14分)解：(1) 8×12×18÷27＝22×23×32÷3 3 ……………………………………………………………4分 ＝8． ……………………………………………………………………………………7分 (2) 9x ＋6 x 4－2x 1 x＝3x ＋3x －2x ……………………………………………………………………6分＝4x ． …………………………………………………………………………………7分17．解：(1) △A 1B 1C 1如右下图； ………………………………………………………………3分(2) A 1(1，3)，B 1(1，0)，C 1(3，0)； …………………………………………………6分(3) 由抛物线y ＝ax 2＋bx ＋c 经过点C 、B 1、C 1，可得：⎩⎪⎨⎪⎧c ＝3a ＋b ＋c ＝09a ＋3b ＋c ＝0， ………………………………………………………………9分 解得：⎩⎪⎨⎪⎧a ＝1b ＝－4c ＝3， …………………………………10分 ∴抛物线的解析式为：y ＝x 2－4x ＋3． ……………11分(答案用一般式或顶点式表示，否则扣2分) (4) 表格填写合理正确得2分，图像正确得2分．x… 0 1 2 3 4 … y ＝x 2－4x＋3 … 3 0 －1 0 3 … 二次函数y ＝x 2－4x ＋3的图像如右图． 18．解：(1) 列树状图如下：………………3分由树状图可知：所有可能出现的结果共12种情况，并且每种情况出现的可能性相等．其中x 与y 的积为偶数有6种． …………………………………………………………………………………4分∴小明获胜的概率P (x 与y 的积为偶数)＝6 12 ＝ 1 2． ………………………………6分 (2) 列树状图如下：……………9分A B C O xy A 1 B 1 C 1 y ＝x 2－4x ＋3 1 2 35 1 2 3 5 1 2 3 5 1 2 3 5 小明 小强小明 小强 1 2 3 5 1 2 3 5 1 2 3 5 1 2 3 5 1 2 3 5由树状图可知，所有可能出现的结果共16种情况，并且每种情况出现的可能性相等．其中x与y的积为偶数有7种． (10)分∴小明获胜的概率P(x与y的积为偶数)＝716 ＜12，……………………………11分(或证明716 ≠916 也可)∴游戏规则不公平．……………………………………………………………………12分19．解：(1) 设这两年该县旅游纯收入的年平均增长率为x．根据题意得：………………1分2000(1＋x)2＝2880．…………………………………………………………4分解得：x1＝0.2＝20%，x2＝－2.2 (不合题意，舍去)．………………………6分答：这两年该县旅游纯收入的年平均增长率为20%．………………………7分(2) 如果到2015年仍保持相同的年平均增长率，则2015年该县旅游纯收入为2880(1＋0.2)2＝4147.2(万元)．………………………9分答：预测2015年该县旅游纯收入约4147.2万元．………………………10分20．解：(1) 连接OC．…………………………………………1分∵AB是⊙O的直径，∴∠ACB＝90°，即∠ACO＋∠OCB＝90°．………2分∵OA＝OC，∴∠A＝∠ACO，………………………………3分∵∠A＝∠PCB，∴∠ACO＝∠PCB．………………………………4分∴∠PCB＋∠OCB＝∠ACO＋∠OCB＝90°，即∠PCO＝90°．∴PC⊥OC．………………………………5分又∵OC为⊙O的半径，∴PC是⊙O的切线．………………………………6分(2) ∵AC＝PC，∴∠A＝∠P，………………………………………7分∴∠PCB＝∠A＝∠P．∴BC＝BP＝1．………………………………………8分∴∠CBO＝∠P＋∠PCB＝2∠PCB．又∵∠COB＝2∠A＝2∠PCB，∴∠COB＝∠CBO，…………………………………9分∴BC＝OC．又∵OB＝OC，∴OB＝OC＝BC＝1，即△OBC为等边三角形．……10分∴∠COB＝60°．………………………………11分∴l⌒BC＝1×60π180＝13π．……………………………12分21．解：(1) DC＋CE＝2；…………………………………3分(2) 结论成立.连接PC，如图．…………………………4分∵△ABC是等腰直角三角形，P是AB的中点，∴CP＝PB，CP⊥AB，∠ACP＝12∠ACB＝45°．ABCOPABCDEP∴∠ACP ＝∠B ＝45°，∠CPB ＝90°． …………………5分∴∠BPE ＝90°－∠CPE ．又∵∠DPC ＝90°－∠CPE ，∴∠DPC ＝∠EPB ． ………………………………6分∴△PCD ≌△PBE ．∴DC ＝EB ， …………………………………………7分∴DC ＋CE ＝EB ＋CE ＝BC ＝2． ……………………8分(3) △CMN 的周长为定值，且周长为2． …………9分在EB 上截取EF ＝DM ，如图， …………………10分由(2)可知：PD ＝PE ，∠PDC ＝∠PEB ， ∴△PDM ≌△PEF ， ………………………………11分∴∠DPM ＝∠EPF ，PM ＝PF ．∵∠NPF ＝∠NPE ＋∠EPF ＝∠NPE ＋∠DPM ＝∠DPE －∠MPN＝45°＝∠NPM ．∴△PMN ≌△PFN ，∴MN ＝NF ． ……………………………………………12分∴MC ＋CN ＋NM ＝MC ＋CN ＋NE ＋EF＝MC ＋CE ＋DM＝DC ＋CE＝2．∴△CMN 的周长是2． …………………………………13分22．解：(1) 令y ＝0，得：x 2－4x ＋1＝0， …………………1分解得：x 1＝2＋3，x 2＝2－3． …………………3分 ∴点A 的坐标为(2－3，0)，点B 的坐标为(2＋3，0)． …4分∴AB 的长为23． ………………………………5分(由韦达定理求出AB 也可)(2) 由已知得点C 的坐标为(0，1)，由y ＝x 2－4x ＋1＝(x ―2)2―3， 可知抛物线的对称轴为直线x ＝2， ……………………6分设△ABC 的外接圆圆心D 的坐标为(2，n )，连接AD 、CD ，∴DC ＝DA ，即22＋(n －1)2＝[2―(2―3)]2＋n 2，……………8分解得：n ＝1， …………………………………………9分∴点D 的坐标为(2，1)，∴△ABC 的外接圆⊙D 半径为2． ……………………10分(3) 解法一：由(2)知，C 是弧MN 的中点．在半径DN 上截取EN ＝ MG ， ……………………11分又∵DM ＝DN ，∴DG ＝DE ．则点G 与点E 关于点D 对称，连接CD 、CE 、PD 、PE ．由圆的对称性可得：图形PMC 的面积与图形PECN 的面积相等． …………………………………………12分由PC 把图形PMCN (指圆弧⌒MCN 和线段PM 、PN 组成的图形)分成两部分，这两部分面积之差为4．可知△PCE 的面积为4．设点P 坐标为(m ，n ) A B C D E M P N F A BC O x yD A B CO xyD EMP N G∴S △CEP ＝2S △CDP ＝2× 1 2·CD ·n －1＝4， ∴n 1＝3，n 2＝－1． ……………………………………13分 由点P 在抛物线y ＝x 2－4x ＋1上，得：x 2－4x ＋1＝3，解得：x 1＝2＋6，x 2＝2－6(舍去)；或x 2－4x ＋1＝－1，解得：x 3＝2＋2，x 4＝2－2(舍去)．∴点P 的坐标为(2＋2，－1)或(2＋6，3)． ……………14分 解法二：设点P 坐标为(m ，n )，点G 坐标为(2，c )，直线PC 的解析式为y ＝kx ＋b ，得：⎩⎨⎧b ＝1n ＝km ＋b ，解得：⎩⎪⎨⎪⎧k ＝n －1 m b ＝1， ∴直线PC 的解析式为y ＝ n －1 m x ＋1． …………………11分当x ＝2时，c ＝ 2(n －1) m ＋1．由(2)知，C 是弧MN 的中点，连接CD ， 图形PCN 的面积与图形PMC 的面积差为：＝S 扇形DCN ＋S △GCD ＋S △PGN －(S 扇形MCD －S △GCD ＋S △PMG )＝2S △GCD ＋S △PGN －S △PMG＝2×12 ×2(c －1)＋1 2 (1＋c )(m ―2)―12 (3―c )(m ―2)＝2(c －1)＋12 (2c ―2)(m ―2)＝(c －1)(2＋m ―2)＝[ 2(c －1) m ＋1―1]m＝2(n －1)＝4．∴n 1＝3，n 2＝－1． ……………………………………13分 由点P 在抛物线y ＝x 2－4x ＋1上，得：x 2－4x ＋1＝3，解得：x 1＝2＋6，x 2＝2－6(舍去)；或x 2－4x ＋1＝－1，解得：x 3＝2＋2，x 4＝2－2(舍去)．∴点P 的坐标为(2＋2，－1)或(2＋6，3)． ……………14分A B C O x y D M P N G。