江苏省泰兴河失中学2019届高三学情调查(三)数学试题

2019届江苏省七市（南通、泰州、扬州、徐州、淮安、宿迁、连云港）高三第三次调研考试数 学 理 科(满分160分，考试时间120分钟)2019．5一、 填空题：本大题共14小题，每小题5分，共70分．1. 已知集合U ＝{－1，0，2，3}，A ＝{0，3}，则∁U A ＝________．2. 已知复数z ＝a ＋i1＋3i(i 是虚数单位)是纯虚数，则实数a 的值为________．3. 右图是一个算法流程图．若输出y 的值为4时，则输入x 的值为________．4. 已知一组数据6，6，9，x ，y 的平均数是8，且xy ＝90，则该组数据的方差为________．5. 一只口袋装有形状、大小都相同的4只小球，其中有3只白球，1只红球．从中1次随机摸出2只球，则2只球都是白色的概率为________．6. 已知函数f(x)＝⎩⎪⎨⎪⎧x 2－2x ，x ≥0，－x 2－2x ，x ＜0，则不等式f(x)＞f(－x)的解集为____________．7. 已知数列{a n }是等比数列，其前n 项和为S n .若a 3－a 2＝4，a 4＝16，则S 3的值为________．8. 在平面直角坐标系xOy 中，双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的右准线与两条渐近线分别交于A ，B 两点．若△AOB 的面积为ab4，则该双曲线的离心率为________．9. 在直角梯形ABCD 中，AB ∥CD ，AB ⊥BC ，AB ＝3 cm ，BC ＝1 cm ，CD ＝2 cm.将此直角梯形绕AB 边所在的直线旋转一周，由此形成几何体的体积为________cm 3.10. 在平面直角坐标系xOy 中，若曲线y ＝sin 2x 与y ＝18tan x 在(π2，π)上交点的横坐标为α，则sin 2α的值为________．11. 如图，在正六边形ABCDEF 中，若AD →＝λAC →＋μAE →(λ，μ∈R )，则λ＋μ的值为________．(第11题)(第12题)12. 如图，有一壁画，最高点A 处离地面6 m ，最低点B 处离地面3.5 m ．若从离地高2 m 的C 处观赏它，则离墙________m 时，视角θ最大．13. 已知函数f(x)＝x 2－2x ＋3a ，g(x)＝2x －1.若对任意x 1∈[0，3]，总存在x 2∈[2，3]，使得|f(x 1)|≤g(x 2)成立，则实数a 的值为________．14. 在平面四边形ABCD 中，∠BAD ＝90°，AB ＝2，AD ＝1.若AB →·AC →＋BA →·BC →＝43CA →·CB →，则CB ＋12CD 的最小值为________．二、 解答题：本大题共6小题，共90分. 解答时应写出必要的文字说明、证明过程或演算步骤．15. (本小题满分14分)在△ABC 中，a ，b ，c 分别为角A ，B ，C 所对边的长，a(sin A －sin B)＝(c －b)(sin B ＋sin C)．(1) 求角C 的值；(2) 若a ＝4b ，求sin B 的值．16.(本小题满分14分)如图，在四棱锥P ABCD 中，底面ABCD 为平行四边形，平面BPC ⊥平面DPC ，BP ＝BC ，点E ，F 分别是PC ，AD 的中点．求证：(1) BE ⊥CD ； (2) EF ∥平面PAB.(本小题满分14分) 17.如图，在平面直角坐标系xOy 中，已知椭圆C ：x 2a 2＋y 2b2＝1(a ＞b ＞0)的上顶点为A(0，3)，圆O：x2＋y2＝a24经过点M(0，1)．(1) 求椭圆C的方程；(2) 过点M作直线l1交椭圆C于P，Q两点，过点M作直线l1的垂线l2交圆O于另一点N.若△PQN的面积为3，求直线l1的斜率．南通风筝是江苏传统手工艺品之一．现用一张长2 m，宽1.5 m的长方形牛皮纸ABCD 裁剪风筝面，裁剪方法如下：分别在边AB，AD上取点E，F，将三角形AEF沿直线EF翻折到A′EF处，点A′落在牛皮纸上，沿A′E，A′F裁剪并展开，得到风筝面AEA′F，如图1.(1) 若点E恰好与点B重合，且点A′在BD上，如图2，求风筝面ABA′F的面积；(2) 当风筝面AEA′F的面积为 3 m2时，求点A′到AB距离的最大值．已知数列{a n }满足(na n －1－2)a n ＝(2a n －1)a n －1(n ≥2)，b n ＝1a n－n(n ∈N *)．(1) 若a 1＝3，求证：数列{b n }是等比数列；(2) 若存在k ∈N *，使得1a k ，1a k ＋1，1a k ＋2成等差数列．①求数列{a n }的通项公式；②求证：ln n ＋12a n ＞ln(n ＋1)－12a n ＋1.已知函数f(x)＝ax 21＋ln x(a ≠0)，e 是自然对数的底数．(1) 当a ＞0时，求f(x)的单调增区间；(2) 若对任意的x ≥12，f(x)≥2e b －1(b ∈R )，求b a的最大值；(3) 若f(x)的极大值为－2，求不等式f(x)＋e x ＜0的解集.2019届高三模拟考试试卷数学附加题(满分40分，考试时间30分钟)21. 【选做题】 在A ，B ，C 三小题中只能选做两题，每小题10分，共20分．若多做，则按作答的前两题计分．解答时应写出必要的文字说明、证明过程或演算步骤．A. (选修42：矩阵与变换)已知a ，b ，c ，d ∈R ，矩阵A ＝⎣⎢⎡⎦⎥⎤a －20 b 的逆矩阵A －1＝⎣⎢⎡⎦⎥⎤1c d 1.若曲线C 在矩阵A 对应的变换作用下得到曲线y ＝2x ＋1，求曲线C 的方程．B. (选修44：坐标系与参数方程)在直角坐标平面内，以原点O 为极点，x 轴的非负半轴为极轴建立极坐标系．已知点A ，B 的极坐标分别为(4，π2)，(22，5π4)，曲线C 的方程为ρ＝r(r>0)．(1) 求直线AB 的直角坐标方程；(2) 若直线AB 和曲线C 有且只有一个公共点，求r 的值．C.(选修45：不等式选讲)已知a ∈R ，若关于x 的方程x 2＋4x ＋|a －1|＋|a|＝0有实根，求a 的取值范围．【必做题】第22，23题，每小题10分，共20分．解答时应写出必要的文字说明、证明过程或演算步骤．22. 现有一款智能学习APP，学习内容包含文章学习和视频学习两类，且这两类学习互不影响．已知该APP积分规则如下：每阅读一篇文章积1分，每日上限积5分；观看视频累计3分钟积2分，每日上限积6分．经过抽样统计发现，文章学习积分的概率分布表如表1所示，视频学习积分的概率分布表如表2所示．文章学习积分 1 2 3 4 5概率1919191612视频学习积分 2 4 6概率161312(1) 现随机抽取1人了解学习情况，求其每日学习积分不低于9分的概率；(2) 现随机抽取3人了解学习情况，设积分不低于9分的人数为ξ，求ξ的概率分布及数学期望．(1) 求2P2－Q2的值；(2) 化简nP n－Q n.2019届高三模拟考试试卷(南通、泰州、徐州等苏北七市联考)数学参考答案及评分标准1. {－1，2}2. －33. －14. 1455. 12 6. (－2，0)∪(2，＋∞) 7. 14 8. 2 9. 7π310. －158 11. 43 12. 6 13. －13 14. 26215. 解：(1) 在△ABC 中， 因为a(sin A －sin B)＝(c －b)(sin B ＋sin C)，由正弦定理a sin A ＝b sin B ＝csin C，所以a(a －b)＝(b ＋c)(c －b)，(3分) 即a 2＋b 2－c 2＝ab.由余弦定理c 2＝a 2＋b 2－2abcos C ，得cos C ＝12.(5分)因为0<C<π，所以C ＝π3.(7分)(2) (解法1)因为a ＝4b 及a 2＋b 2－c 2＝ab ，得c 2＝16b 2＋b 2－4b 2＝13b 2，即c ＝13b.(10分)由正弦定理c sin C ＝b sin B ，得13b 32＝b sin B，所以sin B ＝3926.(14分)(解法2)由正弦定理a sin A ＝bsin B，得sin A ＝4sin B.由A ＋B ＋C ＝π，得sin(B ＋C)＝4sin B.因为C ＝π3，所以12sin B ＋32cos B ＝4sin B ，即7sin B ＝3cos B ．(11分)因为sin 2B ＋cos 2B ＝1，解得sin 2B ＝352.在△ABC 中，因为sin B>0，所以sin B ＝3926.(14分)16. 证明：(1) 在△PBC 中，因为BP ＝BC ，点E 是PC 的中点，所以BE ⊥PC.(2分) 因为平面BPC ⊥平面DPC ，平面BPC ∩平面DPC ＝PC ，BE 平面BPC ， 所以BE ⊥平面PCD.(5分) 因为CD平面DPC ，所以BE ⊥CD.(7分)(2) 如图，取PB 的中点H ，连结EH ，AH. 在△PBC 中，因为点E 是PC 的中点，所以HE ∥BC ，HE ＝12BC.(9分)又底面ABCD 是平行四边形，点F 是AD 的中点，所以AF ∥BC ，AF ＝12BC.所以HE ∥AF ，HE ＝AF ，所以四边形AFEH 是平行四边形，所以EF ∥HA.(12分)因为EF 平面PAB ，HA 平面PAB ，所以EF ∥平面PAB.(14分) 17. 解：(1) 因为椭圆C 的上顶点为A(0，3)，所以b ＝ 3.又圆O ：x 2＋y 2＝14a 2经过点M(0，1)，所以a ＝2.(2分)所以椭圆C 的方程为x 24＋y 23＝1.(4分)(2) 若直线l 1的斜率为0，则PQ ＝463，MN ＝2，所以△PQN 的面积为463，不合题意，所以直线l 1的斜率不为0.(5分)设直线l 1的方程为y ＝kx ＋1，由⎩⎪⎨⎪⎧x 24＋y 23＝1，y ＝kx ＋1消y ，得(3＋4k 2)x 2＋8kx －8＝0.设P(x 1，y 1)，Q(x 2，y 2)，则x 1＝－4k －26·2k 2＋13＋4k 2，x 2＝－4k ＋26·2k 2＋13＋4k 2，所以PQ ＝（x 1－x 2）2＋（y 1－y 2）2＝1＋k 2||x 1－x 2＝46·1＋k 2·2k 2＋13＋4k 2.(8分)由题可知，直线l 2的方程为y ＝－1kx ＋1，即x ＋ky －k ＝0，所以MN ＝21－k 21＋k 2＝21＋k 2.(11分)所以△PQN 的面积S ＝12PQ ·MN ＝12×46·1＋k 2·2k 2＋13＋4k 2·21＋k 2＝3，解得k ＝±12，即直线l 1的斜率为±12.(14分)18. 解：(1) (解法1)建立如图所示的直角坐标系，则B(2，0)，D(0，32)，直线BD 的方程为3x ＋4y －6＝0.(2分) 设F(0，b)(b>0)，因为点F 到AB 与BD 的距离相等，所以b ＝|4b －6|5，解得b ＝23或b ＝－6(舍去)．(4分)所以△ABF 的面积为12×2×23＝23m 2，所以四边形ABA′F 的面积为43 m 2.答：风筝面ABA′F 的面积为43m 2.(6分)(解法2)设∠ABF ＝θ，则∠ABA′＝2θ.在直角三角形ABD 中，tan 2θ＝AD AB ＝34，(2分)所以2tan θ1－tan 2θ＝34，解得tan θ＝13或tan θ＝－3(舍去)． 所以AF ＝ABtan θ＝23.(4分) 所以△ABF 的面积为12×2×23＝23 m 2，所以四边形ABA′F 的面积为43m 2. 答：风筝面ABA′F 的面积为43m 2.(6分) (2) (解法1)建立如图所示的直角坐标系．设AE ＝a ，AF ＝b ，A ′(x 0，y 0)，则直线EF 的方程为bx ＋ay －ab ＝0.因为点A ，A ′关于直线EF 对称，所以⎩⎨⎧y 0x 0＝a b ，bx 02＋ay 02－ab ＝0， 解得y 0＝2a 2b a 2＋b 2.(10分) 因为四边形AEA′F 的面积为3，所以ab ＝3，所以y 0＝23a 3a 4＋3＝23a ＋3a3. 因为0<a ≤2，0<b ≤32，所以233≤a ≤2.(12分) 设f(a)＝a ＋3a 3，233≤a ≤2，则f′(a)＝1－9a 4＝（a 2＋3）（a ＋3）（a －3）a 4. 令f′(a)＝0，得a ＝3或a ＝－3(舍去)．列表如下：a [233，3) 3 (3，2] f′(a) － 0＋ f(a) 单调递减 极小值 单调递增当a ＝3时，f(a)取得极小值，即最小值433， 所以y 0的最大值为32，此时点A′在CD 上，a ＝3，b ＝1. 答：点A′到AB 距离的最大值为32m ．(16分)(解法2)设AE ＝a ，∠AEF ＝θ，则AF ＝atan θ.因为四边形AEA′F 的面积为3，所以AE·AF ＝3，即a 2tan θ＝3，所以tan θ＝3a 2.过点A′作AB 的垂线A′T ，垂足为T ，则A′T ＝A′E ·sin 2θ＝AE·sin 2θ＝asin 2θ(10分)＝a·2sin θcos θsin 2θ＋cos 2θ＝a·2tan θtan 2θ＋1＝a·2×3a 23a 4＋1＝23a ＋3a 3. 因为0<AE ≤2，0<AF ≤32，所以233≤a ≤2.(12分) (下同解法1)19. (1) 证明：由(na n －1－2)a n ＝(2a n －1)a n －1，得1a n ＝2a n －1＋2－n ， 得1a n －n ＝2⎣⎡⎦⎤1a n －1－（n －1），即b n ＝2b n －1. 因为a 1＝3，所以b 1＝1a 1－1＝－23≠0，所以b n b n －1＝2(n ≥2)， 所以数列{b n }是以b 1为首项，2为公比的等比数列．(4分)(2) ①解：设1a 1－1＝λ，由(1)知b n ＝2b n －1， 所以b n ＝2b n －1＝22b n －2＝…＝2n －1b 1，即1a n－n ＝λ·2n －1， 所以1a k＝λ·2k －1＋k.(6分) 因为1a k ，1a k ＋1，1a k ＋2成等差数列，则(λ·2k －1＋k)＋(λ·2k ＋1＋k ＋2)＝2(λ·2k ＋k ＋1)， 所以λ·2k －1＝0，所以λ＝0，所以1a n ＝n ，即a n ＝1n.(10分) ②证明：要证ln n ＋12a n >ln(n ＋1)－12a n ＋1， 即证12(a n ＋a n ＋1)>ln n ＋1n ，即证1n ＋1n ＋1>2ln n ＋1n. 设t ＝n ＋1n ，则1n ＋1n ＋1＝t －1＋t －1t ＝t －1t ，且t>1， 从而只需证：当t>1时，t －1t>2ln t ．(12分) 设f(x)＝x －1x －2ln x(x>1)，则f′(x)＝1＋1x 2－2x ＝(1x－1)2>0， 所以f(x)在(1，＋∞)上单调递增，所以f(x)>f(1)＝0，即x －1x>2ln x. 因为t>1，所以t －1t>2ln t ，所以原不等式得证．(16分) 20. 解：(1) f(x)的定义域为(0，e －1)∪(e －1，＋∞)．由f′(x)＝2ax （1＋ln x ）－ax 2·1x （1＋ln x ）2＝2ax （12＋ln x ）（1＋ln x ）2，(2分) 令f′(x)>0，因为a>0，得x>e －12. 因为e －12>e －1，所以f(x)的单调增区间是(e －12，＋∞)．(4分) (2) 当a<0时，f(1)＝a<0<2e b －1，不合题意；当a>0时，令f′(x)<0，得0<x<e －1或e －1<x<e －12，所以f(x)在区间(0，e －1)和(e －1，e －12)上单调递减． 因为12∈(e －1，e －12)，且f(x)在区间(e －12，＋∞)上单调递增， 所以f(x)在x ＝e －12处取极小值2a e ，即最小值为2a e.(6分) 若x ≥12，f(x)≥2e b －1，则2a e≥2e b －1，即a ≥e b . 不妨设b>0，则b a ≤b e b .(8分) 设g(b)＝b e b (b>0)，则g′(b)＝1－b eb . 当0<b<1时，g ′(b)>0；当b>1时，g ′(b)<0，所以g(b)在(0，1)上单调递增，在(1，＋∞)上单调递减，所以g(b)≤g(1)，即b e b ≤1e， 所以b a 的最大值为1e.(10分) (3) 由(2)知，当a>0时，f(x)无极大值．当a<0时，f(x)在(0，e －1)和(e －1，e －12)上单调递增，在(e －12，＋∞)上单调递减， 所以f(x)在x ＝e －12处取极大值，所以f(e －12)＝2a e＝－2，即a ＝－e.(12分) 设F(x)＝f(x)＋e x ，即F(x)＝e x －ex 21＋ln x， 当x ∈(0，e －1)，1＋ln x<0，所以F(x)>0；当x ∈(e －1，＋∞)，F ′(x)＝e x －ex （1＋2ln x ）（1＋ln x ）2， 由(2)知ex ≤e x ，又1＋2ln x ≤(1＋ln x)2，所以F′(x)≥0，且F(x)不恒为零，所以F(x)在(e －1，＋∞)上单调递增．不等式f(x)＋e x <0，即为F(x)<0＝F(1)，所以e －1<x<1，即不等式的解集为(e －1，1)．(16分)2019届高三模拟考试试卷(南通、泰州、徐州等苏北七市联考)数学附加题参考答案及评分标准21. A. 解： 由题意，得AA －1＝⎣⎢⎡⎦⎥⎤1001，即⎣⎢⎡⎦⎥⎤a －20 b ⎣⎢⎡⎦⎥⎤1c d 1＝⎣⎢⎡⎦⎥⎤a －2d ac －2bd b ＝⎣⎢⎡⎦⎥⎤1001， 所以a ＝1，b ＝1，c ＝2，d ＝0，即矩阵A ＝⎣⎢⎡⎦⎥⎤1－20 1.(5分) 设P(x ，y)为曲线C 上的任意一点，在矩阵A 对应的变换作用下变为点P′(x′，y ′)，则 ⎣⎢⎡⎦⎥⎤x′y′＝⎣⎢⎡⎦⎥⎤1－20 1⎣⎢⎡⎦⎥⎤x y ，即⎩⎪⎨⎪⎧x′＝x －2y ，y ′＝y.(8分) 由已知条件可知P′(x′，y ′)满足y ＝2x ＋1，整理得2x －5y ＋1＝0，所以曲线C 的方程为2x －5y ＋1＝0.(10分)B. 解：(1) 分别将A(4，π2)，B(22，5π4)转化为直角坐标，即A(0，4)，B(－2，－2)， 所以直线AB 的直角坐标方程为3x －y ＋4＝0.(4分)(2) 曲线C 的方程为ρ＝r(r>0)，其直角坐标方程为x 2＋y 2＝r 2.又直线AB 和曲线C 有且只有一个公共点，即直线与圆相切，所以圆心到直线AB 的距离为432＋12＝2105，即r 的值为2105.(10分) C. 解：因为关于x 的方程x 2＋4x ＋|a －1|＋|a|＝0有实根，所以Δ＝16－4(|a －1|＋|a|)≥0，即|a －1|＋|a|≤4.(4分)当a ≥1时，2a －1≤4，得1≤a ≤52； 当0<a<1时，1≤4，恒成立，即0<a<1；当a ≤0时，1－2a ≤4，得－32≤a ≤0. 综上，所求a 的取值范围是－32≤a ≤52.(10分) 22. 解：(1) 由题意，获得的积分不低于9分的情形有因为两类学习互不影响，所以概率P ＝19×12＋16×12＋12×13＋12×12＝59， 所以每日学习积分不低于9分的概率为59.(4分) (2) 随机变量ξ的所有可能取值为0，1，2，3. 由(1)知每个人积分不低于9分的概率为59，则 P (ξ＝0)＝(49)3＝64729；P(ξ＝1)＝C 13(59)(49)2＝240729； P (ξ＝2)＝C 23(59)2(49)＝300729；P(ξ＝3)＝(59)3＝125729. 所以随机变量ξ的概率分布列为(8分)所以E(ξ)＝0×64729＋1×240729＋2×300729＋3×125729＝53. 所以随机变量ξ的数学期望为53.(10分) 23. 解：(1) 由题可知P 2＝1C 04－1C 14＋1C 24－1C 34＋1C 44＝53，Q 2＝－1C 14＋2C 24－3C 34＋4C 44＝103， 所以2P 2－Q 2＝0.(2分)(2) 设T ＝nP n －Q n ，则T ＝(n C 02n －n C 12n ＋n C 22n －…＋n C 2n 2n )－(－1C 12n ＋2C 22n －3C 32n ＋…＋2n C 2n 2n) ＝n C 02n －n －1C 12n ＋n －2C 22n －n －3C 32n ＋…＋－n C 2n 2n①.(6分) 因为C k 2n ＝C 2n －k 2n ，所以T ＝n C 2n 2n －n －1C 2n －12n ＋n －2C 2n －22n －n －3C 2n －32n＋…＋－n C 02n ＝－n C 02n －1－n C 12n ＋2－n C 22n －3－n C 32n ＋…＋n C 2n 2n②， ①＋②，得2T ＝0，即T ＝nP n －Q n ＝0，所以nP n －Q n ＝0.(10分)。

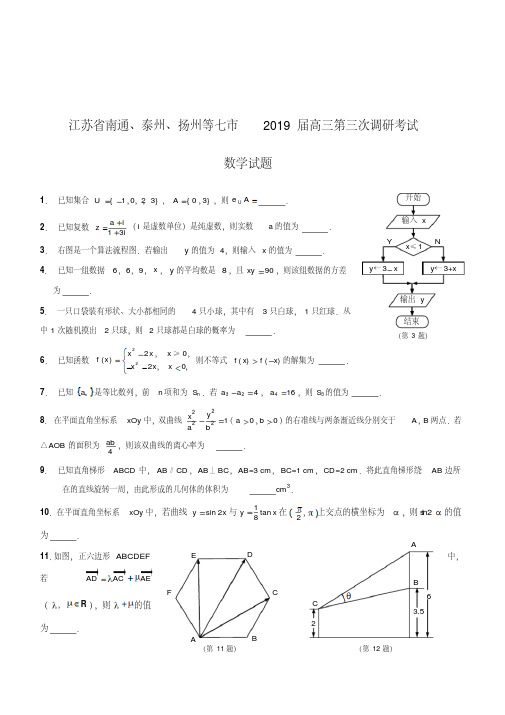
南通市2019届高三第三次调研测试1． 已知集合{1023}U =-，，，，{03}A =，，则U A =ð ▲ ．2． 已知复数i 13i a z +=+（i 是虚数单位）是纯虚数，则实数a 的值为 ▲ ．3． 右图是一个算法流程图．若输出y 的值为4，则输入x 的值为 ▲ ． 4． 已知一组数据6，6，9，x ，y 的平均数是8，且90xy =，则该组数据的方差为 ▲ ．5． 一只口袋装有形状、大小都相同的4只小球，其中有3只白球，1只红球．从中1次随机摸出2只球，则2只球都是白球的概率为 ▲ ．6． 已知函数2220()20x x x f x x x x ⎧-=⎨--<⎩，≥，，， 则不等式()()f x f x >-的解集为 ▲ ．7． 已知{}n a 是等比数列，前n 项和为n S ．若324a a -=，416a =，则3S 的值为 ▲ ．8． 在平面直角坐标系xOy 中，双曲线22221y x a b-=（00a b >>，）的右准线与两条渐近线分别交于A ，B 两点．若△AOB 的面积为4ab ，则该双曲线的离心率为 ▲ ．9． 已知直角梯形ABCD 中，AB ∥CD ，AB ⊥BC ，AB =3 cm ，BC =1 cm ，CD =2 cm ．将此直角梯形绕AB 边所在的直线旋转一周，由此形成的几何体的体积为 ▲ cm 3．10．在平面直角坐标系xOy 中，若曲线sin 2y x =与1tan 8y x =在()2ππ，上交点的横坐标为α，则sin 2α的值为 ▲ ．11．如图，正六边形ABCDEF 中，若AD AC AEλμ=+（λμ∈，R ），则λμ+的值为 ▲ ．12．如图，有一壁画，最高点A 处离地面6 m ，最低点B 处离地面3.5 m ．若从离地高2 m 的C 处观赏它，则离墙 ▲ m 时，视角θ最大．13．已知函数2()23f x x x a =-+，2()1g x x =-．若对任意[]103x ∈，，总存在[]223x ∈，，使得12()()f x g x ≤成立，则实数a 的值为 ▲ ．（第3题）（第11题）（第12题）14．在平面四边形ABCD 中，90BAD ∠=︒， 2AB =，1AD =．若43AB AC B A B C C A C B ⋅+⋅=⋅， 则12CB CD+的最小值为 ▲ ．15．在△ABC 中，a ，b ，c 分别为角A ，B ，C 所对边的长，(sin sin )()(sin sin )a A B c b B C -=-+．（1）求角C 的值；（2）若4a b =，求sin B 的值．16．如图，在四棱锥P －ABCD 中，底面ABCD 是平行四边形，平面BPC ⊥平面DPC ，BP BC =，E ，F 分别是PC ，AD 的中点． 求证：（1）BE ⊥CD ； （2）EF ∥平面P AB ．17．如图，在平面直角坐标系xOy 中，已知椭圆22221y x C a b+=：（0a b >>）的上顶点为(0A ，圆2224a O x y +=：经过点()01M ，． （1）求椭圆C 的方程；（2）过点M 作直线1l 交椭圆C 于P ，Q 两点，过点M 作直线1l 的垂线2l 交圆O 于另一点N ．若△PQN 的面积为3，求直线1l 的斜率．18．南通风筝是江苏传统手工艺品之一．现用一张长2 m ，宽1.5 m 的长方形牛皮纸ABCD 裁剪风筝面，裁剪方法如下：分别在边AB ，AD 上取点E ，F ，将三角形AEF 沿直线EF 翻折到A EF '处，点A '落在牛皮纸上，沿A E '，A F '裁剪并展开，得到风筝面AEA F '，如图1．（1）若点E 恰好与点B 重合，且点A '在BD 上，如图2，求风筝面ABA F '的面积； （2）当风筝面AEA F '2时，求点A '到AB 距离的最大值．（第16题）（第17题）（图1）C（图2）（E ）C19．已知数列{}n a 满足11(2)(21)n n n n na a a a ---=-（2n ≥），1n nb n a =-（n *∈N ）．（1）若1=3a ，证明：{}n b 是等比数列；（2）若存在k *∈N ，使得1k a ，11k a +，21k a +成等差数列．① 求数列{}n a 的通项公式；② 证明：111ln ln(1)22n n n a n a ++>+-．20．已知函数2()1ln ax f x x=+（0a ≠），e 是自然对数的底数． （1）当0a >时，求()f x 的单调增区间；（2）若对任意的12x ≥，1()2e b f x -≥（b ∈R ），求b a 的最大值；（3）若()f x 的极大值为2-，求不等式()e 0x f x +<的解集．21．A ．[选修4-2：矩阵与变换]已知a b c d ∈，，，R ，矩阵20a b -⎡⎤=⎢⎥⎣⎦A 的逆矩阵111c d -⎡⎤=⎢⎥⎣⎦A ．若曲线C 在矩阵A 对应的变换作用下得到曲线21y x =+，求曲线C 的方程． B ．[选修4-4：坐标系与参数方程]在直角坐标平面内，以原点O 为极点，x 轴的非负半轴为极轴建立极坐标系．已知点A ，B 的极坐标分别为()π42，，()5π4，，曲线C 的方程为r ρ=（0r >）．（1）求直线AB 的直角坐标方程；（2）若直线AB 和曲线C 有且只有一个公共点，求r 的值． C ．[选修4-5：不等式选讲]已知a ∈R ，若关于x 的方程2410x x a a ++-+=有实根，求a 的取值范围．22．现有一款智能学习APP ，学习内容包含文章学习和视频学习两类，且这两类学习互不影响．已知该APP 积分规则如下：每阅读一篇文章积1分，每日上限积5分；观看视频累计3分钟 积2分，每日上限积6分．经过抽样统计发现，文章学习积分的概率分布表如表1所示，视频 学习积分的概率分布表如表2所示．（1）现随机抽取1人了解学习情况，求其每日学习积分不低于9分的概率；（2）现随机抽取3人了解学习情况，设积分不低于9分的人数为ξ，求ξ的概率分布及数学期望．23．设202(1)i nn i i n P C =-=∑，212(1)j nn jj njQ C =-⋅=∑． （1）求222P Q -的值；（2）化简n n nP Q -．表1表2南通市2019届高三第三次调研测参考答案1、 {12}-，2、3-3、1-4、1455、126、(20)(2)-+∞，，7、14 8、2 9、73π 10、 11、43 1213、13- 1415、（1）π3C =．（2）sin B =．16、略17、（1）椭圆C 的方程为22143y x +=． （2）若1l 的斜率为0，则PQ ，2MN =， 所以△PQN 的面，不合题意，所以直线1l 的斜率不为0． 设直线1l 的方程为1y kx =+， 由221431y x y kx ⎧+=⎪⎨⎪=+⎩，消y ，得22(34)880k x kx ++-=， 设()11P x y ，，()22Q x y ，，则1x，2x所以PQ12x -=直线2l 的方程为11y x k =-+，即0x ky k +-=，所以．MN == 所以△PQN 的面积12S PQ MN =⋅132==，解得12k =±，即直线1l 的斜率为12±． 18、（1）方法一：建立直角坐标系四边形ABA F '的面积为24m 3．方法二：设ABF θ∠=，则2ABA θ'∠=．在直角△ABD 中，3tan 24AD AB θ==， 所以22tan 341tan θθ=-， 解得1tan 3θ=或tan 3θ=-（舍去）．所以2tan 3AF AB θ==． 所以△ABF 的面积为21222m 233⨯⨯=，所以四边形ABA F '的面积为24m 3．（2）方法一：建立如图所示的直角坐标系． 设AE a =，AF b =，()00A x y '，，则直线EF 的方程为0bx ay ab +-=，因为点A ，A '关于直线EF 对称，所以0000022y ax b bx ay ab ⎧=⎪⎪⎨⎪+-=⎪⎩，，解得20222a b y a b =+． 因为四边形AEA F '所以ab =，所以033y a a=+． 因为02a <≤，302b <≤，2a ≤． 设33()f a a a =+2a ≤．49()1f a a '=-= 令()0f a '=，得a =a =（舍去）． 列表如下：当a ()f a所以0y 的最大值为32，此时点A '在CD上，a =1b =． 答：点A '到AB 距离的最大值为3m 2．方法二：设AE a =，AEF θ∠=，则tan AF a θ=．因为四边形AEA F '的面AE AF ⋅2tan a θ=tan θ．过点A '作AB 的垂线A T '，垂足为T ，则s i n 2s i n 2s i n2A T A E AE a θθθ''=⋅=⋅=A 'ABCDFET2224322sincos 2tan 33sin cos tan 11a a a a a a aθθθθθθ=⋅=⋅=⋅=++++．因为02AE <≤，302AF <≤，2a ≤． （下同方法一）19、（1）由11(2)(21)n n n n na a a a ---=-，得1122n n n a a -=+-，得()11121n n n n a a -⎡⎤-=--⎢⎥⎣⎦，即12n n b b -=因为1=3a ，所以11121=03b a =--≠，所以12n n bb -=（2n ≥），所以{}n b 是以1b 为首项，2为公比等比数列．（2）① 设111a λ-=，由（1）知，12n n b b -=， 所以21121222n n n n b b b b ---====，即112n nn a λ--=⋅，所以112k k k a λ-=⋅+．因为1ka ，11k a +，21k a +成等差数列，则11(2)(22)2(21)k k k k k k λλλ-+⋅++⋅++=⋅++，所以120k λ-⋅=，所以0λ=，所以1n n a =，即1n a n=．② 要证111ln ln(1)22n n n a n a ++>+-，即证111()ln 2n n n a a n +++>，即证1112ln 1n n n n ++>+．设1n t n +=，则111111t t t n n t t -+=-+=-+，且1t >，从而只需证，当1t >时，12ln t t t ->． 设1()2ln f x x x x=--（1x >），则22121()1(1)0f x x x x '=+-=->，所以()f x 在(1)+∞，上单调递增，所以()(1)0f x f >=，即12l n x x x ->，因为1t >，所以12ln t t t ->，所以，原不等式得证． 20、（1）()f x 的定义域为()()110e e --+∞，，． 由， 222112(1ln )2(ln )2()(1ln )(1ln )ax x ax ax x x f x x x +-⋅+'==++ 令()0f x '>，因为0a >，得12e x ->， 因为112ee -->，()f x 的单调增区间是()12e -+∞，． （2）当0a <时，1(1)02e b f a -=<<，不合题意； 当0a >时，令()0f x '<，得10e x -<<或112e e x --<<， 所以()f x 在区间()10e-，和()112ee--，上单调递减． 因为()1121e e 2--∈，，且()f x 在区间()12e -+∞，上单调递增，所以()f x 在12e x -=处取极小值2e a ，即最小值为2e a ． 若12x ∀≥，1()2e bf x -≥，则122e e b a -≥，即e b a ≥．不妨设0b >，则e b b b a ≤． 设()e bb g b =（0b >），则1()e b b g b -'=．当01b <<时，()0g b '>；当1b >时，()0g b '<，所以()g b 在()01，上单调递增；在()1+∞，上单调递减，所以()(1)g b g ≤，即1e ebb ≤，所以b a 的最大值为1e ． （3）由（2）知，当0a >时，()f x 无极大值， 当0a <时，()f x 在()10e -，和()112ee--，上单调递增；在()12e -+∞，上单调递减，所以()f x 在12ex -=处取极大值， 所以122(e)2ea f -==-，即e a =-． 设()()e x F x f x =+，即2e ()e 1ln x x F x x=-+， 当()10e x -∈，，1ln 0x +<，所以()0F x >； 当()1e x -∈+∞，，2e (12ln )()e (1ln )x x x F x x +'=-+， 由（2）知，e e x x ≤，又212ln (1ln )x x ++≤， 所以()0F x '≥，且()F x 不恒为零， 所以()F x 在()1e -+∞，上单调递增．不等式()e 0x f x +<，即为()0(1)F x F <=，所以1e 1x -<<， 即不等式的解集为()1e 1-，． 21A 、由题意得，11001-⎡⎤=⎢⎥⎣⎦AA ，即212210101a c ad a c b d b d b ---⎡⎤⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦， 所以1120a b c d ====，，，，即矩阵1201-⎡⎤=⎢⎥⎣⎦A ． 设()P x y ，为曲线C 上的任意一点，在矩阵A 对应的变换作用下变为点()P x y '''，， 则 1201x x y y '-⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦，即2.x x y y y '=-⎧⎨'=⎩，由已知条件可知，()P x y '''，满足21y x =+，整理得：2510x y -+=， 所以曲线C 的方程为2510x y -+=．21B 、（1）分别将()π42A ，，()5π4B ，转化为直角坐标为()04A ，，()22B --，， 所以直线AB 的直角坐标方程为340x y -+=． （2）曲线C 的方程为r ρ=（0r >），其直角坐标方程为222x y r += 又直线AB 和曲线C 有且只有一个公共点，即直线与圆相切， 所以圆心到直线AB=r21C 、因为关于x 的方程2410x x a a ++-+=有实根， 所以164(1)0a a ∆=--+≥，即41a a -+≤ 当1a ≥时，421a -≤，得512a ≤≤； 当01a <<时，1≤4，恒成立，即01a <<； 当0a ≤时，412a -≤，得032a -≤≤， 综上：所求a 的取值范围为3522a -≤≤．22、（1）由题意，获得的积分不低于9分的情形有：因为两类学习互不影响，所以概率111111115926223229P =⨯+⨯+⨯+⨯=，所以每日学习积分不低于9分的概率为59．（2）随机变量ξ的所有可能取值为0，1，2，3．由（1）每个人积分不低于9分的概率为59．()()3464=0=9729P ξ=；()()()21354240=1=C 99729P ξ=；()()()22354300=2=C 99729P ξ=；()()35125=3=9729P ξ=． 所以，随机变量ξ的概率分布列为所以642403001255()01237297297297293E ξ=⨯+⨯+⨯+⨯=．所以，随机变量ξ的数学期望为53．23、（1）由201234444441111153P C C C C C =-+-+=，2123444441234103Q C C C C =-+-+=，所以2220P Q -=．（2）设n n T nP Q =-，则01221232222222221232()()n n n n n n n n n n n n n n n T C C C C C C C C =-+-⋅⋅⋅+--+-+⋅⋅⋅+ 0123222222123nn n n n nn n n n n C C C C C ----=-+-+⋅⋅⋅+ ① 因为222k n k n n C C -=， 所以2212223022222123n n n n n n n n n n n n n n T C C C C C -------=-+-+⋅⋅⋅+0123222222123nn n n n nn n n n n C C C C C ----=-+-+⋅⋅⋅+ ② ①+②得，20T =，即0n n T nP Q =-=，所以0n n nP Q -=．。

江苏省泰州中学等2019届高三第二学期联合调研测试数学试题一、填空题（本大题共14小题，每小题5分，共计70分．不需要写出解答过程，请将答案填写在答题卡相应的位置上．．．．．．．．．．）1.已知集合，，则集合中元素的个数为____.【答案】4【解析】【分析】先求出集合A B，数出其中元素个数即可.【详解】解：因为集合A＝{l，2，3}，B＝{2，3，4}所以A B＝{l，2，3，4}，有4个元素故答案为：4.【点睛】本题考查了集合的并集运算，属于基础题.2.在复平面内，复数对应的点位于第_______象限．【答案】四【解析】【分析】先对复数进行运算化简，找出其对应的点即可判断出其所在的象限.【详解】解：因为所以复数对应的点为，位于第四象限故答案为：四.【点睛】本题考查了复数的除法运算，复数与复平面中坐标的关系，属于基础题.3.为了解某高中学生的身高情况，现采用分层抽样的方法从三个年级中抽取一个容量为100的样本，其中高一年级抽取24人，高二年级抽取26人．若高三年级共有学生600人，则该校学生总人数为_______．【答案】1200【解析】【分析】先求出高三年级出去的人数和所占比例，再用高三年级学生数除以其所占比例即为总人数.【详解】解：由题意知高三年级抽取了人所以该校学生总人数为人故答案为：1200.【点睛】本题考查了分层抽样，属于基础题.4.从集合A＝{0，1，2，3}中任意取出两个不同的元素，则这两个元素之和为奇数的概率是_______．【答案】【解析】【分析】先列出一共有多少种取法，再找出其中和为奇数的取法，即可求出其概率.【详解】解：集合A中共有4个元素，任取两个不同的元素有（0,1）、（0,2）、（0,3）、（1,2）、（1,3）（2,3）共6种取法，其中两个元素之和为奇数的有（0,1）、（0,3）、（1,2）、（2,3）共4种取法，所以故答案为：.【点睛】本题考查了古典概型，当取法总数较少时可以采用穷举法，属于基础题.5.中国南宋时期的数学家秦九韶提出了一种多项式简化算法，如图是实现该算法的程序框图，若输入的n＝2，x＝1，依次输入的a为1，2，3，运行程序，输出的s的值为_______．【答案】6【解析】【分析】先代入第一次输入的，计算出对应的，判断为否，再代入第二次输入的，计算出对应的，判断仍为否，再代入第三次输入的，计算出对应的，判断为是，得到输出值.【详解】解：第一次输入，得，，判断否；第二次输入，得，，判断否；第三次输入，得，，判断是，输出故答案为：6.【点睛】本题考查了循环结构流程图，要小心每次循环后得到的字母取值，属于基础题.6.若双曲线的离心率为，则实数a的值为_______．【答案】1【解析】【分析】先由双曲线方程求出，再利用列方程求解.【详解】解：因为代表双曲线所以，且，所以解出故答案为：1.【点睛】本题考查了双曲线的离心率，属于基础题.7.若圆锥的侧面积为，底面积为，则该圆锥的体积为。

江苏省泰州中学等2019届高三第二学期联合调研测试数学试题一、填空题（本大题共14小题，每小题5分，共计70分．不需要写出解答过程，请将答案填写在答题卡相应的位置上．．．．．．．．．．）1.已知集合，，则集合中元素的个数为____.【答案】4【解析】【分析】先求出集合A B，数出其中元素个数即可.【详解】解：因为集合A＝{l，2，3}，B＝{2，3，4}所以A B＝{l，2，3，4}，有4个元素故答案为：4.【点睛】本题考查了集合的并集运算，属于基础题.2.在复平面内，复数对应的点位于第_______象限．【答案】四【解析】【分析】先对复数进行运算化简，找出其对应的点即可判断出其所在的象限.【详解】解：因为所以复数对应的点为，位于第四象限故答案为：四.【点睛】本题考查了复数的除法运算，复数与复平面中坐标的关系，属于基础题.3.为了解某高中学生的身高情况，现采用分层抽样的方法从三个年级中抽取一个容量为100的样本，其中高一年级抽取24人，高二年级抽取26人．若高三年级共有学生600人，则该校学生总人数为_______．【答案】1200【解析】【分析】先求出高三年级出去的人数和所占比例，再用高三年级学生数除以其所占比例即为总人数. 【详解】解：由题意知高三年级抽取了人所以该校学生总人数为人故答案为：1200.【点睛】本题考查了分层抽样，属于基础题.4.从集合A＝{0，1，2，3}中任意取出两个不同的元素，则这两个元素之和为奇数的概率是_______．【答案】【解析】【分析】先列出一共有多少种取法，再找出其中和为奇数的取法，即可求出其概率.【详解】解：集合A中共有4个元素，任取两个不同的元素有（0,1）、（0,2）、（0,3）、（1,2）、（1,3）（2,3）共6种取法，其中两个元素之和为奇数的有（0,1）、（0,3）、（1,2）、（2,3）共4种取法，所以故答案为：.【点睛】本题考查了古典概型，当取法总数较少时可以采用穷举法，属于基础题.5.中国南宋时期的数学家秦九韶提出了一种多项式简化算法，如图是实现该算法的程序框图，若输入的n＝2，x＝1，依次输入的a为1，2，3，运行程序，输出的s的值为_______．【答案】6【解析】【分析】先代入第一次输入的，计算出对应的，判断为否，再代入第二次输入的，计算出对应的，判断仍为否，再代入第三次输入的，计算出对应的，判断为是，得到输出值.【详解】解：第一次输入，得，，判断否；第二次输入，得，，判断否；第三次输入，得，，判断是，输出故答案为：6.【点睛】本题考查了循环结构流程图，要小心每次循环后得到的字母取值，属于基础题.6.若双曲线的离心率为，则实数a的值为_______．【答案】1【解析】【分析】先由双曲线方程求出，再利用列方程求解.【详解】解：因为代表双曲线所以，且，所以解出故答案为：1.【点睛】本题考查了双曲线的离心率，属于基础题.7.若圆锥的侧面积为，底面积为，则该圆锥的体积为。

江苏泰州中学2019高三学情诊断测试试题-数学数 学 试 卷 2018.10.8 【一】填空题：本大题共14小题，每题5分，共70分、 2、“X 》1”是“X2》X ”成立的＿＿＿＿＿＿＿条件、〔可选填“充分不必要”、“必要不充分”、“充要”、“既不充分又不必要”〕3、集合M ＝｛X ｜Y ＝x －1｝，N ＝｛Y ｜Y ＝x －1｝，那么M ∩N ＝＿＿＿＿＿＿＿、4、角α的终边经过点(),6P x -，且3tan 5α=-，那么x 的值为、5、在ABC ∆中，假设2cos sin =-A A ，那么A tan ＝＿＿＿＿＿＿＿、6、1sin cos 2αα=+，那么⎪⎭⎫ ⎝⎛+4sin 2cos παα的值为、 7、函数x x y 2cos 2sin 3+-=，⎥⎦⎤⎢⎣⎡∈2,6ππx 的值域为. 8、函数()f x 在定义域R 内可导，假设()(2)f x f x =-，且当(,1)x ∈-∞时，(1)'()0x f x -<，设1(0),(),(3)2a f b f c f ===，那么,,a b c 从小到大排列的顺序为.9、定义在R 上的函数()x f 满足()()()()⎩⎨⎧>---≤-=0,210,8log 2x x f x f x x x f ，那么()3f 的值为、10、直线X ＝A （0《A 《π2）与函数F （X ）＝SINX 和函数G （X ）＝COSX 的图象分别交于M ，N 两点，假设MN ＝15，那么线段MN 的中点纵坐标为、11、函数F （X ）＝｜X2－6｜，假设A 《B 《0，且F （A ）＝F （B ），那么A2B 的最小值是.12、函数F （X ）＝（AX2＋X ）－XLNX 在【1，＋∞）上单调递增，那么实数A 的取值范围是、13、函数()3111,0,,36221,,1.12x x f x x x x ⎧⎡⎤-+∈⎪⎢⎥⎣⎦⎪=⎨⎛⎤⎪∈ ⎥⎪+⎝⎦⎩函数()sin 226g x a x a π=-+，其中0a >、假设存在[]12,0,1x x ∈，使得()()12f x g x =成立，那么实数a 的取值范围是、14、设()f x 是定义在R 上的偶函数，对任意x R ∈，都有()(4)f x f x =+，且当[2,0]x ∈-时，1()12xf x ⎛⎫=- ⎪⎝⎭，假设在区间(2,6]-内关于x 的方程()log (2)0(1)a f x x a -+=>恰有三个不同的实数根，那么a 的取值范围为、【二】解答题：本大题共6小题，共90分，解答应写出文字说明，证明过程或演算步骤.15.〔本小题总分值14分〕集合A ＝｛X ｜（X －2）（X －3A －1）《0｝，函数Y ＝LG 2a －x x －a2＋1的定义域为集合B. 〔Ⅰ〕假设A ＝B ，求实数A 值；〔Ⅱ〕是否存在实数A 的值使φ=⋂B A ，假设存在那么求出实数A 的值，假设不存在说明理由.16.〔本小题总分值14分〕函数()316f x x x =+-.〔Ⅰ〕求曲线()y f x =在点(2,6)-处的切线的方程；〔Ⅱ〕直线l 为曲线()y f x =的切线，且经过原点，求直线l 的方程；〔Ⅲ〕如果曲线()y f x =的某一切与直线134y x =-+垂直，求切点坐标. 17.〔本小题总分值14分〕向量2(3sin ,1),(cos ,cos ).444x x xm n == 〔Ⅰ〕假设1m n ⋅=，求2cos()3x π-的值；〔Ⅱ〕记()f x m n =⋅，在ABC ∆中，角,,A B C 的对边分别是,,a b c ，且满足(2)cos cos a c B b C -=，求函数()f A 的取值范围、18.〔本小题总分值16分〕因发生意外交通事故，一辆货车上的某种液体泄漏到一渔塘中、为了治污，根据环保部门的建议，现决定在渔塘中投放一种可与污染液体发生化学反应的药剂、每投放A 〔1≤A ≤4，且A ∈R 〕个单位的药剂，它在水中释放的浓度Y 〔克／升〕随着时间X 〔天〕变化的函数关系式近似为Y ＝A ·F 〔X 〕，其中F 〔X 〕＝⎩⎪⎨⎪⎧168－x －10≤x ≤4，5－12x 4＜x ≤10.假设多次投放，那么某一时刻水中的药剂浓度为每次投放的药剂在相应时刻所释放的浓度之和、根据经验，当水中药剂的浓度不低于4〔克／升〕时，它才能起到有效治污的作用、〔Ⅰ〕假设一次投放4个单位的药剂，那么有效治污时间可达几天？〔Ⅱ〕假设第一次只能投放2个单位的药剂，6天后可再投放A 个单位的药剂，要使接下来的4天中能够持续有效治污，试求A 的最小值、19.〔本小题总分值16分〕设T 》0，函数F （X ）＝X2（X －T ）的图象与X 轴交于A 、B 两点、〔Ⅰ〕求函数F （X ）的单调区间；〔Ⅱ〕设函数Y ＝F （X ）在点P （X0，Y0）处的切线的斜率为K ，当X0∈（0，1】时，K ≥－12恒成立，求T 的最大值；〔Ⅲ〕有一条平行于X 轴的直线L 恰好与函数Y ＝F （X ）的图象有两个不同的交点C ，D ，假设四边形ABCD 为菱形，求T 的值、20.〔本小题总分值16分〕函数x a x g b x x x f ln )(,)(23=++-=、〔Ⅰ〕假设)(x f 在⎪⎭⎫⎢⎣⎡-∈1,21x 上的最大值为83，求实数b 的值； 〔Ⅱ〕假设对任意[]e x ,1∈，都有x a x x g )2()(2++-≥恒成立，求实数a 的取值范围；〔Ⅲ〕在〔Ⅰ〕的条件下，设()()⎩⎨⎧≥<=1,1,)(x x g x x f x F ，对任意给定的正实数a ，曲线)(x F y =上是否存在两点Q P ,，使得POQ ∆是以〔O 为坐标原点〕为直角顶点的直角三角形，且此三角形斜边中点在y 轴上？请说明理由、江苏省泰州中学2018－2018学年度第一学期学情诊断数学试卷答案2018.10.8【一】填空题：本大题共14小题，每题5分，共70分、1.命题“012,2>++∈∀x x R x ”的否定是、 【答案】012,2≤++∈∃x x R x2、“X 》1”是“X2》X ”成立的＿＿＿＿＿＿＿条件、〔可选填“充分不必要”、“必要不充分”、“充要”、“既不充分又不必要”〕【答案】充分不必要3、集合M ＝｛X ｜Y ＝x －1｝，N ＝｛Y ｜Y ＝x －1｝，那么M ∩N ＝＿＿＿＿＿＿＿、【答案】[)+∞,14、角α的终边经过点(),6P x -，且3tan 5α=-，那么x 的值为、【答案】105、在ABC ∆中，假设2cos sin =-A A ，那么A tan ＝＿＿＿＿＿＿＿、 【答案】1-6、1sin cos 2αα=+，那么⎪⎭⎫ ⎝⎛+4sin 2cos παα的值为、 【答案】22-7、函数x x y 2cos 2sin 3+-=，⎥⎦⎤⎢⎣⎡∈2,6ππx 的值域为. 【答案】[]1,2--8、函数()f x 在定义域R 内可导，假设()(2)f x f x =-，且当(,1)x ∈-∞时，(1)'()0x f x -<，设1(0),(),(3)2a f b f c f ===，那么,,a b c 从小到大排列的顺序为.【答案】c a b <<.9、定义在R 上的函数()x f 满足()()()()⎩⎨⎧>---≤-=0,210,8log 2x x f x f x x x f ，那么()3f 的值为、【答案】3-10、直线X ＝A （0《A 《π2）与函数F （X ）＝SINX 和函数G （X ）＝COSX 的图象分别交于M ，N 两点，假设MN ＝15，那么线段MN 的中点纵坐标为、【答案】71011、函数F （X ）＝｜X2－6｜，假设A 《B 《0，且F （A ）＝F （B ），那么A2B 的最小值是.【答案】－1612、函数F （X ）＝（AX2＋X ）－XLNX 在【1，＋∞）上单调递增，那么实数A 的取值范围是、【答案】【12e，＋∞）13、函数()3111,0,,36221,,1.12x x f x x x x ⎧⎡⎤-+∈⎪⎢⎥⎣⎦⎪=⎨⎛⎤⎪∈ ⎥⎪+⎝⎦⎩函数()sin 226g x a x a π=-+，其中0a >、假设存在[]12,0,1x x ∈，使得()()12f x g x =成立，那么实数a 的取值范围是、【答案】14,23⎡⎤⎢⎥⎣⎦14、设()f x 是定义在R 上的偶函数，对任意x R ∈，都有()(4)f x f x =+，且当[2,0]x ∈-时，1()12xf x ⎛⎫=- ⎪⎝⎭，假设在区间(2,6]-内关于x 的方程()log (2)0(1)a f x x a -+=>恰有三个不同的实数根，那么a 的取值范围为、【答案】【二】解答题：本大题共6小题，共90分，解答应写出文字说明，证明过程或演算步骤.15.〔本小题总分值14分〕集合A ＝｛X ｜（X －2）（X －3A －1）《0｝，函数Y ＝LG 2a －x x －a2＋1的定义域为集合B. 〔Ⅰ〕假设A ＝B ，求实数A 值；〔Ⅱ〕是否存在实数A 的值使φ=⋂B A ，假设存在那么求出实数A 的值，假设不存在说明理由.解：〔Ⅰ〕由于函数的定义域是非空数集，故1≠a .〔1〕当131≠>a a 且时，()13,2+=a A ，()1,22+=a a B ，由B A =可得：⎩⎨⎧+=+=113222a a a ，方程组无解；2分〔2〕当31=a 时，φ=A ，B A =不可能；4分〔3〕当31<a 时，()2,13+=a A ，()1,22+=a a B ，由B A =可得：⎩⎨⎧+==+122132a a a ，1-=a .6分〔Ⅱ〕〔1〕当131≠>a a 且时，()13,2+=a A ，()1,22+=a a B ，由φ=⋂B A 可得：212132≤+≤+a a a 或，又131≠>a a 且，那么a 的值不存在；8分〔2〕当31=a 时，φ=A ，那么φ=⋂B A ，适合题意；10分〔3〕当31<a 时，()2,13+=a A ，()1,22+=a a B ，由φ=⋂B A 可得：131222+≤+≤a a a 或，又31<a ，那么310<≤a .12分∴当⎥⎦⎤⎢⎣⎡∈31,0a 时，φ=⋂B A .14分 16.〔本小题总分值14分〕函数()316f x x x =+-.〔Ⅰ〕求曲线()y f x =在点(2,6)-处的切线的方程；〔Ⅱ〕直线l 为曲线()y f x =的切线，且经过原点，求直线l 的方程；〔Ⅲ〕如果曲线()y f x =的某一切与直线134y x =-+垂直，求切点坐标.解：〔Ⅰ〕13320x y --=4分 〔Ⅱ〕013=-y x 9分 〔Ⅲ〕()()18,1,14,1---14分17.〔本小题总分值14分〕向量2(3sin ,1),(cos ,cos ).444x x xm n == 〔Ⅰ〕假设1m n ⋅=，求2cos()3x π-的值；〔Ⅱ〕记()f x m n =⋅，在ABC ∆中，角,,A B C 的对边分别是,,a b c ，且满足(2)cos cos a c B b C -=，求函数()f A 的取值范围、解：〔Ⅰ〕m n ⋅=2cos cos 444x x x +＝11cos 2222x x ++＝1sin()262x π++2分∵1m n ⋅=，∴1sin()262x π+=，2cos()12sin ()326x x ππ+=-+＝12， ∴21cos()cos()332x x ππ-=-+=-.6分〔Ⅱ〕∵(2)cos cos a c B b C -=，由正弦定理得(2sin sin )cos sin cos A C B B C -=，∴2sin sin cos sin cos AcosB C B B C -=，∴2sin cos sin()A B B C =+，∵A B C π++=∴sin()sin B C A +=，且sin 0A ≠，∴1cos ,23B B π==，10分 ∴203A π<<∴1,sin()16262226A A ππππ<+<<+<又∵()f x m n =⋅=1sin()262x π++，∴()f A =1sin()262A π++， 故函数()f A 的取值范围是〔1，32〕.14分18.〔本小题总分值16分〕因发生意外交通事故，一辆货车上的某种液体泄漏到一渔塘中、为了治污，根据环保部门的建议，现决定在渔塘中投放一种可与污染液体发生化学反应的药剂、每投放A 〔1≤A ≤4，且A ∈R 〕个单位的药剂，它在水中释放的浓度Y 〔克／升〕随着时间X 〔天〕变化的函数关系式近似为Y ＝A ·F 〔X 〕，其中F 〔X 〕＝⎩⎪⎨⎪⎧168－x －10≤x ≤4，5－12x 4＜x ≤10.假设多次投放，那么某一时刻水中的药剂浓度为每次投放的药剂在相应时刻所释放的浓度之和、根据经验，当水中药剂的浓度不低于4〔克／升〕时，它才能起到有效治污的作用、〔Ⅰ〕假设一次投放4个单位的药剂，那么有效治污时间可达几天？〔Ⅱ〕假设第一次只能投放2个单位的药剂，6天后可再投放A 个单位的药剂，要使接下来的4天中能够持续有效治污，试求A 的最小值、解：〔Ⅰ〕因为A ＝4，所以Y ＝⎩⎪⎨⎪⎧648－x －40≤x ≤4，20－2x 4＜x ≤10.2分那么当0≤X ≤4时，由648－x－4≥4，解得X ≥0，所以此时0≤X ≤4.4分当4《X ≤10时，由20－2X ≥4，解得X ≤8，所以此时4《X ≤8.6分综合，得0≤X ≤8，假设一次投放4个单位的制剂，那么有效治污时间可达8天、8分〔Ⅱ〕当6≤X ≤10时，Y ＝2×（5－12X ）＋A ⎣⎢⎡⎦⎥⎤168－x －6－110分 ＝10－X ＋16a 14－x －A ＝（14－X ）＋16a14－x －A －4，因为14－X ∈【4，8】，而1≤A ≤4，所以4a ∈【4，8】，故当且仅当14－X ＝4a 时，Y 有最小值为8a －A －4.14分 令8a －A －4≥4，解得24－162≤A ≤4，所以A 的最小值为24－16 2..16分 19.〔本小题总分值16分〕设T 》0，函数F （X ）＝X2（X －T ）的图象与X 轴交于A 、B 两点、〔Ⅰ〕求函数F （X ）的单调区间；〔Ⅱ〕设函数Y ＝F （X ）在点P （X0，Y0）处的切线的斜率为K ，当X0∈（0，1】时，K ≥－12恒成立，求T 的最大值；〔Ⅲ〕有一条平行于X 轴的直线L 恰好与函数Y ＝F （X ）的图象有两个不同的交点C ，D ，假设四边形ABCD 为菱形，求T 的值、解：〔Ⅰ〕F ′（X ）＝3X2－2TX ＝X （3X －2T ）》0，因为T 》0，所以当X 》2t3或X 《0时，F ′（X ）》0，所以（－∞，0）和（2t3，＋∞）为函数F （X ）的单调增区间；当0《X 《2t 3时，F ′（X ）《0，所以（0，2t3）为函数F （X ）的单调减区间、4分〔Ⅱ〕因为K ＝3X02－2TX0≥－12恒成立，所以2T ≤3X0＋12x0恒成立，6分因为X0∈〔0，1】，所以3X0＋12x0≥23x0×12x0＝6，即3X0＋12x0≥6，当且仅当X0＝66时取等号、所以2T ≤6，即T 的最大值为62、8分〔Ⅲ〕由〔Ⅰ〕可得，函数F （X ）在X ＝0处取得极大值0，在X ＝2t3处取得极小值－4t327、 因为平行于X 轴的直线L 恰好与函数Y ＝F （X ）的图象有两个不同的交点，所以直线L 的方程为Y ＝－4t327、10分令F （X ）＝－4t327，所以X2（X －T ）＝－4t327，解得X ＝2t 3或X ＝－t3、所以C 〔2t 3，－4t327〕，D 〔－t 3，－4t327〕、12分因为A 〔0，0〕，B 〔T ，0〕、易知四边形ABCD 为平行四边形、 AD ＝(－t 3)2＋(－4t327)2，且AD ＝AB ＝T ，所以(－t 3)2＋(－4t327)2＝T ，解得：T ＝3482、16分20.〔本小题总分值16分〕函数x a x g b x x x f ln )(,)(23=++-=、〔Ⅰ〕假设)(x f 在⎪⎭⎫⎢⎣⎡-∈1,21x 上的最大值为83，求实数b 的值； 〔Ⅱ〕假设对任意[]e x ,1∈，都有x a x x g )2()(2++-≥恒成立，求实数a 的取值范围；〔Ⅲ〕在〔Ⅰ〕的条件下，设()()⎩⎨⎧≥<=1,1,)(x x g x x f x F ，对任意给定的正实数a ，曲线)(x F y =上是否存在两点Q P ,，使得POQ ∆是以〔O 为坐标原点〕为直角顶点的直角三角形，且此三角形斜边中点在y 轴上？请说明理由、解：〔Ⅰ〕由()32f x x x b=-++，得()()23232f x x x x x '=-+=--，令()0f x '=，得0x =或23、2分 列表如下：⎫⎪⎭由()28f b -=+，()327f b=+， ∴12()()23f f ->，即最大值为133()288f b -=+=，∴0b =、4分 〔Ⅱ〕由()()22g x x a x≥-++，得()2ln 2x x a x x -≤-、[]1,,ln 1x e x x∈∴≤≤，且等号不能同时取，∴ln ,ln 0x x x x <->即，∴22ln x x a x x -≤-恒成立，即2min2()ln x x a x x -≤-、6分 令()[]()22,1,ln x x t x x e x x -=-，求导得，()()()()212ln ln x x x t x x x -+-'=-，当[]1,x e ∈时，10,ln 1,2ln 0x x x x -≥≤+->，从而()0t x '≥，∴()t x 在[]1,e 上为增函数，∴()()min 11t x t ==-，∴1a ≤-、8分〔Ⅲ〕由条件，()32,1ln ,1x x x F x a x x ⎧-+<=⎨≥⎩， 假设曲线()y F x =上存在两点,P Q 满足题意，那么,P Q 只能在y 轴两侧，不妨设()()(),0P t F t t >，那么()32,Q t t t -+，且1t ≠、POQ∆是以O 〔O 为坐标原点〕为直角顶点的直角三角形，∴0OP OQ ⋅=，∴()()2320t f t t t -++=()*，是否存在,P Q 等价于方程()*在0t >且1t ≠时是否有解、10分①假设01t <<时，方程()*为()()232320t t t t t -+-++=，化简得4210t t -+=， 此方程无解；12分 ②假设1t >时，()*方程为()232ln 0t a t t t-+⋅+=，即()11ln t t a =+，设()()()1ln 1h t t t t =+>，那么()1ln 1h t t t '=++，显然，当1t >时，()0h t '>，即()h t 在()1,+∞上为增函数，∴()h t的值域为()()1,h+∞，即()0,+∞，∴当0a>时，方程()*总有解、∴对任意给定的正实数a，曲线()y F x=上总存在两点,P Q，使得POQ∆是以O〔O为坐标原点〕为直角顶点的直角三角形，且此三角形斜边中点在y轴上、16分。

江苏省泰兴河失中学2011届高三学情调查（三)数 学 试 题一、填空题（每小题5分，共70分）1．已知集合M ＝｛x ｜x ＜3｝，N ＝{x |log 2x ＞1}，则M ∩N ＝__________ 2．命题“2,10x R x∃∈+<”的否定是3．已知函数f （x ） = 3ax －2a + 1在区间 （－1，1）内存在x 0；使f （x 0） = 0，则实数a 的取值范围是 ．4．若函数1(),10()44,01xx x f x x ⎧-≤<⎪=⎨⎪≤≤⎩则4(log 3)f =．5．已知平面向量),2(),3,12(m b m a =+=,且a ∥b ，则实数m 的值等于 6．等差数列}{na 中,10S =120，那么92a a+= ．7．等差数列{a n ｝中,1490,aS S >=，则n S 取最大值时,n =______．8．已知函数f （x ）=|lg x ｜．若0〈a 〈b ，且f （a ）=f （b ）,则a+2b的取值范围是_____ ________．9．已知点P 在曲线41x y e =+上，α为曲线在点P 处的切线的倾斜角,则α的取值范围是_______ _______．10．已知周期函数)(x f 是定义在R 上的奇函数，且)(x f 的最小正周期为3，,2)1(<fm m f 则,)2(=的取值范围为．11．要使sin α－3cos α=m m --464有意义，则应有 ．12．函数f （x ）=2sin （x+4π）+2sinxcosx 在区间⎥⎦⎤⎢⎣⎡2,4ππ上的最大值是 ．13．若)(x f 是偶函数,且当0)1(,1)(,),0[<--=+∞∈x f x x f x 则时的解集是 ．14．对正整数n ，设曲线)1(x xy n-=在2=x 处的切线与y 轴交点的纵坐标为na ，则数列⎭⎬⎫⎩⎨⎧+1n a n 的前n 项和=n S ．二、解答题15．已知函数f （x ）=log 4（4x +1)+kx （x ∈R ）是偶函数． (1）求k 的值；(2）若方程f （x ）- m =0有解,求m 的取值范围．16．已知函数f(x ）=x 3+ax 2+bx+c 在x=32-与x=1时都取得极值．（1)求a 、b 的值与函数f(x ）的单调区间;(2）若对x∈［—1，2］，不等式f （x ）<c 2恒成立,求c 的取值范围．17．如图所示：四棱锥P —ABCD 底面一直角梯形,BA ⊥AD ，CD ⊥AD ，CD=2AB ，PA ⊥底面ABCD,E 为PC 的中点．(1）证明:EB ∥平面PAD ；（2）若PA=AD ，证明：BE ⊥平面PDC ；18．已知函数3223()39f x xax a x a =--+．（1）设1a =，求函数()f x 的极值； （2）若14a >，且当[]1,4x a ∈时，)('x f ≤12a恒成立，试确定a 的取值范围．。

江苏省七市届高三数学第三次调研考试试题(满分分，考试时间分钟)．一、填空题：本大题共小题，每小题分，共分．. 已知集合＝{－，，，}，＝{，}，则∁＝．. 已知复数＝(是虚数单位)是纯虚数，则实数的值为．. 右图是一个算法流程图．若输出的值为时，则输入的值为．. 已知一组数据，，，，的平均数是，且＝，则该组数据的方差为．. 一只口袋装有形状、大小都相同的只小球，其中有只白球，只红球．从中次随机摸出只球，则只球都是白色的概率为．. 已知函数()＝则不等式()＞(－)的解集为．. 已知数列{}是等比数列，其前项和为.若－＝，＝，则的值为．. 在平面直角坐标系中，双曲线－＝(＞，＞)的右准线与两条渐近线分别交于，两点．若△的面积为，则该双曲线的离心率为．. 在直角梯形中，∥，⊥，＝，＝，＝ .将此直角梯形绕边所在的直线旋转一周，由此形成几何体的体积为. . 在平面直角坐标系中，若曲线＝与＝在(，π)上交点的横坐标为α，则α的值为．. 如图，在正六边形中，若＝λ＋μ(λ，μ∈)，则λ＋μ的值为．(第题)(第题). 如图，有一壁画，最高点处离地面，最低点处离地面．若从离地高的处观赏它，则离墙时，视角θ最大．. 已知函数()＝－＋，()＝.若对任意∈[，]，总存在∈[，]，使得()≤()成立，则实数的值为．. 在平面四边形中，∠＝°，＝，＝.若·＋·＝·，则＋的最小值为．二、解答题：本大题共小题，共分. 解答时应写出必要的文字说明、证明过程或演算步骤．. (本小题满分分)在△中，，，分别为角，，所对边的长，( － )＝(－)( ＋ )．() 求角的值；() 若＝，求的值．.(本小题满分分)如图，在四棱锥中，底面为平行四边形，平面⊥平面，＝，点，分别是，的中点．求证：() ⊥；() ∥平面.(本小题满分分).如图，在平面直角坐标系中，已知椭圆：＋＝(＞＞)的上顶点为(，)，圆：＋＝经过点(，)．() 求椭圆的方程；() 过点作直线交椭圆于，两点，过点作直线的垂线交圆于另一点.若△的面积为，求直线的斜率．南通风筝是江苏传统手工艺品之一．现用一张长，宽的长方形牛皮纸裁剪风筝面，裁剪方法如下：分别在边，上取点，，将三角形沿直线翻折到′处，点′落在牛皮纸上，沿′，′裁剪并展开，得到风筝面′，如图.() 若点恰好与点重合，且点′在上，如图，求风筝面′的面积；() 当风筝面′的面积为时，求点′到距离的最大值．已知数列{}满足(－－)＝(－)－(≥)，＝－(∈*)．() 若＝，求证：数列{}是等比数列；() 若存在∈*，使得，，成等差数列．①求数列{}的通项公式；②求证：＋＞(＋)－＋.已知函数()＝)(≠)，是自然对数的底数．() 当＞时，求()的单调增区间；() 若对任意的≥，()≥－(∈)，求的最大值；() 若()的极大值为－，求不等式()＋＜的解集.届高三模拟考试试卷数学附加题(满分分，考试时间分钟). 【选做题】在，，三小题中只能选做两题，每小题分，共分．若多做，则按作答的前两题计分．解答时应写出必要的文字说明、证明过程或演算步骤．. (选修：矩阵与变换)已知，，，∈，矩阵＝)))的逆矩阵－＝.若曲线在矩阵对应的变换作用下得到曲线＝＋，求曲线的方程．. (选修：坐标系与参数方程)在直角坐标平面内，以原点为极点，轴的非负半轴为极轴建立极坐标系．已知点，的极坐标分别为(，)，(，)，曲线的方程为ρ＝(>)．() 求直线的直角坐标方程；() 若直线和曲线有且只有一个公共点，求的值．.(选修：不等式选讲)已知∈，若关于的方程＋＋－＋＝有实根，求的取值范围．【必做题】第，题，每小题分，共分．解答时应写出必要的文字说明、证明过程或演算步骤．. 现有一款智能学习，学习内容包含文章学习和视频学习两类，且这两类学习互不影响．已知该积分规则如下：每阅读一篇文章积分，每日上限积分；观看视频累计分钟积分，每日上限积分．经过抽样统计发现，文章学习积分的概率分布表如表所示，视频学习积分的概率分布表如表所示．表() 现随机抽取人了解学习情况，求其每日学习积分不低于分的概率；() 现随机抽取人了解学习情况，设积分不低于分的人数为ξ，求ξ的概率分布及数学期望．() 求－的值；() 化简－.届高三模拟考试试卷(南通、泰州、徐州等苏北七市联考)数学参考答案及评分标准. {－，}. －. －. . . (－，)∪(，＋∞). . . . －. . . －.. 解：() 在△中，因为( － )＝(－)( ＋ )，由正弦定理)＝)＝)，所以(－)＝(＋)(－)，(分)即＋－＝.由余弦定理＝＋－，得＝.(分)因为<<π，所以＝.(分)() (解法)因为＝及＋－＝，得＝＋－＝，即＝.(分)由正弦定理)＝)，得＝)，所以＝.(分)(解法)由正弦定理)＝)，得＝ .由＋＋＝π，得(＋)＝ .因为＝，所以＋＝，即＝．(分)因为＋＝，解得＝.在△中，因为 >，所以＝.(分) . 证明：() 在△中，因为＝，点是的中点，所以⊥.(分)因为平面⊥平面，平面∩平面＝，?平面，所以⊥平面.(分)因为平面，所以⊥.(分)() 如图，取的中点，连结，.在△中，因为点是的中点，所以∥，＝.(分)又底面是平行四边形，点是的中点，所以∥，＝.所以∥，＝，所以四边形是平行四边形，所以∥.(分)因为平面，平面，所以∥平面.(分). 解：() 因为椭圆的上顶点为(，)，所以＝.又圆：＋＝经过点(，)，所以＝.(分)所以椭圆的方程为＋＝.(分)() 若直线的斜率为，则＝，＝，所以△的面积为，不合题意，所以直线的斜率不为.(分)设直线的方程为＝＋，由消，得(＋)＋－＝.设(，)，(，)，则＝，＝，所以＝＝＝.(分)由题可知，直线的方程为＝－＋，即＋－＝，所以＝＝.(分)所以△的面积＝·＝×·＝，解得＝±，即直线的斜率为±.(分). 解：() (解法)建立如图所示的直角坐标系，则(，)，(，)，直线的方程为＋－＝.(分)设(，)(>)，因为点到与的距离相等，所以＝，解得＝或＝－(舍去)．(分)所以△的面积为××＝，所以四边形′的面积为 .答：风筝面′的面积为 .(分)(解法)设∠＝θ，则∠′＝θ.在直角三角形中，θ＝＝，(分)所以θ－θ)＝，解得θ＝或θ＝－(舍去)．所以＝θ＝.(分)所以△的面积为××＝，所以四边形′的面积为 .答：风筝面′的面积为 .(分)() (解法)建立如图所示的直角坐标系．设＝，＝，′(，)，则直线的方程为＋－＝.因为点，′关于直线对称，所以解得＝.(分)因为四边形′的面积为，所以＝，所以＝＝.因为<≤，<≤，所以≤≤.(分)设()＝＋，≤≤，则′()＝－＝.令′()＝，得＝或＝－(舍去)．列表如下：所以的最大值为，此时点′在上，＝，＝.答：点′到距离的最大值为．(分)(解法)设＝，∠＝θ，则＝θ.因为四边形′的面积为，所以·＝，即θ＝，所以θ＝.过点′作的垂线′，垂足为，则′＝′· θ＝· θ＝θ(分)＝·θθθ＋θ)＝·θθ＋)＝·＝.因为<≤，<≤，所以≤≤.(分)(下同解法). () 证明：由(－－)＝(－)－，得＝＋－，得－＝，即＝－.因为＝，所以＝－＝－≠，所以＝(≥)，所以数列{}是以为首项，为公比的等比数列．(分)() ①解：设－＝λ，由()知＝－，所以＝－＝－＝…＝－，即－＝λ·－，所以＝λ·－＋.(分)因为，，成等差数列，则(λ·－＋)＋(λ·＋＋＋)＝(λ·＋＋)，所以λ·－＝，所以λ＝，所以＝，即＝.(分)②证明：要证＋>(＋)－＋，即证(＋＋)>，即证＋>.设＝，则＋＝－＋＝－，且>，从而只需证：当>时，－> ．(分)设()＝－－ (>)，则′()＝＋－＝(－)>，所以()在(，＋∞)上单调递增，所以()>()＝，即－> .因为>，所以－> ，所以原不等式得证．(分). 解：() ()的定义域为(，－)∪(－，＋∞)．由′()＝）－·(),（＋）)＝）,（＋）)，(分)令′()>，因为>，得>－.因为－>－，所以()的单调增区间是(－，＋∞)．(分)() 当<时，()＝<<－，不合题意；当>时，令′()<，得<<－或－<<－，所以()在区间(，－)和(－，－)上单调递减．因为∈(－，－)，且()在区间(－，＋∞)上单调递增，所以()在＝－处取极小值，即最小值为.(分)若≥，()≥－，则≥－，即≥.不妨设>，则≤.(分)设()＝(>)，则′()＝.当<<时，′()>；当>时，′()<，所以()在(，)上单调递增，在(，＋∞)上单调递减，所以()≤()，即≤，所以的最大值为.(分)() 由()知，当>时，()无极大值．当<时，()在(，－)和(－，－)上单调递增，在(－，＋∞)上单调递减，所以()在＝－处取极大值，所以(－)＝＝－，即＝－.(分)设()＝()＋，即()＝－)，当∈(，－)，＋ <，所以()>；当∈(－，＋∞)，′()＝－）,（＋）)，由()知≤，又＋≤(＋ )，所以′()≥，且()不恒为零，所以()在(－，＋∞)上单调递增．不等式()＋<，即为()<＝()，所以－<<，即不等式的解集为(－，)．(分)届高三模拟考试试卷(南通、泰州、徐州等苏北七市联考)数学附加题参考答案及评分标准. . 解：由题意，得－＝，即)))＝＝，所以＝，＝，＝，＝，即矩阵＝))).(分)设(，)为曲线上的任意一点，在矩阵对应的变换作用下变为点′(′，′)，则＝)))，即(分)由已知条件可知′(′，′)满足＝＋，整理得－＋＝，所以曲线的方程为－＋＝.(分) . 解：() 分别将(，)，(，)转化为直角坐标，即(，)，(－，－)，所以直线的直角坐标方程为－＋＝.(分)() 曲线的方程为ρ＝(>)，其直角坐标方程为＋＝.又直线和曲线有且只有一个公共点，即直线与圆相切，所以圆心到直线的距离为＝，即的值为.(分). 解：因为关于的方程＋＋－＋＝有实根，所以Δ＝－(－＋)≥，即－＋≤.(分)当≥时，－≤，得≤≤；当<<时，≤，恒成立，即<<；当≤时，－≤，得－≤≤.综上，所求的取值范围是－≤≤.(分). 解：() 由题意，获得的积分不低于分的情形有因为两类学习互不影响，所以概率＝×＋×＋×＋×＝，所以每日学习积分不低于分的概率为.(分) () 随机变量ξ的所有可能取值为，，，. 由()知每个人积分不低于分的概率为，则(ξ＝)＝()＝；(ξ＝)＝()()＝；(ξ＝)＝()()＝；(ξ＝)＝()＝.所以随机变量ξ的概率分布列为(分)所以(ξ)＝×＋×＋×＋×＝.所以随机变量ξ的数学期望为.(分)。

江苏省七市2019届高三数学第三次调研考试试题(满分160分，考试时间120分钟)2019．5一、 填空题：本大题共14小题，每小题5分，共70分． 1. 已知集合U ＝{－1，0，2，3}，A ＝{0，3}，则∁U A ＝________． 2. 已知复数z ＝a ＋i1＋3i(i 是虚数单位)是纯虚数，则实数a 的值为________．3. 右图是一个算法流程图．若输出y 的值为4时，则输入x 的值为________．4. 已知一组数据6，6， 9，x ，y 的平均数是8，且xy ＝90，则该组数据的方差为________．5. 一只口袋装有形状、大小都相同的4只小球，其中有3只白球，1只红球．从中1次随机摸出2只球，则2只球都是白色的概率为________．6. 已知函数f(x)＝⎩⎨⎧x 2－2x ，x ≥0，－x 2－2x ，x ＜0，则不等式f(x)＞f(－x)的解集为____________．7. 已知数列{a n }是等比数列，其前n 项和为S n .若a 3－a 2＝4，a 4＝16，则S 3的值为________．8. 在平面直角坐标系xOy 中，双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的右准线与两条渐近线分别交于A ，B 两点．若△AOB 的面积为ab4，则该双曲线的离心率为________． 9. 在直角梯形ABCD 中，AB ∥CD ，AB ⊥BC ，AB ＝3 cm ，BC ＝1 cm ，CD ＝2 cm.将此直角梯形绕AB 边所在的直线旋转一周，由此形成几何体的体积为________cm 3.10. 在平面直角坐标系xOy 中，若曲线y ＝sin 2x 与y ＝18tan x 在(π2，π)上交点的横坐标为α，则sin 2α的值为________．11. 如图，在正六边形ABCDEF 中，若AD →＝λAC →＋μAE →(λ，μ∈R )，则λ＋μ的值为________．(第11题)(第12题)12. 如图，有一壁画，最高点A 处离地面6 m ，最低点B 处离地面3.5 m ．若从离地高2 m 的C 处观赏它，则离墙________m 时，视角θ最大．13. 已知函数f(x)＝x 2－2x ＋3a ，g(x)＝2x －1.若对任意x 1∈[0，3]，总存在x 2∈[2，3]，使得|f(x 1)|≤g(x 2)成立，则实数a 的值为________．14. 在平面四边形ABCD 中，∠BAD ＝90°，AB ＝2，AD ＝1.若AB →·AC →＋BA →·BC →＝4 3CA→·CB→，则CB＋12CD的最小值为________．二、解答题：本大题共6小题，共90分. 解答时应写出必要的文字说明、证明过程或演算步骤．15. (本小题满分14分)在△ABC中，a，b，c分别为角A，B，C所对边的长，a(sin A－sin B)＝(c －b)(sin B＋sin C)．(1) 求角C的值；(2) 若a＝4b，求sin B的值．16.(本小题满分14分)如图，在四棱锥P ABCD中，底面ABCD为平行四边形，平面BPC⊥平面DPC，BP＝BC，点E，F分别是PC，AD的中点．求证：(1) BE⊥CD；(2) EF∥平面PAB.(本小题满分14分)17.如图，在平面直角坐标系xOy 中，已知椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的上顶点为A(0，3)，圆O ：x 2＋y 2＝a 24经过点M(0，1)．(1) 求椭圆C 的方程；(2) 过点M 作直线l 1交椭圆C 于P ，Q 两点，过点M 作直线l 1的垂线l 2交圆O 于另一点N.若△PQN 的面积为3，求直线l 1的斜率．南通风筝是江苏传统手工艺品之一．现用一张长2 m，宽1.5 m的长方形牛皮纸ABCD裁剪风筝面，裁剪方法如下：分别在边AB，AD上取点E，F，将三角形AEF 沿直线EF翻折到A′EF处，点A′落在牛皮纸上，沿A′E，A′F裁剪并展开，得到风筝面AEA′F，如图1.(1) 若点E恰好与点B重合，且点A′在BD上，如图2，求风筝面ABA′F的面积；(2) 当风筝面AEA′F的面积为 3 m2时，求点A′到AB距离的最大值．已知数列{an }满足(nan－1－2)an＝(2an－1)an－1(n≥2)，bn＝1an－n(n∈N*)．(1) 若a1＝3，求证：数列{bn}是等比数列；(2) 若存在k∈N*，使得1ak，1ak＋1，1ak＋2成等差数列．①求数列{an}的通项公式；②求证：ln n＋12an＞ln(n＋1)－12an＋1.已知函数f(x)＝ax21＋ln x(a≠0)，e是自然对数的底数．(1) 当a＞0时，求f(x)的单调增区间；(2) 若对任意的x≥12，f(x)≥2e b－1(b∈R)，求ba的最大值；(3) 若f(x)的极大值为－2，求不等式f(x)＋e x＜0的解集.2019届高三模拟考试试卷数学附加题(满分40分，考试时间30分钟)21. 【选做题】 在A ，B ，C 三小题中只能选做两题，每小题10分，共20分．若多做，则按作答的前两题计分．解答时应写出必要的文字说明、证明过程或演算步骤．A. (选修42：矩阵与变换)已知a ，b ，c ，d ∈R ，矩阵A ＝⎣⎢⎡⎦⎥⎤a －20 b 的逆矩阵A －1＝⎣⎢⎡⎦⎥⎤1c d 1.若曲线C 在矩阵A 对应的变换作用下得到曲线y ＝2x ＋1，求曲线C 的方程．B. (选修44：坐标系与参数方程)在直角坐标平面内，以原点O 为极点，x 轴的非负半轴为极轴建立极坐标系．已知点A ，B 的极坐标分别为(4，π2)，(22，5π4)，曲线C 的方程为ρ＝r(r>0)． (1) 求直线AB 的直角坐标方程；(2) 若直线AB 和曲线C 有且只有一个公共点，求r 的值．C.(选修45：不等式选讲)已知a∈R，若关于x的方程x2＋4x＋|a－1|＋|a|＝0有实根，求a的取值范围．【必做题】第22，23题，每小题10分，共20分．解答时应写出必要的文字说明、证明过程或演算步骤．22. 现有一款智能学习APP，学习内容包含文章学习和视频学习两类，且这两类学习互不影响．已知该APP积分规则如下：每阅读一篇文章积1分，每日上限积5分；观看视频累计3分钟积2分，每日上限积6分．经过抽样统计发现，文章学习积分的概率分布表如表1所示，视频学习积分的概率分布表如表2所示．表1(1) 现随机抽取1人了解学习情况，求其每日学习积分不低于9分的概率；(2) 现随机抽取3人了解学习情况，设积分不低于9分的人数为ξ，求ξ的概率分布及数学期望．(1) 求2P2－Q2的值；(2) 化简nPn －Qn.2019届高三模拟考试试卷(南通、泰州、徐州等苏北七市联考)数学参考答案及评分标准1. {－1，2}2. －33. －14. 1455.126. (－2，0)∪(2，＋∞)7.14 8. 2 9. 7π310. －15811. 4312. 6 13. －1314.26215. 解：(1) 在△ABC中，因为a(sin A－sin B)＝(c－b)(sin B＋sin C)，由正弦定理asin A＝bsin B＝csin C，所以a(a－b)＝(b＋c)(c－b)，(3分) 即a2＋b2－c2＝ab.由余弦定理c2＝a2＋b2－2abcos C，得cos C＝12.(5分)因为0<C<π，所以C＝π3.(7分)(2) (解法1)因为a＝4b及a2＋b2－c2＝ab，得c2＝16b2＋b2－4b2＝13b2，即c＝13b.(10分)由正弦定理csin C＝bsin B，得13b32＝bsin B，所以sin B＝3926.(14分)(解法2)由正弦定理asin A＝bsin B，得sin A＝4sin B.由A＋B＋C＝π，得sin(B＋C)＝4sin B.因为C＝π3，所以12sin B＋32cos B＝4sin B，即7sin B＝3cos B．(11分)因为sin2B＋cos2B＝1，解得sin2B＝3 52 .在△ABC中，因为sin B>0，所以sin B＝3926.(14分)16. 证明：(1) 在△PBC中，因为BP＝BC，点E是PC的中点，所以BE⊥PC.(2分)因为平面BPC⊥平面DPC，平面BPC∩平面DPC＝PC，BE?平面BPC，所以BE⊥平面PCD.(5分)因为CD平面DPC，所以BE⊥CD.(7分)(2) 如图，取PB的中点H，连结EH，AH.在△PBC中，因为点E是PC的中点，所以HE∥BC，HE＝12BC.(9分)又底面ABCD是平行四边形，点F是AD的中点，所以AF∥BC，AF＝12 BC.所以HE∥AF，HE＝AF，所以四边形AFEH是平行四边形，所以EF∥HA.(12分)因为EF平面PAB，HA平面PAB，所以EF∥平面PAB.(14分) 17. 解：(1) 因为椭圆C的上顶点为A(0，3)，所以b＝ 3.又圆O：x2＋y2＝14a2经过点M(0，1)，所以a＝2.(2分)所以椭圆C的方程为x24＋y23＝1.(4分)(2) 若直线l 1的斜率为0，则PQ ＝463，MN ＝2， 所以△PQN 的面积为463，不合题意，所以直线l 1的斜率不为0.(5分) 设直线l 1的方程为y ＝kx ＋1，由⎩⎨⎧x 24＋y 23＝1，y ＝kx ＋1消y ，得(3＋4k 2)x 2＋8kx －8＝0.设P(x 1，y 1)，Q(x 2，y 2)，则x 1＝－4k －26·2k 2＋13＋4k 2，x 2＝－4k ＋26·2k 2＋13＋4k 2，所以PQ＝（x 1－x 2）2＋（y 1－y 2）2＝1＋k 2||x 1－x 2＝46·1＋k 2·2k 2＋13＋4k 2.(8分)由题可知，直线l 2的方程为y ＝－1k x ＋1，即x ＋ky －k ＝0，所以MN ＝21－k 21＋k 2＝21＋k2.(11分) 所以△PQN 的面积S ＝12PQ ·MN ＝12×46·1＋k 2·2k 2＋13＋4k 2·21＋k 2＝3， 解得k ＝±12，即直线l 1的斜率为±12.(14分)18. 解：(1) (解法1)建立如图所示的直角坐标系， 则B(2，0)，D(0，32)，直线BD 的方程为3x ＋4y －6＝0.(2分)设F(0，b)(b>0)，因为点F到AB与BD的距离相等，所以b＝|4b－6|5，解得b＝23或b＝－6(舍去)．(4分)所以△ABF的面积为12×2×23＝23m2，所以四边形ABA′F的面积为43m2.答：风筝面ABA′F的面积为43m2.(6分)(解法2)设∠ABF＝θ，则∠ABA′＝2θ.在直角三角形ABD中，tan 2θ＝ADAB＝34，(2分)所以2tan θ1－tan2θ＝34，解得tan θ＝13或tan θ＝－3(舍去)．所以AF＝ABtan θ＝23.(4分)所以△ABF的面积为12×2×23＝23m2，所以四边形ABA′F的面积为43m2.答：风筝面ABA′F的面积为43m2.(6分)(2) (解法1)建立如图所示的直角坐标系．设AE＝a，AF＝b，A′(x0，y)，则直线EF的方程为bx＋ay－ab＝0. 因为点A，A′关于直线EF对称，所以⎩⎪⎨⎪⎧y 0x 0＝a b ，bx 02＋ay 02－ab ＝0，解得y 0＝2a 2ba 2＋b2.(10分)因为四边形AEA ′F 的面积为3，所以ab ＝3，所以y 0＝23a 3a 4＋3＝23a ＋3a 3.因为0<a ≤2，0<b ≤32，所以233≤a ≤2.(12分)设f(a)＝a ＋3a 3，233≤a ≤2，则f ′(a)＝1－9a4＝（a 2＋3）（a ＋3）（a －3）a 4.令f ′(a)＝0，得a ＝3或a ＝－3(舍去)． 列表如下：当a 所以y 0的最大值为32，此时点A ′在CD 上，a ＝3，b ＝1.答：点A ′到AB 距离的最大值为32m ．(16分)(解法2)设AE＝a，∠AEF＝θ，则AF＝atan θ.因为四边形AEA′F的面积为3，所以AE·AF＝3，即a2tan θ＝3，所以tan θ＝3 a2.过点A′作AB的垂线A′T，垂足为T，则A′T＝A′E·sin 2θ＝AE·sin 2θ＝asin 2θ(10分)＝a·2sin θcos θsin2θ＋cos2θ＝a·2tan θtan2θ＋1＝a·2×3a23a4＋1＝23a＋3a3.因为0<AE≤2，0<AF≤32，所以233≤a≤2.(12分)(下同解法1)19. (1) 证明：由(nan－1－2)an＝(2an－1)an－1，得1an＝2an－1＋2－n，得1an－n＝2⎣⎢⎡⎦⎥⎤1an－1－（n－1），即bn＝2bn－1.因为a1＝3，所以b1＝1a1－1＝－23≠0，所以bnbn－1＝2(n≥2)，所以数列{bn }是以b1为首项，2为公比的等比数列．(4分)(2) ①解：设1a1－1＝λ，由(1)知bn＝2bn－1，所以bn ＝2bn－1＝22bn－2＝…＝2n－1b1，即1an－n＝λ·2n－1，所以1ak＝λ·2k－1＋k.(6分)因为1ak，1ak＋1，1ak＋2成等差数列，则(λ·2k－1＋k)＋(λ·2k＋1＋k＋2)＝2(λ·2k＋k＋1)，所以λ·2k－1＝0，所以λ＝0，所以1an＝n，即an＝1n.(10分)②证明：要证ln n＋12an>ln(n＋1)－12an＋1，即证12(an＋an＋1)>lnn＋1n，即证1n＋1n＋1>2lnn＋1n.设t＝n＋1n，则1n＋1n＋1＝t－1＋t－1t＝t－1t，且t>1，从而只需证：当t>1时，t－1t>2ln t．(12分)设f(x)＝x－1x－2ln x(x>1)，则f′(x)＝1＋1x2－2x＝(1x－1)2>0，所以f(x)在(1，＋∞)上单调递增，所以f(x)>f(1)＝0，即x－1x>2ln x.因为t>1，所以t－1t>2ln t，所以原不等式得证．(16分)20. 解：(1) f(x)的定义域为(0，e－1)∪(e－1，＋∞)．由f′(x)＝2ax（1＋ln x）－ax2·1x（1＋ln x）2＝2ax（12＋ln x）（1＋ln x）2，(2分)令f′(x)>0，因为a>0，得x>e－1 2 .因为e－12>e－1，所以f(x)的单调增区间是(e－12，＋∞)．(4分)(2) 当a<0时，f(1)＝a<0<2e b－1，不合题意；当a>0时，令f′(x)<0，得0<x<e－1或e－1<x<e－1 2，所以f(x)在区间(0，e－1)和(e－1，e－12)上单调递减．因为12∈(e－1，e－12)，且f(x)在区间(e－12，＋∞)上单调递增，所以f(x)在x＝e－12处取极小值2ae，即最小值为2ae.(6分)若?x≥12，f(x)≥2e b－1，则2ae≥2e b－1，即a≥e b.不妨设b>0，则ba≤be b.(8分)设g(b)＝be b(b>0)，则g′(b)＝1－be b.当0<b<1时，g′(b)>0；当b>1时，g′(b)<0，所以g(b)在(0，1)上单调递增，在(1，＋∞)上单调递减，所以g(b)≤g(1)，即be b≤1e，所以ba的最大值为1e.(10分)(3) 由(2)知，当a>0时，f(x)无极大值．当a<0时，f(x)在(0，e－1)和(e－1，e－12)上单调递增，在(e－12，＋∞)上单调递减，所以f(x)在x＝e－12处取极大值，所以f(e－12)＝2ae＝－2，即a＝－e.(12分)设F(x)＝f(x)＋e x，即F(x)＝e x－ex21＋ln x，当x∈(0，e－1)，1＋ln x<0，所以F(x)>0；当x∈(e－1，＋∞)，F′(x)＝e x－ex（1＋2ln x）（1＋ln x）2，由(2)知ex≤e x，又1＋2ln x≤(1＋ln x)2，所以F′(x)≥0，且F(x)不恒为零，所以F(x)在(e－1，＋∞)上单调递增．不等式f(x)＋e x<0，即为F(x)<0＝F(1)，所以e－1<x<1，即不等式的解集为(e －1，1)．(16分)2019届高三模拟考试试卷(南通、泰州、徐州等苏北七市联考)数学附加题参考答案及评分标准21. A. 解： 由题意，得AA －1＝⎣⎢⎡⎦⎥⎤1001，即⎣⎢⎡⎦⎥⎤a －20 b ⎣⎢⎡⎦⎥⎤1c d 1＝⎣⎢⎡⎦⎥⎤a －2d ac －2bdb ＝⎣⎢⎡⎦⎥⎤1001，所以a ＝1，b ＝1，c ＝2，d ＝0，即矩阵A ＝⎣⎢⎡⎦⎥⎤1－20 1.(5分)设P(x ，y)为曲线C 上的任意一点，在矩阵A 对应的变换作用下变为点P ′(x ′，y ′)，则 ⎣⎢⎡⎦⎥⎤x ′y ′＝⎣⎢⎡⎦⎥⎤1－20 1⎣⎢⎡⎦⎥⎤x y ，即⎩⎨⎧x ′＝x －2y ，y ′＝y.(8分) 由已知条件可知P ′(x ′，y ′)满足y ＝2x ＋1，整理得2x －5y ＋1＝0， 所以曲线C 的方程为2x －5y ＋1＝0.(10分)B. 解：(1) 分别将A(4，π2)，B(22，5π4)转化为直角坐标，即A(0，4)，B(－2，－2)，所以直线AB 的直角坐标方程为3x －y ＋4＝0.(4分)(2) 曲线C 的方程为ρ＝r(r>0)，其直角坐标方程为x 2＋y 2＝r 2. 又直线AB 和曲线C 有且只有一个公共点，即直线与圆相切，所以圆心到直线AB 的距离为432＋12＝2105，即r 的值为2105.(10分) C. 解：因为关于x 的方程x 2＋4x ＋|a －1|＋|a|＝0有实根， 所以Δ＝16－4(|a －1|＋|a|)≥0，即|a －1|＋|a|≤4.(4分) 当a ≥1时，2a －1≤4，得1≤a ≤52；当0<a<1时，1≤4，恒成立，即0<a<1；当a≤0时，1－2a≤4，得－32≤a≤0.综上，所求a的取值范围是－32≤a≤52.(10分)22. 解：(1) 由题意，获得的积分不低于9分的情形有所以概率P＝19×12＋16×12＋12×13＋12×12＝59，所以每日学习积分不低于9分的概率为59.(4分)(2) 随机变量ξ的所有可能取值为0，1，2，3.由(1)知每个人积分不低于9分的概率为59，则P(ξ＝0)＝(49)3＝64729；P(ξ＝1)＝C13(59)(49)2＝240729；P(ξ＝2)＝C23(59)2(49)＝300729；P(ξ＝3)＝(59)3＝125729.所以随机变量ξ的概率分布列为(8分)所以E(ξ)＝0×64729＋1×240729＋2×300729＋3×125729＝53.5 3.(10分)所以随机变量ξ的数学期望为。

江苏泰兴三中2019高三下期初调研考试--数学数学【一】填空题〔本大题共14小题，每题5分，共70分、答案写在答卷纸上、〕1、假设全集R U =，集合{}01<+=x x A ，{}03<-=x x B ，那么集合B AC U )(=、2、复数i a z 3)4(2+-=，R a ∈，那么“2a =”是“z 为纯虚数”的_____条件、〔填写“充要”、“充分不必要”、“必要不充分”、“既不充分也不必要”中的一个〕3、如图1,是青年歌手大奖赛上9位评委给某位选手打分的茎叶图， 去掉一个最高分和一个最低分后,所剩数据的平均数为___.4、)2,1(=→a ，)log ,2(2m b -=→，假设→→→→=⋅ba b a ，那么正数m 的值等于、 5、如图2所示的算法流程图中，假设2()2,(),x f x g x x ==那么(3)h 的值等于、6、正六棱锥ABCDEF P -的底面边长为1cm ，侧面积为32cm ，那么该棱锥的体积为3cm 、7、投掷两颗骰子，得到其向上的点数分别为m ，n ，设),(n m a =→，那么满足5<→a 的概率为、8、函数)0)(sin(2)(>+=ωϕωx x f 的图像关于直线3π=x 对称，且12π为函数)(x f 的一个零点，那么ω的最小值为、开始输入x f(x)>g(x)h(x)=f(x)h(x)=g(x)输出h(x)结束是否图2图19、设圆C ：224x y +=的一条切线与x 轴、y 轴分别交于点,A B ，那么AB 的最小值为、 10、数列{}na 满足221221,2,(1cos )sin22n n n n a a a a ππ+===+⋅+，那么该数列的前10项的和为、 11、F 是椭圆2222:1x y C a b+=(0)a b >>的右焦点，点P 在椭圆C 上，线段PF 与圆22214x y b +=相切于点Q ，且→→=QF PQ ，那么椭圆C 的离心率为、 12、如图3基本上由边长为1的正方体叠成的图形图3例如第〔1〕个图形的表面积为6个平方单位，第〔2〕个图形的表面积为18个平方单位，第〔3〕个图形的表面积是36个平方单位、依此规律，那么第n 个图形的表面积是______个平方单位、13、如图4，一块曲线部分是抛物线形的钢板，其底边长为2，高为， 将此钢板切割成等腰梯形的形状，记x CD 2=，梯形面积为S 、那么S 的最大值是、图414、设,x y 是正实数，且1x y +=，那么2221x y x y +++的最小值是.【二】解答题〔本大题共6小题，总分值90分。