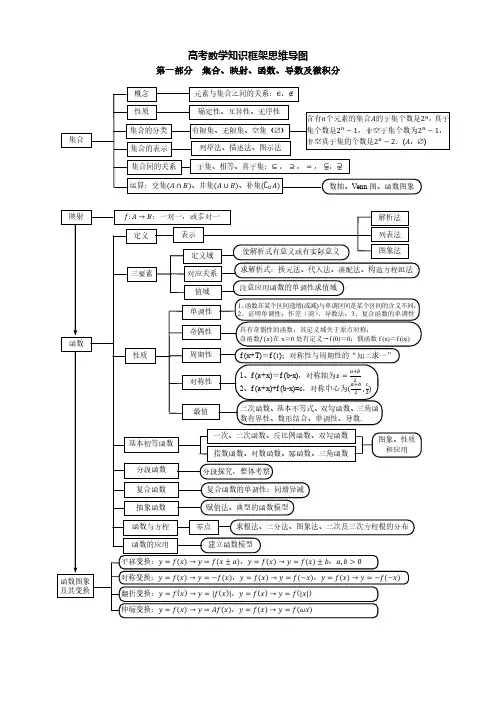
“高频考点透析”考点导图--高中数学(一)
- 格式:doc
- 大小:3.96 MB
- 文档页数:1
x^n=a,则x叫做a的n次根,求方根的过程叫做开方运算,正数a的正n次方根
理数指数幂适用于有理数指数幂的法则
数函数的底判断是增函数还是减函数;实际问题中函数
叫做真数,读作以a为
,自然常数e,叫做ln
性质:
1.值域是实数集R
2.在定义域内,当a>1时是增函数,当0<a小于1时是减
函数
3.图象都通过点(1,0)
指数函数和对数函数的关系当一个函数是一一映射时,可以把这个函数的因变量作为一个新的函数的自变量,而把这个函数的自变量作为新的函数的因变量,称之为反函数
反函数。

一般地我们把研究对象统称为元素,把一些元素组成的总体叫同向可加性我们把只含有一个未知数,并且未知求出相应的一元二次方程的根利用二次函数的图像与X轴的交点确定一元二次不等式的解集如果积xy等于定值P,那么当x=y时,和x+y有最小值如果积xy等于定值S,那么当x=y时,积xy有最大值积定和最小,和定积最大设A、B是非空的实数集,如果按照某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数y和它对应,那么就称f:A→B为从集合A到集合B的一个函数,是幂函数的底数,幂函数的系数是1, 比如2不是幂函数一次函数:二次函数:反比例函数:第五章 三角函数角的定义平面内一条射线绕着它的端点旋转所成的图形叫做角角的分类按照旋转方向正角负角零角按照终边位置第一象限角第二象限角第三象限角第四象限角度量角的两种制度角度制弧度制诱导公式公式一:设α为任意角,终边相同的角的同一三角函数的值相等sin(2kπ+α)=sinα k∈zcos(2kπ+α)=cosα k∈ztan(2kπ+α)=tanα k∈z 公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系sin(π+α)=-sinα k∈zcos(π+α)=-cosα k∈ztan(π+α)=tanα k∈z 公式三:任意角α与 -α的三角函数值之间的关系sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanα弧长与角的换算1°=π/180°,1rad=180°/π弧长公式L=n× π× r/180,L=α× r扇形面积公式S=LR/2三角函数的定义域、值域y=sinαy=cosαy=tanα三角函数的单调性正弦函数余弦函数一周是360度,也是2π弧度,即360°=2π.(n是圆心角度数,r是半径,L是圆心角弧长,α是圆心角度数)(R是扇形半径,L是扇形对应的弧长)定义域是R,值域[-1,1]定义域是R,值域[-1,1]定义域是α≠kπ+π/2区间是(kπ-π/2,kπ+π/2)值域是Ry=sinx在[2kπ-π/2,2kπ+π/2],k∈Z,上是增函数;在[2kπ+π/2,2kπ+3π/2],k∈Z,上是减函数;三角函数y=sin x,它的定义域为全体实数,值域为[-1,1]y=cosx在[2kπ,2kπ+π],k∈Z,上是减函数;在[2kπ+π,2kπ+2π],k∈Z,上是增函数;余弦函数的定义域是整个实数集,值域是[-1,1];余弦函数是周期函数,其最小正周期为2π。

高一数学必修1知识点总结导图1. 数与代数•实数–有理数–无理数•数轴和绝对值•代数式与代数方程•一次函数•二次函数•等差数列•等比数列2. 几何•平面与空间几何初步•平行线与平行四边形•直线之间的大小关系•三角形中的线段•相似三角形•背式与旋转体•直角三角形的应用3. 概率与统计•随机事件与概率•事件的并与交•独立事件与重复试验•抽样调查与统计表4. 函数与方程•函数的定义与性质•函数的图像与性质•二次函数及其图像和性质•一次函数及其图像和性质•函数的运算与复合函数•图像与方程的关系•一元一次方程与一元一次不等式•一元二次方程与一元二次不等式•一元一次方程组与一元一次不等式组•法方程、视角、投影、条件以上导图总结了高一数学必修1的主要知识点,包括数与代数、几何、概率与统计以及函数与方程。
下面将对每个知识点进行详细的解释。
数与代数实数实数是自然数、整数、有理数和无理数的统称。
有理数可以表示为一个整数的比率,无理数则无法表示为有理数的比率,如根号2、圆周率π等。
数轴和绝对值数轴是以一条直线为基础的有向线段,在数轴上我们可以方便地表示和比较数的大小关系。
绝对值是一个数到原点的距离,用来表示这个数的大小,非负数的绝对值等于其本身,负数的绝对值等于其相反数。
代数式与代数方程代数式是由数、字母和运算符号组成的式子,可以进行各种运算。
代数方程是含有未知数的等式,可通过变量的赋值求出未知数的值。
一次函数一次函数是指形如 y = kx + b 的函数,其中 k 是斜率,b 是截距。
一次函数的图像是一条直线,斜率决定了直线的倾斜方向和角度,截距决定了直线与 y 轴的交点位置。
二次函数二次函数是指形如 y = ax^2 + bx + c 的函数,其中 a、b、c 是常数且a ≠ 0。
二次函数的图像是一条抛物线,开口的方向由 a 的正负号决定,a>0 时开口向上,a<0 时开口向下。
等差数列等差数列是指数列中任意两个相邻项之差都相等的数列。



高一数学知识点思维导图大全思维导图是一种图形化的表示方式,可以帮助我们更好地理解和记忆知识点。
在高一数学学习中,掌握并熟悉各个知识点的关系和内在联系对于建立数学思维非常重要。
本文将为大家提供一份高一数学知识点思维导图大全,旨在帮助大家更好地理解和掌握数学知识。
一、函数与方程函数和方程是高一数学的重要基础,掌握好这一部分的知识对于后续的学习非常重要。
1.函数基本概念- 函数的定义- 自变量与因变量- 定义域与值域2.函数的表示与性质- 函数的图像与表达式- 奇偶函数与周期函数- 单调性与极值- 函数的运算与复合3.一次函数与二次函数- 一次函数的图像与性质- 一次函数与斜率- 二次函数的图像与性质- 二次函数与根的关系4.指数函数与对数函数- 指数函数的图像与性质- 指数函数的运算与等式- 对数函数的图像与性质- 对数函数的运算与等式二、平面几何平面几何是数学中的重要分支,它描述了平面中点、直线和图形的性质与关系,是解决空间问题的基础。
1.点、线、面- 点的定义与性质- 直线的定义与性质- 面的定义与性质2.角与三角形- 角的概念与性质- 三角形的分类与性质- 三角形的画法与运算3.四边形与多边形- 正方形、长方形、菱形与平行四边形- 多边形的分类与性质- 多边形的内角和外角4.相似与全等- 相似与全等的定义- 相似与全等的判定条件- 相似与全等的性质与应用三、解析几何解析几何是运用坐标表示和计算几何问题的学科,它通过数学方程与图形之间的关系解决几何问题。
1.平面直角坐标系- 平面直角坐标系的构建- 坐标与距离公式- 斜率与角度2.直线与曲线- 一次函数与二次函数的图像与方程- 圆的方程与性质- 椭圆、双曲线和抛物线的方程与性质3.向量与坐标变换- 向量的定义与运算- 平移、旋转、对称的向量表示- 坐标变换与几何变换四、数列与数学归纳法数列是由一组有序的数所组成的序列,通过研究数列的规律以及数学归纳法,可以解决很多数学问题。