12 杆件结构的计算简图

LIMING UNIVERSITY平面杆件结构的 计算简图13.1 结构的计算简图 13.2 平面杆件结构的分类结构的计算简图LIMING UNIVERSITY13.1 结构的计算简图计算简图——将一个具体的工程结构物用一个简化的受 力图形来表示。

结构计算简图的简化原则是： １）计算简图要能反映实际结构的主要受力和变形特 点，即要使计算结果安全可靠； ２）略去次要因素，便于分析和计算，即计算简图的简 化程度要与计算手段以及对结果的要求相一致。

结构的计算简图LIMING UNIVERSITY结构计算简图的几个要点： 1、杆件构件的简化：以杆件的轴线代替杆件；2、结点的简化（杆件与杆件之间的连接区）： 铰结点：结点杆（焊接）汇交于一点的杆端是用一个完全无磨擦的光滑铰连结。

铰结点所连 各杆端可独自绕铰心自由转动，即各杆端之间的夹角可任意改变。

铰结点结构的计算简图LIMING UNIVERSITY刚结点：钢筋混凝土汇交于一点的杆端是用一个完全不变形的刚性结点连结，形成一个整 体。

刚结点所连各杆端相互之间的夹角不能改变。

组合结点（半铰)：刚结点与铰结点的组合体。

刚结点 组合结点结构的计算简图LIMING UNIVERSITY结点的计算简图结点 计算简图 机动特征各杆之间不能相对移 铰结点 动，可以绕铰结点作自 由转动 刚结点 各杆之间不能相对移 动，也不能相对转动受力特征能承受和传递力，不 能承受和传递力矩 能承受和传递力，也 能承受和传递力矩组合 结点BA杆与AC杆用刚结点相联，其机动和受力特征 同刚结点；BA杆与AD杆用铰结点相联，其机动 和受力特征同铰结点结构的计算简图LIMING UNIVERSITY3、支座的简化： 固定铰支座：可动铰支座：固定铰支座 可动铰支座结构的计算简图LIMING UNIVERSITY固定端支座：定向支座：结构的计算简图LIMING UNIVERSITY支座的计算简图结点 可动 铰支座 固定 铰支座 固定 支座 定向 支座 计算简图 机动特征 杆端A沿水平方向可以相对移 动，绕A点可以自由转动，但 沿竖向不能移动 杆端A绕A点可以自由转动， 但沿任何方向不能移动 杆端不能移动，也不能转动 只允许杆端沿一定方向自由 移动，而沿其它方向不能移 动，也不能转动 受力特征 没有反力矩，水平支座 反力，有竖向支座反力 没有反力矩，有水平支 座反力，竖向支座反力 有反力矩，水平支座反 力，竖向支座反力 沿自由移动方向没有支 座反力，只有与此方向 垂直的支座反力，及反 力矩结构的计算简图LIMING UNIVERSITY四、结构简化实例 单层工业厂房取一榀计算，并 化为平面体系结构的计算简图LIMING UNIVERSITY↓↓↓↓↓↓↓↓↓↓↓↓ ↓↓↓细石混凝土填充结构的计算简图LIMING UNIVERSITY组合式吊车梁FP1横梁AB 和竖杆CD 由钢筋混 凝土做 成，斜杆 AD、BD则 为16锰圆 钢。

结构力学张金生绪论§1 . 结构力学的内容和任务一.对象结构分为:杆系结构,板壳结构,实体结构三.内容 结构组成;内力,位移,临界力计算.二.任务 研究结构的刚度,强度,稳定性的 计算原理和计算方法结构：承受并传递荷载的骨架部分确定计算简图的原则： 1.能反映实际结构的主要力学特性;2.分析计算尽可能简便§2 . 杆件结构的计算简图计算简图:在结构分析当中用来代替实际结构的计算模型(图形)简化内容:1.杆件的简化: 杆件 杆件的轴线2.结点的简化: 刚结点 铰结点 半铰结点(组合结点)半铰结点铰结点刚结点确定计算简图的原则：1.能反映实际结构的主要力学特性;2.分析计算尽可能简便§2 . 杆件结构的计算简图计算简图:在结构分析当中用来代替实际结构的计算模型(图形)简化内容: 1.杆件的简化: 杆件 杆件的轴线2.结点的简化: 刚结点 铰结点 半铰结点(组合结点)3.支座的简化: 固定铰支座 可动较支座 固定端支座 滑动支座(定向支座)确定计算简图的原则：1.能反映实际结构的主要力学特性;2.分析计算尽可能简便§2 . 杆件结构的计算简图计算简图:在结构分析当中用来代替实际结构的计算模型(图形)简化内容: 1.杆件的简化: 杆件 杆件的轴线2.结点的简化: 刚结点 铰结点 半铰结点(组合结点)3.支座的简化: 固定铰支座 可动较支座 固定端支座 滑动支座(定向支座)4.体系的简化: 空间结构 平面结构确定计算简图的原则：1.能反映实际结构的主要力学特性;2.分析计算尽可能简便§2 . 杆件结构的计算简图计算简图:在结构分析当中用来代替实际结构的计算模型(图形)简化内容: 1.杆件的简化: 杆件 杆件的轴线2.结点的简化: 刚结点 铰结点 半铰结点(组合结点)3.支座的简化: 固定铰支座 可动较支座 固定端支座 滑动支座(定向支座)4.体系的简化: 空间结构 平面结构5.荷载的简化: 集中力、集中力偶、分布荷载§3 . 杆件结构的类型1.梁2.拱3.桁架4.刚架5.组合结构第一章杆件体系的几何组成分析(Geometric construction analysis)§1. 几何组成分析本章假定:所有杆件均为刚体§1-1 基本概念一. 几何不变体系几何可变体系几何可变体系不能作为建筑结构结构必须是几何不变体系本章目的:判定一个体系是否能作为结构结构是如何构造的几何形状不能变化的平面物体几何不变体系的自由度一定等于零几何可变体系的自由度一定大于零§1. 几何组成分析§1-1 基本概念一. 几何不变体系几何可变体系二. 刚片几何形状不能变化的平面物体三. 自由度确定体系位置所需的独立坐标数四. 约束(联系) 能减少自由度的装置1. 链杆2. 单铰§1. 几何组成分析§1-1 基本概念一. 几何不变体系 几何可变体系二. 刚片 几何形状不能变化的平面物体 三. 自由度 确定体系位置所需的独立坐标数四. 约束(联系) 能减少自由度的装置1. 链杆 2. 单铰 3. 链杆与单铰的关系4. 虚铰3. 链杆与单铰的关系4. 虚铰§1. 几何组成分析2. 单铰 5. 复铰1. 链杆连接N 个刚片的复铰相当于N-1个单铰§1. 几何组成分析§1-1 基本概念一. 几何不变体系 几何可变体系二. 刚片 几何形状不能变化的平面物体 三. 自由度 确定体系位置所需的独立坐标数四. 约束(联系) 能减少自由度的装置五. 计算自由度0632=−×=W 02936=×−×=W 032333=−×−×=W§1. 几何组成分析五. 计算自由度0632=−×=W 08936=×−×=W 032333=−×−×=W 链杆数单铰数刚片数链杆数结点数−×−×=−×=232W W 计算自由度大于零一定可变;若等于零则一定不变吗§1. 几何组成分析五. 计算自由度链杆数单铰数刚片数链杆数结点数−×−×=−×=232W W 计算自由度大于零一定可变;若等于零则一定不变吗六. 多余约束 必要约束计算自由度小于零一定不变吗计算自由度小于零一定有多余约束§1. 几何组成分析§1-1 基本概念一. 几何不变体系几何可变体系二. 刚片三. 自由度四. 约束(联系) 链杆单铰复铰虚铰实铰五. 计算自由度六. 多余约束必要约束P N=构成无多余约束的几何不变体系构成无多余约束的几何不变体系.§1. 几何组成分析§1-2 无多余约束的几何不变体系的组成规则一. 三刚片规则二元体:在一个体系上用两个不共线的链杆连接一个新结点的装置.二. 两刚片规则在一个体系上加减二元体不影响原体系的机动性质.三. 二元体规则§1. 几何组成分析§1-1 基本概念§1-2 无多余约束的几何不变体系的组成规则§1-3 几何组成分析举例例1: 对图示体系作几何组成分析解: 三刚片三铰相连,三铰不共线,所以该体系为无多余约束的几何不变体系.§1. 几何组成分析§1-3 几何组成分析举例例2: 对图示体系作几何组成分析解:该体系为无多余约束的几何不变体系.方法1: 若基础与其它部分三杆相连,去掉基础只分析其它部分例3: 对图示体系作几何组成分析解: 该体系为无多余约束的几何不变体系.方法2: 利用规则将小刚片变成大刚片.例4: 对图示体系作几何组成分析解: 该体系为瞬变体系.方法3: 将只有两个铰与其它部分相连的刚片看成链杆.方法2: 利用规则将小刚片变成大刚片.例5:对图示体系作几何组成分析解: 该体系为常变体系.方法3: 将只有两个铰与其它部分相连的刚片看成链杆.方法2: 利用规则将小刚片变成大刚片.方法4: 去掉二元体.例6:对图示体系作几何组成分析解: 该体系为无多余约束几何不变体系.方法3: 将只有两个铰与其它部分相连的刚片看成链杆.方法2: 利用规则将小刚片变成大刚片.方法5: 从基础部分(几何不变部分)依次添加.方法4: 去掉二元体.例7: 对图示体系作几何组成分析方法3: 将只有两个铰与其它部分相连的刚片看成链杆.方法2: 利用规则将小刚片变成大刚片.方法5: 从基础部分(几何不变部分)依次添加.方法4: 去掉二元体.解: 该体系为有一个多余约束几何不变体系.练习: 对图示体系作几何组成分析方法3: 将只有两个铰与其它部分相连的刚片看成链杆.方法2: 利用规则将小刚片变成大刚片.方法5: 从基础部分(几何不变部分)依次添加.方法4: 去掉二元体.练习: 对图示体系作几何组成分析方法3: 将只有两个铰与其它部分相连的刚片看成链杆.方法2: 利用规则将小刚片变成大刚片.方法5: 从基础部分(几何不变部分)依次添加.方法4: 去掉二元体.方法1: 若基础与其它部分三杆相连,去掉基础只分析其它部分练习: 对图示体系作几何组成分析方法3: 将只有两个铰与其它部分相连的刚片看成链杆.方法2: 利用规则将小刚片变成大刚片.方法5: 从基础部分(几何不变部分)依次添加.方法4: 去掉二元体.几何组成思考题§几何组成分析的假定和目的是什麽？§何谓自由度？系统自由度与几何可变性有何联系？§不变体系有多余联系时，使其变成无多余联系几何不变体系是否唯一？§瞬变体系有何特点？可变体系时如何区分瞬变还是常变？§瞬铰和实际铰有何异同？§无多余联系几何不变体系组成规则各有什麽限制条件？不满足条件时可变性如何？§按组成规则建立结构有哪些组装格式？组装格式和受力分析有无联系？§如何确定计算自由度？§对体系进行组成分析的步骤如何？几何组成作业题§1-1 b c§1-2 a d g h i j k l §交作业时间:本周 5§1. 几何组成分析作业:1-1 (1-1 (b)b)试计算图示体系的计算自由度 解:由结果不能判定其是否能作为结构1321138−=−×−×=W 110222531−=−×−×+×=W 或:§1. 几何组成分析作业:1-1 (c)试计算图示体系的计算自由度解:由结果可判定其不能作为结构131216=−×=W 13240328=−×−×=W 或:§1. 几何组成分析作业:1-2 (a)试分析图示体系的几何组成从上到下依次去掉二元体或从基础开始依次加二元体.几何不变无多余约束§1. 几何组成分析作业:1-2 (d)试分析图示体系的几何组成依次去掉二元体.几何常变体系§1. 几何组成分析作业:1-2 (f)试分析图示体系的几何组成有一个多余约束的几何不变体系§1. 几何组成分析作业:1-2 (h)( i)试分析图示体系的几何组成瞬变体系几何不变无多余约束作业:试分析图示体系的几何组成有一个无穷远铰:四杆不平行不变平行且各自等长常变平行不等长瞬变§1. 几何组成分析作业:1-2 (j)试分析图示体系的几何组成瞬变体系§1. 几何组成分析L)试分析图示体系的几何组成1-2 (L)作业:1-2 (几何不变无多余约束§1. 几何组成分析例:试分析图示体系的几何组成瞬变体系§1. 几何组成分析练习:试分析图示体系的几何组成几何不变无多余约束一个单刚结点相当于三个约束.单刚结点与其它约束的关系:复刚结点:刚片复刚结点相当于练习:试分析图示体系的几何组成无多余约束几何不变体系有两个多余约束的几何不变体系练习:试分析图示体系的几何组成无多余约束几何不变体系无多余约束的几何不变体系。

结构的计算简图及受力分析3.1 荷载的分类实际的建筑结构由于其作用和工作条件不同,作用在它们上面的力也显示出多种形式。

如图3.1所示的工业厂房结构,屋架所受到的力有:屋面板的自重传给屋架的力,屋架本身的自重,风压力和雪压力以及两端柱或砖墙的支承力等。

图3.1在建筑力学中,我们把作用在物体上的力一般分为两类:一类是主动力,例如重力、风压力等;另一类是约束力,如柱或墙对梁的支承力。

通常把作用在结构上的主动力称为荷载。

荷载多种多样,分类方法各不相同,主要有以下几种分类方法:(1)荷载按其作用在结构上的空间范围可分为集中荷载和分布荷载作用于结构上一点处的荷载称为集中荷载。

满布在体积、面积和线段上的荷载分别称为体荷载、面荷载和线荷载,统称为分布荷载。

例如梁的自重,用单位长度的重力来表示,单位是N/m或kN/m,作用在梁的轴线上,是线荷载。

对于等截面匀质材料梁,单位长度自重不变,可将其称为线均布荷载,常用字母q表示(图3.2)。

当荷载不均匀分布时,称为非均布荷载,如水对水池侧壁的压力是随深度线性增加的,呈三角形分布。

图3.2(2)荷载按其作用在结构上的时间分为恒载和活载恒荷载是指永久作用在结构上的荷载,其大小和位置都不再发生变化,如结构的自重。

活荷载是指作用于结构上的可变荷载。

这种荷载有时存在、有时不存在,作用位置可能是固定的也可能是移动的,如风荷载、雪荷载、吊车荷载等。

各种常用的活荷载可参见《建筑结构荷载规范》。

(3)荷载按其作用在结构上的性质分为静力荷载和动力荷载静力荷载是指荷载从零缓慢增加到一定值,不会使结构产生明显冲击和振动,因而可以忽略惯性力影响的荷载,如结构自重及人群等活荷载。

动力荷载是指大小和方向随时间明显变化的荷载,它使结构的内力和变形随时间变化,如地震力等。

3.2 约束与约束反力1)约束和约束反力的概念所谓约束,是指能够限制某构件位移(包括线位移和角位移)的其他物体(如支承屋架的柱子,见图 3.1)。

结构的计算简图及简化要点Computing Models of Structures and the Main Point of Their Simplification 1.2 结构的计算简图及简化要点教学目标：教学内容：n 结构体系的简化 n 杆件的简化n 杆件间连接的简化n 结构与基础间连接的简化n 荷载的简化n 材料性质的简化n 了解简化原则。

n 理解杆件、结点、支座、荷载等的简化方法。

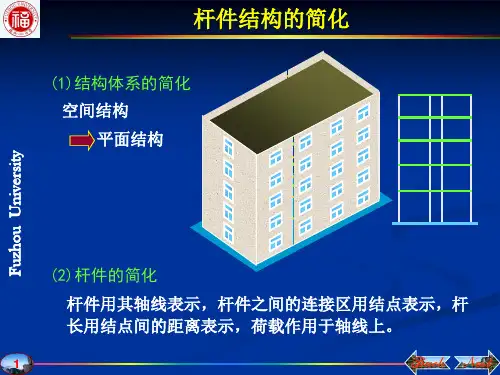
1. 定义与原则结构计算简图的定义：用一个简化的图形来代替实际结构选取计算简图的原则：反映实际 便于计算空间结构平面结构计算简图2. 简化方法Ø杆件的简化Ø杆件间连接的简化Ø结构与基础间连接的简化Ø荷载的简化计算简图Ø 杆件简化杆件——用轴线表示；杆件连接区——用结点表示；杆长——用结点间的距离表示；荷载——作用点移到轴线上。

计算简图Ø 杆件间连接的简化杆件间连接区简化为结点（铰结点和刚结点）（1） 铰结点(Hinge joint)：被连接的杆件在连接处不能相对移动，但可相对转动。

（2） 刚结点(Rigid joint)被连接的杆件在连接处既不能相对移动，又不能相对转动。

预埋钢板焊缝柱屋架柱计算简图梁2. 简化方法Ø 结构与基础间连接的简化结构与基础的连接区简化为支座（support）按受力特征，一般简化为以下四种情况：（1） 滚轴支座（2） 铰支座（3） 定向支座（4） 固定支座（1） 滚轴支座梁 砖墙F y 被支承的部分可以转动和水平移动，但不能竖向移动。

计算简图：用一根支杆表示。

砖墙 （2） 铰支座梁被支承的部分可以转动，但不能移动。

计算简图：用两根相交的支杆表示。

F y F x（3） 定向支座M被支承的部分不能转动,但可以沿一个方向平行滑动。

计算简图：用两根平行支杆表示。

Fy（4） 固定支座M被支承的部分完全被固定。

计算简图：按图表示。