材料模型与状态方程
- 格式:doc
- 大小:359.50 KB
- 文档页数:24

微声聚能穿孔装置优化设计及IED安全销毁实验徐全军;白帆;李裕春;龚自正;张庆明【摘要】Based on the Held initiation theory, and the fact that shaped charge jet against the charge can produce low velocity explosion, this paper presents a new design of micro-acoustic shaped charge device. The orthogonal analysis methods were applied to optimize the charge structure. The experiments indicate that the noise elimination ability and the anti-detonation ability of the device are fine. The simulator charge boxes were destroyed with low velocity detonation, which helps reduce the explosive harm and allows for destroying IED safely.%根据Held引爆理论,利用聚能射流使炸药只燃烧或发生不完全爆轰的特点,设计了微声聚能穿孔装置,并对装药结构进行了正交优化.实验结果表明,装置的消声能力良好,用于销毁模拟爆炸药盒时,装药仅发生低速爆轰,达到了安全销毁简易爆炸装置的目的.【期刊名称】《爆炸与冲击》【年(卷),期】2012(032)001【总页数】5页(P79-83)【关键词】爆炸力学;安全销毁;微声聚能穿孔装置;简易爆炸装置;正交分析【作者】徐全军;白帆;李裕春;龚自正;张庆明【作者单位】解放军理工大学工程兵工程学院,江苏南京210007;解放军理工大学工程兵工程学院,江苏南京210007;解放军理工大学工程兵工程学院,江苏南京210007;北京卫星环境工程所,北京100094;北京理工大学,北京100081【正文语种】中文【中图分类】O383简易爆炸装置(improvised explosive device,IED)是指利用就便器材临时制作的爆炸装置。


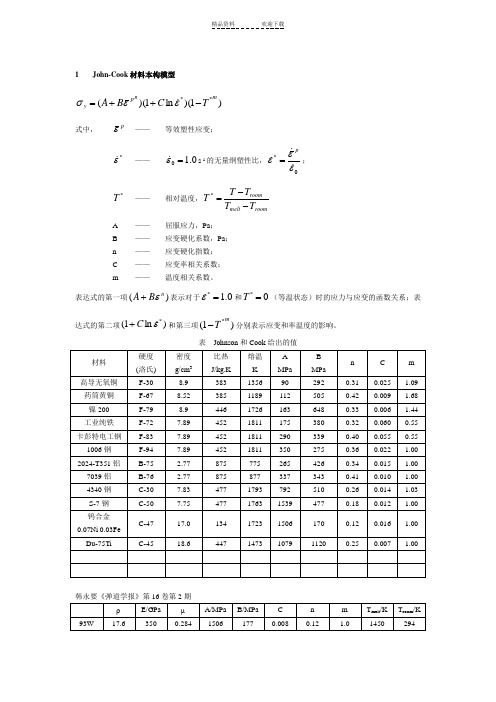
1 John-Cook 材料本构模型)1)(ln 1)((**mnp y T C B A -++=εεσ 式中,pε—— 等效塑性应变;*ε——0.10=εs -1的无量纲塑性比,0*εεε p =;*T——相对温度,roommelt roomT T T T T--=*A —— 屈服应力,Pa ;B —— 应变硬化系数,Pa ; n —— 应变硬化指数;C —— 应变率相关系数;m——温度相关系数。
表达式的第一项)(n B A ε+表示对于0.1*=ε和0*=T (等温状态)时的应力与应变的函数关系;表达式的第二项)ln 1(*εC +和第三项)1(*mT -分别表示应变和率温度的影响。
表 Johnson 和Cook 给出的值韩永要《弹道学报》第16卷第2期(断裂破坏时的)应变]1][ln 1][[*5*421*3T D D e D D D f +++=εεσ其中,D 1、D 2、D 3、D 4、D 5输入参数,σ*是压力与有效应力之比,eff p σσ/*=。
当破坏参数∑∆=fpD εε达到1时,发生破坏。
* Hirofumi Iyama, Kousei Takahashi, Takeshi Hinata, Shigeru Itoh .Numerical Simulation of Aluminum Alloy Forming Using Underwater Shock Wave .8thInternational LS-DYNA Users Conference2 Steinberg-Guinan 材料本构模型定义材料熔化前的剪切模量i m iE E fE c i e R E E h bpV G G --⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-'--+=300313/10p ——压力,V ——相对体积,Ec ——冷压缩能,Em ——熔化能AR R ρ=',R ——气体常数,A ——原子量 屈服强度ii m iE E fE c i y eR E E h pV b --⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-'--'+'=300313/10σσ如果Em 超过Ei ,[]np i y )(10εγβσσ++'= i γ——初始塑性应变,当0σ'超过m σ,设置0σ'等于m σ。

1 John-Cook 材料本构模型)1)(ln 1)((**mnp y T C B A -++=εεσ 式中,pε—— 等效塑性应变;*ε——0.10=εs -1的无量纲塑性比,0*εεε p =;*T——相对温度,roommelt roomT T T T T--=*A —— 屈服应力,Pa ;B —— 应变硬化系数,Pa ; n —— 应变硬化指数;C —— 应变率相关系数;m——温度相关系数。
表达式的第一项)(n B A ε+表示对于0.1*=ε和0*=T (等温状态)时的应力与应变的函数关系;表达式的第二项)ln 1(*εC +和第三项)1(*mT -分别表示应变和率温度的影响。
表 Johnson 和Cook 给出的值韩永要《弹道学报》第16卷第2期(断裂破坏时的)应变]1][ln 1][[*5*421*3T D D e D D D f +++=εεσ其中,D 1、D 2、D 3、D 4、D 5输入参数,σ*是压力与有效应力之比,eff p σσ/*=。
当破坏参数∑∆=fpD εε达到1时,发生破坏。
* Hirofumi Iyama, Kousei Takahashi, Takeshi Hinata, Shigeru Itoh .Numerical Simulation of Aluminum Alloy Forming Using Underwater Shock Wave .8thInternational LS-DYNA Users Conference2 Steinberg-Guinan 材料本构模型定义材料熔化前的剪切模量i m iE E fE c i e R E E h bpV G G --⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-'--+=300313/10p ——压力,V ——相对体积,Ec ——冷压缩能,Em ——熔化能AR R ρ=',R ——气体常数,A ——原子量 屈服强度ii m iE E fE c i y eR E E h pV b --⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-'--'+'=300313/10σσ如果Em 超过Ei ,[]np i y )(10εγβσσ++'= i γ——初始塑性应变,当0σ'超过m σ,设置0σ'等于m σ。

DO1:10.19936/ki.2096-8000.20210428.010陶瓷/UHMWPE层合板/阻尼材料复合靶板防弹性能研究周越松,梁森*,王得盼,刘龙(青岛理工大学机械与汽车工程学院,青岛266520)摘要:提出一种由碳化硼陶瓷、UHMWPE层合板、阻尼材料构成的复合靶板。
应用LS-DYNA动力学软件进行数值仿真分析,研究该靶板在12.7mm穿甲爆炸燃烧弹高速冲击下的性能,并通过实验对数值模拟进行可行性验证。
进一步研究靶板抗侵彻性能随结构几何参数变化的关系,探究阻尼材料的最佳分布位置和最佳厚度。
结果表明:随着陶瓷厚度增大,靶板吸收子弹动能和弹道性能指数呈线性增加;在UHMWPE层合板厚度较大时,增加其厚度对靶板抗侵彻性能的提升更明显;同等面密度条件下,与提高陶瓷或者UHMWPE层合板的厚度相比,涂刷1mm背层阻尼材料时,复合靶板弹道性能指数最高,抗高速侵彻性能最好,为阻尼材料作为减震层在抗高速冲击领域的广泛应用奠定了基础。
关键词:阻尼材料;复合靶板;数值仿真分析;高速冲击;复合材料中图分类号:TB332文献标识码:A文章编号:2096-8000(2021)04-0066-091引言随着科学技术的进步,反装甲武器毁伤效能不断提升,对防护装甲的“轻量级”与“防护性”要求越来越高[1]。
因此,研发防护能力更好、更轻质的防弹靶板迫在眉睫。
目前关于防弹靶板的研究大多集中在防弹新材料和防弹靶板复合结构上。
王亚进等[2]提出了陶瓷/芳纶纤维复合材料防弹板,通过数值模拟方法研究该防弹板抗子弹高速冲击的性能,并对该结构进行优化,为后续轻质复合装甲的研究设计提出了研究方向。
甄建伟等[3]研究了阵列式陶瓷颗粒破片防护层的透波特性,通过采用数值模拟的方法,说明了这种特殊的结构具有降低冲击波破坏的作用。
江怡等⑷用数值分析的方法探究了不同陶瓷种类的抗侵彻性能,深度剖析了陶瓷的抗侵彻原理,为复合靶板中陶瓷材料的选择提供了理论参考。
地下综合管廊燃气舱内爆炸下结构动力响应规律田威; 武泽元; 王亚威; 肖煜强; 张旭东【期刊名称】《《科学技术与工程》》【年(卷),期】2019(019)032【总页数】6页(P31-36)【关键词】地下综合管廊; 隐式-显示顺序求解; 超压层; 耦合作用【作者】田威; 武泽元; 王亚威; 肖煜强; 张旭东【作者单位】长安大学建筑工程学院西安710061【正文语种】中文【中图分类】O383+.2随着中国经济的快速发展,地下综合管廊在城市建设中的得到了广泛的应用,综合管廊是将城市管线集中管理,但燃气管道的泄漏引发的爆炸问题依然存在,如燃气管道发生腐蚀以及设备与设备之间的连接形式存在缺陷、恐怖主义的袭击等爆炸风险。
一旦地下密闭空间发生爆炸事故,其危害性是非常大的,国内外均有类似的地下密闭空间发生爆炸的事故,如重庆的“大溪沟爆炸事件”、青岛的“11·22事件”、德国BASF公司的“地下管廊爆炸事件”、中国台湾的“8·1事件”。
对于密闭狭长空间综合管廊的内爆炸模拟,诸多学者也开展了许多的研究并取得了一定的成果。
孙加超等[1]通过改变炸药量分析了在没有考虑土体和综合管廊结构耦合作用下的综合管廊的动力响应规律。
刘中宪等[2]采取简化燃气爆炸荷载曲线,忽略了冲击波沿纵向的贡献,对燃气在地下综合管廊结构内爆炸进行了近似模拟。
陈长坤等[3]在没有考虑由土体自重产生的初始应力条件下对天然气爆炸荷载作用的圆形单舱地下管廊动力响应规律进行了研究。
地下管廊内燃气爆炸之前,结构会受到土体自重产生的初始应力,会对其产生一定的影响,然而,目前显示求解方法对于处理非常短的瞬间动力问题是非常合适的,但在处理静力问题时显示求解方法就没有隐式求解方法更为奏效,为此,可以结合两种方法的优点进行隐式-显示顺序求解[4]。
故采用ANSYS/LS-DYNA有限元软件,建立考虑土体与综合管廊耦合作用下的典型三舱地下综合管廊模型,并采用隐式-显式顺序求解的分析方法,模拟不同炸药量情况下地下综合管廊的冲击波传播规律和结构毁伤以及位移反应情况,以期提高各舱室及管廊整体结构的抗爆性能,有利于提高城市防灾减灾的能力。
岩土类材料的弹塑性力学模型及本构方程摘要:本文主要结合岩土类材料的特性,开展研究其在受力变形过程中的弹性及塑性变形的特点,描述简化的力学模型特征及对应的适用条件,同时在分析研究其弹塑性力学模型的基础上,探究了关于岩土类介质材料的各种本构模型,如M-C、D-P、Cam、D-C、L-D及节理材料模型等,分析对应使用条件,特点及公式,从而推广到不同的材料本构模型的研究,为弹塑性理论更好的延伸发展做一定的参考性。
关键词:岩土类材料,弹塑性力学模型,本构方程不同的固体材料,力学性质各不相同。
即便是同一种固体材料,在不同的物理环境和受力状态中,所测得的反映其力学性质的应力应变曲线也各不相同。
尽管材料力学性质复杂多变,但仍是有规律可循的,也就是说可将各种反映材料力学性质的应力应变曲线,进行分析归类并加以总结,从而提出相应的变形体力学模型。
第一章岩土类材料地质工程或采掘工程中的岩土、煤炭、土壤,结构工程中的混凝土、石料,以及工业陶瓷等,将这些材料统称为岩土材料。
岩土塑性力学与传统塑性力学的区别在于岩土类材料和金属材料具有不同的力学特性。
岩土类材料是颗粒组成的多相体,而金属材料是人工形成的晶体材料。
正是由于不同的材料特性决定了岩土类材料和金属材料的不同性质。
归纳起来,岩土材料有3点基本特性:1.摩擦特性。
2.多相特性。
3.双强度特性。
另外岩土还有其特殊的力学性质:1.岩土的压硬性,2.岩土材料的等压屈服特性与剪胀性,3.岩土材料的硬化与软化特性。
4.土体的塑性变形依赖于应力路径。
对于岩土类等固体材料往往在受力变形的过程中,产生的弹性及塑性变形具备相应的特点,物体本身的结构以及所加外力的荷载、环境和温度等因素作用,常使得固体物体在变形过程中具备如下的特点。
固体材料弹性变形具有以下特点:(1)弹性变形是可逆的。
物体在变形过程中,外力所做的功以能量(应变能)的形式贮存在物体内,当卸载时,弹性应变能将全部释放出来,物体的变形得以完全恢复; (2)无论材料是处于单向应力状态,还是复杂应力状态,在线弹性变形阶段,应力和应变成线性比例关系;(3)对材料加载或卸载,其应力应变曲线路径相同。
第31 卷第4 期2014 年12 月爆破BLASTINGV o l.31 N o.4D ec.2014d o i:10.3963 /j.i ss n.1001 -487X.2014.04.009空气中TNT 爆炸的数值模拟*胡兆颖,唐德高( 解放军理工大学国防工程学院,南京210007)摘要: 为了研究T N T 炸药爆炸产生的冲击波在空气中的传播规律和预测不同比例距离的超压峰值,应用LS-DYNA有限元软件模拟了7.5 k g T N T 爆炸的冲击波传播过程,揭示其能量衰减规律。
并用2 种经验公式计算不同比例距离的冲击波超压峰值。
对数值模拟结果、经验公式结果和已有的实验数据进行对比。
结果表明: 数值模拟结果与实验数据吻合较好,误差在10% 以内,证明了计算模型和参数的合理性。
2 种经验公式,叶晓华推荐的经验公式与实验数据的误差相对较小,距爆心3.5 m处,误差仅为0.66% 。
说明叶晓华公式相比H e n r yc h 公式更为可靠。
但随着爆距的增大,误差也明显增大。
建议此公式在比例距离小于2.6 m/k g1 /3 时采用。
关键词: 爆炸冲击波; 超压峰值; 有限元; LS-DYNA; 比例距离; 经验公式中图分类号: O625 文献标识码: A 文章编号: 1001 -487X( 2014) 04 -0041 -05Numerical Simulation of TNT Explosion in AirHU Zhao-ying,TANG De-gao( E n g i n ee r i n g I n s tit u t e o f N a ti o n a l D e f e n s e,PL A U n i v o f S c i& T ec h N a n ji n g 210007,C h i n a)A b s t r a c t: T o s t ud y t h e o f s h oc k w ave p r o p aga ti o n b e h av i o r o f T N T ex p l o s i o n i n t h e a i r a nd t o p r e d i c t t h e ove r-p r e ss u r e p ea k i n d iff e r e n t s ca l e d i s t a n ce,t h e fi n it e e l e m e n t s o ft w a r e LS-DYNA w a s u s e d t o s i m u l a t e t h e p r o p aga ti o no f s h oc k w ave b y7.5 k g T N T ex p l o s i o n a nd t o r evea l t h e a tt e nu a ti o n l a w s o f e n e r gy s h oc k w ave.E m p i r i ca l f o r m u l aw a s a l s o u s e d t o ca l c u l a t e t h e p ea k p r e ss u r e i n d iff e r e n t s ca l e d i s t a n ce.B y co m p a r i n g t h e r e s u lt s o f nu m e r i ca l s i m u l a-ti o n a nd e m p i r i ca l f o r m u l a w it h ex p e r i m e n t a l d a t a,t h e r e s u lt s s h o w t h a t t h e s i m u l a ti o n r e s u lt s ag r ee d w e ll w it h ex p e r-i m e n t a l d a t a a nd t h e e rr o r w a s l e ss t h a n 10% .C o m p a r e d w it h t h e ex p e r i m e n t a l d a t a,t h e f o r m u l a pu t f o r w a r d b y Y EX i ao-hu a m a d e a s m a ll e r e rr o r,w h i c h w a s o n l y0.66% 3.5 m e t e rs a w ay f r o m ex p l o s i o n ce n t e r.Re s u lt s h o w s Y E X i-ao-hu a f o r m u l a m o r e r e li a b l e t h a n H e n r yc h f o r m u l a.B u t a s t h e d i s t a n ce i n c r ea s i n g,t h e e rr o r i n c r ea s e do b v i o u s l y.Th e r e f o r e,t h e f o r m u l a co u l d b e a pp li e d w h e n t h e s ca l e d i s t a n ce w a s l e ss t h a n 2.6 m/k g1 /3 .K ey wo r d s: ex p l o s i o n s h oc k w ave;p ea k ove r p r e s s u r e;fi n it e e l e m e n t;LS-DYNA;s ca l e d i s t a n ce;e m p i r i ca lf o r m u l a近年来,由于全球范围内极端势力和分裂势力的盛行,恐怖袭击层出不穷,给人员安全和建筑物造成了重大的损害。
1 John-Cook 材料本构模型)1)(ln 1)((**mnp y T C B A -++=εεσ&式中,pε—— 等效塑性应变;*ε& —— 0.10=ε&s -1的无量纲塑性比,0*εεε&&&p =;*T——相对温度,roommelt roomT T T T T--=*A —— 屈服应力,Pa ;B —— 应变硬化系数,Pa ; n —— 应变硬化指数;C —— 应变率相关系数;m——温度相关系数。
表达式的第一项)(n B A ε+表示对于0.1*=ε&和0*=T (等温状态)时的应力与应变的函数关系;表达式的第二项)ln 1(*ε&C +和第三项)1(*mT -分别表示应变和率温度的影响。
表 Johnson 和Cook 给出的值韩永要《弹道学报》第16卷第2期603钢 7.85 210 0.220 792 180 0.016 0.12 1.0 1520 294(断裂破坏时的)应变]1][ln 1][[*5*421*3T D D e D D D f +++=εεσ其中,D 1、D 2、D 3、D 4、D 5输入参数,*是压力与有效应力之比,eff p σσ/*=。
当破坏参数∑∆=fpD εε达到1时,发生破坏。
* Hirofumi Iyama, Kousei Takahashi, Takeshi Hinata, Shigeru Itoh .Numerical Simulation of Aluminum Alloy Forming Using Underwater Shock Wave .8thInternational LS-DYNA Users ConferenceE/GPaA/MPa B/MPa C n m T melt /K T room /KA70393373430.010.411.002 Steinberg-Guinan 材料本构模型定义材料熔化前的剪切模量i m iE E fE c i e R E E h bpV G G --⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-'--+=300313/10p ——压力,V ——相对体积,Ec ——冷压缩能,Em ——熔化能AR R ρ=',R ——气体常数,A ——原子量 屈服强度ii m iE E fE c i y eR E E h pV b --⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-'--'+'=300313/10σσ如果Em 超过Ei ,[]np i y )(10εγβσσ++'= i γ——初始塑性应变,当0σ'超过m σ,设置0σ'等于m σ。
材料熔化之后,y σ和G 设置为初始值的一半。
$ OFHC 为高导无氧铜,聚能装药药型罩常用材料 *MAT_STEINBERG$ MID R0 G0 SIGO BETA N GAMA SIGM2 8.93 0.477 0.120E-02 36.0 0.450 0.00 0.640E-02 $ B BP H F A TMO GAMO SA2.83 2.83 0.377E-03 0.100E-02 63.5 0.179E+04 2.02 1.50 $ PC SPALL RP FLAG MMN MMX ECO EC1 -9.00 3.00 0.00 0.00 0.00 0.00 0.00 0.00 $ EC2 EC3 EC4 EC5 EC6 EC7 EC8 EC9 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 *EOS_GRUNEISEN$ EOSID C S1 S2 S3 GAMAO A E0 2 0.394 1.49 0.00 0.00 2.02 0.470 0.00 $ V0 1.00M.Katayama, S.Kibe, T.Yamamoto .Numerical and Experimental Study on the Shaped Charge for Space Debris Assessment .Acta Astronauttca Vol.48,No.5-12,pp.363-372,2001maxW.H.Lee, J.W.Painter .Material void-opening computation using particle method .International Journal of Impact Engineering 22(1999)1-22二阶状态方程210221021)()(D C C B B B A A P +++++++=εεμεμμμμμ剪切模量G 与流体应力Y 间的本构关系⎥⎦⎤⎢⎣⎡--⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡-'-++=E x E fE R x E E h P b G G m )(exp 3003)(103/10η⎥⎦⎤⎢⎣⎡--⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡-'-+++=E x E gE R x E E h P qb e Y Y m n )(exp 3003)(1)1(03/10ηβmax 0)1(Y e Y n ≤+β,)('3)()(0x T R x E x E m m +=,α)1()2ex p()(0x ax T x T m m -=31)(20--=a γα,TAD R dx x P x E x '3)()(0-=⎰,ax ax TAD --=0)1()ex p(300γ 00-a3 Mie-Gruneisen 状态方程 定义压缩材料的压力为22332212020)1(1)1(12)21(1⎥⎦⎤⎢⎣⎡+-+---⎥⎦⎤⎢⎣⎡--+=μμμμμμμγμρS S S a C p定义膨胀材料的压力为E a C p )(020μγμρ++=其中:C 为u s -u p 曲线的截距,体积声速S 1、S 2、S 3是u s -u p 曲线斜率的系数,0γ是Gruneisen 常数,1/0-=ρρμ,a 是0γ的一阶体积修正。
(1)Hirofumi Iyama, Kousei Takahashi, Takeshi Hinata, Shigeru Itoh .Numerical Simulation of Aluminum Alloy Forming Using Underwater Shock Wave .8thInternational LS-DYNA Users Conference(2)M. Katayama, S. Kibe, T. Yamamoto .Numerical and Experimental Study on the Shaped Charge for Space Debris Assessment .Acta Astronauttca Vol.48,No.5-12,pp.363-372,2001(3)JingPing Lu, Helen Dorsett, David L. Kennedy .Simulation of Aquarium Tests for PBXW-115(AUST) (4)S. Itoh, H. Hamashima .Determination of JWL Parameters from Underwater Explosion Test (5)Katsuhiko Takahashi, Kenji Murata, Akio Torii, Yukio Kato .Enhancement of Underwater Shock Wave by Metal Confinement4 多线性多项式状态方程 压力由下式定义E C C C C C C C P )(2654332210μμμμμ++++++=其中,1/0-=ρρμ,如果0<μ,则设置022=μC ,026=μC 。
当设置063210=====C C C C C ,154-==γC C 时,就可以用于符合γ律状态方程的气体,其中γ为比热系数。
E P 0)1(ρργ-=5空白材料在仿真计算中,水介质的材料模型可以选用空白材料(NULL),通过此材料来避免计算应力、应变。
在LS-DYNA中为材料模型9。
空白材料模型必须使用状态方程。
6炸药的材料模型在LS-DYNA中,炸药的材料模型一般都选用材料类型8,即MA T_HIGH_EXPLOSIVE_BURN。
需要定义的参数有,密度、爆速与C-J爆轰压力等。
此种材料类型必须与状态方程一块使用。
7 JWL 状态方程炸药爆轰产物的状态方程常采用JWL 方程。
此状态方程通常用于描述高能炸药及爆轰产物,其形式为VEe VR B e VR A p V R V R ϖϖϖ+-+-=--))1()1(2121/g.cm -3(1) Hirofumi Iyama, Kousei Takahashi, Takeshi Hinata, Shigeru Itoh .Numerical Simulation of Aluminum Alloy Forming Using Underwater Shock Wave .8thInternational LS-DYNA Users Conference(2)M.Katayama, S.Kibe, T.Yamamoto .Numerical and Experimental Study on the Shaped Charge for Space Debris Assessment .Acta Astronauttca Vol.48,No.5-12,pp.363-372,2001(3)M.Katayama, S.Kibe .Numerical Study of the Conical Shaped Charge for Space Debris Impact .International Journal of Impact Engineering 26(2001) 357-368(4)Mark Z. Vulitsky, Zvi H. Karni .Ship Structures Subject to High Explosive Detonation .7thInternational LS-DYNA Users Conference(5)金乾坤等.3D Numerical Simulations of Penetration of Oil-Well Perforator into ConcreteTargets .7thInternational LS-DYNA Users Conference(6)W.H.Lee, J.W.Painter .Material void-opening computation using particle method .International Journal of Impact Engineering 22(1999)1-22(7)JingPing Lu, Helen Dorsett, David L.Kennedy .Simulation of Aquarium Tests for PBXW-115(AUST) (8)S. Itoh, H. Hamashima .Determination of JWL Parameters from Underwater Explosion Testb.见LX-10-1炸药的各值,它们是类似的混合炸药James L. O’Daniel, Theodor Krauthammer, Kevin L. Koudela.An UNDEX response validation methodology.International Journal of Impact Engineering 27(2002) 919-937$铝*MAT_JOHNSON_COOK2 2.77 0.2763.37E-03 3.43E-03 0.410 0.100E-01 1.00 0.877E+03 300. 0.100E-050.875E-05 -9.00 3.00 0.00 0.00 0.00 0.00 0.000.00*EOS_GRUNEISEN2 0.5328 1.338 0.00 0.00 2.00 0.00 0.000.00$金属-铜*MAT_JOHNSON_COOK1 8.96 0.478 1.28 0.340000 0.0000000.900E-03 0.292E-02 0.310 0.250E-01 1.09 0.136E+04 294. 0.100E-050.383E-05 -9.00 3.00 0.00 0.00 0.00 0.00 0.000.00*EOS_GRUNEISEN1 0.394 1.49 0.00 0.00 2.02 0.470 0.000.00$炸药*MAT_HIGH_EXPLOSIVE_BURN2 1.7870001 0.8390000 0.3400000 0.0000000 0.0000000 0.0000000 0.0000000*EOS_JWL2 5.8140002 6.8010E-2 4.1000000 1.0000000 0.3500000 0.0900000 1.0000000$空气*MAT_NULL3 1.2250E-3 0.0 17.456E-6 0.0 0.0 0.0 0.0*EOS_LINEAR_POL YNOMIAL3 0.0 0.0 0.0 0.0 0.40 0.4 0.02.5E-6 1.0$水*MAT_NULL4 1.0 -1.00E-4 1E-6 0.0000000 0.0000000 0.0000000 0.0000000*EOS_GRUNEISEN4 .14840 1.7900000 .0000000 .0000000 0.110000 3.0000000 .00000001.0$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$ $ MA TERIAL DEFINITIONS $ $$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$ $*MAT_HIGH_EXPLOSIVE_BURN2 1.7870001 0.8390000 0.3400000 0.0000000 0.0000000 0.0000000 0.0000000*EOS_JWL2 5.8140002 6.8010E-2 4.1000000 1.0000000 0.3500000 0.0900000 1.0000000*INITIAL_DETONA TION2 0.0000000 0.0000000 0.0000000 0.0000000*MAT_NULL1 1.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000$水*MAT_0107 1.000E+00 0.2e-2 0.0 0.000 0.000E-00 2.00*EOS_GRUNEISEN$水$ EOSID C S1 S2 S3 GAMA0 A E06 0.1480 1.79 0 0.0000 1.65 0.0 2.895e-6$ V01.0*EOS_GRUNEISEN$水$ EOSID C S1 S2 S3 GAMA0 A E015 0.1647 1.921 -0.096 0.0000 0.35 0.0 2.895e-6$ V01.0*EOS_GRUNEISEN$水$ EOSID C S1 S2 S3 GAMA0 A E01 0.1480 2.56 -1.986 0.2268 0.50 0.0 2.895e-6$ V01.0$*MAT_JOHNSON_COOK$钨合金9 17.6 1.36 3.50 0.286 0.0000001.806E-02 0.177E-02 0.120 1.600E-02 1.00 1.723E+03 294. 0.100E-050.134E-05 -9.0 2.00 0.00 2.00 0.00 0.00 0.000.00$*EOS_GRUNEISEN$钨合金9 0.399 1.24 0.00 0.00 1.54 0.00 0.000.00$*MAT_PLASTIC_KINEMATIC$树脂8 1.19 0.780E-01 0.000000 0.800E-03 0.00 1.000.00 0.00 2.00$*MAT_PLASTIC_KINEMATIC$钨合金$ mid ro e pr sigy etan beta6 1.862E+01 1.170E+00 0.22 1.790E-02 1.0$ src srp fs0.8$$空气*MAT_NULL4 1.280E-03 0.000E+00 0.000E+00 0.000E+00 0.000E+00*EOS_LINEAR_POL YNOMIAL4 0.000E-00 1.000E-05 0.000E+00 0.000E+00 0.400 0.400 0.000E+00 0.000E+00 0.000E+00$$*MAT_JOHNSON_COOK$铁5 7.83000 0.777.920E-03 5.10E-03 0.260 0.140E-01 1.03 0.1793E+04 294 0.100E-05 0.477E-05 -9.00E+0 3.00 0.0 0.80 0.00 0.00 0.000.00*EOS_GRUNEISEN$铁5 0.4569 1.490 0.00 0.00 2.17 0.46 0.001.00$金属-铜*MAT_JOHNSON_COOK3 8.96 0.478 1.28 0.340000 0.0000000.900E-03 0.292E-02 0.310 0.250E-01 1.09 0.136E+04 294. 0.100E-05 0.383E-05 -9.00 3.00 0.00 0.00 0.00 0.00 0.000.00$金属-铜*EOS_GRUNEISEN3 0.394 1.49 0.00 0.00 2.02 0.470 0.00 0.00$Define Steel 4340*MAT_JOHNSON_COOK1, 7.8400E+00, 0.759E-00, 2.000E+00, 0.320E+00, 0.000E+000.793E-02, 0.510E-02, 2.60E-01, 1.400E-02, 1.030E+00, 1.793E+03, 2.930E+02, 1.000E-05 4.400E-06, 2.000E-02, 2.000E+00, 0.000E+00, 0.80E+00, 2.100E+00, -0.05E+00, 2.000E-03 0.610E+00*EOS_GRUNEISEN1, 4.578E-01, 1.330E+00, 0.000E+00, 0.000E+00, 1.670E+00, 0.430E+00, 0.000E+001.000E+00$ SI unit :cm-g-microsecond$ unit conversion factor$ 1 psi=6895 pa, 1 dyn=1e-5 n,1 bar=1e5 pa,1 g/cm**3=0.0361 lb/in**3,1 lb=0.454kg本参数援引University of Nevada Las Vegas。