湘教版初中数学九年级下《 圆心角、圆周角 》PPT 同课异构课件

探究
量出∠BAC与∠BOC的度数，它们有什么关系？
A
每位同学画一个圆，然后任 意画一个圆周角，以及相应的 圆心角（它所对的弧也是圆周 角所对的弧），量出它们的度 数，看它们之间有什么关系？
O ·
C
B
∠BAC= 1 ∠BOC 2
与同桌或邻近桌的同学交流，猜测一条弧所对的圆周角 与圆心角有什么关系．你能证明这个猜测吗？
情形一 圆周角的一边通过圆心．
∠BAC= 1 ∠BOC 2
A
如图 圆O中，∠BAC的一边AB通过圆心．
由于OA=OC，因此∠C=∠BAC，
O·
C
从而∠BOC=∠C+∠BAC
B
=2∠BAC， 即∠BAC= 1 ∠BOC
2
情形二 圆心在圆心角的内部
如图，圆O在∠BAC的内部．作直径AD，
根据情形一的结果得
∵∠ACD= ∠ ABD ∠ CAB=∠CDB
∴△ACM∽△DBM
C
B M· D
A
O·
•1、书籍是朋友,虽然没有热情,但是非常忠实。2022年3月2日星期三2022/3/22022/3/22022/3/2 •2、科学的灵感，决不是坐等可以等来的。如果说，科学上的发现有什么偶然的机遇的话，那么这种‘偶然的机遇’只能给那些学有素养的人，给那些善于 独立思考的人，给那些具有锲而不舍的人。2022年3月2022/3/22022/3/22022/3/23/2/2022 •3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/3/22022/3/2March 2, 2022 •4、享受阅读快乐，提高生活质量。2022/3/22022/3/22022/3/22022/3/2
1 BOD

A
∵ OA ＝ OC，
∴ ∠C ＝∠BAC，
∴ ∠BOC ＝∠C ＋∠BAC ＝ 2∠BAC，
即∠BAC ＝
1 2
∠BOC．
O
C
B
如何证明一条弧所对的圆周角等于它所对的圆心角的一半？
对于第（2）种情况， 圆心 O 在∠BAC 的内部．
A
作直径 AD， 根据第（1）种情况的结果得
∠BAD
＝
1 2
∠BOD，
3.如图，点 A，B，C 在⊙O 上，AC∥OB．若 ∠OBA = 25°，求∠BOC 的度数.【教材P52页】
解 ∵AC∥OB， ∴∠BAC =∠OBA = 25°. ∵圆形角∠BOC与圆周角∠BAC 所对的弧为B C ， ∴∠BOC = 2∠BAC = 50°
随堂练习
选自《创优作业》
1. 下列结论中,正确的个数有（ B ） ①在同圆或等圆中,同弦所对的弧相等; ②相等的圆周角所对的弧相等; ③圆周角的度数等于它所对弧的度数的一半; ④半圆所对的弦是直径． A. 1 个 B. 2 个 C. 3 个 D. 4 个
A
O
C
B 点击播放
在圆上任取 BC ，画出圆心角∠BOC 和圆周角∠BAC，
圆心与圆周角有几种位置关系？
A A
A
O
C
B
圆周角的一边通过圆心
O
C
B
圆心在圆周角的内部
O
B C
圆心在圆周角的外部
如何证明一条弧所对的圆周角等于它所对的圆心角的一半？
对于第（1）种情况， 圆心 O 在 BAC 的一边 AB 上．
同学们，下课休息十分钟。现在是休
息时间，你们休息一下眼睛，
看看远处，要保护好眼睛哦~站起来 动一动，久坐对身体不好哦~

圆心角、圆周角
圆心角
1.圆的概念是什么？ 圆上任意两点间的部分叫作圆弧，简 称弧。用符号“⌒”表示。
C
·
A B
O
如图圆O上两点A，B间的小于半圆的 部分叫作劣弧，记作：AB
A，B间的大于半圆的部分叫作优弧， 记作：AMB 其中M是圆上一点。 2.圆对称性：
圆是中心对称图形，圆心是它的对称中心。
如图，∠AOB是怎样构成的？ ∠AOB叫作AB所对的圆心角。 AB叫作圆心角∠AOB所对的弧。 两条半径所形成的角叫圆心角。 在生活中，我们常遇到圆心角，如飞镖靶中 有圆心角，还有手表中的时针与分针所成的角也 是圆心角。
A B
D
C
结论：
在同圆或等圆中，如果两个圆心角，两条弧， 两条弦中有一组量相等，那么它们所对应的其余各 组量都分别相等。
1°圆心角
小知识
1°的弧
·
n°的弧
O
n°圆心角
n°的圆心角对着n°的弧， n°的弧对着n°的圆心角。
圆心角的度数与它所对弧的度数相等。
例1.如图，等边△ABC的顶点A，B，C在⊙O上，求 圆心角∠AOB的度数。 A 解：∵△ABC为等边三角形 ∴AB=BC=AC
谢
谢
A'
当∠AOB=∠A'O'B'时，弦AB =
A'B'， AB
= A'B'
3.在同一圆中，∠AOB=∠COD 由旋转不变性得：AB=CD， AB=CD ∠AOB=∠COD AB=CD AB=CD
O ·
D
C
结论：
A B
在同圆中，如果圆心角相等，那么它 们所对的弧相等，所对的弦也相等。
议一议

不成立了，因为一条弦所对的圆周角有两种情况： 优弧上的圆周角和劣弧上的圆周角 .
感悟新知
知2－练
例2 如图 2.2-15， A， B， C， D 是圆上的四个点， ∠ ABD= ∠ DBC．求证：△ ACD 是等腰三角形 .
感悟新知
知2－练
解题秘方：紧扣“同弧所对的圆周角相等”证明 .
证明： ∵ A， B， C， D 是圆上的四个点， ∴∠ ACD= ∠ ABD，∠ DBC= ∠ CAD. 又∵∠ ABD= ∠ DBC，∴∠ ACD= ∠ CAD. ∴△ ACD 是等腰三角形 .
圆 的圆周角
周
定理
角 圆内接四
边形的性质
知3－练
例5 [ 中考·株洲 ]如图 2.2-18， 等边三角形 ABC 的顶点 A 在⊙ O 上，边 AB， AC 与⊙ O 分别交于点 D， E， 点 F 是劣弧 DE 上一点，且与 D， E 不重合，连接 DF， EF，则∠ DFE的度数是( )
A. 50° B. 80° C. 100° D. 130°
2. 推论 2 (1) 直径所对的圆周角是直角； (2)90°的圆周角所对的弦是直径 .
感悟新知
知2－讲
3.“五量关系”定理 在同圆或等圆中，如果两个圆心角、两条弧、两条弧
所对的圆周角、两条弦、两个弦心距中有一组量相等，那 么它们所对应的其余各组量都分别相等 .
感悟新知
知2－讲
特别提醒 “同弧或等弧”若改为“同弦或等弦”结论就
2.2 圆心角、圆周角
第2课时 圆周角
学习目标
1 课时讲解 2 课时流程
圆周角 圆周角定理的推论 圆内接四边形
逐点 导讲练
课堂 小结
作业 提升
感悟新知

学习目标
证明：如图2.2-5，连接OE. ∵ OE=OC，∴∠C= ∠E.
∵ CE∥AB，
∴∠C=∠BOC，∠E=∠AOE. ∴∠BOC=∠AOE.
︵︵ ∴BC = AE .
知2－讲
学习目标
知2－讲
技能提醒: 由例2的结论可知，在同圆中，圆的两条平行弦
所夹的弧相等，以后若遇到圆的两条平行弦，可考 虑运用它们所夹的弧相等证明两条弧所对的弦、圆 心角分别相等.
A. 1
B. 2
C. 3
D. 4
解题秘方：紧扣弧、弦、圆心角之间关系的推论判断.
学习目标
︵︵ 解：∵AB = CD，
∴ AB=CD，故①正确.
︵︵
︵︵
∵AB = CD，∴AC = BD .
∴ AC=BD，∠ AOC= ∠ BOD，故②③④正确.
知3－讲
学习目标
知3－讲
解法提醒： 在同一个圆中， 弧、弦和圆心角中只要有一组
学习目标
知3－讲
拓宽视野: 在同圆或等圆中，两个圆心角、两条弦、两条
弧、两个弦心距中如果有一组量相等，那么它们所 对应的其余各组量也分别相等.
学习目标
知3－讲
︵︵ 例 3 如图2.2-6， 在⊙O中， AB=CD， 则在① AB=CD；
︵︵ ②AC=BD；③∠AOC= ∠BOD；④AC =BD中，正 确的个数是( D )
交，像这样的角叫作圆心角，如图 2.2-1，∠AOB是A︵B所对的圆心角 ︵ ，AB是∠AOB所对的弧. 注意一条 弧所对的圆心角只有一个.
知1－讲
学习目标
特别提醒:
知1－讲
圆心角的条件：
1. 顶点在圆心；
2. 两条边和圆相交.

例2 证明：圆的两条平行弦所夹的弧相等. 已知：如图3-8，圆O中，弦AB与弦CD 平行. ︵ ︵ 求证： AC = BD
图3-8
证明
作直径EF垂直于弦AB， 由于AB∥CD， 因此EF⊥CD. 由于EF⊥AB， ︵ ︵ 因此 AE = BE， 由于EF⊥CD， ︵ ︵ 因此 CE = DE . ︵ ︵ ︵ ︵ 从而 AE -CE = BE - DE ︵ ︵ 即 AC = BD.
E
F 图3-8
练习
1. 如图3-9，圆O中，AB∥CD. 求证：∠AOC=∠BOD. 答 ∵ AB∥CD. ︵ ︵ ∴ AC = BD
（由例题结论得)
∴ ∠AOC=∠BOD.
图3-9
2. 如图3-9，圆O中，AB∥CD. 求证：AC=BD. 答：∵ AB∥CD. ︵ ︵ ∴ AC = BD （由例题结论得） ∴ AC=BD.
A E
●
A E B D
C
O
B D
C
顶点在圆上,并且两边 都与圆相交的角,叫做 圆周角.

类比圆心角探知圆周角


在同圆或等圆中,同弧或等弧所对的圆心角相等.
在同圆或等圆中,同弧或等弧所对的圆周角有什么关系？
为了解决这个问题,我们先探究同弧所对的圆周角 和圆心角之间有的关系.

你会画同弧所对的圆周角和圆心角吗?
图3-9
中考 试题
例1
过⊙O内一点P的最长弦长为10cm，最短弦长 为8cm，那么OP的长为 （ A） A.3cm B.6cm C. 41 cm D. 9cm
解析 如图，过点P 的最长弦为直径AB， 最短弦为CD，且CD⊥AB，则
1 CP= 2CD=4cm，连接OC，则

分析：要证AB ·AC = AE ·AD AC AD AE AB △ADC∽△ABE 或△ACE∽△ADB
B E
A
O DC
1.（兰州·中考）将量角器按如图所示的方式放置在三角 形纸板上，使点C在半圆上．点A，B的读数分别为86°， 30°，则∠ACB的大小为（ ） A.15° B.28° C.29° D.34° 【答案】B
什么？
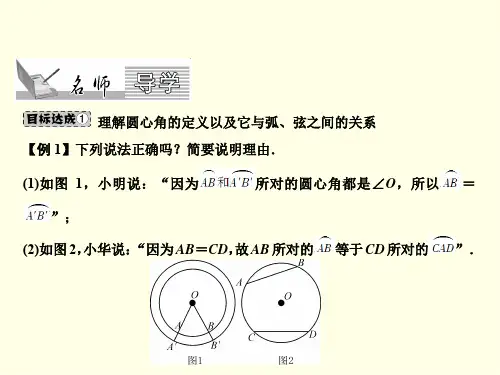
A
A
B
O
C
图(1)
B
●
C
O
图(2) 由此你能得出什么结论?
圆周角定理的推论2
用于构造角
直径（或半圆）所对的圆周角是直角；反之，90°的圆 周角所对的弦是直径.
用于判断某条弦是 否是直径
【例题】
例2.如图,AB是⊙O的直径，BD是弦,延长BD到C,使
DC=BD,AC与AB的大小有什么关系?为什么? A
一、这节课主要学习了两个知识点： 1.圆周角定义. 2.圆周角定理及其定理推论. 二、方法上主要学习了圆周角定理的证明渗透了“特殊 到一般”的思想方法和分类讨论的思想方法. 三、圆周角及圆周角定理及其推论的应用极其广泛，也 是中考的一个重要考点，望同学们灵活运用.
谢谢 观看
A
O
C B
证明：
∠ACB= 1∠AOB 2
∠BAC= 1∠BOC
2
A
∠AOB=2∠BOC
∠ACB=2∠BAC
O
C B
【规律方法】解决圆周角和圆心角的计算和证明问题,要准确
找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理.
当球员在B,D,E处射门 时,他所处的位置对球 门AC分别形成三个张角 ∠ABC, ∠ADC,∠AEC.

圆心角的概念
1．(4 分)如图，AB，CD 为⊙O 的两条直径，弦 DE∥AB，如果∠DOE＝40°，则∠BOC＝( A )
A．110° B．80° C．40° D．70°
2．(4 分)如图，已知⊙O 的半径 OA＝5 cm，弦 CD＝5 cm，则弦 CD 所对的圆心角为__60°__．
圆心角、弦、弧之间的关系
• 9、春去春又回，新桃换旧符。在那桃花盛开的地方，在这醉人芬芳的季节，愿你生活像春天一样阳光，心情像桃花一样美丽，日子像桃子一样甜蜜。 2020/12/162020/12/16Wednesday, December 16, 2020
• 10、人的志向通常和他们的能力成正比例。2020/12/162020/12/162020/12/1612/16/2020 7:07:21 PM • 11、夫学须志也，才须学也，非学无以广才，非志无以成学。2020/12/162020/12/162020/12/16Dec-2016-Dec-20 • 12、越是无能的人，越喜欢挑剔别人的错儿。2020/12/162020/12/162020/12/16Wednesday, December 16, 2020 • 13、志不立，天下无可成之事。2020/12/162020/12/162020/12/162020/12/1612/16/2020
7．(4 分)如图所示，AB，CD，EF 都是⊙O 的直 径，且∠1＝∠2＝∠3，则⊙O 的弦 AC，BE，DF 的大 小关系是__AC＝BE＝DF__．
8．(4 分)一条弦把圆分成 1∶3 两部分，则劣弧所 对的圆心角的度数为__90°__．
9．(8 分)如图所示，点 A，B，C 在⊙O 上，A︵C＝ B︵C，∠C＝30°，求∠A 的度数．

（1）仿第4题得证
（2）∆AOC≌∆BOD ∴∠AOC=∠DBO=60º
∴OC//BD
1.圆是中心对称图形，圆心是它的对称中心。 2.在同圆或等圆中， 如果两个圆心角，两条弧，两条弦中有一组量相等， 那么它们所对应的其余各组都分别相等。 3.圆心角的度数与它所对弧的度数相等。
练 习 巩 固： • 练习第1、2题 作 业 布 置： 习题2.2第1、2题
A
O·
∵CD平分∠ACB，∠ACD= ∠BCD
B
∴AD=BD=
√2 2
AB=5√2cm
D
3.如图，你能设法确定一个圆形纸片的圆心
吗？你有多少种方法？与同学交流一下．
4、在⊙O中，∠CBD=30°,∠BDC=20°,求∠A.
A
∠BAC=∠BDC ∠DAC=∠DBC
∠A=∠BAC+∠DAC =∠BDC+∠DBC =20°+30°=50°
1、如图，点A、B、C、D在同一个圆上，四边形的对
角线把4个内角分成8个角，这些角中哪些是相等的角？
∠2=∠7 ∠1=∠4 ∠3=∠6 ∠5=∠8
D A 1 87
2
2、如图，⊙O直径AB为10cm，弦AC为6cm，
∠ACB的平分线交⊙O于D，求BC、AD、BD
·
3 4
6
5C
B
的长．
C
∵AB是直径，∴ ∠ACB= ∠ADB=90° 在Rt△ABC中，由勾股定理BC=8cm
2、等积式的证明方法；
3、添辅助线的方法。
A O· B
等边三角形，∠DCB=120º
5、如图，已知AB、CD是⊙O的两条直径，
BE是⊙O的一条弦，点C是AE的中点，

B
O.
A C
1、概念的引入和定理的发现：
M O
M O
定义：顶点在圆上，两边都和圆相交的角叫做圆周角。 定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，
都等于该弧所对的圆心角的一半。
2、定理的证明思路：
我们根据圆周角相对于圆心的位置把圆周角分 成三类，先解决一类特殊问题，再把其他两类 转化成特殊问题。
思考: 在同圆或等圆中
相等的圆周角所对的弧 相等吗?
在同圆或等圆中 相等的圆周角所对的弧相等.
A
B
如图,
若
⌒
AC
=
⌒
BD
则 ∠ D=∠A
C
D
∴AB∥CD
例2
如图OA,OB,OC都是⊙O的半径，
已知∠AOB=50°∠BOC=70°求
∠ACB和∠BAC度数
解：∵圆心角∠AOB 与圆周角
∠ACB ⌒AB
。2021年1月12日星期二2021/1/122021/1/122021/1/12
• 15、会当凌绝顶，一览众山小。2021年1月2021/1/122021/1/122021/1/121/12/2021
• 16、如果一个人不知道他要驶向哪头，那么任何风都不是顺风。2021/1/122021/1/12January 12, 2021
B
A
C C
A 图3 D
图4B
3、写出图4中的圆周角：________________________
A
B
E
·
O
C
D
圆周角在我们生活中处处可见，比如，我们从团旗
上的图
案抽象出如图所示图形，图形中就有很多圆周角．
探究
量出∠BAC与∠BOC的度数，它们有什么关系？