最新球体积公式(数学史)讲课稿
- 格式:ppt
- 大小:393.00 KB
- 文档页数:19


人教版六年级数学上册-球体的体积说课稿简介本节课是人教版六年级数学上册的第X单元第X课,主要内容是介绍球体的体积计算方法。
通过本节课的研究,学生将能够理解球体的概念、掌握计算球体体积的方法,并能运用所学知识解决实际问题。
研究目标1. 了解球体的定义和特点;2. 掌握计算球体体积的公式;3. 运用所学知识计算球体的体积。
教学重点1. 球体的定义和特点;2. 如何计算球体的体积。
教学难点1. 运用所学知识解决实际问题。
教学准备1. 教师准备一个球体模型;2. 黑板、彩笔、擦子。
教学过程导入新课1. 教师出示一个球体模型,引导学生观察并提问:“大家知道这是什么几何体吗?”2. 学生回答:“是球体。
”3. 教师继续问:“球体有什么特点?”等待学生回答。
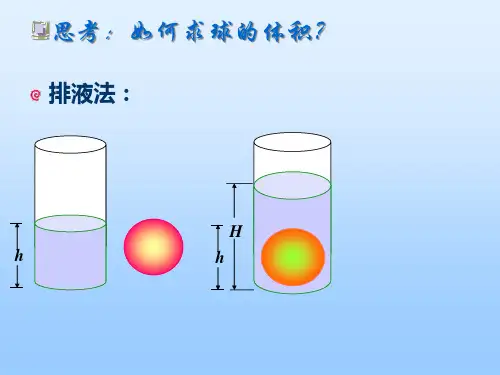
探究球体的体积1. 教师引导学生思考如何计算球体的体积。
2. 教师与学生共同探讨,引导学生找出计算球体体积的方法。
3. 教师板书并解释计算球体体积的公式:$V = \frac{4}{3}\pi r^3$,其中$V$表示体积,$r$表示球体半径。
4. 教师通过几个例子演示如何使用公式计算球体的体积,引导学生进行思考和讨论。
运用所学知识解决实际问题1. 教师设计一些实际问题,要求学生运用所学知识计算球体的体积。
2. 学生独立或小组完成练题,并互相核对答案。
3. 教师给予学生积极的肯定和评价。
总结1. 教师和学生共同总结本节课的研究内容和重点;2. 教师强调掌握计算球体体积的方法,能够运用所学知识解决实际问题。
作业练册上的相关题。
扩展1. 学生可以自行查找更多关于球体的实际应用;2. 学生可以探索其他几何体的体积计算方式。
通过本节课的学习,学生将能够熟练计算球体的体积,并将所学知识应用到实际生活中。
同时,通过探索和扩展,学生能够培养出更好的数学思维能力和解决问题的能力。
希望本节课能够顺利进行,让学生对球体的体积有更深入的理解和掌握。








祖暅原理求球体积公式在咱们的数学世界里,有一个特别厉害的原理叫做祖暅原理。
这祖暅原理啊,可是解决球体积公式的一把神奇钥匙。
咱先来说说祖暅原理到底是啥。
简单来讲,就是两个高度相等的立体,如果在任意等高处的截面面积都相等,那这两个立体的体积就相等。
听起来有点绕是不?咱举个例子。
比如说有两根粗细不一样的柱子,但是从同样的高度去横着切一刀,得到的两个面大小都一样,那这两根柱子的体积就是一样的。
那这祖暅原理和球体积公式有啥关系呢?这就得好好说道说道啦。
咱们可以把球想象成一个特别圆滑的大皮球。
要算出这个大皮球的体积,可不容易。
但是聪明的古人就想到了办法。
假设咱们有一个半球,半径是r 。
然后在半球的旁边放一个圆柱体,圆柱体的底面半径也是 r ,高也是 r 。
接着再在圆柱体上扣掉一个圆锥。
这时候神奇的事情就发生了。
咱们来看看这几个图形在不同高度的截面。
先看半球,在距离球顶高度为 h 的地方,截面是一个圆,这个圆的面积可以通过一些数学知识算出来,是π(r² - h²)。
再看那个组合体,在同样高度 h 的地方,圆柱体的截面是一个半径为 r 的圆,面积是πr²。
圆锥在这个高度的截面也是一个圆,面积是πh²。
所以组合体在这个高度的截面面积就是πr² - πh²,也就是π(r² - h²)。
瞧见没,在任意等高处,半球和这个组合体的截面面积都相等。
根据祖暅原理,它们的体积就相等。
那这个组合体的体积就好算了。
圆柱体的体积是πr²×r = πr³,圆锥的体积是1/3×πr²×r = 1/3πr³。
所以组合体的体积就是πr³ - 1/3πr³ = 2/3πr³。
因为半球的体积和这个组合体的体积相等,所以半球的体积就是2/3πr³,那整个球的体积就是4/3πr³。
体积与体积公式
同学们,我们已经学习了长方体和正方体,也知道了长方体中相交与一点的三条棱的长度分别叫做长方体的长,宽,高。
而正方体是特殊的长方体,正方体中相交与一点的三条棱的长度叫做棱长。
长方体有6个面,相对的两个面向等。
表面积:(长×宽+长×高+宽×高)×2.正方体有6个面,6个面全相等。
表面积:6×边长×边长。
那什么是体积呢?体积又怎么计算呢?下面老师来重点讲一下体积及体积公式。
体积就是物体所占空间的大小。
物体所占空间不同,其体积也不同。
而体积就等于底面积乘以高,用字母表示为v=s h,而长方体和正方体底面的面积就是它们的底面积。
所以它们的体积公式为:
长方体体积=长×宽×高,用字母表示为:v=a·b·h
正方体体积=棱长×棱长×棱长,用字母表示为:v=a·a·a
其中要注意计量体积要用体积单位。
常用的体积单位有立方厘米,立方分米和立方米。
这就是长方体和正方体的体积及体积公式,谢谢大家!。
天眼体积公式范文
首先,我们需要明确球体的定义。
球体是由所有距离一个固定点相等
于半径的点所组成的几何体。
球体具有很多重要的性质和公式,其中包括
体积公式。
球体的体积公式是:V=(4/3)πr³,其中V表示体积,π表示圆周率,r表示球体的半径。
这个公式非常简洁明了,也是很容易理解的。
我们可
以看到,球体的体积与半径的三次方成正比,而与π的比例也是一个常数。
天眼的直径为500米,即半径r=250米(因为r是半径)。
将半径代入球体体积公式中,我们可以得到天眼的体积公式:
V=(4/3)π(250)³
经过计算,我们得到天眼的体积约为523亿立方米。
这是一个非常庞
大的数字,显示出了天眼的巨大规模和令人惊叹的设计。
天眼作为世界上最大的球面射电望远镜,它的体积对应着它的存储和
接收能力,足以收集大量的射电信号,帮助研究人员观测和研究宇宙的奥秘。
由于天眼具有较大的体积,它所能观测的范围也更广阔,能够接收到
更远的射电信号,探测更遥远的宇宙。
通过天眼体积公式,我们可以更好地理解和欣赏天眼的规模和功能。
它的建设和运作无疑是中国在天文学研究方面的一项伟大成就,也是世界
科学技术发展的重要里程碑。
总之,天眼的体积公式是计算球体体积的一种数学公式。
通过该公式,我们可以计算出天眼的巨大体积,进一步认识和理解天眼的规模和功能,
体会到科学研究的伟大力量。
星球体积公式
星球体积公式是一个用来计算星球体积的数学公式。
它被广泛应用于各种领域,如天文学、地质学和物理学等。
这个公式可以帮助我们了解星球的大小和结构,以及它们对我们的生活有何影响。
星球体积公式的基本形式是:
V = (4/3) × π × r³
其中,V表示星球的体积,π是圆周率,r是星球半径。
这个公式的推导是基于几何学原理。
我们知道,球体是一个完全由曲面组成的几何体,其体积可以通过将球体分割成无限小的体积元来计算。
每个体积元的体积可以表示为dV = πr²dh,其中dh是体积元的高度。
通过对所有体积元进行积分,我们可以得到球体的体积公式。
星球体积公式的应用非常广泛。
在天文学中,它通常用于计算行星、卫星和恒星等天体的大小。
例如,我们可以使用这个公式来计算地球的体积,从而了解地球的大小和质量。
在地质学中,这个公式也经常用于计算火山、陨石坑和陨石等天然物体的体积。
此外,在物理学中,星球体积公式也可以应用于计算物体的密度和质量等参数。
当然,这个公式并不完美。
它假设星球是一个完美的球体,而实际
上很少有天体是完全圆形的。
此外,它也没有考虑星球的自转和形变等因素。
因此,在应用这个公式时,我们需要根据实际情况进行适当的修正和调整。
星球体积公式是一个非常有用的数学工具,可以帮助我们了解天体的大小和结构。
虽然它并不完美,但在许多领域仍然被广泛应用。
我们相信,在未来的研究中,这个公式还将发挥更大的作用。