运筹学习题课习题
- 格式:doc
- 大小:147.50 KB
- 文档页数:8

一、回答下面问题(每小题3分)1.在单纯形法计算中,如果不按最小比值规则确定换基变量,则在下一个解中一定会出现。
2. 原问题无界时,其对偶问题,反之,当对偶问题无可行解时,原问题。
3.已知y0为线性规划的对偶问题的最优解,若y0>0,说明在最优生产计划中对应的资源。
4.已知y0为线性规划的对偶问题的最优解,若y0=0,说明在最优生产计划中对应的资源。
5.已知线形规划问题的原问题有无穷多最优解,则其对偶问题的最优解一定是。
6.m个产地n个销地的产销平衡运输问题的模型其决策变量的个数是个;基变量的个数是个;决策变量的系数列向量的特点是。
7.用位势法求解运输问题,位势的含义是;行位势与列位势中有一个的取值是任意的,这是因为。
8.用割平面法求解整数规划,割平面割去了;但未割去。
9.按教材中的符号写出最大流问题的数学模型。
10.什么是截集,何谓最小截集?二、(10分)下表是用单纯形法计算到某一步的表格,已知该线性规划的目标函数值为z=14表1c j x1x2x3x4x3 x12acde11/51σj b-1f g(1)求a—g的值;(8分)(2)表中给出的解是否为最优解。
(2分)三、(每小题6分共12分)车间为全厂生产一种零件,其生产准备费是100元,存贮费是0.05元/天·个,需求量为每天30个,而且要保证供应。
(1)设车间生产所需零件的时间很短(即看成瞬时供应);(2)设车间生产零件的生产率是50个/天。
要求在(1)(2)条件下的最优生产批量Q*,生产间隔期t*和每天的总费用C*。
四、(18分)某公司下属甲、乙两个厂,有A原料360斤,B原料640斤。
甲厂用A、B两种原料生产x1,x2两种产品,乙厂也用A、B两种原料生产x3,x4两种产品。
每种单位产品所消耗各种原料的数量及产值、分配等如下工厂甲分配原料乙分配原料产品x1 x2x3 x4原料AB 8 46 101603305 810 4200310产值(百元) 4 3 3 41.求各厂最优生产计划;(12分)2.问公司能否制定新的资源分配方案使产值更高?(6分)五、(10分)已知有六个村庄,相互间道路的距离如图所示,已知各村庄的小学生数为:A村50人,B村40人,C村40人,D村60人,E村50人,F村90人。
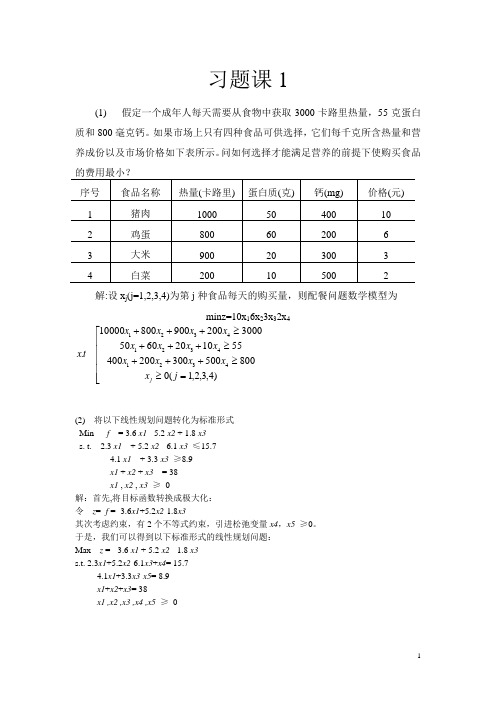
习题课1(1) 假定一个成年人每天需要从食物中获取3000卡路里热量,55克蛋白质和800毫克钙。
如果市场上只有四种食品可供选择,它们每千克所含热量和营养成份以及市场价格如下表所示。
问如何选择才能满足营养的前提下使购买食品解:设x j (j=1,2,3,4)为第j 种食品每天的购买量,则配餐问题数学模型为 minz=10x 16x 23x 32x 4⎢⎢⎢⎢⎢⎣⎡=≥≥+++≥+++≥+++)4,3,2,1(08005003002004005510206050300020090080010000.432143214321j x x x x x x x x x x x x x tx j(2) 将以下线性规划问题转化为标准形式 Min f = 3.6 x1 - 5.2 x2 + 1.8 x3 s. t. 2.3 x1 + 5.2 x2 - 6.1 x3 ≤15.7 4.1 x1 + 3.3 x3 ≥8.9 x1 + x2 + x3 = 38 x1 , x2 , x3 ≥ 0解:首先,将目标函数转换成极大化: 令 z = -f = -3.6x1+5.2x2-1.8x3其次考虑约束,有2个不等式约束,引进松弛变量x4,x5 ≥0。
于是,我们可以得到以下标准形式的线性规划问题: Max z = - 3.6 x1 + 5.2 x2 - 1.8 x3 s.t. 2.3x1+5.2x2-6.1x3+x4= 15.7 4.1x1+3.3x3-x5= 8.9 x1+x2+x3= 38x1 ,x2 ,x3 ,x4 ,x5 ≥ 0(3)用图解法求解下列线性规划问题本例中目标函数与凸多边形的切点是B (2,5),则X *=(2,5)为最优解,m a x Z =20(4) 找出下列线性规划问题的全部基解,基可行解,并找出最优解基本解:X 1=(0,1,4,12,18)’ X 2=(4,0,0,12,6)’ X 3=(6,0,-2,12,0)’ X 4 =(4,3,0,6,0)’ X 5=(0,6,4,0,6)’ X 6=(2,6,2,0,0)’ X 7=((4,6,0,0,-6)’ X 8=(0,9,4,-6,0)’ 其中基本可行解为: X 1, X 2, X 4, X 5 ,X 6 最优解为X *=X 6 =(2,6,2,0,0)’ Z *=36⎪⎪⎩⎪⎪⎨⎧≥≥≤≤+≤++=04155162325max 211212121x x x x x x x x x z ⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤≤++=018236453max 21212121x x x x x x x x z习题课2(1) 用单纯形表求解LP问题Max z = 1500 x1 + 2500 x2s.t. 3 x1 + 2 x2 + x3 = 652 x1 + x2 + x4 = 403 x2 + x5 = 75x1 , x2 , x3 , x4 , x5 ≥0最优解x1 = 5 x2 = 25 x4 = 5(松弛标量,表示B设备有5个机时的剩余)最优值z* = 70000(2)用单纯形法解线性规划问题(唯一解)解:化为标准型列出单纯形表Z*=17/2, X*=(7/2,3/2, 15/2,0,0)’⎪⎪⎩⎪⎪⎨⎧≥=++=++=+++++=-0524261550002max 515214213254321x x x x x x x x x x x x x x z习题课3(1) 用单纯形法求解线性规划问题化成标准形式有加入人工变量则为列出单纯形表 ⎪⎪⎩⎪⎪⎨⎧≥≥≥=+≥-+-≤+++-=000931243max 3213232132131x x x x x x x x x x x x x z ⎪⎪⎩⎪⎪⎨⎧≥=+=--+-=++++++-=-093124003max 5132532143215431x x x x x x x x x x x x x x x z ⎪⎪⎩⎪⎪⎨⎧≥=++=+--+-=+++--+++-=-093124003max 71732653214321765431x x x x x x x x x x x x x Mx Mx x x x x z人工变量已不在基变量中,X*=(0,5/2,3/2,0,0,0,0)’ Z*=3/2注意:(1)在L P 问题的最优解中,人工变量都处在非基变量位置(即取0值),则原问题有最优解,且去掉人工变量后的解为原问题的最优解。


一、选择题1. 2. 3. 4. 5. 6. 7.二、判断题1. 2. 3. 4. 5. 6. 7. 8. 9.三、表上作业法 3. 解:可知,有初始基本可行解1112132122230,10,20,10,35,0x x x x x x ======用闭回路法计算非基变量的检验数:1123(56)(84)10(98)(67)40σσ=+-+=-<=+-+=>因为110σ<,该解并不是最优解。
进行换基迭代,让11x 进基,考虑上述闭回路,调整量min(10,10)10θ==,调整后得到新的调运方案:A2 4 0645945销量10 45 20计算非基变量的检验数得:1223(84)(56)10(95)(47)30σσ=+-+=>=+-+=>故此方案为最优方案,最优解为:11121321222310,0,20,0,45,0x x x x x x ======最优值min 105207456460Z =⨯+⨯+⨯=用电子表格模型求解进行验算:4. 解:用西北角法求得初始基本可行解:1112131421222324313233344,0,0,0;1,2,4,2;0,0,0,4;x x x x x x x x x x x x ============ 用位势法计算检验数:1111212121131322214142233131324323243433333106()210167()861012()9455()12194()731010()47u u v u v v u v u v u u v u v v u v u v v u v u v v u v u v u σσσσσσ=⎧+==-+=⎧⎧⎪=⎪⎪⎪+==-+=⎪⎪⎪=⎪⎪++=-+=⎪⎪⇒=⇒⎨⎨⎨+==-+=-⎪⎪=-⎪⎪+==-+=-=⎪⎪+==-+=⎪⎪⎩=⎩⎪⎪⎪⎪⎪⎩因为3132,σσ小于0,该解不是最优解。

07级工管运筹学期末习题课一、考虑线性规划问题〔P max 0z CXAX bX ==⎧⎨≥⎩(1) 若12,X X 均为〔P 的可行解,[0,1]λ∈,证明12(1)X X λλ+-也是〔P 的可行解;(2) 写出〔P 的对偶模型〔仍用矩阵式表示。
二、有三个线性规划:<Ⅰ> [Min] z =CX <Ⅱ> [Min] z '=C 'X <Ⅲ> [Min] z =CX 约束条件AX =b 约束条件AX =b 约束条件AX =b X ≥0 X ≥0 X ≥0已知X *是<Ⅰ>的最优解,X '*是<Ⅱ>的最优解,X *是<Ⅲ>的最优解,Y *是<Ⅰ>的对偶问题的最优解,试证:〔1()()'-'-≤**C C X X 0; <2> C X X Y b b ()()***-≤-。
三、已知线性规划问题当1t =2t =0时,用单纯形法求得最终表如下:要求:1. 确定23222113*********,,,,,,,,,,a a a a a a b b c c c 的值;2. 当2t =0时,1t 在什么围变化上述最优解不变;3. 当1t =0时,2t 在什么围变化上述最优基不变。
四、某公司准备以甲、乙、丙三种原料生产A 、B 、C 、D 四种型号的产品,每一单位产品对各原料的消耗系数、价格系数及原料成本等已知条件如下表:1x 2x 3x 4x 5x3x 5/20 1/2 1 1/2 0 1x 5/2 1 -1/2 0 -1/6 1/3 j j z c --4-4-21.为解决"在现有原料量限制下,如何安排A、B、C、D四种产品的产量,使总利润〔这里利润简化为销售收入与原料成本之差最大"这一问题,可建立一线性规划模型,令x1、x2、x3、x4依次表示各型号产品的计划产量,试列出这个模型,并记该模型为模型1;2.利用一解线性规划的程序解上述问题〔模型1,得到的部分结果如下:OBJECTIVE FUNCTION V ALUE1> 19923.08V ARIABLEV ALUE REDUCED COSTX1 230.769226 0.000000X2 100.000000 0.000000X3 1238.461548 0.000000X4 0.000000 4.384615ROW SLACK OR SURPLUSDUAL PRICES2> 0.000000 1.3846153> 0.000000 1.2307694> 0.000000 4.000000RANGES IN WHICH THE BASIS IS UNCHANGEDRIGHTHANDSIDERANGESROW CURRENT ALLOWABLE ALLOWABLERHS INCREASEDECREASE2 5500.000000 1499.999878 4025.0000003 3500.000000 500.000000 749.9999394 2000.000000 6192.307617 250.000000根据以上计算结果,分析并回答以下问题:〔1最优生产方案和最大总利润是什么?按此方案生产,现有的原料是否还有剩余?哪一种有剩余?余多少?〔2如果市场上甲原料的价格为4.5〔百元/公斤,那么从市场上购得1000公斤的甲原料扩大生产是否合算〔即总利润是否增加?为什么?〔3若D产品的价格系数增大到34〔百元/公斤,原最优解会否发生变化?为什么?〔4在原考虑的A、B、C、D四种型号产品基础上,如果又提出产品E,它对甲、乙、丙的消耗系数分别为5、6、2,价格系数为74〔百元/公斤,那么原最优方案是否要改变,为什么?〔5若在本题已有已知条件基础上,还要考虑各产品的生产准备费用〔视为固定成本,其中A产品的生产准备费为1000〔百元,B产品的生产准备费为800〔百元,C产品的生产准备费为950〔百元,D产品的生产准备费为750〔百元,而且由于某些原因,A、B、C三种产品至多生产其中的两种。

《运筹学》习题集重点课程建设小组2010.3第一章 线性规划1、将下列线性规划问题化为标准型(1) max Z = 3x 1+ 5x 2- 4x 3+ 2x 4⎪⎪⎩⎪⎪⎨⎧≥=+≥+≤++0x , x , x 9 5x -3x -4x x -13 2x -2x 3x -x 18 3x x -6x 2x s.t.421432143214321 (2) min f = 3x1+ x2+ 4x3+ 2x4 ≤ 1⎪⎪⎩⎪⎪⎨⎧≤≥=++≥+≤+0x 0, x , x 15 2x 3x -4x 2x 7- x -2x 2x -3x 51- 2x - x -3x 2x s.t. 4214214321 43213 (3) min F=x1+x2+x3+x4⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≥+≥+≥+≥+0x ,x ,x ,x 7x x 8x x 6x x 5x x s.t.432143222141 (4) 3213m in x x x F -+=⎪⎪⎩⎪⎪⎨⎧≤≤≥≥0x ,x ,x 4x +5x +x -22x +x -3x +x +x ..32132121321t s2、用图解法求解下列线性规划问题⎪⎪⎩⎪⎪⎨⎧≥≤≤≤+=0x ,x 3 x 122x +3x 6 x -2x ..max )1(211212121t s X X Z⎪⎩⎪⎨⎧≥≥≥++-=0 x ,x 155x -3x 56 7x 4x ..3min )2(21212121t s x x Z3、用单纯形法求解以下线性规划问题⎪⎩⎪⎨⎧≥≤+≤+=0x ,x 5 x x -3 3x -2x ..23max )1(21212121t s x x Z⎪⎩⎪⎨⎧≥≤=++-=0 x ,x ,x 12 x -2x 124x 3x x ..2max )2(3213232132t s x x Z (3) max z = x 1 +2 x 2 +3 x 3(4) max z = 3x 1 + x 2(5) max z = 5x 1 + 2 x 2 + 4 x 34、试用大M 法或两阶段求下述线性规划问题的最优解和最优值(只做一题即可)x 1 + x 2 ≤4-x 1 + x 2 ≤2 6x 1 + 2x 2≤18 x 1 ,x 2 ≥0s.t. x 1 + 2x 2 + 3x 3≤84x 1 + 5x 3≤12 x 1,x 2 ,x 3 ≥0 s.t. 3 x 1 + x 2 + 2 x 3 ≤ 4 6 x 1 + 3 x 2 + 5 x 3 ≤ 10 x 1,x 2,x 3 ≥ 0s.t.(3) max z = 3x 1 – 3 x 2x 1 + x 2 ≥12x 1 + 3x 2 ≤6x 1,x 2 ≥0(4)32122max x x x z +-=s.t.⎪⎪⎩⎪⎪⎨⎧≥≥-≥+-≥++0,,022263213231321x x x x x x x x x x5、写出下列问题的对偶规划(3)s.t.⎪⎩⎪⎨⎧≥≤-+-≥++-+=0,,12222max 32132132121x x x x x x x x x x x Z (4)⎪⎩⎪⎨⎧≥=+-≥+-++-=0,,6242..2min 32121321321x x x x x x x x t s x x x f6、考虑如下线性规划(1)写出对偶规划。
运筹学习题课一、选择题1.用图解法解线性规划时,以下几种情况中不可能出现的是( )。
A. 可行域有界,无有限最优解 B. 可行域无界,有唯一最优解 C. 可行域是空集,无可行解 D. 可行域有界,有多重最优解2.根据线性规划的互补松弛定理,安排生产的产品机会成本一定( )利润. A. 小于B. 等于C. 大于D. 大于等于3.已知某个含10个结点的树图,其中9个结点的次为1,1,3,1,1,1,3,1,3,则另一个结点的次为( )。
A. 3B. 2C. 1D. 以上三种情况均有可能 4.在求解整数规划问题时,不可能出现的是( )。
A. 唯一最优解 B. 无可行解C. 多重最佳解D. 无穷多个最优解5.1m n +-个变量构成一组基变量的充要条件是( )。
A. 1m n +-个变量恰好构成一个闭回路 B. 1m n +-个变量对应的系数列向量线性相关 C. 1m n +-个变量中部分变量构成一个闭回路D.1m n +-个变量不包含任何闭回路6.线性规划具有唯一最优解是指( )。
A. 最优表中存在常数项为零B. 可行解集合有界C. 最优表中存在非基变量的检验数为零D. 最优表中非基变量检验数全部非零 7.有6 个产地4个销地的产销平衡运输问题模型具有特征( )。
A. 有10个变量24个约束 B. 有24个变量10个约束 C. 有24个变量9约束 D. 有9个基变量10个非基变量 8.下列关于网络最大流的说法中,不正确的是( )。
A. 可行流*f 是最大流,当且仅当网络中存在关于*f 的增广链 B. 用标号法求解最大流问题,同时可得到一个最小截集 C. 最小截集的容量的大小影响网络总的输送量的提高 D.网络的最大流需满足容量条件和平衡条件9.如果一个线性规划问题有n 个变量,m 个约束方程()m n <,系数矩阵的行数为m ,则基可行解的个数最为( )。
A.mB.nC.mn CD.nm C10.在一个网络中,如果图形是连通且不含圈的,则这种图形称之为( )。
习 题第二章 线性规划习题2-1 某桥梁工地需集合料3万立方米,集合料含量为:粘土含量不大于0.8%,细沙含量在5%~8%之间,粗沙含量在60%~70%之间,砾石含量在20%~30%之间,现有材料数量及单价如下表所示。
问如何配料才能使集合料的总成本费用最低?(试列出数学模型)。
2—2 将下列线性规划问题化成标准型:① 42154m ax x x x S ++=s.t.⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≥+-≤-+≤+++=+0,,,843104480334304432143432432121x x x x x x x x x x x x x x x② 4321343m in x x x x S --+=s.t.⎪⎪⎪⎩⎪⎪⎪⎨⎧≤≥≤+-≥++=-+≤+0,0,8434040403213242132141x x x x x x x x x x x x x 2—3 用图解法求解下列线性规划问题:2152m ax x x S +=s.t.⎪⎪⎩⎪⎪⎨⎧≥≤+≤≤0,8234212121x x x x x x(答案:19=*S ,()T X 3,2=*。
)2—4 用单纯形法求解下列线性规划问题 ① 321834m in x x x S ++=s.t.⎪⎩⎪⎨⎧≥≥+≤+0,,5223213231x x x x x x x(答案:15=*S ,T X ),0,5,0(=*。
) ② 432132m ax x x x x S -++=s.t. ⎪⎪⎩⎪⎪⎨⎧≥=+++=++=++0,,,1022052153243214321321321x x x x x x x x x x x x x x (答案:15=*S ,T X )0,2/5,2/5,2/5(=*。
)第三章 特殊类型的线性规划习题3-1用表上作业法求解以下运输问题。
3-2某市区交通愿望图有三个始点和三个终点,始点发生的出行交通量a i ,终点吸引的交通量b j 及始终点之间的旅行费用如下所示。
习题:1. 试述LP 模型的要素、组成部分及特征。
判断下述模型是否LP 模型并简述理由。
(式中x ,y 为变量;θ为参数;a,b,c,d,e 为常数。
) (1)max z =2x 1-x 2-3x 3s.t.12312312312135824350,0x x x x x x x x x x x ++=⎧⎪-+≤⎪⎨-+≥⎪⎪≥≤⎩(2)min z =1nk k kx =∏s.t. 1,1,2...,0,1,2...,nik k i k k a x b i m x k m =⎧≥=⎪⎨⎪≥=⎩∑(3)min z =11n ni ijji j a x b y==+∑∑s.t. ,1,2,...,,1,2,...i i j j i i ij x c i m y d j n x y e ⎧≤=⎪≤=⎨⎪+≥⎩(4)max z =1nj jj c x=∑s.t. 1,1,2,...,0,1,2,...nij j i i j ja xb d i m x j n θ=⎧≤+=⎪⎨⎪≥=⎩∑2. 求解下述LP 问题: (1)min w =1234x x x ++s.t. 1231312322410,0,0x x x x x x x x -+=⎧⎪-=⎨⎪≥≥≥⎩ (2)min w = 12323x x x -+s.t. 123123123232234100,0,0x x x x x x x x x -++=⎧⎪++=⎨⎪≥≥≥⎩(3) max z =2.5x 1+x 2s.t. 121212351552100,0x x x x x x +≤⎧⎪+≤⎨⎪≥≥⎩(4) min z =-10x 1-11x 2s.t. 121212123410528220,0x x x x x x x x +≤⎧⎪+≤⎪⎨-≤⎪⎪≥≥⎩3. 用单纯形法求解下述LP 问题:(1)max z = x 1+2x 2+3x 3+4x 4s.t. 123412341,,,0x x x x x x x x +++=⎧⎨≥⎩(2)max z = x 1+x 2+x 3+x 4s.t. 12341234123462,,,0x x x x x x x x x x x x +++=⎧⎪-+-=⎨⎪≥⎩(3)min w = x 2-3x 3+2x 5+2x 6s.t. 23413523562412327438100,1,2,...,6j x x x x x x x x x x x j -++=⎧⎪++=⎪⎨-+++=⎪⎪≥=⎩(4)max z =10 x 1+15x 2+12x 3s.t.12312312312323235226,,0x x x x x x x x x x x x ++≤⎧⎪++≤⎪⎨++≤⎪⎪≥⎩ (5) max w =10 x 1+7x 2+4x 3+3x 4+x 5s.t.12312345123526723482350,1,2,3,4,5j x x x x x x x x x x x x x j ++≤⎧⎪++++≤⎪⎨+++≤⎪⎪≥=⎩4. 试写出下列问题的对偶问题。
(1)max z =4x 1+3x 2+6x 3s.t.123123123123 360 22340 2260,0,0 x x xx x xx x xx x x++≤⎧⎪++≤⎪⎨++≤⎪⎪≥≥≥⎩(2)min w=60x1+10x2+20x3s.t.123123123123321210,0,0 x x xx x xx x xx x x++≥⎧⎪-+≥-⎪⎨+-≥⎪⎪≥≥≥⎩(3)min w=5x1-3x2s.t.123123123123 24221330,0,0 x x xx x xx x xx x x-+≥⎧⎪+-≥⎪⎨--≥⎪⎪≥≥≥⎩(4)max z=4x1+3x2+6x3s.t.1231231232410 253150,0,0 x x xx x xx x x++=⎧⎪++=⎨⎪≥≥≥⎩5. 已知LP问题:min z= 5x1+6x2+3x3s.t.1231231231231231223123 5535020 769307 241510 654510200,0,0 x x xx x xx x xx x xx x xx xx xx x x++≥⎧⎪+-≥⎪⎪+-≥⎪++≥⎪⎨+-≥⎪⎪+≥⎪-≥⎪⎪≥≥≥⎩试通过求解其对偶问题来确定该LP问题的最优解。
6. 用对偶单纯形法求解下述LP问题:(1)min z= x1+x2s.t.1211212245 360,0 x xxx xx x+≥⎧⎪≤⎪⎨+≥⎪⎪≥≥⎩(2) min z = 3x 1+2x 2+x 3s.t. 12313231236430,0,0x x x x x x x x x x ++≤⎧⎪-≥⎪⎨-≥⎪⎪≥≥≥⎩7. 已知LP 问题 max z =-5x 1+5x 2+13x 3 s.t. 12312312332012410900,0,0x x x x x x x x x ++≤⎧⎪++≤⎨⎪≥≥≥⎩试用单纯形法求出最优解,然后分别对下述情况进行灵敏度分析: (1)分别确定参数1122,,c b a 的影响范围。
(2)参数b 1从20变为30。
(3)参数b 2从90变为70。
(4)参数c 3从13变为8。
(5)x 1的系数变为11121205c a a -⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦(6)x 2的系数变为21222625c a a ⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦(7)增加一个约束条件2x 1+3x 2+5x 3≤50 (8)把约束条件2变为10x 1+5x 2+10x 3≤1008. 求解下述运输问题:9. 某厂拟用五台机床加工五种零件,其加工费(元)如下表所示。
若每台机床只加工一种零件则应如何分配任务才能使总加工费最少?10. 五名游泳运动员的四种泳姿的百米最好成绩如下表示。
应从中选哪四个人组成一个4×100米混合泳竭力队?11. 五人翻译五种外文的速度(印刷符号/小时)如下表所示:若规定每人专门负责一个语种的翻译工作,那么,试解答下列问题:(1)应如何指派,使总的翻译效率最高?(2)若甲不懂德文,乙不懂日文,其他数字不变,则应如何指派?(3)若将效益阵中各数字都除以100,然后求解,问最优解有无变化?为什么?12. 某书店希望订购新出版的一部书籍。
据以往经验,新书的销售量可能为50,100,150,或200本。
已知每本新书订购价为4元,零售价6元,剩书的处理价1元。
试分别用乐观准则、悲观准则、折衷准则(α=0.6)和后悔值准则确定该书的订购量。
13. 若上题中书店统计以往这类新书销售量规律如下:试分别用最大可能性准则与EMV准则确定该书的订购量。
14. 某民用电器厂拟生产一种新型家用电器,为使其具有较强的吸引力和竞争力,该厂决定以每件10元的低价出售。
为此已提出三种生产方案:方案Ⅰ需一次性投资10万元,投产后每件产品成本5元;方案Ⅱ需一次性投资16万元,投产后每件产品成本4元;方案Ⅲ需一次性投资25万元,投产后每件产品成本3元。
据市场预测,这种电器的需求量可能为3,12或20万件。
试分别用乐观准则、折衷准则(α=0.8)和后悔值准则进行决策。
15. 若上题中各需求量的概率依次是0.15,0.75,0.10,试分别用最大可能性准则与EMV准则进行决策。
16. 某公司有100万元资金,可投资于A,B,C,D四个项目,但B,C的投资额不能超过60,80万元。
若投资于A,则成功后可获利30%或10%,失败将亏损50%;若投资于B,C,可稳获利20%,12%;若投资于D,则可能盈利30%或10%,也可能亏损10%或20%。
试分别用乐观准则、悲观准则、折衷准则(α=0.6)进行决策。
17. 若上题中投资于A成功的概率为0.8;投资于D盈利30%,10%的概率分别为0.40,0.45;而亏损10%,20%的概率分别是0.10,0.05。
试分别用最大可能性准则与EMV准则进行决策。
18. 拉斯维加斯赌场有一种轮盘赌,其盘上有38个不同的数字。
如果对某个数字下赌,可赢得赌金的35倍,输则赌金全部归赌场老板。
(1)如果某人押1元在某种数字上下赌,写出赌与不赌这两种方案的损益矩阵表;(2)用期望值法进行决策;(3)赌场老板喜欢冒险型顾客还是保守型顾客?(4)赌场老板设置的最大赔率为多少?19. 甲、乙两个企业生产同一种电子产品,两个企业都想通过改革管理获取更多的市场销售份额。
甲企业的策略措施有:(1)降低产品价格;(2)提高产品质量,延长保修年限;(3)推出新产品。
乙企业考虑的策略有:(1)增加广告费用;(2)增设维修网点,扩大维修服务;(3)改进产品性能。
假定市场份额一定,由于各自采取的策略不同,通过预测,今后两个企业的市场占有份额变动情况如下表(正值为甲企业增加的市场占有份额,负值为减少的市场占有份额)。
试通过对策分析,确定两个企业各自的最优策略。
20. A 、B 两家公司的产品竞争性推销,他们各自控制市场的50%。
最近这两家公司都改进了各自的产品,现在都准备发动新的广告宣传。
如果这两家公司都不做广告,那么平分市场的局面将保持不变,但如果有一家公司发动一次强大的广告宣传,那么另一家公司将按比例的失去其一定数量的顾客。
市场调查表面,潜在顾客的50%可通过电视广告争取到,30%可通过报纸,其余20%可通过网络争取到,现在每一家公司的目标是要选择最有利的宣传手段。
(1)把这个问题表达成一个二人有限零和对策,写出局中人A 的赢得矩阵; (2)这个对策有鞍点么?两家公司的最优策略各是什么?21. 三河城由汇合的三条河分割成三个区,如下图。
城市居民40%居住在A 区,30%居住在B 区,30%居住在C 区。
目前,三个区都没有溜冰场,甲、乙两个公司都计划在城中修建溜冰场,公司甲打算修建两个,公司乙打算修建一个。
每个公司都知道,如果在城市的某一个区内设有两个溜冰场,那么这两个溜冰场将把该区的业务平分;如果在一个区内没有修建溜冰场,则该区的业务将平均分散在城市的三个溜冰场中。
每个公司都想把溜冰场设在营业额最多的地方。
(1)把这个问题表述成一个二人有限零和对策,写出公司甲的赢得矩阵。
(2)这个对策有鞍点么?如果有,有几个?甲、乙两个公司的最优策略各B 30%C 30% A 40%是什么?在双方都取得最优策略时,两家公司各占有多大的市场份额?22.某工程队承担一座桥梁的施工任务。
由于施工地区夏季多雨,需停工三个月。
在停工期间该工程队可将机械搬走或留在原处。
如搬走,需搬运费1800元,如留在原处,一种方案是花500元修筑一护堤,防止河水上涨发生高水位的侵袭。