第三章 多元线性回归分析1

简介多元线性回归分析是一种统计技术，用于评估两个或多个自变量与因变量之间的关系。

它被用来解释基于自变量变化的因变量的变化。

这种技术被广泛用于许多领域，包括经济学、金融学、市场营销和社会科学。

在这篇文章中，我们将详细讨论多元线性回归分析。

我们将研究多元线性回归分析的假设，它是如何工作的，以及如何用它来进行预测。

最后，我们将讨论多元线性回归分析的一些限制，以及如何解决这些限制。

多元线性回归分析的假设在进行多元线性回归分析之前，有一些假设必须得到满足，才能使结果有效。

这些假设包括。

1）线性。

自变量和因变量之间的关系必须是线性的。

2）无多重共线性。

自变量之间不应高度相关。

3）无自相关性。

数据集内的连续观测值之间不应该有任何相关性。

4）同质性。

残差的方差应该在自变量的所有数值中保持不变。

5）正态性。

残差应遵循正态分布。

6）误差的独立性。

残差不应相互关联，也不应与数据集中的任何其他变量关联。

7）没有异常值。

数据集中不应有任何可能影响分析结果的异常值。

多重线性回归分析如何工作？多元线性回归分析是基于一个简单的数学方程，描述一个或多个自变量的变化如何影响因变量（Y）的变化。

这个方程被称为"回归方程"，可以写成以下形式。

Y = β0 + β1X1 + β2X2 + ... + βnXn + ε 其中Y是因变量；X1到Xn是自变量；β0到βn是系数；ε是代表没有被任何自变量解释的随机变化的误差项（也被称为"噪音"）。

系数（β0到βn）表示当所有其他因素保持不变时（即当所有其他自变量保持其平均值时），每个自变量对Y的变化有多大贡献。

例如，如果X1的系数为0.5，那么这意味着当所有其他因素保持不变时（即当所有其他独立变量保持其平均值时），X1每增加一单位，Y就会增加0.5单位。

同样，如果X2的系数为-0.3，那么这意味着当所有其他因素保持不变时（即所有其他独立变量保持其平均值时），X2每增加一个单位，Y就会减少0.3个单位。

第三节 多元线性相关与回归分析一、标准的多元线性回归模型上一节介绍的一元线性回归分析所反映的是１个因变量与１个自变量之间的关系。

但是，在现实中，某一现象的变动常受多种现象变动的影响。

例如，消费除了受本期收入水平的影响外，还会受以往消费和收入水平的影响；一个工业企业利润额的大小除了与总产值多少有关外，还与成本、价格等有关。

这就是说，影响因变量的自变量通常不是一个，而是多个。

在许多场合，仅仅考虑单个变量是不够的，还需要就一个因变量与多个自变量的联系来进行考察，才能获得比较满意的结果。

这就产生了测定与分析多因素之间相关关系的问题。

研究在线性相关条件下，两个和两个以上自变量对一个因变量的数量变化关系，称为多元线性回归分析，表现这一数量关系的数学公式，称为多元线性回归模型。

多元线性回归模型是一元线性回归模型的扩展，其基本原理与一元线性回归模型相类似，只是在计算上比较麻烦一些而已。

限于本书的篇幅和程度，本节对于多元回归分析中与一元回归分析相类似的内容，仅给出必要的结论，不作进一步的论证。

只对某些多元回归分析所特有的问题作比较详细的说明。

多元线性回归模型总体回归函数的一般形式如下：t kt k t t u X X Y ++⋯++=βββ221 (7.51)上式假定因变量Y 与(k-1)个自变量之间的回归关系可以用线性函数来近似反映.式中，Y t 是变量Y 的第ｔ个观测值；X jt 是第j 个自变量X j 的第ｔ个观测值(j=1,2,……，k)；u t 是随机误差项；β1，β2，… ，βk 是总体回归系数。

βj 表示在其他自变量保持不变的情况下，自变量X j 变动一个单位所引起的因变量Y 平均变动的数额，因而又叫做偏回归系数。

该式中，总体回归系数是未知的，必须利用有关的样本观测值来进行估计。

假设已给出了ｎ个观测值，同时1ˆβ，2ˆβ…，k βˆ为总体回归系数的估计，则多元线性回归模型的样本回归函数如下：t kt k t t e X X Y ++⋯++=βββˆˆˆ221 (7.52)(t ＝1,2,…,n)式中，e t 是Y t 与其估计t Y ˆ之间的离差，即残差。

一、邹式检验（突变点检验、稳定性检验）1.突变点检验1985—2002年中国家用汽车拥有量（t y ，万辆）与城镇居民家庭人均可支配收入（t x ，元），数据见表。

表 中国家用汽车拥有量（t y ）与城镇居民家庭人均可支配收入（t x ）数据年份 t y （万辆） t x （元）年份 t y （万辆） t x （元）1985 1994 1986 1995 4283 1987 1996 1988 1997 1989 1998 1990 1999 5854 1991 2000 6280 1992 2001 19932002下图是关于t y 和t x 的散点图：从上图可以看出，1996年是一个突变点，当城镇居民家庭人均可支配收入突破元之后，城镇居民家庭购买家用汽车的能力大大提高。

现在用邹突变点检验法检验1996年是不是一个突变点。

：两个字样本（1985—1995年，1996—2002年）相对应的模型回归参数相等HH：备择假设是两个子样本对应的回归参数不等。

1在1985—2002年样本范围内做回归。

在回归结果中作如下步骤(邹氏检验)：1、 Chow 模型稳定性检验（lrtest）用似然比作chow检验，chow检验的零假设：无结构变化，小概率发生结果变化* 估计前阶段模型* 估计后阶段模型* 整个区间上的估计结果保存为All* 用似然比检验检验结构没有发生变化的约束得到结果如下;(如何解释)2.稳定性检验（邹氏稳定性检验）以表为例，在用1985—1999年数据建立的模型基础上，检验当把2000—2002年数据加入样本后，模型的回归参数时候出现显著性变化。

* 用F-test作chow间断点检验检验模型稳定性* chow检验的零假设：无结构变化，小概率发生结果变化* 估计前阶段模型* 估计后阶段模型* 整个区间上的估计结果保存为All* 用F 检验检验结构没有发生变化的约束*计算和显示 F 检验统计量公式，零假设：无结构变化然后 dis f_test 则 得到结果;* F 统计量的临界概率然后 得到结果* F 统计量的临界值然后 得到结果(如何解释)二、似然比（LR ）检验有中国国债发行总量（t DEBT ，亿元）模型如下：0123t t t t t DEBT GDP DEF REPAY u ββββ=++++其中t GDP 表示国内生产总值（百亿元），t DEF 表示年财政赤字额（亿元），t REPAY 表示年还本付息额（亿元）。

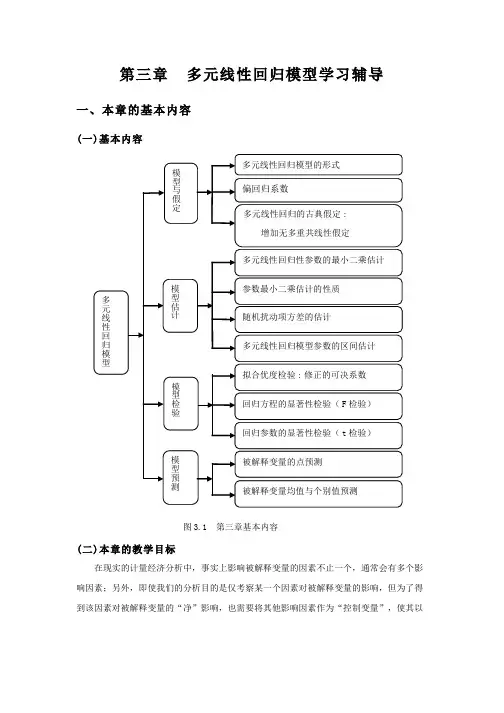
第三章 多元线性回归模型学习辅导一、本章的基本内容(一)基本内容图3.1 第三章基本内容(二)本章的教学目标在现实的计量经济分析中，事实上影响被解释变量的因素不止一个，通常会有多个影响因素；另外，即使我们的分析目的是仅考察某一个因素对被解释变量的影响，但为了得到该因素对被解释变量的“净”影响，也需要将其他影响因素作为“控制变量”，使其以显性形式出现在模型中，以提高模型估计精度。

因此，在对现实经济问题进行计量经济分析时，通常需要建立包含两个及两个以上解释变量的计量模型，此类模型称为多元回归模型。

多元回归模型是在简单回归模型理论基础上的扩展，其建模的理论基础、基本思路、模型估计等与一元回归模型基本一致，只是因解释变量增多，从而带来一些新的内容，比如模型整体显著性检验（F 检验）、修正的可决系数（2R ）以及解释变量之间多重共线性等问题。

本章的教学目标是：深刻理解建立多元回归模型的目的；掌握多元线性回归模型估计、检验的理论与方法；熟练掌握多元线性回归EViews 输出结果的解释。

二、重点与难点分析1.对多元线性回归模型参数意义的理解多元线性回归模型的参数与简单线性回归模型的参数有重要区别。

在多元线性回归模型中，解释变量对应的参数是偏回归系数，表达的是控制其他解释变量不变的条件下，该解释变量的单位变动对被解释变量平均值的“净”影响。

为了更深刻理解偏回归系数，可以两个解释变量的多元线性回归模型为例加以说明1。

例如，被解释变量Y 与解释变量2X 和3X 都有关，如果分别建立模型:多元线性回归: 12233i i i i Y X X u b b b =+++简单线性回归 : 1221i i i Y a a X u =++由于Y 与3X 有关，可以作回归:1332i i i Y b b X u =++，若用OLS 估计其参数，并计算残差213333ˆˆˆi i i i i e Y b b X y b x =--=-，这里的2i e 表示除去3i X 影响后的i Y 。

第三章 多元线性回归模型一、名词解释1、多元线性回归模型：在现实经济活动中往往存在一个变量受到其他多个变量影响的现象，表现在线性回归模型中有多个解释变量，这样的模型被称做多元线性回归模型，多元是指多个解释变量2、调整的可决系数2R ：又叫调整的决定系数，是一个用于描述多个解释变量对被解释变量的联合影响程度的统计量，克服了2R 随解释变量的增加而增大的缺陷，与2R 的关系为2211(1)1n R R n k -=----。

3、偏回归系数：在多元回归模型中，每一个解释变量前的参数即为偏回归系数，它测度了当其他解释变量保持不变时，该变量增加1单位对被解释变量带来的平均影响程度。

4、正规方程组：采用OLS 方法估计线性回归模型时，对残差平方和关于各参数求偏导，并令偏导数为0后得到的方程组，其矩阵形式为ˆX X X Y β''=。

5、方程显著性检验：是针对所有解释变量对被解释变量的联合影响是否显著所作的检验，旨在对模型中被解释变量与解释变量之间的线性关系在总体上是否显著成立作出判断。

二、单项选择题1、C ：F 统计量的意义2、A ：F 统计量的定义3、B ：随机误差项方差的估计值1ˆ22--=∑k n e iσ4、A ：书上P92和P93公式5、C ：A 参看导论部分内容；B 在判断多重共线等问题的时候，很有必要；D 在相同解释变量情况下可以衡量6、C ：书上P99，比较F 统计量和可决系数的公式即可7、A ：书P818、D ：A 截距项可以不管它；B 不考虑beta0；C 相关关系与因果关系的辨析 9、B ：注意！只是在服从基本假设的前提下，统计量才服从相应的分布10、D ：AB 不能简单通过可决系数判断模型好坏，还要考虑样本量、异方差等问题；三、多项选择题1、ACDE ：概念性2、BD ：概念性3、BCD ：总体显著，则至少一个参数不为04、BC ：参考可决系数和F 统计量的公式5、AD ：考虑极端情况，ESS=0，可发现CE 错四、判断题、 1、√2、√3、×4、×：调整的可决系数5、√五、简答题 1、 答：多元线性回归模型与一元线性回归模型的区别表现在如下几个方面：一是解释变量的个数不同；二是模型的经典假设不同，多元线性回归模型比一元线性回归模型多了个“解释变量之间不存在线性相关关系”的假定；三是多元线性回归模型的参数估计式的表达更为复杂。

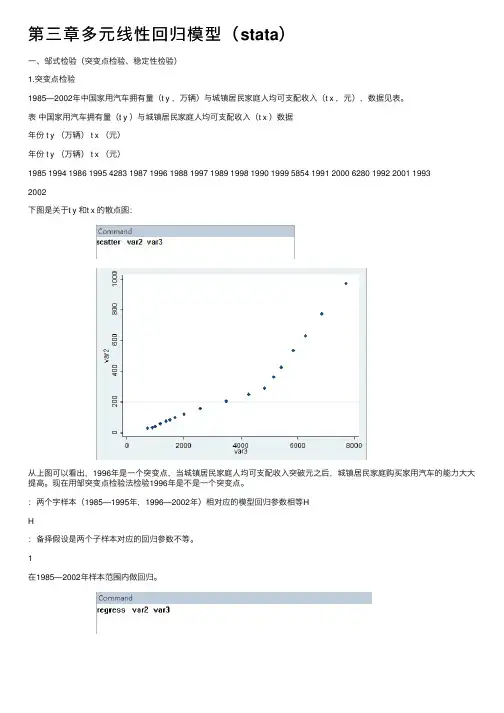
第三章多元线性回归模型（stata）⼀、邹式检验（突变点检验、稳定性检验）1.突变点检验1985—2002年中国家⽤汽车拥有量（t y ，万辆）与城镇居民家庭⼈均可⽀配收⼊（t x ，元），数据见表。

表中国家⽤汽车拥有量（t y ）与城镇居民家庭⼈均可⽀配收⼊（t x ）数据年份 t y （万辆） t x （元）年份 t y （万辆） t x （元）1985 1994 1986 1995 4283 1987 1996 1988 1997 1989 1998 1990 1999 5854 1991 2000 6280 1992 2001 19932002下图是关于t y 和t x 的散点图：从上图可以看出，1996年是⼀个突变点，当城镇居民家庭⼈均可⽀配收⼊突破元之后，城镇居民家庭购买家⽤汽车的能⼒⼤⼤提⾼。

现在⽤邹突变点检验法检验1996年是不是⼀个突变点。

：两个字样本（1985—1995年，1996—2002年）相对应的模型回归参数相等HH：备择假设是两个⼦样本对应的回归参数不等。

1在1985—2002年样本范围内做回归。

在回归结果中作如下步骤(邹⽒检验)：1、 Chow 模型稳定性检验（lrtest）⽤似然⽐作chow检验，chow检验的零假设：⽆结构变化，⼩概率发⽣结果变化* 估计前阶段模型* 估计后阶段模型* 整个区间上的估计结果保存为All* ⽤似然⽐检验检验结构没有发⽣变化的约束得到结果如下;(如何解释)2.稳定性检验（邹⽒稳定性检验）以表为例，在⽤1985—1999年数据建⽴的模型基础上，检验当把2000—2002年数据加⼊样本后，模型的回归参数时候出现显著性变化。

* ⽤F-test作chow间断点检验检验模型稳定性* chow检验的零假设：⽆结构变化，⼩概率发⽣结果变化* 估计前阶段模型* 估计后阶段模型* 整个区间上的估计结果保存为All* ⽤F 检验检验结构没有发⽣变化的约束*计算和显⽰ F 检验统计量公式，零假设：⽆结构变化然后 dis f_test 则得到结果;* F 统计量的临界概率然后得到结果* F 统计量的临界值然后得到结果(如何解释)⼆、似然⽐（LR ）检验有中国国债发⾏总量（t DEBT ，亿元）模型如下：0123t t t t t DEBT GDP DEF REPAY u ββββ=++++其中t GDP 表⽰国内⽣产总值（百亿元），t DEF 表⽰年财政⾚字额（亿元），t REPAY 表⽰年还本付息额（亿元）。