2011年北约数学真题(含解析)

2011年高考数学——北京卷（理科）一．选择题1．已知集合 EMBED Equation.DSMT4 ， EMBED Equation.DSMT4 ．若 EMBED Equation.DSMT4 ，则 EMBED Equation.DSMT4 的取值范围是 （ ）A ． EMBED Equation.DSMT4B ． EMBED Equation.DSMT4C ． EMBED Equation.DSMT4 D ． EMBED Equation.DSMT42．复数 EMBED Equation.DSMT4（ ）A ． EMBED Equation.DSMT4B ． EMBED Equation.DSMT4C ． EMBED Equation.DSMT4 D ． EMBED Equation.DSMT43．在极坐标系中，圆的圆心的极坐标是 （ ） A ． EMBED Equation.DSMT4 B ． EMBED Equation.DSMT4C ． EMBED Equation.DSMT4 D ． EMBED Equation.DSMT44．执行如图所示的程序框图，输出的 EMBED Equation.DSMT4 值为（ ） A ． EMBED Equation.DSMT4 B ． EMBEDEquation.DSMT4 C ． EMBED Equation.DSMT4D ． EMBED Equation.DSMT45．如图， EMBED Equation.DSMT4 ， EMBED Equation.DSMT4， EMBED Equation.DSMT4 分别与圆 EMBED Equation.DSMT4切于点 EMBED Equation.DSMT4 ， EMBED Equation.DSMT4 ， EMBED Equation.DSMT4 ，延长 EMBED Equation.DSMT4与圆 EMBED Equation.DSMT4 交于另一点 EMBEDEquation.DSMT4 ．给出下列三个结论： ① EMBED Equation.DSMT4 ；② EMBED Equation.DSMT4 ；③ EMBED Equation.DSMT4 ． 其中正确结论的序号是 （ ）A ．①②B ．②③C ．①③D ．①②③6．根据统计，一名工人组装第 EMBED Equation.DSMT4 件某产品所用的时间（单位：11s s s -=+0,2i s ==4i <1i i =+s 输出开始结束第4题 CF O EG分钟）为 EMBED Equation.DSMT4（ EMBED Equation.DSMT4 ， EMBEDEquation.DSMT4 为常数），已知工人组装第4件产品用时30分钟，组装第 EMBED Equation.DSMT4 件产品用时15分钟， 那么 EMBED Equation.DSMT4 和 EMBED Equation.DSMT4 的值分别是（ ）A ．75, 25B ．75, 16C ．60, 25D ．60,167．某四面体的三视图如图所示，该四面体四个面的面积中最大的是（ ）A ．8B ． EMBED Equation.DSMT4C ．10D ． EMBED Equation.DSMT48．设 EMBED Equation.DSMT4 ， EMBED Equation.DSMT4 ， EMBED Equation.DSMT4 ， EMBED Equation.DSMT4 （ EMBED Equation.DSMT4 ）．记 EMBED Equation.DSMT4为平行四边形 EMBED Equation.DSMT4 内部（不含边界）的整点的个数，其中整点是指横、纵坐标都是整数的点，则函数 EMBED Equation.DSMT4 的值域为 （ ）A ． EMBED Equation.DSMT4B ． EMBED Equation.DSMT4C ． EMBED Equation.DSMT4 D ． EMBED Equation.DSMT4二．填空题9．在 EMBED Equation.DSMT4 中，若 EMBED Equation.DSMT4 ， EMBED Equation.DSMT4， EMBED Equation.DSMT4 ，则 EMBED Equation.DSMT4_________； EMBED Equation.DSMT4 ________．10．已知向量 EMBED Equation.DSMT4 ， EMBED Equation.DSMT4 ， EMBED Equation.DSMT4 ．若 EMBED Equation.DSMT4 与 EMBED Equation.DSMT4 共线，则 EMBED Equation.DSMT4 ______．11．在等比数列 EMBED Equation.DSMT4 中，若 EMBED Equation.DSMT4 ， EMBED Equation.DSMT4，则公比 EMBED Equation.DSMT4 ； EMBED Equation.DSMT4． 12．用数字2，3组成四位数，且数字2,3 至少都出现一次，这样的四位数共有 个（用数字作答）．13．已知函数 EMBED Equation.DSMT4若关于 EMBED Equation.DSMT4 的方程 EMBED Equation.DSMT4 有两个不同的实根，则实数 EMBED Equation.DSMT4 的取值范围是 ．14．曲线 EMBED Equation.DSMT4 是平面内与两个定点 EMBED Equation.DSMT4 和 EMBED Equation.DSMT4的距离的积等于常数 EMBED Equation.DSMT4 （ EMBED Equation.DSMT4 ）的点的轨迹，给出下列三个结论：①曲线 EMBED Equation.DSMT4 过坐标原点；②曲线 EMBED Equation.DSMT4 关于坐标原点对称；③若点 EMBED Equation.DSMT4 在曲线 EMBED Equation.DSMT4 上，则 EMBED Equation.DSMT4 的面积不大于 EMBED Equation.DSMT4． 其中，所有正确结论的序号是 ．三．解答题15．（13分）已知函数 EMBED Equation.DSMT4．（1）求 EMBED Equation.DSMT4 的最小正周期；（2）求 EMBED Equation.DSMT4 在区间 EMBED Equation.DSMT4上的最大值和最小值．16．（14分）如图，在四棱锥 EMBED Equation.DSMT4 中， EMBED Equation.DSMT4 平面 EMBED Equation.DSMT4 ，底面EMBED Equation.DSMT4 是菱形， EMBED Equation.DSMT4 ， EMBED Equation.DSMT4．（1）求证 EMBED Equation.DSMT4 平面EMBED Equation.DSMT4 ；（2）若 EMBED Equation.DSMT4 ，求 EMBEDEquation.DSMT4 与 EMBED Equation.DSMT4 所成角的余弦值；（3）当平面 EMBED Equation.DSMT4 与平面 EMBED Equation.DSMT4 垂直时，求 EMBEDEquation.DSMT4 的长．17．（13分）以下茎叶图记录了甲、乙两组各四名同学的植树棵数．乙组记录中有一个数据模糊，无法确认，在图中以 EMBED Equation.DSMT4 表示．999X 008甲组乙组 C A B DP（1）如果 EMBED Equation.DSMT4 ，求乙组同学植树棵数的平均数和方差；（2）如果 EMBED Equation.DSMT4 ，分别从甲、乙两组中随机选取一名同学，求这两名同学的植树总棵数 EMBED Equation.DSMT4 的分布列和数学期望．18．（13分）已知函数 EMBED Equation.DSMT4 ．（1）求 EMBED Equation.DSMT4 的单调区间；（2）若对于任意的 EMBED Equation.DSMT4 ，都有 EMBED Equation.DSMT4，求 EMBED Equation.DSMT4 的取值范围．19．（14分）已知椭圆 EMBED Equation.DSMT4，过点 EMBED Equation.DSMT4作圆 EMBED Equation.DSMT4的切线 EMBED Equation.DSMT4 交椭圆 EMBED Equation.DSMT4 于 EMBED Equation.DSMT4 ， EMBED Equation.DSMT4 两点．（1）求椭圆 EMBED Equation.DSMT4 的焦点坐标和离心率；（2）将 EMBED Equation.DSMT4 表示为 EMBED Equation.DSMT4 的函数，并求 EMBED Equation.DSMT4 的最大值．20．（13分）若数列 EMBED Equation.DSMT4 ： EMBED Equation.DSMT4 （ EMBED Equation.DSMT4 ）满足 EMBED Equation.DSMT4（ EMBED Equation.DSMT4 ），则称 EMBED Equation.DSMT4为 EMBED Equation.DSMT4 数列．记 EMBED Equation.DSMT4． （1）写出一个满足 EMBED Equation.DSMT4 ，且 EMBED Equation.DSMT4 的 EMBED Equation.DSMT4 数列 EMBED Equation.DSMT4； （2）若 EMBED Equation.DSMT4， EMBED Equation.DSMT4 ．证明： EMBED Equation.DSMT4 数列 EMBED Equation.DSMT4是递增数列的充要条件是 EMBED Equation.DSMT4； （3）对任意给定的整数 EMBED Equation.DSMT4 （ EMBED Equation.DSMT4），是否存在首项为0的 EMBED Equation.DSMT4 数列 EMBED Equation.DSMT4 ，使得 EMBED Equation.DSMT4?若果存在，写出一个满足条件的 EMBED Equation.DSMT4 数列 EMBED Equation.DSMT4；如果不存在，说明理由．HYPERLINK "/showpic.html" \l"blogid=4dd457800100to0p&url=/orignal/4dd45780t76eca 3d71bb8" \t "_blank" INCLUDEPICTURE"/middle/4dd45780t76eca3d71bb8&690" \*MERGEFORMATINETHYPERLINK "/showpic.html" \l"blogid=4dd457800100to0p&url=/orignal/4dd45780ta53e66861fc5" \t "_blank" INCLUDEPICTURE"/middle/4dd45780ta53e66861fc5&690" \*MERGEFORMATINETHYPERLINK "/showpic.html" \l"blogid=4dd457800100to0p&url=/orignal/4dd45780t76eca 3e4c1a6" \t "_blank" INCLUDEPICTURE"/middle/4dd45780t76eca3e4c1a6&690" \*MERGEFORMATINETHYPERLINK "/showpic.html" \l"blogid=4dd457800100to0p&url=/orignal/4dd45780ta53e672feab7" \t "_blank" INCLUDEPICTURE"/middle/4dd45780ta53e672feab7&690" \*MERGEFORMATINETHYPERLINK "/showpic.html" \l"blogid=4dd457800100to0p&url=/orignal/4dd45780t76ec a3f73edb" \t "_blank" INCLUDEPICTURE"/middle/4dd45780t76eca3f73edb&690" \*MERGEFORMATINETHYPERLINK "/showpic.html" \l"blogid=4dd457800100to0p&url=/orignal/4dd45780ta53e 67c8b2da" \t "_blank" INCLUDEPICTURE"/middle/4dd45780ta53e67c8b2da&690" \* MERGEFORMATINETHYPERLINK "/showpic.html" \l"blogid=4dd457800100to0p&url=/orignal/4dd45780t76ec a400870c" \t "_blank" INCLUDEPICTURE"/middle/4dd45780t76eca400870c&690" \* MERGEFORMATINETHYPERLINK "/showpic.html" \l"blogid=4dd457800100to0p&url=/orignal/4dd45780t76ec a3c042eb" \t "_blank" INCLUDEPICTURE"/middle/4dd45780t76eca3c042eb&690" \* MERGEFORMATINETHYPERLINK "/showpic.html" \l"blogid=4dd457800100to0p&url=/orignal/4dd45780t76ec a3cc5f9e" \t "_blank" INCLUDEPICTURE"/middle/4dd45780t76eca3cc5f9e&690" \* MERGEFORMATINETHYPERLINK "/showpic.html" \l"blogid=4dd457800100to0p&url=/orignal/4dd45780ta53e6 60df7c8" \t "_blank" INCLUDEPICTURE"/middle/4dd45780ta53e660df7c8&690" \* MERGEFORMATINETHYPERLINK "/showpic.html" \l"blogid=4dd457800100to0p&url=/orignal/4dd45780ta53e 64a5792a" \t "_blank" INCLUDEPICTURE"/middle/4dd45780ta53e64a5792a&690" \* MERGEFORMATINET。

2011北约华约自主招生联考笔试试题2011北约华约自主招生联考笔试试题华约试题英语：考题回放：第一项，完型填空，20个空，每空1.5分，共30分；第二项，文章填空，从一篇文章中抽出五个短句，要求考生将抽出的短句填在合适的位置上，每空3分；第三项，将一篇英语短文翻译并概括为200字左右的中文，20分；第四项，翻译，将五个与教育相关的中文句子翻译为英文；第五项，作文，以第四项翻译的内容为背景，请考生谈谈自己的看法。

语文：-《阅读和写作》阅读部分(50分)一、现代文阅读：杨福家的《哥本哈根精神》二、现代文阅读：老舍的《五九》三、古代诗文阅读1.辛弃疾《清平乐校检山园，书所见》2.《南齐书良政》断句3.翻译《论语泰伯》《韩非子外储说右下》4.写作部分(50分)你对忧患意识是怎样认识的？请写一篇文章，谈谈你的思想和认识，角度自选，立意自定，标题自拟；不要编造虚假事实论据，不要套作，不得抄袭。

文科：考题回忆版：1、根据材料论述法国农民与法兰西第三共和国间的关系。

2、北极冰川融化对国际贸易的影响(11分)北极冰川融化对生态环境的影响(10分)。

3、论述题(10分)，给定三段材料，大致内容为：网络在线阅读的弊端在于内容冗杂，使阅读的有效性降低。

它的浏览方式使得读者无法进行更深层次的思考。

网络在线阅读方式的出现所引发的争议在打印机打印取代传统手写等过程中同样有过。

请结合材料分析，人们利用网络在线阅读得到的比失去的要多。

4.阅读材料，回答问题。

材料一“各级领导干部要自觉贯彻群众路线、切实转变作风，多做顺民意、解民忧、得民心的实事，坚决纠正损害群众利益的行为。

”——胡锦涛材料二某地政府官员以破坏了政府办公楼的“风水”为由要强行拆除一座楼房，遭到抵制后说出了“跟政府作对就是恶”的话，在网络上被称为“最雷人官话”之一。

在现实生活中，政府的具体行为并非总是与民众的意愿一致，有时甚至会产生矛盾冲突。

从人民与政府的关系来看，为什么不能说“跟政府作对就是恶”？理科：物理70分，化学30分。

绝密★使用完毕前2011年普通高等学校招生全国统一考试数学（理）（北京卷）本试卷共5页，150分。

考试时间长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第一部分（选择题 共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

（1）已知集合P=｛x ︱x 2≤1｝,M=｛a ｝.若P ∪M=P,则a 的取值范围是（A ）(-∞, -1] （B ）[1, +∞） （C ）[-1，1] （D ）（-∞，-1] ∪[1，+∞） （2）复数212i i-=+（A ）i（B ）-i（C ）（D ）4355i--4355i -+（3）在极坐标系中，圆ρ=-2sin θ的圆心的极坐标系是(A)(B) (C) (1,0)(1,)2π(1,2π-(D)(1，)π（4）执行如图所示的程序框图，输出的s 值为（A ）-3 （B ）-12（C ）13（D ）2（5）如图，AD ，AE ，BC 分别与圆O 切于点D ，E ，F ，延长AF 与圆O 交于另一点G 。

给出下列三个结论：AD+AE=AB+BC+CA ；○1回归往日精品，再现今日辉煌AF·AG=AD·AE○2③△AFB ～△ADG 其中正确结论的序号是（A ）①② （B ）②③ （C ）①③ （D ）①②③（6）根据统计，一名工作组装第4件某产品所用的时间（单位：分钟）为（A ，C 为常数）。

已知工人组装第4件产品用时30分钟，组装第A 件产品用时15分钟，那么C 和A 的值分别是（A ）75，25 （B ）75，16 （C ）60，25 （D ）60，16 (7)某四面体的三视图如图所示，该四面体四个面的面积中，最大的是(A) 8 (B) (C)10 (D) （8）设,，,.记为平行四边形()0,0A ()4,0B ()4,4C t +()(),4D t t R ∈()N t ABCD 内部（不含边界）的整点的个数，其中整点是指横、纵坐标都是整数的点，则函数的值域为()N t（A ） （B ） {}9,10,11{}9,10,12（C ） （D ） {}9,11,12{}10,11,12第二部分 （非选择题 共110分）二、填空题共6小题，每小题5分，共30分。

2011年北大等13校联考数学试卷（文科做1-5题，理科做3-7题）参考思路：1、可以用余弦定理：先利用已知三边求出平行四边形一角的余弦值，则另一角的余弦值可知（互为相反数），再求未知对角线；也可以利用解几中的重要结论：平行四边形的两对角线平方和等于四边平方和（不过要先建立坐标系证明该结论）。

2、最容易想到的方法自然是联立两抛物线方程，解出交点坐标，用两点式或点斜式表示……好吧，我承认这样做有点难算，不过其实也不算太难啦（最后化简结果似乎是不含根式的）。

当然，也可以先设直线方程Y=kX+b，与两抛物线分别联立，再对比所得交点的系数，从而得解（我的一位同学就是这样做的）。

3、常规题。

先求公差，再求通项，再求前n项和，最后利用二次函数的性质解之（注意n 为正整数），或利用an《=0且a（n+1）>=0解之（n和n+1下标）。

4、可以考虑反证法；不然就用余弦定理表示出cosC，把式子分子中的a、b利用原题中的不等式换成c，再用基本不等式，中间经过若干步转换，最后化简为cosC》=0.5，于是得证。

第4题解答：6.最绝的方法：假设存在四个正实数满足题目，不妨按大小排列并计为A,B,C,D(A>B>C>D>0), 则：AB*CD*AC*BD*AD*CB=（ABCD）（ABCD）（ABCD）=2*3*5*6*10*16=28800 因为：27*27*27〈28800〈32*32*32所以：ABCD的值小于32，但是AB=16，CD=2，ABCD=32故不存在四个正实数满足题目。

方法1假设存在四个正实数满足题目，不妨按大小排列并计为A,B,C,D(A>B>C>D>0), 则两两乘积分别为:AB,AC,AD,BC,BD,CD,因为:A>B>C>D>0,所以AB>AC>AD,AB>AC>BC,AD>BD>CD,BC>BD>CD,所以:AB>AC>AD>BC>BD>CD或者AB>AC>BC>AD>BD>CD,所以:AB=16,AC=10,BD=3,CD=2,所以:AB+AC/BD+CD=A/D=16+10/3+2=26/5,所以:AB-AC/BD-CD=A/D=16-10/3-2=6,因为6不等于26/5，所以不存在4个正实数满足题设.从以上解析来看，需要假设4个正实数存，注意到乘积的大小，构造等式AB+AC/BD+CD=AB-AC/BD-CD即可以简单解题。

（ⅰ）若 C 与 C1 ， C2 都外切，则 CC1 r1 r ， CC2 r2 r ，所以 CC1 CC2 r1 r2 ； 若 C 与 C1 ， C2 都内切，则 CC1 r r1 ， CC2 r r2 ，所以 CC2 CC1 r1 r2 ； 所以 CC2 CC1 r1 r2 C1C2 ，由双曲线的定义， C 的圆心的轨迹是以 C1 ， C2 为焦点、实轴长为 （ⅱ）若 C 与 C1 内切， C2 外切，则 CC1 r r1 ， CC2 r2 r ， r1 r2 的双曲线； 所以 CC2 CC1 r1 r2 ；若 C 与 C1 外切， C2 内切，则 CC1 r r1 ， CC2 r r2 ， 所以 CC1 CC2 r1 r2 ；所以 CC2 CC1 r1 r2 C1C2 ，由双曲线的定义， C 的圆心的轨迹是以
值为何？ 解 由 a7 a3 4d 可得公差 d 4 , 从而 a1 21 . 令 21 4( x 1) 0 得 x 6.25 , 故 {an } 从第 7 项开 始为正, 所以 {S n } 的最小项为 S6 66 . 4. 在 ABC 中， a b 2c ，求证： C 60 . 证 根据正弦定理有 sin A sin B 2sin C , 从而有
2011 年北约等十三校联考自主招生数学试卷 厦门一中徐小平
1. 已知平行四边形的其中两条边长为 3 和 5，一条对角线长为 6，求另一条对角线长. 解一 (引理) 平行四边形的对角线平方和等于四边的平方和. 另一对角线长为
2(32 52 ) 62 4 2 . C B 解二 如图, 设 AB 3 , AD 5 , BD 6 , 则据余弦定理有 2 2 2 2 AB AD cos A AB AD BD 2 , 于是 AC 2 DC 2 AD 2 2 DC AD cos CDA D A 32 52 2 AB AD cos A 32 , 从而 AC 4 2 . 2 2 2. 求过抛物线 y 2 x 2 x 1 和 y 5 x 2 x 3 的交点的直线方程. 解 由上述两方程消去二次项可得 6 x 7 y 1 0 , 此即为过两抛物线交点的直线方程. 3. 在等差数列 {an } 中， a3 13, a7 3 ，数列 {an } 的前 n 项和为 S n ，求数列 {S n } 的最小项，并指出其

2011年普通高等学校招生全国统一考试(北京卷)数学(文)本试卷共5页，150分.考试时间长120分钟.考生务必将答案答在答题卡上，在试卷上作答无效.考试结束后，将本试卷和答题卡一并交回.第一部分(选择题共40分)一、选择题共8小题，每小题5分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.1.已知全集U=R,集合P={x︱x2≤1｝,那么A.(-∞, -1] B.[1, +∞)C.[-1，1]D.(-∞，-1] ∪[1，+∞)2.复数 A.i B.-i C. D.3.如果那么A.iB.-iC.D.3.如果那么A.y< x<1B.x< y<1C.1< x <yD.1<y<X4.若p是真命题，q是假命题，则A.p∧q是真命题B.p∨q是假命题C.﹁p是真命题D.﹁q是真命题5.某四棱锥的三视图如图所示，该四棱锥的表面积是A.32B.16+16C.48D.16+326.执行如图所示的程序框图，若输入A的值为2，则输入的P值为A.2B.3C.4D.57.某车间分批生产某种产品，每批的生产准备费用为800元.若每批生产x件，则平均仓储时间为天，且每件产品每天的仓储费用为1元.为使平均没见产品的生产准备费用与仓储费用之和最小，每批应生产产品A.60件B.80件C.100件D.120件8.已知点A(0,2)，B(2,0).若点C在函数y = x的图像上，则使得ΔABC的面积为2的点C 的个数为A.4B.3C.2D.1二、填空题共6小题，每小题5分，共30分.9.在中.若b=5，，sinA=，则a=___________________.10.已知双曲线( >0)的一条渐近线的方程为，则= .11.已知向量a=( ，1)，b=(0，-1)，c=(k，).若a-2b与c共线，则k=________________.12.在等比数列{an}中，a1= ，a4=4，则公比q=______________;a1+a2+…+an= _________________.13.已知函数若关于x 的方程f(x)=k有两个不同的实根，则实数k的取值范围是_______14.设A(0,0),B(4,0),C(t+4,3)，D(t,3)(t R).记N(t)为平行四边形ABCD内部(不含边界)的整点的个数，其中整点是指横、纵坐标都是整数的点，则N(0)= N(t)的所有可能取值为三、解答题6小题，共80分，解答应写出文字说明，演算步骤或证明过程.15.(本小题共13分)已知函数.(Ⅰ)求的最小正周期：(Ⅱ)求在区间上的最大值和最小值.16.(本小题共13分)以下茎叶图记录了甲、乙两组各四名同学的植树棵树.乙组记录中有一个数据模糊，无法确认，在图中以X表示.(1)如果X=8，求乙组同学植树棵树的平均数和方差;(2)如果X=9，分别从甲、乙两组中随机选取一名同学，求这两名同学的植树总棵数为19的概率.(注：方差其中为的平均数)17.(本小题共14分)如图，在四面体PABC中，PC⊥AB，PA⊥BC,点D,E,F,G分别是棱AP,AC,BC,PB的中点.(Ⅰ)求证：DE∥平面BCP;(Ⅱ)求证：四边形DEFG为矩形;(Ⅲ)是否存在点Q，到四面体PABC六条棱的中点的距离相等?说明理由.18.(本小题共13分)已知函数.(Ⅰ)求的单调区间;(Ⅱ)求在区间[0,1]上的最小值.19.(本小题共14分)已知椭圆的离心率为，右焦点为(,0)，斜率为I 的直线与椭圆G交与A、B两点，以AB为底边作等腰三角形，顶点为P(-3,2).(I)求椭圆G的方程;(II)求的面积.20.(本小题共13分)若数列满足，则称为数列，记.(Ⅰ)写出一个E数列A5满足;则称为数列，记(Ⅰ)写出一个E数列A5满足;(Ⅱ)若，n=2000，证明：E数列是递增数列的充要条件是=2011;(Ⅲ)在的E数列中，求使得=0成立得n的最小值.参考答案一、选择题(共8小题，每小题5分，共40分)(1)D (2)A (3)D (4)D(5)B (6)C (7)B (8)A二、填空题(共6小题，每小题5分，共30分)(9) (10)2(11)1 (12)2 (13)(0，1) (14)6 6，7，8，三、解答题(共6小题，共80分)(15)(共13分)解：(Ⅰ)因为所以的最小正周期为(Ⅱ)因为于是，当时，取得最大值2;当取得最小值—1.(16)(共13分)解(1)当X=8时，由茎叶图可知，乙组同学的植树棵数是：8，8，9，10，所以平均数为方差为(Ⅱ)记甲组四名同学为A1，A2，A3，A4，他们植树的棵数依次为9，9，11，11;乙组四名同学为B1，B2，B3，B4，他们植树的棵数依次为9，8，9，10，分别从甲、乙两组中随机选取一名同学，所有可能的结果有16个，它们是：(A1，B1)，(A1，B2)，(A1，B3)，(A1，B4)，(A2，B1)，(A2，B2)，(A2，B3)，(A2，B4)，(A3，B1)，(A2，B2)，(A3，B3)，(A1，B4)，(A4，B1)，(A4，B2)，(A4，B3)，(A4，B4)，用C表示：“选出的两名同学的植树总棵数为19”这一事件，则C中的结果有4个，它们是：(A1，B4)，(A2，B4)，(A3，B2)，(A4，B2)，故所求概率为(17)(共14分)证明：(Ⅰ)因为D，E分别为AP，AC的中点，所以DE//PC。

Ａ ２１； Ｂ ２０； Ｃ １９； Ｄ １８ ４．解法 １ 根 据ａ＋ｂ≥２ｃ，并 运 用 正 弦 定 理 得 ｓｉｎ Ａ＋ｓｉｎ Ｂ≥２ｓｉｎ Ｃ，则
４ｓｉｎ２Ｃｃｏｓ２Ｃ ＝２ｓｉｎ Ｃ≤ｓｉｎ Ａ＋ｓｉｎ Ｂ＝
的方程．
｛ｙ＝２ｘ２ －２ｘ－１，
解法 ２ 联 立 方 程 组
消去 ｙ＝－５ｘ２ ＋２ｘ＋３．
２ ０１１×｜ｘ－２ ０１１１｜＝｜ｘ－１｜＋（｜ｘ－２１｜＋｜ｘ－２１｜）＋
（｜ｘ－３１｜＋｜ｘ－３１｜＋｜ｘ－３１｜）＋ … ＋
（｜ｘ－２ ０１１１｜＋｜ｘ－２ ０１１１｜＋ … ＋｜ｘ－２ ０１１１｜）＝
（｜ｘ－１｜＋｜ｘ－２０１ １１｜）＋（｜ｘ－２１｜＋｜ｘ－２ ０１１１｜）＋
（｜ｘ－２１｜＋｜ｘ－２ ０１１１｜）＋（｜ｘ－３１｜＋｜ｘ－２ ０１１１｜）＋
其２ 个交点为Ａ（ｘ１ ，ｙ１ ）、Ｂ（ｘ２ ，ｙ２ ）．代入点 Ａ 的坐
标
得
烄ｙ１ 烅 烆ｙ１
＝２ｘ１２ －２ｘ１ －１， ＝－５ｘ２１ ＋２ｘ１ ＋３．
① ②
①×５＋②×２ 得 ７ｙ１ ＝－６ｘ１ ＋１，即 ６ｘ１ ＋７ｙ１ －１
＝０．同理得 ６ｘ２ ＋７ｙ２ －１＝０．
所以，两交点 Ａ、Ｂ 都在直线６ｘ＋７ｙ－１＝０ 上，
（｜ｘ－３１｜＋｜ｘ－２ ０１１１｜）＋ …
（※）
其中共有（１＋２＋３＋ … ＋２ ０１１）÷２＝５０３×２ ０１１
解法２ 设等差数列｛ａｎ｝的公差为ｄ，则３＝ａ７ ＝ ａ３ ＋４ｄ＝－１３＋４ｄ，解得ｄ＝４＞０，则通项
ａｎ＝ａ３ ＋（ｎ－３）ｄ＝４ｎ－２５． 令 ａｎ ＝４ｎ－２５＜０，得 正 整 数 ｎ≤６，则
ａ１ ＜ａ２ ＜…＜ａ５ ＜ａ６ ＜０＜ａ７ ＜…， Ｓ１ ＞Ｓ２ ＞…＞Ｓ５ ＞Ｓ６ ＜Ｓ７ ＜Ｓ８ ＜…． 所以，数列Ｓ１ ，Ｓ２ ，…中的第 ６ 项最小，最小值为

2011年普通高等学校招生全国统一考试数学（文）（北京卷） 本试卷共5页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第一部分（选择题 共40分）一、 选择题共8小题，每小题5分，共40分。

在每小题列出四个选项中，选出符合题目要求的一项。

（1） 已知全集U=R ，集合{}21P x x =∣≤，那么U P =ð(A)(,1-∞-) (B)(1,+∞) (C)（-1，1) (D)()()11-∞,-,+∞（2）复数212i i-=+ (A)i (B )i - (C)4355i -- (D)4355i -+ （3）如果1122log log 0x y <<，那么（A ）1y x << (B)1x y << (C)1x y << (D)1y x <<（4）若p 是真命题，q 是假命题，则（A ）p q ∧是真命题 (B)p q ∨是假命题题 (C)p ⌝是真命题 (D)q ⌝是真命（5）某四棱锥的三视图如图所示，该四棱锥的表面积是 (A)32(B)16+(C)48(D)16+（6）执行如图所示的程序框图，若输入A 的值为2，则输出的P 值为(A)2(B)3(C)4(D)5（7）某车间分批生产某种产品，每批的生产准备费用为800元。

若每批生产x 件，则平均仓储时间为8x 天，且每件产品每天的仓储费用为1元。

为使平均到每件产品的生产准备费用与仓储费用之和最小，每批应生产产品（A ）60件 (B)80件 （C ）100件 （D ）120件（8）已知点()()0,2,2,0A B 。

若点C 在函数2y x =的图象上，则使得ABC 的面积为2的点C 的个数为（A ）4 (B)3 (C)2 (D)1第二部分（非选择题 共110分）二、填空题共6小题，每小题5分，共30分。

（9）在ABC 中，若15,,sin 43b B A π=∠==，则a = . （10）已知双曲线2221(0)y x b b-=>的一条渐近线的方程为2y x =，则b = .（11）已知向量),(01),(a b c k ==-=2a b -与c ，共线，则k = .（12）在等比数列{}n a 中，若141,4,2a a ==则公比q = ； 12n a a a ++⋯+= .数 若关于x 的方程()f x k = 有两个不同的实（13）已知函根，则实数k 的取值范围是 . （14）设(0,0),(4,0),(4,3),(,3)(A B C t D t t +∈R )。

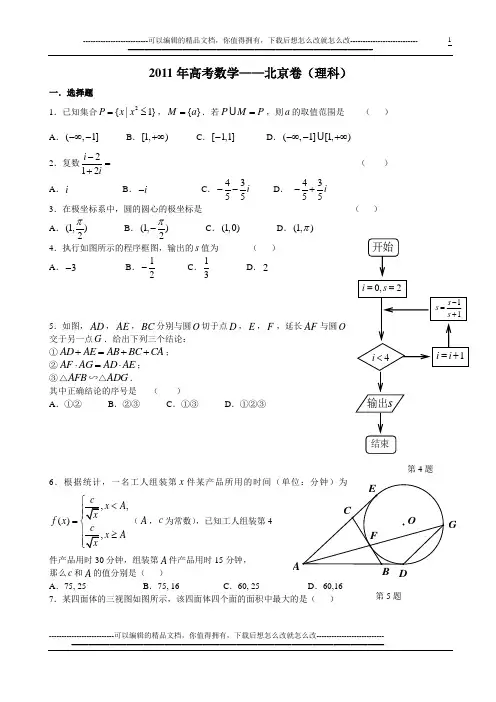
2011年高考数学——北京卷（理科）一．选择题1．已知集合2{|1}P x x =≤，{}M a =．若PM P =，则a 的取值范围是 （ ）A ．(,1]-∞-B ．[1,)+∞C ．[1,1]-D ．(,1][1,)-∞-+∞2．复数212i i-=+ （ ） A ．i B ．i - C ．4355i -- D ． 4355i -+3．在极坐标系中，圆的圆心的极坐标是 （ ）A ．(1,)2π B ．(1,)2π- C ．(1,0) D ．(1,)π4．执行如图所示的程序框图，输出的s 值为 （ ）A ．3-B ．12- C ．13 D ．25．如图，AD ，AE ，BC 分别与圆O 切于点D ，E ，F ，延长AF 与圆O 交于另一点G ．给出下列三个结论： ①AD AE AB BC CA +=++； ②AF AG AD AE ⋅=⋅； ③AFB ADG △△∽．其中正确结论的序号是 （ ）A ．①②B ．②③C ．①③D ．①②③6．根据统计，一名工人组装第x 件某产品所用的时间（单位：分钟）为,,(),cx A xf x cx A x⎧<⎪⎪=⎨⎪≥⎪⎩（A ，c 为常数），已知工人组装第4件产品用时30分钟，组装第A 件产品用时15分钟，那么c 和A 的值分别是（ ）A ．75, 25B ．75, 16C ．60, 25D ．60,16 7．某四面体的三视图如图所示，该四面体四个面的面积中最大的是（ ）11s s s -=+0,2i s ==4i <1i i =+s输出开始结束第4题CB F AODEG第5题A ．8B ．62C ．10D ．82俯视图侧（左）视图正（主）视图3448．设(0,0)A ，(4,0)B ，(4,4)C t +，(,4)D t （t R ∈）．记()N t 为平行四边形ABCD 内部（不含边界）的整点的个数，其中整点是指横、纵坐标都是整数的点，则函数()N t 的值域为 （ ） A ．{9,10,11} B ．{9,10,12} C ．{9,11,12} D ．{10,11,12}二．填空题9．在ABC △中，若5b =，4B π∠=，tan 2A =，则sin A =_________；a =________．10．已知向量(3,1)a =，(0,1)b =-，(,3)c k =．若2a b -与c 共线，则k =______． 11．在等比数列{}n a 中，若112a =，44a =-，则公比q = ；12||||||n a a a +++= ．12．用数字2，3组成四位数，且数字2,3 至少都出现一次，这样的四位数共有 个（用数字作答）．13．已知函数32, 2,()(1), 2.x f x x x x ⎧≥⎪=⎨⎪-<⎩若关于x 的方程()f x k =有两个不同的实根，则实数k 的取值范围是 ．14．曲线C 是平面内与两个定点1(1,0)F -和2(1,0)F 的距离的积等于常数2a （1a >）的点的轨迹，给出下列三个结论：①曲线C 过坐标原点；②曲线C 关于坐标原点对称；③若点P 在曲线C 上，则12F PF △的面积不大于212a ． 其中，所有正确结论的序号是 ．三．解答题15．（13分）已知函数()4cos sin()16f x x x π=+-．（1）求()f x 的最小正周期； （2）求()f x 在区间[,]64ππ-上的最大值和最小值．16．（14分）如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，底面ABCD 是菱形，2AB =，60BAD ∠=．（1）求证BD ⊥平面PAC ；（2）若PA AB =，求PB 与AC 所成角的余弦值； （3）当平面PBC 与平面PDC 垂直时，求PA 的长．17．（13分）以下茎叶图记录了甲、乙两组各四名同学的植树棵数．乙组记录中有一个数据模糊，无法确认，在图中以X 表示．（1）如果8X =，求乙组同学植树棵数的平均数和方差；（2）如果9X =，分别从甲、乙两组中随机选取一名同学，求这两名同学的植树总棵数Y 的分布列和数999X 008111甲组 乙组 C A B D P学期望．18．（13分）已知函数2()()x kf x x k e =-． （1）求()f x 的单调区间；（2）若对于任意的(0,)x ∈+∞，都有1()f x e≤，求k 的取值范围．19．（14分）已知椭圆22:14x G y +=，过点(,0)m 作圆221x y +=的切线l 交椭圆G 于A ，B 两点． （1）求椭圆G 的焦点坐标和离心率；（2）将||AB 表示为m 的函数，并求||AB 的最大值．20．（13分）若数列n A ：12,,,n a a a （2n ≥）满足1||1k k a a +-=（1,2,,1k n =-），则称n A 为E 数列．记12()n n S A a a a =+++．（1）写出一个满足150a a ==，且5()0S A >的E 数列5A ；（2）若112a =，2000n =．证明：E 数列n A 是递增数列的充要条件是2011n a =；（3）对任意给定的整数n （2n ≥），是否存在首项为0的E 数列n A ，使得()0n S A =?若果存在，写出一个满足条件的E 数列n A ；如果不存在，说明理由．--------------------------可以编辑的精品文档，你值得拥有，下载后想怎么改就怎么改--------------------------- ==========================================================--------------------------可以编辑的精品文档，你值得拥有，下载后想怎么改就怎么改--------------------------- ==========================================================================11。

2011 年普通高等学校招生全国统一考试 数学（文）（北京卷）
本试卷共 5 页，150 分。考试时长 120 分钟。考生务必将答案答在答题卡上，在试卷上作答无 效。考试结束后，将本试卷和答题卡一并交回。
第一部分（选择题 共 40 分）
一、选择题共 8 小题，每小题 5 分，共 40 分。在每小题列出四个选项中，选出符合题目要求的一项。
55
(D) 4 3 i 55
【解析】： i 2 1 2i
(i 2)(1 2i) (1 2i)(1 2i)
i 2i2 2 4i 1 4i2
i 2(1) 2 1 4(1)
4i
i
，选
A。
（3）如果 log 1 x log 1 y 0 ，那么 (
2
2
（A） y x 1 (B) x y 1
（6）执行如图所示的程序框图，若输入 A 的值为 2，则输出的 P 值为( )
(A)2
(B)3 (C)4 (D)5
【答案】C
第 1页 （共 7页）
【解析】执行三次循环，S 1 A 2 成立， p 11 2 ，S 1 1 1 1 3 ，S 3 A 2
P 22
2
成立， p 2 1 3 ， S 3 1 3 1 11 ， S 11 A 2 成立， p 3 1 4
y
2x ，则 b
.
【答案】2
第 2页 （共 7页）
【解析】：由
x2
y2 b2
1得渐近线的方程为 x2
y2 b2
0y
bx
即
y
bx ，由一条渐近线的方程
为 y 2x 得b 2
（11）已知向量 a ( 3,1),b (0 1), c (k, 3) 。若 a 2b 与 c ，共线，则 k =

【解析】由通解公式得
y edx ( ex cos x edxdx C)
ex ( cos xdx C)
ex (sin x C) ．
由于 y(0) 0, 故 C =0．所以 y ex sin x ．
(11)【解析】选取 x 为参数，则弧微元 ds 1 y2 dx 1 tan2 xdx sec xdx
x0
xa
ax x0
a1
ax a x0
a1 x0
所以 3 a 0 即 a 3 ．
又因为 0 lim x
x ln(1 t2 )dt
0
xa
ln(1 x2 )
lim
x
axa1
2x
lim
x
1 x2 a(a 1)x
a2
2 a(a 1)
x3a
lim
x
1
x2
所以 3 a 2 ，即 a 1，综合得1 a 3 ．
(15) (本题满分 10 分)
【解析】如果 a 0 时， lim
x ln(1 t2 )dt
0
lim xa
x ln(1 t2 )dt ，
x
xa
x
0
显然与已知矛盾，故 a 0 ．
当 a 0 时，又因为 lim
x ln(1 t2 )dt
0
lim
ln(1
x2 )
lim
x2
lim 1 x3a 0 ．
g(x) f2xy, yg(x) yg(x) f12[xy, yg(x)] x f22[xy, yg(x)]g(x)．
因为 g(x) 在 x 1 可导，且为极值,所以 g(1) 0 ，则
d2z dxdy
|x1
y 1

5
答案： 1、 不妨设角 ADC 为 a,那么角 ABC=π-a。 由余弦定理可得 AC=根号（9+16-24cosa)=根号(1+4+4cosa) 从而可解出 cosa=5/7.即有 sina=2(根号 6)/7. 代入 cosa=5/7,可得 AC=根号（55/7). 所以圆的半径就是 AC/2sina. 2、设 13=a1+md,25=a1+nd,41=a1+kd. 那么我们可得 a1+(m+499(k+m-2n))d=2009. 而实际上这道题是有漏洞的，因为 (m+499(k+m-2n))可能是负的，也就是当这是递减的等差数列的时候，那么 2009 就不在这个 数列中了。 3、 挺简单，设 a=tanx+（根 3）,b=cotx+(根号 3）,假设均为有理数。 那么由(a-（根号 3） ） （b-（根号 3） ）=1 可得（a+b）根号 3=ab+2.若 a+b 非零，除过来就矛盾了。 所以必有 a+b=0，此时 ab+2 也是 0. 显然与 a，b 是有理数矛盾。 4、b=0 的时候可知得有|a|≤1.,此时 a+b≤1.下面考虑 b 不等于 0 的情况。 代入+1 和-1 后得出的式子可以化成|a|≤b+1.....(1)（必有 b≥-1) 对称轴的位置是 x=-a/4b.当对称轴在[-1,1]外的时候 那么 1≤|-a/4b|≤(b+1)/4|b|. 分类讨论后就可以得出 b≤1/3.此时 a+b≤b+1+b≤5/3. 若对称轴在[-1,1]内，则可得 a^2≤8（b-b^2)......(2) 这里注意到(b+1)^2-8(b-b^2)=(3b-1)^2≥0.故只需要(2)式成立,就必有 (1)式也成立。此时用柯西不等式 (a+b-1/2)^2≤（a^2+8(b-1/2)^2)(1+1/8)≤9/4 那么就有了 a+b≤2.等号成立的充要条件是 a=4/3,b=2/3,易验证这是成立的. 比较三种情况，显然 2 是 a+b 的最大值， 5、设优秀有 a 人，及格 b 人，不及格 c 人。 则 a+b+c=333 ① 6a+4b+0c≤1000（这里都取各层次里的最少人，故用小于等于） 即 6a+4b≤1000 即 3a+2b≤500 由①得 2a+2b=666-2c 即 a+666-2c≤500 即 a+166≤2c 若 a≥167 则这 167 人至少共解出 167*6=1002 道题，矛盾 故 a≤166 故 a+166≤166+166≤2c 即 c≥166 所以 c≥166≥a 即不及格得人数大于等于优秀的人数

2011年北京大学研究生入学考试数学分析试题解答SCIbird说明：印象中根据当初论坛上的讨论，北大2011年试题的回忆版与原题多少有些出入，这里根据自己的理解来确定试题。

因为对试卷回忆版第5题搞不清楚，所以略去此题。

其它试题解答，比较基础的试题就写得相对简略一些，难一些的试题就写得详细一些。

试题后的评注是个人对试题的看法。

1. 用确界存在定理证明，如果函数()f x 是区间I 上的连续函数，则()f I 是一个区间。

证明：为证明()f I 是一个区间，实际上只需要证明连续函数具有价值性质即可。

不妨只考虑()()f a f b <情形，其它情况同理。

任取实数c ，满足()()f a c f b <<下面利用确定存在定理证明(,)a b ξ∃∈，使得()f c ξ=. 所用方法非常经典，读者最好熟记此方法。

记集合[,]:{()}S t f a b t c ∈=<，因为()f a c <，所以a S ∈，因此如此定义的集合非空。

由确界存在定理知，上确界sup S ξ=存在且。

由()f x 连续函数，所以()f c ξ≤且a b ξ<<. 下证()f c ξ=：采用反证法。

假设()f c ξ<，因为ξ是内点，所以由连续函数的局部保号性可知存在ξ的一个邻域(,)[,]U a b ξδξδ=−+⊂，使得在U 上满足()f x c <，特别地12()f c ξδ+<，这与sup S ξ=是上确界的定义矛盾！所以()f c ξ=.评注：上面的证明是标准的，读者应该熟练掌握“连续函数取上确界”这种技巧，2009年北大数学分析压轴题的证明方法也取上确界。

印象中北大考研的数学分析试题必有一道试题涉及实数系那几个基本定理的等价性证明或者应用，属于送分题，但前提是你认真准备过。

实数系基本定理有好几个，但在解题或科研中，最常用的是确界存在原理和闭区间套定理。

特别在处理涉及连续函数的1维问题时，确界存在原理往往起到奇兵作用。

2011年北约自主招生联考试题语文：题型包括10道选择题、文言文理解和翻译、现代文阅读、作文等。

10道选择题：辨别字型，主要考察学生的基本功，要求学生选择正确的词语填空，选项主要是让学生区分错别字，比如到底是“果腹”还是“裹腹”；文言文，周密的关于歌舞升平的文章；另一篇韩非子关于国家法律的文章。

一篇古文翻译，但翻译之前，必须自己先断句。

现代文阅读，为一篇散文，主要内容为人与自然。

阅读分析，题为《我们失去了与自然交流的语言》的文章，读完回答问题，最后一题关于环境开发与保护的看法。

古文阅读，韩非子的文章，讨论治国之道，为官清廉、严明法纪的文章，没有断句，要求学生添加句读且翻译；另有一篇宋朝周密的文章。

作文，根据“无尽的远方和无数的人们”作文，要求700-800字，文体不限。

数学：无选择题，题型包括7道解答题，考到的知识点包括三角函数、解析几何等。

前五道文科题较简单，后五道理科题相对难一些。

英语：题型包括选择题、阅读理解题、填空题、改错题。

选择题30道。

阅读理解共4篇文章，每篇文章5个选择题。

30个填空题，前10道是从15个词中选10个填空，中间10道是自己填词，后10道是改错。

完形填空，有首字母和没有首字母的各有一道完形填空；考试中没有翻译，共4篇阅读文章，涉及人文社科学和自然科学，其中还有一篇科技论文，关于科研决策时用到大脑的哪一部分；最后一题为改错题，10句话中，每句都有一个错误，包括拼写、时态、定冠词等错误。

据悉，考生的笔试成绩可在两至三周后在“中国综合性大学自主选拔录取联合考试报名平台”上查询。

政治：材料分析题：根据钱学森的“沙理论”———利用日光、沙漠、生物、植物，将沙漠变为绿洲，创造财富，拉动当地经济发展。

请据此分析“沙理论”蕴含的哲学道理；“沙理论”带动了经济、社会、生物环境的三赢，请分析其中的原因。

历史：8个名词解释：辛丑条约、亚里士多德、楚辞、斯诺、启蒙运动等。

论述题：谈谈中国长城与大运河对中国历史的意义。

2011北约自主招生数学题及解答∎1、已知平行四边形的其中两条边长分别是3和5，一条对角线长是6，求另一条对角线的长。

解：由对角线的平方和等于四边的平方和：所以36+x2=2(9+25)，x2=32，∴x=42。

∎2求过抛物线y=2x2-2x-1，y=-5x2+2x+3交点的直线方程。

解：y=2x2-2x-1y=-5x2+2x+3，5y=10x2-10x-52y=-10x2+4x+6，7y=-6x+1，∴6x+7y-1=0为所求。

∎3、等差数列a1,a2,⋯满足a3=-13，a7=3，这个数列的前n项和为Sn，数列S1,S2,⋯中哪一项最小，并求出这个最小值。

解：d=a7-a37-3=164=4，∴a1=-21，Sn=2n2-23n，当n=234，即n=6时Sn最小，最小为-66。

∎4、∆ABC的三边a,b,c满足a+b≥2c，A,B,C为∆ABC的内角，求证：C≤60°。

解：ab≤(a+b2)2，cosC=a2+b2-c22ab=(a+b)2-2ab-c22ab≥(a+b)2-c2(a+b)22-1=1-2c2(a+b)2≥1-2c24c2=1 2，所以C≤60°。

∎ 5、是否存在四个正实数，它们的两两乘积分别是2,3,5,6,10,16？解：设存在四个正实数分别为a<b<c<d，依题意：ab=2，ac=3，ad=5，bc=6，bd=10，cd=16，∴a2bc=6，∴a=1，b=2，c=3，d=5，而cd=15≠16，故不存在。

或解：∵abcd=32，而(abcd)3=1800×16，不满足，故不存在。

∎6、C1和C2是平面上两个不重合的固定圆，C是该平面上的一个动圆，C和C1，C2都相切，则C的圆心的轨迹是何种曲线？说明理由。

解：设两定圆⊙C1，⊙C2的半径分别为r1,r2，动圆C的半径为R。

⑴当r1=r2①⊙C1与⊙C2相交时a).⊙C与它两都外切，轨迹是线段C1C2的垂直平分线去掉两圆的公共弦；b).⊙C与它两都内切，轨迹是线段C1C2的垂直平分线；c).⊙C与两圆一个内切，一个外切时，|CC1|=r1-R，|CC2|=r2+R，|CC1|+|CC2|=r1+r2，轨迹是以C1、C2为焦点的椭圆。

2011年北约自主招生数学试题1、已知平行四边形两边长分别是3和5，一条对角线是6．求另一条对角线的长度．2、求过抛物线22221,523y x x y x x =--=-++两交点的直线方程．3、等差数列1237,,13, 3..n a a a a n S ⋅⋅⋅=-=满足这个数列的前项和为数列12,⋅⋅⋅S S 中哪一项最小？并求出这个最小值．4、在2,60.ABC a b c C ∆+≥∠≤中，如果证明5、是否存在四个正实数，它们两两乘积分别是2，3，5，6，10，16．6、设12C C 和是平面上两个不重合的固定圆周．设C 是该平面上的一个动圆，它与12C C 和均相 切．问：C 的圆心轨迹是何种曲线？证明你的结论．7、求12120111.x x x -+-+⋅⋅⋅+-的最小值2【参考答案】1、解答：设平行四边形为ABCD ，且6,3,5===AC BC AB ，易得：51cos -=∠ABC ，所以151cos =∠BAC ，24,321515322592==⨯⨯⨯-+=BD BD ． 2、解答：设两条抛物线额交点为),(),,(2211y x B y x A ，联立两条抛物线的方程⎩⎨⎧++-=--=32512222x x y x x y ，消去2x 得：167+-=x y ，B A ,两点的坐标均满足这个方程，所以直线AB 的方程为0176=-+y x ．3、解答：方法一：因为公差4437=-=a a d ，所以03,01,21761>=<-=-=a a a ，所以6S 最小，最小值666-=S ； 方法二：8234232322222-⎪⎭⎫ ⎝⎛-=-=n n n S n ，当6=n 时，n S 的最小值为666-=S ． 4、解答：方法一、在ABC ∆中，由余弦定理得： 21848233222cos 22222222=≥-+=⎪⎭⎫ ⎝⎛+-+≥-+=ab ab ab ab b a ab b a b a ab c b a C ，因为函数x y cos =在),0(π上单调递减，所以3π≤C ． 方法二、依题意得：2cos 2sin 42cos 2sin 2sin 2sin sin B A B A B A B A C B A ++≥-+⇔≥+， 212cos ≤+B A ，因为函数x y cos =在),0(π上单调递减，所以33232πππ≤⇒≥+⇒≥+C B A B A ． 5、解答：假设存在满足题意的四个正实数d c b a ,,,，且假定d c b a <<<<0，依题意得：16,10,3,2====cd bd ac ab ，由前两个式子得32=c b ，由后两个式子得85=c b ，矛盾，所以不存在满足题意的四个数．6、解答：设⊙1C 的半径为1r ，⊙2C 的半径为2r ，⊙C 的半径为r ，且假定21r r ≥．（1）当21r r =时，①若⊙1C 与⊙2C 外离，当⊙C 与⊙1C 、⊙2C 均外切或均内切时，点C 的轨迹是21C C 的中垂线；当⊙C 与⊙1C 、⊙2C 一个外切一个内切时，点C 的轨迹是以21,C C 为焦点，实轴长为21r r +的双曲线； ②若⊙1C 与⊙2C 外切，当⊙C 与⊙1C 、⊙2C 均外切或均内切时，点C 的轨迹是21C C 的中垂线（除去21C C 的中点）；当⊙C 与⊙1C 、⊙2C 一个外切一个内切时，点C 的轨迹是直线21C C （除去21C C 的中点）； ③若⊙1C 与⊙2C 相交，此时⊙C 必与⊙1C 、⊙2C 均外切或均内切，点C 的轨迹是两圆公共弦在圆外部分的两条射线．（2）当21r r >时，①若⊙1C 与⊙2C 外离，当⊙C 与⊙1C 、⊙2C 均外切或均内切时，点C 的轨迹是以21,C C 为焦点，实轴长为21r r -的双曲线；当⊙C 与⊙1C 、⊙2C 一个外切一个内切时，点C 的轨迹是以21,C C 为焦点，实轴长为21r r +的双曲线；②若⊙1C 与⊙2C 外切，当⊙C 与⊙1C 、⊙2C 均外切或均内切时，点C 的轨迹是以21,C C 为焦点，实轴长为21r r -的双曲线（除去⊙1C 与⊙2C 的切点）；当⊙C 与⊙1C 、⊙2C 一个外切一个内切时，点C 的轨迹是直线21C C （除去点21,C C 及⊙1C 与⊙2C 的切点这三个点）；③若⊙1C 与⊙2C 相交，当⊙C 与⊙1C 、⊙2C 均外切或均内切时，点C 的轨迹是以21,C C 为焦点，实轴长为21r r -的双曲线（除去⊙1C 与⊙2C 的两个交点）；当⊙C 与⊙1C 、⊙2C 一个外切一个内切时，点C 的轨迹是以21,C C 为焦点，长轴长为21r r +的椭圆（除去⊙1C 与⊙2C 的两个交点）；④若⊙1C 与⊙2C 内切，当⊙C 与⊙1C 、⊙2C 均外切或均内切时，点C 的轨迹是直线21C C （除去⊙1C 与⊙2C 的切点）；当⊙C 与⊙1C 、⊙2C 一个外切一个内切时，点C 的轨迹是以21,C C 为焦点，长轴长为21r r +的椭圆（除去⊙1C 与⊙2C 的两个切点）；⑤若⊙1C 内含⊙2C ，且不同心，当⊙C 与⊙1C 内切、与⊙2C 外切时，点C 的轨迹是以21,C C 为焦点，长轴长为21r r +的椭圆；当⊙C 与⊙1C 、⊙2C 均内切时，点C 的轨迹是以21,C C 为焦点，长轴长为21r r -的椭圆；⑥若⊙1C 内含⊙2C ，且同心，当⊙C 与⊙1C 内切、与⊙2C 外切时，点C 的轨迹是以1C 为圆心，半径为221r r +的圆；当⊙C 与⊙1C 、⊙2C 均内切时，点C 的轨迹是以1C 为圆心，半径为221r r -的圆． 7、解答：首先设12n a a a ≤≤≤，12()||||||n f x x a x a x a =-+-++-．由绝对值的最高理论知， n 为奇数时，当12n x a +=时，()f x 有最小值；n 为偶数时，当122,n n x a a +⎡⎤∈⎢⎥⎣⎦任何值时，()f x 有最小值． 于是分解之，20111111111()|1|||||||||||||||2233320112011f x x x x x x x x x =-+-+-+-+-+-++-++-个， 共有： 201220111+2+2011==20230662⨯个断点（包括多重）． 设123456111,,,23a a a a a a ======202306612011a =． 因为202306610115332=． 现在求1011533a 和1011534a 的值．设10115331a t =，则121011533t +++≥， 1211011533t +++-<．可得1422t =．且1011533101153411422a a ==，故11422x =时，()f x 的值最小．111111491()112114221423120111832.142214221422142214231422711f =-+-⨯++-⨯+⨯-++⨯-=。

2011 自主招生试题1.语文：第一题是10道选词填空题，考的是不同词汇之间的辨析，比如端倪和端睨，果腹和裹腹等等，难度较低。

第二道题是古文题题目很短：州郡遇圣节锡宴，率命猥妓数十群舞于庭，作“天下太平”字，殊为不经。

而唐《乐府杂录》云：“舞有字，以舞人亚身于地，布成字也。

”王建《宫词》云：“罗衫叶叶绣重重，金凤银鹅各一丛。

每遇舞头分两向，太平万岁字当中。

”则此事由来久矣。

让说明是什么社会现象并联系实际谈谈看法。

感觉应该是从表面太平这种虚假政绩来谈论，为了政绩而粉饰太平的现象。

第三道题是古文翻译，没有短句而且异常的长，是韩非子中的一段话：古者先王尽力于亲民，加事于明法。

彼法明，则忠臣劝；罚必，则邪臣止。

忠劝邪止而地广主尊者，秦是也；群臣朋党比周以隐正道行私曲而地削主卑者，山东是也。

乱弱者亡，人之性也；治强者王，古之道也。

越王勾践恃大朋之龟与吴战而不胜，身臣入宦于吴；反国弃龟，明法亲民以报吴，则夫差为擒。

故恃鬼神者慢于法，恃诸侯者危其国。

第四道是阅读：我们失去了和自然交流的语言不久前我在鄯善迪坎儿村，见一大棵梭梭树长在路旁。

我从小认识梭梭，见了亲切的很，就像看见一个亲人站在那儿。

我对这个村庄也一下有了兴趣。

一棵本来只能当烧柴的梭梭，在村里枝条完好地长了这么多年，一直长到老，谁在护着它呢。

迪坎儿村紧挨沙漠，走进一户人家，门前一渠沟水流，葡萄藤蔓覆盖了整个院落。

转到屋后，发现后墙已经被流沙淹埋掉大半，沙漠从这户人家的后墙根，一望无际地远去，没有一点绿色。

我生活的新疆地域辽阔，大块地存有一些自然风光，除了几个国家级的野生动物保护区，在相对疏松的村镇之间，连绵的农田间隙，还有幸能看到荒野草原、沙漠戈壁，这些暂时没被人侵占的地方，长野草野树，或寸草不生，任风沙吹刮。

不像内地中原，城市村庄紧凑相连，农田密布，整个大地住满人长满人吃的粮食，没有一块闲地供野草生长，更别说有野生动物了。

自然退居到偏远边疆和那些不易人居的荒芜山岭。