风险管理历年计算题汇总

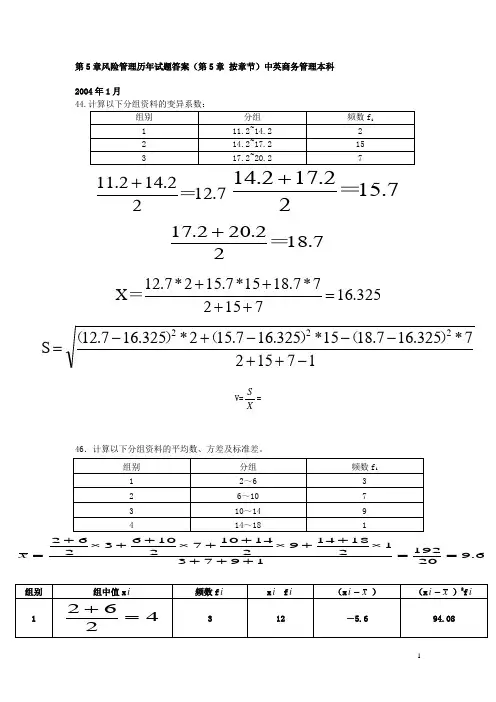
第5章风险管理历年试题答案（第5章 按章节）中英商务管理本科 2004年1月44.计算以下分组资料的变异系数：7.1222.142.11＝+7.1522.172.14＝+ 7.1822.202.17＝+325.1671527*7.1815*7.152*7.12X =++++＝171527*325.167.1815*325.167.152*325.167.12S 222-++---+-=）（）（）（V=XS =46．计算以下分组资料的平均数、方差及标准差。

6.9201921973121814921410721063262==+++⨯++⨯++⨯++⨯+=xs2=12)(2--f fx x iii =1208.204-=10.779283.3779.102===SS(8分)某旅游集团公司风险管理部门发现最近几年该集团各宾馆发生盗窃案件的数目一直处丁二上升趋势．风险管理部门经理建议采用塑料卡式钥匙，在集团下属某家宾馆试行的结果如下．安装整套卡式门锁需2万元，使用寿命6年，安装系统后降低了每年宾馆投保的盗窃险中的自负额，并且还减少了保安方面的服务费用．这两项节省的费用在6年内分布如下：另外，该宾馆的房产部经理打算在该宾馆安装一个取暖照明节能设施．这套系统安装费用集团总经理认为卡式门锁与节能设施都有必要安装，但迫于财务乏力只能支持一项．试用现金流量分析法帮助总经理做出决策．假设投资收益率r 为5％．拆现因子：v=O ．9524．v 2=O ．9071．v 3=O ．8639．v 4=O ．8228．v 5=O ．7836V 6=0．7463．这里V=r+11利用净现值法：在卡式门锁方案下： NPV 1=2000v+4000v 2+6000v 3+8000v 44+10000v 5+12000v 6一20000(2分)=14090(元)(2分)在节能计划方案下：NPV 2=10000v+7000v 2+4000v 3+3000v 4+2000v 5-20000(2分)=3365(元)(2分)因为NPV 1>NPV 2，所以选择风险管理部卡式门锁方案。

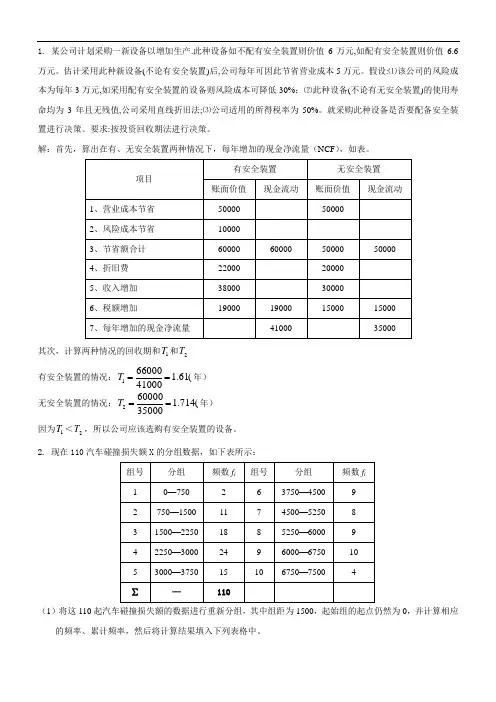
1. 某公司计划采购一新设备以增加生产.此种设备如不配有安全装置则价值6万元,如配有安全装置则价值6.6万元。

估计采用此种新设备(不论有安全装置)后,公司每年可因此节省营业成本5万元。

假设:⑴该公司的风险成本为每年3万元,如采用配有安全装置的设备则风险成本可降低30%；⑵此种设备(不论有无安全装置)的使用寿命均为3年且无残值,公司采用直线折旧法;⑶公司适用的所得税率为50%。

就采购此种设备是否要配备安全装置进行决策。

要求:按投资回收期法进行决策。

解：首先，算出在有、无安全装置两种情况下，每年增加的现金净流量（NCF ），如表。

其次，计算两种情况的回收期和1T 和2T有安全装置的情况：(61.141000660001==T 年）无安全装置的情况：(714.135000600002==T 年） 因为1T ＜2T ，所以公司应该选购有安全装置的设备。

2. 现在110汽车碰撞损失额X 的分组数据，如下表所示：（1）将这110起汽车碰撞损失额的数据进行重新分组，其中组距为1500，起始组的起点仍然为0，并计算相应的频率、累计频率，然后将计算结果填入下列表格中。

（2）在对110起汽车碰撞损失额的数据进行重新分组的基础上，利用损失额和频数这两组数据做出直方图。

（3）损失额不超过6000的概率是多少？47、答：（1）（2）直方图频数454035302520151050 1500 3000 4500 6000 7500 损失（万元）（3）损失额不超过6000的概率是87.3%4.某物业公司过去的经验记录表明，住宅小区每个独立住户大约20年发生一次火灾，假设物业公司的防灾防损部打算用泊松分布来估算住户下一年发生火灾的次数。

试问：（1）每个独立住户每年发生火灾的平均次数是多少？（2）每个独立住户每年不发生火灾的概率是多少？（3）每个独立住户每年发生火灾的次数不超过1次的概率是多少？（4）每个独立住户每年发生火灾次数的方差是多少？（精确到小数点后四位）已知：e-5=0.0067，e-0.05=0.9512，e-1=0.3629。

（风险管理）风险管理历年计算题汇总自考风险管理历年计算题及答案1.（本题9分）某物业公司过去的经验记录表明，住宅小区每个独立住户大约20年发生一次火灾，假设物业公司的防灾防损部打算用泊松分布来估算住户下一年发生火灾的次数。

试问：（1）每个独立住户每年发生火灾的平均次数是多少？（2）每个独立住户每年不发生火灾的概率是多少？（3）每个独立住户每年发生火灾的次数不超过1次的概率是多少？（4）每个独立住户每年发生火灾次数的方差是多少？（精确到小数点后四位）已知：e-5=0.0067，e-0.05=0.9512，e-1=0.3629。

解：（1）（2）无火灾概率即（3）发生火灾次数不超过1概率即（4）S==0.05002.（本题11分）某企业收集整理了去年车间A和车间B由于火灾所造成的损失金额资料如下（单位：百元）：计算损失金额的变异系数并比较两车间损失风险的大小。

（精确到小数点后一位）A：B：S²=12.944S=3.598V=0.3129车间A的风险损失大于车间B的风险损失。

4．假定有一个拥有10辆汽车的车队，根据以往的经验，车队每年均有一次碰撞事故发生，试在车队碰撞事故次数分别服从二项分布和泊松分布的假设条件下估计车队下一年碰撞事故次数为2的概率。

（精确到小数点后4位）解：二项分布：每年发生一次事故，因此事故的概率为p=1÷10=0.1q=1-p=1-0.1=0.9则P（x=2）=×（结果省略）。

泊松分布：记x为一年中发生撞车事故次数。

年平均撞车次数为1,故x服从参数λ=1的泊松分布P（x=2）=e^(-1)*1^2/2!=0.36788请大家注意：泊松分布的分布律γ为年平均事故次数！5．（本题9分）某公司车队统计了近十年本车队发生的车祸次数如下：2，3，3，7，0，6，2，5，1，1试问：（1）车祸次数的众数，全距，算数平均数各是多少？（2）车祸次数的中位数、标准差各是多少？（精确到小数点后两位）（1）众数：1，2，3全距：7-0=7算术平均数：（2）中位数：（2+3）/2=2.标准差：6．（本题11分）某公司一台设备面临火灾风险，其最大可保损失为10万元，假设无不可保损失，现针对火灾风险拟采用以下处理方案：自留风险；购买保费为350元，保额为6万元的保险；购买保费为400元，保额为10万元的保险。

《风险管理》计算题专题公式汇总1.财产直接损失评估方法（一）重置成本法： 财产重置成本＝重置全价－有形损耗－无形损耗＝重置全价×成新率－无形损耗1.直接法：财产重置全价＝直接成本＋间接成本间接成本其分摊方法：（1）按人工成本比例：间接成本＝人工成本总数×分配率（2）单位价格法：间接成本＝工作量×单位价格（按日或时计）（3）直接成本百分率法：间接成本＝直接成本×间接成本占直接成本百分率2. 产出能力比较法：以生产相同的产品的全新财产为标准，通过比较被评估财产与全新财产的产出能力，从而确定财产重置全价3.物价指数法：根据财产帐面原值与物价变动指数估算重置价值。

重置成本法---有形损耗的评估重置成本法---无形损耗的评估财产无形损耗＝生产成本超支额×折现系数n 为被评估财产尚可使用年限；i 为折现率即银行年利率。

（二）现行市价法：通过市场上与被评估财产相同或类似的财产价格，据以确定财产评估价值的方法。

直接法（相同的财产评估）；类比法（类似的财产评估）缺点：受市场影响较大。

（三）收益现值法：对财产在未来产生的收益进行折现来评估财产价值。

1.有限期间各年收益折算法2.无限期收益折现法 ① 永续年金法（适用于各年预期收益相等） ②分段法（适用于未来收益波动较大的情况）5年）各年收益不等，分别折现，5年之后各年收益全部等于G0，用永续年金法将其折算为第6年初的本金再折现。

2.财产间接损失评估（租权利益损失即承租人利益损失）V －租赁价值，T －原定租金，i －年利率，n －从租约合同终止到合同期满的月份总数3.人身风险损失金额评估（1）直接损失金额评估：对员工人身损失的补偿。

个人死亡的年收入能力损失=年净收入个人丧失工作能力的年收入能力损失=年净收入-年生活费用收入能力损失：未来可能获得的收入的现值。

4.损失资料的数字描述描述集中趋势的指标，称位置量数描述离散趋势的指标，称变异量数（1）位置量数1.全距中值（最小观察值＋最大观察值）/22.众数：样本中出现次数最多的观察值。

一、计算分析题1．公司过去8年的财产损失（万元）分别为2，5，5，3，1，6，0，3。

试计算其损失的均值、中值、众数和方差。

答案：均值3.125；中值3；众数3、5；方差为3.862．某企业过去的财产损失（万元）分别为13，25，25，33，11，60，10，22。

试计算其损失的均值、中值、众数和标准差。

答案：均值24.875；中值23.5 ;众数25；标准差15.263．某公司的损失服从正态分布，期望值为20000元，标准差为5000元，如风险经理希望在估计中有95%的置信度，请计算损失可能的变化范围。

如置信度是68%，这个范围如何变化。

答案:3. 如果95%的置信度，t=1.96.损失的范围为：[20000-5000*1.96,20000+5000*1.96]如果68%的置信度，t=1.损失范围为[20000-5000*1,20000+5000*1] 4．某企业租用某建筑物，依规定每月初支付20万元租金，但同等建筑物的市场价值为40万元，后因故于契约届满4年前取消该租约，若市场利率为6%，每月初支付1元年金现值为42.793元，试计算承租合同损失是多少？答案:4. 承租合同损失=（40-20）*42.793=855.86（元）5．某企业重置购进车床一台，市价60000元，运费2500元，直接安装成本400元，间接成本为直接成本的12%，求该车床的重置成本。

答案：5. 重置成本=直接成本+间接成本=（60000+2500+400）*（1+12%）=70448元6．假设某公司年初报表净值为400万元，现在要购买一台机器40万元，如果不购买保险需设立35万元的基金防止损失，如果购买保险则需支出保险费6000元，当银行利率为5%而投资于其它有价证券报酬率为12%时，试计算是否需要买保险。

答案:6. 肯定要买那机器，所以还剩下400-40=360万不买保险：（360-35）*（1+12%）+35*（1+5%）=400.75买保险:(360-0.6)*(1+12%)=402.528所以，402.528》400.75 还是买保险好7．假设某公司欲购入某机器，成本为35万元，使用寿命为30年，利息和维护成本为3万元，固定成本为90万元，变动成本为销货收入的50%，试计算某企业购买机器前后盈亏平衡点。

例1设某企业有一建筑物面临火灾风险。

该建筑物价值1000万元，其中可保价值750万元（已扣除土地及地基价格250万元），并假定如果火灾发生，必导致建筑物全损，同时引起间接损失280万元。

针对这一情况，风险管理者拟定了三个风险处理方案：1．风险残留；2．风险自留并风险控制——通过安装损失预防设备（价值100万元，预计可使用十年，若遇火灾则设备全损）来实现，采用控制手段后可保损失下降1/3，间接损失下降一半；3．购买保险，保险费6万元。

解：建立损失矩阵（不考虑忧虑因素）先看第一方案。

如果火灾发生，则有可保损失750万元，不可保的间接损失280万元，合计1030万元；如果火灾不发生，则无任何损失。

再看第二方案。

如果火灾发生，则有可保损失500万元，预防设备损失100万元，不可保间接损失140万元，合计740万元；如果火灾不发生，则仅支出预防设备折旧费10万元。

最后看第三方案。

如果火灾发生。

则有不可保间接损失280万元，保险费支出6万元，合计286万元；如果火灾不发生，则仅支出保险费6万元。

上述方案最大可能损失分别为1030元，740 元，286 元∴应选方案（3），购买保险。

例2 在例1中，假定火灾发生的概率为5%，但如安装损失预防设备则此概率降至3%，试按损失期望值原则进行决策分析。

解：根据例1的损失矩阵，我们可以算出各方案的损失期望值：（1）风险自留：E1=1030*5%+0*95%=51.5（2）风险自留与风险控制结合：E2=740*3%+10*97%=31.9（3）购买保险：E3=286*5%+6*95%=20例3某公司计划采购一新设备以增加生产。

此种设备如不配有安全装置则价值10万元，如配有安全装置则价值10.5万元。

估计采用此种新设备（不论有无安全装置）后，公司每年可因此节省营业成本5万元。

假设：（1）该公司的风险成本为每年2万元，如采用配有安全装置的设备则风险成本可降低30%；（2）此种设备（不论有无安全装置）的使用寿命决为10年且无残值，公司采用直线折旧法；（3）公司适用的所得税率为50%，要求：就采购此种设备是否要配有安全装置进行决策。

第一章1、核心一级资本充足率、一级资本充足率和资本充足率分别为5%、6%、8%；储备资本要求2.5%、逆周期资本要求0-2.5%、系统重要性银行附加资本要求1%、系统重要性银行资本充足率11.5%、非系统10.5%2、经风险调整的资本收益率RAROC＝（税后净利润－预期损失）/经济资本（或非预期损失）3、正态随机变量X落在距均值1倍、2倍、2.5倍标准差范围内的概率分别为68%、95%、99%4、绝对收益例 500万元的1年期国债，国债的利率5%，到期后绝对收益=500（1-5%）-500=255、百分比收益率例两种资产头寸分别为1000、2000，对应的百分比收益率为6%、10%，则总的资产百分比收益率为1000/3000*6%+2000/3000*10%=8.67%例 6个月100万元理财产品的百分比收益率为2.46%，则年化收益率=（100+100*2.46%）*1.0246-100=4.98%例3个月100万元理财产品的百分比收益率为 1.23%，则年化收益率=（100*1.0123*1.0123*1.0123*1.0123-100）/100=5.01%6、投资组合分散风险的原理例某风险资产的预期收益率8%，标准差0.15，同期国债的无风险收益率4%。

如果希望以该资产和国债构造一个预期收益率6%的资产组合，则投资权重分别多少？8%*X+4%*(1-X)=6% 其中X为资产权重，1-X为国债权重第三章1、企业主要财务比率/指标①盈利能力比率销售毛利率＝[（销售收入－销售成本）/销售收入]×100%销售净利率＝（净利润/销售收入）×100%资产净利率（总资产报酬率）＝净利润/[（期初资产总＋期末资产总）/2] ×100% 净资产收益率（权益报酬率）＝净利润/[(期初所有者权益合计/期末所有者权益合计)/2]×100%总资产收益率＝净利润/平均总资产＝（净利润/销售收入）×（销售收入/平均总资产）②效率比率存货周转率＝产品销售成本/[（期初存货＋期末存货）/2]存货周转天数＝360/存货周转率应收账款周转率＝销售收入/[（期初应收账款＋期末应收账款）/2]应收账款周转天数＝360/应收账款周转率应付账款周转率＝购货成本/[（期初应付账款＋期末应付账款）/2]应付账款周转天数＝360/应付账款周转率流动资产周转率＝销售收入/[（期初流动资产＋期末流动资产）/2]总资产周转率＝销售收入/[（期初资产总额＋期末资产总额）/2]资产回报率（ROA）＝[税后损益＋利息费用×（1－税率）]/平均资产总额权益收益率（ROE）＝税后损益/平均股东权益净额③杠杆比率资产负债率＝（负债总额/资产总额）×100%有形净值债务率＝[负债总额/（股东权益－无形资产净值）×100%利息偿付比率（利息保障倍数）＝（税前净利润＋利息费用）/利息费用＝（经营活动现金流量＋利息费用＋所得税）/利息费用＝[（净利润＋折旧＋无形资产摊销）＋利息费用＋所得税]/利息费用④流动比率流动比率＝流动资产合计/流动负债合计速动比率＝速动资产/流动负债合计其中：速动资产＝流动资产－存货或：速动资产＝流动资产－存货－预付账款－待摊费用违约概率：借款人内部评级1年期违约概率与0.03%中的较高者4、商业银行采用初级内部评级法，除回购类交易有效期限是0.5年外，其他非零售风险暴露的在效期限为2.5年。

三、计算题1．某企业风险管理部整理由于火灾和洪水造成企业每年损失总额资料如下：求：（精确到小数点后1位）（1）损失总额不大于12000元的概率。

（2）损失总额的期望值、标准差和变异系数。

2．某公司计划采购一新设备以增加生产。

这种设备如不配有安全装置则价值10万元，如配有安全装置则价值10.5万元。

估计采用这种新设备（不论有无安全装置）后，公司每年可因此节省营业成本5万元。

假设：①该公司的风险成本为每年2万元，如采用配有安全装置的设备风险成本可降低30%；②这种设备（不论有无安全装置）的使用寿命均为10年且无残值，公司采用直线折旧法；③公司适用的所得税税率为25%。

请采用投资回收期法对采购这种设备是否要配备安全装置进行决策。

3．假定有一个拥有10辆汽车的车队，根据以往的经验，车队每年均有一次碰撞事故发生，试在车队碰撞事故次数分别服从二项分布和泊松分布的假设条件下估计车队下一年碰撞事故次数为2的概率。

（精确到小数点后4位）4设某企业有一建筑物面临火灾风险。

该建筑物价值800万元，其中可保价值600万元（已扣除土地及地基价格200万元），并假设如果火灾发生，必导致建筑物全损，同时引起间接损失200万元。

针对这一情况，风险管理者拟定了三个风险处理方案：（1）风险自留；（2）风险自留并风险控制——通过安装损失预防设备（价值70万元，预计可使用10年，若遇火灾则设备全损）来实现，采用控制手段后可保损失下降三分之一，间接损失下降一半；（3）购买保险，保险费5万元。

试就此建立损失矩阵。

5某公司有6家工厂，假设任何一家在一年中发生火灾概率为0.07，并且各个工厂之间就火灾而言是互不相关的，同一个工厂一年中发生两次以上火灾的概率可以认为是零，请估算该公司下一年度发生火灾的次数分布状况，以及平均将有几家工厂遭受火灾?6. 以下资料是某保险公司1个月内对于投保车损险的客户的赔付数额：（单位：万元）0.12 5.3 7.9 2.5 1.1 4.3 8.5 9.22.343.68 0.54 0.31 1.8 6.24.7 3.231.8 0.2 3.3 1.82.63.54.2 3.7计算这组资料的全距中值、众数和中位数。