微积分(第二版吴传生)第二章 第7节 函数的连续性教案
- 格式:ppt
- 大小:1.52 MB
- 文档页数:10










函数的连续性教案一、教学目标1、理解函数连续性的概念,包括在一点处连续和在区间上连续的定义。
2、能够通过函数的图像和表达式判断函数在某点处的连续性。
3、掌握函数连续性的性质,如连续函数的四则运算、复合函数的连续性等。
4、能够运用函数连续性的概念和性质解决相关的数学问题。
二、教学重难点1、教学重点函数在一点处连续的定义。
函数连续性的性质及其应用。
2、教学难点函数在一点处连续的定义的理解。
运用函数连续性的定义证明函数在某点处连续。
三、教学方法讲授法、讨论法、练习法四、教学过程1、导入(通过展示一些函数的图像,如连续的曲线和不连续的折线)同学们,我们在之前的学习中已经接触过很多函数,大家观察这些函数的图像,有的曲线是平滑的,没有间断点;而有的图像则存在跳跃或者断裂的情况。
今天我们就来深入研究函数的一种重要性质——连续性。
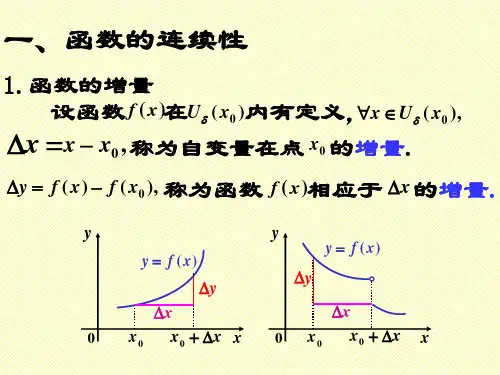
2、函数在一点处连续的定义设函数\(f(x)\)在点\(x_0\)的某一邻域内有定义,如果当自变量的增量\(\Delta x\)趋近于零时,对应的函数增量\(\Delta y = f(x_0 +\Delta x) f(x_0)\)也趋近于零,那么就称函数\(f(x)\)在点\(x_0\)处连续。
用数学语言可以表示为:\(\lim_{\Delta x \to 0} \Delta y =\lim_{\Delta x \to 0} f(x_0 +\Delta x) f(x_0) = 0\)进一步,等价于:\(\lim_{x \to x_0} f(x) = f(x_0)\)(通过具体的函数例子,如\(f(x) = x^2\)在\(x = 1\)处,计算函数增量,帮助学生理解定义)3、函数在一点处连续的充要条件函数\(f(x)\)在点\(x_0\)处连续的充要条件是:函数\(f(x)\)在点\(x_0\)处既左连续又右连续。
左连续:\(\lim_{x \to x_0^} f(x) = f(x_0)\)右连续:\(\lim_{x \to x_0^+} f(x) = f(x_0)\)(举例说明左连续和右连续的情况)4、函数在区间上连续的定义如果函数\(f(x)\)在区间\(I\)内的每一点都连续,就称函数\(f(x)\)在区间\(I\)上连续。
函数的连续性教案教案标题:函数的连续性教案教案目标:1. 了解函数的连续性的概念和意义。
2. 掌握判断函数在给定区间上的连续性的方法。
3. 能够应用函数的连续性性质解决实际问题。
教案步骤:引入:1. 向学生介绍函数的连续性的概念,即函数在某一区间内的图像是连续的。
2. 解释连续性的意义,即函数在某一点上的值与该点附近的值之间没有突变或间断。
探究:1. 提供一个简单的例子,如f(x) = x^2,让学生观察函数图像并讨论函数在整个定义域上的连续性。
2. 引导学生思考如何判断函数在给定区间上的连续性。
提醒学生关注函数在区间端点和内部点上的性质。
3. 引导学生思考连续性的三个基本性质:函数在闭区间上连续的充要条件、函数在开区间上连续的充要条件以及函数在无穷区间上连续的充要条件。
实践:1. 给出一些具体的函数,例如f(x) = sin(x)和g(x) = 1/x,在给定区间上判断它们的连续性。
2. 引导学生使用连续性的性质,结合函数的定义和性质进行判断。
3. 给学生一些实际问题,例如求一个函数在某一点处的极限值,要求学生利用函数的连续性性质进行求解。
总结:1. 总结函数连续性的概念和意义。
2. 强调函数连续性的判断方法和应用。
3. 鼓励学生在实际问题中运用函数连续性的性质解决问题。
教案评估:1. 给学生一些练习题,要求判断给定函数在给定区间上的连续性。
2. 给学生一些应用题,要求利用函数的连续性性质解决实际问题。
3. 收集学生的答案并进行评估,及时纠正他们的错误并给予指导。
教案扩展:1. 引导学生进一步研究函数的间断点和可导性的关系。
2. 探究函数连续性的中值定理及其应用。
3. 引导学生研究其他函数性质与连续性的关系,如函数的单调性和极值点等。
教案资源:1. 函数图像展示工具,如数学软件或在线绘图工具。
2. 练习题和应用题的题目和答案。
3. 相关教材和参考书籍的章节和页码。