当前位置：文档之家 › t分布与检验

t分布与检验

  • 格式：ppt
  • 大小：154.50 KB
  • 文档页数：36

下载文档原格式

  / 36

合集下载

t分布与t检验

t分布与t检验

本讲自测（占一定期末成绩）1【单选题】关于t分布，以下说法不正确的是•A、t分布是一种连续性分布•B、是以0为中心的对称分布•C、t分布就是样本均数的分布•D、当自由度为无穷大时，t分布就是标准正态分布•E、t分布的曲线形状固定正确答案：E 我的答案：E得分：3.3分2【单选题】α=0.05, t＞t0.05,ν，统计上可认为（）•A、两总体均数差别无统计学意义•B、两样本均数差别无统计学意义•C、两总体均数差别有统计学意义•D、两样本均数差别有统计学意义•E、以上均不对正确答案：C 我的答案：A得分：0.0分3【单选题】12名妇女分别用两种测量肺活量的仪器测最大呼气率(l/min)，比较两种方法检测结果有无差别，可进行：•A、卡方检验•B、两独立样本t检验•C、配对卡方检验•D、配对样本t检验正确答案：D 我的答案：D得分：3.3分4【单选题】两样本均数比较，经t 检验，差别有统计学意义时，P 越小，说明：•A、两样本均数差别越大•B、两总体均数差别越大•C、越有理由认为两总体均数不同•D、越有理由认为两样本均数不同•E、样本均数与总体均数不同正确答案：C 我的答案：C得分：3.3分5【单选题】关于学生t分布，下面哪种说法不正确（）。

•A、要求随机样本•B、适用于任何形式的总体分布•C、可用于小样本•D、可用样本标准差S代替总体标准差正确答案：B 我的答案：B得分：3.3分6【单选题】在由两样本均数的差别推断两总体均数的差别的t检验中，检验假设的无效假设是： ( ) •A、两样本均数差别无统计意义•B、两总体均数差别无统计意义•C、两样本均数相等•D、两总体均数相等•E、两总体均数不等正确答案：D 我的答案：D得分：3.3分7【单选题】同一个地区中，随机抽取20名8岁正常男孩，测得其平均收缩压为90.0mmHg，标准差为9.8mmHg。

估计该地8岁正常男孩的平均收缩压的95%置信区间为•A、113.0±×9.8•B、90.0±1.96×9.8•C、90.0±×9.8/•D、90.0±1. 96×9.8/•E、90.0±×9.8正确答案：C 我的答案：C得分：3.3分8【单选题】当自由度ν→∞时,t0.05 值•A、≠1.96•B、＜1.96•C、＝1.96•D、＞1.96正确答案：C 我的答案：B得分：0.0分9【单选题】作两样本均数的t检验，当有差别时，t值越大则•A、两样本均数差异越大•B、两总体均数差异越大•C、越有理由认为两总体均数不同•D、越有理由认为两样本均数不同•E、两样本均数差异越小正确答案：C 我的答案：C得分：3.3分10【单选题】配对t检验的无效假设（双侧检验）一般可表示为________ •A、μ1=μ2•B、μ1≠μ2•C、μd=0•D、μd≠0•E、两样本均数无差别正确答案：C 我的答案：C得分：3.3分11【单选题】在样本均数与总体均数差别的统计学意义检验中，结果为P＜α而拒绝H0，接受H1，原因是_______•A、H1假设成立的可能性大小1-α•B、H0成立的可能性小于α且H1成立的可能性大于1-α•C、从H0成立的总体中抽样得到样本的可能性小于α•D、以上都不对正确答案：C 我的答案：C得分：3.3分12【单选题】两样本比较作t检验，差别有统计学意义时，P值越小说明•A、两样本均数差别越大•B、两总体均数差别越大•C、越有理由认为两总体均数不同•D、越有理由认为两样本均数不同•E、I型错误越大正确答案：C 我的答案：C得分：3.3分13【单选题】在由两样本均数的差别推断两总体均数的差别的t检验中，检验假设的无效假设是：•A、两样本均数差别无统计意义•B、两总体均数差别无统计意义•C、两样本均数相等•D、两总体均数相等•E、两总体均数不等正确答案：D 我的答案：D得分：3.3分14【单选题】与标准正态分布（Z分布）比较，t分布的：•A、均数要小些•B、均数要大些•C、标准差要小些•D、标准差要大些•E、以上都不是正确答案：D 我的答案：D得分：3.3分15【单选题】在研究两种药物治疗高血压的效果的配对t检验中，要求（）。

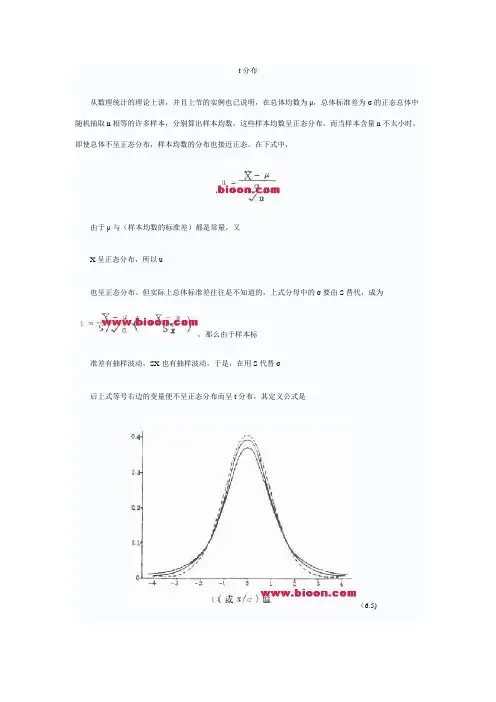
t分布与t检验

t分布与t检验

t分布从数理统计的理论上讲，并且上节的实例也已说明，在总体均数为μ，总体标准差为σ的正态总体中随机抽取n相等的许多样本，分别算出样本均数，这些样本均数呈正态分布。

而当样本含量n不太小时，即使总体不呈正态分布，样本均数的分布也接近正态。

在下式中，由于μ与（样本均数的标准差）都是常量，又X呈正态分布，所以u也呈正态分布。

但实际上总体标准差往往是不知道的，上式分母中的σ要由S替代，成为，那么由于样本标准差有抽样波动，SX也有抽样波动，于是，在用S代替σ后上式等号右边的变量便不呈正态分布而呈t分布，其定义公式是（6.5)t分布也是左右对称，但在总体均数附近的面积较正态分布的少些，两端尾部的面积则比正态分布的多些。

t分布曲线随自由度而不同（如图6.1）。

随着自由度的增大，t分布逐渐接近正态分布，当自由度为无限大时，t分布成为正态分布。

图6.1t分布（实线）与正态分布（虚线）与正态分布相似，我们把t分布左右两端尾部面积之和α=0.05（即每侧尾部面积为0.025）相应的t值称为5%界，符号为t0.05,,，这里ν是自由度。

把左右两端尾部面积之和α为0.01相应的t值称为1%界，符号为t0.01,,。

t的5%界与1%界可查附表3，t值表。

例如当自由度为10-1=9时，t0.05,9=2.262，t0.01,9=3.250。

可信区间的估计一、参数估计的意义一组调查或实验数据，如果是计量资料可求得平均数，标准差等统计指标，如果是计数资料则求百分率藉以概括说明这群观察数据的特征，故称特征值。

由于样本特征值是通过统计求得的，所以又称为统计量以区别于总体特征值。

总体特征值一般称为参数（总体量）。

我们进行科研所要探索的是总体特征值即总体参数，而我们得到的却是样本统计量，用样本统计量估计或推论总体参数的过程叫参数估计。

本章第一节例6.1通过检查110个健康成人的尿紫质算得阳性率为10%，这是样本率，可用它来估计总体率，说明健康成人的尿紫质阳性率水平，这样的估计叫“点估计”。

标准误、t 分布

标准误、t 分布

教 学 内 容 标准误 t分布
二、 t 分布： 三)、应用： 2、t 检验--- 3)、两样本均数的比较： A)、两小样本比较： 检验步骤： 1、建立假设，确定检验水准α 及单双侧 H0：无效假设：(两总体相同)该地急性克山病患者和健康人 的血磷值是否相同， μ 1= μ 2 H1：备择假设：(两总体不同) μ 1 ≠ μ 2 α =0.05 (双侧) 2、选择和计算统计量值： SX1-X2 = t = ( X1-X2 )/SX1-X2 [SC2(1/n1+1/n2)]1/2 = (1.521-1.085)/0.1729 =2.522 3、确定P值：按 v = v1+v2 = n1+n2-2 = 11+13-2 = 22 查t界值 表，得： P < 0.02 4、判断结果： P < 0.05 (α )， 故H1成立， 即该地急性克山病患者和健康人 的血磷值不同。
教 学 内 容 标准误 t分布
二、 t 分布： 三)、应用： 2、t 检验： 3)、两样本均数的比较： A)、两小样本比较： t = (X1-X2)/SX1-X2 B)、两大样本比较： t = (X1-X2)/SX1-X2
v=n1+n2-2 v=n1+n2-2
SX1-X2 = ( S12/n1+S22/n2 )1/2 例： 抽查了25--29岁正常人群的RBC数(mmol/L) 其中男性156人，得均数为4.561，标准差为0.548 ；女性74人，得均数为4.222，标准差为0.442。问 该人群男、女的RBC数有无不同？ 已知样本1 已知样本2 问题： 两样本所属总体 均数是否相同？(μ 1= μ 是否成立 ？)
教 学 内 容 标准误 t分布
二、 t 分布： 三)、应用： 2、t 检验--- 1)、样本均数与总体均数比较：

t检验

t检验

0.25 0.50
1.000 0.816 0.765 0.741 0.727
0.718 0.711 0.706 0.703 0.700
0.686 0.686 0.685 0.685 0.684
0.20 0.40
1.376 1.061 0.978 0.941 0.920
0.906 0.896 0.889 0.883 0.879
0.859 0.858 0.858 0.857 0.856
0.10 0.20
3.078 1.886 1.638 1.533 1.476
1.440 1.415 1.397 1.383 1.372
1.323 1.321 1.319 1.318 1.316
附表2 t 界值表
概 率，P
0.05 0.025 0.01
3.143 2.998 2.896 2.821 2.764
1.721 1.717 1.714 1.711 1.708
2.080 2.074 2.069 2.064 2.060
2.518 2.508 2.500 2.492 2.485
-t
0
t
0.005 0.01
63.657 9.925 5.841 4.604 4.032
接受 H1，差别有统计学意义。结合本题可认 为从事铅作业的男性工人平均血红蛋白含量 低于正常成年男性。
21
f(t)
.4
.3

.2
P .1
0.0 -5.0 -4.0 -3.0 -2.0 -1.0 0.0 1.0 2.0 3.0 4.0 5.0
t
图3-5 例3-5中P值示意图
22
第二节 配对样本均数的t 检验
18

卫生统计学专题八：t检验

卫生统计学专题八：t检验

专题八 t 检验⒈t 检验基础t 检验是一种以t 分布为基础，以t 值为检验统计量资料的假设检验方法。

⑴t 检验的基本思想：假设在H 0成立的条件下做随机抽样，按照t 分布的规律得现有样本统计量t 值的概率为P ，将P 值与事先设定的检验水准进行比较，判断是否拒绝H 0。

⑵t 检验的应用条件：①样本含量较少（n ＜50）；②样本来自正态总体（两样本均数比较时还要求两样本的总体方差相等，即方差齐性）。

【注】实际应用时，与上述条件略有偏离，只要其分布为单峰近似对称分布，对结果影响不大。

⑶t 检验的主要应用：①单个样本均数与总体均数的比较；②配对设计资料的差值均数与总体均数0的比较；③成组设计的两样本均数差异的比较。

⑷单样本t 检验基本公式：t=x0s x μ-=nsx 0μ- υ=n-1⒉z 检验z 分布（标准正态分布）是t 分布的特例，当样本n ≥50或者总体σ已知时用z 检验。

⑴单样本z 检验基本公式：z=nsx 0μ- 或 z=nx 0σμ-⑵单样本z 检验的步骤与单样本t 检验的基本相似。

⒊配对设计均数的比较 配对设计是为了控制某些非处理因素对实验结果的影响而采用的设计方式，应用配对设计可以减少实验误差和个体差异对结果的影响，提高统计处理的效率。

⑴配对设计的主要四种情况：①配对的两受试对象分别接受两种处理，如在动物实验中，常先将动物按照窝别、体重等配对成若干对，同一对的两受试对象随机分配到实验组和对照组，然后观察比较两组的实验结果。

②同一样品用两种不同方法测量同一指标或接受不同处理。

③自身对比，即将同一受试对象（实验或治疗）前后的结果进行比较。

④同一对象的两个部位给予不同处理。

⑵对配对资料的分析：一般用配对t 检验，其检验假设为：差值的总体均数为0即μd =0。

计算统计量的公式为：t=ns 0d d-，υ=n-1式中d 为差值的均数；s d 为差值的标准差；n 为对子数。

⑶关于自身对照（同体比较）的t 检验：①在医学研究中，我们常常对同一批患者治疗前后的某些生理、生化指标进行测量以观察疗效，对于这些资料可以按照配对t 检验。

概率分布与t检验

概率分布与t检验

3
t检验的前提假设包括样本数据来自正态分布总体、 样本数据相互独立且具有相同方差等。
t检验的种类与适用场景
单样本t检验
用于比较一个样本的均值与已知的某个值是否存 在显著差异。
配对样本t检验
用于比较两个相关样本的均值是否存在显著差异， 例如同一组对象在不同条件下的测量结果。
独立样本t检验
用于比较两个独立样本的均值是否存在显著差异， 例如不同组对象在相同条件下的测量结果。
生物统计学
在生物学和医学研究中，概率分布在描述实 验结果的不确定性方面有广泛应用。
02
正态分布
正态分布的定义与特性
定义
正态分布是一种连续概率分布， 其概率密度函数呈钟形曲线，对 称分布。
特性
正态分布具有均值为μ，标准差为σ 的特性，且大部分数据落在μ±3σ 范围内。
正态分布在统计学中的重要性
01
THANKS
感谢观看
检验回归模型的斜率是否显著
在回归分析中，t检验常用于检验回归模型的斜率是否显著。通过比较模型中的 自变量和因变量之间的关系，可以判断自变量对因变量的影响是否具有统计学上 的显著性。
在检验回归模型的斜率是否显著时，需要关注回归模型的整体拟合情况以及自变 量的选择是否合理。同时，需要注意控制其他因素的影响，以避免产生偏倚。
02
03
中心极限定理
在大量独立随机变量的平 均值下，其分布趋近于正 态分布，这是正态分布在 统计学中的基础。
参数估计
正态分布用于估计未知参 数的置信区间和假设检验。
数据分析
在许多领域的数据分析中， 正态分布假设是常用的， 如线性回归、方差分析等。
正态分布在现实生活中的应用
金融

t检验

t 检验
t 检验（t-test）是利用t分布来进行统计量 检验（ test）是利用t 的概率计算的假设检验方法。它主要应用于总体 的概率计算的假设检验方法。它主要应用于总体 方差未知时的小样本资料 n<30） 方差未知时的小样本资料（n<30）。 的小样本资料（
S 均数标准误 S x＝ n
其中， 其中，

【例4-3】某名优绿茶含水量标准为不超过5.5 某名优绿茶含水量标准为不超过5.5 ％。现有一批该绿茶 从中随机抽出8 现有一批该绿茶， ％。现有一批该绿茶，从中随机抽出8个样品测 定其含水量， 5.6％， ％，标准差 定其含水量，平均含水量 ＝5.6％，标准差 S＝0.3％。问该批绿茶的含水量是否超标？ 0.3％。问该批绿茶的含水量是否超标？ ％。问该批绿茶的含水量是否超标 符合t检验条件，为单尾检验。 符合t检验条件，为单尾检验。 1） （1）提出无效假设与备择假设
µ H0： ≤ µ ＝5.5％， A： > µ0 ％，H µ ％，
0
x
（2）计算 t 值 ）
S 0.003 ＝ .001 Sx ＝ ＝ 0 n 8 x − µ0 0.056−0.055 t＝ ＝ ＝ .000 1 Sx 0.001
df =n −1= 8−1= 7
（3）查临界t值，作出统计推断 查临界t
（4）查临界t值，作出统计推断 查临界t
由 =15， 值表（附表3 df =15，查t值表（附表3）得
t0.01（15）=2.947，因为|t|>t0.01， =2.947，因为| |>t P<0.01， 故应否定H0，接受HA， 表明 <0.01， 故应否定H 新老工艺的每100g加工出的果冻量差异极 新老工艺的每100g加工出的果冻量差异极 显著。（在统计量t上标记**） 显著。（在统计量 上标记**） 。（在统计量t

第5章t检验


1. 建立检验假设，确定检验水准 H0: σ12= σ 22 两组体重的总体方差相等 H1: σ12≠ σ22 两组体重的总体方差不等 α=0.05 2. 计算检验统计量 已知：n1=12 X1=45.75 S12=17.659 n2=13 X2=36.538 S22=3.269
S1 (较大） 17.659 F 2 5.402 S 2（较小） 3.269
注： P<0.01 差别有高度统计学意义 (P越小，越有理由拒绝H0）。
第三节
配对样本t检验
d 0 d t Sd Sd / n
配对设计主要有以下两种形式：
①同源配对： 同一受试对象处理前后的数据；同一受 试对象两个部位的数据；同一样品用两 种方法（仪器）检验的结果； ②异源配对： 配对的两个受试对象分别接受两种处理 后的数据。
第四节 两独立样本 t 检验 Two independent sample t-test • 又称成组t检验 • 适用于完全随机设计的两样本均数的比 较
将受试对象完全 随机地分配到两 组中
一、总体方差相等时的两独立样本 t 检验
应用条件：1. 两样本所代表的总体服从正态分布
2. 两总体方差具有齐性
s1 s12 17.659 2 sx 1.472 1 n n1 12 1
2 s2 s2 3.269 2 sx 2.179 2 n n2 12 2 2
2
三、完全随机分组两组几何均数比较的t检验
宜用几何平均数表示集中水平的资料，不服从 正态分布，但是测量值的对数值服从正态分布， 如抗体滴度的资料。此时可对lgx进行t检验。
t
' 2 2 S x t (1 ) S x t ( 2 )

t分布的概念表和查表方法

t分布介绍在和中，学生t-分布（t-distribution），可简称为t分布，用于根据小样本来估计呈且方差未知的总体的均值。

如果总体方差已知（例如在样本数量足够多时），则应该用正态分布来估计总体均值。

t分布曲线形态与n（确切地说与自由度df）大小有关。

与标准正态分布曲线相比，自由度df越小，t分布曲线愈平坦，曲线中间愈低，曲线双侧尾部翘得愈高；自由度df愈大，t分布曲线愈接近正态分布曲线，当自由度df=∞时，t分布曲线为标准正态分布曲线。

目录123456历史在和统计学中，学生t-分布（Student's t-distribution）经常应用在对呈的总体的进行估计。

它是对两个差异进行测试的学生t测定的基础。

t检定改进了Z检定（en:Z-test），不论样本数量大或小皆可应用。

在样本数量大（超过120等）时，可以应用Z检定，但Z检定用在小的样本会产生很大的误差，因此样本很小的情况下得改用学生t检定。

在数据有三组以上时，因为误差无法压低，此时可以用代替学生t检定。

当母群体的是未知的但却又需要估计时，我们可以运用学生t-分布。

学生t-分布可简称为t分布。

其推导由于1908年首先发表，当时他还在都柏林的健力士酿酒厂工作。

因为不能以他本人的名义发表，所以论文使用了学生（Student）这一笔名。

之后t检验以及相关理论经由的工作发扬光大，而正是他将此分布称为学生分布。

定义由于在实际工作中，往往σ是未知的，常用s作为σ的估计值，为了与u变换区别，称为t变换，统计量t 值的分布称为t分布。

假设X服从标准正态分布N（0,1），Y服从分布，那么的分布称为自由度为n 的t分布，记为。

分布密度函数，其中，Gam(x)为伽马函数。

扩展（normal distribution）是数理统计中的一种重要的理论分布，是许多的理论基础。

正态分布有两个参数，μ和σ，决定了正态分布的位置和形态。

为了应用方便，常将一般的正态变量X通过u变换[(X-μ)/σ]转化成标准正态变量u，以使原来各种形态的正态分布都转换为μ=0，σ=1的（standard normal distribution），亦称u分布。

2 概率分布与t检验


σ 2π 其中µ为平均数 为平均数， 为方差，则称随机变量x服从 其中 为平均数，σ2为方差，则称随机变量 服从 正态分布，记为x~N(µ,σ2) 正态分布，记为
f ( x) =
e
2σ 2
相应的概率分布函数为 相应的概率分布函数为 概率分布函数
F (x) = 1
σ
2π
∫
x
−∞
e
−
( x− µ )2 2σ
Sx = S n =
∑ (x − x)
n(n − 1)
2
=
∑x
2
− (∑ x) / n
2
n(n − 1)
样本标准差与样本标准误是两个不同的统计量。 样本标准差与样本标准误是两个不同的统计量。 两个不同的统计量 二者的区别在于： 二者的区别在于： 在于
是样本中各观测值x 样本标准差S是样本中各观测值 1,x2,x3…,变异程度的一个 , 指标， 对该样本代表性的强弱。 指标，反映了 x 对该样本代表性的强弱。 样本标准误是样本平均数的标准差，它是 x 抽样误差的估 样本标准误是样本平均数的标准差， 样本平均数的标准差 计值， 精确性的高低。 计值，说明了 x 精确性的高低。
对于无限总体， 对于无限总体，返置与否都可保证各个 无限总体 体被抽到的机会相等。 体被抽到的机会相等。 对于有限总体 就应该采取返置抽样， 有限总体， 对于有限总体，就应该采取返置抽样， 否则各个体被抽到的机会就不相等。 否则各个体被抽到的机会就不相等。
1.2 中心极限定理
若有一随机变量服从总体平均数为μ 若有一随机变量服从总体平均数为μ、 总体平均数为 方差为σ 的分布， 方差为σ2的分布，则从这个总体中随机 的样本， 抽取容量为n的样本， 的不断增大， 随样本容量n的不断增大，其样本平均
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

t分布表的使用:
例：自由度为10，P(t>1.812)=P(t<-1.812)=0.05 P(︱t︱>1.812)=P(t>1.812)+P(t<-1.812)=0.1
0.05 0.05
-1.812
0
1.812
t分布表举例：
例：变量X表示面包房每日出售的面包量， 在15天内，出售面包的样本方差为16。假 定真实的出售量为70条，求任意15天内出 售面包平均数量为74条的概率。 分析：本例中已知样本方差S² =16，则S=4， 总体均值（真实的出售量）=70，运用t变量 公式得： 74 70 t 3.873 4 15
表示随机变量X服从正态分布。 符号~表示随机变量服从什么样的分布； N表示正态分布； ，² 为正态分布的（总体）均值（或期望）和 方差。 X是一个连续型随机变量，可在区间（－∞,+∞） 内任意取值。
正态曲线下的区域示意图
68%（近似） 95%（近似） 99.7%（近似）

-3
-Hale Waihona Puke -2(X ) t ~t S 20
X
19
查t分布表得：当自由度为19时， P(-2.861≦t≦2.861)=0.99
整理得出：
X 2.861S X 2.861S 0.99 P n n
X
将已知条件代入，得： 5.22≦ x ≦7.78 （近似值） 由于该区间包括了零假设值7.5，因此，我 们不拒绝零假设：真实的x =7.5。
按照上述步骤，首先运用t变量公式，求出 t变量。
72 70 t 1.936 4 / 15
查t分布表，当自由度为14时，t值大于等于 1.761的概率为0.05，大于等于2.145的概率为 0.025，因此，t值取1.936的概率介于0.025与 0.05之间。
查t分布表的注意事项：
⑴ 自由度为（n-1），而不是n。
X t S n
_
根据统计理论得知：变量t服从自由度为(n-1)的 t分布。
注意：在这里，自由度为(n-1)，而不是n。
结论：从正态总体中抽取随机样本，若该正态 总体的均值为，但方差² 用其估计量S² 来代替， 则其样本均值服从t分布。通常用符号t 表示， 其中k表示自由度。
k
k=120(正态） K=20 K=5
Z ~ N(0,1 )
任一给定均值和方差的正态变量都可转化为标准正 态变量，将其标准化可以大大简化计算。
例：变量X表示面包房每日出售的面包量，假 定它服从均值为70、方差为9的正态分布，即 X~N(70,9)，求任给一天，出售面包数量大于 75条的概率。 首先，定义变量Z，Z=(75-70)/3≈1.67 求：P(Z>1.67) 查正态分布表得： P(0≦Z≦1.67)=0.4525 则：P(Z>1.67)=0.5-0.4525=0.0475 即每天出售面包的数量超过75条的概率为 0.0475。

t分布与正态分布：
当k增大时，t分布的方差接近于标准正态分布方差值1。
例如：当k=10时，t分布的方差为10/8=1.25；
当k=30时，t分布的方差为30/28=1.07；
当k=100时，t分布的方差为100/98=1.02；
结论：随着自由度的逐渐增大，t分布近似于正态分布。
注意：对于t分布，不要求其样本容量很大，k=30时，t 分布与正态分布已很近似。
0 不同自由度下的分布
t分布的性质

⑴ t分布与正态分布相类似，具有对称性。 ⑵ t分布的均值与标准正态分布均值相同， 为0，但方差为k/(k-2)。由此，在求t分布的 方差时定义自由度必须大于2。 标准正态分布的方差等于1，因此，t分布方 差总大于标准分布的方差，也就是说，t分布 比正态分布略“胖”些。
正态分布
1.1
什么是正态分布？
对于连续型随机变量而言，正态分布是最
重要的一种概率分布，其形状似“钟型”。
经验表明：对于其值依赖于众多微小因素
且每一因素均产生微小的或正或负影响的 连续型随机变量来说，正态分布是一个相 当好的描述模型。如身高、体重、考试成 绩等。
为了方便，通常用：
X ~ N ( , 2 )
用假设的语言，将x =13称为零假设，用符号H0 表示。即，H0: x =13 与零假设相对应的是备择假设，用符号H1表示， 备择假设有以下几种形式： H1： x＞13 称为单边备择假设； H1： x＜13 称为单边备择假设； H1： x≠13 称为双边备择假设。 为了检验零假设（和备择假设）,根据样本数据及 统计理论建立判定规则来判断样本信息是否支持 零假设。若支持，不拒绝零假设，反之拒绝零假 设，接受备择假设。 建立判定规则有两种方法：置信区间法、显著性 检验法。
4.1 置信区间法

在上述例子中，我们知道样本均值服从均值为x ， 方差为² /n的正态分布，由于真实的方差未知， 以样本方差代替。在这种情况下，样本均值服从 t分布，从而得到x 的一个95%的置信区间： 10.63≦ x ≦12.36 （近似值）

置信区间提供了在某一置信度下（如95%）真实 的x 的取值范围。因此，如果这个区间不包括零 假设中的值，如x =13，则拒绝零假设，即我们 以95%的置信度拒绝零假设。反之，接受零假设。

查t分布表，自由度为(n-1)=15-1=14 当自由度为14时，查表得，t值大于等于 2.977的概率为0.005，大于等于4.140的概 率为0.0005，所以，t值大于等于3.873的 概率介于0.0005~0.005之间。 练习1：
上例中其他条件不变，现假定15天 内出售面包的平均数量为72条，求获得 此数量的概率。
接受区域：上述不等式所描述的置信区间称为 接受区域。 零假设的临界区域（或拒绝区域）：接受区域 以外的称为零假设的临界区域或拒绝区域。 临界值：接受区域的上界和下界称为临界值。 它们是接受或拒绝零假设的分界线。 归纳：如果参数值在零假设下位于接受区域内， 则不拒绝零假设，若落在接受区域以外（即落 在拒绝区域内），则拒绝零假设。
当自由度为49时，在5%的显著水平下，查表 得临界的t值为-2.0096和2.0096 （见下图） ， 获此t值小于或等于-2.0096的概率为2.5%，获 得此t值大于或等于2.0096的概率也为2.5%。
95% t =-3.5 =2.5% =2.5%
-2.0096
0
2.0096
t检验的显著性：双边检验
P/E 6 7 8 9 10 11 12 13 14 15 16 18
频数 2 2 5 6 5 7 5 4 3 4 6 1 总计：50
均值=11.5
样本方差=9.2755 样本标准差=3.0456
假设的样本（50支股票的P/E值）
假设检验

假设真实的x 取某一特定值，如x =13。 然后去检验这个假设，检验结果是接受或 拒绝该假设？下面以此为例说明。
3
1.2 正态分布的性质：

⑴ 正态分布曲线以均值为中心，对称分布。 ⑵ 正态分布的概率密度函数呈中间高、两边 低，在均值处达到最高，向两边逐渐降低， 即随机变量在远离均值处取值的概率逐渐变 小。 ⑶ 正态曲线下的面积约有68%位于± 两 值之间；约有95%面积位于±2之间；约有 99.7%的面积位于± 3之间。这些区域可用 作概率的度量。
显然，t值位于t分布的左侧拒绝区域。因此， 拒绝零假设。
t检验小结
零H0
备择假设
临界区域，拒绝H0，若
x= 0
x>0
x= 0
x<0
x= 0
x≠0
最后一列给出了t临界值，第一个下标表示显著水平，d.t代表自由度。
⑵ t分布表具有对称性，t值大于等于 某一特定值的概率与t值小于等于该特
定值相反数的概率相等。

关注某一总体，如纽约股票交易市场的
1758支（90年9月4日）股票，想要研究该
总体某一方面的统计特征，比如说股票价
格与收入比（P/E）的平均值。在总体中抽
取随机样本，如50支股票，求样本中每一
支股票的P/E值，然后再计算平均P/E值， 就称为总体平均P/E的估计量
准正态分布。
1
2
不同均值，同方差的两个正态分布图
不同均值，不 同方差
1
2
相同均值，不 同方差
1=2
标准正态分布

如果变量X的均值为，方差为，定义一个 新的变量Z，
Z
X

则根据性质5，变量Z的均值为0，方差为1。 在统计学中，我们称之为单位或标准正态 变量，用符号表示为：

f(Z)
0.4525
0.0475
0
1.67
标准正态变量概率密度函数
t分布
回忆：若样本均值 X ~ N ( ,
_ 2
n) ，则
变量Z服从标准正态分布。
X 即： Z ~ N (0,1) n
_
假定已知和² 的估计量S² ，则可以 用样本标准差（S）代替总体标准差 （），得到一个新的变量t。
H0：x =7.5
99%
0.5%
0.5%
5.22
7.5 7.78
a) x的99%的置信区间
4.3 显著性检验

显著性检验是一种两者择一的假设检验，现通 过P/E一例加以说明。 根据以下公式可知：

(X ) t S n
X
服从自由度为(n-1)的t分布。在具体应用中，、 S、n已知， x 未知。

⑷
正态分布可由两个参数，² 来描 述，即一旦知道，² 的值，就可以根 据附录表查到随机变量X落于某一区 间的概率值。 两个（或多个）正态分布随机变量 的线性组合仍服从正态分布。该性质 很重要，解释如下：