玻尔理论的基本假设现象氢原子光谱是分立线状共23页

玻尔的氢原子理论：原子只能处在一系列具有不连续能量的稳定状态，简称定态。

定态时，核外电子在一定的轨道上作圆周运动，不辐射电磁波.: 原子从一个定态跃迁到另一个定态时，会辐射或吸收一个能量为h 的光子.1. 定态假设n k E E h2.频率假设n kE E 一、玻尔的氢原子理论的三个基本假设...3 ,2 ,1π2 n n hn r m Lv 3.轨道角动量量子化假设n 称为轨道量子数称为约化普朗克常量2h第n 个定态电子的轨道半径为:玻尔半径二、氢原子轨道半径和能量的计算库仑力=向心力v nE n +e-e m m p r n 角动量量子化条件（1）（2）运动轨道是量子化的23...n ，，对应的定态分别称为第一激发态、第二激发态……n=1对应的定态称为基态能量量子化夫兰克-赫兹实验证实了原子能级的存在121E (n 1,2,3,)n基态能量meE .eV h412201368不连续的分立能量称为能级（3）（1）1122211n n (n )E E E E n (n )n E:n 三、对应原理这符合玻尔的对应原理n n r ,E 0,E 0电子能量趋于连续。

,n 对应原理：在极限条件下，新理论应与旧理论形式一致。

新理论应包含一定经验范围内证明是正确的旧理论。

在量子数n 很大时，玻尔氢原子理论应与经典理论一致。

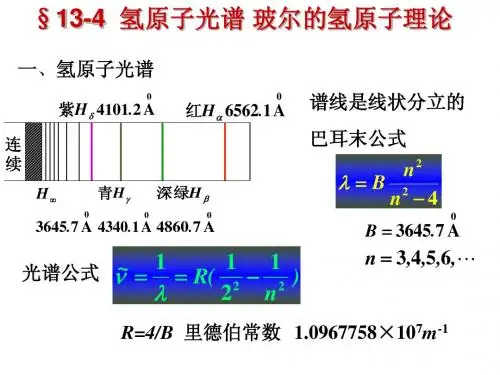
四、玻尔氢原子理论值和实验值比较原因在于原理论假设氢核静止; 而实际核与电子一起绕它们的质心旋转，这时应用折合质量μ代替mn k E E νh423220me 118h k n－（1）42322111=()8 0νme νλc εh c k n2211=R()() n k k n （2）赖曼系k=1巴耳末系k=2氢原子能级图0n kh E E 光子能量：-13.6-1.51-3.39E n (eV)n = 1n = 2n = 3n = 4n = 5n = 6n 213.6E -eVn根学派的领头人。

玻尔氢原子理论的三条假说N.玻尔首创的第一个将量子概念应用于原子现象的理论。

1911年E.卢瑟福提出原子核式模型，这一模型与经典物理理论之间存在着尖锐矛盾，原子将不断辐射能量而不可能稳定存在；原子发射连续谱，而不是实际上的离散谱线。

玻尔着眼于原子的稳定性，吸取了M.普朗克、A.爱因斯坦的量子概念，于1913年考虑氢原子中电子圆形轨道运动，提出原子结构的玻尔理论[1]。

理论的三条基本假设是：①定态假设：原子只能处于一系列不连续的能量的状态中，在这些状态中原子是稳定的，这些状态叫定态。

原子的不同能量状态跟电子沿不同的圆形轨道绕核运动相对应，原子的定态是不连续的，因此电子的可能轨道的分布也是不连续的，电子在这些可能的轨道上的运动是一种驻波形式的振动。

②跃迁假设：原子系统从一个定态过渡到另一个定态，伴随着光辐射量子的发射和吸收。

辐射或吸收的光子的能量由这两种定态的能量差来决定，即hν=|E初-E末|③轨道量子化：电子绕核运动，其轨道半径不是任意的，只有电子在轨道上的角动量满足下列条件的轨道才是可能的：mvr=nh/（2π）（n=1，2，3…）式中的n是正整数，称为量子数。

玻尔理论在氢原子中的应用⑴氢原子核外电子轨道的半径— 1 —设电子处于第n条轨道，轨道半径为（rn），根据玻尔理论的轨道量子化得m（vn）（rn）=mvr=nh/（2π）（n=1，2，3…）①电子绕核作圆周运动时,由电子和原子核之间的库仑力来提供向心力,所以有m（vn）^2/（rn)=1/（4πε0）*[e^2/（rn）^2]②由①②式可得（rn）=ε0h^2*n^2/(πme^2)（n=1，2，3…）当n=1时,第一条轨道半径为r1=ε0h^2/(πme^2)=5.3*10^-11(m),其他可能的轨道半径为（rn）=r1,4r1,9r1,25r1…⑵氢原子的能级当电子在第n条轨道上运动时，原子系统的总能量E叫做第n 条轨道的能级，其数值等于电子绕核转动时的动能和电子与原子的电势能的代数和En=1/2*m*(vn)^2-e^2/(4πε0（rn))③由②式得1/2*m*(vn)^2=e^2/(8πε0（rn))④将④式代入③式得En=-me^4/(8(ε0)^2h^2n^2)⑤这就是氢原子的能级公式当n=1时,第一条轨道的能级为E1==-me^4/(8(ε0)^2h^2)=-13.6eV.其他可能轨道的能级为En=E1/n^2=-13.6/n^2(eV)(n=2,3,4…)由轨道半径的表达式可以看出,量子数n越大,轨道的半径越大,— 2 —能级越高.n=1时能级最低,这时原子所处的状态称为基态,n=2,3,4,5…时原子所处的状态称为激发态.⑶玻尔理论对氢光谱的解释由玻尔理论可知,氢原子中的电子从较高能级(设其量子数为n)向较低能级(设其量子数为m)跃迁时,它向外辐射的光子能量为hν=En-Em=-me^4/(8(ε0)^2h^2)(1/n^2-1/m^2)由于c=λν,上式可化为1/λ=me^4/(8(ε0)^2h^2)(1/m^2-1/n^2)将上式和里德伯公式作比较得R=me^4/(8(ε0)^2h^3c)=1.097373*10^7m^(-1)这个数据和实验所得的数据1.0967758*10^7m^(-1)基本一致,因此用玻尔理论能较好的解释氢原子的光谱规律,包括氢原子的各种谱线系.例如:赖曼系、巴尔末系、帕邢系、布喇开系等的规律。