假言命题

判断推理假言命题摘要：一、假言命题的概念与分类1.充分条件假言命题2.必要条件假言命题3.充分必要条件假言命题4.无效假言命题二、假言命题的推理规则1.肯定前件，肯定后件2.否定前件，否定后件3.肯定前件，否定后件4.否定前件，肯定后件三、假言命题的应用1.题目解析方法2.解题技巧与策略四、实战演练与解析正文：一、假言命题的概念与分类假言命题是逻辑推理中的一种基本类型，它描述了两个事物之间的条件关系。

根据条件关系的不同，假言命题可分为以下四种类型：1.充分条件假言命题：若A，则B。

例如，若下雨，则地面湿润。

2.必要条件假言命题：只有A，才B。

例如，只有认真学习，才能取得好成绩。

3.充分必要条件假言命题：A当且仅当B。

例如，成年人当且仅当具有民事行为能力。

4.无效假言命题：A不管B。

例如，不管天气如何，我都要去散步。

二、假言命题的推理规则假言命题的推理规则有四种，分别是：1.肯定前件，肯定后件：若A，则B。

已知A成立，可以推出B成立。

2.否定前件，否定后件：若A，则B。

已知A不成立，可以推出B不成立。

3.肯定前件，否定后件：若A，则B。

已知A成立，可以推出B不成立。

4.否定前件，肯定后件：若A，则B。

已知A不成立，可以推出B成立。

三、假言命题的应用假言命题在逻辑推理题中占有很大比重。

要解答这类题目，首先要熟练掌握各类假言命题的推理规则，其次要学会运用规则进行题目解析。

1.题目解析方法：阅读题目，识别假言命题类型，根据题干给出的条件进行推理。

2.解题技巧与策略：熟悉假言命题的推理规则，善于寻找题干中的关键信息，灵活运用规则进行推理。

四、实战演练与解析【例题】已知：若小明去健身房，则他会跑步；小明去了健身房。

问：小明会不会跑步？解答：根据充分条件假言命题的推理规则，已知小明去了健身房，可以推出他会跑步。

所以，小明会跑步。

通过以上内容，我们对假言命题的概念、分类和推理规则有了更深入的了解。

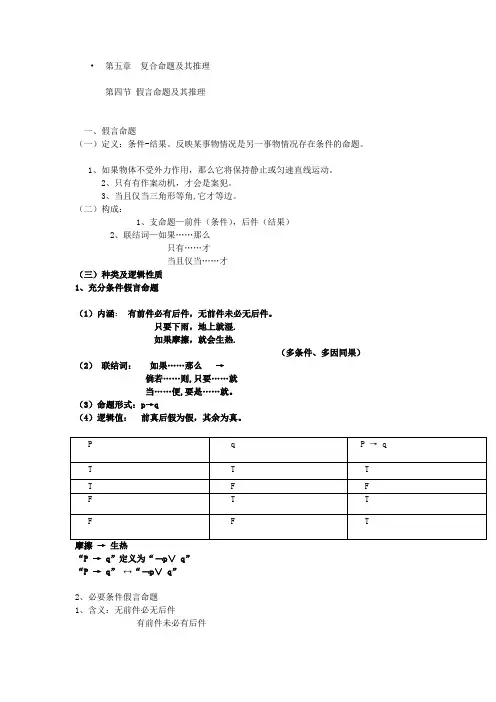
•第五章复合命题及其推理第四节假言命题及其推理一、假言命题（一）定义：条件-结果。

反映某事物情况是另一事物情况存在条件的命题。

1、如果物体不受外力作用，那么它将保持静止或匀速直线运动。

2、只有有作案动机，才会是案犯。

3、当且仅当三角形等角,它才等边。

（二）构成：1、支命题—前件（条件），后件（结果）2、联结词—如果……那么只有……才当且仅当……才（三）种类及逻辑性质1、充分条件假言命题（1）内涵：有前件必有后件，无前件未必无后件。

只要下雨，地上就湿.如果摩擦，就会生热.（多条件、多因同果）（2）联结词：如果……那么→倘若……则,只要……就当……便,要是……就。

（3）命题形式：p→q（4）逻辑值：前真后假为假，其余为真。

摩擦→生热“P →q”定义为“﹁p∨ q”“P →q” ↔“﹁p∨ q”2、必要条件假言命题1、含义：无前件必无后件有前件未必有后件只有阳光充足，庄稼才能长好。

只有努力学习，才能取得好成绩。

（复合条件、合因一果）2、联结词：只有……才←除非…不，必须…才，不…就不3、命题形式：p←q，﹁p→﹁q4、逻辑值：前假后真为假，其余为真。

3、充分必要条件假言命题1、含义：前件既是后件的充分条件，也是后件的必要条件，反过来一样，后件既是前件的充分条件也是前件的必要条件。

当且仅当三角形等角，则三角形等边。

人不犯我，我不犯人；人若犯我，我必犯人。

（唯一条件联系）2、联结词：↔当且仅当……才如果且只有……才3、命题形式：p↔q 当且仅当p，才q如果p那么q，且只有p才q4、逻辑值：前后件一真一假时为假等角↔等边“P ↔q” ↔“q↔p ”三种条件之间有内在联系（1）意义：弄清可以实现它们之间的转换推演，使表达方式多样活泼。

（2）充分与必要的前后件之间有固定的逻辑关系：前件是后件的充分，则后件是前件的必要。

（p→q）↔（ q ← p ）摩擦→生热努力学习←好成绩二、假言推理（一）定义：前提中有假言命题，据其逻辑特性进行的推理。

[例1] p.天下雨; q.地湿
2.必要条件
如果一种事物情况p不存在，则另一种事物情况q就一 定不存在；如果p存在，则q可能存在，也可能不存在， 这样，p就是q的必要条件。
如果无p，就无q；如果有p，未必就有q（可能有， 可能没有）。
“无之必不然，有之未必然”。
[例2] p. 一人年满18岁; q.他入党
[例1]如果天下雨，那么地就湿； 今天天下雨；
所以，今天地湿。
（1）肯定前件式： 在前提中肯定假言命题的前 件，结论肯定它的后件。
逻辑形式：
如果p，那么q p 所以，q
（（p→q）∧ p）→q
[例2]如果天下雨，那么地就湿； 今天地不湿； 所以，今天天没有下雨。
逻辑形式： 如果p，那么q 非q 所以，非p
1. p(T) q (T) 2. p(T) q (F) 3. p(F) q (T) 4. p(F) q (F)
命题的真值
p← q (T) p← q (F) p← q (F) p← q (T)
充分必要条件假言命题的真值表：
p
q
p↔q
T
T
T
T
F
F
F
T
F
F
F
T
（三）
下列命题是何种命题？写出形式，判定真值。
（3）必要条件假言命题的逻辑值
一个必要假言命题的真假，取决于、而且仅 仅取决于其前件是否是后件的必要条件，如果 是，命题真；否则，命题假。
前件是否是后件的必要条件，可以通过前件与后件的 真假关系来反映。
一个必要条件假言命题前 件和后件的真假组合有四 种：
1. p(T) q (T) 2. p(T) q (F) 3. p(F) q (T) 4. p(F) q (F)

假言命题名词解释假言命题是数理逻辑中十分重要的概念，也被广泛应用于哲学、语言学等领域。

它是由前提和结论两部分构成的陈述性语句，表达的是一种条件关系。

本文将对假言命题的定义、符号表示及相关概念进行解释和探讨。

1、假言命题的定义假言命题又称为条件命题，它是指由前提和结论两个陈述性语句组成，其中前提为条件语句（if-then语句），结论则为相应的结果语句。

假言命题可以用一种简洁的形式来表示，即p→q，其中p为前提，q为结论。

例如，“如果今天下雨，那么我就不去打篮球”就是一个假言命题。

另外，需要注意的是，假言命题只有在前提成立的情况下，结论才成立。

如果前提不成立，则结论可以是成立也可以是不成立，因此假言命题并不具有直接的确定性。

2、符号表示为了简化假言命题的表达方式，数理逻辑使用了一种符号表示法。

其中，箭头“→”被用来表示“如果……，则……”的关系，即前提和结果的关系。

例如，p→q表示“如果p，则q”或“p导致q”。

此外，还有一些常用符号可以和箭头一起使用，例如“∧”表示“与”、“∨”表示“或”、“¬”表示“非”等，这些符号常常可以用来表示逻辑命题的复合关系。

3、相关概念除了假言命题本身，还有一些相关的、重要的概念需要了解。

3.1 反命题反命题是指将假言命题中的前提和结论都取反得到的命题。

例如，对于假言命题“如果今天下雨，那么我就不去打篮球”，其反命题为“如果今天不下雨，那么我就去打篮球”。

需要注意的是，有些假言命题的反命题并不等价于原命题，因为它们的真假性可能会发生变化。

3.2 逆命题逆命题是指将假言命题中的前提和结论交换位置得到的命题。

例如，对于假言命题“如果今天下雨，那么我就不去打篮球”，其逆命题为“如果我不去打篮球，那么今天就下雨”。

同样需要注意的是，有些假言命题的逆命题也不等价于原命题，因为它们的真假性也可能会发生变化。

3.3 逆否命题逆否命题是指先将假言命题中的前提和结论交换位置，再分别取反得到的命题。

假言命题推理技巧假言命题推理是逻辑推理中的一个重要部分，它涉及到条件和结论的关系。

如果一个命题的结论只有在特定条件下才成立，则这种命题被称为假言命题。

假言命题可以分为两类：充分条件假言命题和必要条件假言命题。

充分条件假言命题是指一个条件（前件）存在，则另一个条件（后件）一定存在的命题。

它的逻辑形式是“如果P，则Q”。

例如，“如果天下雨，那么地面会湿。

”在这个例子中，“天下雨”是“地面会湿”的充分条件。

必要条件假言命题是指一个条件（前件）不存在，则另一个条件（后件）一定不存在的命题。

它的逻辑形式是“除非P，否则Q”。

例如，“除非你吃饭，否则你会饿。

”在这个例子中，“你吃饭”是“你不会饿”的必要条件。

在处理假言命题推理时，可以使用以下技巧：1. 理解逻辑形式：理解充分条件假言命题和必要条件假言命题的逻辑形式，可以帮助你更好地理解它们的含义和推理方式。

2. 寻找关键信息：在处理实际问题时，你需要找到关键的信息，如前提条件、结论和推理规则。

这些信息将帮助你进行正确的推理。

3. 使用逻辑符号：使用逻辑符号来表示前提条件和结论，可以使你的推理更加清晰和准确。

例如，你可以使用P表示前提条件，Q表示结论。

4. 应用推理规则：根据不同的逻辑形式，应用相应的推理规则。

对于充分条件假言命题，可以使用肯定前件或否定后件的推理规则；对于必要条件假言命题，可以使用否定前件或肯定后件的推理规则。

5. 注意例外情况：在处理假言命题推理时，需要注意可能的例外情况。

这些例外情况可能会使你的推理出现错误。

通过掌握这些技巧，你可以更好地理解和处理假言命题推理问题。

假言命题题目
假言命题题目示例如下：
1. 如果一个人不抽烟，那么他的血液中的胆固醇含量一定很低。

2. 如果一个人经常喝酒，那么他患心脏病的几率一定很高。

3. 如果一个人经常运动，那么他的身体一定很健康。

4. 如果一个人没有定期体检，那么他患癌症的几率一定很高。

5. 如果一个人经常吃蔬菜和水果，那么他的身体一定很健康。

6. 如果一个人经常熬夜，那么他的身体一定很虚弱。

7. 如果一个人经常读书，那么他的思维一定很敏捷。

8. 如果一个人经常旅游，那么他的视野一定很开阔。

9. 如果一个人经常学习新知识，那么他的能力一定很强。

10. 如果一个人经常练习口语，那么他的表达能力一定很好。

非q 所以，非P 即：
【 (p→q ) ∧﹃q】 → ﹃p
二、假言推理——2、必要条件假言推理
该推理指前提中有一个是必要条件假言命题，结论和 另一前提是性质命题。
p
q p←q 真 真 真：肯定后件就要肯定前件——用来推理
真 假 真：肯定前件不能肯定后件，否定后件不能
否定前件——防止推理错误
假 真 假：逻辑值为假，不能用来推理 假 假 真：否定前件就要否定后件——用来推理
2、必要条件假言命题
即前件是后件的必要条件的命题。必要条件就是：作为 产生某个结果的条件，它是必不可少的（唯一的），没有 这个条件，就一定没有相应的结果；但即使有了这个条件 也不一定有相应的结果（可能有，也可能无），因为可能
不充分，所以还需要别的条件辅助。
如：／只有认识错误，才能改正错误。（光认识错误，不 一定能改） 公式为：只有p，才q 或： P←q “←”读作“逆蕴涵”，
充分条件假言命题真值表
p 真 假 假 真 q 真 真 假 假 P→ｑ 真 真 真 假 p
必要条件假言命题真值表
q 真 假 假 真 P←ｑ 真 真 真 假
真 真 假 假
p 真 假 真 假
q 真 假 假 真
P←→ｑ 真 真 假 假
假 言 命 题 真 值 表
充 分 必 要 条 件
4、假言命题之间的转换 （1）充分――转换为必要： 如果p，则q――只有q，才可能p。即一个充分条件产 生了一个结果，只有从这个结果，才可以肯定这个充分条 件的存在的可能；如果没有这一结果，肯定没有任何产生 这一结果的充分条件。 ／如果物体摩擦，就会生热 ―― 只有物体发热了，才说明 有摩擦的可能（不发热，肯定没有摩擦）。 ／如果骄傲，就会落后 ―― 只有落后了，才说明他可能有 骄傲情绪（没落后，就肯定没有骄傲）。 注意，转换前后两个命题不能互相脱离而孤立地看， 如上句“有摩擦”，是承接原句来的，如果脱离了原句， 则不一定生热是“有摩擦”。表达上要合情理。如把上例 说成“只有生热，才摩擦”，“只有落后，他才骄傲”， 就匪夷所思。

逻辑知识之假言命题一、定义：所谓假言命题就是陈述某一事物情况是另一件事物情况的条件的命题，假言命题亦称条件命题。

例如：1. 如果在淀粉溶液里加入碘酒，那么淀粉溶液会变蓝。

2. 只有水分充足，庄稼才能茁壮生长。

3. 一个代数方程能得到根的计算公式当且仅当这个代数方程的次数不超过四。

二、分类：逻辑学考察的事物间的条件关系有三种：1. 如果有事物情况A，则必然有事物情况B；如果没有事物情况A而未必有事物情况B，A就是B的充分而不必要的条件，简称充分条件。

2. 如果没有事物情况A，则必然没有事物情况B；如果有事物情况A而未必有事物情况B，A就是B的必要而不充分的条件，简称必要条件。

3. 如果有事物情况A，则必然有事物情况B；如果没有事物情况A，则必然没有事物情况B，A就是B的充分必要条件。

例如：例1.A下雨；B地湿。

例2.A不断呼吸；B人能活着。

例3.A三角形等边；B三角形等角。

例1中的A是B的充分条件；例2中的A是B的必要条件；例3中的A是B的充分必要条件。

与此相应，假言命题也有三种，即：充分条件假言命题、必要条件假言命题和充分必要条件假言命题。

根据三种不同的假言命题的逻辑性质，相应地，也就有三种不同的假言推理。

1、充分条件假言命题：充分条件假言命题是陈述某一事物情况是另一件事物情况的充分条件的假言命题。

“如果，那么”是充分条件假言命题的联结词；“如果”后面的支命题称为前件；“那么”后面的支命题称为后件。

用p表示前件，用q表示后件，充分条件假言命题的的命题形式可表示为：如果p，那么q符号为：p→q(读作“p蕴涵q”）。

例如“如果物体不受外力作用，那么它将保持静止或匀速直线运动”是一个充分条件假言命题。

充分条件假言命题与其支命题（前件、后件）之间的真假关系是：如果前件真而后件假，则该充分条件假言命题才是假的；如果不是“前件真而后件假”，则该充分条件假言命题是真的。

这种真假关系可用下面的真值表来表示：p q 如果p，那么q______________________________真真真真假假假真真假假真2、必要条件假言命题：必要条件假言命题是陈述某一事物情况是另一件事物情况的必要条件的假言命题。

假言命题逻辑联词大全
1. 否定，表示命题的否定，常用符号为¬或~。

例如，¬P表示命题P的否定。

2. 合取，表示命题的合取（且），常用符号为∧或&。

例如，P∧Q表示命题P和Q同时成立。

3. 析取，表示命题的析取（或），常用符号为∨或|。

例如，P∨Q表示命题P或Q至少有一个成立。

4. 条件，表示命题的条件（如果...则...），常用符号为→。

例如，P→Q表示如果命题P成立，则命题Q也成立。

5. 双条件，表示命题的双条件（当且仅当），常用符号为↔。

例如，P↔Q表示命题P和Q同时成立或同时不成立。

6. 充分条件，表示命题的充分条件（如果...则...），常用符号为⇒。

例如，P⇒Q表示如果命题P成立，则命题Q也成立。

7. 必要条件，表示命题的必要条件（只有...才...），常用符
号为⇐。

例如，P⇐Q表示只有当命题Q成立时，命题P才成立。

8. 互斥，表示命题的互斥（不可能同时成立），常用符号为⊥。

例如，P⊥Q表示命题P和Q不可能同时成立。

以上是常见的假言命题逻辑联词，它们用于描述命题之间的逻
辑关系。

在逻辑推理和证明中，这些联词可以帮助我们分析和推导
命题之间的逻辑结构和关联性。

请看下列符号式：它们是否是有效式？
p→q p→q q←p q←p
0推理的相关知识，回答下列问题： (1)只有认真贯彻落实党的十七大精神，才能使中国发展得更好更快。要使中国发展得更好更快，所以，必须认真贯彻落实党的十七大精神。 问：这一推理属于何种形式的推理？试写出它的推理形式。 (2)某学园门口挂了一块牌子：“不懂几何者禁入”，某日来了一群懂几何的人。请问：这群人是否应该被允许进入？请说明你的理由。 (3)只有减少工业二氧化碳排放量，才能减缓温室效应。我们要减缓温室效应。 请问：以上述命题为前提，能否得出必然真的结论？如果能，结论是什么？
练习：
用p、q、r……等分别表示不同内容的简单命题，并用符号表示其逻辑联结词，写出下列复合命题的逻辑形式：
只有小芸、小茜同去，小耿才去。
广泛阅读优秀的读物，平时从各个渠道留心生活里的那些优美的有用的语言材料，不断地充实自己的语言积累，才能使自己的头脑里有一个丰富的语言宝库。
如果人们要使工作得到预想的效果，那么就要使自己的思想合乎客观外界的规律性。
补充：（4）设p为一前件，对任何后件q而言，要使“如果p，那么q”为真，请问：p应该取真值还是假值？
见教材112-113
（前件假，后件假，整个命题真。）
假如国内房价大致回落到2007年初的水平，那么2008年到2010年投资买房者的资产会缩水。
关于假言命题的说明：
充分条件假言命题与必要条件假言命题之间的相互转换
真假包公： 只要知道“石龟眼中流出的是血”，就是真包公；（说明：这个大前提是王丞相的看法，他把它看作充要条件，这是恰当的。所以这个前提是真的。） “真包公”知道“石龟眼中流出的是血”， 所以他就是真包公。（结论真） 只要知道“石龟眼中流出的是血”，就是真包公；（说明：这个大前提是王丞相的看法，他把它看作充要条件，这是恰当的。所以这个前提是真的。） “假包公”不知道“石龟眼中流出的是血”， 所以他不是真包公。（结论真）

第一章假言命题第一节充分条件1.只要诊断准确并且救治及时，那么这个病人就不会死亡。

现在这个病人不幸死亡了。

如果上述断定是真的，下面也一定真的是：A.对这个病人诊断不准确，但救治及时B.对这个病人诊断是准确的，但救治不及时C.如果这个病人死亡的原因是诊断不准确，那么救治不及时不会是原因D.如果对这个病人的诊断是准确的，那么，造成死亡的原因一定是救治不及时2.有人对“不到长城非好汉”这句名言的理解是：“如果不到长城，就不是好汉。

”假定这种理解为真，则下列哪项判断必然为真：A.到了长城的人就一定是好汉B.如果是好汉，他一定到过长城C.只有好汉，才到过长城D.不到长城，也会是好汉3.企业应事先征询气象预报。

因为如果不这样，企业就不会生产出适销对路的产品。

据此，可推出：A.如果企业事先征询气象预报，就会生产出适销对路的产品B.企业只有事先征询气象预报，才会生产出适销对路的产品C.企业事先征询气象预报，一定会提高经济效益和社会效益D.因人类认识的局限，目前气象预报的准确率还未达到较高水平4.如果赵川参加宴会，那么钱华、孙旭和李元将一起参加宴会。

如果上述断定是真的，那么，以下哪项也是真的：A.如果赵川没参加宴会，那么钱、孙、李三人中至少有一人没参加宴会B.如果赵川没参加宴会，那么钱、孙、李三人都没参加宴会C.如果钱、孙、李都参加宴会，那么赵川参加宴会D.如果孙旭没参加宴会，那么赵川和李元不会都参加宴会5.张明说：如果选李明当教练，那么王芳就要当领队。

李红：我不同意。

以下哪项最符合李红的意思：A.选李明当教练，但不能让王芳当领队B.如果选李明当教练，就不能让王芳当领队C.不选李明当教练，但要让王芳当领队D.如果不选李明当教练，就要让王芳当领队第二节必要条件1.以前在农村，只有男孩子才有读书的权力。

张飞农村出来，并顺利的考上大学。

那么张飞：A.与父母的关系搞得很好B.有头脑，接受了新思想C.是男孩，并受到了家里的重视D.是女孩，并受到家里的重视2.张三：只有正式党员才可以举手表决。

第四节假言命题及其推理一、假言命题假言命题是陈述某一事物情况存在是另一事物情况存在的条件的命题。

[例1] 如果一个人的行为没有社会危害性，那么就不能认为是犯罪。

[例2] 如果当事人是在违背自己意愿的情况下签订的合同，那么该合同无效。

[例3] 只要驳倒了被告的辩解，原告就能胜诉。

假言命题由联结词“如果……那么……”和支命题构成。

假言命题的逻辑联结词“如果……那么……”可以用蕴涵词“→”表示。

“如果”后面的支命题称作假言命题的前件，“那么”后面的支命题称作假言命题的后件。

在日常用语中，假言命题逻辑联结词的语言形式是多种多样的，除了“如果……那么……”外，还有“如果……则……”、“假如……那么……”、“只要……就……”，“……则……”等等。

假言命题的形式为：如果p，那么q。

用蕴涵词表示为：p→q。

由于假言命题是陈述事物情况之间的条件关系的命题，因此，一个假言命题的真假就只取决于其前件与后件的关系是否确实反映了事物情况之间的条件关系。

假言命题陈述前件蕴涵后件，也就是说，它陈述了前件真时，后件一定是真的。

假言从真值表中可以看出，当p真而q假时p→q为假。

当p真q也真，或者p假而q真，或者p假q也假时，p→q都是真的。

如上述[例1]，如果事实上一个人的行为没有社会危害性，而却被认为有罪，那么这个假言命题就是假的。

若不是这样，而是事实上某人的行为没有社会危害性并且不认为是犯罪，或某人的行为有社会危害性而被认为是犯罪，或者某人的行为有社会危害性而不认为是犯罪，这个假言命题都是真的。

需要指出的是，逻辑学虽然只从形式方面研究命题的真假性质，但在假言命题中，如果只考虑前、后件的真值关系，而不考虑前、后件的内容联系，那么就会出现前、后件没有内容上的联系，只是形式上正确的假言命题，这种假言命题被称为蕴涵怪论。

[例1]如果刑法是程序法，那么民法是实体法。

[例2]如果一个10周岁的儿童有选举权，那么某甲应该被判死刑。

[例1]中，前件“刑法是程序法”事实上是假的。

假言言语理解
假言命题是逻辑学中的一种命题，它表示一个条件和结论的关系，其中结论的真实性取决于条件的真实性。

假言命题通常由一个前件和一个后件组成，表示为 "如果P，那么Q"。

其中P是前件，Q是后件。

在逻辑学中，假言命题可以分为以下三种类型：
1. 充分条件假言命题：如果P，那么Q，其中P存在时Q一定存在。

2. 必要条件假言命题：只有当P，才Q，其中P不存在时Q一定不存在。

3. 充分必要条件假言命题：当且仅当P，才Q，其中P存在时Q一定存在，P不存在时Q一定不存在。

在理解假言命题时，需要注意以下几点：
1. 假言命题的前件和后件之间存在逻辑联系，这种联系表明了条件和结论之间的依赖关系。

2. 假言命题的真假取决于前件和后件之间的逻辑关系，如果前件为真而后件为假，则整个假言命题为假。

3. 在推理过程中，可以利用假言命题的性质进行推理，例如传递性、逆否律等。

在日常生活中，我们经常遇到假言命题的应用。

例如，“如果天下雨，那么地面会湿”，“只有努力学习，才能取得好成绩”等。

正确理解和应用假言命题可以帮助我们更好地进行逻辑推理和问题解决。

一、假言命题的概念及分类所谓假言命题就是陈述事物情况之间条件关系的命题，亦称条件命题。

根据肢命题间条件关系的不同可以分为三种：充分条件假言命题、必要条件假言命题和充分必要条件假言命题。

充分条件假言命题是陈述某一事物情况是另一件事物情况的充分条件的假言命题。

所谓A 是B的充分条件是指一种“充足但不必需〞的条件，即由A这个条件就能得出B结论；但没有这个条件却不一定得不出这个结论。

充分条件假言命题最常用的联结词是“如果……那么……〞；“如果〞后面的肢命题称为前件；“那么〞后面的肢命题称为后件。

其他常用的还有“只要……，就……、一……，就……、假设……，那么……、……必须……〞。

必要条件假言命题是陈述某一事物情况是另一件事物情况的必要条件的假言命题。

所谓“C“C是D的必需但不充足的条件，C与其他条件一起才能得到D，是D的必要条件〞含义就是：没有C就一定得不到D〞。

“只有……，才……〞是必要条件假言命题最常用的联结词。

其他常用的还有“不……,不……、除非……,否那么不……、没有……，没有……〞。

充分必要条件假言命题是陈述某一事物情况是另一件事物情况的充分必要条件的假言命题。

逻辑联结词通常为“当且仅当〞。

日常词项中通常还用：“只要而且只有……，才……、假设……那么……，且假设不……那么不……、当且仅当……那么……〞。

充分必要条件的含义是“充足且必需〞的意思。

“E是F的充分必要条件〞的含义是：“E是F的充足且必需的条件〞。

二、充分条件和必要条件的转化所以，“如果p，那么q〞等值于“只有q，才p〞；“只有p，才q〞等值于“如果q，那么p〞。

例如，“如果小红不吃饭，那么小明吃饭〞等值于“只有小明吃饭，小红才不吃饭〞。

“小红不吃饭〞是“小明吃饭〞的充分条件，同时，“小明吃饭〞是“小红不吃饭〞的必要条件。

充分条件和必要条件之间的转化关系虽然比较简单，但是在公务员考试中会经常出现。

例题：最近的一那么调查报告显示，参加民意测验的人中，有50％的人认为选举产生的官员如被控告有罪的就应辞职，而有35%的人认为只有中选产生的官员被宣判有罪时，他们才应当辞职。

逻辑结构
逻辑结构
假言命题由两部分组成：前件（条件 ）和后件（结论）。前件表示条件， 后件表示结论。
逻辑符号
在逻辑学中，我们通常用“→”表示 “如果...那么...”的逻辑关系。
特点与作用
特点
假言命题的特点是它表达了一个条件关系，即一个条件的成立将导致另一个条件的成立。
作用
假言命题在逻辑推理和论证中起着重要的作用，因为它可以表达因果关系或逻辑条件，帮助我们理解和解释事物 的规律和现象。
析取规则
如果"P或Q"是真的，那么P→Q和Q→P都是假的。
合取规则
如果"P和Q"是真的，那么P→Q和Q→P都是真的。
传递规则与反传递规则
要点一
传递规则
如果"如果P，则Q"和"如果Q，则R"都是真的，那么"如果P ，则R"也是真的。
要点二
反传递规则
如果"如果P，则Q"和"如果Q，则P"都是假的，那么"如果 P，则Q"和"如果¬Q，则¬P"都是真的。
假言命题翻译
目录
• 假言命题概述 • 假言命题的逻辑关系 • 假言命题的表示方法 • 假言命题的推理规则 • 假言命题的应用场景 • 假言命题的实例分析
01
假言命题概述
定义与分类
定义
假言命题是一种逻辑命题，它表达一个条件陈述，即如果一个条件成立，那么另一个条件也会 成立。
分类
根据条件和结论之间的关系，假言命题可以分为充分条件假言命题、必要条件假言命题和充分 必要条件假言命题。
实例五：自然灾害的预警系统
总结词
自然灾害预警系统通过监测自然现象建 立假言命题，预测灾害并发出预警。

假言命题例子
1. 如果明天下雨，那咱就不去爬山了。

就像上次，天气预报说明天会有暴雨，那咱还能傻愣愣地去爬山吗？肯定不能呀！
2. 要是你不好好学习，将来可就没有好出路啊！你想想那些整天混日子不学习的人，最后不都没啥好结果吗？
3. 只要你坚持锻炼，身体肯定会越来越健康的。

你看小区里的王大爷，每天坚持晨练，现在身体多棒啊！
4. 倘若你对别人撒谎，那别人还会相信你吗？这就好比你盖房子用了劣质材料，房子能牢固吗？
5. 假如你总是半途而废，怎么能做成大事呢？就像跑马拉松，中途放弃的人可尝不到冲过终点线的喜悦呀！
6. 要是你不懂得感恩，谁还愿意一直帮你呢？你想想那些忘恩负义的人，最后不是都众叛亲离了吗？
7. 只要你对生活充满热情，生活也会回馈你美好的呀！这跟你对花精心浇灌，花就会绽放得灿烂是一个道理嘛！
8. 倘若你不尊重别人，又怎么能奢求别人尊重你呢？这不是显而易见的事情吗？
我的观点结论就是：假言命题在我们的生活中随处可见呀，它能让我们更清晰地思考事情之间的逻辑关系呢！。