直线与平面、平面与平面平行的判定(附答案)
- 格式:docx
- 大小:576.96 KB
- 文档页数:12

专题十二空间直线、平面的平行知识精讲一知识结构图二.学法指导1.空间两条直线平行的证明一是定义法:即证明两条直线在同一个平面内且两直线没有公共点;二是利用平面图形的有关平行的性质,如三角形中位线,梯形,平行四边形等关于平行的性质;三是利用基本事实4:找到一条直线,使所证的直线都与这条直线平行.2.求证角相等一是用等角定理;二是用三角形全等或相似.3.利用直线与平面平行的判定定理证明线面平行,关键是寻找平面内与已知直线平行的直线.4.证线线平行的方法常用三角形中位线定理、平行四边形性质、平行线分线段成比例定理、基本事实4等.5.线面平行的性质和判定经常交替使用,也就是通过线线平行得到线面平行,再通过线面平行得线线平行.利用线面平行的性质定理解题的具体步骤:(1)确定(或寻找)一条直线平行于一个平面;(2)确定(或寻找)过这条直线且与这个平行平面相交的平面;(3)确定交线;(4)由性质定理得出线线平行的结论.6.平面与平面平行的判定方法:(1)定义法:两个平面没有公共点.(2)判定定理:一个平面内的两条相交直线分别平行于另一个平面.(3)转化为线线平行:平面α内的两条相交直线与平面β内的两条相交直线分别平行,则α∥β.(4)利用平行平面的传递性:若α∥β,β∥γ,则α∥γ.7.应用平面与平面平行性质定理的基本步骤:8.证明直线与直线平行的方法(1)平面几何中证明直线平行的方法.如同位角相等,两直线平行;三角形中位线的性质;平面内垂直于同一直线的两条直线互相平行等.(2)基本事实4.(3)线面平行的性质定理. (4)面面平行的性质定理. 9. 证明直线与平面平行的方法:(1)线面平行的判定定理.(2)两个平面平行,其中一个平面内的任意一条直线平行于另一个平面.三.知识点贯通知识点1 基本事实4、等角定理的应用1.基本事实4文字表述:平行于同一条直线的两条直线平行.这一性质叫做空间平行线的传递性. 符号表述:⎭⎪⎬⎪⎫a ∥b b ∥c ⇒a ∥c . 2.等角定理如果空间中两个角的两条边分别对应平行,那么这两个角相等或互补. 例题1.如图,在正方体ABCD A 1B 1C 1D 1中,M ,M 1分别是棱AD 和A 1D 1的中点.(1)求证:四边形BB 1M 1M 为平行四边形; (2)求证:∠BMC =∠B 1M 1C 1.【解析】 (1)∵ABCD A 1B 1C 1D 1为正方体.∴AD =A 1D 1,且AD ∥A 1D 1,又M,M1分别为棱AD,A1D1的中点,∴AM=A1M1且AM∥A1M1,∴四边形AMM1A1为平行四边形,∴MM1=AA1且MM1∥AA1.又AA1=BB1且AA1∥BB1,∴MM1=BB1且MM1∥BB1,∴四边形BB1M1M为平行四边形.(2)由(1)知四边形BB1M1M为平行四边形,∴B1M1∥BM.同理可得四边形CC1M1M为平行四边形,∴C1M1∥CM.∵∠BMC和∠B1M1C1方向相同,∴∠BMC=∠B1M1C1.知识点二直线与平面平行的判定直线与平面平行的判定例题2:如图,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.求证:(1)EH∥平面BCD;(2)BD∥平面EFGH.【解析】(1)∵EH为△ABD的中位线,∴EH∥BD.∵EH⊄平面BCD,BD⊂平面BCD,∴EH∥平面BCD.(2)∵BD∥EH,BD⊄平面EFGH,EH⊂平面EFGH,∴BD∥平面EFGH.知识点三直线与平面平行的判定与性质直线与平面平行的判定及性质例题3已知直线a,l,平面α,β满足α∩β=l,a∥α,a∥β.求证:a∥l.【证明】如图所示,过a作平面γ交平面α于b,∵a∥α,∴a∥b.同样过a作平面δ交平面β于c,∵a∥β,∴a∥c.则b∥c.又∵b⊄β,c⊂β,∴b∥β.又∵b⊂α,α∩β=l,∴b∥l.又∵a∥b,∴a∥l.知识点四平面与平面平行的判定1.平面与平面平行的判定(1)文字语言:如果一个平面内的两条相交直线与另一个平面平行,那么这两个平面平行.(2)符号语言:a⊂β,b⊂β,a∩b=P,a∥α,b∥α⇒β∥α.(3)图形语言:如图所示.例题4.如图,在正方体ABCDA1B1C1D1中,M、E、F、N分别是A1B1、B1C1、C1D1、D1A1的中点.求证:(1)E、F、B、D四点共面;(2)平面MAN∥平面EFDB.【解析】(1)连接B1D1,∵E、F分别是边B1C1、C1D1的中点,∴EF∥B1D1.而BD∥B1D1,∴BD∥EF.∴E、F、B、D四点共面.(2)易知MN∥B1D1,B1D1∥BD,∴MN∥BD.又MN⊄平面EFDB,BD⊂平面EFDB.∴MN∥平面EFDB.连接MF.∵M、F分别是A1B1、C1D1的中点,∴MF∥A1D1,MF=A1D1.∴MF∥AD且MF=AD.∴四边形ADFM是平行四边形,∴AM∥DF.又AM⊄平面BDFE,DF⊄平面BDFE,∴AM∥平面BDFE.又∵AM∩MN=M,∴平面MAN∥平面EFDB.知识点五平面与平面平行的性质1.平面与平面平行的性质定理(1)文字语言:两个平面平行,如果另一个平面与这两个平面相交,那么两条交线平行.(2)符号语言:α∥β,α∩γ=a,β∩γ=b⇒a∥b.(3)图形语言:如图所示.(4)作用:证明两直线平行.例题5 如图,已知平面α∥平面β,P ∉α且P ∉β,过点P 的直线m 与α、β分别交于A 、C ,过点P 的直线n 与α、β分别交于B 、D ,且P A =6,AC =9,PD =8,求BD 的长.【解析】 因为AC ∩BD =P ,所以经过直线AC 与BD 可确定平面PCD ,因为α∥β,α∩平面PCD =AB ,β∩平面PCD =CD ,所以AB ∥CD .所以P A AC =PB BD ,即69=8-BDBD . 所以BD =245.五 易错点分析易错一 等角定理的运用例题5.已知角α和角β的两边分别平行且一组边方向相同,另一组边的方向相反,若α=45°,则β= . 【答案】135°【解析】由等角定理可知β=135°. 误区警示利用等角定理求角的大小,应注意两角的边的方向之间的关系。
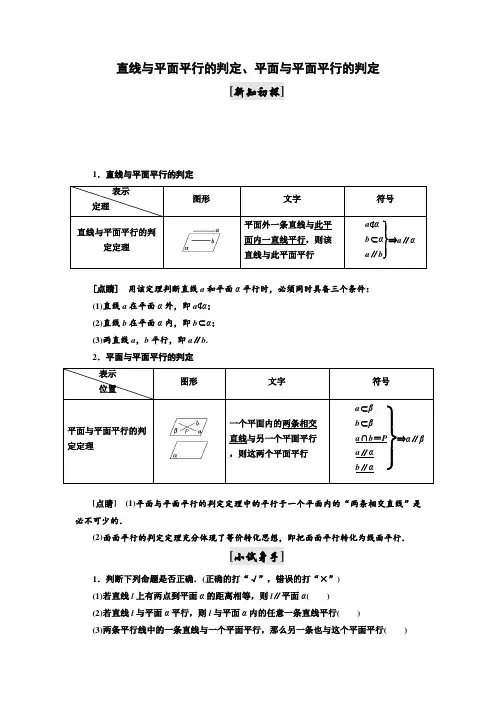
直线与平面平行的判定、平面与平面平行的判定[新知初探]1.直线与平面平行的判定[点睛]用该定理判断直线a和平面α平行时,必须同时具备三个条件:(1)直线a在平面α外,即a⊄α;(2)直线b在平面α内,即b⊂α;(3)两直线a,b平行,即a∥b.2.平面与平面平行的判定[点睛](1)平面与平面平行的判定定理中的平行于一个平面内的“两条相交直线”是必不可少的.(2)面面平行的判定定理充分体现了等价转化思想,即把面面平行转化为线面平行.[小试身手]1.判断下列命题是否正确.(正确的打“√”,错误的打“×”)(1)若直线l上有两点到平面α的距离相等,则l∥平面α()(2)若直线l与平面α平行,则l与平面α内的任意一条直线平行()(3)两条平行线中的一条直线与一个平面平行,那么另一条也与这个平面平行()答案:(1)× (2)× (3)×2.能保证直线a 与平面α平行的条件是( ) A .b ⊂α,a ∥bB .b ⊂α,c ∥α,a ∥b ,a ∥cC .b ⊂α,A ,B ∈a ,C ,D ∈b ,且AC ∥BD D .a ⊄α,b ⊂α,a ∥b解析:选D 由线面平行的判定定理可知,D 正确.3.若一个平面内的两条直线分别平行于另一个平面内的两条直线,则这两个平面的位置关系是( )A .一定平行B .一定相交C .平行或相交D .以上判断都不对解析:选C 可借助于长方体判断两平面对应平行或相交.直线与平面平行的判定[典例] 如图,在正方体ABCD -A 1B 1C 1D 1中,E ,F ,G 分别是BC ,CC 1,BB 1的中点,求证:EF ∥平面AD 1G .[证明] 连接BC 1,则由E ,F 分别是BC ,CC 1的中点,知EF ∥BC 1. 又AB 綊A 1B 1綊D 1C 1,所以四边形ABC 1D 1是平行四边形, 所以BC 1∥AD 1,所以EF ∥AD 1. 又EF ⊄平面AD 1G ,AD 1⊂平面AD 1G , 所以EF ∥平面AD 1G .利用直线和平面平行的判定定理证明线面平行的关键是在平面内找一条直线与已知直线平行,常利用平行四边形、三角形中位线、平行公理等.已知有公共边AB 的两个全等的矩形ABCD 和ABEF 不同在一个平面内,P ,Q 分别是对角线AE ,BD 上的点,且AP =DQ .求证:PQ ∥平面CBE .证明:如图,作PM ∥AB 交BE 于点M ,作QN ∥AB 交BC 于点N ,连接MN ,则PM ∥QN ,PM AB =EP EA ,QN CD =BQ BD .∵EA =BD ,AP =DQ ,∴EP =BQ . 又∵AB =CD ,∴PM 綊QN ,∴四边形PMNQ 是平行四边形,∴PQ ∥MN . 又∵PQ ⊄平面CBE ,MN ⊂平面CBE , ∴PQ ∥平面CBE .平面与平面平行的判定[典例] 已知,点P 是△ABC 所在平面外一点,点A ′,B ′,C ′分别是△PBC ,△PAC ,△PAB 的重心.(1)求证:平面A ′B ′C ′∥平面ABC . (2)求A ′B ′∶AB 的值.[解] (1)证明:如图,连接PA ′,并延长交BC 于点M ,连接PB ′,并延长交AC 于点N ,连接PC ′,并延长交AB 于点Q ,连接MN ,NQ .∵A ′,B ′,C ′分别是△PBC ,△PAC ,△PAB 的重心, ∴M ,N ,Q 分别是△ABC 的边BC ,AC ,AB 的中点,且PA ′A ′M =PB ′B ′N =2,∴A ′B ′∥MN .同理可得B ′C ′∥NQ .∵A ′B ′∥MN ,MN ⊂平面ABC ,A ′B ′⊄平面ABC , ∴A ′B ′∥平面ABC . 同理可证B ′C ′∥平面ABC .又∵A ′B ′∩B ′C ′=B ′,A ′B ′⊂平面A ′B ′C ′,B ′C ′⊂平面A ′B ′C ′, ∴平面A ′B ′C ′∥平面ABC .(2)由(1)知A ′B ′∥MN ,且A ′B ′MN =PA ′PM =23,即A ′B ′=23MN .∵M ,N 分别是BC ,AC 的中点,∴MN =12AB .∴A ′B ′=23MN =23×12AB =13AB ,∴A ′B ′AB =13,即A ′B ′∶AB 的值为13.两个平面平行的判定定理是确定面面平行的重要方法.解答问题时一定要寻求好判定定理所需要的条件,特别是相交的条件,即与已知平面平行的两条直线必须相交,才能确定面面平行.如图,在三棱柱ABC -A 1B 1C 1中,E ,F ,G ,H 分别 是AB ,AC ,A 1B 1,A 1C 1的中点. 求证:(1)B ,C ,H ,G 四点共面; (2)平面EFA 1∥平面BCHG .证明:(1)∵GH 是△A 1B 1C 1的中位线, ∴GH ∥B 1C 1.又B 1C 1∥BC ,∴GH ∥BC , ∴B ,C ,H ,G 四点共面.(2)∵E ,F 分别为AB ,AC 的中点,∴EF ∥BC . ∵EF ⊄平面BCHG ,BC ⊂平面BCHG , ∴EF ∥平面BCHG .∵A 1G 綊EB ,∴四边形A 1EBG 是平行四边形, ∴A 1E ∥GB .∵A 1E ⊄平面BCHG ,GB ⊂平面BCHG , ∴A 1E ∥平面BCHG .∵A 1E ∩EF =E ,∴平面EFA 1∥平面BCHG .平行中探索存在性问题[典例] 在三棱柱ABC -A 1B 1C 1中,D ,E 分别是线段BC ,CC 1的中点,在线段AB 上是否存在一点M ,使直线DE ∥平面A 1MC ?请证明你的结论.[解] 如图,取线段AB 的中点M ,连接A 1M ,MC ,A 1C ,AC 1,设O 为A 1C ,AC 1的交点.由已知,O 为AC 1的中点.连接MD ,OE ,则MD ,OE 分别为△ABC ,△ACC 1的中位线, 所以MD 綊12AC ,OE 綊12AC ,因此MD 綊OE .连接OM ,从而四边形MDEO 为平行四边形,则DE ∥MO . 因为直线DE ⊄平面A 1MC ,MO ⊂平面A 1MC , 所以直线DE ∥平面A 1MC .即线段AB 上存在一点M (线段AB 的中点),使直线DE ∥平面A 1MC .平行中探索存在性问题的判定是高考的常考内容,多出现在解答题中.证明线面平行的关键是找线线平行,注意利用所给几何体中隐含的线线位置关系,当题目中有中点时,一般考虑先探索中点,再用中位线定理找平行关系.[活学活用]如图所示,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为CC1,C1D1,DD1,CD的中点.N为BC的中点.试在E,F,G,H四个点中找两个点,使这两个点与点N确定一个平面α,且平面α∥平面BB1D1D.解:由面面平行的判定定理,若使平面α∥平面BB1D1D,只需在平面α内有两条相交直线平行于平面BB1D1D,或在平面α内有两条相交直线平行于平面BB1D1D内的两条相交直线即可.连接HN,HF,NF,易知HN∥BD,HF∥DD1,所以平面NHF∥平面BB1D1D,即在E,F,G,H四个点中,由H,F两点与点N确定的平面α满足条件.层级一学业水平达标1.下列选项中,一定能得出直线m与平面α平行的是()A.直线m在平面α外B.直线m与平面α内的两条直线平行C.平面α外的直线m与平面内的一条直线平行D.直线m与平面α内的一条直线平行解析:选C选项A不符合题意,因为直线m在平面α外也包括直线与平面相交;选项B与D不符合题意,因为缺少条件m⊄α;选项C中,由直线与平面平行的判定定理,知直线m与平面α平行,故选项C符合题意.2.已知α,β是两个不重合的平面,下列选项中,一定能得出平面α与平面β平行的是()A.平面α内有一条直线与平面β平行B.平面α内有两条直线与平面β平行C.平面α内有一条直线与平面β内的一条直线平行D.平面α与平面β不相交解析:选D选项A、C不正确,因为两个平面可能相交;选项B不正确,因为平面α内的这两条直线必须相交才能得到平面α与平面β平行;选项D正确,因为两个平面的位置关系只有相交与平行两种.故选D.3.在三棱锥A-BCD中,E,F分别是AB和BC上的点,若AE∶EB=CF∶FB=2∶5,则直线AC与平面DEF的位置关系是()A.平行B.相交C.直线AC在平面DEF内D.不能确定解析:选A∵AE∶EB=CF∶FB=2∶5,∴EF∥AC.又EF⊂平面DEF,AC⊄平面DEF,∴AC∥平面DEF.4.已知a,b,c,d是四条直线,α,β是两个不重合的平面,若a∥b∥c∥d,a⊂α,b⊂α,c⊂β,d⊂β,则α与β的位置关系是()A.平行B.相交C.平行或相交D.以上都不对解析:选C根据图1和图2可知α与β平行或相交.5.如图,下列正三棱柱ABC-A1B1C1中,若M,N,P分别为其所在棱的中点,则不能得出AB∥平面MNP的是()解析:选C在图A、B中,易知AB∥A1B1∥MN,所以AB∥平面MNP;在图D中,易知AB∥PN,所以AB∥平面MNP.故选C.6.已知l,m是两条直线,α是平面,若要得到“l∥α”,则需要在条件“m⊂α,l∥m”中另外添加的一个条件是________.解析:根据直线与平面平行的判定定理,知需要添加的一个条件是“l⊄α”.答案:l⊄α7.已知A,B两点是平面α外两点,则过A,B与α平行的平面有________个.解析:当A,B两点在平面α异侧时,不存在这样的平面.当A,B两点在平面同侧时,若直线AB∥α,则存在一个,否则不存在.答案:0或18.如图,在五面体FE-ABCD中,四边形CDEF为矩形,M,N分别是BF,BC的中点,则MN与平面ADE的位置关系是________.解析:∵M,N分别是BF,BC的中点,∴MN∥CF.又四边形CDEF为矩形,∴CF∥DE,∴MN∥DE.又MN⊄平面ADE,DE⊂平面ADE,∴MN∥平面ADE.答案:平行9.如图所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD.E,F,G分别为线段PC,PD,BC的中点,现将△PDC折起,使点P∉平面ABCD.求证:平面PAB∥平面EFG.证明:∵PE=EC,PF=FD,∴EF∥CD,又∵CD∥AB,∴EF∥AB.又EF⊄平面PAB,∴EF∥平面PAB.同理可证EG∥平面PAB.又∵EF∩EG=E,∴平面PAB∥平面EFG.10.已知正方形ABCD,如图(1)E,F分别是AB,CD的中点,将△ADE沿DE折起,如图(2)所示,求证:BF∥平面ADE.证明:∵E,F分别为AB,CD的中点,∴EB=FD.又∵EB∥FD,∴四边形EBFD为平行四边形,∴BF∥ED.∵DE⊂平面ADE,而BF⊄平面ADE,∴BF∥平面ADE.层级二应试能力达标1.若直线l不平行于平面α,且l⊄α,则()A.α内的所有直线与l异面B.α内不存在与l平行的直线C.α内存在唯一的直线与l平行D.α内的直线与l都相交解析:选B若在平面α内存在与直线l平行的直线,因l⊄α,故l∥α,这与题意矛盾.2.在正方体EFGH-E1F1G1H1中,下列四对截面彼此平行的一对是()A.平面E1FG1与平面EGH1B.平面FHG1与平面F1H1GC.平面F1H1H与平面FHE1D.平面E1HG1与平面EH1G解析:选A画出相应的截面如图所示,即可得答案.3.已知P是正方体ABCD-A1B1C1D1的棱DD1上任意一点(不是端点),则在正方体的12条棱中,与平面ABP平行的有()A.3个B.6个C.9个D.12个解析:选A因为棱AB在平面ABP内,所以只要与棱AB平行的棱都满足题意,即A1B1,D1C1,DC.4.A,B是直线l外的两点,过A,B且和l平行的平面有()A.0个B.1个C.无数个D.以上都有可能解析:选D若AB与l平行,则和l平行的平面有无数个;若AB与l相交,则和l 平行的平面没有;若AB与l异面,则和l平行的平面有一个.5.已知三棱柱ABC-A1B1C1,D,E,F分别是棱AA1,BB1,CC1的中点,则平面DEF 与平面ABC的位置关系是________.解析:∵D,E,F分别是棱AA1,BB1,CC1的中点,∴在平行四边形AA1B1B与平行四边形BB1C1C中,DE∥AB,EF∥BC,∴DE∥平面ABC,EF∥平面ABC.又DE∩EF=E,∴平面DEF ∥平面ABC.答案:平行6.如图是一几何体的平面展开图,其中ABCD为正方形,E,F,G,H分别为PA,PD,PC,PB的中点.在此几何体中,给出下面四个结论:①平面EFGH∥平面ABCD;②直线PA∥平面BDG;③直线EF∥平面PBC;④直线EF∥平面BDG.其中正确的序号是________.解析:作出立体图形,可知平面EFGH ∥平面ABCD ;PA ∥平面BDG ;EF ∥HG ,所以EF ∥平面PBC ;直线EF 与平面BDG 不平行.答案:①②③7.如图所示,在正方体ABCD -A 1B 1C 1D 1中,S 是B 1D 1的中点,E ,F ,G 分别是BC ,DC 和SC 的中点.求证:平面EFG ∥平面BDD 1B 1.证明:如图所示,连接SB ,SD , ∵F ,G 分别是DC ,SC 的中点, ∴FG ∥SD .又∵SD ⊂平面BDD 1B 1,FG ⊄平面BDD 1B 1, ∴FG ∥平面BDD 1B 1. 同理可证EG ∥平面BDD 1B 1, 又∵EG ⊂平面EFG ,FG ⊂平面EFG ,EG ∩FG =G , ∴平面EFG ∥平面BDD 1B 1.8.如图,已知底面是平行四边形的四棱锥P -ABCD ,点E 在PD 上,且PE ∶ED =2∶1,在棱PC 上是否存在一点F ,使BF ∥平面AEC ?若存在,请证明你的结论,并说出点F 的位置;若不存在,请说明理由.解:当F 是棱PC 的中点时,BF ∥平面AEC .证明如下:取PE 的中点M ,连接FM ,则FM ∥CE .因为FM ⊄平面AEC , EC ⊂平面AEC , 所以FM ∥平面AEC .由EM =12PE =ED ,得E 为MD 的中点,连接BM ,BD ,设BD ∩AC =O ,则O 为BD 的中点. 连接OE ,则BM ∥OE .因为BM ⊄平面AEC ,OE ⊂平面AEC , 所以BM ∥平面AEC .又因为FM ⊂平面BFM ,BM ⊂平面BFM ,FM ∩BM =M , 所以平面BFM ∥平面AEC ,所以平面BFM 内的任何直线与平面AEC 均没有公共点. 又BF ⊂平面BFM ,所以BF 与平面AEC 没有公共点,所以BF∥平面AEC.。


2.2.直线、平面平行的判定及其性质2.2.1 直线与平面平行的判定●知识梳理1、直线与平面平行的判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
简记为:线线平行,则线面平行。
符号表示:a αb β => a∥αa∥b●知能训练一.选择题1.已知m,n是两条不同直线,α,β,γ是三个不同平面,下列命题中正确的是()A.若m∥α,n∥α,则m∥n B.若α⊥γ,β⊥γ,则α∥βC.若m∥α,m∥β,则α∥βD.若m⊥α,n⊥α,则m∥n2.若直线l不平行于平面α,且l⊄α,则()A.α内存在直线与l异面B.α内存在与l平行的直线C.α内存在唯一的直线与l平行D.α内的直线与l都相交3.如图,M是正方体ABCD-A1B1C1D1的棱DD1的中点,给出下列命题①过M点有且只有一条直线与直线AB、B1C1都相交;②过M点有且只有一条直线与直线AB、B1C1都垂直;③过M点有且只有一个平面与直线AB、B1C1都相交;④过M点有且只有一个平面与直线AB、B1C1都平行.其中真命题是()A.②③④B.①③④C.①②④D.①②③4.正方体ABCD-A1B1C1D1中M,N,Q分别是棱D1C1,A1D1,BC的中点.P在对角线BD1上,且BP=BD1,给出下面四个命题:(1)MN∥面APC;(2)C1Q∥面APC;(3)A,P,M三点共线;(4)面MNQ∥面APC.正确的序号为()A.(1)(2)B.(1)(4)C.(2)(3)D.(3)(4)5.在正方体ABCD-A1B1C1D1的各个顶点与各棱中点共20个点中,任取两点连成直线,所连的直线中与A1BC1平行的直线共有()A.12条B.18条C.21条D.24条6.直线a∥平面α,P∈α,那么过P且平行于a的直线()A.只有一条,不在平面α内B.有无数条,不一定在平面α内C.只有一条,且在平面α内D.有无数条,一定在平面α内7.如果直线a∥平面α,那么直线a与平面α内的()A.一条直线不相交B.两条直线不相交C.无数条直线不相交D.任意一条直线不相交8.如图在正方体ABCD-A1B1C1D1中,与平面AB1C平行的直线是()A.DD1B.A1D1C.C1D1D.A1D9.如图,在三棱柱ABC-A1B1C1中,点D为AC的中点,点D1是A1C1上的一点,若BC1∥平面AB1D1,则等于()A.1/2B.1 C.2 D.310.下面四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形是()A.①②B.①④C.②③D.③④11.如图,正方体的棱长为1,线段B′D′上有两个动点E,F,EF=,则下列结论中错误的是()A.AC⊥BEB.EF∥平面ABCDC.三棱锥A-BEF的体积为定值D.异面直线AE,BF所成的角为定值二.填空题12.如图,在正方体ABCD-A1B1C1D1中,E,F,G,H,M分别是棱AD,DD1,D1A1,A1A,AB的中点,点N在四边形EFGH的四边及其内部运动,则当N只需满足条件时,就有MN⊥A1C1;当N只需满足条件时,就有MN∥平面B1D1C.13.如图,正方体ABCD-A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上,若EF∥平面AB1C,则线段EF的长度等于.三.解答题14.如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.(1)求证:AB 1∥平面BC1D;(2)若BC=3,求三棱锥D-BC1C的体积.2.2.2 平面与平面平行的判定●知识梳理1、两个平面平行的判定定理:一个平面内的两条交直线与另一个平面平行,则这两个平面平行。
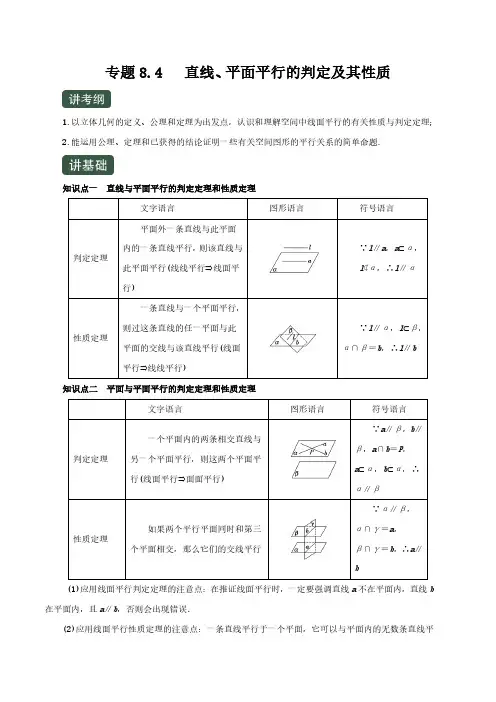
专题8.4 直线、平面平行的判定及其性质1.以立体几何的定义、公理和定理为出发点,认识和理解空间中线面平行的有关性质与判定定理;2.能运用公理、定理和已获得的结论证明一些有关空间图形的平行关系的简单命题.知识点一直线与平面平行的判定定理和性质定理文字语言图形语言符号语言判定定理平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行(线线平行⇒线面平行)∵l∥a,a⊂α,l⊄α,∴l∥α性质定理一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行(线面平行⇒线线平行)∵l∥α,l⊂β,α∩β=b,∴l∥b知识点二平面与平面平行的判定定理和性质定理文字语言图形语言符号语言判定定理一个平面内的两条相交直线与另一个平面平行,则这两个平面平行(线面平行⇒面面平行)∵a∥β,b∥β,a∩b=P,a⊂α,b⊂α,∴α∥β性质定理如果两个平行平面同时和第三个平面相交,那么它们的交线平行∵α∥β,α∩γ=a,β∩γ=b,∴a∥b(1)应用线面平行判定定理的注意点:在推证线面平行时,一定要强调直线a不在平面内,直线b 在平面内,且a∥b,否则会出现错误.(2)应用线面平行性质定理的注意点:一条直线平行于一个平面,它可以与平面内的无数条直线平行,但这条直线与平面内的任意一条直线可能平行,也可能异面.(3)线面平行的判定定理和性质定理使用的区别:如果结论中有a ∥α,则要用判定定理,在α内找与a 平行的直线;如果条件中有a ∥α,则要用性质定理,找(或作)过a 且与α相交的平面.应用定理证明有关平行问题时,一定要满足定理的前提条件.(4)面面平行判定定理的一个推论:如果一个平面内的两条相交直线分别平行于另一个平面内的两条相交直线,则这两个平面平行.符号表示:a ⊂α,b ⊂α,a ∩b =O ,a ′⊂β,b ′⊂β,a ′∩b ′=O ′,a ∥a ′,b ∥b ′⇒α∥β.【知识必备】1.两个平面平行,其中一个平面内的任意一条直线平行于另一个平面. 2.夹在两个平行平面之间的平行线段长度相等. 3.经过平面外一点有且只有一个平面与已知平面平行. 4.两条直线被三个平行平面所截,截得的对应线段成比例. 5.同一条直线与两个平行平面所成角相等.6.如果两个平面分别平行于第三个平面,那么这两个平面互相平行.考点一 与线、面平行相关命题的判定【例1】【2019年高考全国Ⅱ卷】设α,β为两个平面,则α∥β的充要条件是( ) A .α内有无数条直线与β平行 B .α内有两条相交直线与β平行 C .α,β平行于同一条直线D .α,β垂直于同一平面【解析】由面面平行的判定定理知:α内两条相交直线都与β平行是αβ∥的充分条件,由面面平行性质定理知,若αβ∥,则α内任意一条直线都与β平行,所以α内两条相交直线都与β平行是αβ∥的必要条件,故选B .【举一反三】【2019年高考北京卷】已知l ,m 是平面α外的两条不同直线.给出下列三个论断: ①l ⊥m ;②m ∥α;③l ⊥α.以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:__________. 【解析】将所给论断,分别作为条件、结论,得到如下三个命题: (1)如果l ⊥α,m ∥α,则l ⊥m ,正确;(2)如果l ⊥α,l ⊥m ,则m ∥α,不正确,有可能m 在平面α内; (3)如果l ⊥m ,m ∥α,则l ⊥α,不正确,有可能l 与α斜交、l ∥α.故答案为:如果l⊥α,m∥α,则l⊥m.【举一反三】(一中2019届高三模拟)(1)在空间中,a,b,c是三条不同的直线,α,β是两个不同的平面,则下列命题中的真命题是( )A.若a⊥c,b⊥c,则a∥bB.若a⊂α,b⊂β,α⊥β,则a⊥bC.若a∥α,b∥β,α∥β,则a∥bD.若α∥β,a⊂α,则a∥β(2)下列四个正方体中,A,B,C为所在棱的中点,则能得出平面ABC∥平面DEF的是( )【解析】(1)对于A,若a⊥c,b⊥c,则a与b可能平行、异面、相交,故A是假命题;对于B,设α∩β=m,若a,b均与m平行,则a∥b,故B是假命题;对于C,a,b可能平行、异面、相交,故C是假命题;对于D,若α∥β,a⊂α,则a与β没有公共点,则a∥β,故D是真命题.(2)在B中,如图,连接MN,PN,∵A,B,C为正方体所在棱的中点,∴AB∥MN,AC∥PN,∵MN∥DE,PN∥EF,∴AB∥DE,AC∥EF,∵AB∩AC=A,DE∩EF=E,AB,AC⊂平面ABC,DE,EF⊂平面DEF,∴平面ABC∥平面DEF. 故B正确【变式1】(贵州凯里一中2019届高三模拟)(1)下列命题正确的是( )A.若两条直线和同一个平面平行,则这两条直线平行B.若一条直线与两个平面所成的角相等,则这两个平面平行C.若一条直线与两个相交平面都平行,则这条直线与这两个平面的交线平行D.若两个平面垂直于同一个平面,则这两个平面平行【解析】(1)A选项中两条直线可能平行也可能异面或相交;对于B选项,如图,在正方体ABCD-A1B1C1D1中,平面ABB1A1和平面BCC1B1与B1D1所成的角相等,但这两个平面垂直;D选项中两平面也可能相交.C正确.考点二直线与平面平行的判定与性质【典例2】(陕西西安中学2019届高三质检)如图所示,斜三棱柱ABCA1B1C1中,点D,D1分别为AC,A1C1的中点.求证:(1)AD1∥平面BDC1;(2)BD∥平面AB1D1.【证明】(1)∵D1,D分别为A1C1,AC的中点,四边形ACC1A1为平行四边形,∴C1D1DA,∴四边形ADC1D1为平行四边形,∴AD1∥C1D.又AD1⊄平面BDC1,C1D⊂平面BDC1,∴AD1∥平面BDC1.(2)连接DD1,∵BB1∥平面ACC1A1,BB1⊂平面BB1D1D,平面ACC1A1∩平面BB1D1D=DD1,∴BB1∥DD1,又∵D1,D分别为A1C1,AC的中点,∴BB1=DD1,故四边形BDD1B1为平行四边形,∴BD∥B1D1,又BD⊄平面AB1D1,B1D1⊂平面AB1D1,∴BD∥平面AB1D1.考点三面面平行的判定与性质【典例3】(广西柳州高级中学2019届高三模拟)如图,在三棱柱ABCA1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:(1)B,C,H,G四点共面;(2)平面EFA1∥平面BCHG.【证明】(1)∵在△A1B1C1中,G,H分别是A1B1,A1C1的中点,∴GH∥B1C1.又∵B1C1∥BC,∴GH∥BC,∴GH与BC确定一个平面α,∴G,H,B,C∈α,∴B,C,H,G四点共面.(2)∵E,F分别是AB,AC的中点,∴EF∥BC,∵EF⊄平面BCHG,BC⊂平面BCHG,∴EF∥平面BCHG.易证A1G EB,∴四边形A1EBG是平行四边形,∴A1E∥GB.∵A1E⊄平面BCHG,GB⊂平面BCHG.∴A1E∥平面BCHG.∵A1E∩EF=E,且A1E⊂平面EFA1,EF⊂平面EFA1,∴平面EFA1∥平面BCHG.【方法技巧】证明面面平行的常用方法(1)面面平行的定义,即证两个平面没有公共点(不常用);(2)面面平行的判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行(主要方法);(3)利用垂直于同一条直线的两个平面平行(客观题常用);(4)如果两个平面同时平行于第三个平面,那么这两个平面平行(客观题常用);(5)利用“线线平行”“线面平行”“面面平行”的相互转化进行证明.【变式3】(广东中山一中2019届高三模拟)如图所示,在四棱锥EABCD中,△ABD为正三角形,CB =CD,EC⊥BD.(1)求证:BE=DE;(2)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.证明:(1)取BD的中点O,连接OC,OE.∵CB=CD,∴CO⊥BD.又∵EC⊥BD,EC∩CO=C,∴BD⊥平面OEC.∵OE⊂平面OEC,∴BD⊥OE.又∵O为BD中点,∴OE为BD的垂直平分线,∴BE=DE.(2)取AB的中点N,连接DN,MN.∵M为AE的中点,∴MN∥BE.∵△ABD为等边三角形,N为AB的中点,∴DN⊥AB.∵∠BCD=120°,CD=CB,∴∠OBC=30°,∴∠CBN=90°,即CB⊥AB,∴DN∥CB.∵DN∩MN=N,BE∩CB=B,∴平面MND∥平面BEC.又∵DM⊂平面MND,∴DM∥平面BEC.。
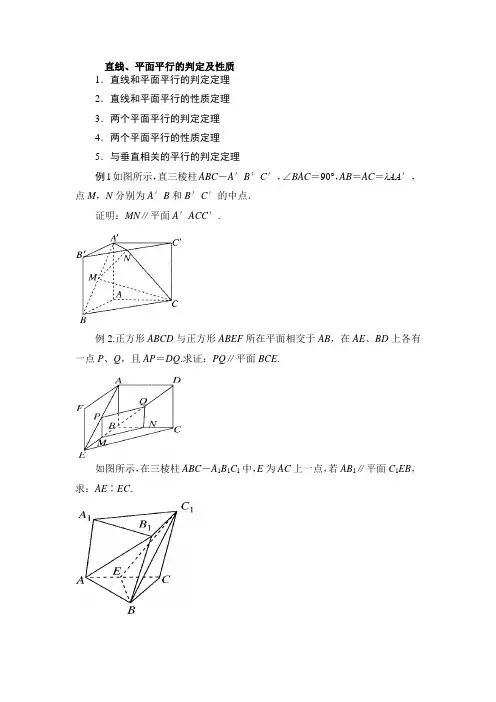
直线、平面平行的判定及性质1.直线和平面平行的判定定理2.直线和平面平行的性质定理3.两个平面平行的判定定理4.两个平面平行的性质定理5.与垂直相关的平行的判定定理例1如图所示,直三棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=λAA′,点M,N分别为A′B和B′C′的中点.证明:MN∥平面A′ACC′.例2.正方形ABCD与正方形ABEF所在平面相交于AB,在AE、BD上各有一点P、Q,且AP=DQ.求证:PQ∥平面BCE.如图所示,在三棱柱ABC-A1B1C1中,E为AC上一点,若AB1∥平面C1EB,求:AE∶EC.例3如图所示,正方体ABCD—A1B1C1D1中,M、N、E、F分别是棱A1B1,A1D1,B1C1,C1D1的中点.求证:平面AMN∥平面EFDB.例4如图所示,平面α∥平面β,点A∈α,C∈α,点B∈β,D∈β,点E、F分别在线段AB,CD上,且AE∶EB=CF∶FD.求证:EF∥β.练习题:1.(课本习题改编)给出下列四个命题:①若一条直线与一个平面内的一条直线平行,则这条直线与这个平面平行;②若一条直线与一个平面内的两条直线平行,则这条直线与这个平面平行;③若平面外的一条直线和这个平面内的一条直线平行,则这条直线和这个平面平行;④若两条平行直线中的一条与一个平面平行,则另一条也与这个平面平行.其中正确命题的个数是________个.1.下列命题中正确的是________.①若直线a不在α内,则a∥α;②若直线l上有无数个点不在平面α内,则l∥α;③若直线l与平面α平行,则l与α内的任意一条直线都平行;④如果两条平行线中的一条与一个平面平行,那么另一条也与这个平面平行;⑤若l与平面α平行,则l与α内任何一条直线都没有公共点;⑥平行于同一平面的两直线可以相交.2.(2014·合肥一检)给出下列关于互不相同的直线l、m、n和平面α、β、γ的三个命题:①若l与m为异面直线,l⊂α,m⊂β,则α∥β;②若α∥β,l⊂α,m⊂β,则l∥m;③若α∩β=l,β∩γ=m,γ∩α=n,l∥γ,则m∥n.1.已知两条不同直线l1和l2及平面α,则直线l1∥l2的一个充分条件是() A.l1∥α且l2∥αB.l1⊥α且l2⊥αC.l1∥α且l2⊄αD.l1∥α且l2⊂α答案 B解析l1⊥α且l2⊥α⇒l1∥l2.2.(2012·四川)下列命题正确的是()A.若两条直线和同一个平面所成的角相等,则这两条直线平行B.若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D.若两个平面都垂直于第三个平面,则这两个平面平行答案 C解析若两条直线和同一平面所成的角相等,则这两条直线可平行、可异面、可相交,A项不正确;如果到一个平面距离相等的三个点在同一条直线上或在这个平面的两侧,那么经过这三个点的平面与这个平面相交,B项不正确.3.(2013·浙江)设m,n是两条不同的直线,α,β是两个不同的平面() A.若m∥α,n∥α,则m∥nB.若m∥α,m∥β,则α∥βC.若m∥n,m⊥α,则n⊥αD.若m∥α,α⊥β,则m⊥β答案 C解析A项中,直线m,n可能平行,也可能相交或异面,直线m,n的关系是任意的;B项中,α与β也可能相交,此时直线m平行于α,β的交线;D 项中,m也可能平行于β.故选C项.4.设α,β表示平面,m,n表示直线,则m∥α的一个充分不必要条件是()A .α⊥β且m ⊥βB .α∩β=n 且m ∥nC .m ∥n 且n ∥αD .α∥β且m ⊂β答案 D解析 若两个平面平行,其中一个面内的任一直线均平行于另一个平面,故选D.5.若空间四边形ABCD 的两条对角线AC 、BD 的长分别是8、12,过AB 的中点E 且平行于BD 、AC 的截面四边形的周长为( )A .10B .20C .8D .4答案 B解析 设截面四边形为EFGH ,F 、G 、H 分别是BC 、CD 、DA 的中点,∴EF =GH =4,FG =HE =6.∴周长为2×(4+6)=20.6.在正方体ABCD -A 1B 1C 1D 1中,棱长为a ,M 、N 分别为A 1B 和AC 上的点,A 1M =AN =2a3,则MN 与平面BB 1C 1C 的位置关系是( )A .相交B .平行C .垂直D .不能确定答案 B解析 连接CD 1,在CD 1上取点P ,使D 1P =2a3,∴MP ∥BC ,PN ∥AD 1. ∴MP ∥面BB 1C 1C ,PN ∥面AA 1D 1D . ∴面MNP ∥面BB 1C 1C ,∴MN ∥面BB 1C 1C .7.如图所示,四个正方体图形中,A 、B 为正方体的两个顶点,M 、N 、P 分别为其所在棱的中点,能得出AB ∥面MNP 的图形的序号是________(写出所有符合要求的图形序号).答案①③8. 棱锥P-ABCD的底面是一直角梯形,AB∥CD,BA⊥AD,CD=2AB,P A⊥底面ABCD,E为PC的中点,则BE与平面P AD的位置关系为________.答案平行解析取PD的中点F,连接EF.在△PCD中,EF綊12CD.又∵AB∥CD且CD=2AB,∴EF=12CD且CD=2AB.∴EF綊AB,∴四边形ABEF是平行四边形,∴EB∥AF.又∵EB⊄平面P AD,AF⊂平面P AD,∴BE∥平面P AD.9. 如图所示,ABCD-A1B1C1D1是棱长为a的正方体,M、N分别是下底面的棱A1B1、B1C1的中点,P是上底面的棱AD上的一点,AP=a3,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ=________.答案22 3a解析 如图所示,连接AC ,易知MN ∥平面ABCD .∴MN ∥PQ .又∵MN ∥AC ,∴PQ ∥AC . 又∵AP =a 3,∴PD AD =DQ CD =PQ AC =23. ∴PQ =23AC =232a =223a .10.考查下列三个命题,在“________”处都缺少同一个条件,补上这个条件使其构成真命题(其中l 、m 为直线,α、β为平面),则此条件为________.①⎭⎬⎫m ⊂αl ∥m⇒l ∥α;②⎭⎬⎫l ∥m m ∥α⇒l ∥α;③⎭⎬⎫l ⊥βα⊥β⇒l ∥α. 答案 l ⊄α解析 ①体现的是线面平行的判定定理,缺的条件是“l 为平面α外的直线”,即“l ⊄α”,它也同样适合②③,故填l ⊄α.11.在四面体ABCD 中,M 、N 分别是面△ACD 、△BCD 的重心,则四面体的四个面中与MN 平行的是________.答案 平面ABC 和平面ABD解析 连接AM 并延长交CD 于E ,连接BN 并延长交CD 于F .由重心的性质可知,E 、F 重合为一点,且该点为CD 的中点E .由EM MA =EN NB =12,得MN ∥AB .因此MN ∥平面ABC 且MN ∥平面ABD .12.过三棱柱ABC —A 1B 1C 1的任意两条棱的中点作直线,其中与平面ABB 1A 1平行的直线共有________条.答案 6解析 过三棱柱ABC —A 1B 1C 1的任意两条棱的中点作直线,记AC ,BC ,A 1C 1,B 1C 1的中点分别为E ,F ,E 1,F 1,则直线EF ,EF 1,EE 1,FF 1,E 1F ,E 1F 1均与平面ABB1A 1平行,故符合题意的直线共6条.13. 如图所示,已知ABCD-A1B1C1D1是棱长为3的正方体,点E在AA1上,点F在CC1上,G在BB1上,且AE=FC1=B1G=1,H是B1C1的中点.(1)求证:E、B、F、D1四点共面;(2)求证:平面A1GH∥平面BED1F.答案(1)略(2)略解析(1)连接FG.∵AE=B1G=1,∴BG=A1E=2.∴BG綊A1E,∴A1G∥BE.又∵C1F綊B1G,∴四边形C1FGB1是平行四边形.∴FG綊C1B1綊D1A1.∴四边形A1GFD1是平行四边形.∴A1G綊D1F,∴D1F綊EB.故E、B、F、D1四点共面.(2)∵H是B1C1的中点,∴B1H=32.又B1G=1,∴B1GB1H=23.又FCBC=23,且∠FCB=∠GB1H=90°,∴△B1HG∽△CBF.∴∠B1GH=∠CFB=∠FBG,∴HG∥FB.又由(1)知,A1G∥BE,且HG∩A1G=G,FB∩BE=B,∴平面A1GH∥平面BED1F.14. 如图所示,四棱锥P—ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别为PC、PD、BC的中点.(1)求证:P A∥平面EFG;(2)求三棱锥P—EFG的体积.答案(1)略(2)1 6解析(1)如图所示,取AD的中点H,连接GH,FH.∵E,F分别为PC,PD的中点,∴EF∥CD.∵G,H分别是BC,AD的中点,∴GH∥CD.∴EF∥GH,∴E,F,H,G四点共面.∵F,H分别为DP,DA的中点,∴P A∥FH.∵P A⊄平面EFG,FH⊂平面EFG,∴P A∥平面EFG.(2)∵PD⊥平面ABCD,CG⊂平面ABCD,∴PD⊥CG.又∵CG⊥CD,CD∩PD=D,∴GC⊥平面PCD.∵PF =12PD =1,EF =12CD =1, ∴S △PEF =12EF ·PF =12. 又GC =12BC =1,∴V P —EFG =V G —PEF =13×12×1=16.15.一个多面体的直观图和三视图如图所示(其中M ,N 分别是AF ,BC 中点).(1)求证:MN ∥平面CDEF ; (2)求多面体A —CDEF 的体积. 答案 (1)略 (2)83解析 (1)证明 由三视图知,该多面体是底面为直角三角形的直三棱柱,且AB =BC =BF =2,DE =CF =22,∴∠CBF =90°.取BF 中点G ,连接MG ,NG ,由M ,N 分别是AF ,BC 中点,可知:NG ∥CF ,MG ∥EF .又MG ∩NG =G ,CF ∩EF =F ,∴平面MNG ∥平面CDEF ,∴MN ∥平面CDEF .(2)作AH ⊥DE 于H ,由于三棱柱ADE —BCF 为直三棱柱,∴AH ⊥平面CDEF ,且AH = 2.∴V A -CDEF =13S 四边形CDEF ·AH =13×2×22×2=83.16. 如图所示,三棱柱ABC -A 1B 1C 1,底面为正三角形,侧棱A 1A ⊥底面ABC ,点E 、F 分别是棱CC 1、BB 1上的点,点M 是线段AC 上的动点,EC =2FB .当点M 在何位置时,BM ∥平面AEF?答案当M为AC中点时,BM∥平面AEF.解析方法一:如图所示,取AE的中点O,连接OF,过点O作OM⊥AC 于点M.∵侧棱A1A⊥底面ABC,∴侧面A1ACC1⊥底面ABC.∴OM⊥底面ABC.又∵EC=2FB,∴OM∥FB綊12EC.∴四边形OMBF为矩形.∴BM∥OF.又∵OF⊂面AEF,BM⊄面AEF,故BM∥平面AEF,此时点M为AC的中点.方法二:如图所示,取EC的中点P,AC的中点Q,连接PQ、PB、BQ. ∴PQ∥AE.∵EC=2FB,∴PE綊BF,PB∥EF.∴PQ∥平面AEF,PB∥平面AEF.又PQ∩PB=P,∴平面PBQ ∥平面AEF .又∵BQ ⊂面PQB ,∴BQ ∥平面AEF .故点Q 即为所求的点M ,此时点M 为AC 的中点.17. (2013·福建)如图所示,在四棱锥P -ABCD 中,PD ⊥平面ABCD ,AB ∥DC ,AB ⊥AD ,BC =5,DC =3,AD =4,∠P AD =60°.(1)当正视方向与向量AD →的方向相同时,画出四棱锥P -ABCD 的正视图(要求标出尺寸,并写出演算过程);(2)若M 为P A 的中点,求证:DM ∥平面PBC ;(3)求三棱锥D -PBC 的体积.答案 (1)略 (2)略 (3)8 3解析 方法一:(1)在梯形ABCD 中,过点C 作CE ⊥AB ,垂足为E ,由已知得,四边形ADCE 为矩形,AE =CD =3,在Rt △BEC 中,由BC =5,CE =4,依勾股定理,得BE =3,从而AB =6.又由PD ⊥平面ABCD ,得PD ⊥AD .从而在Rt △PDA 中,由AD =4,∠P AD =60°,得PD =4 3.正视图如图所示.(2) 取PB 中点N ,连接MN ,CN .在△P AB 中,∵M 是P A 中点,∴MN ∥AB ,MN =12AB =3.又CD ∥AB ,CD =3,∴MN ∥CD ,MN =CD .∴四边形MNCD 为平行四边形.∴DM ∥CN .又DM ⊄平面PBC ,CN ⊂平面PBC ,∴DM ∥平面PBC .(3)V D -PBC =V P -DBC =13S △DBC ·PD ,又S △DBC =6,PD =43,所以V D -PBC =8 3.方法二:(1)同方法一.(2) 取AB 的中点E ,连接ME ,DE .在梯形ABCD 中,BE ∥CD ,且BE =CD ,∴四边形BCDE 为平行四边形.∴DE ∥BC .又DE ⊄平面PBC ,BC ⊂平面PBC ,∴DE∥平面PBC.又在△P AB中,ME∥PB,ME⊄平面PBC,PB⊂平面PBC,∴ME∥平面PBC.又DE∩ME=E,∴平面DME∥平面PBC.又DM⊂平面DME,∴DM∥平面PBC.(3)同方法一.。
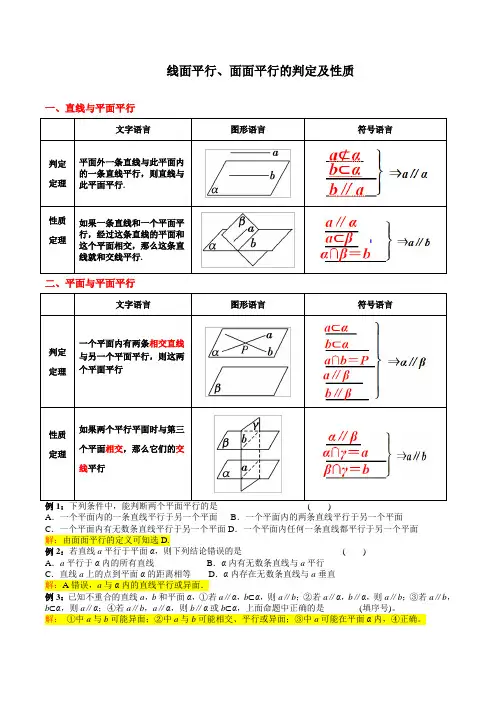
线面平行、面面平行的判定及性质一、直线与平面平行文字语言图形语言符号语言判定定理平面外一条直线与此平面内的一条直线平行,则直线与此平面平行.性质定理如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行.二、平面与平面平行文字语言图形语言符号语言判定定理一个平面内有两条相交直线与另一个平面平行,则这两个平面平行性质定理如果两个平行平面时与第三个平面相交,那么它们的交线平行A.一个平面内的一条直线平行于另一个平面B.一个平面内的两条直线平行于另一个平面C.一个平面内有无数条直线平行于另一个平面D.一个平面内任何一条直线都平行于另一个平面解:由面面平行的定义可知选D.例2:若直线a平行于平面α,则下列结论错误的是()A.a平行于α内的所有直线B.α内有无数条直线与a平行C.直线a上的点到平面α的距离相等D.α内存在无数条直线与a垂直解:A错误,a与α内的直线平行或异面.例3:已知不重合的直线a,b和平面α,①若a∥α,b⊂α,则a∥b;②若a∥α,b∥α,则a∥b;③若a∥b,b⊂α,则a∥α;④若a∥b,a∥α,则b∥α或b⊂α,上面命题中正确的是________(填序号)。
解:①中a与b可能异面;②中a与b可能相交、平行或异面;③中a可能在平面α内,④正确。
例4:已知α、β是平面,m 、n 是直线,给出下列命题:①若m ⊥α,m ⊂β,则α⊥β.②若m ⊂α,n ⊂α,m ∥β,n ∥β,则α∥β.③如果m ⊂α,n ⊄α,m 、n 是异面直线,那么n 与α相交.④若α∩β=m ,n ∥m ,且n ⊄α,n ⊄β,则n ∥α且n ∥β其中正确命题的个数是 ( ) A .1 B .2 C .3 D .4解:对于①,由定理“如果一个平面经过另一个平面的一条垂线,那么这两个平面垂直”得知,①正确;对于②,注意到直线m ,n 可能是两条平行直线,此时平面α,β可能是相交平面,因此②不正确;对于③,满足条件的直线n 可能平行于平面α,因此③不正确;对于④,由定理“如果平面外一条直线平行于平面内一条直线,那么这条直线平行于这个平面”得知,④正确.综上所述,其中正确的命题是①④,选B.例5:已知m ,n 表示两条不同直线,α,β,γ表示不同平面,给出下列三个命题:(1)⎩⎪⎨⎪⎧ m ⊥αn ⊥α⇒m ∥n ;(2)⎩⎪⎨⎪⎧ m ⊥αm ⊥n ⇒n ∥α (3)⎩⎪⎨⎪⎧m ⊥αn ∥α⇒m ⊥n 其中真命题的个数为 ( ) A .0 B .1 C .2 D .3 解:若⎩⎪⎨⎪⎧ m ⊥α,n ⊥α,则m ∥n ,即命题(1)正确;若⎩⎪⎨⎪⎧ m ⊥α,m ⊥n ,则n ∥α或n ⊂α,即命题(2)不正确;若⎩⎪⎨⎪⎧m ⊥αn ∥α,则m ⊥n ,即命题(3)正确;综上可得,真命题共有2个.选C例6:已知m 、n 、l 1、l 2表示直线,α、β表示平面.若m ⊂α,n ⊂α,l 1⊂β,l 2⊂β,l 1∩l 2=M ,则以下条件中,能推出α∥β的是 ( )A .m ∥β且l 1∥αB .m ∥β且n ∥βC .m ∥β且n ∥l 2D .m ∥l 1且n ∥l 2解:由定理“如果一个平面内有两条相交直线分别与另一个平面平行,那么这两个平面平行”可得,由选项D 可推知α∥β.例7:在下列条件中,可判断平面α与β平行的是( ).A. α、β都平行于直线lB. α内存在不共线的三点到β的距离相等C. l 、m 是α内两条直线,且l ∥β,m ∥βD. l 、m 是两条异面直线,且l ∥α,m ∥α,l ∥β,m ∥β 解:排除法,A中α、β可以是相交平面;B中三点可面平面两侧;C中两直线可以不相交.故选D,也可直接证明.例8:经过平面外的两点作该平面的平行平面可以作( ).A. 0个B. 1个C. 0个或1个D. 1个或2个解:这两点可以是在平面同侧或两侧.选C 。


一、选择题1.能保证直线a与平面α平行的条件是a bA.错误!未找到引用源。
,错误!未找到引用源。
,∥a bB.错误!未找到引用源。
,∥cα,a∥b,a∥cC.错误!未找到引用源。
,∥D.错误!未找到引用源。
,A∈a,B∈a,C∈b,D∈b且AC=BD2.下列说法中正确的是A.若直线a平行于平面α内的无数条直线,则a∥αB.若直线a∥b,直线b⊂α,则a∥αC.若一个平面内的两条直线分别平行于另一个平面内的两条直线,则这两个平面平行D.若一个平面内的两条相交直线分别平行于另一个平面内的两条相交直线,则这两个平面平行3.两个平面平行的条件是A.一个平面内的一条直线平行于另一个平面B.一个平面内的两条直线平行于另一个平面C.一个平面内的无数条直线平行于另一个平面D.一个平面内的任意一条直线平行于另一个平面4.平面α内有不共线的三点到平面β的距离相等且不为零,则α与β的位置关系为A.平行B.相交C.平行或相交D.可能重合5.设P是异面直线,a b外的一点,则过点P且与,a b都平行的平面A.有且只有一个B.恰有两个C.没有或只有一个D.有无数个6.如图,在正方体ABCD-A′B′C′D′中,E,F分别为平面ABCD和平面A′B′C′D′的中心,则正方体的六个面中与EF平行的平面有A.1个B.2个C.3个D.4个7.点E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点,则空间四边形的六条棱中与平面EFGH平行的条数是A.0 B.1C.2 D.38.下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是A.①③B.①④C.①③D.②④二、填空题9.在三棱台错误!未找到引用源。
中,错误!未找到引用源。
,点错误!未找到引用源。
、错误!未找到引用源。
分别是棱错误!未找到引用源。
、错误!未找到引用源。
的中点,则在三棱台的各棱所在的直线中,与平面错误!未找到引用源。

第4节直线、平面平行的判定及其性质考试要求1。
以立体几何的定义、公理和定理为出发点,认识和理解空间中线面平行的有关性质与判定定理;2.能运用公理、定理和已获得的结论证明一些有关空间图形的平行关系的简单命题。
知识梳理1.直线与平面平行(1)直线与平面平行的定义直线l与平面α没有公共点,则称直线l与平面α平行。
(2)判定定理与性质定理文字语言图形表示符号表示判定定理平面外一条直线与此平面内的一条直线平行,则该直线平行于此平面a⊄α,b⊂α,a∥b⇒a∥α性质定理一条直线和一个平面平行,则过这条a∥α,a⊂β,α∩β直线的任一平面与此平面的交线与该直线平行=b⇒a∥b2。
平面与平面平行(1)平面与平面平行的定义没有公共点的两个平面叫做平行平面.(2)判定定理与性质定理文字语言图形表示符号表示判定定理一个平面内的两条相交直线与另一个平面平行,则这两个平面平行a⊂α,b⊂α,a∩b=P,a∥β,b∥β⇒α∥β性质定两个平面平行,则其中一个平面内的直线平行于α∥β,a⊂α⇒a∥β理另一个平面如果两个平行平面同时和第三个平面相交,那么它们的交线平行α∥β,α∩γ=a,β∩γ=b⇒a∥b3。
与垂直相关的平行的判定(1)a⊥α,b⊥α⇒a∥b.(2)a⊥α,a⊥β⇒α∥β。
[常用结论与易错提醒]1.平行关系的转化2。
平面与平面平行的六个性质(1)两个平面平行,其中一个平面内的任意一条直线平行于另一个平面。
(2)夹在两个平行平面间的平行线段长度相等。
(3)经过平面外一点有且只有一个平面与已知平面平行。
(4)两条直线被三个平行平面所截,截得的对应线段成比例.(5)如果两个平面分别和第三个平面平行,那么这两个平面互相平行.(6)如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线,那么这两个平面平行.诊断自测1.判断下列说法的正误。
(1)若一条直线和平面内一条直线平行,那么这条直线和这个平面平行。
()(2)若直线a∥平面α,P∈α,则过点P且平行于直线a的直线有无数条。
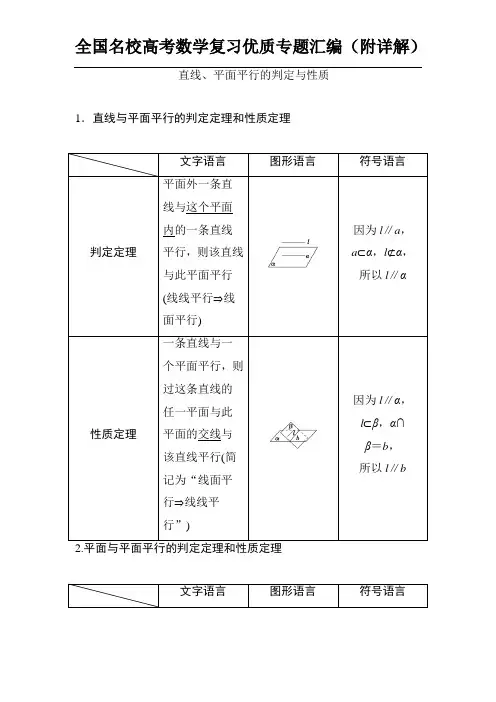
直线、平面平行的判定与性质1.直线与平面平行的判定定理和性质定理(1)垂直于同一条直线的两个平面平行,即若a ⊥α,a ⊥β,则α∥β; (2)垂直于同一个平面的两条直线平行,即若a ⊥α,b ⊥α,则a ∥b ; (3)平行于同一个平面的两个平面平行,即若α∥β,β∥γ,则α∥γ.判断正误(正确的打“√”,错误的打“×”)(1)若一条直线平行于一个平面内的一条直线,则这条直线平行于这个平面.( )(2)若一条直线平行于一个平面,则这条直线平行于这个平面内的任一条直线.( )(3)若直线a 与平面α内无数条直线平行,则a ∥α.( )(4)如果一个平面内的两条直线平行于另一个平面,那么这两个平面平行.( )(5)如果两个平面平行,那么分别在这两个平面内的两条直线平行或异面.( )答案:(1)× (2)× (3)× (4)× (5)√(教材习题改编)如果直线a ∥平面α,那么直线a 与平面α内的( )A .一条直线不相交B .两条直线不相交C .无数条直线不相交D .任意一条直线都不相交解析:选D.因为a ∥平面α,直线a 与平面α无公共点,因此a 和平面α内的任意一条直线都不相交,故选D.a 、b 、c 为三条不重合的直线,α、β、γ为三个不重合的平面,现给出四个命题: ①⎭⎪⎬⎪⎫c ∥αc ∥β⇒α∥β ②⎭⎪⎬⎪⎫α∥γβ∥γ⇒α∥β ③⎭⎪⎬⎪⎫c ∥αa ∥c ⇒a ∥α ④⎭⎪⎬⎪⎫a ∥γα∥γ⇒a ∥α其中正确的命题是________.解析:②正确.①错在α与β可能相交.③④错在a 可能在α内. 答案:②(教材习题改编)在正方体ABCD -A1B 1C 1D 1中,E 是DD 1的中点,则BD 1与平面ACE 的位置关系为________.解析:如图,连接AC ,BD 交于O 点,连接OE ,因为OE ∥BD 1,而OE ⊂平面ACE ,BD 1⊄平面ACE ,所以BD 1∥平面ACE .答案:平行线面平行的判定与性质(高频考点)平行关系是空间几何中的一种重要关系,包括线线平行、线面平行、面面平行,其中线面平行在高考试题中出现的频率很高,一般出现在解答题的某一问中.高考对线面平行的判定与性质的考查主要有以下三个命题角度:(1)线面位置关系的判断;(2)线面平行的证明;(3)线面平行性质的应用.[典例引领]角度一线面位置关系的判断设m,n表示不同直线,α,β表示不同平面,则下列结论中正确的是()A.若m∥α,m∥n,则n∥αB.若m⊂α,n⊂β,m∥β,n∥α,则α∥βC.若α∥β,m∥α,m∥n,则n∥βD.若α∥β,m∥α,n∥m,n⊄β,则n∥β【解析】A错误,n有可能在平面α内;B错误,平面α有可能与平面β相交;C错误,n也有可能在平面β内;D正确,易知m∥β或m⊂β,若m⊂β,又n∥m,n⊄β,所以n∥β,若m∥β,过m作平面γ交平面β于直线l,则m∥l,又n∥m,所以n∥l,又n⊄β,l⊂β,所以n∥β.【答案】 D角度二线面平行的证明在正方体ABCD-A1B1C1D1中,E,F,G,H分别是BC,CC1,C1D1,A1A的中点.求证:(1)BF∥HD1;(2)EG∥平面BB1D1D.【证明】(1)如图所示,取BB1的中点M,连接MH,MC1,易证四边形HMC1D1是平行四边形,所以HD1∥MC1.又因为在平面BCC1B1中,BM綊FC1,所以四边形BMC1F为平行四边形,所以MC1∥BF,所以BF∥HD1.(2)取BD的中点O,连接EO,D1O,则OE∥DC且OE=12DC,又D1G∥DC且D1G=12DC,所以OE綊D1G,所以四边形OEGD1是平行四边形,所以GE∥D1O.又D1O⊂平面BB1D1D,GE⊄平面BB1D1D,所以EG∥平面BB1D1D.角度三线面平行性质的应用B1C1D1中,E为线段AD上的任意一如图,在四棱柱ABCD-A点(不包括A,D两点),平面CEC1与平面BB1D交于FG.证明:FG∥平面AA1B1B.【证明】在四棱柱ABCD-A1B1C1D1中,BB1∥CC1,BB1⊂平面BB1D,CC1⊄平面BB1D,所以CC1∥平面BB1D,又CC1⊂平面CEC1,平面CEC1与平面BB1D交于FG,所以CC1∥FG,因为BB1∥CC1,所以BB1∥FG,而BB1⊂平面AA1B1B,FG⊄平面AA1B1B,所以FG∥平面AA1B1B.证明直线与平面平行的常用方法(1)定义法:证明直线与平面没有公共点,通常要借助于反证法来证明.(2)判定定理法:在利用判定定理时,关键是找到平面内与已知直线平行的直线,可先直观判断题中是否存在这样的直线,若不存在,则需作出直线,常考虑利用三角形的中位线、平行四边形的对边平行或过已知直线作一平面,找其交线进行证明.[通关练习]1.(优质试题·高考全国卷Ⅰ)如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是()解析:选A.对于选项B,如图所示,连接CD,因为AB∥CD,M,Q分别是所在棱的中点,所以MQ∥CD,所以AB∥MQ,又AB⊄平面MNQ,MQ⊂平面MNQ,所以AB∥平面MNQ.同理可证选项C,D中均有AB∥平面MNQ.故选A.2.如图,四棱锥P-ABCD中,底面ABCD为矩形,F是AB的中点,E是PD的中点.(1)证明:PB ∥平面AEC ;(2)在PC 上求一点G ,使FG ∥平面AEC ,并证明你的结论.解:(1)证明:连接BD 与AC 交于点O ,连接EO . 因为四边形ABCD 为矩形, 所以O 为BD 的中点. 又E 为PD 的中点, 所以EO ∥PB .因为EO ⊂平面AEC ,PB ⊄平面AEC , 所以PB ∥平面AEC .(2)PC 的中点G 即为所求的点. 证明如下: 连接GE 、FG , 因为E 为PD 的中点, 所以GE 綊12CD .又F 为AB 的中点,且四边形ABCD 为矩形, 所以F A 綊12CD . 所以F A 綊GE .所以四边形AFGE 为平行四边形,所以FG ∥AE .又FG ⊄平面AEC ,AE ⊂平面AEC ,所以FG∥平面AEC.面面平行的判定与性质[典例引领]B1C1中,E,F,G,如图所示,在三棱柱ABC-AH分别是AB,AC,A1B1,A1C1的中点,求证:(1)B,C,H,G四点共面;(2)平面EF A1∥平面BCHG.【证明】(1)因为G,H分别是A1B1,A1C1的中点,所以GH∥B1C1,又B1C1∥BC,所以GH∥BC,所以B,C,H,G四点共面.(2)在△ABC中,E,F分别为AB,AC的中点,所以EF∥BC,因为EF⊄平面BCHG,BC⊂平面BCHG,所以EF∥平面BCHG.又因为G,E分别为A1B1,AB的中点,所以A1G綊EB,所以四边形A1EBG是平行四边形,所以A1E∥GB.因为A1E⊄平面BCHG,GB⊂平面BCHG,所以A1E∥平面BCHG.又因为A1E∩EF=E,所以平面EF A1∥平面BCHG.1.在本例条件下,若D为BC1的中点,求证:HD∥平面A1B1BA.证明:如图所示,连接HD,A1B,因为D为BC1的中点,H为A1C1的中点,所以HD∥A1B,又HD⊄平面A1B1BA,A1B⊂平面A1B1BA,所以HD∥平面A1B1BA.2.在本例条件下,若D1,D分别为B1C1,BC的中点,求证:平面A1BD1∥平面AC1D.证明:如图所示,连接A1C交AC1于点M,因为四边形A1ACC1是平行四边形,所以M是A1C的中点,连接MD,因为D为BC的中点,所以A1B∥DM.因为A1B⊂平面A1BD1,DM⊄平面A1BD1,。
2.2.3直线与平面平行的性质2.2.4平面与平面平行的性质1.理解直线与平面、平面与平面平行的性质定理的含义.(重点)2.能用三种语言准确描述直线与平面、平面与平面平行的性质定理.(重点) 3.能用直线与平面、平面与平面平行的性质定理证明一些空间平行关系的简单命题.(难点)[基础·初探]教材整理1直线与平面平行的性质定理阅读教材P58~P59“例3”以上的内容,完成下列问题.自然语言一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行符号语言a∥α,a⊂β,α∩β=b⇒a∥b图形语言作用证明两直线平行判断(正确的打“√”,错误的打“×”)(1)一条直线如果和一个平面平行,它就和这个平面内的无数条直线平行.()(2)一条直线和一个平面平行,它就和这个平面内的任何直线无公共点.()(3)过直线外一点,有且仅有一个平面和已知直线平行.()(4)如果直线l和平面α平行,那么过平面α内一点和直线l平行的直线在α内.()【解析】由线面平行的性质定理知(1)(4)正确;由直线与平面平行的定义知(2)正确;因为经过一点可作一条直线与已知直线平行,而经过这条直线可作无数个平面,故(3)错.【答案】(1)√(2)√(3)×(4)√教材整理2平面与平面平行的性质定理阅读教材P60“思考”以下至P61“练习”以上的内容,完成下列问题.自然语言如果两个平行平面同时和第三个平面相交,那么它们的交线平行符号语言α∥β,α∩γ=a,β∩γ=b⇒a∥b图形语言作用证明两直线平行已知平面α∥平面β,过平面α内的一条直线a的平面γ,与平面β相交,交线为直线b,则a,b的位置关系是()A.平行B.相交C.异面D.不确定【解析】由面面平行的性质定理可知a∥b.【答案】 A[小组合作型]线面平行性质定理的应用面为平行四边形,求证:AB∥平面EFGH.图2-2-15【精彩点拨】要证明AB∥平面EFGH,只需证AB平行于平面EFGH内的某一条直线,由于EFGH是平行四边形,可利用其对边平行的特点,达到证题的目的.【自主解答】∵四边形EFGH为平行四边形,∴EF∥HG.∵HG⊂平面ABD,EF⊄平面ABD,∴EF∥平面ABD.∵EF⊂平面ABC,平面ABC∩平面ABD=AB,∴EF∥AB.∵AB⊄平面EFGH,EF⊂平面EFGH,∴AB∥平面EFGH.运用线面平行的性质定理时,应先确定线面平行,再寻找过已知直线的平面与平面相交的交线,然后确定线线平行.应认真领悟线线平行与线面平行的相互转化关系.[再练一题]1.如图2-2-16,在三棱柱ABC-A1B1C1中,过AA1作一平面交平面BCC1B1于EE1.求证:AA1∥EE1.图2-2-16【证明】在三棱柱ABC-A1B1C1中,AA1∥BB1,∵AA1⊄平面BCC1B1,BB1⊂平面BCC1B1,∴AA1∥平面BCC1B1.∵AA1⊂平面AEE1A1,平面AEE1A1∩平面BCC1B1=EE1,∴AA1∥EE1.面面平行性质定理的应用α与β之间),直线PB,PD分别与α,β相交于点A,B和C,D.图2-2-17(1)求证:AC∥BD;(2)已知P A=4,AB=5,PC=3,求PD的长.【精彩点拨】(1)利用面面平行的性质定理直接证明即可.(2)利用平行线分线段成比例定理可求得PD.【自主解答】(1)证明:∵PB∩PD=P,∴直线PB和PD确定一个平面γ,则α∩γ=AC,β∩γ=BD.又α∥β,∴AC∥BD.(2)由(1)得AC∥BD,∴P AAB=PCCD,∴45=3CD,∴CD=154,∴PD =PC +CD =274.1.利用面面平行的性质定理判定两直线平行的步骤:(1)先找两个平面,使这两个平面分别经过这两条直线中的一条;(2)判定这两个平面平行;(3)再找一个平面,使这两条直线都在这个平面上;(4)由性质定理得出线线平行.2.应用面面平行的性质定理时,往往需要“作”或“找”辅助平面,但辅助平面不可乱作,要想办法与其他已知量联系起来.[再练一题]2.如图2-2-18,在三棱柱ABC -A 1B 1C 1中,M 是A 1C 1的中点,平面AB 1M ∥平面BC 1N ,AC ∩平面BC 1N =N .求证:N 为AC 的中点.图2-2-18【证明】 因为平面AB 1M ∥平面BC 1N ,平面ACC 1A 1∩平面AB 1M =AM ,平面BC 1N ∩平面ACC 1A 1=C 1N ,所以C 1N ∥AM ,又AC ∥A 1C 1,所以四边形ANC 1M 为平行四边形, 所以AN ∥C 1M 且AN =C 1M , 又C 1M =12A 1C 1,A 1C 1=AC ,所以AN =12AC ,所以N 为AC 的中点.[探究共研型]平行关系的综合应用探究1 【提示】 应着力寻找过已知直线的平面与已知平面的交线,有时为了得到交线还需作出辅助平面,而且证明与平行有关的问题时,要与公理4等结合起来使用,扩大应用的范畴.探究2面面平行的判定定理与性质定理各有什么作用?【提示】两个平面平行的判定定理与性质定理的作用,关键都集中在“平行”二字上.判定定理解决了“在什么样的条件下两个平面平行”;性质定理揭示了“两个平面平行之后它们具有什么样的性质”.前者给出了判定两个平面平行的一种方法;后者给出了判定两条直线平行的一种方法.探究3你能总结一下线线平行与线面平行、面面平行之间的转化关系吗?【提示】三种平行关系可以任意转化,其相互转化关系如图所示:如图2-2-19,在正方体ABCD-A1B1C1D1中,点N在BD上,点M在B1C上,且CM=DN.求证:MN∥平面AA1B1B.图2-2-19【精彩点拨】用判定定理证明较困难,可通过证明过MN的平面与平面AA1B1B平行,得到MN∥平面AA1B1B.【自主解答】如图,作MP∥BB1交BC于点P,连接NP,∵MP∥BB1,∴CMMB1=CPPB.∵BD=B1C,DN=CM,∴B1M=BN,∴CMMB1=DNNB,∴CPPB=DNNB,∴NP∥CD∥AB.∵NP⊄平面AA1B1B,AB⊂平面AA1B1B,∴NP∥平面AA1B1B.∵MP∥BB1,MP⊄平面AA1B1B,BB1⊂平面AA1B1B,∴MP∥平面AA1B1B.又∵MP⊂平面MNP,NP⊂平面MNP,MP∩NP=P,∴平面MNP∥平面AA1B1B.∵MN⊂平面MNP,∴MN∥平面AA1B1B.1.三种平行关系的转化要灵活应用线线平行、线面平行和面面平行的相互联系、相互转化.在解决立体几何中的平行问题时,一般都要用到平行关系的转化.转化思想是解决这类问题的最有效的方法.2.面面平行的性质定理的几个推论(1)两个平面平行,其中一个平面内的任意一条直线平行于另一个平面.(2)夹在两平行平面间的平行线段相等.(3)经过平面外的一点有且只有一个平面与已知平面平行.(4)两条直线被三个平行平面所截,截得的对应线段成比例.[再练一题]3.如图2-2-20,在四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=2CD,E,E1分别是棱AD,AA1上的点.设F是棱AB的中点,证明:直线EE1∥平面FCC1.图2-2-20【证明】因为F为AB的中点,所以AB=2AF.又因为AB=2CD,所以CD=AF.因为AB∥CD,所以CD∥AF,所以AFCD为平行四边形.所以FC∥AD.又FC⊄平面ADD1A1,AD⊂平面ADD1A1,所以FC∥平面ADD1A1.因为CC1∥DD1,CC1⊄平面ADD1A1,DD1⊂平面ADD1A1,所以CC1∥平面ADD1A1,又FC∩CC1=C,所以平面ADD1A1∥平面FCC1.又EE1⊂平面ADD1A1,所以EE1∥平面FCC1.1.正方体ABCD-A1B1C1D1中,E,F,G分别是A1B1,CD,B1C1的中点,则正确命题是()图2-2-21A.AE⊥CGB.AE与CG是异面直线C.四边形AEC1F是正方形D.AE∥平面BC1F【解析】由正方体的几何特征知,AE与平面BCC1B1不垂直,则AE⊥CG 不成立;由于EG∥A1C1∥AC,故A,E,G,C四点共面,所以AE与CG是异面直线错误;在四边形AEC1F中,AE=EC1=C1F=AF,但AF与AE不垂直,故四边形AEC1F是正方形错误;由于AE∥C1F,由线面平行的判定定理,可得AE∥平面BC1F.故选D.【答案】 D2.如图2-2-22,四棱锥P-ABCD中,M,N分别为AC,PC上的点,且MN ∥平面P AD,则()图2-2-22A.MN∥PDB.MN∥P AC.MN∥ADD.以上均有可能B[∵MN∥平面P AD,平面P AC∩平面P AD=P A,MN⊂平面P AC,∴MN ∥P A.]3.已知直线l∥平面α,l⊂平面β,α∩β=m,则直线l,m的位置关系是________.【解析】由直线与平面平行的性质定理知l∥m.【答案】平行4.过两平行平面α,β外的点P的两条直线AB与CD,它们分别交α于A,C两点,交β于B,D两点,若P A=6,AC=9,PB=8,则BD的长为________.【解析】两条直线AB与CD相交于P点,所以可以确定一个平面,此平面与两平行平面α,β的交线AC∥BD,所以P APB=ACBD,又P A=6,AC=9,PB=8,故BD=12.【答案】125.如图2-2-23,α∩β=CD,α∩γ=EF,β∩γ=AB,AB∥α.求证:CD∥EF.图2-2-23【证明】因为AB∥α,AB⊂β,α∩β=CD,所以AB∥CD.同理可证AB∥EF,所以CD∥EF.学业分层测评(十一)(建议用时:45分钟)[学业达标]一、选择题1.直线a∥平面α,α内有n条直线交于一点,那么这n条直线中与直线a 平行的()A.至少有一条B.至多有一条C.有且只有一条D.没有【解析】过a和平面内n条直线的交点只有一个平面β,所以平面α与平面β只有一条交线,且与直线a平行,这条交线可能不是这n条直线中的一条,也可能是.故选B.【答案】 B2.设a,b是两条直线,α,β是两个平面,若a∥α,a⊂β,α∩β=b,则α内与b相交的直线与a的位置关系是()A.平行B.相交C.异面D.平行或异面【解析】条件即为线面平行的性质定理,所以a∥b,又a与α无公共点,故选C.【答案】 C3.下列命题中不正确的是()A.两个平面α∥β,一条直线a平行于平面α,则a一定平行于平面βB.平面α∥平面β,则α内的任意一条直线都平行于平面βC.一个三角形有两条边所在的直线平行于一个平面,那么三角形所在平面与这个平面平行D.分别在两个平行平面内的两条直线只能是平行直线或者是异面直线【解析】选项A中直线a可能与β平行,也可能在β内,故选项A不正确;三角形两边必相交,这两条相交直线平行于一个平面,那么三角形所在的平面与这个平面平行,所以选项C正确;依据平面与平面平行的性质定理可知,选项B,D也正确,故选A.【答案】 A4.如图2-2-24,在长方体ABCD-A1B1C1D1中,E,F分别是棱AA1和BB1的中点,过EF的平面EFGH分别交BC和AD于G,H,则GH与AB的位置关系是()图2-2-24A.平行B.相交C.异面D.平行或异面【解析】由长方体性质知:EF∥平面ABCD,∵EF⊂平面EFGH,平面EFGH∩平面ABCD=GH,∴EF∥GH,又∵EF∥AB,∴GH∥AB,∴选A.【答案】 A5.设平面α∥平面β,A∈α,B∈β,C是AB的中点,当点A、B分别在平面α,β内运动时,动点C()A.不共面B.当且仅当点A、B分别在两条直线上移动时才共面C.当且仅当点A、B分别在两条给定的异面直线上移动时才共面D.无论点A,B如何移动都共面【解析】无论点A、B如何移动,其中点C到α、β的距离始终相等,故点C在到α、β距离相等且与两平面都平行的平面上.【答案】 D二、填空题6.如图2-2-25,正方体ABCD-A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上,若EF∥平面AB1C,则线段EF的长度等于________.图2-2-25【解析】因为EF∥平面AB1C,EF⊂平面ABCD,平面AB1C∩平面ABCD=AC,所以EF∥AC.又点E为AD的中点,点F在CD上,所以点F是CD的中点,所以EF=12AC= 2.【答案】 27.如图2-2-26所示,直线a∥平面α,A∉α,并且a和A位于平面α两侧,点B,C∈a,AB、AC分别交平面α于点E,F,若BC=4,CF=5,AF=3,则EF=________.图2-2-26【解析】EF可看成直线a与点A确定的平面与平面α的交线,∵a∥α,由线面平行的性质定理知,BC∥EF,由条件知AC=AF+CF=3+5=8.又EFBC=AFAC,∴EF=AF×BCAC=3×48=32.【答案】3 2三、解答题8.如图2-2-27所示,四边形ABCD是矩形,P∉平面ABCD,过BC作平面BCFE交AP于点E,交DP于点F,求证:四边形BCFE为梯形.图2-2-27【证明】∵四边形ABCD是矩形,∴BC∥AD.∵AD⊂平面APD,BC⊄平面APD,∴BC∥平面APD.又平面BCFE∩平面APD=EF,∴BC∥EF,∴AD∥EF.又E,F是△APD边上的点,∴EF≠AD,∴EF≠BC.∴四边形BCFE是梯形.9.如图2-2-28,S是平行四边形ABCD所在平面外一点,M,N分别是SA,BD上的点,且AMSM=DNNB,求证:MN∥平面SBC.图2-2-28【证明】在AB上取一点P,使APBP=AMSM,连接MP,NP,则MP∥SB.∵SB⊂平面SBC,MP⊄平面SBC,∴MP∥平面SBC.又AMSM=DNNB,∴APBP=DNNB,∴NP∥AD.∵AD∥BC,∴NP∥BC.又BC⊂平面SBC,NP⊄平面SBC,∴NP∥平面SBC.又MP∩NP=P,∴平面MNP∥平面SBC,而MN⊂平面MNP,∴MN∥平面SBC.[能力提升]10.对于直线m、n和平面α,下列命题中正确的是()A.如果m⊂α,n⊄α,m、n是异面直线,那么n∥αB.如果m⊂α,n⊄α,m、n是异面直线,那么n与α相交C.如果m⊂α,n∥α,m、n共面,那么m∥nD.如果m∥α,n∥α,m、n共面,那么m∥n【解析】对于A,如图(1)所示,此时n与α相交,故A不正确;对于B,如图(2)所示,此时m,n是异面直线,而n与α平行,故B不正确;对于D,如图(3)所示,m与n相交,故D不正确.故选C.图(1)图(2)图(3)【答案】 C11.如图2-2-29,三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,点E,F分别是棱CC1,BB1上的点,点M是线段AC上的动点,EC=2FB=2,当点M在何位置时,BM∥平面AEF.图2-2-29【解】如图,取EC的中点P,AC的中点Q,连接PQ,PB,BQ,则PQ ∥AE.因为EC=2FB=2,所以PE=BF.所以四边形BFEP为平行四边形,所以PB ∥EF.又AE,EF⊂平面AEF,PQ,PB⊄平面AEF,所以PQ∥平面AEF,PB∥平面AEF.又PQ∩PB=P,所以平面PBQ∥平面AEF.又BQ⊂平面PBQ,所以BQ∥平面AEF.故点Q即为所求的点M,即点M为AC的中点时,BM∥平面AEF.。
空间直线、平面的平行考试要求 1.理解空间中直线与直线、直线与平面、平面与平面的平行关系,并加以证明.2.掌握直线与平面、平面与平面平行的判定与性质,并会简单应用.知识梳理1.线面平行的判定定理和性质定理文字语言图形语言符号语言判定定理如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行错误!⇒a∥α性质定理一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么该直线与交线平行错误!⇒a∥b2.面面平行的判定定理和性质定理文字语言图形语言符号语言判定定理如果一个平面内的两条相交直线与另一个平面平行,那么这两个平面平行错误!⇒β∥α性质定理两个平面平行,如果另一个平面与这两个平面相交,那么两条交线平行错误!⇒a∥b常用结论(1)垂直于同一条直线的两个平面平行,即若a⊥α,a⊥β,则α∥β.(2)平行于同一个平面的两个平面平行,即若α∥β,β∥γ,则α∥γ.(3)垂直于同一个平面的两条直线平行,即a⊥α,b⊥α,则a∥b.(4)若α∥β,a⊂α,则a∥β.思考辨析判断下列结论是否正确(请在括号中打“√”或“×”)(1)若一条直线平行于一个平面内的一条直线,则这条直线平行于这个平面.( ×)(2)若直线a∥平面α,P∈α,则过点P且平行于直线a的直线有无数条.( ×)(3)若直线a⊂平面α,直线b⊂平面β,a∥b,则α∥β.( ×)(4)如果两个平面平行,那么分别在这两个平面内的两条直线平行或异面.( √)教材改编题1.下列说法中,与“直线a∥平面α”等价的是( )A.直线a上有无数个点不在平面α内B.直线a与平面α内的所有直线平行C.直线a与平面α内无数条直线不相交D.直线a与平面α内的任意一条直线都不相交答案 D解析因为a∥平面α,所以直线a与平面α无交点,因此a和平面α内的任意一条直线都不相交.2.已知不重合的直线a,b和平面α,则下列选项正确的是( )A.若a∥α,b⊂α,则a∥bB.若a∥α,b∥α,则a∥bC.若a∥b,b⊂α,则a∥αD.若a∥b,a⊂α,则b∥α或b⊂α答案 D解析若a∥α,b⊂α,则a∥b或异面,A错;若a∥α,b∥α,则a∥b或异面或相交,B错;若a∥b,b⊂α,则a∥α或a⊂α,C错;若a∥b,a⊂α,则b∥α或b⊂α,D对.3.如图是长方体被一平面所截得的几何体,四边形EFGH为截面,则四边形EFGH的形状为______.答案平行四边形解析∵平面ABFE∥平面DCGH,又平面EFGH∩平面ABFE=EF,平面EFGH∩平面DCGH=HG,∴EF∥HG.同理EH∥FG,∴四边形EFGH是平行四边形.题型一 直线与平面平行的判定与性质 命题点1 直线与平面平行的判定例1 如图,在四棱锥P -ABCD 中,底面ABCD 是平行四边形,E ,F 分别是BC ,PD 的中点,求证:(1)PB ∥平面ACF ;(2)EF ∥平面PAB .证明 (1)如图,连接BD 交AC 于O ,连接OF ,∵四边形ABCD 是平行四边形, ∴O 是BD 的中点,又∵F 是PD 的中点,∴OF ∥PB , 又∵OF ⊂平面ACF ,PB ⊄平面ACF , ∴PB ∥平面ACF .(2)取PA 的中点G ,连接GF ,BG . ∵F 是PD 的中点, ∴GF 是△PAD 的中位线, ∴GF 綉12AD ,∵底面ABCD 是平行四边形,E 是BC 的中点, ∴BE 綉12AD ,∴GF 綉BE ,∴四边形BEFG 是平行四边形, ∴EF ∥BG ,又∵EF ⊄平面PAB ,BG ⊂平面PAB , ∴EF ∥平面PAB .命题点2 直线与平面平行的性质例2 如图所示,在四棱锥P-ABCD中,四边形ABCD是平行四边形,M是PC的中点,在DM 上取一点G,过G和PA作平面交BD于点H.求证:PA∥GH.证明如图所示,连接AC交BD于点O,连接OM,∵四边形ABCD是平行四边形,∴O是AC的中点,又M是PC的中点,∴PA∥OM,又OM⊂平面BMD,PA⊄平面BMD,∴PA∥平面BMD,又平面PAHG∩平面BMD=GH,∴PA∥GH.教师备选如图,四边形ABCD是矩形,P∉平面ABCD,过BC作平面BCFE交AP于点E,交DP于点F,求证:四边形BCFE是梯形.证明∵四边形ABCD为矩形,∴BC∥AD.∵AD⊂平面PAD,BC⊄平面PAD,∴BC∥平面PAD.∵平面BCFE∩平面PAD=EF,BC⊂平面BCFE,∴BC∥EF.∵AD=BC,AD≠EF,∴BC≠EF,∴四边形BCFE是梯形.思维升华(1)判断或证明线面平行的常用方法①利用线面平行的定义(无公共点).②利用线面平行的判定定理(a⊄α,b⊂α,a∥b⇒a∥α).③利用面面平行的性质(α∥β,a⊂α⇒a∥β).④利用面面平行的性质(α∥β,a⊄β,a∥α⇒a∥β).(2)应用线面平行的性质定理的关键是确定交线的位置,有时需要经过已知直线作辅助平面确定交线.跟踪训练1 如图所示,已知四边形ABCD是正方形,四边形ACEF是矩形,M是线段EF的中点.(1)求证:AM∥平面BDE;(2)若平面ADM∩平面BDE=l,平面ABM∩平面BDE=m,试分析l与m的位置关系,并证明你的结论.(1)证明如图,记AC与BD的交点为O,连接OE.因为O,M分别为AC,EF的中点,四边形ACEF是矩形,所以四边形AOEM是平行四边形,所以AM∥OE.又因为OE⊂平面BDE,AM⊄平面BDE,所以AM∥平面BDE.(2)解l∥m,证明如下:由(1)知AM∥平面BDE,又AM⊂平面ADM,平面ADM∩平面BDE=l,所以l∥AM,同理,AM∥平面BDE,又AM⊂平面ABM,平面ABM∩平面BDE=m,所以m∥AM,所以l∥m.题型二平面与平面平行的判定与性质例3 如图所示,在三棱柱ABC-A1B1C1中,过BC的平面与上底面A1B1C1交于GH(GH与B1C1不重合).(1)求证:BC∥GH;(2)若E,F,G分别是AB,AC,A1B1的中点,求证:平面EFA1∥平面BCHG.证明(1)∵在三棱柱ABC-A1B1C1中,∴平面ABC∥平面A1B1C1,又∵平面BCHG∩平面ABC=BC,且平面BCHG∩平面A1B1C1=HG,∴由面面平行的性质定理得BC∥GH.(2)∵E,F分别为AB,AC的中点,∴EF∥BC,∵EF⊄平面BCHG,BC⊂平面BCHG,∴EF∥平面BCHG.又G,E分别为A1B1,AB的中点,A1B1綉AB,∴A1G綉EB,∴四边形A1EBG是平行四边形,∴A1E∥GB.∵A1E⊄平面BCHG,GB⊂平面BCHG,∴A1E∥平面BCHG.又∵A1E∩EF=E,A1E,EF⊂平面EFA1,∴平面EFA1∥平面BCHG.延伸探究在本例中,若将条件“E,F,G分别是AB,AC,A1B1的中点”变为“点D,D1分别是AC,A1C1上的点,且平面BC1D∥平面AB1D1”,试求ADDC的值.解如图,连接A1B交AB1于O,连接OD1.由平面BC 1D ∥平面AB 1D 1, 且平面A 1BC 1∩平面BC 1D =BC 1, 平面A 1BC 1∩平面AB 1D 1=D 1O , 所以BC 1∥D 1O ,则A 1D 1D 1C 1=A 1OOB=1. 又由题设A 1D 1D 1C 1=DC AD, 所以DC AD=1,即AD DC=1. 教师备选如图,在三棱柱ABC -A 1B 1C 1中,E ,F ,G 分别为B 1C 1,A 1B 1,AB 的中点.(1)求证:平面A 1C 1G ∥平面BEF ;(2)若平面A 1C 1G ∩BC =H ,求证:H 为BC 的中点. 证明 (1)∵E ,F 分别为B 1C 1,A 1B 1的中点, ∴EF ∥A 1C 1,∵A 1C 1⊂平面A 1C 1G ,EF ⊄平面A 1C 1G , ∴EF ∥平面A 1C 1G ,又F ,G 分别为A 1B 1,AB 的中点, ∴A 1F =BG , 又A 1F ∥BG ,∴四边形A 1GBF 为平行四边形, 则BF ∥A 1G ,∵A 1G ⊂平面A 1C 1G ,BF ⊄平面A 1C 1G , ∴BF ∥平面A 1C 1G ,又EF ∩BF =F ,EF ,BF ⊂平面BEF , ∴平面A 1C 1G ∥平面BEF .(2)∵平面ABC∥平面A1B1C1,平面A1C1G∩平面A1B1C1=A1C1,平面A1C1G与平面ABC有公共点G,则有经过G的直线,设交BC于点H,如图,则A1C1∥GH,得GH∥AC,∵G为AB的中点,∴H为BC的中点.思维升华证明面面平行的常用方法(1)利用面面平行的判定定理.(2)利用垂直于同一条直线的两个平面平行(l⊥α,l⊥β⇒α∥β).(3)利用面面平行的传递性,即两个平面同时平行于第三个平面,则这两个平面平行(α∥β,β∥γ⇒α∥γ).跟踪训练2 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形.(1)证明:平面A1BD∥平面CD1B1;(2)若平面ABCD∩平面CD1B1=直线l,证明:B1D1∥l.证明(1)由题设知BB1綉DD1,所以四边形BB1D1D是平行四边形,所以BD∥B1D1.又BD⊄平面CD1B1,B1D1⊂平面CD1B1,所以BD∥平面CD1B1.因为A1D1綉B1C1綉BC,所以四边形A1BCD1是平行四边形,所以A1B∥D1C.又A1B⊄平面CD1B1,D1C⊂平面CD1B1,所以A1B∥平面CD1B1.又因为BD∩A1B=B,BD,A1B⊂平面A1BD,所以平面A1BD∥平面CD1B1.(2)由(1)知平面A1BD∥平面CD1B1,又平面ABCD∩平面CD1B1=直线l,平面ABCD∩平面A1BD=直线BD,所以直线l∥直线BD,在四棱柱ABCD-A1B1C1D1中,四边形BDD1B1为平行四边形,所以B 1D 1∥BD ,所以B 1D 1∥l .题型三 平行关系的综合应用例4 如图,在正方体ABCD -A 1B 1C 1D 1中,P ,Q 分别为对角线BD ,CD 1上的点,且CQ QD 1=BP PD =23.(1)求证:PQ ∥平面A 1D 1DA ;(2)若R 是AB 上的点,AR AB的值为多少时,能使平面PQR ∥平面A 1D 1DA ?请给出证明. (1)证明 连接CP 并延长,与DA 的延长线交于M 点,如图,连接MD 1,因为四边形ABCD 为正方形, 所以BC ∥AD ,故△PBC ∽△PDM , 所以CP PM =BP PD =23,又因为CQ QD 1=BP PD =23, 所以CQ QD 1=CP PM =23, 所以PQ ∥MD 1.又MD 1⊂平面A 1D 1DA ,PQ ⊄平面A 1D 1DA , 故PQ ∥平面A 1D 1DA .(2)解 当AR AB 的值为35时,能使平面PQR ∥平面A 1D 1DA .如图,证明如下:因为AR AB =35,即BR RA =23, 故BR RA =BP PD. 所以PR ∥DA .又DA ⊂平面A 1D 1DA ,PR ⊄平面A 1D 1DA , 所以PR ∥平面A 1D 1DA ,又PQ ∥平面A 1D 1DA ,PQ ∩PR =P ,PQ ,PR ⊂平面PQR , 所以平面PQR ∥平面A 1D 1DA . 教师备选如图,四边形ABCD 与ADEF 均为平行四边形,M ,N ,G 分别是AB ,AD ,EF 的中点.求证:(1)BE ∥平面DMF ; (2)平面BDE ∥平面MNG .证明 (1)如图,连接AE ,则AE 必过DF 与GN 的交点O ,连接MO ,则MO 为△ABE 的中位线,所以BE ∥MO . 又BE ⊄平面DMF ,MO ⊂平面DMF , 所以BE ∥平面DMF .(2)因为N ,G 分别为平行四边形ADEF 的边AD ,EF 的中点,所以DE ∥GN , 又DE ⊄平面MNG ,GN ⊂平面MNG , 所以DE ∥平面MNG . 又M 为AB 的中点,所以MN 为△ABD 的中位线,所以BD ∥MN , 又MN ⊂平面MNG ,BD ⊄平面MNG , 所以BD ∥平面MNG ,又DE ,BD ⊂平面BDE ,DE ∩BD =D ,所以平面BDE ∥平面MNG .思维升华 证明平行关系的常用方法熟练掌握线线、线面、面面平行关系间的相互转化是解决线线、线面、面面平行的综合问题的关键.面面平行判定定理的推论也是证明面面平行的一种常用方法.跟踪训练3 如图所示,四边形EFGH 为空间四边形ABCD 的一个截面,若截面为平行四边形. (1)求证:AB ∥平面EFGH ;(2)若AB =4,CD =6,求四边形EFGH 周长的取值范围.(1)证明 ∵四边形EFGH 为平行四边形, ∴EF ∥HG .∵HG ⊂平面ABD ,EF ⊄平面ABD , ∴EF ∥平面ABD . 又∵EF ⊂平面ABC , 平面ABD ∩平面ABC =AB , ∴EF ∥AB ,又∵AB ⊄平面EFGH ,EF ⊂平面EFGH , ∴AB ∥平面EFGH . (2)解 设EF =x (0<x <4), 由(1)知EF ∥AB , ∴CF CB =EF AB =x4, 与(1)同理可得CD ∥FG , ∴FG CD =BF BC, 则FG 6=BF BC=BC -CF BC =1-x4, ∴FG =6-32x .∴四边形EFGH 的周长L =2⎝⎛⎭⎪⎫x +6-32x =12-x .又∵0<x <4,∴8<L <12,故四边形EFGH 周长的取值范围是(8,12).课时精练1.(2022·宁波模拟)下列命题中正确的是( )A.若a,b是两条直线,且a∥b,那么a平行于经过b的任何平面B.若直线a和平面α满足a∥α,那么a与α内的任何直线平行C.平行于同一条直线的两个平面平行D.若直线a,b和平面α满足a∥b,a⊂α,b⊄α,则b∥α答案 D解析A中,a可以在过b的平面内;B中,a与α内的直线也可能异面;C中,两平面可能相交;D中,由直线与平面平行的判定定理知b∥α,正确.2.(2022·呼和浩特模拟)设a,b是两条不同的直线,α,β是两个不同的平面,则α∥β的一个充分条件是( )A.存在一条直线a,a∥α,a∥βB.存在一条直线a,a⊂α,a∥βC.存在两条平行直线a,b,a⊂α,b⊂β,a∥β,b∥αD.存在两条异面直线a,b,a⊂α,b⊂β,a∥β,b∥α答案 D解析对于A,一条直线与两个平面都平行,两个平面不一定平行,故A不正确;对于B,一个平面中的一条直线平行于另一个平面,两个平面不一定平行,故B不正确;对于C,两个平面中的两条直线平行,不能保证两个平面平行,故C不正确;对于D,如图,在直线b上取点B,过点B和直线a确定一个平面γ,交平面β于a′,因为a∥β,所以a∥a′,又a′⊄α,a⊂α,所以a′∥α,又因为b∥α,b∩a′=B,b⊂β,a′⊂β,所以β∥α.3.(2022·广州模拟)如图,在三棱柱ABC-A1B1C1中,AM=2MA1,BN=2NB1,过MN作一平面分别交底面△ABC的边BC,AC于点E,F,则( )A.MF∥EBB.A1B1∥NEC.四边形MNEF为平行四边形D.四边形MNEF为梯形答案 D解析由于B,E,F三点共面,F∈平面BEF,M∉平面BEF,故MF,EB为异面直线,故A错误;由于B1,N,E三点共面,B1∈平面B1NE,A1∉平面B1NE,故A1B1,NE为异面直线,故B错误;∵在平行四边形AA1B1B中,AM=2MA1,BN=2NB1,∴AM∥BN,AM=BN,故四边形AMNB为平行四边形,∴MN∥AB.又MN⊄平面ABC,AB⊂平面ABC,∴MN∥平面ABC.又MN⊂平面MNEF,平面MNEF∩平面ABC=EF,∴MN∥EF,∴EF∥AB,显然在△ABC中,EF≠AB,∴EF≠MN,∴四边形MNEF为梯形,故C错误,D正确.4.(2022·杭州模拟)已知P为△ABC所在平面外一点,平面α∥平面ABC,且α交线段PA,PB,PC于点A′,B′,C′,若PA′∶AA′=2∶3,则S△A′B′C′∶S△ABC等于( )A.2∶3B.2∶5C.4∶9D.4∶25答案 D解析∵平面α∥平面ABC,∴A′C′∥AC,A′B′∥AB,B′C′∥BC,∴S△A′B′C′∶S△ABC=(PA′∶PA)2,又PA′∶AA′=2∶3,∴PA′∶PA=2∶5,∴S△A′B′C′∶S△ABC=4∶25.5.(多选)(2022·济宁模拟)如图,在下列四个正方体中,A,B为正方体的两个顶点,D,E,F为所在棱的中点,则在这四个正方体中,直线AB与平面DEF平行的是( )答案AC解析对于A,AB∥DE,AB⊄平面DEF,DE⊂平面DEF,∴直线AB与平面DEF平行,故A正确;对于B,如图,取正方体所在棱的中点G,连接FG并延长,交AB延长线于H,则AB与平面DEF相交于点H,故B错误;对于C,AB∥DF,AB⊄平面DEF,DF⊂平面DEF,∴直线AB与平面DEF平行,故C正确;对于D,AB与DF所在平面的正方形对角线有交点B,DF与该对角线平行,∴直线AB与平面DEF相交,故D错误.6.(多选)如图,透明塑料制成的长方体容器ABCD-A1B1C1D1内灌进一些水,固定容器一边AB 于地面上,再将容器倾斜,随着倾斜程度的不同,有下面几个结论,其中正确的是( )A .没有水的部分始终呈棱柱形B .水面EFGH 所在四边形的面积为定值C .随着容器倾斜程度的不同,A 1C 1始终与水面所在平面平行D .当容器倾斜如图(3)所示时,AE ·AH 为定值 答案 AD解析 根据棱柱的特征(有两个面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边都互相平行),结合题中图形易知A 正确;由题图可知水面EFGH 的边EF 的长保持不变,但邻边的长却随倾斜程度而改变,可知B 错误;因为A 1C 1∥AC ,AC ⊂平面ABCD ,A 1C 1⊄平面ABCD ,所以A 1C 1∥平面ABCD ,当平面EFGH 不平行于平面ABCD 时,A 1C 1不平行于水面所在平面,故C 错误;当容器倾斜如题图(3)所示时,因为水的体积是不变的,所以棱柱AEH -BFG 的体积V 为定值,又V =S △AEH ·AB ,高AB 不变,所以S △AEH 也不变,即AE ·AH 为定值,故D 正确.7.考查①②两个命题,①⎭⎪⎬⎪⎫m ⊂αl ∥m ⇒l ∥α;②⎭⎪⎬⎪⎫l ∥m m ∥α ⇒l ∥α,它们都缺少同一个条件,补上这个条件就可以使其构成真命题(其中l ,m 为直线,α为平面),则此条件为__________. 答案 l ⊄α解析 ①由线面平行的判定定理知l ⊄α;②由线面平行的判定定理知l ⊄α.8.如图所示,在正四棱柱ABCD —A 1B 1C 1D 1中,E ,F ,G ,H 分别是棱CC 1,C 1D 1,D 1D ,DC 的中点,N 是BC 的中点,点M 在四边形EFGH 及其内部运动,则M 只需满足条件______,就有MN ∥平面B 1BDD 1.(注:请填上你认为正确的一个条件即可,不必考虑全部可能情况)答案 点M 在线段FH 上(或点M 与点H 重合) 解析 连接HN ,FH ,FN (图略), 则FH ∥DD 1,HN ∥BD ,∴平面FHN ∥平面B 1BDD 1,只需M ∈FH , 则MN ⊂平面FHN ,∴MN ∥平面B 1BDD 1.9.如图,在正方体ABCD -A 1B 1C 1D 1中,E ,F ,G ,H 分别是BC ,CC 1,C 1D 1,AA 1的中点,求证:(1)BF ∥HD 1; (2)EG ∥平面BB 1D 1D ; (3)平面BDF ∥平面B 1D 1H . 证明 如图.(1)取B 1B 的中点M ,连接HM ,MC 1,易证四边形HMC 1D 1是平行四边形, ∴HD 1∥MC 1. 又MC 1∥BF , ∴BF ∥HD 1.(2)取BD 的中点O ,连接OE ,OD 1, 则OE 綉12DC .又D 1G 綉12DC ,∴OE 綉D 1G .∴四边形OEGD 1是平行四边形, ∴EG ∥D 1O .又D 1O ⊂平面BB 1D 1D ,EG ⊄平面BB 1D 1D , ∴EG ∥平面BB 1D 1D .(3)由(1)知BF ∥HD 1,由题意易证B 1D 1∥BD .又B 1D 1,HD 1⊂平面B 1D 1H ,BF ,BD ⊂平面BDF ,且B 1D 1∩HD 1=D 1,DB ∩BF =B , ∴平面BDF ∥平面B 1D 1H .10.如图,在四棱锥P -ABCD 中,AD ∥BC ,AB =BC =12AD ,E ,F ,H 分别为线段AD ,PC ,CD 的中点,AC 与BE 交于O 点,G 是线段OF 上一点.(1)求证:AP ∥平面BEF ; (2)求证:GH ∥平面PAD . 证明 (1)如图,连接EC , 因为AD ∥BC ,BC =12AD ,所以BC ∥AE ,BC =AE ,所以四边形ABCE 是平行四边形, 所以O 为AC 的中点. 又因为F 是PC 的中点, 所以FO ∥AP , 因为FO ⊂平面BEF ,AP ⊄平面BEF ,所以AP ∥平面BEF .(2)连接FH ,OH ,因为F ,H 分别是PC ,CD 的中点, 所以FH ∥PD ,因为PD ⊂平面PAD ,FH ⊄平面PAD , 所以FH ∥平面PAD .又因为O 是BE 的中点,H 是CD 的中点, 所以OH ∥AD ,因为AD ⊂平面PAD ,OH ⊄平面PAD , 所以OH ∥平面PAD .又FH ∩OH =H ,FH ,OH ⊂平面OHF , 所以平面OHF ∥平面PAD . 又因为GH ⊂平面OHF , 所以GH ∥平面PAD .11.(多选)已知α,β是两个平面,m,n是两条直线.下列命题正确的是( )A.如果m∥n,n⊂α,那么m∥αB.如果m∥α,m⊂β,α∩β=n,那么m∥nC.如果α∥β,m⊂α,那么m∥βD.如果α⊥β,α∩β=n,m⊥n,那么m⊥β答案BC解析如果m∥n,n⊂α,那么m∥α或m⊂α,故A不正确;如果m∥α,m⊂β,α∩β=n,那么m∥n,这就是线面平行推得线线平行的性质定理,故B正确;如果α∥β,m⊂α,那么m∥β,这就是利用面面平行推线面平行的性质定理,故C正确;缺少m⊂α这个条件,故D不正确.12.(2022·福州检测)如图所示,正方体ABCD-A1B1C1D1中,点E,F,G,P,Q分别为棱AB,C1D1,D1A1,D1D,C1C的中点,则下列叙述中正确的是( )A.直线BQ∥平面EFGB.直线A1B∥平面EFGC.平面APC∥平面EFGD.平面A1BQ∥平面EFG答案 B解析过点E,F,G的截面如图所示(H,I分别为AA1,BC的中点),连接A1B,BQ,AP,PC,易知BQ与平面EFG相交于点Q,故A错误;∵A1B∥HE,A1B⊄平面EFG,HE⊂平面EFG,∴A1B∥平面EFG,故B正确;AP⊂平面ADD1A1,HG⊂平面ADD1A1,延长HG与PA必相交,故C错误;易知平面A1BQ与平面EFG有交点Q,故D错误.13.(多选)(2022·临沂模拟)如图1,在正方形ABCD 中,点E 为线段BC 上的动点(不含端点),将△ABE 沿AE 翻折,使得二面角B -AE -D 为直二面角,得到图2所示的四棱锥B -AECD ,点F 为线段BD 上的动点(不含端点),则在四棱锥B -AECD 中,下列说法正确的有( )图1 图2A .B ,E ,C ,F 四点不共面 B .存在点F ,使得CF ∥平面BAE C .三棱锥B -ADC 的体积为定值D .存在点E 使得直线BE 与直线CD 垂直 答案 AB解析 对于A ,假设直线BE 与直线CF 在同一平面上,所以E 在平面BCF 上, 又因为E 在折前线段BC 上,BC ∩平面BCF =C ,所以E 与C 重合,与E 异于C 矛盾, 所以直线BE 与直线CF 必不在同一平面上,即B ,E ,C ,F 四点不共面,故A 正确; 对于B ,如图,当点F 为线段BD 的中点,EC =12AD 时,直线CF ∥平面BAE ,证明如下:取AB 的中点G ,连接GE ,GF , 则EC ∥FG 且EC =FG ,所以四边形ECFG 为平行四边形, 所以FC ∥EG ,又因为EG ⊂平面BAE , 则直线CF 与平面BAE 平行,故B 正确;对于C ,在三棱锥B -ADC 中,因为点E 的移动会导致点B 到平面ACD 的距离发生变化,所以三棱锥B -ADC 的体积不是定值,故C 不正确;对于D ,过D 作DH ⊥AE 于H ,因为平面BAE ⊥平面AECD ,平面BAE ∩平面AECD =AE ,所以DH ⊥平面BAE ,所以DH ⊥BE ,若存在点E 使得直线BE 与直线CD 垂直,DH ⊂平面AECD ,且DC ⊂平面AECD ,DH ∩DC =D ,所以BE ⊥平面AECD ,所以BE ⊥AE ,与△ABE 是以B 为直角的三角形矛盾,所以不存在点E 使得直线BE 与直线CD 垂直,故D 不正确.14.如图,在长方体ABCD -A 1B 1C 1D 1中,AD =DD 1=1,AB =3,E ,F ,G 分别是AB ,BC ,C 1D 1的中点,点P 在平面ABCD 内,若直线D 1P ∥平面EFG ,则线段D 1P 长度的最小值是________.答案72解析 如图,连接D 1A ,AC ,D 1C .因为E ,F ,G 分别为AB ,BC ,C 1D 1的中点, 所以AC ∥EF ,又EF ⊄平面ACD 1,AC ⊂平面ACD 1, 则EF ∥平面ACD 1.同理可得EG ∥平面ACD 1,又EF ∩EG =E ,EF ,EG ⊂平面EFG ,所以平面ACD 1∥平面EFG . 因为直线D 1P ∥平面EFG , 所以点P 在直线AC 上.在△ACD 1中,易得AD 1=2,AC =2,CD 1=2, 所以1AD C S △=12×2×22-⎝⎛⎭⎪⎫222=72, 故当D 1P ⊥AC 时,线段D 1P 的长度最小,最小值为7212×2=72.15.(2022·合肥市第一中学模拟)正方体ABCD -A 1B 1C 1D 1的棱长为1,点M ,N 分别是棱BC ,CC 1的中点,动点P 在正方形BCC 1B 1(包括边界)内运动,且PA 1∥平面AMN ,则PA 1的长度范围为( )A.⎣⎢⎡⎦⎥⎤1,52B.⎣⎢⎡⎦⎥⎤324,52C.⎣⎢⎡⎦⎥⎤324,32 D.⎣⎢⎡⎦⎥⎤1,32答案 B解析 取B 1C 1的中点E ,BB 1的中点F ,连接A 1E ,A 1F ,EF , 取EF 的中点O ,连接A 1O ,如图所示,∵点M ,N 分别是棱长为1的正方体ABCD -A 1B 1C 1D 1中棱BC ,CC 1的中点, ∴AM ∥A 1E ,MN ∥EF ,∵AM ∩MN =M ,A 1E ∩EF =E ,AM ,MN ⊂平面AMN ,A 1E ,EF ⊂平面A 1EF , ∴平面AMN ∥平面A 1EF ,∵动点P 在正方形BCC 1B 1(包括边界)内运动, 且PA 1∥平面AMN ,∴点P 的轨迹是线段EF ,∵A 1E =A 1F =12+⎝ ⎛⎭⎪⎫122=52,EF =1212+12=22,∴A 1O ⊥EF ,∴当P 与O 重合时,PA 1的长度取最小值A 1O , A 1O =⎝ ⎛⎭⎪⎫522-⎝ ⎛⎭⎪⎫242=324,当P 与E (或F )重合时,PA 1的长度取最大值A 1E 或A 1F ,A 1E =A 1F =52.∴PA 1的长度范围为⎣⎢⎡⎦⎥⎤324,52.16.如图,正方体ABCD -A 1B 1C 1D 1中,棱长为a ,M ,N 分别为AB 1,A 1C 1上的点,A 1N =AM .(1)求证:MN ∥平面BB 1C 1C ;(2)求MN 的最小值.(1)证明 如图,作NE ∥A 1B 1交B 1C 1于点E ,作MF ∥AB 交BB 1于点F ,连接EF , 则NE ∥MF .∵NE ∥A 1B 1,∴NEA 1B 1=C 1NA 1C 1.又MF ∥AB ,∴MF AB =B 1MAB 1,∵A 1C 1=AB 1,A 1N =AM ,∴C 1N =B 1M .∴NE A 1B 1=MF AB,又AB =A 1B 1,∴NE =MF .∴四边形MNEF 是平行四边形,∴MN ∥EF , 又MN ⊄平面BB 1C 1C ,EF ⊂平面BB 1C 1C , ∴MN ∥平面BB 1C 1C .(2)解 设B 1E =x ,∵NE ∥A 1B 1, ∴B 1E B 1C 1=A 1NA 1C 1.又∵MF ∥AB ,∴B 1F BB 1=B 1M AB 1,∵A 1N =AM ,A 1C 1=AB 1=2a ,B 1C 1=BB 1=a ,B 1E =x ,∴B 1E B 1C 1+B 1F BB 1=A 1N A 1C 1+B 1MAB 1,∴x a +B 1F a =1,∴B 1F =a -x ,从而MN =EF =B 1E 2+B 1F 2 =x 2+a -x2 =2⎝ ⎛⎭⎪⎫x -a 22+⎝ ⎛⎭⎪⎫a 22, ∴当x =a 2时,MN 的最小值为22a .。
直线与平⾯、平⾯与平⾯平⾏的判定(附答案)直线与平⾯、平⾯与平⾯平⾏的判定[学习⽬标] 1.理解直线与平⾯平⾏、平⾯与平⾯平⾏判定定理的含义.2.会⽤图形语⾔、⽂字语⾔、符号语⾔准确描述直线与平⾯平⾏、平⾯与平⾯平⾏的判定定理,并知道其地位和作⽤.3.能运⽤直线与平⾯平⾏的判定定理、平⾯与平⾯平⾏的判定定理证明⼀些空间线⾯关系的简单问题.知识点⼀直线与平⾯平⾏的判定定理思考若⼀条直线平⾏于⼀个平⾯内的⼀条直线,则这条直线和这个平⾯平⾏吗?答根据直线与平⾯平⾏的判定定理可知该结论错误. 知识点⼆平⾯与平⾯平⾏的判定定理思考如果⼀条直线与两个平⾏平⾯中的⼀个平⾏,那么这条直线与另⼀个平⾯也平⾏吗?答不⼀定.这条直线与另⼀个平⾯平⾏或在另⼀个平⾯内.题型⼀直线与平⾯平⾏的判定定理的应⽤例1 如图,空间四边形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点.求证:(1)EH ∥平⾯BCD ; (2)BD ∥平⾯EFGH .证明 (1)∵EH 为△ABD 的中位线,∴EH ∥BD .∵EH ?平⾯BCD ,BD ?平⾯BCD ,∴EH∥平⾯BCD.(2)∵BD∥EH,BD?平⾯EFGH,EH?平⾯EFGH,∴BD∥平⾯EFGH.跟踪训练1在四⾯体A-BCD中,M,N分别是△ABD和△BCD的重⼼,求证:MN∥平⾯ADC.证明如图所⽰,连接BM,BN并延长,分别交AD,DC于P,Q两点,连接PQ.因为M,N分别是△ABD和△BCD的重⼼,所以BM∶MP=BN∶NQ=2∶1.所以MN∥PQ.⼜因为MN?平⾯ADC,PQ?平⾯ADC,所以MN∥平⾯ADC.题型⼆⾯⾯平⾏判定定理的应⽤例2如图所⽰,在三棱柱ABC-A1B1C1中,点D,E分别是BC与B1C1的中点.求证:平⾯A1EB∥平⾯ADC1.证明由棱柱性质知,B1C1∥BC,B1C1=BC,⼜D,E分别为BC,B1C1的中点,所以C1E綊DB,则四边形C1DBE为平⾏四边形,因此EB∥C1D,⼜C1D?平⾯ADC1,EB?平⾯ADC1,所以EB∥平⾯ADC1.连接DE,同理,EB1綊BD,所以四边形EDBB1为平⾏四边形,则ED綊B1B.因为B1B∥A1A,B1B=A1A(棱柱的性质),所以ED綊A1A,则四边形EDAA1为平⾏四边形,所以A 1E ∥AD ,⼜A 1E ?平⾯ADC 1,AD ?平⾯ADC 1,所以A 1E ∥平⾯ADC 1.由A 1E ∥平⾯ADC 1,EB ∥平⾯ADC 1, A 1E ?平⾯A 1EB ,EB ?平⾯A 1EB ,且A 1E ∩EB =E ,所以平⾯A 1EB ∥平⾯ADC 1.跟踪训练2 已知ABCD -A 1B 1C 1D 1是棱长为3的正⽅体,点E 在AA 1上,点F 在CC 1上,点G 在BB 1上,且AE =FC 1=B 1G =1,H 是B 1C 1的中点. 求证:(1)E ,B ,F ,D 1四点共⾯; (2)平⾯A 1GH ∥平⾯BED 1F .证明 (1)∵AE =B 1G =1,∴BG =A 1E =2. ⼜∵BG ∥A 1E ,∴四边形A 1EBG 是平⾏四边形,∴A 1G ∥BE .连接FG .∵C 1F =B 1G ,C 1F ∥B 1G ,∴四边形C 1FGB 1是平⾏四边形,∴FG =C 1B 1=D 1A 1,FG ∥C 1B 1∥D 1A 1,∴四边形A 1GFD 1是平⾏四边形,∴A 1G ∥D 1F ,∴D 1F ∥EB . 故E ,B ,F ,D 1四点共⾯. (2)∵H 是B 1C 1的中点,∴B 1H =32.⼜∵B 1G =1,∴B 1G B 1H =23.⼜FC BC =23,且∠FCB =∠GB 1H =90°,∴△B 1HG ∽△CBF ,∴∠B 1GH =∠CFB =∠FBG ,∴HG ∥FB .⼜由(1)知,A 1G ∥BE ,且HG ∩A 1G =G ,FB ∩BE =B ,∴平⾯A 1GH ∥平⾯BED 1F .题型三线⾯平⾏、⾯⾯平⾏判定定理的综合应⽤例3 在正⽅体ABCD -A 1B 1C 1D 1中,O 为底⾯ABCD 的中⼼,P 是DD 1的中点,设Q 是CC 1上的点.问:当点Q 在什么位置时,平⾯D 1BQ ∥平⾯P AO ?请说明理由.解当Q 为CC1的中点时,平⾯D 1BQ ∥平⾯P AO .理由如下:连接PQ .∵Q 为CC 1的中点,P 为DD 1的中点,∴PQ ∥DC ∥AB ,PQ =DC =AB ,∴四边形ABQP 是平⾏四边形,∴QB ∥P A . ⼜∵O 为DB 的中点,∴D 1B ∥PO . ⼜∵PO ∩P A =P ,D 1B ∩QB =B ,∴平⾯D 1BQ ∥平⾯P AO .跟踪训练3 如图,三棱柱ABC -A 1B 1C 1的底⾯为正三⾓形,侧棱A 1A ⊥底⾯ABC ,E ,F 分别是棱CC 1,BB 1上的点,EC =2FB .M 是线段AC 上的动点,当点M 在何位置时,BM ∥平⾯AEF ?请说明理由.解当M 为AC 中点时,BM ∥平⾯AEF .理由如下:⽅法⼀如图1,取AE 的中点O ,连接OF ,OM . ∵O ,M 分别是AE ,AC 的中点,∴OM ∥EC ,OM =12EC .⼜∵BF ∥CE ,EC =2FB ,∴OM ∥BF ,OM =BF ,∴四边形OMBF 为平⾏四边形,∴BM ∥OF . ⼜∵OF ?⾯AEF ,BM ?⾯AEF ,∴BM ∥平⾯AEF .⽅法⼆如图2,取EC 的中点P ,连接PM ,PB . ∵PM 是△ACE 的中位线,∴PM ∥AE .∵EC=2FB=2PE,CC1∥BB1,∴PE=BF,PE∥BF,∴四边形BPEF是平⾏四边形,∴PB∥EF.⼜∵PM?平⾯AEF,PB?平⾯AEF,∴PM∥平⾯AEF,PB∥平⾯AEF.⼜∵PM∩PB=P,∴平⾯PBM∥平⾯AEF.⼜∵BM?⾯PBM,∴BM∥平⾯AEF.⾯⾯平⾏的判定例4已知在正⽅体ABCD-A′B′C′D′中,M,N分别是A′D′,A′B′的中点,在该正⽅体中是否存在过顶点且与平⾯AMN平⾏的平⾯?若存在,试作出该平⾯,并证明你的结论;若不存在,请说明理由.分析根据题意画出正⽅体,根据平⾯AMN的特点,试着在正⽅体中找出⼏条平⾏于该平⾯的直线,然后作出判断,并证明.解如图,与平⾯AMN平⾏的平⾯有以下三种情况:下⾯以图①为例进⾏证明.如图①,取B′C′的中点E,连接BD,BE,DE,ME,B′D′,可知四边形ABEM是平⾏四边形,所以BE∥AM.⼜因为BE?平⾯BDE,AM?平⾯BDE,所以AM∥平⾯BDE.因为MN是△A′B′D′的中位线,所以MN∥B′D′.因为四边形BDD′B′是平⾏四边形,所以BD∥B′D′.所以MN∥BD.⼜因为BD?平⾯BDE,MN?平⾯BDE,所以MN∥平⾯BDE.⼜因为AM?平⾯AMN,MN?平⾯AMN,且AM∩MN=M,所以由平⾯与平⾯平⾏的判定定理可得,平⾯AMN∥平⾯BDE.1.过直线l外两点,作与l平⾏的平⾯,则这样的平⾯()A.不可能作出B.只能作出⼀个C.能作出⽆数个D.上述三种情况都存在2.经过平⾯α外两点,作与α平⾏的平⾯,则这样的平⾯可以作()A.1个或2个B.0个或1个C.1个D.0个3.若线段AB,BC,CD不共⾯,M,N,P分别为线段AB,BC,CD的中点,则直线BD与平⾯MNP的位置关系是()A.平⾏B.直线在平⾯内C.相交D.以上均有可能4.在正⽅体EFGH-E1F1G1H1中,下列四对截⾯彼此平⾏的⼀对是()A.平⾯E1FG1与平⾯EGH1B.平⾯FHG1与平⾯F1H1GC.平⾯F1H1H与平⾯FHE1D.平⾯E1HG1与平⾯EH1G5.梯形ABCD中,AB∥CD,AB?平⾯α,CD?平⾯α,则直线CD与平⾯α的位置关系是________.⼀、选择题1.下列说法正确的是()①若⼀个平⾯内有两条直线都与另⼀个平⾯平⾏,则这两个平⾯平⾏;②若⼀个平⾯内有⽆数条直线都与另⼀个平⾯平⾏,则这两个平⾯平⾏;③若⼀个平⾯内任何⼀条直线都平⾏于另⼀个平⾯,则这两个平⾯平⾏;④若⼀个平⾯内的两条相交直线都与另⼀个平⾯平⾏,则这两个平⾯平⾏.A.①③B.②④C.②③④D.③④2.平⾯α与平⾯β平⾏的条件可以是()A.α内有⽆穷多条直线与β平⾏B.直线a∥α,a∥β,且直线a不在α与β内C.直线a?α,直线b?β,且b∥α,a∥βD.α内的任何直线都与β平⾏3.六棱柱的表⾯中,互相平⾏的平⾯最多有()A.2对B.3对C.4对D.5对4.如果直线a平⾏于平⾯α,那么下列命题正确的是()A.平⾯α内有且只有⼀条直线与a平⾏B.平⾯α内有⽆数条直线与a平⾏C.平⾯α内不存在与a平⾏的直线D.平⾯α内的任意直线与直线a都平⾏5.在空间四边形ABCD中,E,F分别为AB,AD上的点,且AE∶EB=AF∶FD=1∶4,⼜H,G分别为BC,CD的中点,则()A.BD∥平⾯EFG,且四边形EFGH是平⾏四边形B.EF∥平⾯BCD,且四边形EFGH是梯形C.HG∥平⾯ABD,且四边形EFGH是平⾏四边形D.EH∥平⾯ADC,且四边形EFGH是梯形6.平⾯α内有不共线的三点到平⾯β的距离相等且不为零,则α与β的位置关系为()A.平⾏B.相交C.平⾏或相交D.可能重合7.已知直线l,m,平⾯α,β,下列命题正确的是()A.l∥β,l?α?α∥βB.l∥β,m∥β,l?α,m?α?α∥βC.l∥m,l?α,m?β?α∥βD.l∥β,m∥β,l?α,m?α,l∩m=M?α∥β⼆、填空题8.三棱锥SABC中,G为△ABC的重⼼,E在棱SA上,且AE=2ES,则EG与平⾯SBC的关系为________.9.如图是正⽅体的平⾯展开图.在这个正⽅体中,①BM∥平⾯DE;②CN∥平⾯AF;③平⾯BDM∥平⾯AFN;④平⾯BDE∥平⾯NCF.以上四个命题中,正确命题的序号是________.10.右图是⼀⼏何体的平⾯展开图,其中四边形ABCD为正⽅形,E,F,G,H分别为P A,PD,PC,PB的中点,在此⼏何体中,给出下⾯五个结论:①平⾯EFGH∥平⾯ABCD;②P A∥平⾯BDG;③EF∥平⾯PBC;④FH∥平⾯BDG;⑤EF∥平⾯BDG;其中正确结论的序号是________.三、解答题11.如图,在已知四棱锥P-ABCD中,底⾯ABCD为平⾏四边形,点M,N,Q分别在P A,BD,PD上,且PM∶MA=BN∶ND=PQ∶QD.求证:平⾯MNQ∥平⾯PBC.12.如图,在正四棱柱ABCD-A1B1C1D1中,M是棱AB的中点,点N在侧⾯AA1D1D上运动,点N满⾜什么条件时,MN∥平⾯BB1D1D?当堂检测答案1.答案 D解析设直线外两点为A、B,若直线AB∥l,则过A、B可作⽆数个平⾯与l平⾏;若直线AB与l异⾯,则只能作⼀个平⾯与l平⾏;若直线AB与l相交,则过A、B没有平⾯与l 平⾏.2.答案 B解析①当经过两点的直线与平⾯α平⾏时,可作出⼀个平⾯β使β∥α.②当经过两点的直线与平⾯α相交时,由于作出的平⾯⼜⾄少有⼀个公共点,故经过两点的平⾯都与平⾯α相交,不能作出与平⾯α平⾏的平⾯.故满⾜条件的平⾯有0个或1个. 3.答案 A解析连接NP,因为N、P分别是BC、CD的中点,M是AB的中点,AB、BC、CD不共⾯,所以直线BD不在平⾯MNP上.∴直线BD与平⾯MNP平⾏.4.答案 A解析如图,∵EG∥E1G1,EG?平⾯E1FG1,E1G1?平⾯E1FG1,∴EG∥平⾯E1FG1,⼜G1F∥H1E,同理可证H1E∥平⾯E1FG1,⼜H1E∩EG=E,∴平⾯E1FG1∥平⾯EGH1.5.答案CD∥α解析因为AB∥CD,AB?平⾯α,CD?平⾯α,由线⾯平⾏的判定定理可得CD∥α.课时精练答案⼀、选择题1.答案 D解析如图,长⽅体ABCD-A1B1C1D1中,在平⾯ABCD内,在AB上任取⼀点E,过点E作EF∥AD,交CD于点F,则由线⾯平⾏的判定定理,知EF,BC都平⾏于平⾯ADD1A1,⽤同样的⽅法可以在平⾯ABCD内作出⽆数条直线都与平⾯ADD1A1平⾏,但是平⾯ABCD与平⾯ADD 1A 1不平⾏,因此①②都错;③正确,事实上,因为⼀个平⾯内任意⼀条直线都平⾏于另⼀个平⾯,所以这两个平⾯必⽆公共点(要注意“任意⼀条直线”与“⽆数条直线”的区别);④是平⾯与平⾯平⾏的判定定理,正确. 2.答案 D解析对于A 项,当α与β相交时,α内也有⽆数条直线都与交线平⾏,故A 错误;对于B 项,当a 平⾏于α与β的交线时,也能满⾜,但此时α与β相交,故B 错误;对于C 项,当a 和b 都与α与β的交线平⾏时,也能满⾜,但此时α与β相交,故C 错误;对于D 项,α内的任何直线都与β平⾏,故在⼀个平⾯内存在两条相交直线平⾏于另⼀平⾯,故D 正确. 3.答案 C解析侧⾯中有3对,对⾯相互平⾏,上下两底⾯也相互平⾏. 4.答案 B解析如图,直线B 1C 1∥平⾯ABCD ,B 1C 1∥BC ,B 1C 1∥AD ,B 1C 1∥EF (E ,F 为中点)等,平⾯ABCD 内平⾏于BC 的所有直线均与B 1C 1平⾏.但AB 与B 1C 1不平⾏.5.答案 B解析易证EF ∥平⾯BCD .由AE ∶EB =AF ∶FD ,知EF ∥BD ,且EF =15BD .⼜因为H ,G 分别为BC ,CD 的中点,所以HG ∥BD ,且HG =12BD .综上可知,EF ∥HG ,EF ≠HG ,所以四边形EFGH 是梯形,且EF ∥平⾯BCD . 6.答案 C解析若三点分布于平⾯β的同侧,则α与β平⾏,若三点分布于平⾯β的两侧,则α与β相交. 7.答案 D解析如图所⽰,在长⽅体ABCDA 1B 1C 1D 1中,AB ∥CD ,则AB ∥平⾯DC 1,AB ?平⾯AC ,但是平⾯AC 与平⾯DC 1不平⾏,所以A 错误;取BB 1的中点E ,CC 1的中点F ,则可证EF ∥平⾯AC ,B1C1∥平⾯AC.EF?平⾯BC1,B1C1?平⾯BC1,但是平⾯AC与平⾯BC1不平⾏,所以B 错误;可证AD∥B1C1,AD?平⾯AC,B1C1?平⾯BC1,⼜平⾯AC与平⾯BC1不平⾏,所以C错误;很明显D是⾯⾯平⾏的判定定理,所以D正确.⼆、填空题8.答案平⾏解析如图,延长AG交BC于F,连接SF,则由G为△ABC的重⼼知AG∶GF=2,⼜AE∶ES=2,∴EG∥SF,⼜SF?平⾯SBC,EG?平⾯SBC,∴EG∥平⾯SBC.9.答案①②③④解析以ABCD为下底⾯还原正⽅体,如图:则易判定四个命题都是正确的.10.答案①②③④解析把图形还原为⼀个四棱锥,然后根据线⾯、⾯⾯平⾏的判定定理判断即可.三、解答题11.证明因为PM∶MA=BN∶ND=PQ∶QD,所以MQ∥AD,NQ∥BP.因为BP?平⾯PBC,NQ?平⾯PBC,所以NQ∥平⾯PBC.⼜因为底⾯ABCD为平⾏四边形,所以BC∥AD,所以MQ∥BC.因为BC?平⾯PBC,MQ?平⾯PBC,所以MQ∥平⾯PBC.⼜因为MQ∩NQ=Q,所以根据平⾯与平⾯平⾏的判定定理,得平⾯MNQ∥平⾯PBC.12.解如图,在正四棱柱ABCD-A1B1C1D1中,分别取棱A1B1,A1D1,AD的中点E,F,G,连接ME,EF,FG,GM.因为M是AB的中点,所以ME∥AA1∥FG,且ME=AA1=FG.所以四边形MEFG是平⾏四边形.因为ME∥BB1,BB1?平⾯BB1D1D,ME?平⾯BB1D1D,所以ME∥平⾯BB1D1D.在△A1B1D1中,因为EF∥B1D1,B1D1?平⾯BB1D1D,EF?平⾯BB1D1D,所以EF∥平⾯BB1D1D.⼜因为ME∩EF=E,且ME?平⾯MEFG,EF?平⾯MEFG,所以平⾯MEFG∥平⾯BB1D1D.在FG上任取⼀点N,连接MN,所以MN?平⾯MEFG.所以MN与平⾯BB1D1D⽆公共点.所以MN∥平⾯BB1D1D.总之,当点N在平⾯AA1D1D内的直线FG上(任意位置)时,都有MN∥BB1D1D,即当点N在矩形AA1D1D中过A1D1与AD的中点的直线上运动时,都有MN∥平⾯BB1D1D.。
直线与平面、平面与平面平行的判定[学习目标] 1.理解直线与平面平行、平面与平面平行判定定理的含义.2.会用图形语言、文字语言、符号语言准确描述直线与平面平行、平面与平面平行的判定定理,并知道其地位和作用.3.能运用直线与平面平行的判定定理、平面与平面平行的判定定理证明一些空间线面关系的简单问题.知识点一直线与平面平行的判定定理语言叙述符号表示图形表示平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行⎭⎪⎬⎪⎫a⊄αb⊂αa∥b⇒a∥α思考若一条直线平行于一个平面内的一条直线,则这条直线和这个平面平行吗答根据直线与平面平行的判定定理可知该结论错误.知识点二平面与平面平行的判定定理语言叙述符号表示图形表示一个平面内的两条相交直线与另一个平面平行,则这两个平面平行⎭⎪⎬⎪⎫a⊂α,b⊂αa∩b=Aa∥β,b∥β⇒α∥β思考如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面也平行吗答不一定.这条直线与另一个平面平行或在另一个平面内.题型一直线与平面平行的判定定理的应用例1 如图,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.求证:(1)EH∥平面BCD;(2)BD∥平面EFGH.证明(1)∵EH为△ABD的中位线,∴EH∥BD.∵EH⊄平面BCD,BD⊂平面BCD,∴EH∥平面BCD.(2)∵BD∥EH,BD⊄平面EFGH,EH⊂平面EFGH,∴BD∥平面EFGH.跟踪训练1 在四面体A-BCD中,M,N分别是△ABD和△BCD的重心,求证:MN∥平面ADC.证明如图所示,连接BM,BN并延长,分别交AD,DC于P,Q两点,连接PQ.因为M,N分别是△ABD和△BCD的重心,所以BM∶MP=BN∶NQ=2∶1.所以MN∥PQ.又因为MN⊄平面ADC,PQ⊂平面ADC,所以MN∥平面ADC.题型二面面平行判定定理的应用例2 如图所示,在三棱柱ABC-A1B1C1中,点D,E分别是BC与B1C1的中点.求证:平面A1EB∥平面ADC1.证明由棱柱性质知,B1C1∥BC,B1C1=BC,又D,E分别为BC,B1C1的中点,所以C1E綊DB,则四边形C1DBE为平行四边形,因此EB∥C1D,又C1D⊂平面ADC1,EB⊄平面ADC1,所以EB∥平面ADC1.连接DE,同理,EB1綊BD,所以四边形EDBB1为平行四边形,则ED綊B1B.因为B1B∥A1A,B1B=A1A(棱柱的性质),所以ED綊A1A,则四边形EDAA1为平行四边形,所以A1E∥AD,又A1E⊄平面ADC1,AD⊂平面ADC1,所以A1E∥平面ADC1.由A1E∥平面ADC1,EB∥平面ADC1,A1E⊂平面A1EB,EB⊂平面A1EB,且A1E∩EB=E,所以平面A1EB∥平面ADC1.跟踪训练2 已知ABCD-A1B1C1D1是棱长为3的正方体,点E在AA1上,点F在CC1上,点G在BB1上,且AE=FC1=B1G=1,H是B1C1的中点.求证:(1)E,B,F,D1四点共面;(2)平面A1GH∥平面BED1F.证明(1)∵AE=B1G=1,∴BG=A1E=2.又∵BG∥A1E,∴四边形A1EBG是平行四边形,∴A1G∥BE.连接FG.∵C1F=B1G,C1F∥B1G,∴四边形C1FGB1是平行四边形,∴FG=C1B1=D1A1,FG∥C1B1∥D1A1,∴四边形A1GFD1是平行四边形,∴A1G∥D1F,∴D1F∥EB.故E,B,F,D1四点共面.(2)∵H是B1C1的中点,∴B1H=32 .又∵B 1G =1,∴B 1G B 1H =23.又FC BC =23,且∠FCB =∠GB 1H =90°, ∴△B 1HG ∽△CBF ,∴∠B 1GH =∠CFB =∠FBG ,∴HG ∥FB .又由(1)知,A 1G ∥BE ,且HG ∩A 1G =G ,FB ∩BE =B , ∴平面A 1GH ∥平面BED 1F .题型三 线面平行、面面平行判定定理的综合应用例3 在正方体ABCD -A 1B 1C 1D 1中,O 为底面ABCD 的中心,P 是DD 1的中点,设Q 是CC 1上的点.问:当点Q 在什么位置时,平面D 1BQ ∥平面PAO 请说明理由.解 当Q 为CC 1的中点时,平面D 1BQ ∥平面PAO .理由如下:连接PQ .∵Q 为CC 1的中点,P 为DD 1的中点, ∴PQ ∥DC ∥AB ,PQ =DC =AB ,∴四边形ABQP 是平行四边形,∴QB ∥PA .又∵O为DB的中点,∴D1B∥PO.又∵PO∩PA=P,D1B∩QB=B,∴平面D1BQ∥平面PAO.跟踪训练3 如图,三棱柱ABC-A1B1C1的底面为正三角形,侧棱A1A⊥底面ABC,E,F分别是棱CC1,BB1上的点,EC=是线段AC上的动点,当点M在何位置时,BM∥平面AEF请说明理由.解当M为AC中点时,BM∥平面AEF.理由如下:方法一如图1,取AE的中点O,连接OF,OM.∵O,M分别是AE,AC的中点,∴OM∥EC,OM=12 EC.又∵BF∥CE,EC=2FB,∴OM∥BF,OM=BF,∴四边形OMBF为平行四边形,∴BM∥OF.又∵OF⊂面AEF,BM⊄面AEF,∴BM∥平面AEF.方法二如图2,取EC的中点P,连接PM,PB.∵PM是△ACE的中位线,∴PM∥AE.∵EC=2FB=2PE,CC1∥BB1,∴PE=BF,PE∥BF,∴四边形BPEF是平行四边形,∴PB∥EF.又∵PM⊄平面AEF,PB⊄平面AEF,∴PM∥平面AEF,PB∥平面AEF.又∵PM∩PB=P,∴平面PBM∥平面AEF.又∵BM⊂面PBM,∴BM∥平面AEF.面面平行的判定例4 已知在正方体ABCD-A′B′C′D′中,M,N分别是A′D′,A′B′的中点,在该正方体中是否存在过顶点且与平面AMN平行的平面若存在,试作出该平面,并证明你的结论;若不存在,请说明理由.分析根据题意画出正方体,根据平面AMN的特点,试着在正方体中找出几条平行于该平面的直线,然后作出判断,并证明.解如图,与平面AMN平行的平面有以下三种情况:下面以图①为例进行证明.如图①,取B′C′的中点E,连接BD,BE,DE,ME,B′D′,可知四边形ABEM是平行四边形,所以BE∥AM.又因为BE⊂平面BDE,AM⊄平面BDE,所以AM∥平面BDE.因为MN是△A′B′D′的中位线,所以MN∥B′D′.因为四边形BDD′B′是平行四边形,所以BD∥B′D′.所以MN∥BD.又因为BD⊂平面BDE,MN⊄平面BDE,所以MN∥平面BDE.又因为AM⊂平面AMN,MN⊂平面AMN,且AM∩MN=M,所以由平面与平面平行的判定定理可得,平面AMN∥平面BDE.1.过直线l外两点,作与l平行的平面,则这样的平面( )A.不可能作出B.只能作出一个C.能作出无数个D.上述三种情况都存在2.经过平面α外两点,作与α平行的平面,则这样的平面可以作( )个或2个个或1个个个3.若线段AB,BC,CD不共面,M,N,P分别为线段AB,BC,CD的中点,则直线BD与平面MNP的位置关系是( )A.平行B.直线在平面内C.相交D.以上均有可能4.在正方体EFGH-E1F1G1H1中,下列四对截面彼此平行的一对是( )A.平面E1FG1与平面EGH1B.平面FHG1与平面F1H1GC.平面F1H1H与平面FHE1D.平面E1HG1与平面EH1G5.梯形ABCD中,AB∥CD,AB⊂平面α,CD⊄平面α,则直线CD与平面α的位置关系是________.一、选择题1.下列说法正确的是( )①若一个平面内有两条直线都与另一个平面平行,则这两个平面平行;②若一个平面内有无数条直线都与另一个平面平行,则这两个平面平行;③若一个平面内任何一条直线都平行于另一个平面,则这两个平面平行;④若一个平面内的两条相交直线都与另一个平面平行,则这两个平面平行.A.①③B.②④C.②③④D.③④2.平面α与平面β平行的条件可以是( )A.α内有无穷多条直线与β平行B.直线a∥α,a∥β,且直线a不在α与β内C.直线a⊂α,直线b⊂β,且b∥α,a∥βD.α内的任何直线都与β平行3.六棱柱的表面中,互相平行的平面最多有( )对对对对4.如果直线a平行于平面α,那么下列命题正确的是( )A.平面α内有且只有一条直线与a平行B.平面α内有无数条直线与a平行C.平面α内不存在与a平行的直线D.平面α内的任意直线与直线a都平行5.在空间四边形ABCD中,E,F分别为AB,AD上的点,且AE∶EB=AF∶FD=1∶4,又H,G分别为BC,CD的中点,则( )∥平面EFG,且四边形EFGH是平行四边形∥平面BCD,且四边形EFGH是梯形∥平面ABD,且四边形EFGH是平行四边形∥平面ADC,且四边形EFGH是梯形6.平面α内有不共线的三点到平面β的距离相等且不为零,则α与β的位置关系为( )A.平行B.相交C.平行或相交D.可能重合7.已知直线l,m,平面α,β,下列命题正确的是( )∥β,l⊂α⇒α∥β∥β,m∥β,l⊂α,m ⊂α⇒α∥β∥m,l⊂α,m⊂β⇒α∥β∥β,m∥β,l⊂α,m⊂α,l∩m=M⇒α∥β二、填空题8.三棱锥SABC中,G为△ABC的重心,E在棱SA上,且AE=2ES,则EG与平面SBC的关系为________.9.如图是正方体的平面展开图.在这个正方体中,①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.以上四个命题中,正确命题的序号是________.10.右图是一几何体的平面展开图,其中四边形ABCD为正方形,E,F,G,H分别为PA,PD,PC,PB的中点,在此几何体中,给出下面五个结论:①平面EFGH∥平面ABCD;②PA∥平面BDG;③EF∥平面PBC;④FH∥平面BDG;⑤EF∥平面BDG;其中正确结论的序号是________.三、解答题11.如图,在已知四棱锥P-ABCD中,底面ABCD为平行四边形,点M,N,Q分别在PA,BD,PD上,且PM∶MA=BN∶ND=PQ∶QD.求证:平面MNQ∥平面PBC.12.如图,在正四棱柱ABCD-A1B1C1D1中,M是棱AB的中点,点N在侧面AA1D1D上运动,点N满足什么条件时,MN∥平面BB1D1D当堂检测答案1.答案D解析设直线外两点为A、B,若直线AB∥l,则过A、B可作无数个平面与l平行;若直线AB与l异面,则只能作一个平面与l平行;若直线AB与l相交,则过A、B没有平面与l平行.2.答案B解析①当经过两点的直线与平面α平行时,可作出一个平面β使β∥α.②当经过两点的直线与平面α相交时,由于作出的平面又至少有一个公共点,故经过两点的平面都与平面α相交,不能作出与平面α平行的平面.故满足条件的平面有0个或1个.3.答案A解析连接NP,因为N、P分别是BC、CD的中点,M是AB的中点,AB、BC、CD不共面,所以直线BD不在平面MNP上.∴直线BD与平面MNP平行.4.答案A解析如图,∵EG∥E1G1,EG⊄平面E1FG1,E1G1⊂平面E1FG1,∴EG∥平面E1FG1,又G1F∥H1E,同理可证H1E∥平面E1FG1,又H1E∩EG=E,∴平面E1FG1∥平面EGH1.5.答案CD∥α解析因为AB∥CD,AB⊂平面α,CD⊄平面α,由线面平行的判定定理可得CD∥α.课时精练答案一、选择题1.答案D解析如图,长方体ABCD-A1B1C1D1中,在平面ABCD内,在AB上任取一点E,过点E作EF∥AD,交CD于点F,则由线面平行的判定定理,知EF,BC都平行于平面ADD1A1,用同样的方法可以在平面ABCD内作出无数条直线都与平面ADD1A1平行,但是平面ABCD与平面ADD1A1不平行,因此①②都错;③正确,事实上,因为一个平面内任意一条直线都平行于另一个平面,所以这两个平面必无公共点(要注意“任意一条直线”与“无数条直线”的区别);④是平面与平面平行的判定定理,正确.2.答案D解析 对于A 项,当α与β相交时,α内也有无数条直线都与交线平行,故A 错误;对于B 项,当a 平行于α与β的交线时,也能满足,但此时α与β相交,故B 错误;对于C 项,当a 和b 都与α与β的交线平行时,也能满足,但此时α与β相交,故C 错误;对于D 项,α内的任何直线都与β平行,故在一个平面内存在两条相交直线平行于另一平面,故D 正确. 3.答案 C解析 侧面中有3对,对面相互平行,上下两底面也相互平行. 4.答案 B解析 如图,直线B 1C 1∥平面ABCD ,B 1C 1∥BC ,B 1C 1∥AD ,B 1C 1∥EF (E ,F 为中点)等,平面ABCD 内平行于BC 的所有直线均与B 1C 1平行.但AB与B 1C 1不平行.5.答案 B解析 易证EF ∥平面BCD .由AE ∶EB =AF ∶FD ,知EF ∥BD ,且EF =15BD .又因为H ,G 分别为BC ,CD 的中点,所以HG∥BD,且HG=12BD.综上可知,EF∥HG,EF≠HG,所以四边形EFGH是梯形,且EF∥平面BCD.6.答案C解析若三点分布于平面β的同侧,则α与β平行,若三点分布于平面β的两侧,则α与β相交.7.答案D解析如图所示,在长方体ABCDA1B1C1D1中,AB∥CD,则AB∥平面DC1,AB⊂平面AC,但是平面AC与平面DC1不平行,所以A错误;取BB1的中点E,CC1的中点F,则可证EF∥平面AC,B1C1∥平面⊂平面BC1,B1C1⊂平面BC1,但是平面AC与平面BC1不平行,所以B错误;可证AD∥B1C1,AD⊂平面AC,B1C1⊂平面BC1,又平面AC与平面BC1不平行,所以C错误;很明显D是面面平行的判定定理,所以D正确.二、填空题8.答案平行解析如图,延长AG交BC于F,连接SF,则由G为△ABC的重心知AG∶GF=2,又AE∶ES=2,∴EG∥SF,又SF⊂平面SBC,EG⊄平面SBC,∴EG∥平面SBC.9.答案①②③④解析以ABCD为下底面还原正方体,如图:则易判定四个命题都是正确的.10.答案①②③④解析把图形还原为一个四棱锥,然后根据线面、面面平行的判定定理判断即可.三、解答题11.证明因为PM∶MA=BN∶ND=PQ∶QD,所以MQ∥AD,NQ∥BP.因为BP⊂平面PBC,NQ⊄平面PBC,所以NQ∥平面PBC.又因为底面ABCD为平行四边形,所以BC∥AD,所以MQ∥BC.因为BC⊂平面PBC,MQ⊄平面PBC,所以MQ∥平面PBC.又因为MQ∩NQ=Q,所以根据平面与平面平行的判定定理,得平面MNQ∥平面PBC.12.解如图,在正四棱柱ABCD-A1B1C1D1中,分别取棱A1B1,A1D1,AD的中点E,F,G,连接ME,EF,FG,GM.因为M是AB的中点,所以ME∥AA1∥FG,且ME=AA1=FG.所以四边形MEFG是平行四边形.因为ME∥BB1,BB1⊂平面BB1D1D,ME⊄平面BB1D1D,所以ME∥平面BB1D1D.在△A1B1D1中,因为EF∥B1D1,B1D1⊂平面BB1D1D,EF⊄平面BB1D1D,所以EF∥平面BB1D1D.又因为ME∩EF=E,且ME⊂平面MEFG,EF⊂平面MEFG,所以平面MEFG∥平面BB1D1D.在FG上任取一点N,连接MN,所以MN⊂平面MEFG.所以MN与平面BB1D1D无公共点.所以MN∥平面BB1D1D.总之,当点N在平面AA1D1D内的直线FG上(任意位置)时,都有MN∥BB1D1D,即当点N在矩形AA1D1D中过A1D1与AD的中点的直线上运动时,都有MN∥平面BB1D1D.。
直线、平面平行的判定及其性质考点梳理1.直线与平面平行(1)判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行(线线平行⇒线面平行).即:a⊄α,b⊂α,且a∥b⇒a∥α.其他判定方法;α∥β,a⊂α⇒a∥β.(2)性质定理:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行(线面平行⇒线线平行).即:a∥α,a⊂β,α∩β=l⇒a∥l.2.平面与平面平行(1)判定定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行(线面平行⇒面面平行).即:a⊂α,b⊂α,a∩b=M,a∥β,b∥β⇒α∥β.(2)性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.即:α∥β,γ∩α=a,γ∩β=b⇒a∥b.一个转化关系平行问题的转化关系两点提醒(1)在推证线面平行时,必须满足三个条件:一是直线a在已知平面外;二是直线b在已知平面内;三是两直线平行.(2)把线面平行转化为线线平行时,必须说清经过已知直线的平面与已知平面相交,则该直线与交线平行.考点自测1.若两条直线都与一个平面平行,则这两条直线的位置关系是().A.平行B.相交C.异面D.以上均有可能解析借助长方体模型易得.答案 D2.在空间中,下列命题正确的是().A.平行直线的平行投影重合B.平行于同一直线的两个平面平行C.垂直于同一平面的两个平面平行D.垂直于同一平面的两条直线平行解析选项A,平行直线的平行投影可以依然是两条平行直线;选项B,两个相交平面的交线与某一条直线平行,则这条直线平行于这两个平面;选项C,两个相交平面可以同时垂直于同一个平面;选项D,正确.答案 D3.(2013·长沙模拟)若直线a⊥b,且直线a∥平面α,则直线b与平面α的位置关系是( ).A .b ⊂αB .b ∥αC .b ⊂α或b ∥αD .b 与α相交或b ⊂α或b ∥α解析 可以构造一草图来表示位置关系,经验证,当b 与α相交或b ⊂α或b ∥α时,均满足直线a ⊥b ,且直线a ∥平面α的情况,故选D.答案 D4.在空间中,下列命题正确的是( ).A .若a ∥α,b ∥a ,则b ∥αB .若a ∥α,b ∥α,a ⊂β,b ⊂β,则β∥αC .若α∥β,b ∥α,则b ∥βD .若α∥β,a ⊂α,则a ∥β解析 若a ∥α,b ∥a ,则b ∥α或b ⊂α,故A 错误;由面面平行的判定定理知,B 错误;若α∥β,b ∥α,则b ∥β或b ⊂β,故C 错误.答案 D5.在正方体ABCDA 1B 1C 1D 1中,E 是DD 1的中点,则BD 1与平面ACE 的位置关系为________.解析 如图.连接AC 、BD 交于O 点,连接OE ,因为OE ∥BD 1,而OE ⊂平面ACE ,BD 1⊄平面ACE ,所以BD 1∥平面ACE .答案 平行考向一 线面平行的判定及性质【例1】►(2012·辽宁)如图,直三棱柱ABCA ′B ′C ′,∠BAC=90°,AB =AC =2,AA ′=1,点M ,N 分别为A ′B 和B ′C ′的中点.(1)证明:MN ∥平面A ′ACC ′; (2)求三棱锥A ′MNC 的体积.(锥体体积公式V =13Sh ,其中S 为底面面积,h 为高)[审题视点] (1)连接AB ′,AC ′,在△AC ′B ′中由中位线定理可证MN ∥AC ′,则线面平行可证;此问也可以应用面面平行证明.(2)证A ′N ⊥平面NBC ,故V A ′MNC =V A ′NBC -V MNBC =12V A ′NBC ,体积可求.(1)证明 法一 连接AB ′,AC ′,如图由已知∠BAC =90°,AB =AC ,三棱柱ABCA ′B ′C ′为直三棱柱,所以M 为AB ′中点.又因为N 为B ′C ′的中点,所以MN ∥AC ′. 又MN ⊄平面A ′ACC ′,AC ′⊂平面A ′ACC ′, 因此MN ∥平面A ′ACC ′.法二 取A ′B ′的中点P ,连接MP ,NP ,AB ′,如图,而M ,N 分别为AB ′与B ′C ′的中点,所以MP ∥AA ′,PN ∥A ′C ′,所以MP ∥平面A ′ACC ′,PN ∥平面A ′ACC ′. 又MP ∩NP =P ,因此平面MPN ∥平面A ′ACC ′. 而MN ⊂平面MPN ,因此MN ∥平面A ′ACC ′.(2)解 法一 连接BN ,如图由题意A ′N ⊥B ′C ′,平面A ′B ′C ′∩平面B ′BCC ′=B ′C ′,所以A ′N ⊥平面NBC .又A ′N =12B ′C ′=1,故V A ′MNC =V NA ′MC =12V NA ′BC =12V A ′NBC =16.法二 V A ′MNC =V A ′NBC -V MNBC =12V A ′NBC =16.(1)证明直线与平面平行的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质,或者构造平行四边形、寻找比例式证明两直线平行.注意说明已知的直线不在平面内.(2)证明直线与平面平行的方法:①利用定义结合反证;②利用线面平行的判定定理;③利用面面平行的性质.【训练1】 如图,在四棱锥P ABCD 中,底面ABCD 是矩形,P A ⊥平面ABCD ,AP =AB ,BP =BC =2,E ,F 分别是PB ,PC 的中点.(1)证明:EF ∥平面P AD ; (2)求三棱锥EABC 的体积.(1)证明 在△PBC 中,E ,F 分别是PB ,PC 的中点, ∴EF ∥BC .又BC ∥AD ,∴EF ∥AD . 又∵AD ⊂平面P AD ,EF ⊄平面P AD , ∴EF ∥平面P AD .(2)解 连接AE ,AC ,EC ,过E 作EG ∥P A 交AB 于点G ,则EG ⊥平面ABCD ,且EG =12P A .在△P AB 中,AP =AB ,∠P AB =90°,BP =2, ∴AP =AB =2,EG =22. ∴S △ABC =12AB ·BC =12×2×2= 2.∴V EABC =13S △ABC ·EG =13×2×22=13.考向二 面面平行的判定和性质【例2】►(2013·济南调研) 如图,在正方体ABCDA 1B 1C 1D 1中,M 、N 、P 分别为所在边的中点.求证:平面MNP ∥平面A 1C 1B .[审题视点] 利用面面平行判定定理的证明即可. 证明如图,连接D 1C ,则MN 为△DD 1C 的中位线,∴MN ∥D 1C . ∵D 1C ∥A 1B ,∴MN ∥A 1B . 同理可证,MP ∥C 1B .而MN 与MP 相交,MN ,MP 在平面MNP 内,A 1B ,C 1B 在平面A 1C 1B 内, ∴平面MNP ∥平面A 1C 1B .要证面面平行需证线面平行,要证线面平行需证线线平行,因此“面面平行”问题最终转化为“线线平行”问题来解决.【训练2】 如图,在三棱柱ABCA 1B 1C 1中,E ,F ,G ,H 分别是AB ,AC ,A 1B 1,A 1C 1的中点,求证:(1)B ,C ,H ,G 四点共面; (2)平面EF A 1∥平面BCHG .证明 (1)∵GH 是△A 1B 1C 1的中位线,∴GH ∥B 1C 1. 又∵B 1C 1∥BC ,∴GH ∥BC , ∴B ,C ,H ,G 四点共面.(2)∵E 、F 分别为AB 、AC 的中点,∴EF ∥BC ,∵EF⊄平面BCHG,BC⊂平面BCHG,∴EF∥平面BCHG.∵A1G綉EB,∴四边形A1EBG是平行四边形,∴A1E∥GB.∵A1E⊄平面BCHG,GB⊂平面BCHG.∴A1E∥平面BCHG.∵A1E∩EF=E,∴平面EF A1∥平面BCHG.考向三线面平行中的探索性问题【例3】►如图所示,在三棱柱ABCA1B1C1中,A1A⊥平面ABC,若D是棱CC1的中点,问在棱AB上是否存在一点E,使DE∥平面AB1C1?若存在,请确定点E的位置;若不存在,请说明理由.[审题视点] 取AB、BB1的中点分别为E、F,证明平面DEF∥平面AB1C1即可.解存在点E,且E为AB的中点.下面给出证明:如图,取BB1的中点F,连接DF,则DF∥B1C1.∵AB的中点为E,连接EF,则EF∥AB1.B1C1与AB1是相交直线,∴平面DEF∥平面AB1C1.而DE⊂平面DEF,∴DE∥平面AB1C1.解决探究性问题一般要采用执果索因的方法,假设求解的结果存在,从这个结果出发,寻找使这个结论成立的充分条件,如果找到了符合题目结果要求的条件,则存在;如果找不到符合题目结果要求的条件(出现矛盾),则不存在.【训练3】如图,在四棱锥P ABCD中,底面是平行四边形,P A⊥平面ABCD,点M、N分别为BC、P A的中点.在线段PD上是否存在一点E,使NM∥平面ACE?若存在,请确定点E的位置;若不存在,请说明理由.解在PD上存在一点E,使得NM∥平面ACE.证明如下:如图,取PD 的中点E ,连接NE ,EC ,AE , 因为N ,E 分别为P A ,PD 的中点, 所以NE 綉12AD .又在平行四边形ABCD 中,CM 綉12AD .所以NE 綉MC ,即四边形MCEN 是平行四边形.所以NM 綉EC .又EC ⊂平面ACE ,NM ⊄平面ACE ,所以MN ∥平面ACE , 即在PD 上存在一点E ,使得NM ∥平面ACE .规范解答13——如何作答平行关系证明题【命题研究】 通过近三年的高考试题分析,对线面平行、面面平行的证明一直受到命题人的青睐,多以多面体为载体,证明线面平行和面面平行,题型为解答题,题目难度不大.【真题探究】► (本小题满分12分)(2012·山东)如图,几何体EABCD 是四棱锥,△ABD 为正三角形,CB =CD ,EC ⊥BD . (1)求证:BE =DE ;(2)若∠BCD =120°,M 为线段AE 的中点,求证:DM ∥平面BEC . [教你审题] 一审 取BD 的中点O ,证明BD ⊥EO ;二审 取AB 中点N ,证明平面DMN ∥平面BEC ;找到平面BCE 和平面ADE 的交线EF ,证明DM ∥EF .[规范解答] 证明 (1)图(a)如图(a),取BD的中点O,连接CO,EO.由于CB=CD,所以CO⊥BD,(2分)又EC⊥BD,EC∩CO=C,CO,EC⊂平面EOC,所以BD⊥平面EOC,(4分)因此BD⊥EO,又O为BD的中点,所以BE=DE.(6分)(2)法一如图(b),取AB的中点N,连接DM,DN,MN,图(b)因为M是AE的中点,所以MN∥BE.又MN⊄平面BEC,BE⊂平面BEC,∴MN∥平面BEC.(8分)又因为△ABD为正三角形,所以∠BDN=30°,又CB=CD,∠BCD=120°,因此∠CBD=30°,所以DN∥BC.(10分)又DN⊄平面BEC,BC⊂平面BEC,所以DN∥平面BEC. 又MN∩DN=N,故平面DMN∥平面BEC,又DM⊂平面DMN,所以DM∥平面BEC.(12分)法二如图(c),延长AD,BC交于点F,连接EF.图(c)因为CB=CD,∠BCD=120°,所以∠CBD =30°. 因为△ABD 为正三角形, 所以∠BAD =60°,∠ABC =90°, 因此∠AFB =30°, 所以AB =12AF .(8分)又AB =AD ,所以D 为线段AF 的中点.连接DM ,由点M 是线段AE 的中点,因此DM ∥EF .(10分)又DM ⊄平面BEC ,EF ⊂平面BEC , 所以DM ∥平面BEC .(12分)[阅卷老师手记] (1)对题目已知条件分析不深入,不能将已知条件与所证问题联系起来; (2)识图能力差,不能观察出线、面之间的隐含关系,不能作出恰当的辅助线或辅助面; (3)答题不规范,跳步、漏步等.证明线面平行问题的答题模板(一)第一步:作(找)出所证线面平行中的平面内的一条直线; 第二步:证明线线平行;第三步:根据线面平行的判定定理证明线面平行; 第四步:反思回顾.检查关键点及答题规范. 证明线面平行问题的答题模板(二)第一步:在多面体中作出要证线面平行中的线所在的平面;第二步:利用线面平行的判定定理证明所作平面内的两条相交直线分别与所证平面平行;第三步:证明所作平面与所证平面平行; 第四步:转化为线面平行; 第五步:反思回顾.检查答题规范. 【试一试】如图,在几何体ABCDEFG 中,下底面ABCD 为正方形,上底面EFG 为等腰直角三角形,其中EF ⊥FG ,且EF ∥AD ,FG ∥AB ,AF ⊥面ABCD ,AB =2FG =2,BE =BD ,M 是DE 的中点.(1)求证:FM ∥平面CEG ; (2)求几何体GEFC 的体积. (1)证明取CE 的中点N ,连接MN ,GN ,则MN 綉FG 綉12AB .故四边形MNGF 为平行四边形. ∴MF ∥GN .又MF ⊄平面CEG ,GN ⊂平面CEG , ∴FM ∥平面CEG .(2)解 在Rt △ABD 中,AB =AD =2,BD =22, ∴BE =2 2.∵AF ⊥平面ABCD ,AB ⊂平面ABCD , ∴AF ⊥AB .在正方形ABCD 中,AB ⊥AD . 又AD ∩AF =A ,∴AB ⊥平面ADEF .又AE ⊂平面ADEF ,∴AB ⊥AE . ∴在Rt △ABE 中,AE =8-4=2.又在Rt △AEF 中,EF =1,∴AF =4-1= 3. 又EF ∥AD ,EF ⊄平面ABCD ,AD ⊂平面ABCD , ∴EF ∥平面ABCD .同理由FG ∥AB ,可得FG ∥平面ABCD .又EF ∩FG =F ,EF ⊂平面EFG ,FG ⊂平面EFG . ∴平面EFG ∥平面ABCD . 又AF ⊥平面ABCD ,AF =3, ∴点C 到平面EFG 的距离等于3, ∴V GEFC =V CEFG =13×S △EFG ·d=13×⎝⎛⎭⎫12×1×1×3=36A级基础演练(时间:30分钟满分:55分)一、选择题(每小题5分,共20分)1.一条直线l上有相异三个点A、B、C到平面α的距离相等,那么直线l与平面α的位置关系是().A.l∥αB.l⊥αC.l与α相交但不垂直 D.l∥α或l⊂α解析l∥α时,直线l上任意点到α的距离都相等;l⊂α时,直线l上所有的点到α的距离都是0;l⊥α时,直线l上有两个点到α距离相等;l与α斜交时,也只能有两个点到α距离相等.答案 D2.平面α∥平面β,点A,C∈α,B,D∈β,则直线AC∥直线BD的充要条件是().A.AB∥CD B.AD∥CB C.AB与CD相交D.A,B,C,D四点共面解析充分性:A,B,C,D四点共面,由平面与平面平行的性质知AC∥BD.必要性显然成立.答案 D3.(2012·北京模拟)以下命题中真命题的个数是().①若直线l平行于平面α内的无数条直线,则直线l∥α;②若直线a在平面α外,则a∥α;③若直线a∥b,b⊂α,则a∥α;④若直线a∥b,b⊂α,则a平行于平面α内的无数条直线.A.1 B.2 C.3 D.4解析命题①l可以在平面α内,不正确;命题②直线a与平面α可以是相交关系,不正确;命题③直线a可以在平面α内,不正确;命题④正确.答案 A4.(2013·汕头质检)若m、n为两条不重合的直线,α、β为两个不重合的平面,则下列命题中正确的是().A.若m、n都平行于平面α,则m、n一定不是相交直线B.若m、n都垂直于平面α,则m、n一定是平行直线C.已知α、β互相平行,m、n互相平行,若m∥α,则n∥βD.若m、n在平面α内的射影互相平行,则m、n互相平行解析A中,m、n可为相交直线;B正确;C中,n可以平行β,也可以在β内;D中,m、n也可能异面.故正确的命题是B.答案 B二、填空题(每小题5分,共10分)5.过三棱柱ABCA1B1C1的任意两条棱的中点作直线,其中与平面ABB1A1平行的直线共有________条.解析过三棱柱ABCA1B1C1的任意两条棱的中点作直线,记AC,BC,A1C1,B1C1的中点分别为E,F,E1,F1,则直线EF,E1F1,EE1,FF1,E1F,EF1均与平面ABB1A1平行,故符合题意的直线共6条.答案 66.α、β、γ是三个平面,a 、b 是两条直线,有下列三个条件:①a ∥γ,b ⊂β;②a ∥γ,b ∥β;③b ∥β,a ⊂γ.如果命题“α∩β=a ,b ⊂γ,且________,则a ∥b ”为真命题,则可以在横线处填入的条件是________(把所有正确的题号填上).解析 ①中,a ∥γ,a ⊂β,b ⊂β,β∩γ=b ⇒a ∥b (线面平行的性质).③中,b ∥β,b ⊂γ,a ⊂γ,β∩γ=a ⇒a ∥b (线面平行的性质).答案 ①③三、解答题(共25分)7.(12分)如图,在四面体ABCD 中,F 、E 、H 分别是棱AB 、BD 、AC 的中点,G 为DE 的中点.证明:直线HG ∥平面CEF .证明 法一 如图,连接BH ,BH 与CF 交于K ,连接EK .∵F 、H 分别是AB 、AC 的中点,∴K 是△ABC 的重心,∴BK BH =23.又据题设条件知,BE BG =23,∴BK BH =BE BG ,∴EK ∥GH .∵EK ⊂平面CEF ,GH ⊄平面CEF ,∴直线HG ∥平面CEF .法二如图,取CD 的中点N ,连接GN 、HN .∵G 为DE 的中点,∴GN ∥CE .∵CE ⊂平面CEF ,GN ⊄平面CEF ,∴GN ∥平面CEF .连接FH ,EN∵F 、E 、H 分别是棱AB 、BD 、AC 的中点, ∴FH 綉12BC ,EN 綉12BC ,∴FH 綉EN ,∴四边形FHNE 为平行四边形,∴HN ∥EF . ∵EF ⊂平面CEF ,HN ⊄平面CEF ,∴HN ∥平面CEF .HN ∩GN =N ,∴平面GHN ∥平面CEF .∵GH ⊂平面GHN ,∴直线HG ∥平面CEF .8.(13分)如图,已知ABCDA 1B 1C 1D 1是棱长为3的正方体,点E 在AA 1上,点F 在CC 1上,G 在BB 1上,且AE =FC 1=B 1G =1,H 是B 1C 1的中点.(1)求证:E ,B ,F ,D 1四点共面;(2)求证:平面A 1GH ∥平面BED 1F .证明 (1)∵AE =B 1G =1,∴BG =A 1E =2,∴BG =A 1E ,∴A 1G =BE .又同理,C 1F 綉B 1G ,∴四边形C 1FGB 1是平行四边形, ∴FG 綉C 1B 1綉D 1A 1,∴四边形A 1GFD 1是平行四边形. ∴A 1G 綉D 1F ,∴D 1F 綉EB ,故E 、B 、F 、D 1四点共面.(2)∵H 是B 1C 1的中点,∴B 1H =32.又B 1G =1,∴B 1G B 1H =23.又FC BC =23,且∠FCB =∠GB 1H =90°,∴△B 1HG ∽△CBF ,∴∠B 1GH =∠CFB =∠FBG , ∴HG ∥FB .又由(1)知A 1G ∥BE ,且HG ∩A 1G =G , FB ∩BE =B ,∴平面A 1GH ∥平面BED 1F .。
直线与平面、平面与平面平行的判定[学习目标] 1.理解直线与平面平行、平面与平面平行判定定理的含义.2.会用图形语言、文字语言、符号语言准确描述直线与平面平行、平面与平面平行的判定定理,并知道其地位和作用.3.能运用直线与平面平行的判定定理、平面与平面平行的判定定理证明一些空间线面关系的简单问题.知识点一直线与平面平行的判定定理语言叙述符号表示图形表示平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行⎭⎪⎬⎪⎫a⊄αb⊂αa∥b⇒a∥α思考若一条直线平行于一个平面内的一条直线,则这条直线和这个平面平行吗?答根据直线与平面平行的判定定理可知该结论错误.知识点二平面与平面平行的判定定理语言叙述符号表示图形表示一个平面内的两条相交直线与另一个平面平行,则这两个平面平行⎭⎪⎬⎪⎫a⊂α,b⊂αa∩b=Aa∥β,b∥β⇒α∥β思考如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面也平行吗?答不一定.这条直线与另一个平面平行或在另一个平面内.题型一直线与平面平行的判定定理的应用例1如图,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.求证:(1)EH∥平面BCD;(2)BD∥平面EFGH.证明(1)∵EH为△ABD的中位线,∴EH∥BD.∵EH⊄平面BCD,BD⊂平面BCD,∴EH∥平面BCD.(2)∵BD∥EH,BD⊄平面EFGH,EH⊂平面EFGH,∴BD∥平面EFGH.跟踪训练1在四面体A-BCD中,M,N分别是△ABD和△BCD的重心,求证:MN∥平面ADC.证明如图所示,连接BM,BN并延长,分别交AD,DC于P,Q两点,连接PQ.因为M,N分别是△ABD和△BCD的重心,所以BM∶MP=BN∶NQ=2∶1.所以MN∥PQ.又因为MN⊄平面ADC,PQ⊂平面ADC,所以MN∥平面ADC.题型二面面平行判定定理的应用例2如图所示,在三棱柱ABC-A1B1C1中,点D,E分别是BC与B1C1的中点.求证:平面A1EB∥平面ADC1.证明由棱柱性质知,B1C1∥BC,B1C1=BC,又D,E分别为BC,B1C1的中点,所以C1E綊DB,则四边形C1DBE为平行四边形,因此EB∥C1D,又C1D⊂平面ADC1,EB⊄平面ADC1,所以EB∥平面ADC1.连接DE,同理,EB1綊BD,所以四边形EDBB1为平行四边形,则ED綊B1B.因为B1B∥A1A,B1B=A1A(棱柱的性质),所以ED綊A1A,则四边形EDAA1为平行四边形,所以A 1E ∥AD ,又A 1E ⊄平面ADC 1,AD ⊂平面ADC 1, 所以A 1E ∥平面ADC 1.由A 1E ∥平面ADC 1,EB ∥平面ADC 1, A 1E ⊂平面A 1EB ,EB ⊂平面A 1EB ,且A 1E ∩EB =E ,所以平面A 1EB ∥平面ADC 1.跟踪训练2 已知ABCD -A 1B 1C 1D 1是棱长为3的正方体,点E 在AA 1上,点F 在CC 1上,点G 在BB 1上,且AE =FC 1=B 1G =1,H 是B 1C 1的中点. 求证:(1)E ,B ,F ,D 1四点共面; (2)平面A 1GH ∥平面BED 1F .证明 (1)∵AE =B 1G =1,∴BG =A 1E =2. 又∵BG ∥A 1E ,∴四边形A 1EBG 是平行四边形, ∴A 1G ∥BE .连接FG .∵C 1F =B 1G ,C 1F ∥B 1G , ∴四边形C 1FGB 1是平行四边形, ∴FG =C 1B 1=D 1A 1,FG ∥C 1B 1∥D 1A 1, ∴四边形A 1GFD 1是平行四边形, ∴A 1G ∥D 1F ,∴D 1F ∥EB . 故E ,B ,F ,D 1四点共面. (2)∵H 是B 1C 1的中点,∴B 1H =32.又∵B 1G =1,∴B 1G B 1H =23.又FC BC =23,且∠FCB =∠GB 1H =90°, ∴△B 1HG ∽△CBF ,∴∠B 1GH =∠CFB =∠FBG ,∴HG ∥FB .又由(1)知,A 1G ∥BE ,且HG ∩A 1G =G ,FB ∩BE =B , ∴平面A 1GH ∥平面BED 1F .题型三 线面平行、面面平行判定定理的综合应用例3 在正方体ABCD -A 1B 1C 1D 1中,O 为底面ABCD 的中心,P 是DD 1的中点,设Q 是CC 1上的点.问:当点Q 在什么位置时,平面D 1BQ ∥平面P AO ?请说明理由.解 当Q 为CC 1的中点时,平面D 1BQ ∥平面P AO .理由如下: 连接PQ .∵Q 为CC 1的中点,P 为DD 1的中点, ∴PQ ∥DC ∥AB ,PQ =DC =AB , ∴四边形ABQP 是平行四边形,∴QB ∥P A . 又∵O 为DB 的中点,∴D 1B ∥PO . 又∵PO ∩P A =P ,D 1B ∩QB =B , ∴平面D 1BQ ∥平面P AO .跟踪训练3 如图,三棱柱ABC -A 1B 1C 1的底面为正三角形,侧棱A 1A ⊥底面ABC ,E ,F 分别是棱CC 1,BB 1上的点,EC =2FB .M 是线段AC 上的动点,当点M 在何位置时,BM ∥平面AEF ?请说明理由.解 当M 为AC 中点时,BM ∥平面AEF .理由如下: 方法一 如图1,取AE 的中点O ,连接OF ,OM . ∵O ,M 分别是AE ,AC 的中点, ∴OM ∥EC ,OM =12EC .又∵BF ∥CE ,EC =2FB ,∴OM ∥BF ,OM =BF , ∴四边形OMBF 为平行四边形,∴BM ∥OF . 又∵OF ⊂面AEF ,BM ⊄面AEF , ∴BM ∥平面AEF .方法二 如图2,取EC 的中点P ,连接PM ,PB . ∵PM 是△ACE 的中位线, ∴PM ∥AE .∵EC=2FB=2PE,CC1∥BB1,∴PE=BF,PE∥BF,∴四边形BPEF是平行四边形,∴PB∥EF.又∵PM⊄平面AEF,PB⊄平面AEF,∴PM∥平面AEF,PB∥平面AEF.又∵PM∩PB=P,∴平面PBM∥平面AEF.又∵BM⊂面PBM,∴BM∥平面AEF.面面平行的判定例4已知在正方体ABCD-A′B′C′D′中,M,N分别是A′D′,A′B′的中点,在该正方体中是否存在过顶点且与平面AMN平行的平面?若存在,试作出该平面,并证明你的结论;若不存在,请说明理由.分析根据题意画出正方体,根据平面AMN的特点,试着在正方体中找出几条平行于该平面的直线,然后作出判断,并证明.解如图,与平面AMN平行的平面有以下三种情况:下面以图①为例进行证明.如图①,取B′C′的中点E,连接BD,BE,DE,ME,B′D′,可知四边形ABEM是平行四边形,所以BE∥AM.又因为BE⊂平面BDE,AM⊄平面BDE,所以AM∥平面BDE.因为MN是△A′B′D′的中位线,所以MN∥B′D′.因为四边形BDD′B′是平行四边形,所以BD∥B′D′.所以MN∥BD.又因为BD⊂平面BDE,MN⊄平面BDE,所以MN∥平面BDE.又因为AM⊂平面AMN,MN⊂平面AMN,且AM∩MN=M,所以由平面与平面平行的判定定理可得,平面AMN∥平面BDE.1.过直线l外两点,作与l平行的平面,则这样的平面()A.不可能作出B.只能作出一个C.能作出无数个D.上述三种情况都存在2.经过平面α外两点,作与α平行的平面,则这样的平面可以作()A.1个或2个B.0个或1个C.1个D.0个3.若线段AB,BC,CD不共面,M,N,P分别为线段AB,BC,CD的中点,则直线BD与平面MNP的位置关系是()A.平行B.直线在平面内C.相交D.以上均有可能4.在正方体EFGH-E1F1G1H1中,下列四对截面彼此平行的一对是()A.平面E1FG1与平面EGH1B.平面FHG1与平面F1H1GC.平面F1H1H与平面FHE1D.平面E1HG1与平面EH1G5.梯形ABCD中,AB∥CD,AB⊂平面α,CD⊄平面α,则直线CD与平面α的位置关系是________.一、选择题1.下列说法正确的是()①若一个平面内有两条直线都与另一个平面平行,则这两个平面平行;②若一个平面内有无数条直线都与另一个平面平行,则这两个平面平行;③若一个平面内任何一条直线都平行于另一个平面,则这两个平面平行;④若一个平面内的两条相交直线都与另一个平面平行,则这两个平面平行.A.①③B.②④C.②③④D.③④2.平面α与平面β平行的条件可以是()A.α内有无穷多条直线与β平行B.直线a∥α,a∥β,且直线a不在α与β内C.直线a⊂α,直线b⊂β,且b∥α,a∥βD.α内的任何直线都与β平行3.六棱柱的表面中,互相平行的平面最多有()A.2对B.3对C.4对D.5对4.如果直线a平行于平面α,那么下列命题正确的是()A.平面α内有且只有一条直线与a平行B.平面α内有无数条直线与a平行C.平面α内不存在与a平行的直线D.平面α内的任意直线与直线a都平行5.在空间四边形ABCD中,E,F分别为AB,AD上的点,且AE∶EB=AF∶FD=1∶4,又H,G分别为BC,CD的中点,则()A.BD∥平面EFG,且四边形EFGH是平行四边形B.EF∥平面BCD,且四边形EFGH是梯形C.HG∥平面ABD,且四边形EFGH是平行四边形D.EH∥平面ADC,且四边形EFGH是梯形6.平面α内有不共线的三点到平面β的距离相等且不为零,则α与β的位置关系为()A.平行B.相交C.平行或相交D.可能重合7.已知直线l,m,平面α,β,下列命题正确的是()A.l∥β,l⊂α⇒α∥βB.l∥β,m∥β,l⊂α,m⊂α⇒α∥βC.l∥m,l⊂α,m⊂β⇒α∥βD.l∥β,m∥β,l⊂α,m⊂α,l∩m=M⇒α∥β二、填空题8.三棱锥SABC中,G为△ABC的重心,E在棱SA上,且AE=2ES,则EG与平面SBC的关系为________.9.如图是正方体的平面展开图.在这个正方体中,①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.以上四个命题中,正确命题的序号是________.10.右图是一几何体的平面展开图,其中四边形ABCD为正方形,E,F,G,H分别为P A,PD,PC,PB的中点,在此几何体中,给出下面五个结论:①平面EFGH∥平面ABCD;②P A∥平面BDG;③EF∥平面PBC;④FH∥平面BDG;⑤EF∥平面BDG;其中正确结论的序号是________.三、解答题11.如图,在已知四棱锥P-ABCD中,底面ABCD为平行四边形,点M,N,Q分别在P A,BD,PD上,且PM∶MA=BN∶ND=PQ∶QD.求证:平面MNQ∥平面PBC.12.如图,在正四棱柱ABCD-A1B1C1D1中,M是棱AB的中点,点N在侧面AA1D1D上运动,点N满足什么条件时,MN∥平面BB1D1D?当堂检测答案1.答案D解析设直线外两点为A、B,若直线AB∥l,则过A、B可作无数个平面与l平行;若直线AB与l异面,则只能作一个平面与l平行;若直线AB与l相交,则过A、B没有平面与l 平行.2.答案B解析①当经过两点的直线与平面α平行时,可作出一个平面β使β∥α.②当经过两点的直线与平面α相交时,由于作出的平面又至少有一个公共点,故经过两点的平面都与平面α相交,不能作出与平面α平行的平面.故满足条件的平面有0个或1个.3.答案A解析连接NP,因为N、P分别是BC、CD的中点,M是AB的中点,AB、BC、CD不共面,所以直线BD不在平面MNP上.∴直线BD与平面MNP平行.4.答案A解析如图,∵EG∥E1G1,EG⊄平面E1FG1,E1G1⊂平面E1FG1,∴EG∥平面E1FG1,又G1F∥H1E,同理可证H1E∥平面E1FG1,又H1E∩EG=E,∴平面E1FG1∥平面EGH1.5.答案CD∥α解析因为AB∥CD,AB⊂平面α,CD⊄平面α,由线面平行的判定定理可得CD∥α.课时精练答案一、选择题1.答案D解析如图,长方体ABCD-A1B1C1D1中,在平面ABCD内,在AB上任取一点E,过点E作EF∥AD,交CD于点F,则由线面平行的判定定理,知EF,BC都平行于平面ADD1A1,用同样的方法可以在平面ABCD内作出无数条直线都与平面ADD1A1平行,但是平面ABCD与平面ADD 1A 1不平行,因此①②都错;③正确,事实上,因为一个平面内任意一条直线都平行于另一个平面,所以这两个平面必无公共点(要注意“任意一条直线”与“无数条直线”的区别);④是平面与平面平行的判定定理,正确. 2.答案 D解析 对于A 项,当α与β相交时,α内也有无数条直线都与交线平行,故A 错误;对于B 项,当a 平行于α与β的交线时,也能满足,但此时α与β相交,故B 错误;对于C 项,当a 和b 都与α与β的交线平行时,也能满足,但此时α与β相交,故C 错误;对于D 项,α内的任何直线都与β平行,故在一个平面内存在两条相交直线平行于另一平面,故D 正确. 3.答案 C解析 侧面中有3对,对面相互平行,上下两底面也相互平行. 4.答案 B解析 如图,直线B 1C 1∥平面ABCD ,B 1C 1∥BC ,B 1C 1∥AD ,B 1C 1∥EF (E ,F 为中点)等,平面ABCD 内平行于BC 的所有直线均与B 1C 1平行.但AB 与B 1C 1不平行.5.答案 B解析 易证EF ∥平面BCD .由AE ∶EB =AF ∶FD ,知EF ∥BD ,且EF =15BD .又因为H ,G 分别为BC ,CD 的中点, 所以HG ∥BD ,且HG =12BD .综上可知,EF ∥HG ,EF ≠HG ,所以四边形EFGH 是梯形,且EF ∥平面BCD . 6.答案 C解析 若三点分布于平面β的同侧,则α与β平行,若三点分布于平面β的两侧,则α与β相交. 7.答案 D解析 如图所示,在长方体ABCDA 1B 1C 1D 1中,AB ∥CD , 则AB ∥平面DC 1,AB ⊂平面AC , 但是平面AC 与平面DC 1不平行,所以A 错误;取BB 1的中点E ,CC 1的中点F ,则可证EF ∥平面AC ,B1C1∥平面AC.EF⊂平面BC1,B1C1⊂平面BC1,但是平面AC与平面BC1不平行,所以B 错误;可证AD∥B1C1,AD⊂平面AC,B1C1⊂平面BC1,又平面AC与平面BC1不平行,所以C错误;很明显D是面面平行的判定定理,所以D正确.二、填空题8.答案平行解析如图,延长AG交BC于F,连接SF,则由G为△ABC的重心知AG∶GF=2,又AE∶ES=2,∴EG∥SF,又SF⊂平面SBC,EG⊄平面SBC,∴EG∥平面SBC.9.答案①②③④解析以ABCD为下底面还原正方体,如图:则易判定四个命题都是正确的.10.答案①②③④解析把图形还原为一个四棱锥,然后根据线面、面面平行的判定定理判断即可.三、解答题11.证明因为PM∶MA=BN∶ND=PQ∶QD,所以MQ∥AD,NQ∥BP.因为BP⊂平面PBC,NQ⊄平面PBC,所以NQ∥平面PBC.又因为底面ABCD为平行四边形,所以BC∥AD,所以MQ∥BC.因为BC⊂平面PBC,MQ⊄平面PBC,所以MQ∥平面PBC.又因为MQ∩NQ=Q,所以根据平面与平面平行的判定定理,得平面MNQ∥平面PBC.12.解如图,在正四棱柱ABCD-A1B1C1D1中,分别取棱A1B1,A1D1,AD的中点E,F,G,连接ME,EF,FG,GM.因为M是AB的中点,所以ME∥AA1∥FG,且ME=AA1=FG.所以四边形MEFG是平行四边形.因为ME∥BB1,BB1⊂平面BB1D1D,ME⊄平面BB1D1D,所以ME∥平面BB1D1D.在△A1B1D1中,因为EF∥B1D1,B1D1⊂平面BB1D1D,EF⊄平面BB1D1D,所以EF∥平面BB1D1D.又因为ME∩EF=E,且ME⊂平面MEFG,EF⊂平面MEFG,所以平面MEFG∥平面BB1D1D.在FG上任取一点N,连接MN,所以MN⊂平面MEFG.所以MN与平面BB1D1D无公共点.所以MN∥平面BB1D1D.总之,当点N在平面AA1D1D内的直线FG上(任意位置)时,都有MN∥BB1D1D,即当点N在矩形AA1D1D中过A1D1与AD的中点的直线上运动时,都有MN∥平面BB1D1D.。