二年级奥数讲义上

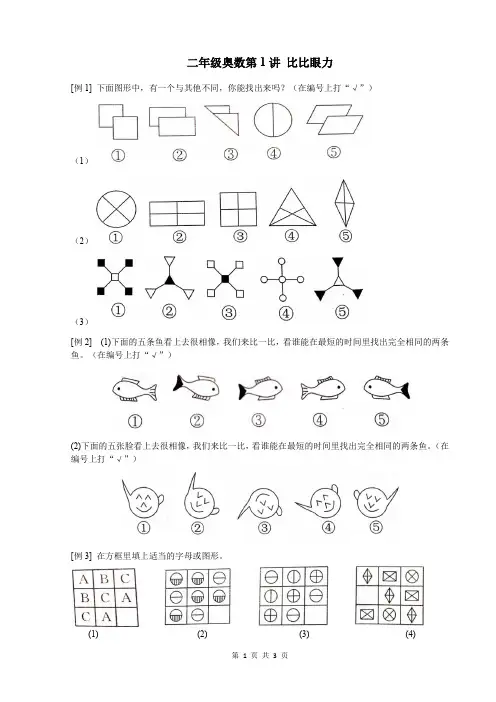
二年级奥数第1讲比比眼力
[例1] 下面图形中，有一个与其他不同，你能找出来吗？（在编号上打“√”）
（1）
（2）
（3）
[例2] (1)下面的五条鱼看上去很相像，我们来比一比，看谁能在最短的时间里找出完全相同的两条鱼。

（在编号上打“√”）
(2)下面的五张脸看上去很相像，我们来比一比，看谁能在最短的时间里找出完全相同的两条鱼。

（在编号上打“√”）
[例3] 在方框里填上适当的字母或图形。

(1)(2) (3) (4)
[例4] 请根据前三个图形的变化规律，画出第四个图形。

(1)
(2)
[例5] 仔细观察，第四幅图应怎样画？
(1)
(2)
(3)
第1讲作业
1、下面图形中，有一个与其他不同，你能找出来吗？（在编号上打“√”）
2、下面图形中，有两幅完全相同，请你找一找。

（在编号上打“√”）（1）
（2）
3、仔细观察下图，第四幅图应画什么图形？第十幅图应画什么图形？
4、仔细观察，想一想第三幅图应该怎样画？。

第4讲数字问题重点摘要小朋友们一定都会数数吧，每一个数都是由一个或几个数字组成的，我们一般所说的“数”是指自然数，“数字”只是0、1、2、3、4、5、6、7、8、9这10种。

只有今天我们主要来研究数字与数之间的关系。

精讲精练例题1、小钱在家看《十万个为什么》，他从第5页看到第11页，小钱一共看了几页？解：从第1页到第11页共有11页，从第1页到第4页共有4页，11页去掉4页，还有11-4=7页。

例题2、龙龙是个小淘气，上个学期结束时，妈妈他的数学课本，缺少了第5页，第21页，第22页，第23页，甜甜的数学课本共缺少了多少张？解：一般在课本印刷时，都是把一页奇数页码和一页偶数页码放在一张书页的正反两面上，所以龙龙一定缺了三张书页，分别是（21，22），（23,24），（5，6）或（20，21），（22,23），（4，5）。

例题3、从1开始的15个自然数中一共包含了多少个数字？解：采取分段计数的方法：1至9中一共有9个数字，10至15中一共有12个数字，所以一共有9+12=21个数字。

例题4、有一本漫画书，在编排页码时一共用了31个数字。

这本漫画书一共有多少页？（一般我们用从1开始的连续自然数来编排页码）解：因为31＞9，所以一定排到了两位数的页码，每个两位数都包含2个数字，所以两位数的页码一共有（31-9）÷2=11页，这本漫画书一共有11+9=20页。

跟进练习1、《新华字典》从第11页看到第31页一共用了多少个页码？解：一共用了31-10=22个页码。

2、一本书缺少的页码是20，21，35，36，37，100，104，105。

这本书一共缺多少张纸？解：这本书缺少（19,20），（21,22），（35,36），（37,38），（99,100），（103,104），（105,106）共7张纸。

3、一本书共有34页，在这本书的页码中共用了多少个数字？解：页码1～9，每个页码用1个数字，9个页码共用9个数字；页码10—34，共34-9=25页，每个页码用2个数字，25个页码共用2×25＝50个数字，一共用了9+50=59个数字。

第十四讲数规则图形前续知识点：二年级第一讲；XX模块第X讲后续知识点：X年级第X讲；XX模块第X讲只需换风格就行，与其它的风格相符．在数图形的时候，要认真仔细，必须要做到有次序、有条理，保证不重不漏，这样才能数得又快又准．【提示】找规律哦．数一数，下图共有几个点？并且列出算式．列算式：数一数，下图共有几个点？并且列出算式．例题1列算式：练习1【提示】从上到下，按行来数．数一数，下图共有几个点？并且列出算式．列算式：数一数，下图共有几个点？并且列出算式．例题2 列算式：练习2【提示】这是空心的哦，数的时候一共要注意正方形角的地方．数一数，下图共有几个点？并且列出算式．列算式：数一数，下图共有几个点？并且列出算式．例题3列算式：练习3【提示】在数图形时，要做到数和形结合，适当分类，找出规律，做到不重不漏．上题中的四种图形，都可以用同一种方法数，你知道是什么方法吗？仔细想想看，能发现什么规律呢？数一数，回答问题，并列出算式．例题4 共有几条线段？ 列算式：共有几个角？ 列算式：共有几个三角形？ 列算式：共有几个长方形？ 列算式：【提示】分层来数哦！请你帮小猪数一数，下图中共有几个三角形？例题6数一数，下图中共有几个三角形，并且列出算式？例题5列算式：练习4 数一数．下图中共有几条横着的线段？列算式：下图中共有几个三角形？ 列算式：【提示】分层来数哦！课堂内外小知识——猫和蜘蛛是“几何专家”在寒冷的冬天，猫睡觉时总要把身体抱成一个球形，因为球形使身体的表面积最小．这样，身体露在冷空气中的表面积最小，因而散发的热量也最少．蜘蛛结的“八卦”网，既复杂又非常美丽，这种八角形的几何图案，即使人们用直尺和圆规也难画得如蜘蛛网那样匀称．作业1.数一数，下图共有几个点？并且列出算式．列算式：2.数一数，下图共有几个点？并且列出算式．列算式：3.小狗用棋子摆成一个三角形，请你数一数，小狗一共用了几个棋子？并且列出算式．列算式：4.观察下图，数一数．共有几条横着的线段？列算式：共有几个三角形？列算式：5.数一数，下图共有几个三角形？并且列出算式．列算式：第十四讲 数规则图形1. 例题1答案：25详解：通过观察发现，每一行是5个棋子，一共5行，那么可以列出如下算式：5525⨯=（个）；5555525++++=（个）；12345432125++++++++=（个）．（方法不唯一）2. 例题2答案：45 详解：观察图形，从上到下看，都是1，2，3，4，5，6，7，8，9．所以共有12345678945++++++++=（个）．计算时，可以用凑十法．（方法不唯一）3. 例题3答案：20详解：方法一：每条边上有6个棋子，那么4条边，所以就是4624⨯=个，但是这时候把角的地方算了2次，那么就应该是24420-=个．方法二：每条边上有6个棋子，因为角的地方比较特殊，所以先不看，那么每条边上只看4个棋子，4条边，所以就是4416⨯=（个），再加上开始没算的4个，16420+=（个）． 方法三：用分组法，如下图所以：列算式为4520⨯=（个）．4. 例题4答案：（1）15；（2）10；（3）10；（4）6 详解：（1）如下图所示：把每个点标上字母.我们知道，两点间的直线部分是一条线段；从A 点出发的线段有AB 、AC 、AD 、AE 、AF 共有5条线段；同理，从B 出发的线段有： BC 、BD 、BE 、BF 共有4条线段；从C 出发的线段有： CD 、CE 、CF 共有3条线段；从D 出发的线段有： DE 、DF 共有2条线段；从E 出发的线段有：EF 共有1条线段． 列算式：5432115++++=（条）；（2）如下图所示：把每个点标上字母.(1)从AF 出发的长方形有：AFGB 、AFHC 、AFID 、AFJE 共有4个长方形；同理，从BG 出发的长方形有：BGHC 、BGID 、BGJE 共有3个长方形；从CH 出发的长方形有：CHID 、CHJE 共有2个长方形；从DI 出发的长方形有：DIJE 共有1个长方形．列算式：432110+++=（个）．（3）如下图所示：把点和线标上字母．我们知道，从一个点起，用尺子向不同方向画两条射线，就得到一个角，角有一个顶点、两条边． 以OA 为边的角有：∠AOB 、∠AOC 、∠AOD 、∠AOE ，共4个角；以OB 为边的角有：∠BOC 、∠BOD 、∠BOE ，共3个角；以OC 为边的角有：∠COD 、∠COE ，共2个角；以OD 为边的角有：∠DOE ，共1个角．列算式：432110+++=（个）．（4）如下图所示：把每个点标上字母.从OA 出发的三角形有：AOB 、AOC 、AOD 共有3个三角形；同理，从OB 出发的三角形有：BOC 、BOD 共有2个三角形；从OC 出发的三角形有：COD 共有1个三角形．总数列算式：3216++=（个）．5. 例题5答案：12详解：如下图所示：把每个点标上字母.这是一个比较复杂的图形，可以把它分成上下两层，先数上层有：从OA 出发的三角形有：AOB 、AOC 、AOD 共有3个三角形；同理，从OB 出发的三角形有：BOC 、BOD 共有2个三角形；从OC 出发的三角形有：COD 共有1个三角形．上层总数为：3216++=（个）．(4) OA B C D (3) O AB CD E A B C D E FG H I J (2)再数整体有：从OE 出发的三角形有：EOF 、EOG 、EOH 共有3个三角形；同理，从OF 出发的三角形有：FOG 、FOH 共有2个三角形；从OG 出发的三角形有：GOH 共有1个三角形．整体总数为：3216++=（个）．所以共有6612+=（个）三角形．6. 例题6答案：15详解：如下图所示：把每个点标上字母.把它分成上层、下层和整体三部分，先数上层有：从OA 出发的三角形有：AOB 、AOC 、AOD 共有3个三角形；同理，从OB 出发的三角形有：BOC 、BOD 共有2个三角形；从OC 出发的三角形有：COD 共有1个三角形．上层总数为： 3216++=（个）．再看下层：有ABE 、ACF 、ADG ，共有3个三角形．最后看整体：从OA 出发的三角形有：AOE 、AOF 、AOG 共有3个三角形；从OE 出发的三角形有：EOF 、EOG 共有2个三角形；从OF 出发的三角形有：FOG 共有1个三角形．整体总数为：3216++=（个）． 所以共有66315++=（个）三角形．7. 练习1答案：16简答：仔细观察发现，将这个图形旋转后，这个图像就是一个正方形，每一行是4个，一共4行，那么列算式：4416⨯=（个）或123432116++++++=（个）。

复习排队问题1.25个小朋友排队，从左边数起小林是第12个，从右边数起小刚是第9个，小林和小刚之间隔着几个小朋友？2.同学们排队做操，第一排有18个小朋友，从前面数起青青是第6个，从后面数起兰兰是第7个，青青和兰兰中间有几个小朋友？3.有30个工人排成一行，其中有两个工人戴帽子，从左往右数，第7个戴红帽子，从右往左数，第8个戴蓝帽子，戴帽子的两个工人中间有几个人？4.20个小朋友排队，从左边数起小华是第11 个，从右边数起，小飞是第16个，小华和小飞之间有几个小朋友？5.体操表演时，四（1）班同学排成6列做操，每列人数同样多。

小明站在第一列，从前面数、从后面数他都是第5个。

四（1）班一共有多少个同学在做操？6.二年级同学排成8列体操表演，每列人数同样多。

小青站在第一列，从前面数、从后面数她都是第4个。

二年级一共有多少个同学参加体操表演？7.幼儿园小朋友排成方队做操，不管是从前边还是从后边数，不管是从左边还是从右边数，李东都排在第4个，这个方队里一共有多少个小朋友？8.四年级组织合唱队，每队人数同样多。

小亮从左往右数排第4，从右往左数排第5，从前面数排第3，从后面数排第4。

这个合唱队一共有多少人？余数的妙用1.（1）○□□△○□□△○□□△……第22个图形是（）.（2）○◎□○◎□○◎□○……第20个图形是（）.2.电视塔上有一串彩灯，按“红、黄、绿、白”的顺序排列起来，请你算一算，第14盏彩灯是什么颜色?第27盏、第36盏彩灯又是什么颜色?3．一列数按“1， 4， 2， 8， 5， 7， 1， 4， 2， 8， 5， 7， 1， 4， 2， 8， 5， 7……”排列，问第50个数字是几?第96个数字是几?4．2007年5月1日是星期二，再过20天是星期几?5．王老师把1～64号拼音卡片依次发给甲、乙、丙、丁四个小朋友，第59号卡片应发给谁?6.有一列数：1，3，5，1，3，5，1，3，5……第35个数字是几?这35个数的和是多少?7、一列数按“3， 8， 5， 1， 6， 1， 7， 1， 3， 8， 5， 1， 6， 1， 7， 1， 3， 8， 5， 1， 6， 1， 7， 1……”排列，第40个数字是几?第71个数字是几?8. 明明问芳芳：“今天是星期二，再过22天是星期几?”9.今年“六一”儿童节是星期五，再过19天是星期几?10.老师有1～53号卡片，依次发给小红、冬冬、兰兰和小林四个人，问第38张卡片应发给谁?11.胡老师把1～40号拼音卡片，依次发给小伟、小冬、小军、小辉、小燕，问第27张卡片应发给谁？1.今天是星期一，再过18天，妈妈就要带小明去看马戏。

第一讲 趣题巧解二前续知识点：二年级第一讲；XX 模块第X 讲 后续知识点：X 年级第X 讲；XX 模块第X 讲小高小高 墨莫 卡莉娅萱萱 阿呆 阿瓜 墨爷爷高爷爷小山羊小高墨莫萱萱卡莉娅阿呆阿瓜墨爷爷高爷爷小山羊!把里面的人物换成相应红字标明的人物，没有红字标明的人物用路人甲、乙代替即可．本讲我们将学习一些非常有趣而巧妙的数学题．首先是“空瓶换水”问题，这种题目都会规定，几个喝完的空瓶子可以去换一瓶新的饮料，新的饮料喝完了又会有新的空瓶子，几个新的空瓶子又可以去换一瓶新的饮料……如果这样循环下去，是不是就一直能换到新饮料呢？【提示】按照3个空瓶换1瓶可乐的规定，一直换到剩下的空瓶不能够再换为止．有的同学发现，需要多个空瓶去换一瓶可乐，所以当空瓶数不够的时候，就换不了可乐了．这种说法一定正确吗？冷饮店规定，用3个空可乐瓶可以换1瓶可乐．丁丁和一些同学进店后，共买了7瓶可乐．如果每人喝1瓶可乐，那么最多有几人能喝到可乐？例题1阿瓜看到冷饮店的规定（用3个空可乐瓶可以换1瓶可乐）后，也带着一些同学来到店里，共买了5瓶可乐．如果每人喝1瓶可乐，那么最多有几人能喝到可乐？练习1【提示】用“直接换”的方法时，如果最后剩余多个空瓶，可尝试先借再还，从而喝到更多的雪碧．只有保证借来之后能够如数还回去，才可以借空瓶．蘑菇园的糖果店规定，吃完糖果后，用5个空盒可以换1盒糖果．蘑菇园的小朋友们进店后，共买了8盒糖果．如果每人吃1盒糖果，那么最多有几人能吃到糖果？学习“空瓶换水”问题要保证借来空瓶之后能够如数还回去，才可以先借再还，获得更多的饮料．这是一个隐藏的条件，题目中没有说不可以借，所以发现这个隐藏条件是解题的关键．很多有趣的题目中都有隐藏条件，接下来我们一起看看“渡河”问题，找找其中的隐藏条件．冷饮店规定，喝完雪碧后，用4个空雪碧瓶可以换1瓶雪碧．小高和一些同学进店后，共买了12瓶雪碧．如果每人喝1瓶雪碧，那么最多有几人能喝到雪碧？例题2练习2【提示】小船不能没有“驾驶员”哦！渡河问题的隐藏条件是必须有一个人充当船夫的角色，把船划回来，这样每次渡河的人数就不是小船本身的载重人数，而需要减去一个人．当然，最后一次渡河不需要减去一个人．这是一个隐藏条件，帮助我们发现渡河问题的规律．发现规律也是我们解决问题的关键．接下来学习的“量水”问题，就需要大家通过尝试发现规律，从而解决问题．有10只小动物要过河到对岸（从一个岸边到另一个岸边算渡河1次）．现在只有1条小船，并且最多能容纳4只小动物．那么至少要渡几次，才能把10只小动物全部渡到对岸？例题3班长林林带着9名小朋友去春游，他们要乘一条小木船到河对岸的公园（从一个岸边到另一个岸边算渡河1次）．现在只有1条小木船，并且这条小木船最多能坐5名小朋友．那么至少要渡几次，才能把所有的小朋友都渡到河对岸？练习3【提示】把大勺子盛满水，倒入空的小勺子，当小勺子盛满水时，大勺子里还剩多少克水？练习 459 小象有两个不同大小的空勺子、一个杯子和一个桶．大勺子一次能装25克水，小勺子一次能装15克水．现在有一桶水，你能用这两个勺子往杯子里倒入35克水吗？例题 4有一堆大米、一架天平和两个砝码（一个重9克，一个重5克）．你能用这两个砝码称出13克大米吗？【提示】最轻能称出几克的重量？最重能称出几克的重量？最轻和最重之间有哪些重量？尝试称出每一种重量．师生共35人外出春游．到达后，班主任要给每人买一瓶矿泉水，给了班长买矿泉水的钱．班长到商店后，发现商店正在进行促销活动，规定每5个空瓶可换1瓶矿泉水，班长只要买多少瓶矿泉水，就可以保证每人一瓶？【提示】买4瓶矿泉水够5个人喝，而且没有剩余空瓶．买水的数量和人数有什么关系？课堂内外例题6奇奇猫有三个砝码，重量分别为1克、2克和5克，用这3个砝码一次能够称出几种不同重量的物体？（砝码可以放在天平的两边）例题 5分西瓜孙悟空和猪八戒外出旅行，天气很热，两人走在路上，又累又渴．突然看到前面有个老农在卖西瓜．看着又大又圆的西瓜，八戒乐了，喜滋滋地跑上前去问老农：“嗨，请问这个西瓜卖多少钱？”老农告诉他价钱，八戒一摸口袋，钱只够买l个西瓜的了．没办法，就买1个吧．可是就八戒的那个大肚皮，1个西瓜怎么够呢?而且还是和猴哥两个人一起吃．两人把西瓜抱到一棵大树下，八戒拿着借来的水果刀，傻笑着对悟空说：“猴哥，这次我来分西瓜吧．以前师傅在的时候都是你做主，现在也该我做主一次了．”悟空一看他那模样，就明白八戒是想给自己多分一点，心里面当然不乐意了．这么热的天，俺老孙还想要那块大点的西瓜呢：“不行不行，师傅说了，我是师兄，你要听我的，我来分．”八戒当然不肯答应，于是两个人就争执了起来，谁也不肯让步．西瓜也就一直放在旁边．卖瓜的老农在一旁听得不耐烦了，心想，这两个人怎么这么烦啊，连个西瓜也切不好．老农灵机一动，想了个办法，他走上前去，对悟空和八戒说：“两位不要吵了，我有一个办法，保准你们满意．”两个人听了，半信半疑．老农接着说：“你们两人呐，一个切西瓜，把西瓜切成两半，另外一个负责分切好的西瓜．”“就这么简单？我们两个人都满意?”“没错，你们试试!”小朋友们，你们知道为什么这样规定后，两个人都能满意吗？作业1.阿呆去商店买瓶装饮料，发现店里规定，用4个空瓶可以换一瓶新的饮料．阿呆买了10瓶饮料，他实际上最多可以喝到几瓶？2.商店规定，用3个空瓶子可以换一瓶新的饮料．瓜瓜买了6瓶饮料，那么他实际上最多可以喝到喝到几瓶？3.果果和小朋友们一起玩划船渡河游戏，他们一共有10人，现在只有1条小木船，并且这条小木船最多能坐3名小朋友．那么至少要渡几次，才能把所有的小朋友都渡到河对岸（从一个岸边到另一个岸边算渡河1次）？4.小象有两个不同大小的空勺子、一个空杯子和一个装满水的桶．大勺子一次能装40克水，小勺子一次能装30克水．它能用这两个勺子往空杯子里倒入50克水吗？5.皮皮有3个砝码，重量分别为2克、3克和4克，用这3个砝码可以一次称出几种不同重量的物体？（砝码可以放在天平的两边．）第一讲 趣题巧解二1. 例题1答案：10详解：方法一：直接换．买了7瓶可乐，喝完后得到7个空瓶可换2瓶可乐，剩余1个空瓶，换来的2瓶可乐喝完后得到2个空瓶，和剩余的1个空瓶一起又能换1瓶可乐，喝完后此时还剩1个空瓶，不能够再换了．所以总共喝到72110++=（瓶）．如图所示：画图时，瓶水分离，“√”代表无瓶的可乐，“○”代表空瓶，换完后把空瓶划掉．方法二：“砸瓶大法”由于“等式两边同时去掉相同部分，等式仍然成立．”如图所示，在等式两边各“砸掉”1个空瓶，得到2个空瓶可换1瓶“无瓶可乐”．所以总共喝到7310+=（瓶）．2. 例题2答案：16详解：方法一：直接换．如图所示，换1次后，剩余3个空瓶，先借1个空瓶，用4个空瓶又能换1瓶雪碧，喝完后把得到的1个空瓶再还回去．所以总共喝到123116++=（瓶）．一人喝1瓶雪碧，所以有16人喝到雪碧．砸瓶后开始：换1次：换2次：表示1瓶可乐．方法二：“砸瓶大法”，不需要分析是否借瓶，更简便通用．如图所示，总共喝到12416+=（瓶）．3. 例题3答案：5 详解：选1只小动物当“驾驶员”，“驾驶员”把剩下的小动物分批送到对岸，根据小船的容量，每次能送3只到对岸，“驾驶员”再把船划回去载其它的小动物，直到最后一次把全部的小动物送过去，“驾驶员”就不需要返回了．如图所示，“○”代表小动物，至少要渡5次，才能把10只小动物全部渡到对岸．砸瓶后还1瓶开始：换1换2次：4. 例题4答案：能详解：第一步：先把大勺子盛满水倒入空杯子里，这时杯子里有25克水．第二步：再把大勺子盛满水，倒入空的小勺子，直到小勺子水满为止，这时大勺子里还剩251510-=（克）水．第三步：把这10克水倒入杯子里，251035+=（克）．此时杯子里有35克水．5. 例题5答案：8详解：最轻能称出1克，最重能称出1258++=（克）．用1、2、5这3个数进行加减计算，凑出1——8之间所有的数：123+=（克），541-=（克），156+=（克），257+=（克），1258++=（克）．所以，能够称出8种不同重量的物体．6. 例题6答案：28详解：根据规定“每5个空瓶可换1瓶矿泉水”，那么买4瓶水够5个人喝．3557÷=，4728⨯=（瓶）．7.练习1答案：7简答：用“砸瓶大法”，如图所示，在等式两边各“砸掉”1个空瓶，得到2个空瓶可换1瓶“无瓶可乐”．所以总共喝到527+=（瓶）．驾驶员2次2次1次8.练习2答案：10简答：用“砸瓶大法”，如图所示，在等式两边各“砸掉”1个空盒，得到4个空盒可换1盒“无盒糖果”．所以总共吃到8210+=（盒）．9.练习3答案：5简答：选班长当“驾驶员”，注意班长和9名小朋友去春游，说明一共有10人．如图所示，那么至少要渡5次，才能把所有的小朋友都渡到河对岸．驾驶员2次2次1次砸盒后砸瓶后10.练习4 答案：能 简答：第一步：在天平一边放入9克的砝码，另一边放大米，直到天平平衡为止，称出9克的大米．第二步：在天平一边放入9克的砝码，另一边放入5克的砝码，此时天平不平，在5克砝码的那一边放大米，直到天平平衡为止，954-=（克），称出4克的大米．9413+=（克），共称出13克大米． 11.作业1 答案：13 简答：首先买了10瓶饮料，然后10个空瓶可以换2瓶饮料剩2个空瓶，然后4个空瓶又可以换1瓶，102113++=． 12.作业2 答案：9 简答：首先是买的6瓶饮料，然后6个空瓶换2瓶饮料，接着借一瓶喝完，和之前的两个空瓶一起还掉借的那一瓶，6219++=． 13.作业3 答案：9 简答：每次送过去2个人，因为船上的3个人中有一个人必须把船划回来，最后一次两个人划船过河． 14.作业4 答案：能 简答：大勺子装满40克水，往小勺子里倒，并且把小勺子倒满，这时大勺子还剩下10克水，把这10克水倒入杯子里，最后大勺子装满40克水倒入杯子，这样杯子里就有50克水了． 15. 作业5答案：8简答：1克、2克、3克、4克、5克、6克、7克、9克．。

奥数春季班讲义姓名：学校：目录第01讲按规律填图 (3)第02讲巧填竖式 (5)第03讲余数 (7)第04讲切蛋糕找规律 (9)第05讲页码问题 (11)第06讲填图与拆数 (13)第07讲考虑所有可能情况（一） (16)第08讲考虑所有可能情况（二） (18)第09讲机智题 (20)第10讲猜猜凑凑 (24)第11讲列表尝试法 (27)第12讲灵感题 (29)第13讲一笔画问题 (33)第14讲七座桥问题 (36)第15讲整数的分拆 (40)第01讲按规律填图【知识梳理】找规律就像苹果香蕉梨水壶里面谁是不同的？【典型例题】【例题1】下面一组图中，有一个是不同的，你能找到它吗？①②③【例题2 】根据规律接着画。

○○○○△△△○□□○【例题3 】在方框里填上适当的字母。

A B CB C AC A【例题4】请你根据前三个图形的变化规律，画出第四个图形来。

【例题5】※★★§§☆☆§※☆★※【课堂练习】【练习1】下面一组图形，其中有一个是不相同的，你能找出来吗？【练习2】找出与其他图形不同的那组图。

●△■○△●△●□●○▲●□●□（1）（2）（3）（4）【练习3】按顺序仔细观察图，第三幅图“？”处该怎么填？●○●■□■▲？▲【练习4】按规律在空格里画上图形。

【练习5△△△△△△△△△△△▲△△△△△△△▲△△▲△△△△△△▲△△△▲△△【练习6○□□︱－↓↑－○←□○第02讲巧填竖式【知识梳理】算式谜”是一种常见的猜谜游戏。

通常是给出一个式子，但式子中却含有一些用汉字、字母等表示的特定的数字。

要求我们根据一定的法则和逻辑推理的方法，找到要填的数字。

解答这类题目，要分析算式的特点，运用加、减的运算法则来安排每一个数。

一个算式中填几个数时，要选好先填什么，再填什么，选准“突破口”，其他就好填了【典型例题】【例1】根据给出的算式，请推算出每个图形代表一个什么数字。

※ 4＋2○※=（）○=（）8 9【例2】猜一猜，每个汉字各表示什么数字？学学－4 生8学=（）生=（）【例3】在□里填合适的数，使算式成立。

第二讲巧填算符本讲内容重点：括号( )——改变运算顺序四则运算中，先乘除，后加减，有括号，就先算括号里的课前活动——抢24点游戏规则：用扑克牌上的这四个数，利用“＋、－、×、÷、( )”组成一个结果是24的算式，四个数的位置可以变化。

【例1】(★★)在下面的式子中适当的地方填上括号使等式成立。

36－12－10＝347×5－3＝1420－5÷5＋8＝11【例2】(★★★)将“＋、－、×、÷”分别填入下面等式的○里，使等式成立。

⑴7○2○4＝10○2○5⑵12○4○9＝2○8○4⑶2○8○5＝2○10○4【拓展】(★★★竞赛)在下面的○中填入“＋”、“－”、“×”、“÷”，使算式成立。

⑴16○2○5＝3⑵3○6○7＝45⑶1○2○3○4＝1⑷1○2○3○4＝24【例3】(★★★)在合适的地方填上“＋”，使等式成立。

(位置相邻的两个数字可以组成一个数)⑴ 1 2 3 4 5 ＝60⑵ 1 2 3 4 5 6 ＝102⑶ 1 2 3 4 5 6 ＝75【例4】(★★★★)在下面每两个数字之间填上“＋”或“－”，使等式成立。

（1）1 2 3 4 5 6 ＝1（2）1 2 3 4 5 6 ＝3【例5】(★★★★)在下面每两个数之间填“＋”、“－”、“×”、“÷”合适的符号，也可以添加( )，使算式成立。

（1） 1 2 3 4 5 ＝0（2） 1 2 3 4 5 ＝ 2【例6】(★★★★★)将“＋、－、×、÷、( )”填入合适的地方，使下面的等式成立。

⑴ 4 4 4 4 4＝1⑵ 4 4 4 4 4＝2⑶ 4 4 4 4 4＝3【拓展】下面的算式中，有一处运算符号填错了，造成这个等式不成立，请你改一处的运算符号，使等式成立。

12÷3－4＋5＋6＋7－8－9－10＝9。