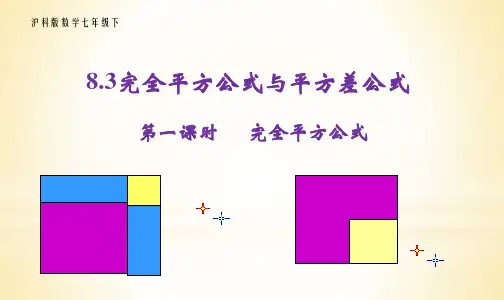
完全平方公式的结果 是三项,
结果不同: 即 (a b)2=a2 2ab+b2;
平方差公式的结果 是两项, 即 (a+b)(a−b)=a2−b2.
在解题过程中要准确确定a和b、对照公式原形的 两边, 做到不丢项、不弄错符号、2ab时不少乘2; 首项、末项是乘积被平方时要注意添括号, 是运用 完全平方公式进行多项式乘法的关键.
语言表述:
两数和(差)的平方等于这两数的平方和加 上(减去)这两数乘积的两倍. (a−b)2 = a2 −ab −b(a−b) = a2−2ab+b2 .
例题解析
1 2
注意 使用完全平方公式与平方差公式的使用一样, 先把要计算的式子与完全平方公式对照, 明确个是 a , 哪个是 b.
解:(1) (2x−3)2 = (2x )2 − 2 • 2x • 3+ 32 = 4x2 − 12x + 9 ;
1.8 完全平方公式(一)
回顾 & 思考☞
平方差公式 (a+b)(a−b)= a2 − b2
公式的结构特征: 左边是 两个二项式的乘积, 即两数和与这两数差的积. 右边是 两数的平方差.
应用平方差公式的注意事项:
☾ 弄清在什么情况下才能使用平方差公式:
对于一般两个二项式的积, 看准有无相等的“项”和 符号相反的“项”; 仅当把两个二项式的积变 成公式标准形式后,才能使用平方差公式。
解题规律:
当所给的二项式的符号相同时,就用“和”的完全平方式; 当所给的二项式的符号不同时,就用“差”的完全平方式。
6.填空: 1) a2+ 2ab +b2=(a+b)2 2) a2+ (-2ab)+b2=(a - b)2 3) 4a2+ 4ab +b2=(2a+b)2 4) 4a2+ (-4ab) +b2=(2a - b)2 5) (2a )2+4ab+b2=( 2a +b)2 6) a2-8ab+16b2=( a-4b )2 7.如果 x2 +mx+4是完全平方式,那么 m的值是多少?