围岩正应力计算公式

第六章地下洞室围岩应力与围岩压力计算第一节概述一、地下洞室的定义与分类1、定义: 地下洞室(underground cavity)是指人工开挖或天然存在于岩土体中作为各种用途的地下空间。

2、地下洞室的分类按用途：矿山巷道（井）、交通隧道、水工隧道、地下厂房（仓库）、地下军事工程按洞壁受压情况：有压洞室、无压洞室按断面形状：圆形、矩形、城门洞形、椭圆形按与水平面关系：水平洞室、斜洞、垂直洞室（井）按介质类型：岩石洞室、土洞二、洞室围岩的力学问题（1）围岩应力重分布问题——计算重分布应力1）天然应力:人类工程活动之前存在于岩体中的应力。

又称地应力、初始应力、一次应力等。

2）重分布应力:由于工程活动改变了的岩体中的应力。

又称二次分布应力等。

地下开挖破坏了岩体天然应力的相对平衡状态，洞室周边岩体将向开挖空间松胀变形，使围岩中的应力产生重分布作用，形成新的应力状态，称为重分布应力状态。

（2）围岩变形与破坏问题——计算位移、确定破坏范围在重分布应力作用下，洞室围岩将向洞内变形位移。

如果围岩重分布应力超过了岩体的承受能力，围岩将产生破坏。

（3）围岩压力问题——计算围岩压力围岩变形破坏将给地下洞室的稳定性带来危害，因而，需对围岩进行支护、衬砌，变形破坏的围岩将对支衬结构施加一定的荷载，称为围岩压力(或称山岩压力、地压等)。

（4）有压洞室围岩抗力问题——计算围岩抗力在有压洞室中，作用有很高的内水压力，并通过衬砌或洞壁传递给围岩，这时围岩将产生一个反力，称为围岩抗力。

天然应力，没有工程活动 开挖洞室后的应立场，为重分布应力，与天然应力有所改变在附近开挖第二个洞室，则视前一个洞室开挖后的应力场为天然应力，第二个洞室开挖后的应力场为重分布应力第二节围岩重分布应力计算一、围岩重分布应力的概念围岩：洞室开挖后，应力重分布影响范围内的岩体。

围岩（重分布）应力：应力重分布影响范围内岩体的应力。

围岩应力与围岩性质、洞形、洞室受外力状态有关。

计算题四、岩石的强度特征(1) 在劈裂法测定岩石单轴抗拉强度的试验中，采用的立方体岩石试件的边长为5cm，一组平行试验得到的破坏荷载分别为16.7、17.2、17.0kN，试求其抗拉强度。

解：由公式σt=2P t/πa2=2×P t×103/3.14×52×10-4=0.255P t(MPa)σt1=0.255×16.7=4.2585σt2=0.255×17.2=4.386σt3=0.255×17.0=4.335则所求抗拉强度：σt==(4.2585+4.386+4.335)/3=4.33MPa。

(2) 在野外用点荷载测定岩石抗拉强度，得到一组数据如下：试计算其抗拉强度。

(K=0.96)解：因为K=0.96，P t、D为上表数据，由公式σt=KI s=KP t/D2代入上述数据依次得：σt=8.3、9.9、10.7、10.1、7.7、8.7、10.4、9.1。

求平均值有σt=9.4MPa。

(3) 试导出倾斜板法抗剪强度试验的计算公式。

解：如上图所示：根据平衡条件有：Σx=0τ-P sinα/A-P f cosα/A=0τ=P (sinα- f cosα)/AΣy=0σ-P cosα-P f sinα=0σ=P (cosα+ f sinα)式中：P为压力机的总垂直力。

σ为作用在试件剪切面上的法向总压力。

τ为作用在试件剪切面上的切向总剪力。

f为压力机整板下面的滚珠的磨擦系数。

α为剪切面与水平面所成的角度。

则倾斜板法抗剪强度试验的计算公式为:σ=P(cosα+ f sinα)/Aτ=P(sinα- f cosα)/A(4) 倾斜板法抗剪强度试验中，已知倾斜板的倾角α分别为30º、40º、50º、和60º，如果试样边长为5cm,据经验估计岩石的力学参数c=15kPa，φ=31º，试估计各级破坏荷载值。

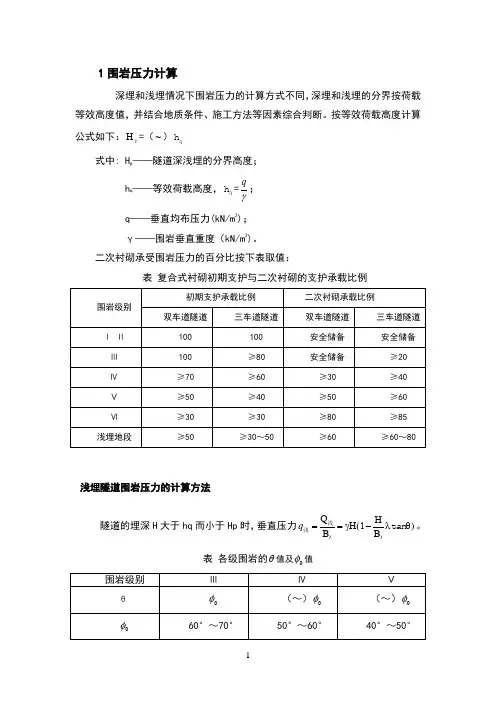
1围岩压力计算深埋和浅埋情况下围岩压力的计算方式不同，深埋和浅埋的分界按荷载等效高度值，并结合地质条件、施工方法等因素综合判断。

按等效荷载高度计算公式如下：HP =（~）qh式中: Hp——隧道深浅埋的分界高度；hq ——等效荷载高度，qh=qγ；q——垂直均布压力(kN/m2)；γ——围岩垂直重度（kN/m3)。

二次衬砌承受围岩压力的百分比按下表取值：表复合式衬砌初期支护与二次衬砌的支护承载比例浅埋隧道围岩压力的计算方法隧道的埋深H大于hq而小于Hp时，垂直压力QB Bt tqH==γH(1-λθ)浅浅tan。

表各级围岩的θ值及φ值2(tan 1)tan tan tan c cc ϕ+ϕβϕ+ϕ-θc tan =tan侧压力系数()tan tan tan tan tan tan tan tan cc c β-ϕλ=β1+βϕ-θ+ϕθ⎡⎤⎣⎦作用在支护结构两侧的水平侧压力为：e 1=γh λ ； e 2=γ(h+Ht)λ 侧压力视为均布压力时：Ⅴ级围岩的等效荷载高度hq=×24×[1+×(10-5)]= Hp==27m,H<Hq,故为浅埋。

取φ0=45°，θ=φ0=27°，h=20m ，tan β=,λ=,tan θ=, 计算简图：()212+1e =e e垂直压力q=19×20×20×10)=mPg=πdγ=π××25=m地基反力P=me1=γhλ=19×20×=e2=γ(h+Ht)λ=19×(20+×=水平均布松动压力e=(e1+e2)/2=mⅤ级围岩二衬按承受50%围岩压力进行计算，则垂直压力为q×50%=m地基反力为P×50%=m水平压力为e×50%=m2衬砌结构内力计算表等效节点荷载表轴力、剪力、弯矩详细数据50+0557********51+05409972930652+05240502556953+052115954+0517015内力图分析（1）轴力：由ANSYS建模分析围岩衬砌内力得出轴力图如图，最大轴力出现在仰拱段，其值为。

精心整理§2.1隧道围岩重分布应力的计算隧道开挖前，岩体中每个质点均受到天然应力的作用而处于相对平衡状态；隧洞开挖后，洞壁岩体因失去了原有岩体的支撑，破坏了原有的平衡状态，从而产生向洞内空间的膨胀变形，其结果又改变了相邻质点的相对平衡关系，引起应力、应变和能量的重新调整，达到新的平衡关系，形成新的应力状态。

2.1.1弹性围岩重分布应力对于那些坚硬致密的块状岩体，当天然应力大约等于或小于其单轴抗压强度的一般时，隧道开挖后的围岩将呈弹性变形状态。

这类围岩可近似视为各向同性、连续、均质的线弹性体，其围岩应力重分布可用弹性力学的基本理论来分析，隧洞半径相对于洞长很小时，可按平面应变问题考虑，围岩重分布应力可用柯西（Kirsh ）课题求解。

图2-1是柯西课题的简化模型。

设无限大弹性薄板，在边界上受沿X 方向的外力P 作用，薄板中有一半径为R 0的圆形小孔。

取如图极坐标，薄板中任一点（，）的应力及方向如图所示，按平面问题考虑，不计体力，则点的各应力分量，即径向应力、环向应力和剪应力与应力函数间的关系，根据弹性理论可表示为：22222221111r r r r r r r r r θθθθφφσθφσφφτ∂∂=+∂∂∂=∂∂∂⎫⎪⎪⎪⎪=⎬⎪⎪⎪⎪⎭-∂∂∂（2-1） 上式的边界条件为：()()()()000cos 222sin 22r r br r b r r r br bp p bR p b R b R σθτθστ====⎫=+⎪⎪⎪=-⎬⎪⎪==⎪⎭（2-2）设满足该方程的应力函数φ是：()222ln cos 2A r Br Cr Dr F φθ-=++++（2-3）带入上式并考虑边界条件，可求得应力函数为：22220022200ln 1cos 22222pR R r r r R R r φθ⎡⎤=-----⎢⎥⎢⎥⎣⎦（2-4） 代入可得各应力分量：2400244200423(1)(1)cos 2232(122r R R r r R R rprp θθσθτθ⎪⎡⎤⎪=+-+⎢⎥⎬⎢⎥⎪⎣⎦⎪⎪=--+⎪⎭（2-5） 式中，x σ,θσ,r θτ分别为M 点的径向应力、环向应力和剪应力，以压应力为正，拉应力为负;θ为M 点的极角，自水平轴(x 轴)起始，反时针方向为正；r 为径向半径。

隧道塌落拱的计算支护结构物在控制围岩的变形、松散或防止岩块坍塌的过程中，自身将受到由于围岩的变形或岩块坍塌所产生的力的作用。

我们把这种来自围岩的，作用在支护结构物上的力称做“山体压力”。

当山体压力作用于支护结构物时，支护结构物对图岩也产生了反作用力。

因此，这个概念反映了围岩与支护结构物之间的相互关系。

在地下工程的长期实践中人们发现，在一般随况下，围岩的这种坍塌是有一定限度的。

当坍塌致使洞室形状改变到一定程度时，将不再发展，即使不加支护，围岩自身亦可建立起新的平衡。

这也就是说，如果不加支护，洞空开挖前后围岩力学形态将经历“相对平衡——变形、破坏、坍塌——相对平衡”的过程，这种过程的最终产物就是“坍落拱”。

对此，有不少技术工作者总结了这种规律，并建立了一些简单的数学公式来描述不加支护情况下围岩最终坍塌的范围即坍落拱的形状。

主要有以下五种方法：1. 三角形公式如图a 示：（注：以下所有图示均以单线铁路隧道Ⅴ级围岩为例） 侧壁稳定时其高度为：ϕtg b h = 侧壁不稳定时其高度为：ϕϕtg b tg h +-︒⨯=)2/45(H h －坍落洪高；b －洞室跨度之半；H －隧道开挖高度；φ－岩体内摩擦角。

图a(单位：mm)2. 轴变论公式20世纪50年代末。

我国学者于学馥教授提出了轴变论，他提出了在二维应力场中，使围岩保持稳定的最佳洞形是具有一定轴比的椭圆。

1978年瑞合兹（） 和贝觉克门（）又从理论计算方面解决了这一问题。

从围岩稳定的观点选择最佳洞形，就是要找具有最小应力集中的洞形，这种洞形称为“谐洞”。

形成“谐洞”的条件为：如图b 所示。

λ1=qq －椭圆轴比；λ－围岩侧压力系数，据有关资料，当埋深小于500m 时，λ=～，松散软弱地层中，λ=～。

图b(单位：mm)塌落拱高度即为椭圆长轴，即：λab =a －椭圆短轴长，等于隧道开挖半径；b －椭圆长轴长。

3. 梯形公式包里索夫等人从层状岩体坍落后出现的块体平衡出发，认为在层状围岩中坍落拱的形状为一梯形，如图c 所示，其高度为：()a a L h h cos sin 1⨯+=式中：h －塌落拱高度，m ；L －洞室跨度,m ；a －层面倾角；图c （单位：mm ）δδζtg a nr h a L h i i n 2cos 04.0cos 1-=其中：ζ－压缩蠕变系数，可取ζ=～；h i －层厚，即层面间距,m ；n －承载能力安全系数，可取n =4；δn －抗压强度,N/cm 2；γi －岩体容重,t/m 3；δ－冒落边界与层面间的交角，根据试验资料，对坚硬裂隙性岩石当沉积深度不大和中等时，这个倾角δ等于60°～80°。

第一节概述1．地下洞室（underground cavity）：指人工开挖或天然存在于岩土体中作为各种用途的构筑物。

2．我国古代的采矿巷道，埋深60m，距今约3000年左右（西周）。

目前，地下洞室的最大埋深已达2500m，跨度已过50m，同时还出现有群洞。

3．分类：按作用分类：交通隧洞（道）、水工隧洞、矿山巷道、地下厂房仓库、地铁等等；按内壁有无水压力：有压洞室和无压洞室；按断面形状为：圆形、矩形或门洞形和马蹄形洞室等；按洞轴线与水平面间的关系分为：水平洞室、竖井和倾斜洞室三类；按介质，土洞和岩洞。

4．地下洞室→引发的岩体力学问题过程：地下开挖→天然应力失衡，应力重分布→洞室围岩变形和破坏→洞室的稳定性问题→初砌支护：围岩压力、围岩抗力（有内压时）（洞室的稳定性问题主要研究围岩重分布应力与围岩强度间的相对关系）第二节围岩重分布应力计算1．围岩：指由于人工开挖使岩体的应力状态发生了变化，而这部分被改变了应力状态的岩体。

2．地下洞室围岩应力计算问题可归纳的三个方面：①开挖前岩体天然应力状态（一次应力、初始应力和地应力）的确定；②开挖后围岩重分布应力（二次应力）的计算；③支护衬砌后围岩应力状态的改善。

3．围岩的重分布应力状态（二次应力状态）：指经开挖后岩体在无支护条件下，岩体经应力调整后的应力状态。

一、无压洞室围岩重分布应力计算1．弹性围岩重分布应力坚硬致密的块状岩体，当天然应力，地下洞室开挖后围岩将呈弹性变形状态。

这类围岩可近似视为各向同性、连续、均质的线弹性体，其围岩重分布应力可用弹性力学方法计算。

重点讨论圆形洞室。

（1）圆形洞室深埋于弹性岩体中的水平圆形洞室，可以用柯西求解，看作平面应变问题处理。

无限大弹性薄板，沿X方向的外力为P，半径为R0的小圆孔，如图8.1所示。

任取一点M（r,θ）按平面问题处理，不计体力。

则：图8.1柯西课题分析示意图……………………①式中为应力函数，它是和的函数，也是和的函数。