2009年中考试题专题之23-圆与圆的位置关系试题及答案

圆与圆的位置综合练习一．选择题（共10小题）1．（2010•防城港）在数轴上，点A所表示的实数是﹣2，⊙A的半径为2，⊙B的半径为1，若⊙B与⊙A外切，则在数轴上点B所表示的实数是（）A．1B．﹣5 C．1或﹣5 D．﹣1或﹣32．（2009•肇庆）若⊙O1与⊙O2相切，且O1O2=5，⊙O1的半径r1=2，则⊙O2的半径r2是（）A．3B．5C．7D．3或73．（2009•临沂）已知⊙O1和⊙O2相切，⊙O1的直径为9cm，⊙O2的直径为4cm．则O1O2的长是（）A．5cm或13cm B．2.5cm C．6.5cm D．2.5cm或6.5cm4．（2009•佛山）将两枚同样大小的硬币放在桌上，固定其中一枚，而另一枚则沿着其边缘滚动一周，这时滚动的硬币滚动了（）A．1圈B．1.5圈C．2圈D．2.5圈5．（2009•滨州）已知两圆半径分别为2和3，圆心距为d，若两圆没有公共点，则下列结论正确的是（）A．0＜d＜1 B．d＞5 C．0＜d＜1或d＞5 D．0≤d＜1或d＞56．（2008•雅安）已知两圆圆心距是5，半径分别为2和3，则两圆的位置关系为（）A．相离B．相交C．内切D．外切7．（2008•宁夏）已知⊙O1和⊙O2相切，两圆的圆心距为9cm，⊙O1的半径为4cm，则⊙O2的半径为（）A．5cm B．13cm C．9cm或13cm D．5cm或13cm8．（2007•肇庆）若两圆没有公共点，则两圆的位置关系是（）A．外离B．外切C．内含D．外离或内含9．（2007•襄阳）如图，△ABC是边长为10的等边三角形，以AC为直径作⊙O，D是BC上一点，BD=2，以点B 为圆心，BD为半径的⊙B与⊙O的位置关系为（）A．相交B．外离C．外切D．内切10．（2007•泰安）半径分别为13和15的两圆相交，且公共弦长为24，则两圆的圆心距为（）A．或14 B．或4C．14 D．4或14二．填空题（共8小题）11．（2012•攀枝花）如图，以BC为直径的⊙O1与⊙O2外切，⊙O1与⊙O2的外公切线交于点D，且∠ADC=60°，过B点的⊙O1的切线交其中一条外公切线于点A．若⊙O2的面积为π，则四边形ABCD的面积是_________．12．（2011•绍兴）如图，相距2cm的两个点A、B在直线l上．它们分别以2cm/s和1cm/s的速度在l上同时向右平移，当点A，B分别平移到点A1，B1的位置时，半径为1cm的⊙A1，与半径为BB1的⊙B相切．则点A平移到点A1，所用的时间为_________s．13．（2010•宁夏）如图是三根外径均为1米的圆形钢管堆积图和主视图，则其最高点与地面的距离是_________米．14．（2008•绍兴）如图中的圆均为等圆，且相邻两圆外切，圆心连线构成正三角形，记各阴影部分面积从左到右依次为S1，S s，S3，…，S n，则S12：S4的值等于_________．15．（2008•三明）如图，在以O为圆心的两个同心圆中，大圆的直径AB交小圆于C、D两点，AC=CD=DB，分别以C、D为圆心，以CD为半径作圆．若AB=6cm，则图中阴影部分的面积为_________cm2．16．（2007•河池）若两圆的半径分别为5cm和3cm，圆心距为1cm，则这两个圆的位置关系是_________．17．（2004•郫县）已知半径3cm，4cm的两圆外切，那么半径为6cm且与这两圆都相切的圆共有_________个．18．（2000•嘉兴）如图，⊙O1与⊙O2交于点A，B，延长⊙O2的直径CA交⊙O1于点D，延长⊙O2的弦CB交⊙O1于点E．已知AC=6，AD：BC：BE=1：1：5，则DE的长是_________．三．解答题（共5小题）19．（2012•鼓楼区二模）如图，已知边长为10的菱形ABCD，对角线BD、AC交于点O，AC=12，点P在射线BD 上运动，过点P分别向直线AB、AD作垂线，垂足分别为E、F．（1）对角线BD长为_________；（2）设PB=x，以PO为半径的⊙P与以DF为半径的⊙D相切时，求x的值．20．（2008•静安区二模）如图，在四边形ABCD中，∠B=90°，AD∥BC，AB=4，BC=12，点E在边BA的延长线上，AE=2，点F在BC边上，EF与边AD相交于点G，DF⊥EF，设AG=x，DF=y．（1）求y关于x的函数解析式，并写出定义域；（2）当AD=11时，求AG的长；（3）如果半径为EG的⊙E与半径为FD的⊙F相切，求这两个圆的半径．21．如图，正方形网格中，每个小正方形的边长为1个单位，以O为原点建立平面直角坐标系，圆心为A（3，0）的⊙A被y轴截得的弦长BC=8．解答下列问题：（1）求⊙A 的半径；（2）请在图中将⊙A 先向上平移6 个单位，再向左平移8个单位得到⊙D，并写出圆心D的坐标；（3）观察你所画的图形，对⊙D 与⊙A 的位置关系作出合情的猜想，并直接写出你的结论．聪明的小伙伴，你完成整张试卷全部试题的解答后，如果还有时间对问题（3）的猜想结论给出证明，将酌情另加1～5分，并计入总分．22．如图，在平台上用直径为100mm的两根圆钢棒嵌在大型工件的两侧，测量大的圆形工件的直径，设两圆钢棒的外侧的距离为xmm，工件的直径为Dmm．（1）求出D（mm）与x（mm）之间的函数关系式；（2）当图形工件的直径D小于圆钢棒的直径时，上面所求得的D与x的函数关系式还是否仍然适用？请说明理由．23．实验探究：同学们，你注意过烟盒里的香烟是如何摆放的吗？已知，一个烟盒的长为56mm，宽为22mm，高为87mm，一根烟的直径是8mm，若把20根香烟摆放在烟盒中，请你探究合理的摆放方法．圆与圆的位置综合练习参考答案与试题解析一．选择题（共10小题）1．（2010•防城港）在数轴上，点A所表示的实数是﹣2，⊙A的半径为2，⊙B的半径为1，若⊙B与⊙A外切，则在数轴上点B所表示的实数是（）A．1B．﹣5 C．1或﹣5 D．﹣1或﹣3考点：圆与圆的位置关系．专题：压轴题．分析：本题直接告诉了两圆的半径及位置关系，根据数量关系与两圆位置关系的对应情况便可直接得出答案．外离，则P＞R+r；外切，则P=R+r；相交，则R﹣r＜P＜R+r；内切，则P=R﹣r；内含，则P＜R﹣r．（P表示圆心距，R，r分别表示两圆的半径）．解答：解：设数轴上点B所表示的实数是b，则AB=||b﹣（﹣2）|=|b+2|，⊙B与⊙A外切时，AB=2+1，即|b+2|=3，解得b=1或﹣5，故选C．点评：本题考查了由数量关系及两圆位置关系求圆心坐标的方法．2．（2009•肇庆）若⊙O1与⊙O2相切，且O1O2=5，⊙O1的半径r1=2，则⊙O2的半径r2是（）A．3B．5C．7D．3或7考点：圆与圆的位置关系．专题：压轴题．分析：两圆相切，包括了内切或外切，即d=R+r，d=R﹣r，分别求解．解答：解：∵这两圆相切∴⊙O1与⊙O2的位置关系是内切或外切，O1O2=5，⊙O1的半径r1=2，所以r1+r2=5或r2﹣r1=5，解得r2=3或7．故选D．点评：本题考查了由两圆位置关系来判断半径和圆心距之间数量关系的方法．两圆的半径分别为R和r，且R≥r，圆心距为d：外离d＞R+r；外切d=R+r；相交R﹣r＜d＜R+r；内切d=R﹣r；内含d＜R﹣r．3．（2009•临沂）已知⊙O1和⊙O2相切，⊙O1的直径为9cm，⊙O2的直径为4cm．则O1O2的长是（）A．5cm或13cm B．2.5cm C．6.5cm D．2.5cm或6.5cm考点：圆与圆的位置关系．专题：压轴题．分析：半径不相等的两圆相切有两种情况：内切和外切，不要只考虑其中一种情况．由⊙O1与⊙O2的直径分别为9cm和4cm得两圆的半径分别为4.5cm、2cm；当两圆外切时，O1O2=4.5+2=6.5（cm）；当两圆内切时，O1O2=4.5﹣2=2.5（cm），所以O1O2的值为6.5cm或2.5cm．注意，相同半径的两圆只有外切与外离，而没有内切与内含的位置关系．解答：解：∵⊙O1和⊙O2相切，∴两圆可能内切和外切，∴当两圆外切时，O1O2=4.5+2=6.5（cm）；当两圆内切时，O1O2=4.5﹣2=2.5（cm）；∴O1O2的长是2.5cm或6.5cm．∴故选D．点评：本题考查两圆的位置关系．特别注意：两圆相切，则可能有两种情况，内切或外切．4．（2009•佛山）将两枚同样大小的硬币放在桌上，固定其中一枚，而另一枚则沿着其边缘滚动一周，这时滚动的硬币滚动了（）A．1圈B．1.5圈C．2圈D．2.5圈考点：圆与圆的位置关系．专题：压轴题；转化思想．分析：根据自身的周长和滚动的周长求解．解答：解：设圆的半径是r，则另一枚沿着其边缘滚动一周所走的路程是以2r为半径的圆周长，即是4πr，它自身的周长是2πr．即一共滚了2圈．故选C．点评：此题要特别注意正确分析另一枚则沿着其边缘滚动一周所走的路程．5．（2009•滨州）已知两圆半径分别为2和3，圆心距为d，若两圆没有公共点，则下列结论正确的是（）A．0＜d＜1 B．d＞5 C．0＜d＜1或d＞5 D．0≤d＜1或d＞5考点：圆与圆的位置关系．专题：压轴题．分析：若两圆没有公共点，则可能外离或内含，据此考虑圆心距的取值范围．解答：解：若两圆没有公共点，则可能外离或内含，外离时的数量关系应满足d＞5；内含时的数量关系应满足0≤d＜1．故选D．点评：考查了两圆的位置关系和数量关系之间的等价关系．6．（2008•雅安）已知两圆圆心距是5，半径分别为2和3，则两圆的位置关系为（）A．相离B．相交C．内切D．外切考点：圆与圆的位置关系．专题：压轴题．分析：由两圆的半径分别2和3，圆心距为5，根据两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系即可得出两圆位置关系．解答：解：∵两圆的半径分别为2和3，圆心距为5，又∵2+3=5，∴两圆的位置关系是外切．故选D．点评：此题考查了圆与圆的位置关系．解题的关键是掌握两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系．7．（2008•宁夏）已知⊙O1和⊙O2相切，两圆的圆心距为9cm，⊙O1的半径为4cm，则⊙O2的半径为（）A．5cm B．13cm C．9cm或13cm D．5cm或13cm考点：圆与圆的位置关系．专题：压轴题；分类讨论．分析：根据两圆的位置关系与圆心距和两圆半径之间的数量关系之间的联系即可解决问题．设两圆的半径分别为R和r，且R≥r，圆心距为d：外离，则d＞R+r；外切，则d=R+r；相交，则R﹣r＜d＜R+r；内切，则d=R﹣r；内含，则d＜R﹣r．解答：解：两圆相切时，有两种情况：内切和外切．当外切时，另一圆的半径=9+4=13cm；当内切时，另一圆的半径=9﹣4=5cm．故选D．点评：本题考查了两圆相切时，两圆的半径与圆心距的关系，注意有两种情况．8．（2007•肇庆）若两圆没有公共点，则两圆的位置关系是（）A．外离B．外切C．内含D．外离或内含考点：圆与圆的位置关系．分析：此题要求两个圆的位置关系，可观察两个圆之间的交点个数，一个交点两圆相切（内切或外切），两个交点两圆相交，没有交点两圆相离（外离或内含）．解答：解：外离或内含时，两圆没有公共点．故选D．点评：此题考查的是两个圆之间的位置关系，解此类题目时可根据两个圆的交点个数来判断两个圆的位置关系．9．（2007•襄阳）如图，△ABC是边长为10的等边三角形，以AC为直径作⊙O，D是BC上一点，BD=2，以点B 为圆心，BD为半径的⊙B与⊙O的位置关系为（）A．相交B．外离C．外切D．内切考点：圆与圆的位置关系；等边三角形的性质．专题：压轴题．分析：要判断两圆的位置关系，需要明确两圆的半径和两圆的圆心距，再根据数量关系进一步判断两圆的位置关系．设两圆的半径分别为R和r，且R≥r，圆心距为d：外离，则d＞R+r；外切，则d=R+r；相交，则R﹣r＜d＜R+r；内切，则d=R﹣r；内含，则d＜R﹣r．解答：解：根据题意，得：圆O的直径是10，点B到点O的距离是5，则5＞5+2，所以⊙B与⊙O的位置关系为外离．故选B．点评：本题考查了由数量关系来判断两圆位置关系的方法．10．（2007•泰安）半径分别为13和15的两圆相交，且公共弦长为24，则两圆的圆心距为（）A．或14 B．或4C．14 D．4或14考点：相交两圆的性质．分析：利用了连心线垂直平分公共弦，勾股定理求解，注意两圆相交的情况有两种情况．解答：解：如图，圆A与圆B相交于点C，D，CD与AB交于点E，AC=15，BC=13，由于连心线AB垂直平分CD，有CE=12，△ACE，△BCE是直角三角形，由勾股定理得，AE=9，BE=5，而两圆相交的情况有两种，当为左图时，AB=AE﹣BE=9﹣5=4，当为右图时，AB=AE+BE=14．故选D．点评：本题利用了连心线垂直平分公共弦，勾股定理．二．填空题（共8小题）11．（2012•攀枝花）如图，以BC为直径的⊙O1与⊙O2外切，⊙O1与⊙O2的外公切线交于点D，且∠ADC=60°，过B点的⊙O1的切线交其中一条外公切线于点A．若⊙O2的面积为π，则四边形ABCD的面积是12．考点：相切两圆的性质；含30度角的直角三角形；勾股定理；矩形的判定与性质；切线长定理．专题：计算题；压轴题．分析：设⊙O1的半径是R，求出⊙O2的半径是1，连接DO2，DO1，O2E，O1H，AO1，作O2F⊥BC于F，推出D、O2、O1三点共线，∠CDO1=30°，求出四边形CFO2E是矩形，推出O2E=CF，CE=FO2，∠FO2O1=∠CDO1=30°，推出R+1=2（R﹣1），求出R=3，求出DO1，在Rt△CDO1中，由勾股定理求出CD，求出AH==AB，根据梯形面积公式得出×（AB+CD）×BC，代入求出即可．解答：解：∵⊙O2的面积为π，设⊙O2的半径是r，则π×r2=π∴⊙O2的半径是1，∵AB和AH是⊙O1的切线，∴AB=AH，设⊙O1的半径是R，连接DO2，DO1，O2E，O1H，AO1，作O2F⊥BC于F，∵⊙O1与⊙O2外切，⊙O1与⊙O2的外公切线DC、DA，∠ADC=60°，∴D、O2、O1三点共线，∠CDO1=30°，∴∠DAO1=60°，∠O2EC=∠ECF=∠CFO2=90°，∴四边形CFO2E是矩形，∴O2E=CF，CE=FO2，∠FO2O1=∠CDO1=30°，∴DO2=2O2E=2，∠HAO1=60°，∵O1O2=2O1F（在直角三角形中，30度角所对的直角边等于斜边的一半），又∵O1F=R﹣1，O1O2=R+1，∴R+1=2（R﹣1），解得：R=3，即DO1=2+1+3=6，在Rt△CDO1中，由勾股定理得：CD=3，∵∠HO1A=90°﹣60°=30°，HO1=3，∴AH==AB，∴四边形ABCD的面积是：×（AB+CD）×BC=×（+3）×（3+3）=12．故答案为：12．点评：本题考查的知识点是勾股定理、相切两圆的性质、含30度角的直角三角形、矩形的性质和判定，本题主要考查了学生能否运用性质进行推理和计算，题目综合性比较强，有一定的难度．12．（2011•绍兴）如图，相距2cm的两个点A、B在直线l上．它们分别以2cm/s和1cm/s的速度在l上同时向右平移，当点A，B分别平移到点A1，B1的位置时，半径为1cm的⊙A1，与半径为BB1的⊙B相切．则点A平移到点A1，所用的时间为或3s．考点：圆与圆的位置关系．专题：压轴题；数形结合；分类讨论．分析：首先设点A平移到点A1，所用的时间为ts，根据题意求得AB=2cm，AA1=2tcm，BB1=tcm，再分别从内切与外切四种情况分析求解，即可求得答案．解答：解：设点A平移到点A1，所用的时间为ts，根据题意得：AB=2cm，AA1=2tcm，A1B=（2﹣2t）cm，BB1=tcm，如图，此时外切：2﹣2t=1+t，∴t=；如图，此时内切：2﹣2t=1﹣t，∴t=1，此时两圆心重合，舍去；或2﹣2t=t﹣1，解得：t=1，此时两圆心重合，舍去；如图，此时内切：2t﹣t+1=2，∴t=1，此时两圆心重合，舍去；如图：此时外切：2t﹣t﹣1=2，∴t=3．∴点A平移到点A1，所用的时间为1或3s．故答案为：或3．点评：此题考查了圆与圆的位置关系．解题的关键是注意数形结合与方程思想，分类讨论思想的应用，注意别漏解．13．（2010•宁夏）如图是三根外径均为1米的圆形钢管堆积图和主视图，则其最高点与地面的距离是米．考点：相切两圆的性质．专题：压轴题．分析：连接三个圆的圆心，构造等边三角形．根据等边三角形的性质进行求解．解答：解：连接三个圆的圆心，构造等边三角形，则等边三角形的边长是1．根据等边三角形的三线合一和勾股定理，得等边三角形的高是．则其最高点与地面的距离是（1+）米．点评：此题主要是构造等边三角形，根据等边三角形的性质进行计算．14．（2008•绍兴）如图中的圆均为等圆，且相邻两圆外切，圆心连线构成正三角形，记各阴影部分面积从左到右依次为S1，S s，S3，…，S n，则S12：S4的值等于19：7．考点：相切两圆的性质．专题：压轴题；规律型．分析：首先正确求得第一个图形的面积，然后结合图形发现面积增加的规律，从而进行分析求解．解答：解：设圆的半径是1，在第一个图形中，阴影部分的面积是3π﹣π=π；观察图形发现：阴影部分的面积依次增加1.5π．所以第四个图形的面积是2.5π+1.5π×3=7π，第12个图形的面积是2.5π+1.5π×11=19π．所以它们的比值是．点评：此类题的关键是找规律，根据规律进行计算．15．（2008•三明）如图，在以O为圆心的两个同心圆中，大圆的直径AB交小圆于C、D两点，AC=CD=DB，分别以C、D为圆心，以CD为半径作圆．若AB=6cm，则图中阴影部分的面积为4πcm2．考点：圆与圆的位置关系．分析：根据圆的中心对称性，大圆与小圆之间的部分全等，故阴影部分的面积是两圆面积差的一半．解答：解：观察图形，发现：阴影部分的面积是两圆面积差的一半，即S阴影=（S大圆﹣S小圆）=（π×32﹣π×12）=4π．点评：这里要能够把阴影部分合到一起整体计算．16．（2007•河池）若两圆的半径分别为5cm和3cm，圆心距为1cm，则这两个圆的位置关系是内含．考点：圆与圆的位置关系．分析：先计算两圆半径的和与差，再与圆心距比较，得出结论．解答：解：因为5﹣3＞1，根据圆心距与半径之间的数量关系可知，⊙O1与⊙O2的位置关系是内含．点评：本题考查了由数量关系来判断两圆位置关系的方法．设两圆的半径分别为R和r，且R≥r，圆心距为d：外离d＞R+r；外切d=R+r；相交R﹣r＜d＜R+r；内切d=R﹣r；内含d＜R﹣r．17．（2004•郫县）已知半径3cm，4cm的两圆外切，那么半径为6cm且与这两圆都相切的圆共有4个．考点：圆与圆的位置关系．专题：压轴题．分析：两圆相切有内切和外切两种情况，本题只要画出图形加以判断即可．解答：解：如图：与两圆相切的有4个．点评：本题考查的是圆与圆的位置关系，解此类题目常常要结合图形再进行判断．18．（2000•嘉兴）如图，⊙O1与⊙O2交于点A，B，延长⊙O2的直径CA交⊙O1于点D，延长⊙O2的弦CB交⊙O1于点E．已知AC=6，AD：BC：BE=1：1：5，则DE的长是9．考点：圆内接四边形的性质；解分式方程；圆与圆的位置关系；相交两圆的性质；相似三角形的判定与性质．专题：压轴题．分析：连接公共弦AB，构成圆内接四边形ABED，根据圆内接四边形的性质，可证明△ABC∽△EDC，从而得出与AD、BC、BE有关的比例线段，根据AD：BC：BE=1：1：5，设线段长度，代入比例式可求CD、CE的长，在Rt△EDC中，用勾股定理求ED．解答：解：连接AB，在圆内接四边形ABED中，∠BAC=∠E，∠ABC=∠EDC，因为AC为⊙O2直径，则∠ABC=90°，于是△ABC∽△EDC，因为AD：BC：BE=1：1：5，所以，设AD=x，BC=x，BE=5x；于是：=，即6x2=36+6x，x2﹣x﹣6=0，解得x=3，x=﹣2（负值设去），在Rt△EDC中，ED==9．点评：本题考查的是对圆心角和圆周角的关系，以及圆的内接四边形的外角和相应的内对角关系的应用．解答此类题关键是通过角的关系，在解题中应用中间角来寻找等量关系．三．解答题（共5小题）19．（2012•鼓楼区二模）如图，已知边长为10的菱形ABCD，对角线BD、AC交于点O，AC=12，点P在射线BD 上运动，过点P分别向直线AB、AD作垂线，垂足分别为E、F．（1）对角线BD长为16；（2）设PB=x，以PO为半径的⊙P与以DF为半径的⊙D相切时，求x的值．考点：相切两圆的性质；勾股定理；菱形的性质．分析：（1）根据菱形性质求出AO长，OB=OD，AC⊥BD，根据勾股定理求出BO，即可求出BD；（2）设PB=x，则PD=BD﹣PB=16﹣x．在Rt△PFD中，求出DF=DP•cos∠ADB=（16﹣x），分为两种情况：①当⊙P与⊙D外切时：第一种情况，当P点在点O的左侧，PO=8﹣x，根据相切两圆性质得出PO+DF=PD，代入得出方程（8﹣x）+（16﹣x）=16﹣x，求出x即可；第二种情况，当P点在点O的右侧，PO=x﹣8，根据相切两圆的性质得出PO+DF=PD，代入得出方程（x﹣8）+（16﹣x）=16﹣x，求出方程的解即可；②当⊙P与⊙D内切时：第三种情况，PO=PB﹣OB=x﹣8，根据OP﹣DF═PD，得出方程（x﹣8）﹣（16﹣x）=16﹣x，求出即可；第四种情况，点P在点D右侧时，PF=OD=8，则DP=10，PB=26．解答：（1）解：∵四边形ABCD是菱形，∴AO=OC=AC=6，OB=OD，AC⊥BD，由勾股定理得：BO===8，∴BD=16，故答案为：16．（2）PB=x，则PD=BD﹣PB=16﹣x．∵PF⊥AD，∴在Rt△PFD中，DF=DP•cos∠ADB=（16﹣x）；①当⊙P与⊙D外切时：情况一：当P点在点O的左侧，PO=OB﹣PB=8﹣x，此时PO+DF=PD，∴（8﹣x）+（16﹣x）=16﹣x，解得，x=6；情况二：当P点在点O的右侧，PO=PB﹣OB=x﹣8，此时PO+DF=PD，∴（x﹣8）+（16﹣x）=16﹣x，解得，x=；②当⊙P与⊙D内切时：情况三：点P在D的左侧时，PO=PB﹣OB=x﹣8，∵PD＞DF，∴DF﹣OP═PD，∴（x﹣8）﹣（16﹣x）=16﹣x，解得，x=；情况四：点P在点D右侧时，DF=OD=8，则DP=10，PB=26，综上所述，PB的长为6或或或26．点评：本题考查了解直角三角形，菱形的性质，勾股定理，相切两圆的性质等知识点，主要考查学生综合运用性质进行推理和计算的能力，题目综合性比较强，难度偏大，注意要进行分类讨论．20．（2008•静安区二模）如图，在四边形ABCD中，∠B=90°，AD∥BC，AB=4，BC=12，点E在边BA的延长线上，AE=2，点F在BC边上，EF与边AD相交于点G，DF⊥EF，设AG=x，DF=y．（1）求y关于x的函数解析式，并写出定义域；（2）当AD=11时，求AG的长；（3）如果半径为EG的⊙E与半径为FD的⊙F相切，求这两个圆的半径．考点：相似三角形的判定与性质；勾股定理；相切两圆的性质．专题：压轴题；探究型．分析：（1）先根据AD∥BC，∠B=90°求出∠EAG=∠B=90°，在Rt△AEG中根据勾股定理可用x表示出EG的值，再根据平行线分线段成比例可得出=，进而可得到关于x、y的关系式，由二次根式有意义的条件求出x的取值范围即可；（2）由△DFG∽△EAG可得到=，可用x表示出GD的值，再把AD=11代入即可求出x的值，进而得出AG的长；（3）①当⊙E与⊙F外切时，EF=EG+FD=EG+FG，再由△DFG∽△EAG即可求出AG=AE=2，进而可得出⊙E与⊙F的半径；②当⊙E与⊙F内切时，EF=FD﹣EG，再把EF、FD及ED的关系式代入即可求出x的值，由勾股定理即可求出两圆的半径．解答：解：（1）∵AD∥BC，∠B=90°，∴∠EAG=∠B=90°，∴EG==，∵=，∴FG===，∵∠DFG=∠EAG=90°，∠EGA=∠DGF，△DFG∽△EAG，∴=，∴=，∴y关于x的函数解析式为y=，定义域为0＜x≤4．（2）∵△DFG∽△EAG，∴=，∴=，∴GD=．当AD=11时，x+=11，x1=1，x2=，经检验它们都是原方程的根，且符合题意，所以AG的长为1或．（3）当⊙E与⊙F外切时，EF=EG+FD=EG+FG，∴FD=FG，∵△DFG∽△EAG，∴∠E=∠AGE=∠FGD=∠GDF．∴AG=AE=2；∴⊙E的半径EG=，⊙F的半径FD=．当⊙E与⊙F内切时，EF=FD﹣EG，∴3=﹣，∵≠0，∴3=，∴x=1，∴⊙E的半径EG==，⊙F的半径FD=，∴⊙E的半径为2，⊙F的半径为4；或⊙E的半径为，⊙F的半径为4．点评：本题考查的是相似三角形的判定与性质、勾股定理及两圆相切的性质，涉及面较广，难度较大，在解（3）时要注意分两圆外切与内切两种情况进行讨论．21．如图，正方形网格中，每个小正方形的边长为1个单位，以O为原点建立平面直角坐标系，圆心为A（3，0）的⊙A被y轴截得的弦长BC=8．解答下列问题：（1）求⊙A 的半径；（2）请在图中将⊙A 先向上平移6 个单位，再向左平移8个单位得到⊙D，并写出圆心D的坐标；（3）观察你所画的图形，对⊙D 与⊙A 的位置关系作出合情的猜想，并直接写出你的结论．聪明的小伙伴，你完成整张试卷全部试题的解答后，如果还有时间对问题（3）的猜想结论给出证明，将酌情另加1～5分，并计入总分．考点：垂径定理；勾股定理；圆与圆的位置关系；坐标与图形变化-平移．专题：作图题．分析：（1）连接AB，根据垂径定理求出BO，根据勾股定理求出AB即可；（2）根据已知画出图形即可，根据平移规律求出D的坐标即可；（3）根据图形即可得出结论．解答：（1）解：∵x轴⊥y轴，A在x轴上，∴BO=CO=4，连接AB，由勾股定理得：AB==5，答：⊙A的半径是5．（2）解：如图：圆心D的坐标是（﹣5，6）．（3）解：⊙D 与⊙A 的位置关系是外切．点评：本题考查了对勾股定理，垂径定理，圆与圆的位置关系，坐标与图形变化﹣平移等知识点的应用，解此题的关键是根据题意画出图形，培养了学生分析问题的能力，同时也培养了学生观察图形的能力，题型较好，难度适中．22．如图，在平台上用直径为100mm的两根圆钢棒嵌在大型工件的两侧，测量大的圆形工件的直径，设两圆钢棒的外侧的距离为xmm，工件的直径为Dmm．（1）求出D（mm）与x（mm）之间的函数关系式；（2）当图形工件的直径D小于圆钢棒的直径时，上面所求得的D与x的函数关系式还是否仍然适用？请说明理由．考点：相切两圆的性质；勾股定理；切线的性质．专题：计算题．分析：（1）设三圆的圆心分别为A、B、C，连接AB，则AB过切点E，连接AC，则AC过切点F，连接BC，AN，AN交BC于M，由题意得出AB=AC=50+，BC=x﹣（50+50）=x﹣100，AN=﹣50，在△ABM中根据勾股定理得出D和x的方程，求出即可；（2）根据（1）结合图形仍能得出函数解析式，即可得出答案．解答：（1）解：如图设三圆的圆心分别为A、B、C，连接AB，则AB过切点E，连接AC，则AC过切点F，连接BC，AN，AN交BC于M，由题意得：AB=AC=50+，BC=x﹣（50+50）=x﹣100，AN=﹣50，∵AC=AB，AM⊥BC，∴BM=CM=（x﹣100）=x﹣50，在Rt△ABM中，由勾股定理得：AB2=AM2+BM2，∴=+，即D=x2﹣x+25．（2）解：当图形工件的直径D小于圆钢棒的直径时，上面所求得的D与x的函数关系式能仍然适用，因为那样时，三圆同时与平台相切，有两大圆都与小圆相切时，得出的方程与（1）中的方程相同，所有上面所求得的D与x的函数关系式能仍然适用．点评：本题考查了相切两圆的性质，切线的性质，勾股定理等知识点的应用，能根据题意得出方程是解此题的关键，主要考查学生的观察能力和构造直角三角形的能力，题目比较典型，有一定的难度．23．实验探究：同学们，你注意过烟盒里的香烟是如何摆放的吗？已知，一个烟盒的长为56mm，宽为22mm，高为87mm，一根烟的直径是8mm，若把20根香烟摆放在烟盒中，请你探究合理的摆放方法．考点：相切两圆的性质；勾股定理．专题：计算题．分析：分为两种情况：（1）并列摆放，根据烟的直径和烟盒的长、宽得出只能放14根；（2）若错位摆放，连接O1O2、O2O3、O3O1，解答：解：（1）若并列摆放，如图①，因为烟的直径为8mm，所以AD方向上能并排放（根）烟，而在AB方向上，因为8×3=24＞22，所以只能放两根，即烟盒只能放2×7=14（根）烟，此法不行．（2）若错位摆放，如图②，连接O1O2、O2O3、O3O1，则O2O3=O3O1=8mm，△O1O2O3为等腰三角形，过O3作O3E⊥O1O2，则E是O1O2的中点．=7（mm）．所以在Rt△O1O3E中，（mm）．故排列后中排所需空间长度=（mm），三排所需宽度为AB=22mm，故此摆放符合要求．点评：本题考查了对相切两圆的性质，勾股定理，等腰三角形性质的运用，主要培养学生分析问题和解决问题的能力，注意：分类讨论啊．。

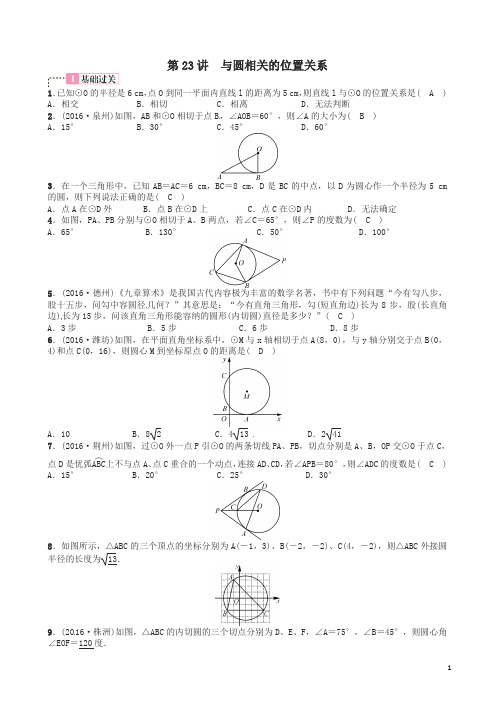
第23讲 与圆相关的位置关系1．已知⊙O 的半径是6 cm ，点O 到同一平面内直线l 的距离为5 cm ，则直线l 与⊙O 的位置关系是( A ) A ．相交 B ．相切 C ．相离 D ．无法判断2．(2016·泉州)如图，AB 和⊙O 相切于点B ，∠AOB ＝60°，则∠A 的大小为( B ) A ．15° B ．30° C ．45° D ．60°3．在一个三角形中，已知AB ＝AC ＝6 cm ，BC ＝8 cm ，D 是BC 的中点，以D 为圆心作一个半径为5 cm 的圆，则下列说法正确的是( C )A ．点A 在⊙D 外B ．点B 在⊙D 上C ．点C 在⊙D 内 D ．无法确定 4．如图，PA 、PB 分别与⊙O 相切于A 、B 两点，若∠C＝65°，则∠P 的度数为( C ) A ．65° B ．130° C ．50° D ．100°5．(2016·德州)《九章算术》是我国古代内容极为丰富的数学名著，书中有下列问题“今有勾八步，股十五步，问勾中容圆径几何？”其意思是：“今有直角三角形，勾(短直角边)长为8步，股(长直角边)长为15步，问该直角三角形能容纳的圆形(内切圆)直径是多少？”( C ) A ．3步 B ．5步 C ．6步 D ．8步6．(2016·潍坊)如图，在平面直角坐标系中，⊙M 与x 轴相切于点A(8，0)，与y 轴分别交于点B(0，4)和点C(0，16)，则圆心M 到坐标原点O 的距离是( D )A ．10B ．8 2C ．413D ．2417．(2016·荆州)如图，过⊙O 外一点P 引⊙O 的两条切线PA 、PB ，切点分别是A 、B ，OP 交⊙O 于点C ，点D 是优弧ABC ︵上不与点A 、点C 重合的一个动点，连接AD 、CD ，若∠APB＝80°，则∠ADC 的度数是( C ) A ．15° B ．20° C ．25° D ．30°8．如图所示，△ABC 的三个顶点的坐标分别为A(－1，3)、B(－2，－2)、C(4，－2)，则△ABC 外接圆9．(2016·株洲)如图，△ABC 的内切圆的三个切点分别为D 、E 、F ，∠A ＝75°，∠B ＝45°，则圆心角∠EOF＝120度．10．(2016·益阳)如图，四边形ABCD 内接于⊙O，AB 是直径，过C 点的切线与AB 的延长线交于P 点，若∠P＝40°，则∠D 的度数为115°．11．(2016·天津)在⊙O 中，AB 为直径，C 为⊙O 上一点．(1)如图1，过点C 作⊙O 的切线，与AB 的延长线相交于点P ，若∠CAB＝27°，求∠P 的大小； (2)如图2，D 为⊙O 上一点，且OD 经过AC 的中点E ，连接DC 并延长，与AB 的延长线相交于点P ，若∠CAB ＝10°，求∠P 的大小．解：(1)连接OC ，∵⊙O 与PC 相切于点C ， ∴OC ⊥PC ，即∠OCP＝90°. ∵∠CAB ＝27°，∴∠COB ＝2∠CAB＝54°.在Rt △OPC 中，∠P ＋∠COP＝90°， ∴∠P ＝90°－∠COP＝36°. (2)∵E 为AC 的中点，∴OD ⊥AC ，即∠AEO＝90°.在Rt △AOE 中，由∠EAO＝10°， 得∠AOE＝90°－∠EAO＝80°.∴∠ACD ＝12∠AOD＝40°.∵∠ACD 是△ACP 的一个外角， ∴∠P ＝∠ACD－∠CAP＝30°.12．(2016·永州)如图，△ABC 是⊙O 的内接三角形，AB 为直径，过点B 的切线与AC 的延长线交于点D ，E 是BD 中点，连接CE.(1)求证：CE 是⊙O 的切线；(2)若AC ＝4，BC ＝2，求BD 和CE 的长．解：(1)证明：连接OC. ∵BD 是⊙O 的切线，∴∠ABD ＝90°，即∠OBC ＋∠DBC＝90°. ∵AB 是⊙O 的直径，∴∠ACB ＝90°，∠BCD ＝90°. ∵E 是BD 中点，∴CE ＝12BD ＝BE.∴∠BCE ＝∠CBE. ∵OB ＝OC ，∴∠OCB ＝∠OBC.∵∠OBC ＋∠DBC＝90°， ∴∠BCE ＋∠BCO＝90°， 即∠OCE＝90°. ∴CE 是⊙O 的切线． (2)∵∠ACB＝90°，∴AB ＝AC 2＋BC 2＝42＋22＝2 5.∵tanA ＝BD AB ＝BC AC ＝24＝12，∴BD ＝12AB ＝ 5.∴CE ＝12BD ＝52.13．(2016·宜昌)在公园的O 处附近有E 、F 、G 、H 四棵树，位置如图所示(图中小正方形的边长均相等)．现计划修建一座以O 为圆心，OA 为半径的圆形水池，要求池中不留树木，则E 、F 、G 、H 四棵树中需要被移除的为( A )A ．E 、F 、GB ．F 、G 、HC ．G 、H 、ED ．H 、E 、F14．(2016·鄂州)如图所示，AB 是⊙O 的直径，AM 、BN 是⊙O 的两条切线，D 、C 分别在AM 、BN 上，DC 切⊙O 于点E.连接OD 、OC 、BE 、AE ，BE 与OC 相交于点P ，AE 与OD 相交于点Q ，已知AD ＝4，BC ＝9.以下结论：①⊙O 的半径为132；②OD∥B E ；③PB＝181313；④tan ∠CEP ＝23.其中正确结论有( B )A ．1个B ．2个C ．3个D ．4个15．(2016·武汉)如图，点C 在以AB 为直径的⊙O 上，AD 与过点C 的切线垂直，垂足为点D ，AD 交⊙O 于点E.(1)求证：AC 平分∠DAB；(2)连接BE 交AC 于点F ，若cos ∠CAD ＝45，求AFFC的值．解：(1)证明：连接OC ，由题意知OC⊥CD.又∵AD⊥CD，∴OC ∥AD.∴∠OCA ＝∠DAC. 又∵∠OCA＝∠OAC，∴∠DAC ＝∠OAC，即AC 平分∠DAB.(2)设AC ＝5x ，AD ＝4x ， 则DC ＝3x ，BE 与CO 相交于点G ，连接BC. ∵∠BEA ＝90°，∴四边形DEGC 是矩形． ∴EG ＝BG ＝3x. ∵∠CBG ＝∠CAD， ∴BG BC ＝45.∴BC＝154x. ∴CG ＝94x.∵AE ＝AD －DE ＝AD －CG ＝74x.由(1)知AD∥OC，△AEF ∽△CGF.∴AF CF ＝AE CG ＝74x94x ＝79.16．(2016·德州)如图，⊙O 是△ABC 的外接圆，AE 平分∠BAC 交⊙O 于点E ，交BC 于点D ，过点E 作直线l∥B C.(1)判断直线l 与⊙O 的位置关系，并说明理由；(2)若∠ABC 的平分线BF 交AD 于点F ，求证：BE ＝EF ； (3)在(2)的条件下，若DE ＝4，DF ＝3，求AF 的长．解：(1)直线l 与⊙O 相切．理由：连接OE 、OB 、OC. ∵AE 平分∠BAC， ∴∠BAE ＝∠CAE. ∴BE ︵＝CE ︵.∴∠BOE ＝∠COE. 又∵OB＝OC ， ∴OE ⊥BC. ∵l ∥BC ， ∴OE ⊥l.∴直线l 与⊙O 相切．(2)证明：∵BF 平分∠ABC， ∴∠ABF ＝∠CBF.又∵∠CBE＝∠CAE＝∠BAE， ∴∠CBE ＋∠CBF＝∠BAE＋∠ABF. 又∵∠EFB＝∠BAE＋∠ABF， ∴∠EBF ＝∠EFB. ∴BE ＝EF.(3)由(2)得BE ＝EF ＝DE ＋DF ＝7. ∵∠DBE ＝∠BAE，∠DEB ＝∠BEA， ∴△BED ∽△AEB. ∴DE BE ＝BE AE ，即47＝7AE. 解得AE ＝494.∴AF ＝AE －EF ＝494－7＝214.17．如图，直线AB 与⊙O 相切于点A ，弦CD∥AB，E ，F 为圆上的两点，且∠CDE＝∠ADF.若⊙O 的半径为52，CD ＝4，则弦EF 的长为( B )A ．4B ．2 5C ．5D ．6。

中考复习之圆与圆的位置关系一、选择题：1.如果两圆的半径长分别为 6 和2，圆心距为 3，那么这两个圆的位置关系是【】A.外离B．相切C．相交D．内含2.若两圆的半径分别为 2cm 和6cm，圆心距为 4cm，则这两圆的位置关系是【】A.内含 B．内切 C．外切 D．外离3.如图，用邻边分别为 a，b（a＜b）的矩形硬纸板裁出以 a 为直径的两个半圆，再裁出与矩形的较长边、两个半圆均相切的两个小圆．把半圆作为圆锥形圣诞帽的侧面，小圆恰好能作为底面，从而做成两个圣诞帽（拼接处材料忽略不计），则 a 与b 满足的关系式是【】A．b= a B．b= 5+1a2C．b=5a2D．b= 2a4.已知⊙O1与⊙O2外切，O1O2=8cm，⊙O1的半径为5cm，则⊙O2的半径是【】A.13cm.B. 8cmC. 6cmD. 3cm5.已知两圆半径分别为7，3，圆心距为4，则这两圆的位置关系为【】A.外离B.内切C.相交D.内含6.若⊙O1，⊙O2的半径是r1=2, r2=4，圆心距d=5，则这两个圆的位置关系是【】A.内切B.相交C.外切D.外离7.已知⊙O1、⊙O2的半径分别为3cm、5cm，且它们的圆心距为8cm，则⊙O1与⊙O2的位置关系是【】A.外切B．相交C．内切D．内含8.⊙O1和⊙O2的半径分别是3cm 和4cm，如果O1O2＝7cm，则这两圆的位置关系是【】A.内含B．相交C．外切D．外离9.若两圆的半径分别为2 和4，且圆心距为7，则两圆的位置关系为【】A.外切B. 内切C. 外离D. 相交10.如图，平面直角坐标系中，⊙O半径长为 1.点⊙P（a,0），⊙P的半径长为 2，把⊙P向左平移，当⊙P与⊙O相切时，a 的值为【】（A）3 （B）1 （C）1，3 （D）±1，±311.已知两圆外切，圆心距为5cm，若其中一个圆的半径是3cm，则另一个圆的半径是【】A.8cm B．5cm C．3cm D．2cm12.⊙O1的半径为3 厘米，⊙O2的半径为2 厘米，圆心距O1O2=5 厘米，这两圆的位置关系是【】A.内含B．内切C．相交D．外切13.已知两圆的半径分别为1 和3，当这两圆内含时，圆心距d 的范围是【】A. 0<d<2B. 1<d<2C. 0<d<3D. 0≤d<214.圆心距为2 的两圆相切，其中一个圆的半径为1，则另一个圆的半径为【】(A)1 (B)3 (C)1 或2 (D)1 或315.第三十奥运会将于 2012 年7 月27 日在英国伦敦开幕，奥运会旗图案有五个圆环组成，下图也是一幅五环图案，在这个五个圆中，不存在的位置关系是【】 A 外离 B 内切 C 外切 D 相交16.已知两圆相外切，连心线长度是 10 厘米，其中一圆的半径为 6 厘米，则另一圆的半径是【】A．16 厘米B．10 厘米C．6 厘米D．4 厘米17.如果两圆的半径分别为4 和6，圆心距为10，那么这两圆的位置关系是【】A.内含B．外离C．相交D．外切18.已知⊙O1与⊙O2的半径分别为4 和6，O1O2＝2，则⊙O1与⊙O2的位置关系是【】A.内切B．相交C．外切D．外离19.如图，⊙O1，⊙O，⊙O2的半径均为2cm，⊙O3，⊙O4的半径均为1cm，⊙O与其他4个圆均相外切，图形既关于O1O2所在直线对称，又关于O3O4所在直线对称，则四边形O1O4O2O3的面积为【】A．12cm2B．24cm2C．36cm2D．48cm220.已知两圆的半径分别是3 和4，圆心距的长为1，则两圆的位置关系为：【】A.外离B．相交C．内切D．外切21.已知两圆半径为5cm 和3cm，圆心距为3cm，则两圆的位置关系是【】A.相交B．内含C．内切D．外切22.定圆O 的半径是4cm，动圆P 的半径是2cm，动圆在直线l 上移动，当两圆相切时，OP 的值是【】A.2cm 或6cm B．2cm C．4cmD．6cm23.若两圆的半径是方程x2﹣5x+6=0 的两个根，且圆心距是5，则这两圆的位置关系是【】A.内切B．相交C．外切D．外离24.已知两圆的直径分别为2cm 和4cm，圆心距为3cm，则这两个圆的位置关系是【】A.相交B．外切C．外离D．内含25.已知两圆的半径分别为3cm、4cm，圆心距为8cm，则两圆的位置关系是【】A.外离B．相切C．相交D．内含二、填空题：1.半径分别为3cm 和4cm 的两圆内切，这两圆的圆心距为cm．2.如图，⊙M与⊙N外切，MN＝10cm，若⊙M的半径为6cm，⊙N的半径为cm。

专题23 圆的有关位置关系☞解读考点☞2年中考【2015年题组】1．（2015贵港）如图，已知P是⊙O外一点，Q是⊙O上的动点，线段PQ的中点为M，连接OP，OM．若⊙O 的半径为2，OP=4，则线段OM的最小值是（）A．0 B．1 C．2 D．3【答案】B．考点：1．点与圆的位置关系；2．三角形中位线定理；3．最值问题；4．轨迹．2．（2015湘西州）⊙O的半径为5cm，点A到圆心O的距离OA=3cm，则点A与圆O的位置关系为（）A．点A在圆上 B．点A在圆内 C．点A在圆外 D．无法确定【答案】B．【解析】试题分析：∵⊙O的半径为5cm，点A到圆心O的距离为3cm，即点A到圆心O的距离小于圆的半径，∴点A在⊙O内．故选B．考点：点与圆的位置关系．3．（2015泸州）如图，PA、PB分别与⊙O相切于A、B两点，若∠C=65°，则∠P的度数为（）A．65° B．130° C．50° D．100°【答案】C．【解析】试题分析：∵PA、PB是⊙O的切线，∴OA⊥AP，OB⊥BP，∴∠OAP=∠OBP=90°，又∵∠AOB=2∠C=130°，则∠P=360°﹣（90°+90°+130°）=50°．故选C．考点：切线的性质．4．（2015宜昌）如图，圆形铁片与直角三角尺、直尺紧靠在一起平放在桌面上．已知铁片的圆心为O，三角尺的直角顶点C落在直尺的10cm处，铁片与直尺的唯一公共点A落在直尺的14cm处，铁片与三角尺的唯一公共点为B，下列说法错误的是（）A．圆形铁片的半径是4cm B．四边形AOBC为正方形C．弧AB的长度为4πcm D．扇形OAB的面积是4πcm2【答案】C．考点：1．切线的性质；2．正方形的判定与性质；3．弧长的计算；4．扇形面积的计算；5．应用题；6．综合题．5．（2015襄阳）点O是△ABC的外心，若∠BOC=80°，则∠BAC的度数为（）A．40° B．100° C．40°或140° D．40°或100°【答案】C．【解析】试题分析：如图所示：∵O是△ABC的外心，∠BOC=80°，∴∠A=40°，∠A′=140°，故∠BAC的度数为：40°或140°．故选C．考点：1．三角形的外接圆与外心；2．圆周角定理；3．分类讨论．6．（2015齐齐哈尔）如图，两个同心圆，大圆的半径为5，小圆的半径为3，若大圆的弦AB与小圆有公共点，则弦AB的取值范围是（）A．8≤AB≤10 B．8＜AB≤10 C．4≤AB≤5 D．4＜AB≤5【答案】A．考点：1．直线与圆的位置关系；2．勾股定理；3．垂径定理．7．（2015河池）我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”．如图，直线l：y kx=+与x轴、y轴分别交于A、B，∠OAB=30°，点P在x轴上，⊙P与l相切，当P在线段OA上运动时，使得⊙P成为整圆的点P个数是（）A．6 B．8 C．10 D．12【答案】A．【解析】试题分析：∵直线l：y kx=+与x轴、y轴分别交于A、B，∴B（0，，∴OB=RT△AOB中，∠OAB=30°，∴OA，∵⊙P与l相切，设切点为M，连接PM，则PM⊥AB，∴PM=12 PA，设P（x，0），∴PA=12﹣x，∴⊙P的半径PM=12PA=162x-，∵x为整数，PM为整数，∴x可以取0，2，4，6，8，10，共6个数，∴使得⊙P成为整圆的点P个数是6．故选A．考点：1．切线的性质；2．一次函数图象上点的坐标特征；3．新定义；4．动点型；5．综合题．8．（2015贺州）如图，BC是⊙O的直径，AD是⊙O的切线，切点为D，AD与CB的延长线交于点A，∠C=30°，给出下面四个结论：①AD=DC；②AB=BD；③AB=12BC；④BD=CD，其中正确的个数为（）A．4个 B．3个 C．2个 D．1个【答案】B．故选B．考点：切线的性质．9．（2015南京）如图，在矩形ABCD 中，AB =4，AD =5，AD ，AB ，BC 分别与⊙O 相切于E ，F ，G 三点，过点D 作⊙O 的切线BC 于点M ，切点为N ，则DM 的长为（ ）A ．133 B ．92 C ．【答案】A ．考点：1．切线的性质；2．矩形的性质；3．综合题．10．（2015天水）相切两圆的半径分别是5和3，则该两圆的圆心距是 ． 【答案】2或8． 【解析】试题分析：若两圆内切，圆心距为5﹣3=2；若两圆外切，圆心距为5+3=8，故答案为：2或8． 考点：1．圆与圆的位置关系；2．分类讨论．11．（2015上海市）在矩形ABCD 中，AB =5，BC =12，点A 在⊙B 上，如果⊙D 与⊙B 相交，且点B 在⊙D 内，那么⊙D 的半径长可以等于 ．（只需写出一个符合要求的数） 【答案】14（答案不唯一）．考点：1．圆与圆的位置关系；2．点与圆的位置关系；3．开放型．12．（2015盐城）如图，在矩形ABCD中，AB=4，AD=3，以顶点D为圆心作半径为r的圆，若要求另外三个顶点A、B、C中至少有一个点在圆内，且至少有一个点在圆外，则r的取值范围是．【答案】3＜r＜5．【解析】试题分析：在直角△ABD中，CD=AB=4，AD=3，则BD．由图可知3＜r＜5．故答案为：3＜r＜5．考点：点与圆的位置关系．13．（2015上海市）在矩形ABCD中，AB=5，BC=12，点A在⊙B上，如果⊙D与⊙B相交，且点B在⊙D内，那么⊙D的半径长可以等于．（只需写出一个符合要求的数）【答案】14（答案不唯一）．【解析】试题分析：∵矩形ABCD中，AB=5，BC=12，∴AC=BD=13，∵点A在⊙B上，∴⊙B的半径为5，∵如果⊙D 与⊙B相交，∴⊙D的半径R满足8＜R＜18，∵点B在⊙D内，∴R＞13，∴13＜R＜18，∴14符合要求，故答案为：14（答案不唯一）．考点：1．圆与圆的位置关系；2．点与圆的位置关系；3．开放型．14．（2015义乌）在Rt△ABC中，∠C=90°，BC=3，AC=4，点P在以C为圆心，5为半径的圆上，连结PA，PB．若PB=4，则PA的长为．【答案】3考点：1．点与圆的位置关系；2．勾股定理；3．垂径定理；4．分类讨论．15．（2015徐州）如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，若∠C=20°，则∠CDA= °．【答案】125．【解析】试题分析：连接OD，则∠ODC=90°，∠COD=70°，∵OA=OD，∴∠ODA=∠A=12∠COD=35°，∴∠CDA=∠CDO+∠ODA=90°+35°=125°，故答案为：125．考点：切线的性质．16．（2015镇江）如图，AB是⊙O的直径，OA=1，AC是⊙O的弦，过点C的切线交AB的延长线于点D，若BD1，则∠ACD= °．【答案】112.5．考点：切线的性质．17．（2015贵阳）小明把半径为1的光盘、直尺和三角尺形状的纸片按如图所示放置于桌面上，此时，光盘与AB，CD分别相切于点N，M．现从如图所示的位置开始，将光盘在直尺边上沿着CD向右滚动到再次与AB 相切时，光盘的圆心经过的距离是．．【答案】3考点：1．切线的性质；2．轨迹；3．应用题；4．综合题．18．（2015泰安）如图，AB是⊙O的直径，且经过弦CD的中点H，过CD延长线上一点E作⊙O的切线，切点为F．若∠ACF=65°，则∠E= ．【答案】50°．【解析】，∵EF 试题分析：连接DF，连接AF交CE于G，∵AB是⊙O的直径，且经过弦CD的中点H，∴AC AD是⊙O的切线，∴∠GFE=∠GFD+∠DFE=∠ACF=65°，∵∠FGD=∠FCD+∠CFA，∵∠DFE=∠DCF，∠GFD=∠AFC，∠EFG=∠EGF=65°，∴∠E=180°﹣∠EFG﹣∠EGF=50°，故答案为：50°．考点：切线的性质．19．（2015鄂州）已知点P是半径为1的⊙O外一点，PA切⊙O于点A，且PA=1，AB是⊙O的弦，AB连接PB，则PB= ．【答案】1考点：1．切线的性质；2．分类讨论；3．综合题．20．（2015广元）如图，在⊙O中，AB是直径，点D是⊙O上一点，点C是AD的中点，弦CE⊥AB于点E，过点D的切线交EC的延长线于点G，连接AD，分别交CF、BC于点P、Q，连接AC．给出下列结论：①∠BAD=∠ABC；②GP=GD；③点P是△ACQ的外心．其中正确结论是________ （只需填写序号）．【答案】②③．则正确的选项序号有②③．故答案为：②③．考点：1．切线的性质；2．圆周角定理；3．三角形的外接圆与外心；4．相似三角形的判定与性质；5．压轴题．21．（2015荆州）如图，OA在x轴上，OB在y轴上，OA=8，AB=10，点C在边OA上，AC=2，⊙P的圆心P在线段BC上，且⊙P与边AB，AO都相切．若反比例函数kyx=（0k≠）的图象经过圆心P，则k= ．【答案】﹣5．考点：1．切线的性质；2．一次函数图象上点的坐标特征；3．反比例函数图象上点的坐标特征；4．综合题；5．压轴题．22．（2015杭州）如图1，⊙O的半径为r（r＞0），若点P′在射线OP上，满足OP′•OP=2r，则称点P′是点P关于⊙O的“反演点”．如图2，⊙O的半径为4，点B在⊙O上，∠BOA=60°，OA=8，若点A′，B′分别是点A，B关于⊙O的反演点，求A′B′的长．【答案】【解析】考点：1．点与圆的位置关系；2．勾股定理；3．新定义．23．（2015北海）如图，AB、CD为⊙O的直径，弦AE∥CD，连接BE交CD于点F，过点E作直线EP与CD的延长线交于点P，使∠PED=∠C．（1）求证：PE是⊙O的切线；（2）求证：ED平分∠BEP；（3）若⊙O的半径为5，CF=2EF，求PD的长．【答案】（1）证明见试题解析；（2）证明见试题解析；（3）103．【解析】试题分析：（1）如图，连接OE，证明OE⊥PE即可得出PE是⊙O的切线；（2）由圆周角定理得到∠AEB=∠CED=90°，进而得到∠3=∠4，结合已知条件证得结论；（3）设EF=x，则CF=2x，在RT△OEF中，根据勾股定理求出EF的长，进而求得BE，CF的长，在RT△AEB 中，根据勾股定理求出AE的长，然后根据△AEB∽△EFP，求出PF的长，即可求得PD的长．考点：1．切线的判定；2．相似三角形的判定与性质；3．圆的综合题；4．压轴题．24．（2015南宁）如图，AB 是⊙O 的直径，C ，G 是⊙O 上两点，且AC =CG ，过点C 的直线CD ⊥BG 于点D ，交BA 的延长线于点E ，连接BC ，交OD 于点F ．（1）求证：CD 是⊙O 的切线． （2）若32FD OF ，求∠E 的度数． （3）连接AD ，在（2）的条件下，若CD =3，求AD 的长．【答案】（1）证明见试题解析；（2）30°；（3 【解析】试题解析：（1）如图1，连接OC ，AC ，CG ，∵AC =CG ，∴AC CG =，∴∠ABC =∠CBG ，∵OC =OB ，∴∠OCB =∠OBC ，∴∠OCB =∠CBG ，∴OC ∥BG ，∵CD ⊥BG ，∴OC ⊥CD ，∴CD 是⊙O 的切线； （2）∵OC ∥BD ，∴△OCF ∽△BDF ，△EOC ∽△EBD ，∴23OC OF BD DF ==，∴23OC OE BD BE ==，∵OA =OB ，∴AE =OA =OB ，∴OC =12OE ，∵∠ECO =90°，∴∠E =30°；（3）如图2，过A 作AH ⊥DE 于H ，∵∠E =30°，∴∠EBD =60°，∴∠CBD =12∠EBD =30°，∵CD ∴BD =3，DE =，BE =6，∴AE =13BE =2，∴AH =1，∴EH =，∴DH =，在R t △DAH 中，AD考点：1．圆的综合题；2．切线的判定与性质；3．相似三角形的判定与性质；4．压轴题．25．（2015桂林）如图，四边形ABCD 是⊙O 的内接正方形，AB =4，PC 、PD 是⊙O 的两条切线，C 、D 为切点． （1）如图1，求⊙O 的半径；（2）如图1，若点E 是BC 的中点，连接PE ，求PE 的长度；（3）如图2，若点M 是BC 边上任意一点（不含B 、C ），以点M 为直角顶点，在BC 的上方作∠AMN =90°，交直线CP 于点N ，求证：AM =MN ．【答案】（1）（2）（3）证明见试题解析．（2）如图1，连接EO，OP，∵点E是BC的中点，∴OE⊥BC，∠OCE=45°，则∠E0P=90°，∴EO=EC=2，OP=4，∴PE=（3）如图2，在AB上截取BF=BM，∵AB=BC，BF=BM，∴AF=MC，∠BFM=∠BMF=45°，∵∠AMN=90°，∴∠AMF+∠NMC=45°，∠FAM+∠AMF=45°，∴∠FAM=∠NMC，∵由（1）得：PD=PC，∠DPC=90°，∴∠DCP=45°，∴∠MCN=135°，∵∠AFM=180°﹣∠BFM=135°，在△AFM和△CMN中，∵∠FAM=∠CMN，AF=MC，∠AFM=∠MCN，∴△AFM≌△CMN（ASA），∴AM=MN．考点：1．圆的综合题；2．切线的性质；3．正方形的判定与性质；4．全等三角形的判定与性质；5．压轴题．26．（2015柳州）如图，已知抛物线21(76)2y x x =--+的顶点坐标为M ，与x 轴相交于A ，B 两点（点B 在点A 的右侧），与y 轴相交于点C ．（1）用配方法将抛物线的解析式化为顶点式：2()y a x h k =-+（0a ≠），并指出顶点M 的坐标； （2）在抛物线的对称轴上找点R ，使得CR +AR 的值最小，并求出其最小值和点R 的坐标； （3）以AB 为直径作⊙N 交抛物线于点P （点P 在对称轴的左侧），求证：直线MP 是⊙N 的切线．【答案】（1）21725()228y x =--+，M （72，258）；（2），（72，54-）；（3）证明见试题解析．试题解析：（1）∵21(76)2y x x =--+=21725()228x --+，∴抛物线的解析式化为顶点式为：21725()228y x =--+，顶点M 的坐标是（72，258）；（2）∵21(76)2y x x =--+，∴当y =0时，21(76)02x x --+=，解得x =1或6，∴A （1，0），B （6，0），∵x =0时，y =﹣3，∴C （0，﹣3）．连接BC ，则BC 与对称轴x =72的交点为R ，连接AR ，则CR +AR =CR +BR =BC ，根据两点之间线段最短可知此时CR+AR的值最小，最小值为BC．设直线BC的解析式为考点：1．二次函数综合题；2．最值问题；3．切线的判定；4．压轴题．【2014年题组】1．（2014·扬州）如图，圆与圆的位置关系没有（）A．相交 B．相切 C．内含 D．外离[【答案】A ．考点：圆与圆的位置关系．2．（2014· 山东省淄博市）如图，直线AB 与⊙O 相切于点A ，弦CD ∥AB ，E ，F 为圆上的两点，且∠CDE =∠ADF ．若⊙O 的半径为52，CD =4，则弦EF 的长为（ ）A ． 4B ．C ． 5D ． 6【答案】B ． 【解析】试题分析：连接OA ，并反向延长交CD 于点H ，连接OC ，∵直线AB 与⊙O 相切于点A ，∴OA ⊥AB ，∵弦CD ∥AB ，∴AH ⊥CD ，∴CH =12CD =12×4=2，∵⊙O 的半径为52，∴OA =OC =52，∴OH =32=，∴AH =OA +OH =52+32=4，∴AC ==．∵∠CDE =∠ADF ，∴CE AF =，∴EF AC =，∴EF =AC =B ．考点：切线的性质．3．（2014·四川省广安市）如图，矩形ABCD 的长为6，宽为3，点O 1为矩形的中心，⊙O 2的半径为1，O 1O 2⊥AB 于点P ，O 1O 2=6．若⊙O 2绕点P 按顺时针方向旋转360°，在旋转过程中，⊙O 2与矩形的边只有一个公共点的情况一共出现（ ）A ． 3次B ．4次C ．5次D ．6次【答案】B ．考点：直线与圆的位置关系．4．（2014·泸州）如图，⊙1O ，⊙2O 的圆心1O ，2O 都在直线l 上，且半径分别为2cm ，3cm ，12O O 8cm ．若⊙1O 以1cm /s 的速度沿直线l 向右匀速运动（⊙2O 保持静止），则在7s 时刻⊙1O 与⊙2O 的位置关系是（ ）A ．外切B ．相交C ．内含D ．内切 【答案】D ． 【解析】试题分析：∵O1O2=8cm，⊙O1以1cm/s的速度沿直线l向右运动，7s后停止运动，∴7s后两圆的圆心距为：1cm．根据两圆的位置关系的判定：外切（两圆圆心距离等于两圆半径之和），内切（两圆圆心距离等于两圆半径之差），外离（两圆圆心距离大于两圆半径之和），相交（两圆圆心距离小于两圆半径之和大于两圆半径之差），内含（两圆圆心距离小于两圆半径之差）．因此，∵⊙O1和⊙O2的半径分别为2㎝和3㎝，且O1O2＝12㎝，∴3－2=1，即两圆圆心距离等于两圆半径之差．∴⊙O1和⊙O2的位置关系是内切．故选D．考点：1．面动平移问题；2．两圆的位置关系．5．（2014·黔西南）已知两圆半径分别为3、5，圆心距为8，则这两圆的位置关系为（）A．外离 B．内含 C．相交 D．外切【答案】D．考点：圆与圆的位置关系．6．（2014·桂林）两圆的半径分别为2和3，圆心距为7，则这两圆的位置关系为（）A．外离 B．外切 C．相交 D．内切【答案】A．【解析】试题分析：根据两圆的位置关系的判定：外切（两圆圆心距离等于两圆半径之和），内切（两圆圆心距离等于两圆半径之差），外离（两圆圆心距离大于两圆半径之和），相交（两圆圆心距离小于两圆半径之和大于两圆半径之差），内含（两圆圆心距离小于两圆半径之差）．因此，∵两圆的半径分别为2和3，圆心距为 ，即两圆圆心距离大于两圆半径之和．7，∴23<7∴这两圆的位置关系为外离．故选A．考点：两圆的位置关系．7．（2014·北海）若两圆的半径分别是1cm和4cm，圆心距为5cm，则这两圆的位置关系是（）A．内切 B．相交 C．外切 D．外离【答案】C．考点：两圆的位置关系．8．（2014·甘肃省白银市）已知⊙O的半径是6cm，点O到同一平面内直线l的距离为5cm，则直线l与⊙O 的位置关系是（）A．相交 B．相切 C．相离 D．无法判断【答案】A．【解析】试题分析：设圆的半径为r，点O到直线l的距离为d，∵d=5，r=6，∴d＜r，∴直线l与圆相交．故选A．考点：直线与圆的位置关系．9．（2014·资阳）已知⊙O1与⊙O2的圆心距为6，两圆的半径分别是方程x2﹣5x+5=0的两个根，则⊙O1与⊙O2的位置关系是．【答案】相离．【解析】试题分析：∵两圆的半径分别是方程x2﹣5x+5=0的两个根，∴两半径之和为5，∵⊙O1与⊙O2的圆心距为6，∴6＞5，∴⊙O1与⊙O2的位置关系是相离．故答案为：相离．考点：1．根与系数的关系；2．圆与圆的位置关系．10．（2014·宜宾）如图，已知AB为⊙O的直径，AB=2，AD和BE是圆O的两条切线，A、B为切点，过圆上一点C作⊙O的切线CF，分别交AD、BE于点M、N，连接AC、CB，若∠ABC=30°，则AM= ．考点：切线的性质．11．（2014·福建省莆田市）如图，AB是⊙O的直径，C是⊙O上的一点，过点A作AD⊥CD于点D，交⊙O 于点E，且BC CE=（1）求证：CD是⊙O的切线；（2）若tan∠CAB=34，BC=3，求DE的长．【答案】（1）证明见解析；（2）95．【解析】试题分析：（1）连结OC，由BC CE=，根据圆周角定理得∠1=∠2，而∠1=∠OCA，则∠2=∠OCA，则可判断OC∥AD，由于AD⊥CD，所以OC⊥CD，然后根据切线的判定定理得到CD是⊙O的切线；（2）连结BE交OC于F，由AB是⊙O的直径得∠ACB=90°，在Rt△ACB中，根据正切的定义得AC=4，考点：切线的判定．☞考点归纳归纳 1：点和圆的位置关系基础知识归纳：设⊙O的半径是r，点P到圆心O的距离为d，则有：d<r点P在⊙O内；d=r点P在⊙O上；d>r点P在⊙O外．基本方法归纳：点的位置可以确定该点到圆心距离与半径的关系，反过来已知点到圆心距离与半径的关系可以确定该点与圆的位置关系．注意问题归纳：符号“⇔”读作“等价于”，它表示从符号“⇔”的左端可以得到右端，从右端也可以得到左端．【例1】在数轴上，点A所表示的实数为3，点B所表示的实数为a，⊙A的半径为2，下列说法中不正确的是（）A．当a＜5时，点B在⊙A内B．当1＜a＜5时，点B在⊙A内C．当a＜1时，点B在⊙A外D．当a＞5时，点B在⊙A外【答案】A．考点：点与圆的位置关系．归纳 2：直线与圆的位置关系基础知识归纳：直线和圆有三种位置关系，具体如下：（1）相交：直线和圆有两个公共点时，叫做直线和圆相交，这时直线叫做圆的割线，公共点叫做交点；（2）相切：直线和圆有唯一公共点时，叫做直线和圆相切，这时直线叫做圆的切线，（3）相离：直线和圆没有公共点时，叫做直线和圆相离．如果⊙O的半径为r，圆心O到直线l的距离为d，那么：直线l与⊙O相交d<r；直线l与⊙O相切d=r；直线l与⊙O相离d>r；注意问题归纳：直线与圆的位置关系，解题的关键是了解直线与圆的位置关系与d与r的数量关系．【例2】已知⊙O的半径r=3，设圆心O到一条直线的距离为d，圆上到这条直线的距离为2的点的个数为m，给出下列命题：①若d＞5，则m=0；②若d=5，则m=1；③若1＜d＜5，则m=3；④若d=1，则m=2；⑤若d＜1，则m=4．其中正确命题的个数是（）A． 1 B． 2 C． 4 D． 5【答案】C．考点：直线与圆的位置关系．归纳 3：圆和圆的位置关系基础知识归纳：如果两个圆没有公共点，那么就说这两个圆相离，相离分为外离和内含两种．如果两个圆只有一个公共点，那么就说这两个圆相切，相切分为外切和内切两种．如果两个圆有两个公共点，那么就说这两个圆相交．基本方法归纳：设两圆的半径分别为R和r，圆心距为d，那么两圆外离d>R+r两圆外切d=R+r两圆相交R-r<d<R+r（R≥r）两圆内切d=R-r（R>r）两圆内含d<R-r（R>r）【例3】如图，当半径分别是5和r的两圆⊙O1和⊙O2外切时，它们的圆心距O1O2=8，则⊙O2的半径r为（）A． 12 B． 8 C． 5 D． 3【答案】D．【解析】试题分析：根据两圆外切，圆心距等于两圆半径之和，得该圆的半径是8-5=3．故选D．考点：圆与圆的位置关系．☞1年模拟1．（2015届广东省湛江第二中学校级模拟）已知⊙O的半径为2，圆心O到直线l的距离PO=1，则直线l 与⊙O的位置关系是（）A．相切 B．相离 C．相交 D．无法判断【答案】C．考点：直线与圆的位置关系．2．（2015届江苏省盐城校级模拟）在数轴上，点A所表示的实数为3，点B所表示的实数为a，⊙ A的半径为2，下列说法中不正确的是（）A．当a＜5时，点B在⊙A内B．当1＜a＜5时，点B在⊙A内C．当a＜1时，点B在⊙A外D．当a＞5时，点B在⊙A外【答案】A．【解析】试题分析：由于圆心A在数轴上的坐标为3，圆的半径为2，∴当d=r时，⊙A与数轴交于两点：1、5，故当a=1、5时点B在⊙A上；当d＜r即当1＜a＜5时，点B在⊙A内；当d＞r即当a＜1或a＞5时，点B在⊙A外．由以上结论可知选项B、C、D正确，选项A错误．故选A．考点：点与圆的位置关系．3．（2015届四川省广安市校级模拟）如图所示，△ABC 的内切圆⊙O 与AB 、BC 、AC 分别相切于点D 、E 、F ，若∠DEF =52°，则∠A 的度数是【答案】76°．考点：1三角形的内切圆与内心；2．圆周角定理；3．切线的性质．4．（2015届湖南省长沙麓山国际等四校联考）Rt ABC ∆中，90,6,8C AC BC ∠===．则ABC ∆的内切圆半径r =______． 【答案】2． 【解析】试题分析：利用面积分割法可得出直角三角形内切圆的半径r 与三角形的三边之间的关系为：cb a abr ++=其中：a ，b 是直角三角形的两条直角边，c 是直角三角形的斜边由勾股定理可求出斜边AB =10 所以内切圆半径2108686=++⨯=r考点：直角三角形的内切圆和内心．5．（2015届北京市怀柔区一模）已知两圆的半径分别为2cm 和4cm ，它们的圆心距为6cm ，则这两个圆的位置关系是 ． 【答案】外切． 【解析】试题分析：圆心距6=两个半径之和，所以这两个圆相外切． 考点：圆有关的位置关系．6．（2015届河南省三门峡市一模）两圆的圆心距d =6，两圆的半径长分别是方程01272=+-x x 的两根，则这两个圆的位置关系是 ． 【答案】内切．考点：1．圆与圆的位置关系；2．解一元二次方程-因式分解法．7．（2015届江西省南昌市一模）如图，两圆圆心相同，大圆的弦AB 与小圆相切，AB =2n ，则图中阴影部分的面积是（ ）．A ．n 2π B .2n 2π C .4n 2π D .8n 2π 【答案】A ． 【解析】试题分析：设AB 于小圆切于点C ，连接OC ，OB ．∵AB 于小圆切于点C ，∴OC ⊥AB ，∴BC =AC =12AB =12×2n =n ∵圆环（阴影）的面积=π•OB 2-π•OC 2=π（OB 2-OC 2） 又∵直角△OBC 中，OB 2=OC 2+BC 2∴圆环（阴影）的面积=π•OB 2-π•OC 2=π（OB 2-OC 2）=π•BC 2=n 2π． 故选A ．考点：1．垂径定理的应用；2．切线的性质．8．（2015届四川中江县校级模拟）如图所示，图①中圆与正方形各边都相切，设这个圆的周长为；图②中的四个圆的半径相等，并依次外切，且与正方形的边相切，设这四个圆的周长为；图③中的九个圆的半径相等，并依次外切，且与正方形的边相切，设这九个圆的周长为；…．依此规律，当正方形边长为2时，= ____________．【答案】10100π．考点：1．相切两圆的性质；2．规律型：图形的变化类．9．（2015届山东省滕州市校级模拟）已知P是⊙O外一点，PA切⊙O于A，PB切⊙O于B．若PA＝6，则PB ＝．【答案】6．【解析】试题分析：∵PA、PB都是⊙O的切线，且A、B是切点，∴PA=PB，即PB=6．考点：切线长定理．10．（2015届江苏省如皋市校级模拟）如图，AB是⊙O的直径，点C在AB的延长线上，CD切⊙O于点D，连接AD．若∠A=25°，则∠C= 度．【答案】40°．考点：1．切线的性质；2．圆周角定理．。

专题23 圆与圆的位置关系【阅读与思考】两圆的半径与圆心距的大小量化确定圆与圆的外离、外切、相交、内切、内含五种位置关系.圆与圆相交、相切等关系是研究圆与圆位置关系的重点，解题中经常用到相关性质. 解圆与圆的位置关系问题，往往需要添加辅助线，常用的辅助线有： 1.相交两圆作公共弦或连心线；2.相切两圆作过切点的公切线或连心线；3.有关相切、相离两圆的公切线问题常设法构造相应的直角三角形. 熟悉以下基本图形和以上基本结论.【例题与求解】【例1】 如图，大圆⊙O 的直径a AB cm ，分别以OA ，OB 为直径作⊙O 1和⊙O 2，并在⊙O 与⊙O 1和⊙O 2的空隙间作两个等圆⊙O 3和⊙O 4，这些圆互相内切或外切，则四边形3241O O O O 的面积为________cm 2. （全国初中数学竞赛试题） 解题思路：易证四边形3241O O O O 为菱形，求其面积只需求出两条对角线的长.O O 2O 1O 3O 4BA【例2】 如图，圆心为A ，B ，C 的三个圆彼此相切，且均与直线l 相切.若⊙A ，⊙B ，⊙C 的半径分别为a ，b ，c （b a c <<<0），则a ，b ，c 一定满足的关系式为（ ） A .c a b +=2 B .c a b +=2C .b ac 111+= D .ba c 111+= （天津市竞赛试题） 解题思路：从两圆相切位置关系入手，分别探讨两圆半径与分切线的关系，解题的关键是作圆的基本辅助线.lC A 1C 1B 1BA【例3】 如图，已知两圆内切于点P ，大圆的弦AB 切小圆于点C ，PC 的延长线交大圆于点D .求证： （1）∠APD =∠BPD ；（2）CB AC PC PB PA ∙+=∙2. （天津市中考试题）解题思路：对于（1），作出相应辅助线；对于（2），应化简待证式的右边，不妨从AC ·BC =PC ·CD 入手.PBCDA【例4】 如图⊙O 1和⊙O 2相交于点A 及B 处，⊙O 1的圆心落在⊙O 2的圆周上，⊙O 1的弦AC 与⊙O 2交于点D .求证：O 1D ⊥BC .（全俄中学生九年级竞赛试题）解题思路：连接AB ，O 1B ，O 1C ，显然△O 1BC 为等腰三角形，若证O 1D ⊥BC ，只需证明O 1D 平分∠B O 1C .充分运用与圆相关的角.O 1O 2D BCA【例5】 如图，在直角梯形ABCD 中，AD ∥BC ，AB ⊥BC ，AD =1,AB =2，DC =22，点P 在边BC 上运动（与B ，C 不重合）.设PC =x ，四边形ABPD 的面积为y . （1）求y 关于x 的函数关系式，并写出自变量x 的取值范围； （2）若以D 为圆心，21为半径作⊙D ，以P 为圆心，以PC 的长为半径作⊙P ，当x 为何值时，⊙D 与⊙P 相切？并求出这两圆相切时四边形ABPD 的面积. （河南省中考题） 解题思路：对于（2），⊙P 与⊙D 既可外切，也可能内切，故需分类讨论，解题的关键是由相切两圆的性质建立关于x 的方程.DCPBA【例6】 如图，ABCD 是边长为a 的正方形，以D 为圆心，DA 为半径的圆弧与以BC 为直径的半圆交于另一点P ，延长AP 交BC 于点N ，求NCBN的值. （全国初中数学联赛试题） 解题思路：AB 为两圆的公切线，BC 为直径，怎样产生比例线段？丰富的知识，不同的视角激活想象，可生成解题策略与方法.N PB A CD【能力与训练】A 级1.如图，⊙A ，⊙B 的圆心A ，B 在直线l 上，两圆的半径都为1cm .开始时圆心距AB ＝4cm ，现⊙A ，⊙B 同时沿直线l 以每秒2cm 的速度相向移动，则当两圆相切时，⊙A 运动的时间为_______秒.（宁波市中考试题）2.如图，O 2是⊙O 1上任意一点，⊙O 1和⊙O 2相交于A ，B 两点，E 为优弧AB 上的一点，EO 2及延长线交⊙O 2于C ，D ，交AB 于F ，且CF ＝1，EC ＝2，那么⊙O 2的半径为_______.（四川省中考试题）（第1题图） （第2题图） （第3题图）3.如图，半圆O 的直径AB ＝4,与半圆O 内切的动圆O 1与AB 切于点M .设⊙O 1的半径为y ，AM 的长为x ，则y 与x 的函数关系是_________________.（要求写出自变量x 的取值范围）（昆明市中考试题）4.已知直径分别为151+和315-的两个圆，它们的圆心距为115-，这两圆的公切线的条数是__________.5.如图，⊙O 1和⊙O 2相交于点A ，B ，且⊙O 2的圆心O 2在圆⊙O 1的圆上，P 是⊙O 2上一点.已知∠A O 1B ＝60°，那么∠APB 的度数是（ ）A .60°B .65°C .70°D .75°（甘肃省中考试题） 6.如图，两圆相交于A 、B 两点，过点B 的直线与两圆分别交于C ，D 两点.若⊙O 1半径为5，⊙O 2的半径为2，则AC ：AD 为（ ）A .52:3B .3:52C .1:52D .2:5（第5题图） （第6题图） （第7题图）7.如图，⊙O 1和⊙O 2外切于点T ，它们的半径之比为3:2，AB 是它们的外公切线，A ，B 是切点，AB ＝64，那么⊙O 1和⊙O 2的圆心距是（ ）A .65B .10C .610D .1339208.已知两圆的半径分别为R 和r （r R >），圆心距为d .若关于x 的方程0)(222=-+-d R rx x 有两相等的实数根，那么这两圆的位置关系是（ ）A .外切B .内切C .外离D .外切或内切lB A FC EB AD O 1O 2O 1B O M A O 1O 2PBAO 2DBCAO 1BATO 1O 2。

P O 2O 1中考数学复习《圆与圆的位置关系》练习题（含答案）一、选择题1.如图，在Rt △ABC 中，∠C =90°，AC =8，BC =6，DE ∥BC ，且AD =2CD ，则以D 为圆心DC 为半径的⊙D 和以E 为圆心EB 为半径的⊙E 的位置关系是 （ ）（A ）外离； （B ）外切； （C ）相交； （D ）不能确定．2.已知半径分别为5cm 和8cm 的两圆相交，则它们的圆心距可能是（ ）A ．1cmB ．3cmC ．10cmD ．15cm3.已知两圆的半径分别为3和4，圆心距为1，则两圆的位置关系是 （ ）Ａ．相交 Ｂ．内切 Ｃ．外切 Ｄ．内含 4.已知半径分别是3和5的两个圆没有公共点，那么这两个圆的圆心距d 的取值范围是（ ） A ．8d > B ． 2d > C ．02d ≤< D ． 8d >或02d ≤<5.已知两圆半径分别为4和7，圆心距为3，那么这两个圆的位置关系是（ ）．A . 内含B . 内切C . 相交D . 外切6.如图，已知⊙01与⊙02关于y 轴对称，点01的坐标为（- 4，0）.两圆相交于A 、B ，且01A ⊥02A ，则图中阴影部分的面积是（ ）A.4π – 8B.8π – 16C. 16π – 16D.16π – 32二、填空题1.如图，⊙O 1和⊙O 2的半径为2和3，连接O 1O 2，交⊙O 2于点P ，O 1O 2=7，若将⊙O 1绕点P 按顺时针方向以30°/秒的速度旋转一周，请写出⊙O 1与⊙O 2相切时的旋转时间为_______秒．2．已知⊙O 1的半径为3，⊙O 2的半径为5， O 1O 2＝7，则⊙O 1、⊙O 2的位置关系是ABC ED (第1题图)3．已知⊙1O 和⊙2O 的半径分别为3cm 和5cm ，且它们内切，则12O O 等于 ▲ cm ．4.已知⊙O 1的半径为3，⊙O 2的半径为5， O 1O 2＝7，则⊙O 1、⊙O 2的位置关系是 ▲ ．5.如图，在△ABC 中，∠A=90，分别以B 、C 为圆心的两个等圆外切，两圆的半径都为2cm ，则图中阴影部分的面积为 ．6.已知ABC △的三边分别是a b c ，，，两圆的半径12r a r b ==，，圆心距d c =，则这两 个圆的位置关系是 ．7.如果半径为3cm 的⊙O 1与半径为4cm 的⊙O 2内切，那么两圆的圆心距O 1O 2＝ cm ．【原创】8.要在一个矩形纸片上画出半径分别是4cm 和1cm 的两个外切圆，该矩形纸片面积的最小值是 .第5题选择题1、C2、C3、B4、D5、B6、B填空题1、【答案】 3或6或92、答案：相交3、答案：24、答案：相交：5、答案: 2cm6、答案:相交7、答案：18、答案： 72.。

中考试题专题之23-圆与圆的地点关系试题及答案一．选择1. （泸州）已知⊙ O1与⊙ O2的半径分别为 5cm 和 3cm，圆心距 020=7cm ，则两圆的地点关系为A ．外离B ．外切C．订交D．内切2.( 滨州 )已知两圆半径分别为 2 和 3，圆心距为d，若两圆没有公共点，则以下结论正确的是（）A ．0 d 1B．d5C．0 d 1或 d 5D．0≤d 1 或 d53.（台州市）大圆半径为6，小圆半径为3，两圆圆心距为10，则这两圆的地点关系为（）A ．外离B．外切Ｃ．订交D．内含4.（ 2009 桂林百色）右图是一张卡通图，图中两圆的地点关系（）A ．订交B．外离C．内切 D ．内含5．若两圆的半径分别是1cm 和 5cm，圆心距为6cm，则这两圆的地点关系是（）A ．内切B ．订交C．外切D．外离6（衢州）外切两圆的圆心距是7，此中一圆的半径是4，则另一圆的半径是A．11B．7C．4D．37.（舟山）外切两圆的圆心距是7，此中一圆的半径是4，则另一圆的半径是A．11B．7C．4D．38. . （益阳市）已知⊙ O1和⊙ O2的半径分别为 1 和 4，假如两圆的地点关系为订交，那么圆心距 O1O2的取值范围在数轴上表示正确的选项是012345012345012345012345A ．B．C． D ．9. （宜宾）若两圆的半径分别是2cm 和 3cm,圆心距为 5cm，则这两个圆的地点关系是（）A. 内切B. 订交C.外切D. 外离10.. （ 2009 肇庆） 10．若⊙O1与⊙O2相切，且O1O2 5 ，⊙O1的半径 r12 ，则⊙O2的半径r2是（）A ．3B．5C．7 D ． 3 或711. ．(湖州 )已知⊙O1与⊙O2外切，它们的半径分别为 2 和3，则圆心距O1O2的长是（）A ．O1O2 =1B ．O1O2＝5C．１＜O1O2＜５D．O1O2＞５12.（兰州）已知两圆的半径分别为A ．外离B ．外切3cm 和2cm，圆心距为C．订交5cm，则两圆的地点关系是D．内切.13.（遂宁）如图，把⊙ O1向右平移 8 个单位长度得⊙ O2，两圆订交于 A.B ，且 O1A ⊥ O2A ，则图中暗影部分的面积是A.4 π-8B. 8π-16C.16 π-16D. 16π-3214．（赤峰市）若两圆的直径分别是是（）A. 内切B. 订交C.外切2cm 和 10cm，圆心距为D.外离8cm，则这两个圆的地点关系.15.（常德市）如图4，两个齐心圆的半径分别为3cm和5cm，弦AB 与小圆相切于点C，则 AB 的长为（）A ． 4cm C．6cm B． 5cm D． 8cm·OA C B16.（ 2009 湖北荆州年）8．如图，两齐心圆的圆心为O，大圆的弦AB切小圆于P，两圆的半径分别为6，3，则图中暗影部分的面积是（）A．93B．63C．933D．632OA BP17．（新疆乌鲁木齐市）若订交两圆的半径分别为 1 和 2，则此两圆的圆心距可能是（）．A．1B．2C． 3D． 418.(陕西省 )图中圆与圆之间不一样的地点关系有A．2 种B．3 种C．4 种【】D．5 种19．（重庆）已知⊙O1的半径为3cm，⊙O2的半径为4cm，两圆的圆心距O1O2为7cm，则⊙O1与⊙O2的地点关系是．20.（宜宾）若两圆的半径分别是A. 内切B. 订交2cm 和C.外切3cm,圆心距为 5cm，则这两个圆的地点关系是D. 外离（）二．填空21（.济宁市）已知两圆的半径分别是 2 和 3，圆心距为6，那么这两圆的地点关系是.22. （宁波市）如图，⊙ A.⊙B的圆心距 AB4cm ，现⊙ A .⊙B 同时沿直线A.B 在直线l上，两圆的半径都为1cm，开始时圆心l 以每秒2cm的速度相向挪动，则当两圆相切时，⊙ A 运动的时间为秒．23. （齐齐哈尔市）已知订交两圆的半径分别为圆的圆心距是 ______________．5cm 和 4cm，公共弦长为6cm ，则这两个24.. （锦州）如图 6 所示，点 A.B 在直线 MN 上，AB=11cm ，⊙ A. ⊙ B的半径均为 1cm，⊙ A 以每秒 2cm 的速度自左向右运动，与此同时，⊙B 的半径也不停增大，其半径r(cm) 与时间r=1+t(t ≥，0)当点 A 出发后 ____ 秒两圆相切 .t( 秒 )之间的关系式为25.（锦州）图 7-1 中的圆与正方形各边都相切，设这个圆的面积为S1；图 7-2 中的四个圆的半径相等，并挨次外切，且与正方形的边相切，设这四个圆的面积之和为 S2；图 7-3 中的九个圆半径相等，并挨次外切，且与正方形的各边相切，设这九个圆的面积之和为S3，依此规律，当正方形边长为 2 时，第 n 个图中全部圆的面积之和S n=________.26.（重庆）已知⊙O1的半径为3cm，⊙O2的半径为4cm，两圆的圆心距 O1O2为7cm，则⊙O1与⊙O2的地点关系是．27. （莆田）已知⊙O1和⊙O2的半径分别是一元二次方程x1x20 的两根，且OO1 22，则⊙O 和⊙O 的地点关系是12．28.．（ 09 湖北宜昌）如图，日蚀图中表示太阳和月亮的分别为两个圆，这两个圆的地点关系是．29.（浙江省绍兴市）如图，⊙ A，⊙B的半径分别为1cm，2cm，圆心距AB为5cm．假如⊙ A 由图示地点沿直线 AB 向右平移3cm，则此时该圆与⊙ B 的地点关系是_____________．30.（ 2009 威海）如图，⊙ O1和⊙ O2的半径为 1 和 3，连结 O1O2，交⊙ O2于点 P，O1O2=8，若将⊙ O1绕点P按顺时针方向旋转 360°，则⊙ O1与⊙ O2共相切 _______次．31.（ 2009是黑龙江大兴安岭）已知相切两圆的半径分别为．5cm 和4cm ，这两个圆的圆心距32.（2009襄樊市）已知O1和O2的半径分别为 3cm 和 2cm，且O1O2则O1与1cm，O2的地点关系为．分析：此题考察圆与圆的地点关系，已知O1和 O2的半径分别为3cm 和 2cm，且O1O21cm，因此r1r2 d ，因此O1 与O2的地点关系为为内切，故填内切。

本题考点与圆有关的位置关系
整理表
姓名:
职业工种:
申请级别:
受理机构:
填报日期:
A4打印/ 修订/ 内容可编辑
如图，已知⊙是以数轴的原点为圆心，半径为1的圆，,点在数轴上运动，若过点且与平行的直线与⊙有公共点, 设，则的取值范围是（）
A．－1≤ ≤ 1 B．≤ ≤C．0≤≤ D．＞
思路分析：
根据题意，因为点与平行，与⊙有公共点，可知当直线与圆相切时，求出与数轴相交点的值，即可得出x的取值范围.
解答过程：
如下图，作OA的平行线与圆相切于点E、F，与坐标轴相交于点C、D.
∵ OA∥DF
∴∠AOB=∠ODF=45°OF=1,
∴OD=，同理可得出OC= -
∵点且与平行的直线与⊙有公共点,
∴≤≤
答案：B
拓展提升：
本题考查勾股定理与相切的综合运用.
整理丨尼克
本文档信息来自于网络，如您发现内容不准确或不完善，欢迎您联系我修正；如您发现内容涉嫌侵权，请与我们联系，我们将按照相关法律规定及时处理。

中考数学真题《圆的有关位置关系》专项测试卷(附答案)学校:___________班级：___________姓名：___________考号：___________（45题）一、单选题1．（2023·四川眉山·统考中考真题）如图，AB 切O 于点B 连接OA 交O 于点C BD OA ∥交O 于点D 连接CD 若25OCD ∠=︒则，A ∠的度数为（ ）A ．25︒B ．35︒C ．40︒D ．45︒2．（2023·重庆·统考中考真题）如图，AC 是O 的切线 B 为切点 连接OA OC ，．若30A ∠=︒ 23AB = 3BC =则，OC 的长度是（ ）A ．3B ．3C 13D ．63．（2023·重庆·统考中考真题）如图，AB 为O 的直径 直线CD 与O 相切于点C 连接AC若50ACD ∠=︒则，BAC ∠的度数为（ ）A ．30︒B ．40︒C ．50︒D ．60︒4．（2023·湖北武汉·统考中考真题）如图，在四边形ABCD 中 ,AB CD AD AB ⊥∥ 以D 为圆心 AD 为半径的弧恰好与BC 相切 切点为E ．若13AB CD =则，sin C 的值是（ ）A ．23 B 5C ．34 D 75．（2023·四川泸州·统考中考真题）如图，在Rt ABC △中 90C ∠=︒ 点D 在斜边AB 上 以AD 为直径的半圆O 与BC 相切于点E 与AC 相交于点F 连接DE ．若8AC = 6BC =则，DE 的长是（ ）A 410B 810C ．8027D ．83二 填空题6．（2023·浙江嘉兴·统考中考真题）如图，点A 是O 外一点 AB AC 分别与O 相切于点B C 点D 在BDC 上 已知50A ∠=︒则，D ∠的度数是___________．7．（2023·黑龙江·统考中考真题）如图，AB 是O 的直径 PA 切O 于点A PO 交O 于点C 连接BC 若28B ∠=︒则，P ∠=__________︒．8．（2023·湖南·统考中考真题）如图，AD 是O 的直径 AB 是O 的弦 BC 与O 相切于点B 连接OB 若65ABC ∠=︒则，BOD ∠的大小为__________．9．（2023·山东滨州·统考中考真题）如图，,PA PB 分别与O 相切于,A B 两点 且56APB ∠=︒．若点C 是O 上异于点,A B 的一点则，ACB ∠的大小为___________．10．（2023·浙江宁波·统考中考真题）如图，在Rt ABC △中 90C ∠=︒ E 为AB 边上一点 以AE 为直径的半圆O 与BC 相切于点D 连接AD 3,35BE BD ==P 是AB 边上的动点 当ADP △为等腰三角形时 AP 的长为_____________．11．（2023·河南·统考中考真题）如图，PA 与O 相切于点A PO 交O 于点B 点C 在PA 上 且CB CA =．若5OA = 12PA =则，CA 的长为______．12．（2023·湖北·统考中考真题）如图，在ABC 中 70ACB ABC ∠=︒，△的内切圆O 与AB BC ，分别相切于点D E 连接DE AO ，的延长线交DE 于点F 则，AFD ∠=_________．13．（2023·湖南·统考中考真题）如图，在Rt ABC △中 90,8,6ACB AC BC ∠=︒==．以点C 为圆心 r 为半径作圆 当所作的圆与斜边AB 所在的直线相切时 r 的值为________．14．（2023·山东烟台·统考中考真题）如图，在直角坐标系中 A 与x 轴相切于点,B CB 为A 的直径 点C 在函数(0,0)ky k x x =>>的图象上 D 为y 轴上一点 ACD 的面积为6则，k 的值为________．15．（2023·四川·统考中考真题）如图，45ACB ∠=︒ 半径为2的O 与角的两边相切 点P 是⊙O 上任意一点 过点P 向角的两边作垂线 垂足分别为E F 设2t PE PF =则，t 的取值范围是 _____．16．（2023·湖南岳阳·统考中考真题）如图，在O 中 AB 为直径 BD 为弦 点C 为BD 的中点 以点C 为切点的切线与AB 的延长线交于点E ．（1）若30,6A AB ∠=︒=则，BD 的长是_________（结果保留π）（2）若13CF AF =则，CE AE =_________．17．（2023·上海·统考中考真题）在ABC 中7,3,90AB BC C ==∠=︒ 点D 在边AC 上 点E 在CA 延长线上 且CD DE = 如果B 过点A E 过点D 若B 与E 有公共点 那么E 半径r 的取值范围是________．三 解答题18．（2023·浙江绍兴·统考中考真题）如图，AB 是O 的直径 C 是O 上一点 过点C 作O 的切线CD 交AB 的延长线于点D 过点A 作AE CD ⊥于点E ．(1)若25EAC ∠=︒ 求ACD ∠的度数．(2)若2,1OB BD == 求CE 的长．19．（2023·湖南张家界·统考中考真题）如图，O 是ABC 的外接圆 AD 是O 的直径F 是AD 延长线上一点 连接CD CF ， 且DCF CAD ∠=∠．(1)求证：CF 是O 的切线(2)若直径310,cos 5AD B == 求FD 的长．20．（2023·江西·统考中考真题）如图，在ABC 中 464AB C =∠=︒， 以AB 为直径的O 与AC 相交于点D E 为ABD 上一点 且40ADE ∠=︒．(1)求BE 的长(2)若76EAD ∠=︒ 求证：CB 为O 的切线．21．（2023·江苏连云港·统考中考真题）如图，在ABC 中 AB AC = 以AB 为直径的O 交边AC 于点D 连接BD 过点C 作CE AB ∥．(1)请用无刻度的直尺和圆规作图：过点B 作O 的切线 交CE 于点F （不写作法 保留作图痕迹 标明字母）(2)在（1）的条件下 求证：BD BF =．22．（2023·辽宁·统考中考真题）如图，AB是O的直径点C E，在O上2CAB EAB∠=∠点F在线段AB的延长线上且AFE ABC∠=∠．(1)求证：EF与O相切(2)若41sin5BF AFE=∠=，求BC的长．23．（2023·山东东营·统考中考真题）如图，在ABC中AB AC=以AB为直径的O交BC于点D DE AC⊥垂足为E．(1)求证：DE是O的切线(2)若30C∠=︒23CD=求BD的长．24．（2023·内蒙古赤峰·统考中考真题）如图，AB 是O 的直径 C 是O 上一点过点C 作CD AB ⊥于点E 交O 于点D 点F 是AB 延长线上一点 连接CF AD 2FCD DAF ∠=∠．(1)求证：CF 是O 切线(2)若10AF2sin 3F = 求CD 的长．25．（2023·湖南常德·统考中考真题）如图，四边形ABCD 是O 的内接四边形 AB 是直径 C 是BD 的中点 过点C 作CE AD ⊥交AD 的延长线于点E ．(1)求证：CE 是O 的切线(2)若6BC = 8AC = 求,CE DE 的长．26．（2023·内蒙古通辽·统考中考真题）如图，AB 为O 的直径 D E 是O 上的两点 延长AB 至点C 连接CD BDC A∠=∠．(1)求证：ACD DCB∽(2)求证：CD是O的切线(3)若3tan,105E AC==求O的半径．27．（2023·广东深圳·统考中考真题）如图，在单位长度为1的网格中点O A B均在格点上3OA= 2AB=以O为圆心OA为半径画圆请按下列步骤完成作图并回答问题：⊙过点A作切线AC且4AC=（点C在A的上方）⊙连接OC交O于点D⊙连接BD与AC交于点E．(1)求证：BD为O的切线(2)求AE的长度．28．（2023·黑龙江绥化·统考中考真题）已知：点P是O外一点．(1)尺规作图：如图，过点P 作出O 的两条切线PE PF 切点分别为点E 点F ．（保留作图痕迹 不要求写作法和证明）(2)在（1）的条件下 若点D 在O 上（点D 不与E F 两点重合） 且30EPF ∠=︒．求EDF ∠的度数．29．（2023·黑龙江齐齐哈尔·统考中考真题）如图，在Rt ABC △中 90B AD 平分BAC ∠交BC 于点D 点E 是斜边AC 上一点 以AE 为直径的O 经过点D 交AB 于点F 连接DF ．(1)求证：BC 是O 的切线(2)若5BD = tan 3ADB ∠= 求图中阴影部分的面积（结果保留π）．30．（2023·福建·统考中考真题）如图，已知ABC 内接于,O CO 的延长线交AB 于点D 交O 于点E 交O 的切线AF 于点F 且AF BC ∥．(1)求证：AO BE ∥(2)求证：AO 平分BAC ∠．31．（2023·湖北荆州·统考中考真题）如图，在菱形ABCD 中 DH AB ⊥于H 以DH 为直径的O 分别交AD BD 于点E F 连接EF ．(1)求证：⊙CD 是O 的切线⊙DEF DBA ∽(2)若5AB = 6DB = 求sin DFE ∠．32．（2023·广西·统考中考真题）如图，PO 平分APD ∠ PA 与O 相切于点A 延长AO 交PD 于点C 过⊥垂足为B．点O作OB PD(1)求证：PB是O的切线(2)若O的半径为4 5OC=求PA的长．33．（2023·湖北黄冈·统考中考真题）如图，ABC中以AB为直径的O交BC于点D DE是O的切线⊥垂足为E延长CA交O于点F．且DE AC=(1)求证：AB AC(2)若3,6AE DE==求AF的长．34．（2023·湖南郴州·统考中考真题）如图，在O中AB是直径点C是圆上一点．在AB的延长线上取一点D 连接CD 使BCD A ∠=∠．(1)求证：直线CD 是O 的切线(2)若120ACD ∠=︒ 3CD = 求图中阴影部分的面积（结果用含π的式子表示）．35．（2023·湖北十堰·统考中考真题）如图，在Rt ABC △中 90,C AC BC ∠=︒= 点O 在AB 上 以O 为圆心 OA 为半径的半圆分别交,AC BC AB 于点,,D E F 且点E 是弧DF 的中点．(1)求证：BC 是O 的切线(2)若2CE 求图中阴影部分的面积（结果保留π）．36．（2023·四川内江·统考中考真题）如图，以线段AB 为直径作O 交射线AC 于点C AD 平分CAB ∠交O 于点D 过点D 作直线DE AC ⊥ 交AC 的延长线于点E 交AB 的延长线于点F ．连接BD 并延长交AC的延长线于点M．(1)求证：直线DE是O的切线(2)当30F∠=︒时判断ABM的形状并说明理由(3)在（2）的条件下1ME=连接BC交AD于点P求AP的长．37．（2023·湖北随州·统考中考真题）如图，AB是O的直径点E C在O上点C是BE的中点AE 垂直于过C点的直线DC垂足为D AB的延长线交直线DC于点F．(1)求证：DC是O的切线(2)若2AE=1sin3AFD∠=⊙求O的半径⊙求线段DE的长．38．（2023·山东枣庄·统考中考真题）如图，AB为O的直径点C是AD的中点过点C做射线BD的垂线垂足为E．(1)求证：CE 是O 切线(2)若34BE AB ==， 求BC 的长(3)在（2）的条件下 求阴影部分的面积（用含有π的式子表示）．39．（2023·山东临沂·统考中考真题）如图，O 是ABC 的外接圆 BD 是O 的直径 ,AB AC AE BC =∥ E 为BD 的延长线与AE 的交点．(1)求证：AE 是O 的切线(2)若75,2ABC BC ∠=︒= 求CD 的长．40．（2023·湖南永州·统考中考真题）如图，以AB 为直径的O 是ABC 的外接圆 延长BC 到点D ．使得BAC BDA ∠=∠ 点E 在DA 的延长线上 点AM 在线段AC 上 CE 交BM 于N CE 交AB 于G ．(1)求证：ED 是O 的切线(2)若,65,AC BD AC CD ==> 求BC 的长(3)若DE AM AC AD ⋅=⋅ 求证：BM CE ⊥．41．（2023·山东烟台·统考中考真题）如图，在菱形ABCD 中 对角线,AC BD 相交于点,E O 经过,A D 两点 交对角线AC 于点F 连接OF 交AD 于点G 且AG GD =．(1)求证：AB 是O 的切线(2)已知O 的半径与菱形的边长之比为5:8 求tan ADB ∠的值．42．（2023·江苏扬州·统考中考真题）如图，在ABC 中 90ACB ∠=︒ 点D 是AB 上一点 且12BCD A ∠=∠ 点O 在BC 上 以点O 为圆心的圆经过C D 两点．(1)试判断直线AB 与O 的位置关系 并说明理由(2)若3sin ,5B O =的半径为3 求AC 的长．43．（2023·四川乐山·统考中考真题）如图，已知O 是Rt ABC △的外接圆 90ACB ∠=︒ D 是圆上一点 E 是DC 延长线上一点 连结AD AE ， 且AD AE CA CE ==，．(1)求证：直线AE 是O 是的切线(2)若2sin 3E =O 的半径为3 求AD 的长．44．（2023·甘肃兰州·统考中考真题）如图，ABC 内接于O AB 是O 的直径 BC BD = DE AC ⊥于点E DE 交BF 于点F 交AB 于点G 2BOD F ∠=∠ 连接BD ．(1)求证：BF是O的切线(2)判断DGB的形状并说明理由(3)当2BD=时求FG的长．=BD是边AC上的中线过点C作45．（2023·湖北·统考中考真题）如图，等腰ABC内接于O AB ACAE FC．AB的平行线交BD的延长线于点E BE交O于点F连接,(1)求证：AE为O的切线BC=求FC的长．(2)若O的半径为56参考答案一单选题1．（2023·四川眉山·统考中考真题）如图，AB切O于点B连接OA交O于点C BD OA∥交O于点∠的度数为（）D连接CD若25OCD∠=︒则，AA ．25︒B ．35︒C ．40︒D ．45︒【答案】C 【分析】如图，连接OB 证明90∠=︒ABO 25CDB ∠=︒ 可得250BOC BDC ∠=∠=︒ 从而可得40A ∠=︒．【详解】解：如图，连接OB⊙AB 切O 于点B⊙90∠=︒ABO⊙BD OA ∥ 25OCD ∠=︒⊙25CDB ∠=︒⊙250BOC BDC ∠=∠=︒⊙40A ∠=︒故选：C.【点睛】本题考查的是切线的性质 圆周角定理的应用 三角形的内角和定理的应用 掌握基本图形的性质是解本题的关键．2．（2023·重庆·统考中考真题）如图，AC 是O 的切线 B 为切点 连接OA OC ，．若30A ∠=︒ 23AB = 3BC =则，OC 的长度是（ ）A ．3B ．3C 13D ．6【答案】C 【分析】根据切线的性质及正切的定义得到2OB = 再根据勾股定理得到13OC =【详解】解：连接OB⊙AC 是O 的切线 B 为切点⊙OB AC ⊥⊙30A ∠=︒ 23AB =⊙在Rt OAB 中 3tan 232OB AB A =⋅∠== ⊙3BC =⊙在Rt OBC 中 2213OC OB BC +故选：C ．【点睛】本题考查了切线的性质 锐角三角函数 勾股定理 掌握切线的性质是解题的关键．3．（2023·重庆·统考中考真题）如图，AB 为O 的直径 直线CD 与O 相切于点C 连接AC 若50ACD ∠=︒则，BAC ∠的度数为（ ）A ．30︒B ．40︒C ．50︒D ．60︒【答案】B 【分析】连接OC 先根据圆的切线的性质可得90OCD ∠=︒ 从而可得40OCA ∠=︒ 再根据等腰三角形的性质即可得．【详解】解：如图，连接OC直线CD 与O 相切OC CD ∴⊥90OCD ∴∠=︒50ACD ∠=︒40OCA ∴∠=︒OA OC =40BAC OCA ∴∠=∠=︒故选：B ．【点睛】本题考查了圆的切线的性质 等腰三角形的性质 熟练掌握圆的切线的性质是解题关键． 4．（2023·湖北武汉·统考中考真题）如图，在四边形ABCD 中 ,AB CD AD AB ⊥∥ 以D 为圆心 AD 为半径的弧恰好与BC 相切 切点为E ．若13AB CD =则，sin C 的值是（ ）A ．23B 5C ．34D 7【答案】B 【分析】作CF AB ⊥延长线于F 点 连接DE 根据圆的基本性质以及切线的性质 分别利用勾股定理求解在Rt DEC △和Rt BFC △ 最终得到DE 即可根据正弦函数的定义求解．【详解】解：如图所示 作CF AB ⊥延长线于F 点 连接DE⊙AD AB ⊥ AB CD ∥⊙90FAD ADC F ∠=∠=∠=︒⊙四边形ADCF 为矩形 AF DC = AD FC =⊙AB 为D 的切线由题意 BE 为D 的切线⊙DE BC ⊥ AB BE = ⊙13AB CD = ⊙设AB BE a 3CD a = CE x =则2BF AF AB CD AB a =-=-= BC BE CE a x =+=+在Rt DEC △中 222229DE CD CE a x =-=-在Rt BFC △中 ()()222222FC BC BF a x a =-=+-⊙DE DA FC ==⊙()()222292a x a x a -=+-解得：2x a =或3x a =-（不合题意 舍去）⊙2CE a = ⊙2222945DE CD CE a a a --= ⊙55sin DE a C DC === 故选：B ．【点睛】本题考查圆的切线的判定与性质 解直角三角形 以及正弦函数的定义等 综合性较强 熟练运用圆的相关性质以及切线的性质等是解题关键．5．（2023·四川泸州·统考中考真题）如图，在Rt ABC △中 90C ∠=︒ 点D 在斜边AB 上 以AD 为直径的半圆O 与BC 相切于点E 与AC 相交于点F 连接DE ．若8AC = 6BC =则，DE 的长是（ ）A 410B 810C ．8027 D ．83【答案】B【分析】连接OE AE 首先根据勾股定理求出2210AB AC BC + 然后证明出BCA BEO ∽利用相似三角形的性质得到409OE = 103BE = 证明出DBE EBA ∽ 利用相似三角形的性质求出810DE =【详解】如图所示 连接OE AE⊙90C ∠=︒ 8AC = 6BC = ⊙2210AB AC BC +⊙以AD 为直径的半圆O 与BC 相切于点E⊙OE BC ⊥⊙90C ∠=︒⊙90C OEB ︒∠=∠=⊙AC OE ∥⊙A EOB ∠=∠⊙BCA BEO ∽ ⊙6OE OB BE AC AB == 即108106OE OEBE-== ⊙409OE = 103BE = ⊙108633CE CB BE =-=-=⊙228103AE AC CE =+=⊙90OEB ∠=︒ ⊙90OED DEB ∠+∠=︒⊙90ODE EAD ∠+∠=︒ ODE OED ∠=∠⊙EAD DEB ∠=∠又⊙B B ∠=∠⊙DBE EBA ∽ ⊙DE BE AE AB = 即103810103DE = ⊙解得810DE =故选：B ．【点睛】此题考查了圆与三角形综合题 切线的性质定理 相似三角形的性质和判定 勾股定理等知识 解题的关键是熟练掌握以上知识点．二 填空题6．（2023·浙江嘉兴·统考中考真题）如图，点A 是O 外一点 AB AC 分别与O 相切于点B C 点D 在BDC 上 已知50A ∠=︒则，D ∠的度数是___________．【答案】65︒【分析】连接,CO BO 根据切线的性质得出90ACO ABO ∠=∠=︒ 根据四边形内角和得出130COB ∠=︒ 根据圆周角定理即可求解．【详解】解：如图,CO BO⊙AB AC 分别与O 相切于点B C⊙90ACO ABO ∠=∠=︒⊙50A ∠=︒⊙360909050130COB ∠=︒-︒-︒-︒=︒⊙BC BC = ⊙1652D BOC ∠=∠=︒ 故答案为：65︒．【点睛】本题考查了切线的性质 圆周角定理 求得130COB ∠=︒是解题的关键．7．（2023·黑龙江·统考中考真题）如图，AB 是O 的直径 PA 切O 于点A PO 交O 于点C 连接BC 若28B ∠=︒则，P ∠=__________︒．【答案】34【分析】首先根据等边对等角得到28B OCB ∠=∠=︒ 然后利用外角的性质得到56AOC B OCB ∠=∠+∠=︒ 利用切线的性质得到90OAP ∠=︒ 最后利用三角形内角和定理求解即可．【详解】解：⊙28B ∠=︒ OB OC =⊙28B OCB ∠=∠=︒⊙56AOC B OCB ∠=∠+∠=︒⊙PA 切O 于点A⊙90OAP ∠=︒⊙18034P OAP AOP ∠=︒-∠-∠=︒．故答案为：34．【点睛】此题考查了切线的性质和三角形的外角的性质 三角形内角和定理等知识 解题的关键是熟练掌握以上知识点．8．（2023·湖南·统考中考真题）如图，AD 是O 的直径 AB 是O 的弦 BC 与O 相切于点B 连接OB 若65ABC ∠=︒则，BOD ∠的大小为__________．【答案】50︒【分析】证明90OBC ∠=︒ 可得906525OBD ∠=︒-︒=︒ 结合OB OA = 证明25A OBA ∠=∠=︒ 再利用三角形的外角的性质可得答案．【详解】解：⊙BC 与O 相切于点B⊙90OBC ∠=︒⊙65ABC ∠=︒⊙906525OBD ∠=︒-︒=︒⊙OB OA =⊙25A OBA ∠=∠=︒⊙22550BOD ∠=⨯︒=︒故答案为：50︒【点睛】本题考查的是圆的切线的性质 等腰三角形的性质 三角形的外角的性质 熟记基本图形的性质是解本题的关键．9．（2023·山东滨州·统考中考真题）如图，,PA PB 分别与O 相切于,A B 两点 且56APB ∠=︒．若点C 是O 上异于点,A B 的一点则，ACB ∠的大小为___________．【答案】62︒或118︒【分析】根据切线的性质得到90∠=∠=︒PAO PBO 根据四边形内角和为360︒ 得出AOB ∠ 然后根据圆周角定理即可求解．【详解】解：如图所示 连接,AC BC 当点C 在优弧AB 上时⊙,PA PB 分别与O 相切于,A B 两点⊙90∠=∠=︒PAO PBO⊙56APB ∠=︒．⊙360909056124AOB ∠=︒-︒-︒-︒=︒⊙AB AB = ⊙1622ACB AOB ∠=∠=︒ 当点C '在AB 上时⊙四边形AC BC '是圆内接四边形⊙180118C C '∠=︒-∠=︒故答案为：62︒或118︒．【点睛】本题考查了切线的性质 圆周角定理 多边形内角和 熟练掌握切线的性质与圆周角定理是解题的关键．10．（2023·浙江宁波·统考中考真题）如图，在Rt ABC △中 90C ∠=︒ E 为AB 边上一点 以AE 为直径的半圆O 与BC 相切于点D 连接AD 3,35BE BD ==P 是AB 边上的动点 当ADP △为等腰三角形时 AP 的长为_____________．【答案】2306【分析】连接OD 勾股定理求出半径 平行线分线段成比例 求出CD 的长 勾股定理求出AC 和AD 的长 分AP AD =和AP PD =两种情况进行求解即可．【详解】解：连接OD⊙以AE 为直径的半圆O 与BC 相切于点D⊙OD BC ⊥ OA OE OD ==⊙90ODB ∠=︒设OA OE OD r ===则，3OB OE BE r =+=+在Rt ODB △中：222OD BD OB += 即：(()222353r r +=+ 解得：6r =⊙6OA OE OD ===⊙9OB = 15AB = 12AE =⊙90C ODB ∠=∠=︒⊙OD AC ∥ ⊙9362OB DB OA DC === ⊙35DB = ⊙5CD = ⊙5BC DB CD =+= ⊙2210AC AB BC -= ⊙22230AD AC CD +=⊙ADP △为等腰三角形当AD AP =时 30AP =当PA PD =时⊙OA OD =⊙点P 与点O 重合⊙6AP OA ==不存在PD AD =的情况综上：AP 的长为306． 故答案为：2306．【点睛】本题考查切线的性质 平行线分线段成比例 勾股定理 等腰三角形的定义．熟练掌握切线的性质 等腰三角形的定义 确定点P 的位置 是解题的关键．11．（2023·河南·统考中考真题）如图，PA 与O 相切于点A PO 交O 于点B 点C 在PA 上 且CB CA =．若5OA = 12PA =则，CA 的长为______．【答案】103【分析】连接OC 证明OAC OBC ≌ 设CB CA x ==则，12PC PA CA x =-=- 再证明PAO PBC ∽ 列出比例式计算即可．【详解】如图，连接OC⊙PA 与O 相切于点A⊙90OAC ∠=︒⊙OA OB CA CB OC OC =⎧⎪=⎨⎪=⎩, ⊙OAC OBC ≌⊙90OAC OBC ∠=∠=︒⊙90PAO PBC ∠=∠=︒⊙P P ∠=∠⊙PAO PBC ∽ ⊙PO AO PC BC= ⊙5OA = 12PA = ⊙2251213PO +设CB CA x ==则，12PC PA CA x =-=- ⊙13512x x=- 解得103x =故CA 的长为103故答案为：103． 【点睛】本题考查了切线的性质 三角形全等的判定和性质 勾股定理 三角形相似的判断和性质 熟练掌握性质是解题的关键．12．（2023·湖北·统考中考真题）如图，在ABC 中 70ACB ABC ∠=︒，△的内切圆O 与AB BC ，分别相切于点D E 连接DE AO ，的延长线交DE 于点F 则，AFD ∠=_________．【答案】35︒【分析】如图所示 连接OE OD OB ，， 设OB DE 、交于H 由内切圆的定义结合三角形内角和定理求出125AOB ∠=︒ 再由切线长定理得到BD BE = 进而推出OB 是DE 的垂直平分线 即90OHF ∠=︒则，35AFD AOH OHF =-=︒∠∠∠．【详解】解：如图所示 连接OE OD OB ，， 设OB DE 、交于H⊙O 是ABC 的内切圆⊙OA OB 、分别是CAB CBA ∠、∠的角平分线 ⊙1122OAB CAB OBA CBA ==∠∠，∠∠ ⊙70ACB ∠=︒⊙180110CAB CBA ACB +=︒-=︒∠∠∠ ⊙115522OAB OBA CBA CAB +=+=︒∠∠∠∠ ⊙180125AOB OAB OBA =︒--=︒∠∠∠⊙O 与AB BC ，分别相切于点D E⊙BD BE =又⊙OD OE =⊙OB 是DE 的垂直平分线⊙OB DE ⊥ 即90OHF ∠=︒⊙35AFD AOH OHF =-=︒∠∠∠故答案为：35︒．【点睛】本题主要考查了三角形内切圆 切线长定理 三角形内角和定理 线段垂直平分线的判定 三角形外角的性质 正确作出辅助线是解题的关键．13．（2023·湖南·统考中考真题）如图，在Rt ABC △中 90,8,6ACB AC BC ∠=︒==．以点C 为圆心 r 为半径作圆 当所作的圆与斜边AB 所在的直线相切时 r 的值为________．【答案】245【分析】根据勾股定理 得228610AB =+= 根据切线的性质 得到圆的半径等于AB 边上的高 根据直角三角形的面积不变性计算即可．【详解】⊙90,8,6ACB AC BC ∠=︒== ⊙228610AB +=根据切线的性质 得到圆的半径等于AB 边上的高 ⊙1122AB r AC BC ⨯=⨯, ⊙8624105AC BCr AB ⨯⨯=== 故答案为：245．【点睛】本题考查了勾股定理 切线的性质 熟练掌握勾股定理 切线的性质是解题的关键． 14．（2023·山东烟台·统考中考真题）如图，在直角坐标系中 A 与x 轴相切于点,B CB 为A 的直径点C 在函数(0,0)ky k x x =>>的图象上 D 为y 轴上一点 ACD 的面积为6则，k 的值为________．【答案】24 【分析】设,k C a a ⎛⎫⎪⎝⎭则，,k OB a AC a ==则，122kAC BC a == 根据三角形的面积公式得出162ACD S AC OB =⋅= 列出方程求解即可． 【详解】解：设,k C a a ⎛⎫⎪⎝⎭⊙A 与x 轴相切于点B⊙BC x ⊥轴 ⊙,kOB a AC a ==则，点D 到BC 的距离为a⊙CB 为A 的直径⊙122k AC BC a == ⊙16224ACD k k S a a =⋅⋅== 解得：24k =故答案为：24．【点睛】本题主要考查了切线的性质 反比例函数的图象和性质 解题的关键掌握切线的定义：经过半径外端且垂直于半径的直线是圆的切线 以及反比例函数图象上点的坐标特征．15．（2023·四川·统考中考真题）如图，45ACB ∠=︒ 半径为2的O 与角的两边相切 点P 是⊙O 上任意一点 过点P 向角的两边作垂线 垂足分别为E F 设2t PE PF =则，t 的取值范围是 _____．【答案】22224t ≤ 【分析】利用切线的性质以及等腰直角三角形的性质求得222CD DH == 再求得t PE PQ EQ =+= 分两种情况讨论 画出图形 利用等腰直角三角形的性质即可求解．【详解】解：设O 与ACB ∠两边的切点分别为D G 连接OG OD 、 延长DO 交CB 于点H由90OGC ODC OGH ∠=∠=∠=︒⊙45ACB ∠=︒⊙45OHC ∠=︒ ⊙222OH OG == ⊙222CD DH ==如图，延长EP 交CB 于点Q同理2PQ PF = ⊙2t PE PF =⊙t PE PQ EQ =+=当EQ 与O 相切时 EQ 有最大或最小值连接OP⊙D E 都是切点⊙90ODE DEP OPE ∠=∠=∠=︒⊙四边形ODEP 是矩形⊙OD OP =⊙四边形ODEP 是正方形⊙t 的最大值为24EQ CE CD DE ==+=如图，同理 t 的最小值为2EQ CE CD DE ==-=综上 t 的取值范围是22224t ≤≤． 故答案为：22224t ≤．【点睛】本题考查了切线的性质 等腰直角三角形的性质 勾股定理 求得t EQ =是解题的关键． 16．（2023·湖南岳阳·统考中考真题）如图，在O 中 AB 为直径 BD 为弦 点C 为BD 的中点 以点C 为切点的切线与AB 的延长线交于点E ．（1）若30,6A AB ∠=︒=则，BD 的长是_________（结果保留π）（2）若13CF AF =则，CE AE =_________． 【答案】2π12 【分析】（1）连接,OC OD 根据点C 为BD 的中点 根据已知条件得出120BOD ∠=︒ 然后根据弧长公式即可求解（2）连接OC 根据垂径定理的推论得出OC BD ⊥ EC 是O 的切线则，OC EC ⊥,得出EC BD ∥ 根据平行线分线段成比例得出13EB AB = 设2EB a =则，6AB a = 勾股定理求得EC ,J 进而即可求解． 【详解】解：（1）如图，连接,OC OD⊙点C 为BD 的中点⊙BC CD =又⊙30A ∠=︒⊙260BOC COD A ∠=∠=∠=︒⊙120BOD ∠=︒⊙6AB = ⊙132OB AB == ⊙120π32π180BD l =⨯⨯= 故答案为：2π．（2）解：如图，连接OC⊙点C 为BD 的中点⊙BC CD =⊙OC BD ⊥⊙EC 是O 的切线⊙OC EC ⊥,⊙EC BD ∥ ⊙CF EB AF AB = ⊙13CF AF = ⊙13EB AB = 设2EB a =则，6AB a = 3,5BO a EO EB BO a ==+= ⊙2222534EC EO CO a a --= 268AE a a a =+= ⊙4182CE a AE a ==． 故答案为：12．【点睛】本题考查了垂径定理 圆周角定理 切线的性质 弧长公式 平行线分线段成比例定理等知识 综合性较强 熟练掌握和灵活运用相关知识是解题的关键．17．（2023·上海·统考中考真题）在ABC 中7,3,90AB BC C ==∠=︒ 点D 在边AC 上 点E 在CA 延长线上 且CD DE = 如果B 过点A E 过点D 若B 与E 有公共点 那么E 半径r 的取值范围是________． 1010r ≤【分析】先画出图形 连接BE 利用勾股定理可得294BE r + 210AC = 10210r <≤ 再根据B 与E 有公共点可得一个关于r 的不等式组 然后利用二次函数的性质求解即可得．【详解】解：由题意画出图形如下：连接BEB 过点A 且7AB =B ∴的半径为7 E 过点D 它的半径为r 且CD DE =2CE CD DE r ∴=+=3,90BC C =∠=︒22294BE BC CE r ∴++ 22210AC AB BC - D 在边AC 上 点E 在CA 延长线上CD AC CE AC ≤⎧∴⎨>⎩ 即2102210r r ⎧≤⎪⎨>⎪⎩10210r <≤ B 与E 有公共点AB DE BE AB DE ∴-≤≤+ 即22947794r r r r ++-≤+⎪⎩①②不等式⊙可化为2314400r r --≤解方程2314400r r --=得：2r =-或203r = 画出函数231440y r r =--的大致图象如下：由函数图象可知 当0y ≤时 2023r -≤≤即不等式⊙的解集为2023r -≤≤ 同理可得：不等式⊙的解集为2r ≥或203r ≤-则不等式组的解集为2023r ≤≤又10210r <≤ 半径r 1010r ≤ 1010r ≤．【点睛】本题考查了勾股定理 圆与圆的位置关系 二次函数与不等式 根据圆与圆的位置关系正确建立不等式组是解题关键．三 解答题18．（2023·浙江绍兴·统考中考真题）如图，AB 是O 的直径 C 是O 上一点 过点C 作O 的切线CD 交AB 的延长线于点D 过点A 作AE CD ⊥于点E ．(1)若25EAC ∠=︒ 求ACD ∠的度数．(2)若2,1OB BD == 求CE 的长．【答案】(1)115︒ (2)253CE = 【分析】（1）根据三角形的外角的性质 ACD AEC EAC ∠=∠+∠即可求解．（2）根据CD 是O 的切线 可得90OCD ∠=︒ 在Rt OCD △中 勾股定理求得5CD 根据OC AE ∥ 可得CDODCE OA = 进而即可求解．【详解】（1）解：⊙AE CD ⊥于点E⊙90AEC ∠=︒⊙9025115ACD AEC EAC ∠=∠+∠=︒+︒=︒．（2）⊙CD 是O 的切线 OC 是O 的半径⊙90OCD ∠=︒．在Rt OCD △中⊙2,3OC OB OD OB BD ===+= ⊙225CD OD OC -⊙90OCD AEC ∠=∠=︒⊙OC AE ∥ ⊙CD OD CE OA = 532= ⊙253CE =．【点睛】本题考查了三角形外角的性质 切线的性质 勾股定理 平行线分线段成比例熟练掌握以上知识是解题的关键．19．（2023·湖南张家界·统考中考真题）如图，O 是ABC 的外接圆 AD 是O 的直径 F 是AD 延长线上一点 连接CD CF ， 且DCF CAD ∠=∠．(1)求证：CF 是O 的切线(2)若直径310,cos 5AD B == 求FD 的长． 【答案】(1)详见解析 (2)907【分析】(1)根据直径所对的圆周角是直角 余角的性质即可求得结论(2)根据已知条件可知FCD FAC ∽ 再根据正切的定义和相似三角形的性质得到线段的关系即可求得线段FD 的长度．【详解】（1）证明：连接OC⊙AD 是O 的直径⊙90ACD ∠=︒⊙90ADC CAD ∠+∠=︒又⊙OC OD =⊙ADC OCD ∠=∠又⊙DCF CAD ∠=∠⊙90DCF OCD ∠+∠=︒即OC FC ⊥⊙FC 是O 的切线（2）解：⊙3,cos 5B ADC B ∠=∠=⊙3cos 5ADC ∠= ⊙在Rt ACD 中 3cos ,10,5CD ADC AD AD∠=== ⊙3cos 106,5CD AD ADC =⋅∠=⨯= ⊙228AC AD CD - ⊙34CD AC = ⊙FCD FAC F F ∠=∠∠=∠，⊙FCD FAC ∽ ⊙34CD FC FD AC FA FC === 设3FD x =则，4310FC x AF x ==+，又⊙2FC FD FA =⋅即2(4)3(310)x x x =+ 解得307x =（取正值） ⊙9037FD x ==【点睛】本题考查了圆周角的性质 切线的判定定理 正切的定义 相似三角形的性质和判定 找出正切的定义与相似三角形相似比的关联是解题的关键．20．（2023·江西·统考中考真题）如图，在ABC 中 464AB C =∠=︒， 以AB 为直径的O 与AC 相交于点D E 为ABD 上一点 且40ADE ∠=︒．(1)求BE 的长(2)若76EAD ∠=︒ 求证：CB 为O 的切线．【答案】(1)109π (2)见解析【分析】（1）如图所示 连接OE 先求出2OE OB OA === 再由圆周角定理得到280AOE ADE ==︒∠∠进而求出100∠=︒BOE 再根据弧长公式进行求解即可（2）如图所示 连接BD 先由三角形内角和定理得到64AED ∠=︒则，由圆周角定理可得64ABD AED ==︒∠∠ 再由AB 是O 的直径 得到90ADB ∠=︒ 进而求出26BAC ∠=︒ 进一步推出90ABC ∠=︒ 由此即可证明BC 是O 的切线．【详解】（1）解：如图所示 连接OE⊙AB 是O 的直径 且4AB =⊙2OE OB OA ===⊙E 为ABD 上一点 且40ADE ∠=︒⊙280AOE ADE ==︒∠∠⊙180100BOE AOE ∠=︒-=︒∠⊙BE 的长1002101809ππ⨯⨯==（2）证明：如图所示 连接BD⊙76EAD ∠=︒ 40ADE ∠=︒⊙18064AED EAD ADE =︒--=︒∠∠∠⊙64ABD AED ==︒∠∠⊙AB 是O 的直径⊙90ADB ∠=︒⊙9026BAC ABD =︒-=︒∠∠⊙64C ∠=︒⊙18090ABC C BAC =︒--=︒∠∠∠ 即AB BC ⊥⊙OB 是O 的半径⊙BC 是O 的切线．【点睛】本题主要考查了切线的判定 求弧长 圆周角定理 三角形内角和定理等等 正确作出辅助线是解题的关键．21．（2023·江苏连云港·统考中考真题）如图，在ABC 中 AB AC = 以AB 为直径的O 交边AC 于点D 连接BD 过点C 作CE AB ∥．(1)请用无刻度的直尺和圆规作图：过点B 作O 的切线 交CE 于点F （不写作法 保留作图痕迹 标明字母）(2)在（1）的条件下 求证：BD BF =．【答案】(1)见解析(2)见解析【分析】（1）根据尺规作图 过点B 作AB 的垂线 交CE 于点F 即可求解（2）根据题意切线的性质以及直径所对的圆周角是直角 证明BDC BFC ∠=∠ 根据平行线的性质以及等腰三角形的性质得出BCD BCF =∠ 进而证明()AAS BCD BCF ≌ 即可得证．【详解】（1）解：方法不唯一 如图所示．（2）⊙AB AC =⊙A ABC CB =∠∠．又⊙CE AB ∥⊙ABC BCF ∠=∠⊙BCF ACB =∠∠．⊙点D 在以AB 为直径的圆上⊙90ADB ∠=︒⊙=90BDC ∠︒．又⊙BF 为O 的切线⊙90ABF ∠=︒．⊙CE AB ∥⊙180BFC ABF ∠+∠=︒⊙90BFC ∠=︒⊙BDC BFC ∠=∠．⊙在BCD △和BCF △中,,,BCD BCF BDC BFC BC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩⊙()AAS BCD BCF ≌．⊙BD BF =．【点睛】本题考查了作圆的切线 切线的性质 直径所对的圆周角是直角 全等三角形的性质与判定 熟练掌握以上知识是解题的关键．22．（2023·辽宁·统考中考真题）如图，AB 是O 的直径 点C E ，在O 上 2CAB EAB ∠=∠ 点F 在线段AB 的延长线上 且AFE ABC ∠=∠．(1)求证：EF 与O 相切(2)若41sin 5BF AFE =∠=， 求BC 的长．【答案】(1)见解析 (2)245BC = 【分析】（1）利用圆周角定理得到2EOB EAB ∠=∠ 结合已知推出CAB EOB ∠=∠ 再证明OFE ABC ∽△△ 推出90OEF C ∠=∠=︒ 即可证明结论成立（2）设O 半径为x 则，1=+OF x 在Rt OEF △中 利用正弦函数求得半径的长 再在Rt ABC △中 解直角三角形即可求解．【详解】（1）证明：连接OE⊙=BE BE ⊙2EOB EAB ∠=∠⊙2CAB EAB ∠=∠⊙CAB EOB ∠=∠⊙AB 是O 的直径⊙90C ∠=︒⊙AFE ABC ∠=∠⊙OFE ABC ∽△△⊙90OEF C ∠=∠=︒⊙OE 为O 半径⊙EF 与O 相切（2）解：设O 半径为x 则，1=+OF x⊙AFE ABC ∠=∠ 4sin 5AFE ∠=⊙4sin 5ABC ∠= 在Rt OEF △中 90OEF ∠=︒ 4sin 5AFE ∠=⊙45OE OF = 即415x x =+ 解得4x =经检验 4x =是所列方程的解⊙O 半径为4则，8AB =在Rt ABC △中 90C ∠=︒ 4sin 5ABC ∠=8AB = ⊙32sin 5A AB C AB C ∠==⋅ ⊙22245BC AB AC =-=． 【点睛】本题考查了圆的切线的判定 圆周角定理 解直角三角形以及相似三角形的判定和性质等知识 熟练掌握圆的相关知识和相似三角形的判定和性质是解题的关键．23．（2023·山东东营·统考中考真题）如图，在ABC 中 AB AC = 以AB 为直径的O 交BC 于点D DE AC ⊥ 垂足为E ．(1)求证：DE 是O 的切线(2)若30C ∠=︒ 23CD = 求BD 的长．【答案】(1)见解析 (2)43π 【分析】（1）如图：OD 然后根据等边对等角可得B ODB ∠=∠ B C ∠=∠即ODB C ∠=∠ 再根据OD AC ∥可得ODE DEC ∠=∠ 进而得到90ODE ∠=︒即可证明结论（2）如图：连接AD 有圆周角定理可得AD BC ⊥ 再解直角三角形可得4AC = 进而得到11222OB AB AC === 然后说明120BOD ∠=︒ 最后根据弧长公式即可解答． 【详解】（1）证明：如图：连接OD⊙OB OD =⊙B ODB ∠=∠,⊙AB AC =⊙B C ∠=∠,⊙ODB C ∠=∠,⊙OD AC ∥,⊙ODE DEC ∠=∠。